微铣削加工在航空航天、医疗器械、电子和汽车等行业中应用广泛^{[ [1]  KANG I S, KIM J S, KANG M C, et al. Tool condition and machined surface monitoring for micro-lens array fabrication in mechanical machining[J]. Journal of Materials Processing Technology, 2008, 201(1–3): 585–589.
1 ]}。微铣削加工零件对表面质量要求较高，但由于刀具尺寸小且磨损迅速，导致刀具表面粗糙度增加、几何精度下降和存在毛刺等问题，恶化的加工质量进一步缩短刀具寿命，显著影响微细产品的整体加工质量^{[ [2]  ZHANG X W, YU T B, ZHAO J. Surface generation modeling of micro milling process with stochastic tool wear[J]. Precision Engineering, 2020, 61: 170–181.
2 ]}。因此，监测刀具磨损状态以避免刀具过早失效进而恶化加工质量则非常重要。刀具磨损主要表现形式为侧面磨损^{[ [3]  DAI Y Q, ZHU K P. A machine vision system for micro-milling tool condition monitoring[J]. Precision Engineering, 2018, 52: 183–191.
3 ]}，其过程分为初期磨损、正常磨损和急剧磨损3个阶段，准确预测急剧磨损阶段的起点一直是研究的重点。

刀具磨损的测量方法有直接测量和间接测量^{[ [4]  JARDINE A K S, LIN D M, BANJEVIC D. A review on machinery diagnostics and prognostics implementing condition-based maintenance[J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1483–1510.
4 ]}。直接测量方法包括放射线法、接触法和机器视觉检测法，其中机器视觉检测法因其非接触性被广泛研究。Dai等^{[ [3]  DAI Y Q, ZHU K P. A machine vision system for micro-milling tool condition monitoring[J]. Precision Engineering, 2018, 52: 183–191.
3 ]}开发一种在线机器视觉系统，通过远心镜头和光源相机成像，能有效测量刀具的渐进磨损量。FernGndez–Robles等^{[ [5]  FERNÁNDEZ-ROBLES L, CHARRO N, SÁNCHEZ-GONZÁLEZ L, et al. Tool wear estimation and visualization using image sensors in micro milling manufacturing[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2018: 399–410.
[6]  FERNÁNDEZ-ROBLES L, SÁNCHEZ-GONZÁLEZ L, DÍEZ-GONZÁLEZ J, et al. Use of image processing to monitor tool wear in micro milling[J]. Neurocomputing, 2021, 452: 333–340.
5-6 ]}提出基于形态学操作和k-means算法的系统，磨损预测精度达90.24%，实际磨损面积预测误差仅为5%。然而，机器视觉系统在铣削过程中会受到切削液、残留材料、光照条件等因素影响，限制其工业应用。间接测量方法通过监测加工过程中的切削力^{[ [7]  LI W J, LIU T S. Time varying and condition adaptive hidden Markov model for tool wear state estimation and remaining useful life prediction in micro-milling[J]. Mechanical Systems and Signal Processing, 2019, 131: 689–702.
[8]  HUANG Z W, ZHU J M, LEI J T, et al. Tool wear predicting based on multi-domain feature fusion by deep convolutional neural network in milling operations[J]. Journal of Intelligent Manufacturing, 2020, 31(4): 953–966.
7-8 ]}、振动^{[ [9]  HUANG Z W, ZHU J M, LEI J T, et al. Tool wear monitoring with vibration signals based on short-time Fourier transform and deep convolutional neural network in milling[J]. Mathematical Problems in Engineering, 2021, 2021: 9976939.
9 ]}、电流^{[ [10]  ZHOU Y Q, SUN W F. Tool wear condition monitoring in milling process based on current sensors[J]. IEEE Access, 2020, 8: 95491–95502.
10 ]}和声发射^{[ [11]  KHRIPUNOV N V, VASKIN K Y. Tool life estimation using acoustic emission signal[J]. IOP Conference Series: Materials Science and Engineering, 2020, 709(3): 033088.
11 ]}等参数变化来表征刀具磨损状态。Li等^{[ [12]  LI X, LIM B S, ZHOU J H, et al. Fuzzy neural network modelling for tool wear estimation in dry milling operation[C]//Annual Conference of the PHM Society. Melville: American Institute of Physics, 2009.
12 ]}通过声发射传感器采集铣削力信号，并利用模糊神经网络预测刀具磨损，结果显示实际值与预测值高度相关。Wu等^{[ [13]  WU D Z, JENNINGS C, TERPENNY J, et al. A comparative study on machine learning algorithms for smart manufacturing: Tool wear prediction using random forests[J]. Journal of Manufacturing Science and Engineering, 2017, 139(7): 071018.
13 ]}通过实时监测切削力、振动和声发射信号，并使用机器学习算法对刀具磨损进行预测，结果表明随机森林模型性能优于其他算法。然而，这些方法在微铣削加工中的应用受到限制，因材料去除量小且容易受到切削液的影响，使得精确采集信号变得困难，并增加成本。

许多研究表明，刀具磨损会导致加工表面质量变差^{[ [14]  OLIAEI S N B, KARPAT Y. Experimental investigations on micro milling of stavax stainless steel[J]. Procedia CIRP, 2014, 14: 377–382.
[15]  GAO Q, LI W M, CHEN X Y. Surface quality and tool wear in micro-milling of single-crystal aluminum[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(16): 5597–5609.
14-15 ]}，通过分析加工表面图像可以间接监测刀具磨损。Dutta等^{[ [16]  DUTTA S, KANWAT A, PAL S K, et al. Correlation study of tool flank wear with machined surface texture in end milling[J]. Measurement, 2013, 46(10): 4249–4260.
16 ]}通过灰度共生矩阵和游程统计技术分析端铣表面图像，发现所提取纹理特征与刀具磨损特征高度相关。Datta等^{[ [17]  DATTA A, DUTTA S, PAL S K, et al. Progressive cutting tool wear detection from machined surface images using Voronoi tessellation method[J]. Journal of Materials Processing Technology, 2013, 213(12): 2339–2349.
17 ]}利用Voronoi多边形细分法提取出车削加工表面纹理特征，并证明了这些特征可用于刀具状态监控。他们的研究通过分析加工表面图像间接预测刀具磨损方向有重大意义，但在微切削加工领域的研究尚不深入，同时这些图像纹理分析方法对图像质量要求较高，鲁棒性有待提高。因此，本文提出了一种采用多重分形分析处理加工表面图像，以捕捉微小纹理变化的方法。该方法对刀具磨损的变化高度敏感，能够有效检测早期磨损。

在工业应用中，精确预测刀具磨损对提高生产效率和降低成本至关重要。为实现高效且准确的预测，选择合适的预测模型是预测工作中非常重要的环节。本研究重点考察支持向量回归 （SVR）模型，并与高斯过程回归 （GPR）和随机森林 （RF）两种流行的回归模型进行对比。SVR模型因其优越的非线性建模能力和鲁棒性，在多个领域表现突出，本文特别关注SVR模型在刀具磨损预测中的优势。

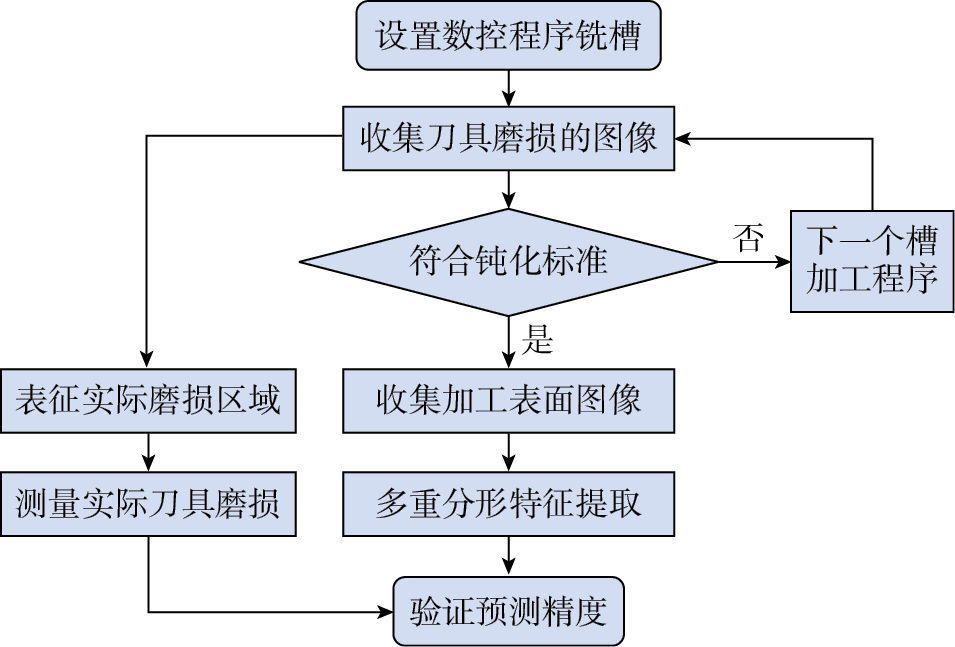
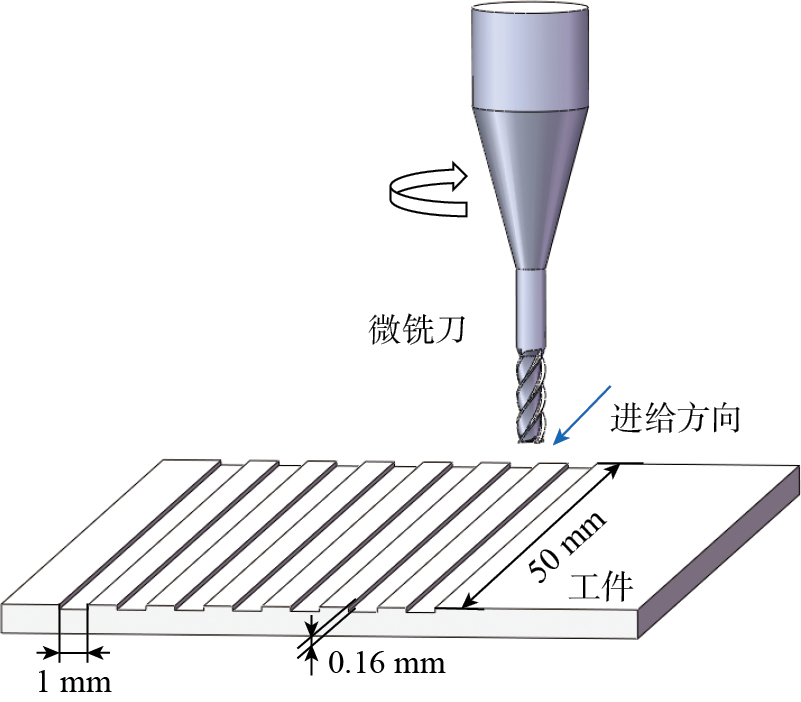
为探究微铣削加工表面分形特征预测刀具磨损的能力，共设计9组铣削试验进行验证，如表1所示。铣削试验在VDLS600立式加工中心上进行，工件材料为9Cr18不锈钢，尺寸为50 mm×80 mm×50 mm。试验采用株洲钻石切削刀具公司生产的AlTiN涂层硬质合金四刃微型立铣刀 （XD1.0L30B2H3N4–FRS），刀具直径为1 mm，切削刃长1.5 mm，螺旋角为30°，刀具总长为40 mm。试验流程如图1所示，正式进行试验前，先将工件固定在机床上并对其上表面进行面铣，以确保刀具与加工表面垂直。由于不锈钢材料在切削加工时具有塑性变形大、摩擦力大及导热系数较低的特点，因此加工时使用切削液以防止刀具磨损过快。正式试验采用全铣槽模式进行，图2为加工过程示意图。每铣削50 mm槽后，采用自制图像采集系统获取加工过程刀具磨损图像，其中图像采集系统主要由工业相机、远心镜头、LED环形光源和图像采集软件组成，相机和镜头的具体参数详见表2，试验设置如图3所示。为避免获取刀具磨损时因频繁拆卸刀具而影响加工一致性，试验中直接在机床上获取刀具磨损图像。为消除切屑和切削液的影响，在获取图像前使用气枪保持适当距离对刀具进行清洁，此操作发生在加工停止后，不会影响加工稳定性，且有助于提高图像采集质量，确保磨损区域清晰可见。每组试验均进行至刀具磨损达到失效标准^{[ [18]  ALHADEFF L L, MARSHALL M B, CURTIS D T, et al. Protocol for tool wear measurement in micro-milling[J]. Wear, 2019, 420–421: 54–67.
18 ]}，如式 （1）所示，其中KT为刀具的径向磨损，D为刀具直径。

获取清晰且高质量的加工表面图像对后续多重分形特征的提取至关重要。为防止加工过程中切削液残留影响图像质量，采集前需使用清洗剂对工件进行清洗。由于在铣削过程中，刀具刚切入材料时会导致切削力突然增加，可能会产生较大的冲击力和振动，从而使工件和刀具表面的不稳定性增加。此外，当刀具切出材料时，切削力突然减小，可能会导致工件表面出现毛刺或不连续的切削痕迹。相比之下，在铣削过程的中间位置，刀具和工件之间的切削力相对稳定，从而工件表面的切削效果相对均匀，因此，表面质量通常会比刚切入和切出材料的部位更加平滑和均匀。考虑到以上因素，选择在加工槽的中间位置 （图4中标红部位）进行图像采集，以确保获得的图像能够较好地反映加工表面的整体质量。

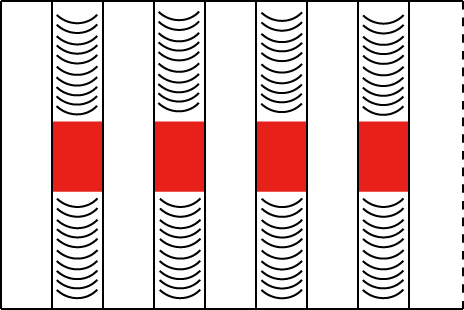
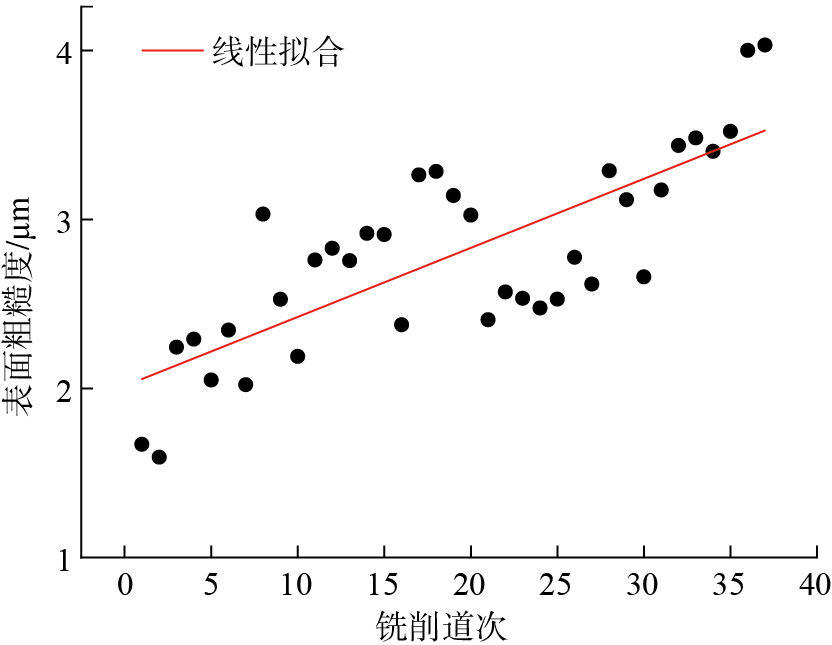
图5为加工表面纹理图像，可以看出加工工件表面图像随着铣削道次的增加，表面纹理由深变浅、由较规则变得相对杂乱无章。此外，可观察到加工槽底部的宽度随铣削道次增加逐渐变窄，这些变化反映出刀具磨损和工件加工几何精度之间存在很大的关联性。通过分析图像特征，可以一定程度反映工件加工质量的变化情况，从而进行刀具磨损预测。在表面粗糙度方面，本文通过基恩士VK–X1100形状激光测量显微镜获取了加工工件表面的三维图像，并提取了表面粗糙度数据。如图6所示，尽管由于加工过程的随机性，个别道次的粗糙度值存在一定波动，但整体上加工工件表面粗糙度随刀具磨损程度的增加而增加。这一现象表明，刀具磨损不仅影响工件的几何精度，还会导致表面粗糙度的增加。通过以上分析，说明加工工件的几何精度和表面粗糙度随刀具磨损变化有强关联关系，是凭借加工表面纹理特征来进行刀具磨损预测的基础。

在刀具磨损预测研究中，为准确评估预测效果，需将预测结果与实际刀具磨损情况进行对比。因此，准确描述刀具磨损类型并量化磨损程度是后续预测工作的关键前提。与常规切削相比，微铣削刀具磨损主要磨损表现为刀具刃口磨损、刀口磨损和刀具半径减小^{[ [6]  FERNÁNDEZ-ROBLES L, SÁNCHEZ-GONZÁLEZ L, DÍEZ-GONZÁLEZ J, et al. Use of image processing to monitor tool wear in micro milling[J]. Neurocomputing, 2021, 452: 333–340.
6 ]}。其中，新刀具刃口表面光滑平整、切削刃锋利，切割材料时仅发生轻微刀具材料剥落，但随着磨损程度的进一步加深，刀具材料剥落加重导致切削刃的后刀面磨损清晰可见。Alhadeff等^{[ [18]  ALHADEFF L L, MARSHALL M B, CURTIS D T, et al. Protocol for tool wear measurement in micro-milling[J]. Wear, 2019, 420–421: 54–67.
18 ]}提出一种用于微铣加工中刀具磨损测量的协议，通过从不同方位获取刀具磨损信息来描述多种刀具磨损类型。但由于微铣刀主齿面存在螺旋刀具齿面，导致周向定位失败使得图像采集系统刀具原位磨损检测困难^{[ [19]  ZHANG X H, YU H Y, LI C C, et al. Study on in situ tool wear detection during micro end milling based on machine vision[J]. Micromachines, 2023, 14(1): mi14010100.
19 ]}。综上，选择从刀具端面采集的磨损图像来更准确、全面地评价刀具在微铣削加工过程的磨损行为。

在加工过程中，刀具尖端的材料可能会脱落，暴露出基体材料。通过适当调节光源位置，即可利用图像采集系统清晰地观察到刀具的磨损区域。此外，随着铣削距离的增加，刀具磨损程度逐渐加重。图7清晰地展示出这一变化趋势。

为提取准确的刀具磨损信息，需先对刀具磨损区域进行表征，Zhang等^{[ [19]  ZHANG X H, YU H Y, LI C C, et al. Study on in situ tool wear detection during micro end milling based on machine vision[J]. Micromachines, 2023, 14(1): mi14010100.
19 ]}通过与常规尺寸立铣刀的磨损规律对比，提出微面铣刀磨损状态的相应评价指标为：磨损面积S、侧面磨损VB和径向磨损KT，本试验根据实际情况采用相同指标描述刀具磨损量，如图8所示。

在本研究中，为精确量化刀具磨损状态，采用ImageJ软件作为分析工具，聚焦于VB、KT及S的精确测量。ImageJ提供了两种策略以提取磨损区域特征：自动阈值分割与手动测量。鉴于加工过程中刀具表面磨损区域可能因多种因素 （如材料不均、加工条件波动）而呈现非均匀高亮和粗糙度变化，自动阈值分割法可能引入显著误差，因此，本研究优先选择边界清晰的手动测量方法，以确保磨损数据的准确性，见图9。尽管手动测量在精度上具有优势，但需强调应标准化操作，使人为误差最小化。因此在实际工作中，应采取多项标准化措施。首先，统一刀具磨损图像的拍摄方位，确保每次拍摄时刀刃所处位置保持一致；其次，通过ImageJ软件进行图像校正，以保证刀具在垂直对称状态。为确保测量一致性，指定单一操作者进行手动测量，每项测量均进行10次重复操作，并取其平均值作为实际磨损值。这些措施共同作用可有效减少人为误差，提高数据准确性和可比性。图10展示了3种不同磨损类型 （磨损面积、侧面磨损量和端面磨损量）的测量结果，各切削刃的磨损程度展现出一定的非均匀性，这主要归因于铣削过程中工件材料的非均质特性及主轴径向跳动的影响。然而，从整体视角分析，各刃的磨损趋势具有高度一致性，验证了所采集数据的可靠性与有效性。

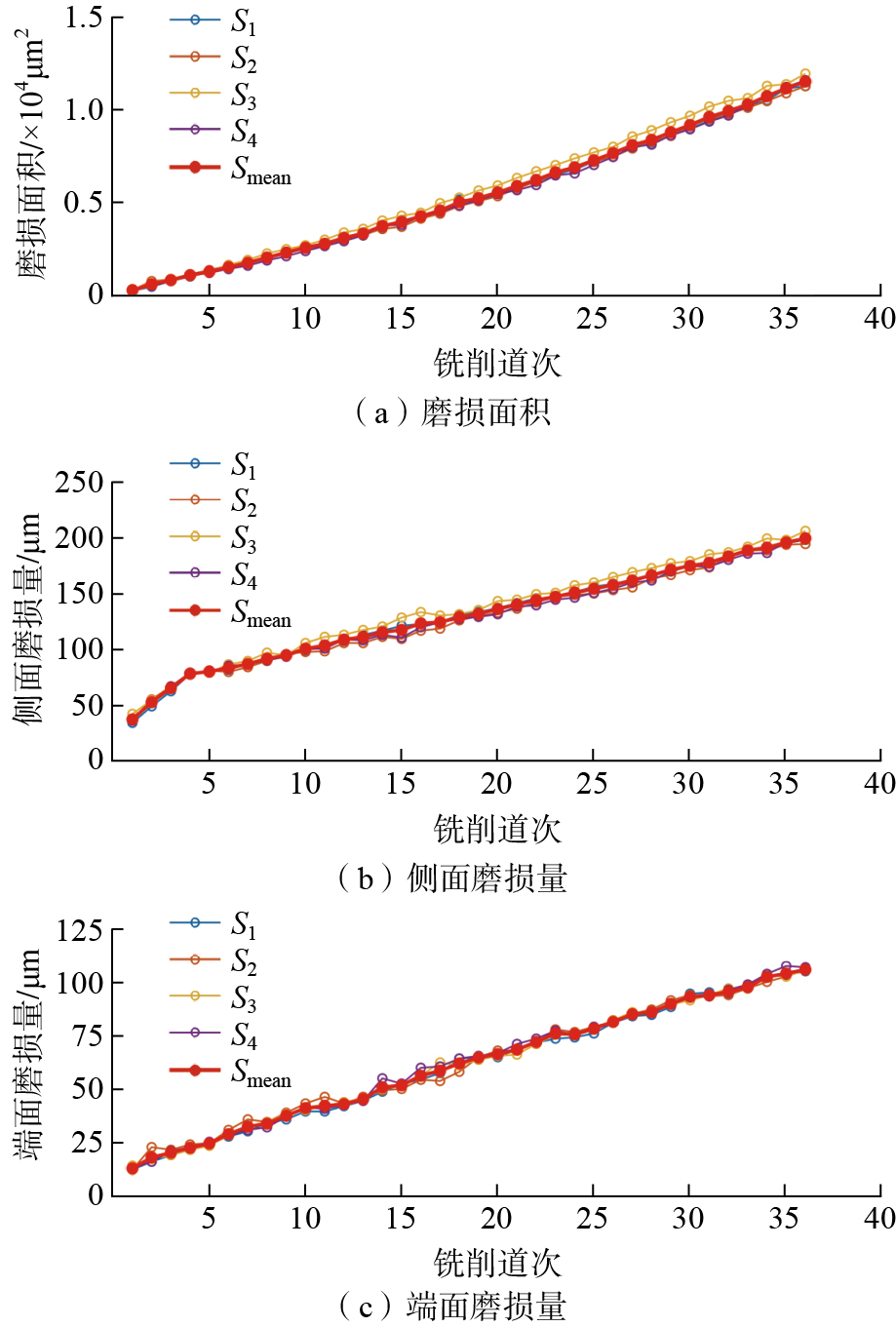
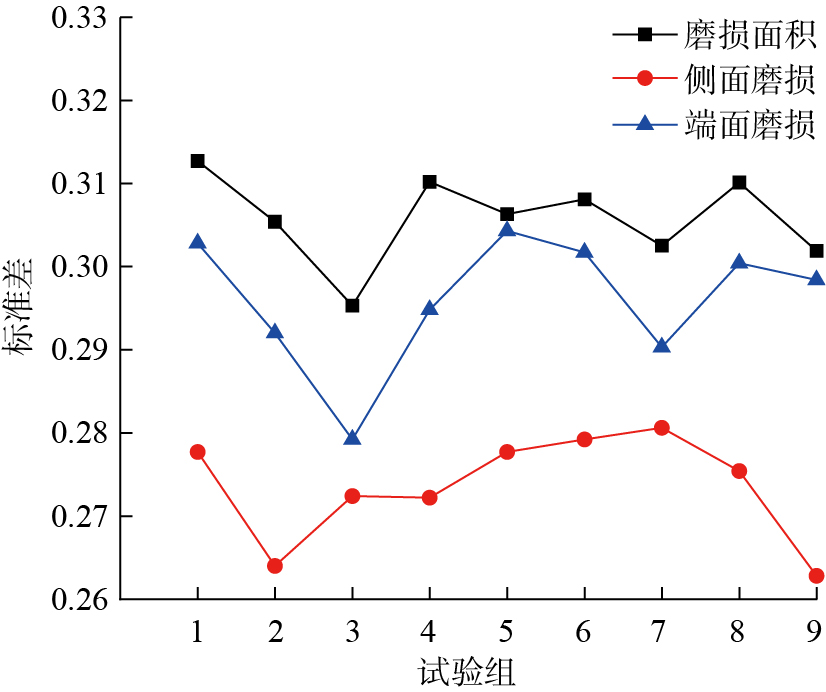
在后续的磨损预测中实际上只需1个磨损指标来衡量刀具的磨损程度，但由于刀具磨损的随机性会导致磨损值的波动，为尽量减少随机误差的影响，决定选择3个指标中离散程度最小的1个。首先，由于3个指标的数值大小不同，为更好地进行对比，对数值进行归一化处理，使所有磨损指标的数值都处于 （0，1）区间。然后计算9组试验中3个磨损指标：磨损面积、侧面磨损量和端面磨损量的平均标准差分别为0.3058、0.2736和0.2960（图11）。可以看出，侧面磨损的标准差明显小于另外两个磨损指标，间接说明侧面磨损引入的随机误差较小。综上所述，为保证数据的准确性和可靠性，后续分析将重点聚焦于4个切削刃的平均侧面磨损数据。

分形是一种具有自相似性的几何结构，其部分结构与整体结构在某种程度上相似，且具备标度不变性，可用分形维数来度量其复杂度。然而，分形维数无法描述局部的不规则性，多重分形分析可以在不同位置和尺度上描述这种局部特征。加工表面纹理展示出分形特征^{[ [20]  全书海. 基于表面灰度图像的加工表面形貌分形特征研究[D]. 武汉: 武汉理工大学, 2003.QUAN Shuhai. Study on fractal characteristics of machined surface morphology based on surface gray image[D]. Wuhan: Wuhan University of Technology, 2003.
20 ]}，通过多重分形分析能定量描述其奇异性分布。常见的多重分形谱计算方法有盒计数法、结构函数法和多重分形去趋势波动分析 （MFDFA），但它们在捕捉复杂局部特征方面存在局限。而小波leaders相比之下优势明显，能更全面、准确地分析信号的多重分形特性，尤其在图像处理上更具灵活性和计算效率，以下是该算法的详细描述。

首先，对于一个d维的信号X（x）进行离散小波变换 （DWT），计算不同尺度j和位置k上的小波变换系数$c_{j,k}^{(i)}$。其中，d为信号的维度大小；R^d为d维欧几里得空间；${\psi }_{j,k}^{\left(i\right)}\left(x\right)$为第i个母小波在尺度j和位置k的扩展和平移形式 （式3）。

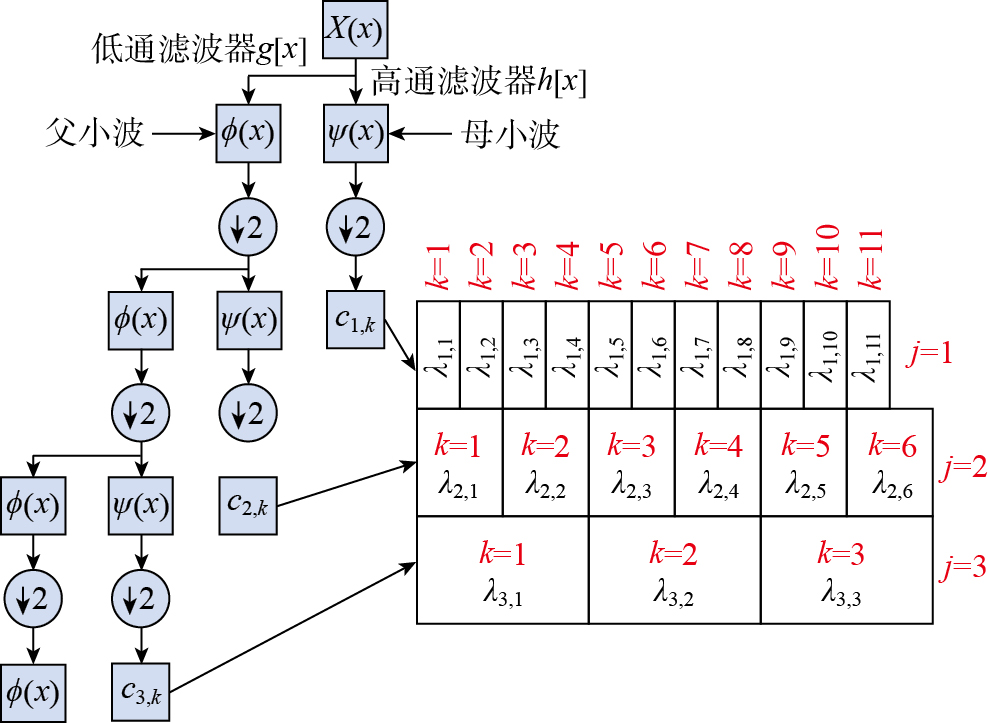
为捕获信号的多重分形特性，计算小波leaders，其定义尺度j和位置k处的3个相邻区间内所有小波变换系数的最大值l^(∞)（j，k），具体过程如图12所示。对于给定信号X（x），通过高通滤波器和低通滤波器分别得到母小波 （高频部分）和父小波 （低频部分）。信号的低频部分通常携带主要信息，为了在不同尺度上捕捉信号特征，需逐级分解信号。原始信号经过3次滤波和下采样后，得到不同尺度和位置的小波变换系数c₁，k，c₂，k，c₃，k用于小波leaders的计算。

接下来是对信号X（x）的多重分形谱计算，首先要定义结构函数S_q（j），即小波leaders的q阶矩的平均值，其中，q为不同的阶数；n_j为尺度j上的区间数目。

多重分形谱的核心是标度指数ζ（q），用于描述结构函数随尺度j的变化关系。假设结构函数S_q（q）与尺度j存在以下关系

通过对数变换得到

式中，C为常数。通过多个尺度j上线性回归方法拟合出log₂S_q（j）与j之间的关系，可以得到标度指数ζ（q）。

为绘制多重分形谱图需计算Holder指数h以及对应的分形维数D（h）。其中，Holder指数h描述信号的局部光滑性，表示标度指数ζ（q）对q的导数。

分形维数D（h）表示具有特定Holder指数h的点集的分形维数。用于描述这些点在整个信号中的分布情况。可通过对标度指数ζ（q）进行Legendre变换得到。

小波leaders的对数累积量是在多重分形分析中用于描述信号统计特性的工具。第m阶对数累积量C_m是对标度指数ζ（q）的对数展开式中的系数。对于多重分形信号，标度指数ζ（q）通常具有以下形式

本研究基于Matlab 2023a提取的9组试验表面纹理图像来获取特征数据，根据不同的q阶矩函数可以得到对应的广义分形维数D（q）和广义Holder指数h（q），其中q（q = [±1，±2，±3，±4，±5]）及缩放范围j（j = [3，4，5，6]^{[ [21]  LEONARDUZZI R, WENDT H, ABRY P, et al. P-exponent and p-leaders, part II: Multifractal analysis. relations to detrended fluctuation analysis[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 448: 319–339.
21 ]}）用来估计多重分形谱。不同铣削道次加工图像可以得到对应q值下的分形维数D（q）和广义Holder指数h（q）并绘制多重分形谱，结果如图13所示。通过多重分形谱可得，随着铣削道次的增加多重分形谱呈现右移的趋势，说明多重分形特征对于刀具磨损所引起的加工表面纹理变化存在一定的映射关系，可以用来预测刀具磨损。

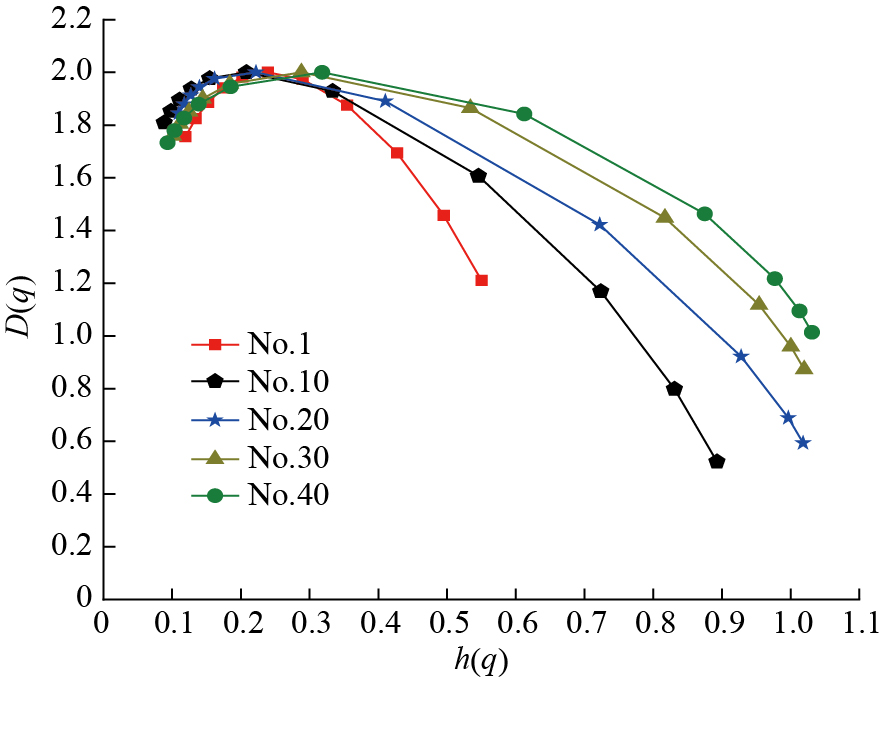
通过多重分形谱提取的特征包括最小奇异性指数及其对应的多重分形维数D_min、最大奇异性指数h_max及其对应的多重分形维数D_max、谱宽Δh （h_max–h_min）、谱高差ΔD （D_max–D_min）及最大分形维数D（h）对应的Holder指数h_D。此外，三阶对数累积量C₁、C₂、C₃提供关于时间序列偏斜度和非高斯性的信息，辅助分析时间序列的非线性特征和高阶统计特性。为研究不同工艺参数下图像纹理多重分形特征预测刀具磨损的有效性，将9组铣削试验中的不同转速n和进给速度f纳入数据集作为特征，共同构建32个特征值，具体特征详见表3。

在刀具磨损预测中，选择合适的预测模型至关重要，能够预防质量问题和停机损失，提高加工质量并降低成本。SVR在处理高维数据、保证泛化能力、对异常值的鲁棒性及小样本学习方面表现优异^{[ [22]  黄贤振, 孙良仕, 高娓, 等. 基于SFS–SVR的高速铣削刀具剩余使用寿命预测[J]. 东北大学学报(自然科学版), 2023, 44(6): 824–831.HUANG Xianzhen, SUN Liangshi, GAO Wei, et al. Remaining useful life prediction of cutting tools based on SFS–SVR in high speed milling operations[J]. Journal of Northeastern University (Natural Science), 2023, 44(6): 824–831.
22 ]}，因此，本文建立SVR模型来监测刀具寿命。

SVR的目标是找到一个函数f（x）能够以尽可能小的误差预测目标变量y。通过引入一个Ò –不敏感损失函数，使得在Ò范围内的预测误差不会对模型的损失产生影响，即对小于Ò的误差不予考虑，只有超过Ò的误差才会被计入损失。其定义如下

本文特征数据属于非线性数据，处理非线性数据时，SVR可以使用核函数将数据映射到高维空间中，在高维空间中进行线性回归。常用的核函数K（x_i，x_j）包括径向基函数 （RBF核）、多项式核、线性核等。本文采用的RBF核，因具有强大的非线性映射能力、灵活性和局部性特征，使得RBF核在SVM和SVR中广泛应用，其形式为

式中，γ为一个超参数，控制核函数的宽度或相似度的度量，在核函数中的作用至关重要，可影响模型的性能和泛化能力。通过核函数K（x_i，x_j），输入数据被隐式地映射到一个高维空间。在这个高维空间中，非线性关系可能变成线性关系，可以应用线性SVR的原理。非线性SVR的回归函数表示为

式中，α_i和${\alpha }_i^{*}$为拉格朗日乘子。

非线性SVR的优化问题与线性SVR类似，但需在高维空间中进行，其定义见式 （15），ζ_i和${\zeta }_i^{*}$为松弛变量，表示超过Ò范围的误差 （式16）。

其约束条件为

非线性SVR能够充分利用提取的多维特征，通过核函数映射到高维空间，在此空间中，刀具磨损与其影响因素之间的复杂关系得以更好地表示和学习。这样，非线性SVR可以显著提高刀具磨损预测的精度和可靠性，为制造过程的优化提供强有力的支持。

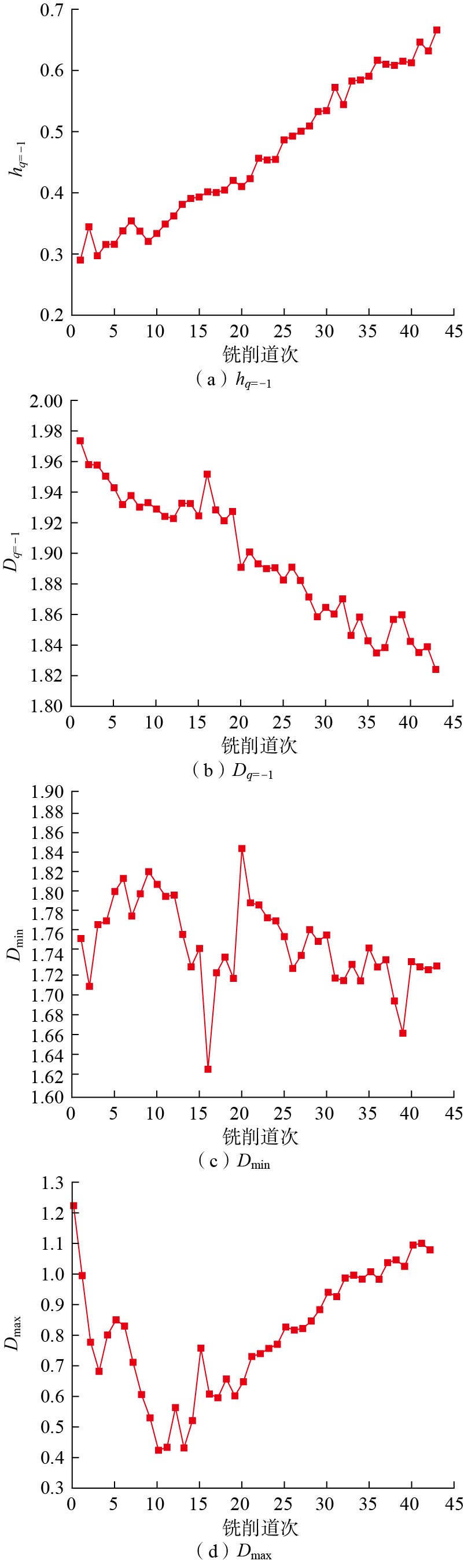
从1.3节中得到的多维特征数据中，并非所有特征都适用于刀具磨损预测。图14显示出以h_{q = –1}、Dq _{= –1}、D_min、D_max特征为例的趋势变化。可以看出h_{q = –1}随着铣削道次增加而增大；Dq _{= –1}随铣削道次增加而减小，虽然有轻微波动，但这两个特征与刀具磨损趋势高度相关。而D_max的趋势表现为初期减小后再增大，主要是因为新刀具开始切削时受到较大冲击力，切削力尚未稳定，导致表面生成的切屑不均匀，从而分形维数较高，这一点在图5中也有体现。相比之下，D_min则没有明显的变化规律。这些不同的特征参数反映出加工表面不同的微观特征变化，说明并非所有特征都能有效反映由刀具磨损引起的加工表面变化，因此为最大程度上提升预测精度，避免不相关因素的影响应进行特征筛选^{[ [23]  KONG D D, CHEN Y J, LI N, et al. Tool wear monitoring based on kernel principal component analysis and v-support vector regression[J]. The International Journal of Advanced Manufacturing Technology, 2017, 89(1): 175–190.
23 ]}。

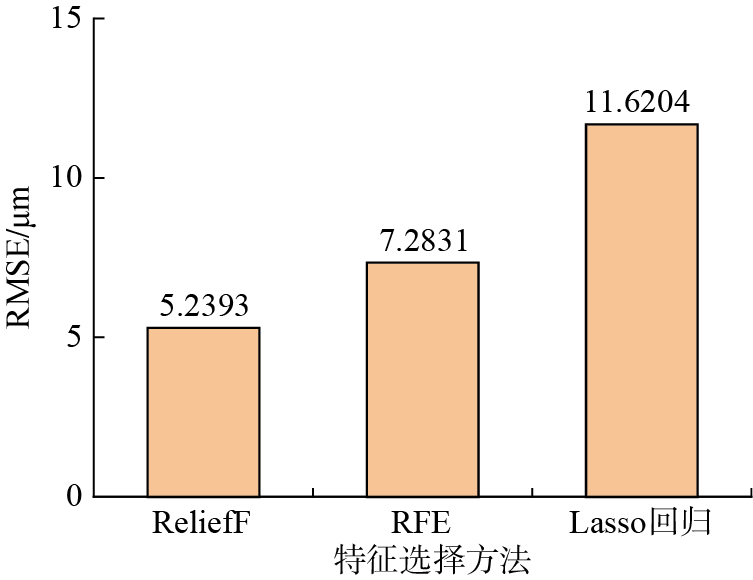
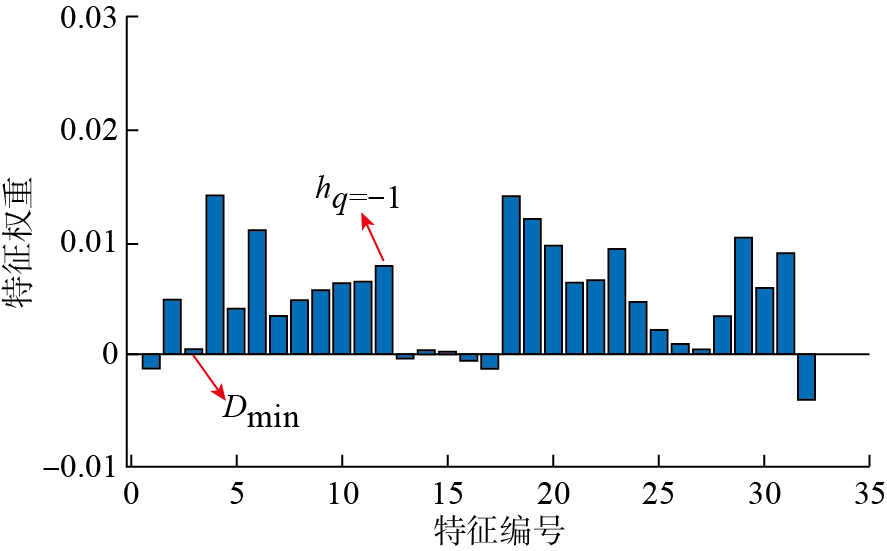
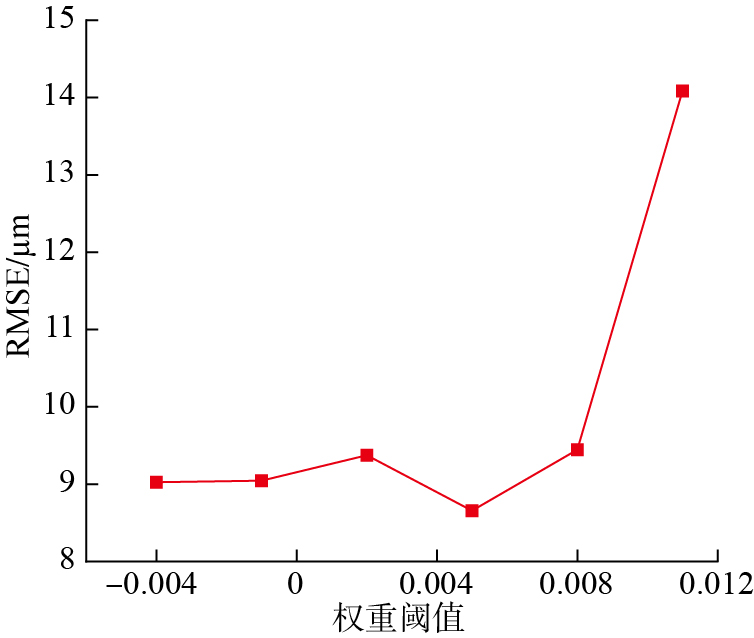
此外，特征筛选不仅可以剔除不相关或冗余的特征，还能提高模型的精度缩短运行时间。在本研究中，比较了3种典型特征选择算法：过滤法 （ReliefF）、封装法 （RFE）和嵌入法 （Lasso回归）。比较结果如图15所示，ReliefF的均方根误差 （RMSE）为5.2393 μm，明显优于RFE的7.2831 μm和Lasso回归的11.6204 μm。Relief F在计算效率和稳定性方面表现更佳，尤其适合本研究样本量较小（325个样本）的情况。因此，考虑到本研究的数据特性，RFE和Lasso回归可能会产生过拟合并且计算成本较高的问题，综合评估后，认为ReliefF更适合的作为本文特征选择方法。图16展示了使用ReliefF算法提取的特征权重图，权重大小反映了各特征对刀具磨损的影响程度。特征权重越大，说明该特征对目标变量的影响越显著。从图16中可观察到h_{q = –1}特征的权重较高，而D_min的权重相对较低，这与图14中反映的结果一致。为剔除不相关的特征，设定一个特征权重选择阈值，权重大于该阈值的特征被保留，小于该阈值的特征被剔除。如图17所示，通过对不同阈值的交叉验证，确定在RMSE最小时，对应的最佳权重阈值为0.005。因此，选择特征权重需大于该阈值的特征，这些特征与刀具磨损的相关性较高，将用于后续的预测模型中。

本文根据9组铣削试验中提取的加工表面多重分形特征值及对应的刀具磨损值构建9组数据集，总计325个样本，为验证模型的泛化能力，采用留一法交叉验证 （LOOCV），此方法几乎利用所有样本进行训练，因此这种方法在样本量较少的情况下尤为重要。最终，计算不同工艺参数下每组试验的预测结果，如表4所示。模型的预测效果通过均方根误差 （RMSE）、平均相对误差 （MRE）和决定系数 （R²）3个指标进行评价。结果显示，9组试验中刀具达到磨钝标准时（侧面磨损约为200 μm），最大RMSE为13.800 μm，最大MRE为7.50%，R²均在0.9以上，表明预测效果良好。

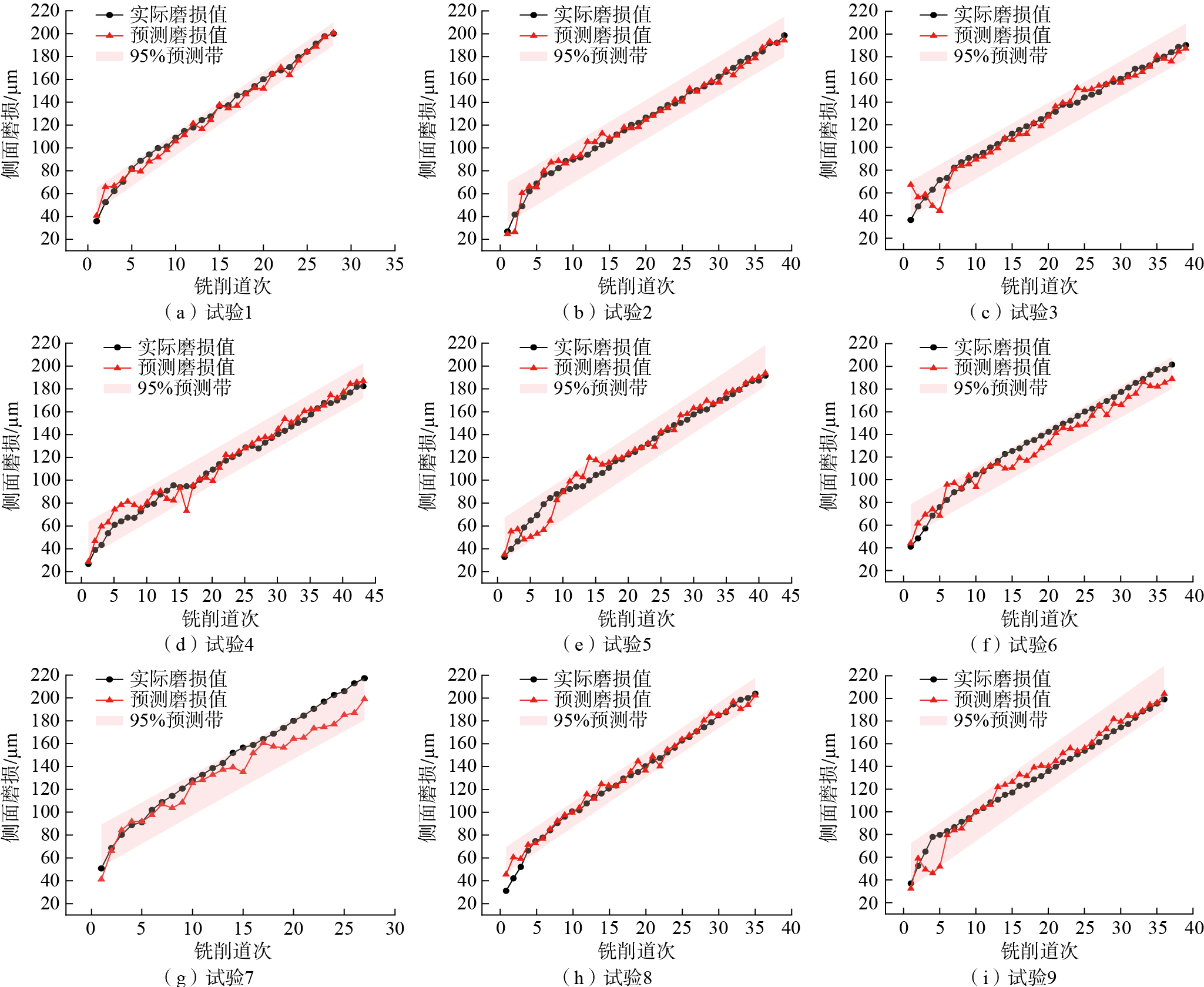
图18展示了9组试验中实际磨损值与预测磨损值的对比情况。可以看到，预测曲线与实际磨损曲线高度一致，且实际磨损值均位于预测值的95%预测带内。值得注意的是，试验7的预测效果较差，如图18（g）所示。通过分析发现，试验7仅铣削27道槽就达到磨钝标准，因本组试验的预测模型是通过其余8组试验数据训练得出的，从而导致预测值曲线略低于实际磨损曲线。表明本组参数会导致刀具磨损加剧，为提升整体模型的泛化能力，后续可通过增加试验次数来覆盖更广泛的参数范围。从整体试验组的结果观察 （图18），刀具磨损初期的预测曲线波动幅度较大，主要是因为新刀具通常有一层保护涂层，在最初的几次切削中尚未完全磨合。此外，新刀具在开始使用时可能需要一段时间才能达到最佳稳定性，因而导致了加工初期表面纹理较为混乱。这些因素会导致在进行多重分形分析计算时特征值出现波动，使得预测磨损值与实际磨损值间有一定误差。但在后期，整体曲线趋向稳定，并与实际磨损高度重合。众所周知，换刀的评判标准通常根据刀具后期的磨损状态，这进一步说明该方法用于刀具磨损预测的可行性。

为验证特征选择算法的有效性，分别对未进行特征选择的数据和经过特征选择的数据进行训练预测。表4和5分别展示了9组试验数据在经过和未经过特征选择后的SVR模型预测结果。图19展示这9组试验预测结果的均值对比图，结果显示，经过特征选择后，预测结果的RMSE和MRE均相对降低，R²则相对提高，表明特征选择能够有效提升预测模型的性能。

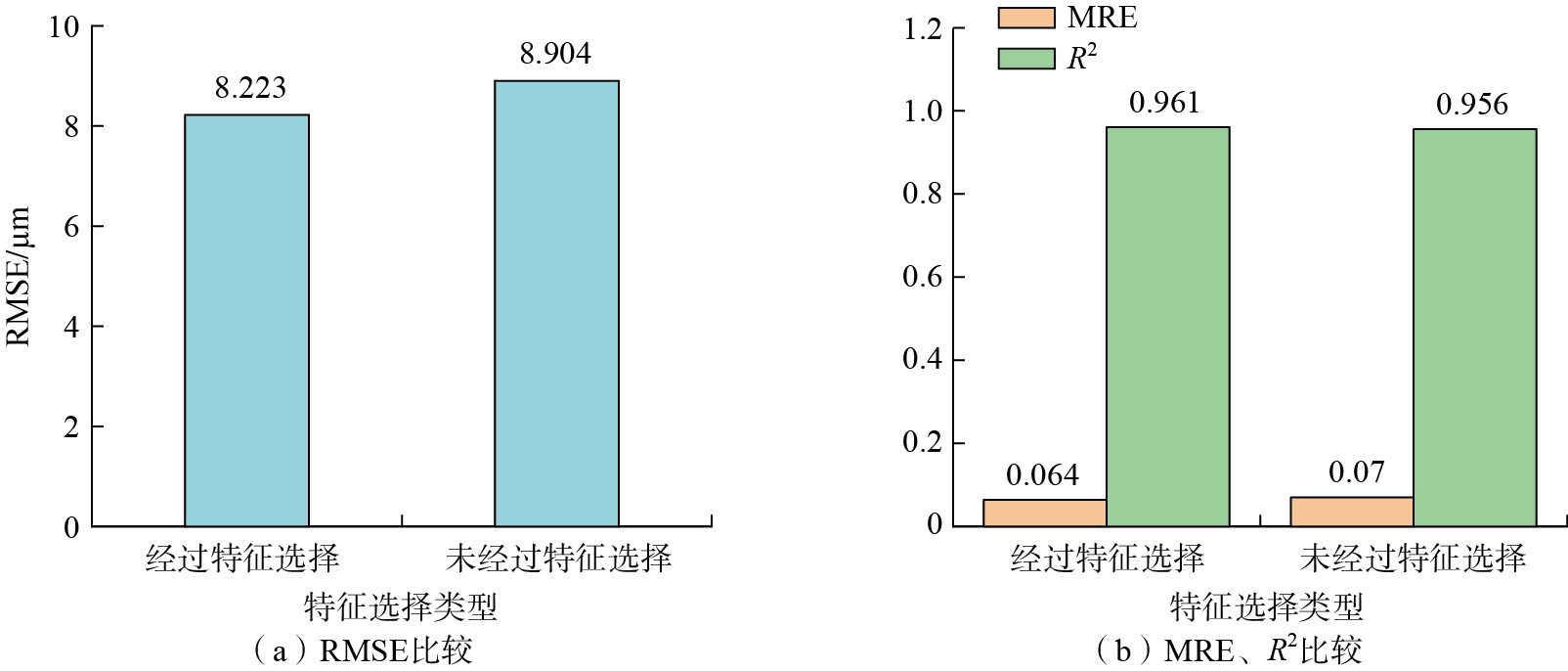
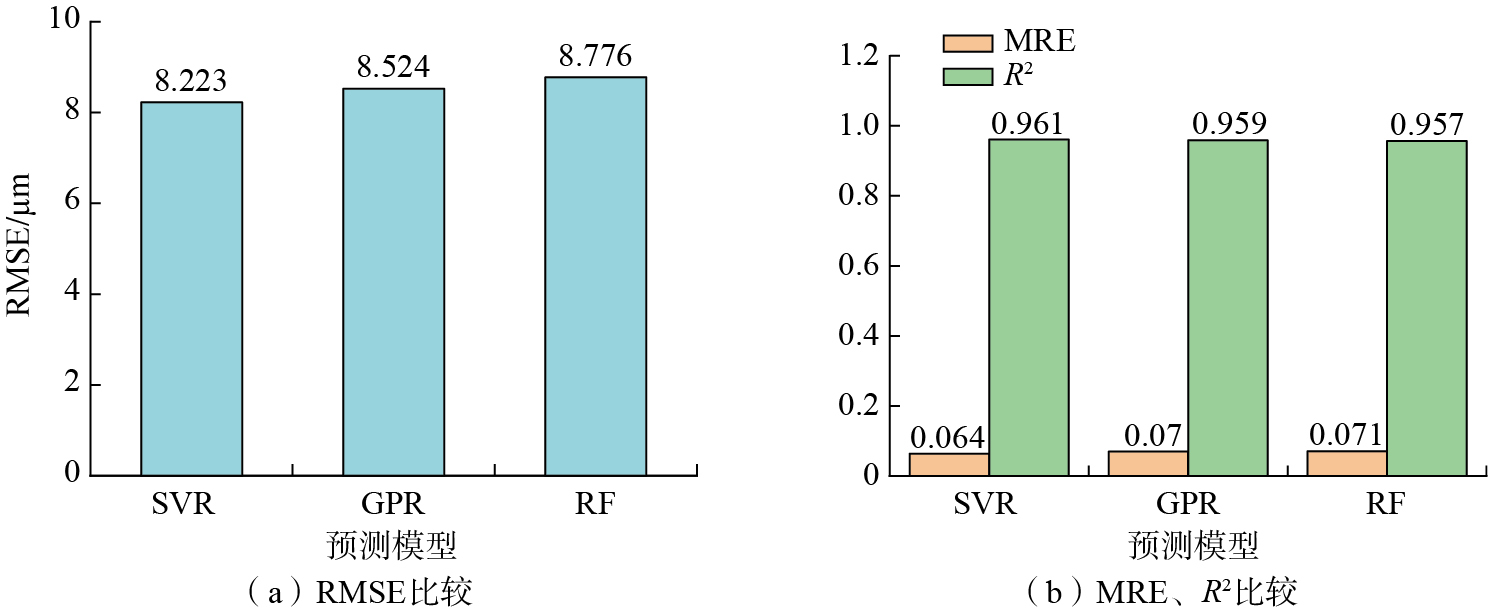
表6和7分别记录了GPR和RF模型在刀具侧面磨损预测中的表现，涵盖训练集和测试集的RMSE、MRE以及R²。图20展示了3种模型的预测效果对比，试验结果表明，SVR模型在预测准确性方面显著优于GPR和RF模型，特别是在处理非线性数据时，其优势尤为明显，主要归因于SVR强大的非线性建模能力和较高的鲁棒性。尽管GPR和RF模型在训练集上表现良好，但在测试集上的预测效果不及SVR，这是由于SVR具有更强的泛化能力，能够更好地适应数据中刀具磨损的随机性特征。因此，SVR模型在通过加工表面纹理特征预测刀具磨损方面，更能满足实际应用中的需求，显示出更强的适应性和准确性。

（1）本文提出了一种综合多重分形分析法和加工参数的刀具磨损预测新方法。通过对加工表面纹理特征的多重分形分析，能够更精确地捕捉到表面细微变化，有效反映刀具的磨损状态。试验验证了多重分形小波leaders提取的表面纹理特征与刀具磨损之间的显著相关性。

（2）建立了一种基于过滤法 （ReliefF）特征选择算法和支持向量回归 （SVR）的高精度刀具磨损预测模型。在325个样本的基础上，通过ReliefF特征选择算法优化后的特征集显著提高了预测模型的准确性。试验结果显示，SVR模型在与高斯过程回归 （GPR）和随机森林 （RF）模型的对比中表现优越，具有更高的预测精度和泛化性能，更符合刀具磨损的随机特性。

（3）提供了一种结合多重分形特征、加工参数和先进特征选择及回归算法的综合预测框架。该框架为智能制造中的刀具状态监测提供新的思路，并通过试验验证了刀具在不同加工条件下的实用性。试验结果表明，该方法在多个试验条件下表现出高效的预测能力，平均均方根误差 （RMSE）仅为8.223 μm，平均决定系数 （R²）达到0.961，平均预测精度为93.6%。

尽管本研究取得显著成果，但试验条件相对有限，获取的试验样本数量较少，未来需要在更广泛的加工环境中验证方法的普适性。同时，不同材料的加工特性可能对纹理特征的提取和分析带来影响，未来研究应进一步探索材料特性对预测模型的影响。