飞机机体结构具有制造精度要求高、零件数量大、装配层级多、整体刚度低、装配协调关系复杂等特点，飞机装配工作量在整个飞机制造过程中占比高达50%~60%^{[ [1]  陈文亮, 潘国威, 丁力平. 飞机数字化装配技术发展现状[J]. 航空制造技术, 2016, 59(8): 26–30.CHEN Wenliang, PAN Guowei, DING Liping. Development of aircraft digital assembly technology[J]. Aeronautical Manufacturing Technology, 2016, 59(8): 26–30.
1 ]}。飞机机翼是飞机产生升力以支持飞机在空中飞行的主要部件，其制造精度对飞机性能指标起决定性作用，其形状、翼型和结构直接影响飞机稳定性、操纵性和可靠性等^{[ [2]  MENG Y S, YAN L, HUANG W, et al. Structural design and analysis of a composite wing with high aspect ratio[J]. Journal of Zhejiang University: Science A, 2019, 20(10): 781–793.
2 ]}。翼盒不仅是机翼的主承力结构，还是飞机油箱，内部存储了飞机所需的大部分燃油。翼盒主要由前后梁、上下壁板和翼肋组成，装配过程一般为，先由前后梁及翼肋组成翼盒骨架，最后安装上下壁板形成整个翼盒^{[ [3]  王静, 路畅, 邬盼盼, 等. 基于组合梁结构的复合材料机翼设计及验证[J]. 复合材料科学与工程, 2023(7): 50–56.WANG Jing, LU Chang, WU Panpan, et al. Design and verification of composite wing based on composite beam structure[J]. Composites Science and Engineering, 2023(7): 50–56.
3 ]}。翼盒一般为扁平盒状结构且内部空间由若干个肋隔开，通常在壁板上留有用于装配和检修的椭圆形开口，施工空间开敞性差，导致翼盒成为机翼装配中难度最大的部分^{[ [4]  黄春, 李光丽, 袁士平, 等. 机翼翼盒装配间隙精密补偿研究[J]. 航空制造技术, 2013, 56(20): 63–66.HUANG Chun, LI Guangli, YUAN Shiping, et al. Research on active compensation for assembly gap of aircraft wing box[J]. Aeronautical Manufacturing Technology, 2013, 56(20): 63–66.
4 ]}。机器人具有使用灵活性高、装配质量高、作业空间小等优点，可以在一定程度上提高飞机翼盒装配的效率。但由于翼盒装配的复杂性，导致机器人的装配效率及质量都非常依赖机器人路径规划的合理性和准确性。

机械臂路径规划是其运动控制中的关键环节^{[ [5]  杨旭海, 周文皓, 李育峰, 等. 采摘机械臂路径规划算法研究现状综述[J]. 中国农机化学报, 2023, 44(5): 161–169.YANG Xuhai, ZHOU Wenhao, LI Yufeng, et al. Review of path planning algorithms for picking manipulator[J]. Journal of Chinese Agricultural Mechanization, 2023, 44(5): 161–169.
5 ]}，与移动机器人的路径规划不同，机械臂路径规划不仅需要考虑末端执行器与障碍物的碰撞，还要考虑各连杆之间的运动关系及其与环境障碍物的相互碰撞^{[ [6]  刘建春, 秦昆, 林彦锋, 等. 双机械臂碰撞检测算法研究[J]. 机械传动, 2021, 45(1): 40–44, 70.LIU Jianchun, QIN Kun, LIN Yanfeng, et al. Research on collision detection algorithm of dual manipulator[J]. Journal of Mechanical Transmission, 2021, 45(1): 40–44, 70.
6 ]}。根据算法的核心思想和底层数据结构，机械臂路径规划方法可分为4类：基于搜索、基于优化、基于学习和基于采样的路径规划算法^{[ [7]  KARUR K, SHARMA N, DHARMATTI C, et al. A survey of path planning algorithms for mobile robots[J]. Vehicles, 2021, 3(3): 448–468.
7 ]}。基于搜索的算法能够生成高质量的路径，精确搜索最优路径，但在高维空间中计算量较大，难以应对复杂环境，因此更适用于低维空间^{[ [8]  HA J, AN B, KIM S. Reinforcement learning heuristic A[J]. IEEE Transactions on Industrial Informatics, 2023, 19(3): 2307–2316.
[9]  REHMAN T U, YOUSAF M, JING L. A*–FastIsomap: An improved performance of classical isomap based on A* search algorithm[J]. Neural Processing Letters, 2023, 55(9): 12719–12736.
8-9 ]}；基于优化的算法适应性强，能处理复杂环境，但收敛速度较慢，易陷入局部最优^{[ [10]  YANG J, WANG Y D, CHEN Y, et al. Detection of weeds growing in Alfalfa using convolutional neural networks[J]. Agronomy, 2022, 12(6): 1459.
[11]  ZUCKER M, RATLIFF N, DRAGAN A D, et al. CHOMP: Covariant Hamiltonian optimization for motion planning[J]. The International Journal of Robotics Research, 2013, 32(9–10): 1164–1193.
10-11 ]}；基于学习的算法在多目标规划和自适应优化中具有优势，但存在训练时间长、数据依赖性强及计算资源消耗大的问题^{[ [12]  何启嘉, 王启明, 李佳璇, 等. 基于优势竞争网络的转运机器人路径规划[J]. 清华大学学报(自然科学版), 2022, 62(11): 1751–1757.HE Qijia, WANG Qiming, LI Jiaxuan, et al. Transport robot path planning based on an advantage dueling double deep Q-network[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(11): 1751–1757.
[13]  IRIONDO A, LAZKANO E, ANSUATEGI A, et al. Learning positioning policies for mobile manipulation operations with deep reinforcement learning[J]. International Journal of Machine Learning and Cybernetics, 2023, 14(9): 3003–3023.
12-13 ]}；基于采样的路径规划算法（如快速扩展随机树（Rapidly-exploring random tree，RRT）^{[ [14]  QIE T Q, WANG W D, YANG C, et al. A path planning algorithm for autonomous flying vehicles in cross-country environments with a novel TF–RRT method[J]. Green Energy and Intelligent Transportation, 2022, 1(3): 100026.
14 ]}和概率路线图（Probabilistic roadmap，PRM）^{[ [15]  KAVRAKI L E, SVESTKA P, LATOMBE J C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces[J]. IEEE Transactions on Robotics and Automation, 1996, 12(4): 566–580.
15 ]}），由于在高维空间和复杂环境中的优异表现、简单易实现等优点，特别适合于离线计算和反复查询的应用场景。其中，PRM算法具有较高的灵活性，可根据具体应用需求调整采样策略、连接策略和优化策略，能够在不同的环境和约束条件下进行定制化配置，被广泛应用于机械臂路径规划、移动机器人导航及其他需要在复杂环境中进行路径生成和优化的任务中^{[ [16]  林俊志, 席万强, 周俊, 等. 基于改进PRM和APF的移动机器人路径规划[J]. 国外电子测量技术, 2022, 41(12): 1–6.LIN Junzhi, XI Wanqiang, ZHOU Jun, et al. Path planning of mobile robots based on improved PRM and APF[J]. Foreign Electronic Measurement Technology, 2022, 41(12): 1–6.
16 ]}。

PRM算法通过在构型空间（Configuration space）中进行采样、碰撞检测及测试相邻采样点的连通性来构建路径图。其主要优点在于算法复杂度与路径难度相关，而与构型空间的大小和维度无关，因此在高维空间中表现良好^{[ [17]  封澳, 杨锦宇, 谢玉阳, 等. 基于改进PRM算法的机器人路径规划[J]. 计算机技术与发展, 2024, 34(2): 127–133.FENG Ao, YANG Jinyu, XIE Yuyang, et al. Robot path planning based on improved PRM algorithm[J]. Computer Technology and Development, 2024, 34(2): 127–133.
17 ]}。然而，当起始点和目标点之间存在密集障碍或狭窄通道时，PRM算法的效率显著下降。同时，PRM算法需对整个构型空间进行采样，可能导致不必要的计算资源浪费。针对这些问题，国内外学者提出了多种改进方案。Kurniawati等^{[ [18]  KURNIAWATI H, HSU D. Workspace-based connectivity oracle: An adaptive sampling strategy for PRM planning[C]//International Workshop Algorithmic Foundations Robotics. Heidelberg: Springer Berlin Heidelberg, 2008.
18 ]}提出在采样阶段对障碍物边界进行采样，并评估最优可行区域，从而优化采样策略；李琼琼等^{[ [19]  李琼琼, 徐溢琪, 布升强, 等. 基于修正PRM算法的智能车辆路径规划研究[J]. 森林工程, 2022, 38(5): 179–186.LI Qiongqiong, XU Yiqi, BU Shengqiang, et al. Smart vehicle path planning based on modified PRM algorithm[J]. Forest Engineering, 2022, 38(5): 179–186.
19 ]}提出了一种基于空间主轴线的伪随机采样策略，改进了采样点生成方式，减少了规划时间；Aria^{[ [20]  ARIA M. Optimal path planning using informed probabilistic road map algorithm[J]. Journal of Engineering Research, 2014: ASSEEE.16105.
20 ]}提出了一种Informed–PRM算法，将PRM算法与信息搜索算法相结合，采用两种信息引导的搜索方法，使得路径规划能够更快速地收敛，并有效减少路径规划的成本；宁新杰等^{[ [21]  宁新杰, 崔炜, 徐照翔, 等. 改进概率路标图算法[J]. 计算机工程与设计, 2021, 42(12): 3422–3427.NING Xinjie, CUI Wei, XU Zhaoxiang, et al. Improved probabilistic roadmap algorithm[J]. Computer Engineering and Design, 2021, 42(12): 3422–3427.
21 ]}则通过边集优化和引入道格拉斯–普克算法，在PRM学习阶段减少了路径图中的冗余点，进而减少了查询阶段的计算量。

针对传统PRM算法采样点分布不均、冗余点过多、路径图构建复杂及路径折点过多等问题，本文提出了若干改进措施。首先，引入Halton序列优化采样策略，以实现采样点在构型空间中的均匀分布；其次，提出基于控制点的椭圆区域冗余点优化策略，并结合局部敏感哈希函数，从而提高路径图构建和搜索效率；最后，采用B样条曲线对生成的路径进行平滑处理，进一步满足机器人的运动约束。

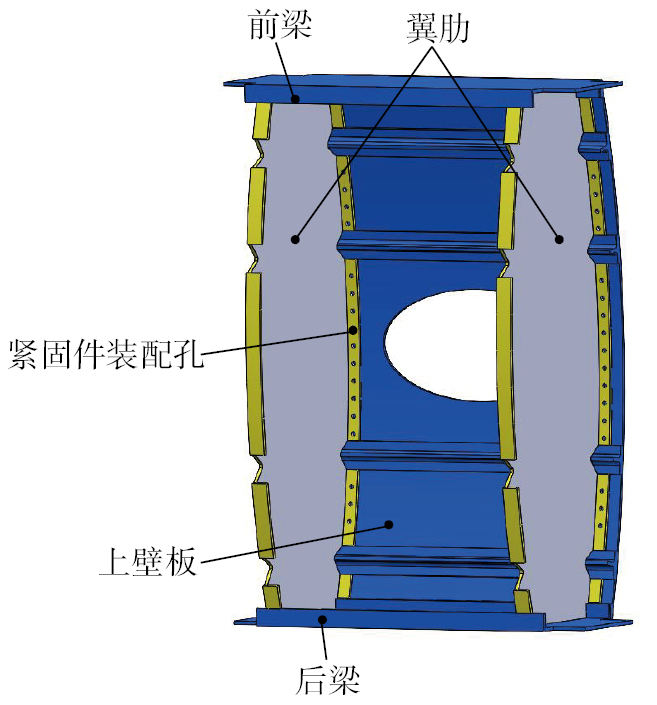
大型飞机的机翼长度通常超过10 m，为简化研究，选取翼展方向的翼盒截面作为研究模型。如图1所示，典型复合材料翼盒由上下壁板、前后梁及若干翼肋构成，是机翼结构中承载与传递载荷的核心部件。翼盒的设计目标是轻量化、高强度与高刚度，广泛采用复合材料进行制造，且壁板通过蒙皮与长桁共固化成型技术进行制备。为便于装配与后期维护，复合材料壁板通常预留椭圆形开口，用于内部空间检修和操作。翼肋与壁板连接区域通过紧固件装配孔来实现高精度装配与结构固定。

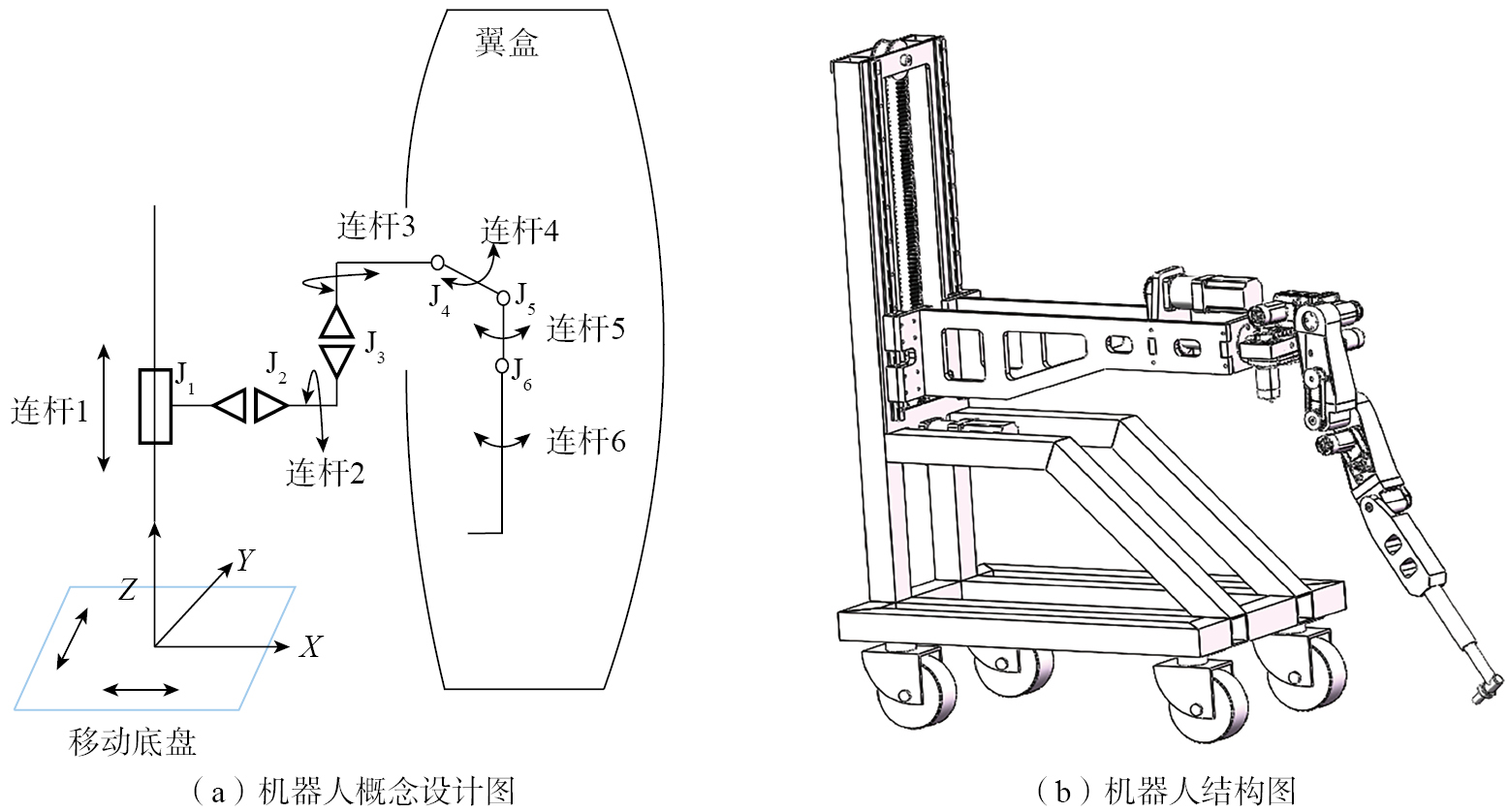
复合材料翼盒内部紧固件装配机器人的拟人化概念设计及结构如图2所示。机器人的机械臂由多个自由度构成，通过功能分区模拟人体动作，以满足复杂装配需求。基础部分为移动底盘，提供平面运动自由度，确定机械臂相对于翼盒的初始位置。关节1（J₁）采用棱镜副设计，模拟人体蹲下与站立动作，满足翼盒高度方向的需求，并驱动后臂连杆进入翼盒内部。为了覆盖装配工作的圆周范围，机械臂通过旋转轴驱动的连杆2和连杆3实现肩部横摆和上臂横滚功能，旋转角度分别为360°和180°。肩部末端设置关节4（J₄），模拟肩关节的俯仰动作；连杆4通过关节5（J₅）连接连杆5，模拟肘部弯曲功能；连杆5通过关节6（J₆）连接连杆6，模拟手部及工具操作。关节4、5、6的旋转轴平行，协调运动以驱动末端执行器在指定角度范围内摆动，精确定位并完成紧固件的装配任务。

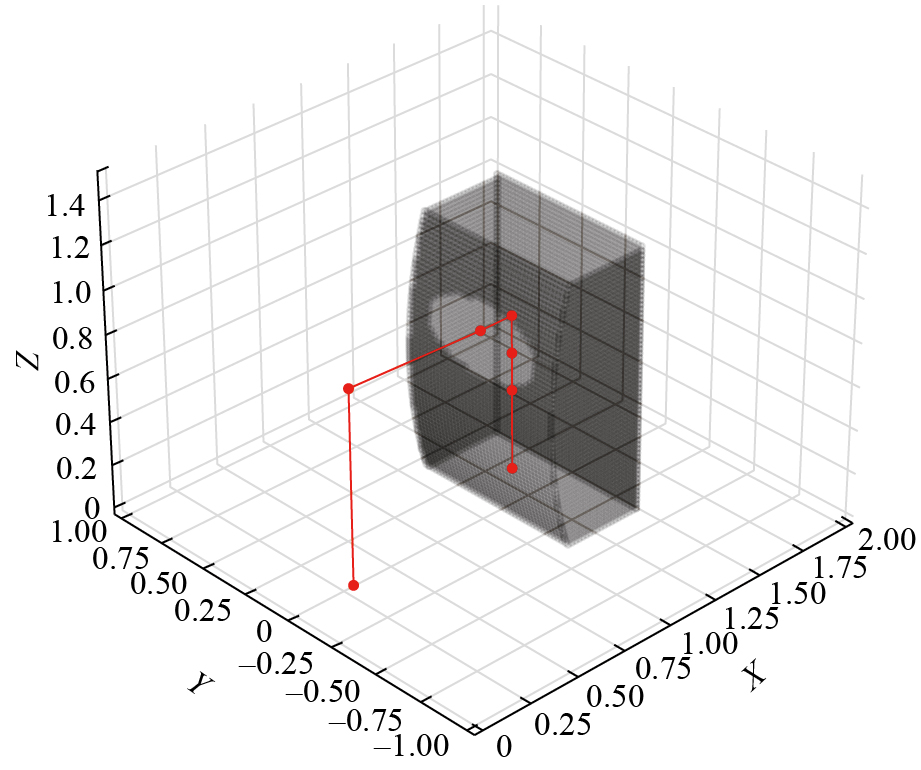
机械臂的碰撞检测与移动机器人不同，主要侧重于确保各连杆在运动过程中避免与障碍物或自身发生碰撞，从而保障机械臂的安全与任务执行效率。为了简化翼盒紧固件装配过程中碰撞检测的计算，采用k–d树法（K–dimension tree）构建障碍物模型，并使用圆柱形包围盒（Axis-aligned bounding box，AABB）来表示机械臂连杆。根据机械臂的结构与装配过程，可能发生碰撞的连杆包括连杆3、4、5和6，因此，仅对这些连杆进行碰撞检测。在Python中，首先将机械臂拆分为6个主要部分，使用圆柱体包围盒对每个部分进行替换，并用线段表示机械臂结构。随后，利用k–d树算法将翼盒障碍物转化为高效的空间数据结构，以便快速进行点查询和邻近搜索。简化后的机械臂与翼盒障碍物如图3所示，其中红色线段包含机械臂的6个端点，黑色区域表示翼盒障碍物在k–d树中的数据分布。

为了判断翼盒障碍物是否与连杆圆柱体发生碰撞，设机械臂某个圆柱体轴线的两端点分别为p_i=（x_i，y_i，z_i）和p_i+1=（x_i+1，y_i+1，z_i+1），则该轴线对应线段p_ip_i+1的表达式为

式中，t为参数。为了计算连杆圆柱体到翼盒障碍物空间点的最短距离，使用Python中的cKDTree模块构建快速查询树，假设查询树中某一点的空间坐标为p_n=（x_n，y_n，z_n），则p_n到线段p_ip_i+1或延长线的投影t_proj为

根据t_proj的值，可以得到p_n到线段p_ip_i+1的距离为

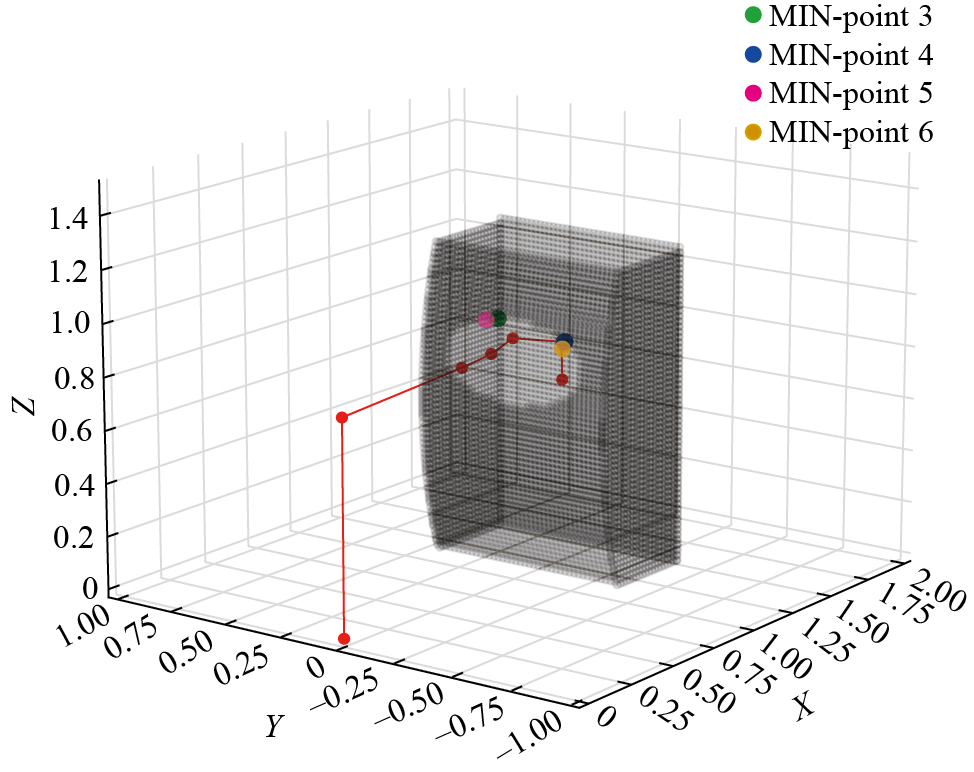
式中，p_n+1是当0≤t_proj≤1时，p_n在线段p_ip_i+1的投影点。通过计算查询树中距离线段p_ip_i+1最近的点，可以得到路径上连杆3、4、5、6到障碍物的最小距离，若该最小距离大于连杆圆柱体的半径，则可判断翼盒障碍物与连杆未发生碰撞。图4展示了在某一姿态下，翼盒障碍物到连杆3、4、5、6的最近点及最小距离，通过对比最小距离与连杆圆柱体的半径，验证了该姿态下机械臂与翼盒障碍物未发生碰撞。

PRM是一种基于概率采样的路径规划算法，通过在构型空间C中随机采集样点并进行连接，构建无向路径图（Roadmap）以搜索有效路径。PRM算法分为采样阶段和查询阶段。

采样阶段：PRM算法在构型空间中按照某种采样策略采集N个采样点X_i（i=1，2，…，N），去除落在障碍物空间中的采样点，随后得到一组有效采样点集合V；然后根据设定的连接准则将有效采样点通过直线段连接起来，且连线的长度d（X_i，X_j）≤R，其中R为PRM算法的最大连通半径，最终形成一张无向路径图G（V^*，E），其中V^*代表顶点集合，E代表无碰撞的边（顶点间连线）的集合，V^*和E的初始状态均为空。

查询阶段：在采样阶段得到的无向路径图G（V^*，E）中加入起始点q_init与目标点q_goal，使用图搜索算法（如Dijkstra算法、A*算法）查询从起始点到目标点的路径。

传统PRM算法广泛应用于复杂环境中的离线规划、多机器人系统及高维构型空间的路径规划。然而，该算法仍存在以下主要问题。

（1）随机采样点的质量低：采用随机采样策略，导致采样点在构型空间中的分布不均，进而影响规划路径的质量和稳定性。

（2）路径图构建效率低下：传统PRM算法对整个构型空间进行采样，并采用固定的连接策略（如距离阈值），生成大量冗余点，导致路径图过于密集，增加了计算时间和复杂度。

（3）路径折点过多：由于采样点通过直线连接，导致最终路径中的折点过多，降低了路径的可读性和执行效率。

针对传统PRM算法的不足，选择以下4个方面进行改进：改进采样策略，设计一种冗余点优化策略，改进路线图构建方式及局部路径优化。

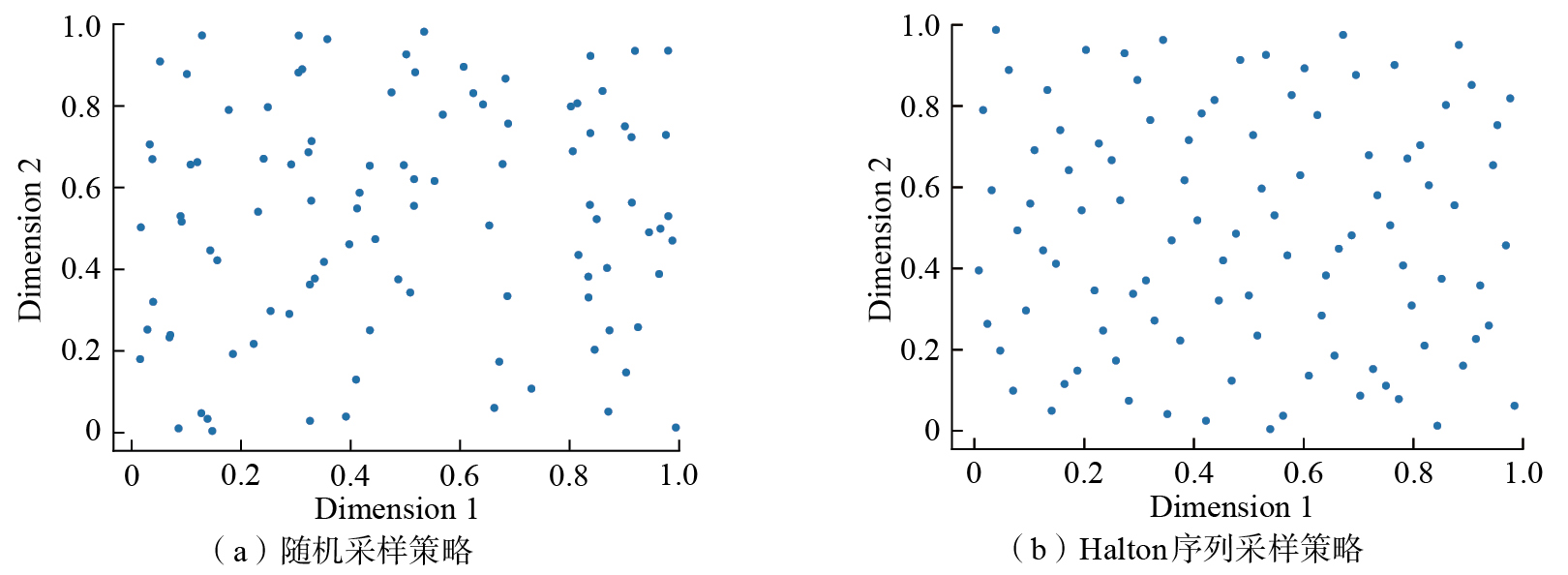
传统PRM算法采用随机采样策略，导致采样点分布不均、采样质量低。为提高采样质量，本文引入Halton序列进行采样优化。Halton序列是一种低差异、非周期且伪随机的序列，广泛应用于Monte Carlo模拟等数值方法。与常规伪随机数序列相比，Halton序列具有更均匀的分布，能提供更好的数值稳定性和计算效率。Halton序列通过选取质数作为基数，根据维度数量选择相应数量的质数，利用质数的数位构造序列，从而生成在每个维度上独立且均匀分布的点，这一方法有效改进了采样过程，提升了路径规划的精度与效率。

使用Halton序列取代传统的随机取样，可使采样点的分布相对更加均匀，同时又保持了部分随机性。图5对比了随机采样和Halton序列采样（选取质数2和3作为Halton序列的基数）的采样点分布图。可以看出，相比于随机采样，Halton采样策略的采样点分布更均匀，能确保每个子区域有采样点，从而提高了采样点质量，增强了路径搜索的稳定性，有效解决了随机采样中因采样点数不足而导致的搜索空间不完整问题。

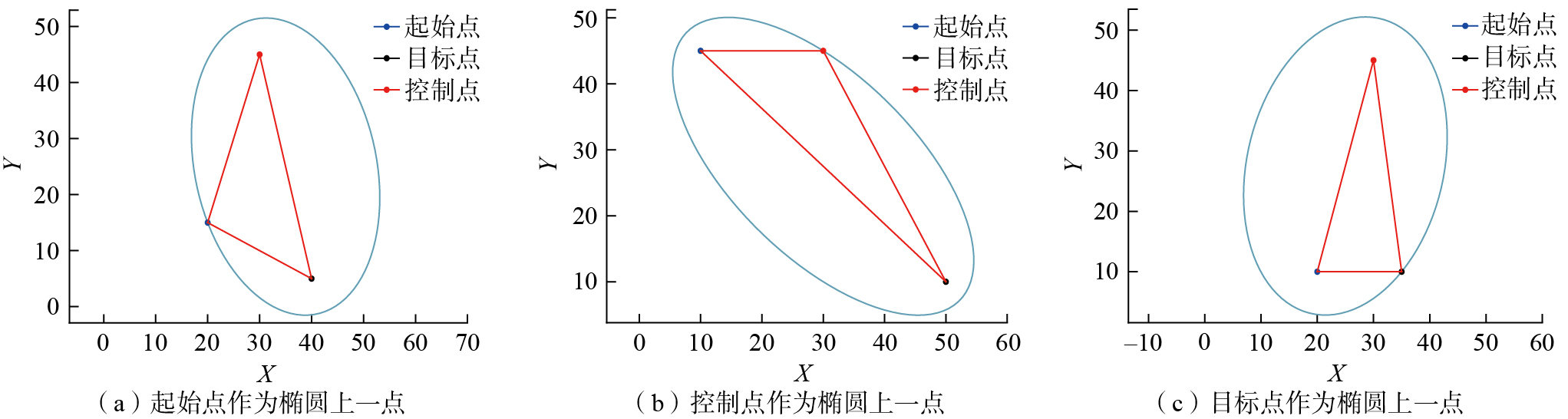
在PRM算法的采样阶段，通常在整个构型空间C中进行采样，随着构型空间C的增大，采样点数量增加。为了确保最终能够找到合适的路径，往往会生成大量冗余点，将显著影响规划时间和效率。为此，提出一种基于控制点的椭圆区域冗余点优化策略，旨在减少采样阶段的冗余点并提高路径图的构建效率。

根据椭圆的定义，椭圆上任一点P到焦点F₁、F₂的距离之和为常数。因此，已知椭圆的2个焦点和其上一点即可确定椭圆区域。在PRM算法中，除了起始点和目标点外，增加一个固定的控制点，该点位置根据实际构型空间确定，一旦选定，不再更改。起始点、控制点和目标点确定一个三角形，以三角形最长边的两端点为椭圆的焦点，另外一个点位于椭圆曲线上，从而确定椭圆区域。在采样阶段，对于生成的每个采样点，若位于椭圆区域内，则保留该点；若位于椭圆区域外，则剔除该点，即不参与路径图的构建。图6展示了不同起始点和目标点的椭圆区域形成机制，其中，蓝色表示起始点，黑色表示目标点，红色表示固定的控制点。在60×60的构型空间中，选取（30，45）作为控制点。

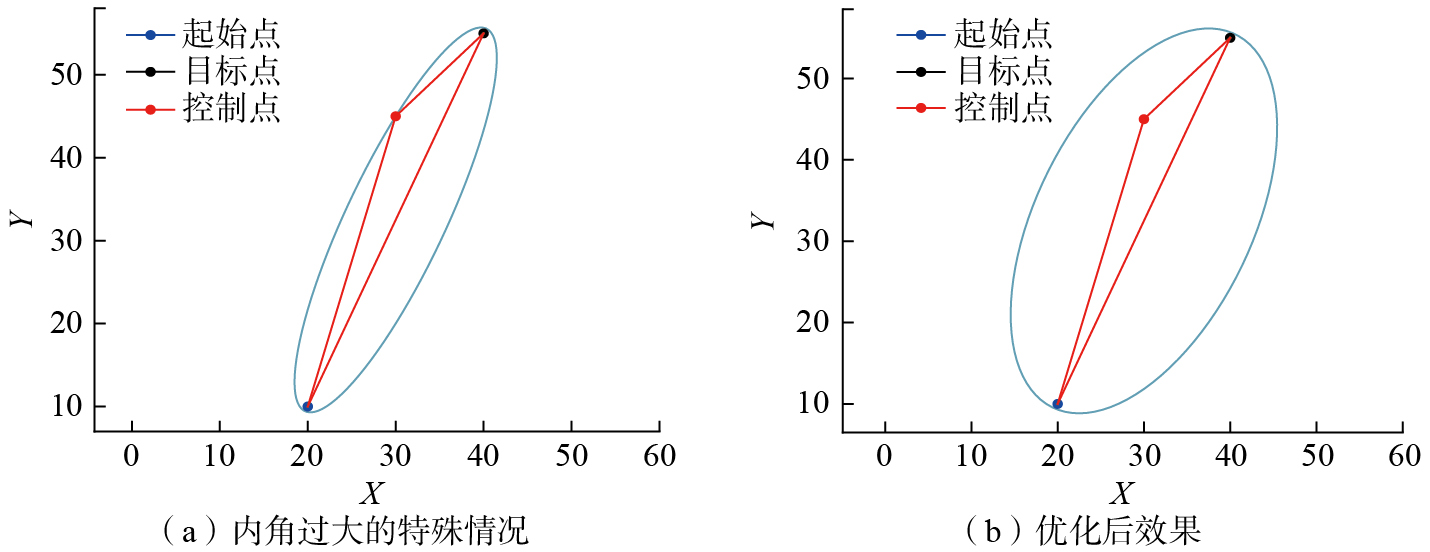
为了确保椭圆区域内包含足够的采样点，当起始点、目标点和控制点形成的三角形最大内角过大时，椭圆可能出现“扁平”的特殊情况，导致椭圆区域内的点过少，进而影响路径规划的成功率，如图7（a）所示。为解决这一问题，当三角形的最大内角超过某一阈值时，仍然以三角形最长边的两端点作为椭圆的焦点，并将椭圆的短轴长度设置为长轴的一半，如图7（b）所示。这一调整保证了椭圆区域的适当大小，确保椭圆区域包含足够的采样点，从而提升路径规划的稳定性。

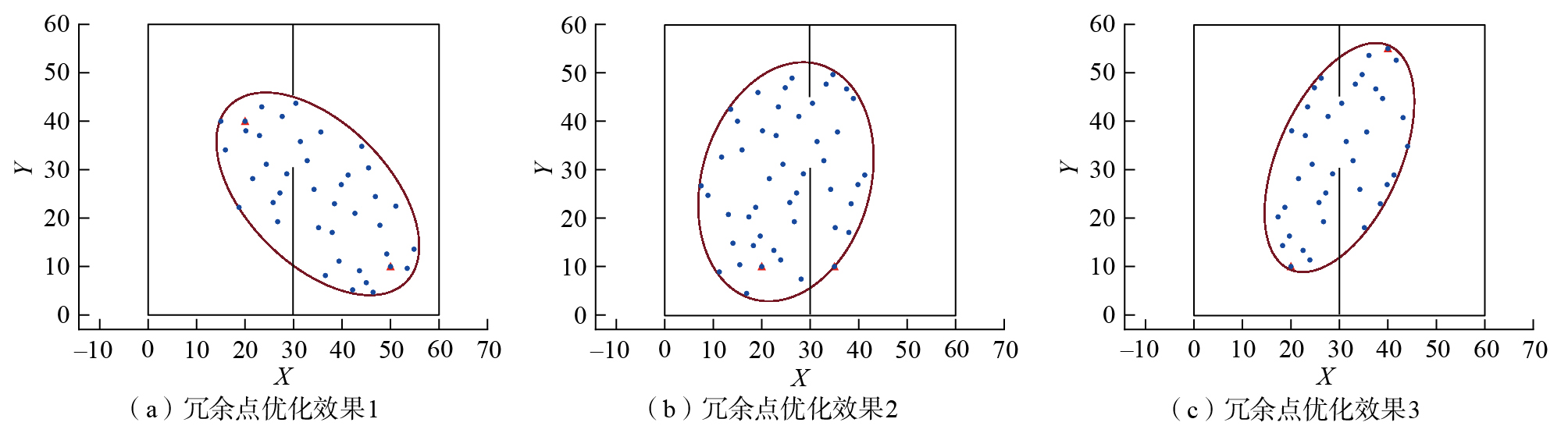
根据翼盒装配的应用需求，在60×60的构型空间中选定控制点（30，45），该点在路径规划过程中保持不变。随机选择起始点和目标点，采用基于控制点的椭圆区域冗余点优化策略得到不同起始点和目标点配置下的优化效果，如图8所示，其中红色三角形代表起始点和目标点，黑色边框表示构型空间。可以看出，该策略不仅保留了起始点和目标点周围的采样点，确保路径规划的稳定性，还去除了构型空间中的冗余点。在Python环境中对该冗余点优化策略进行重复试验，使用不同的起始点及终点，每组试验重复50次以消除随机性。试验结果表明，采用此策略后，路线图构建时间较标准PRM算法减少约25.9%~28.5%（根据Python试验所得），提高了路径规划效率。

在连接采样点时，PRM算法通常使用精确的最近邻搜索，计算查询点与构型空间中所有其他点的距离，并根据碰撞检测和连接长度找到符合条件的近邻点。尽管精确最近邻搜索能够准确找到符合条件的近邻点，并稳定构建路径图，但其计算资源消耗较大，导致规划效率低下，特别是在高维空间和大规模数据集中的情况下，搜索效率急剧下降。然而，近似最近邻搜索（Approximate nearest neighbor search，ANNS）是一种优化算法，能够在大规模数据集中快速查找与查询点最相似的近邻点。尽管ANNS不能保证找到绝对最近的近邻点，但该算法在高维数据空间中显著提高了检索效率，适用于牺牲精度以换取更快检索速度的场景。

局部敏感哈希（Locality sensitive hashing，LSH）函数是一种近似最近邻搜索方法，其基本思想是将高维向量映射到低维空间，并将相似的向量映射到同一哈希桶中。LSH函数满足两个条件：（1）若D（x，y）≤r₁，则$P_{r_R}$[h（x）=h（y）]≥P₁；（2）若D（x，y）≤r₂，则$P_{r_R}$[h（x）=h（y）]≥P₂。其中，D（x，y）表示x和y之间的欧式距离；r₁≤r₂、h（x）和h（y）分别表示对x和y进行的哈希变换。满足以上条件的哈希函数h（x）称作（d₁，d₂，P₁，P₂）敏感的函数簇。

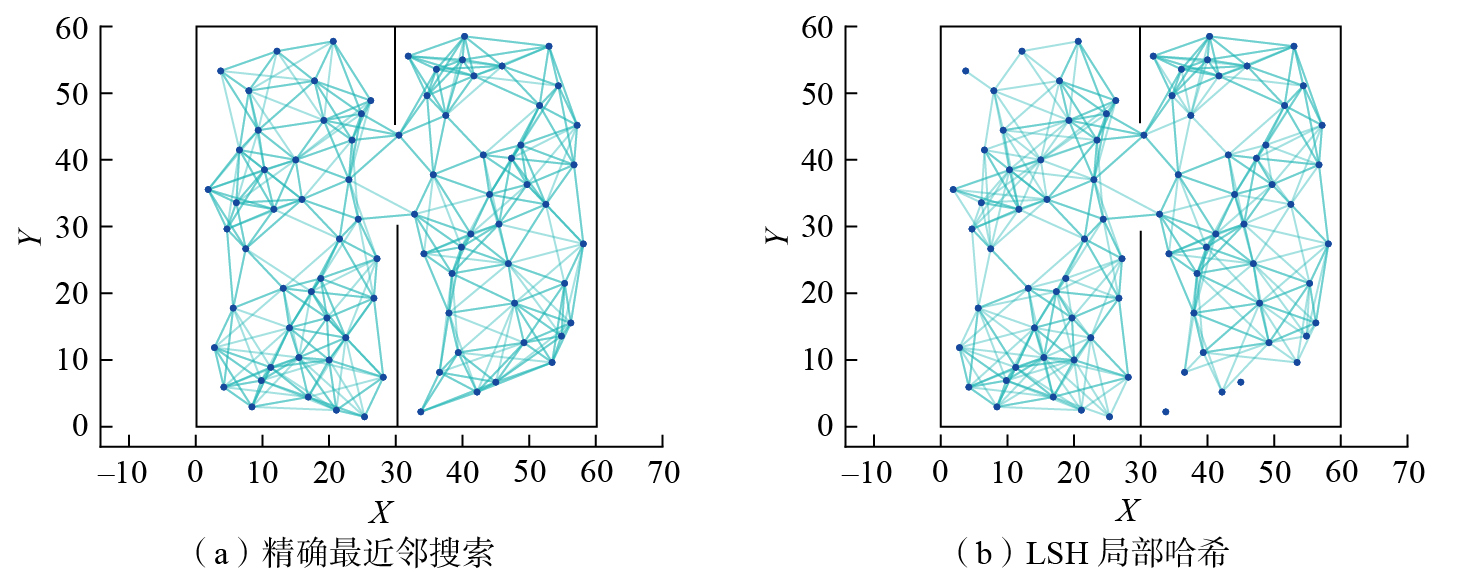
在二维空间中，采用5个哈希函数对2.2节中获得的有效采样点集合进行映射处理，并加入哈希表。随后，对于集合中的每个点，查询哈希表中8个近邻点，并通过直线连接查询点与这些近邻点，对连接线与障碍物进行碰撞检测，保留未发生碰撞的连线，最终构建无向路径图。图9对比了精确最近邻搜索与近似最近邻搜索（LSH局部哈希）所构建的路径图。可以看出，使用LSH局部哈希所得到的路径图更加简洁。在Python环境中对精确最近邻搜索及LSH局部哈希进行重复试验，每组试验重复10次以消除随机性。相比精确最近邻搜索，LSH局部哈希节省了12.35%~25.21%的搜索时间（根据Python试验所得），且随着采样点数量的增加，搜索效率显著提高。引入LSH局部哈希函数后，改进的PRM算法在保证规划成功率的同时，减少了路径图的构建时间。

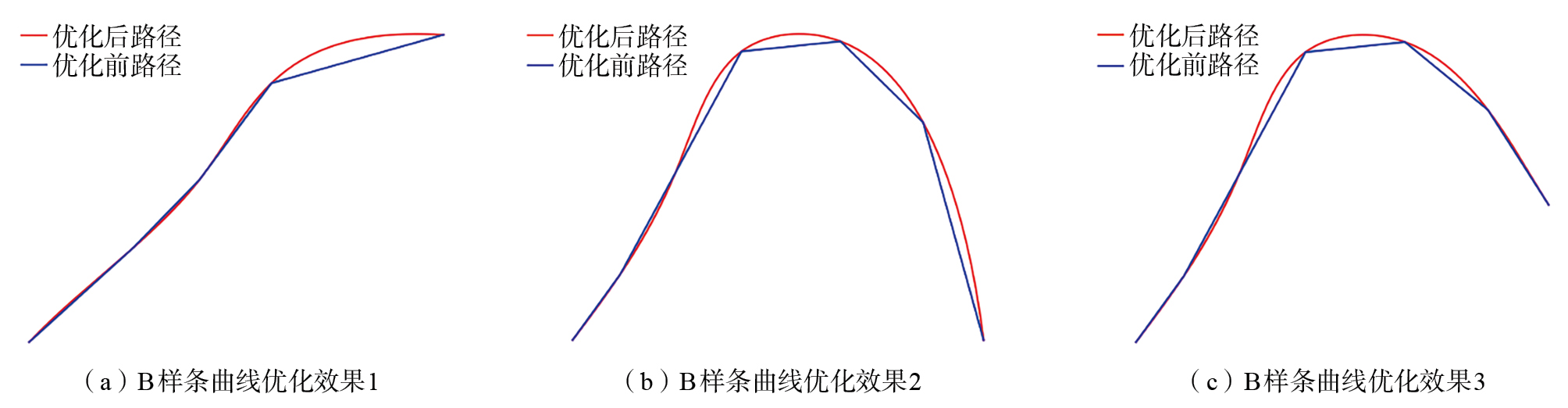
传统PRM算法在路径图构建阶段使用直线连接，导致生成的路径存在“折点”，需要通过平滑处理以适应机械臂的实际运动。B样条曲线通过控制点局部控制曲线形状，并在保证通过所有给定点的同时调整样条形态，直至符合要求。与贝塞尔曲线相比，B样条曲线不依赖于控制点数量来确定阶次，因此在路径规划中得到广泛应用。

B样条曲线方程可表示为

式中，P_i（i=0，1，…，n）为控制点（坐标）；B_i，k（i=0，1，…，n）为k次规范B样条的基函数，最高次数是k，与控制点P_i相对应，k≥1；u为自变量。

根据PRM算法最终生成的路径点数，选用准均匀B样条曲线对最终路径进行优化，即起始点和目标点作为两端节点[0，1]，在重复度为次数k的基础上加1（即k+1），则u₀=u₁=…=u_k，u_n+1=u_n+2=…=u_n+k+1，所有内部节点重复度为k+1。图10为经过B样条曲线优化后的路径，其中蓝色折线表示优化前路径，红色曲线表示优化后路径。可以看出，优化后的路径更加平滑，且与原路径保持一致，更适合实际机械臂的运动轨迹。

为了检验本文所提改进PRM算法的规划效率，在Python环境中针对传统PRM算法和改进PRM算法进行多次仿真试验，改进PRM算法的控制点根据地图大小进行选择，连通半径R=20，每个采样点连接的近邻点数量L=8，计算机参数为CPU型号i7–12700F、内存32 GB、硬盘1 TB、Window10操作系统。

针对翼盒装配机器人的实际工作环境，在60×60的构型空间内随机选择起始点和目标点，并应用改进PRM算法进行路径规划。控制点选择（30，45），传统PRM算法和改进PRM算法分别在构型空间中以60、90和120个采样点进行采样。每组仿真试验重复10次，计算路径长度和规划时间的平均值，试验结果如表1所示，所规划路径如图11所示。由表1可知，当采样点数量分别为60、90和120时，改进PRM算法的规划时间较传统PRM算法分别减少了37.32%、39.0%和46.99%（平均减少41.1%）。同时，随着采样点数量的增加，改进PRM算法的路径长度逐渐减小，表明该算法的运行效率更优。

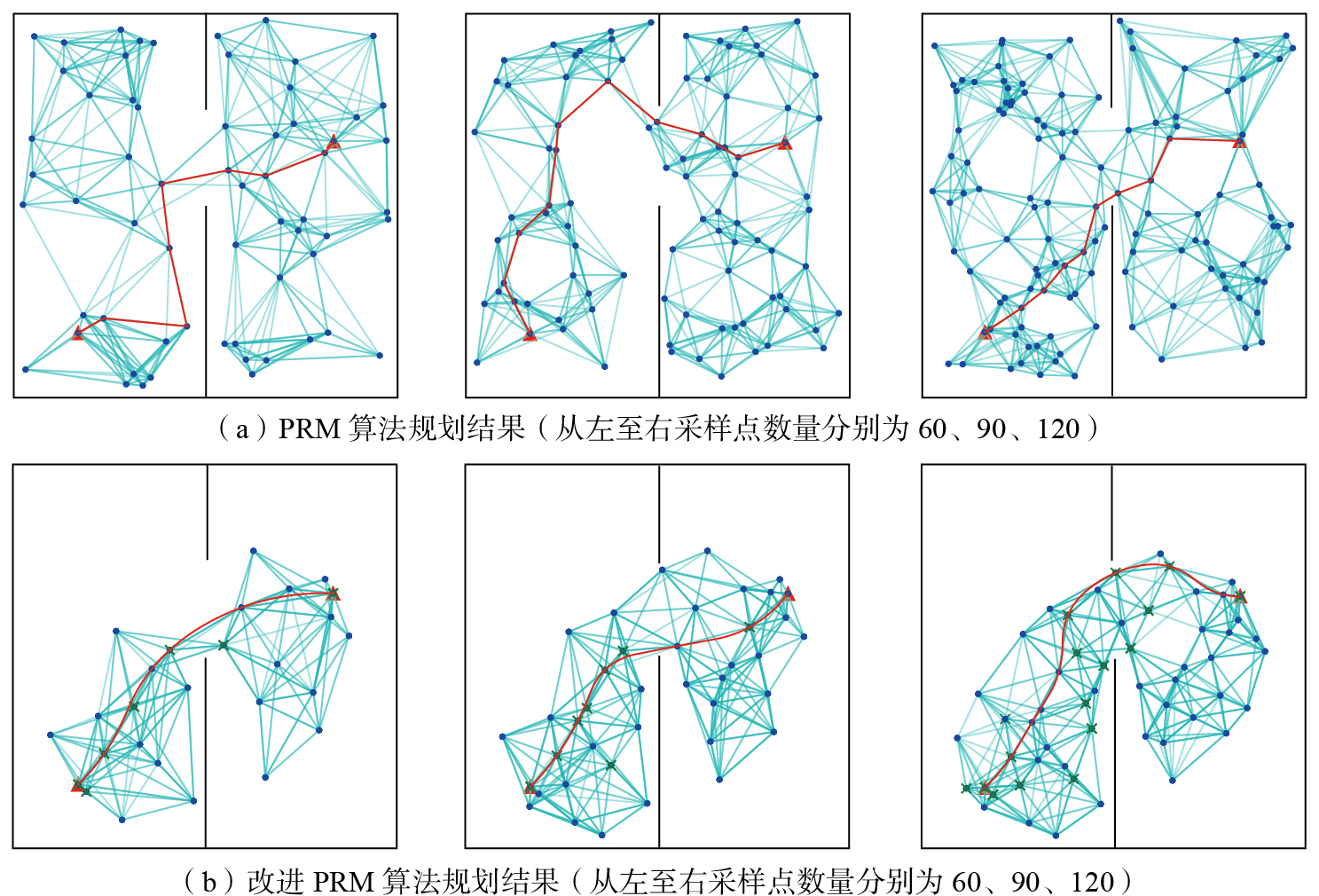
由图11可知，当采样点数量较少（N=60）时，由于随机采样策略导致构型空间中某些区域采样点分布不均，传统PRM算法生成的规划路径存在较多折点，且采样质量较低；随着采样点数量增多，尽管采样质量有所提升，但仍存在冗余点。在不同采样点数量下，改进PRM算法不仅保证了采样点均匀分布，还有效保留了起点、终点及路径中间的关键采样点，去除了冗余点，提高了规划成功率，显著提升了路径规划效率。

为验证改进PRM算法在不同环境下的性能，选取了3张具有不同规模和复杂度的测试地图。测试地图1为简单环境，障碍物数量较少且规则，适用于考察算法在低复杂度环境中的基本功能；测试地图2增大了规模并提高了障碍物的复杂度，测试算法在中等复杂度场景中的表现；测试地图3进一步增加了障碍物的数量和不规则分布，用于检验算法在高复杂度环境中的鲁棒性与效率。每张地图根据大小确定控制点，最大连通半径R为20，每个采样点连接8个近邻点。为了评估算法的准确性，每张地图进行了50次仿真试验，计算路径长度、规划时间的均值，并统计路径搜索成功率。试验数据见表2，测试地图和规划结果如图12所示。

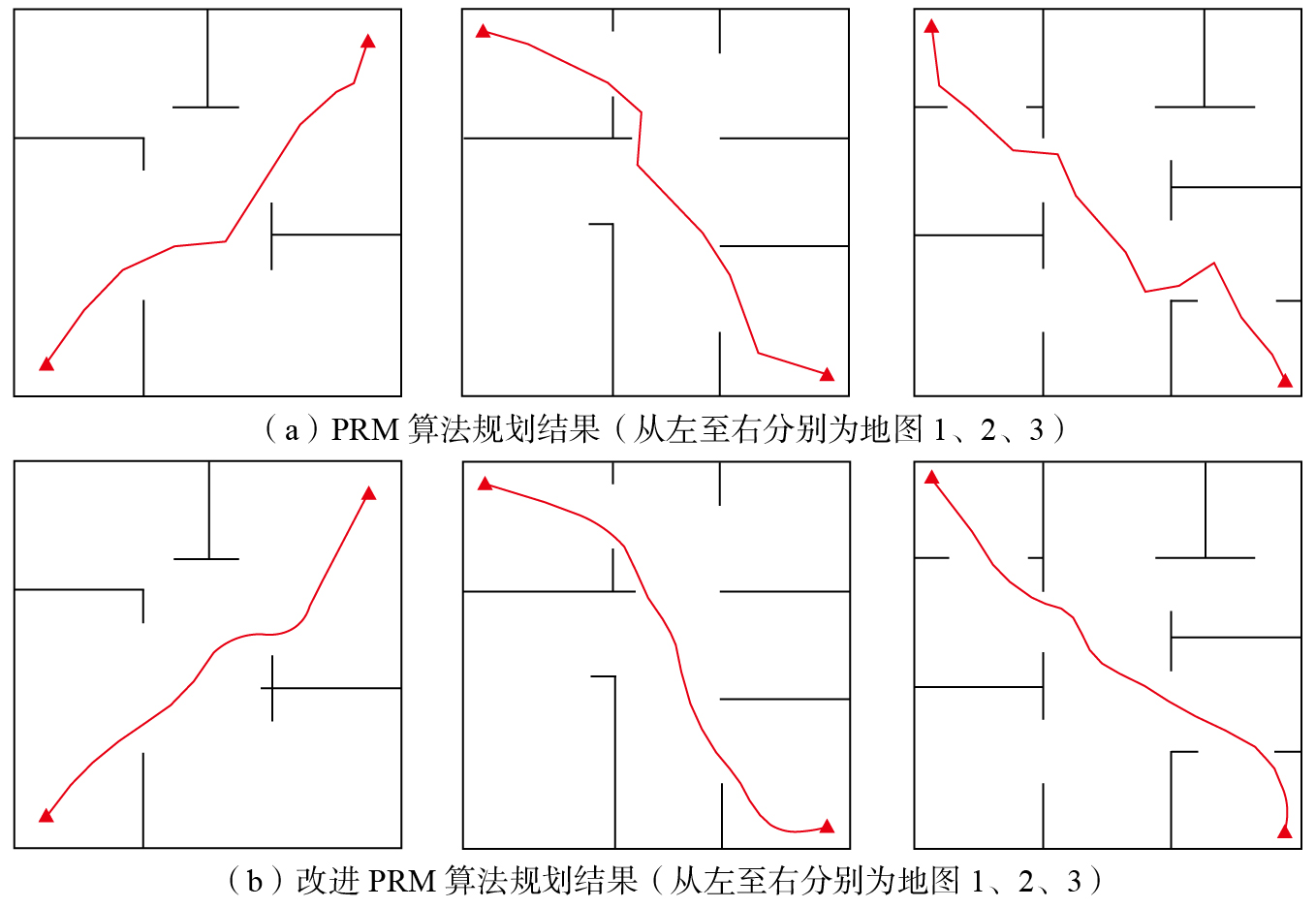
由表2和图12可知，对于测试地图1，传统PRM算法和改进PRM算法在不同采样点数量下均表现出较高的成功率（>90%），且改进PRM算法在路径长度和规划时间方面的表现明显优于传统PRM算法。相比之下，测试地图2的构型空间和地图复杂度有所增加，改进PRM算法在成功率、路径长度和规划时间方面的表现明显优于传统PRM算法。对于更加复杂的测试地图3，在采样点较多时，改进PRM算法不仅提高了路径规划的成功率，且路径质量更加可靠。通过对比3个测试地图的试验结果可知，改进PRM算法采用Halton序列进行采样，确保了较高的采样质量，使得平均路径长度小于传统PRM算法。同时，尽管采用LSH局部哈希函数构建路径图牺牲了一定的搜索精度，致使成功率未明显超过传统PRM算法，但该策略显著减少了规划时间。经过B样条曲线优化后，改进PRM算法的规划路径中去除了折点，变得更加平滑，适合机械臂的运动和控制需求。

由于翼盒装配机械臂工作环境为高维空间，因此，应重点评估该算法在高维空间中的表现。本研究基于实际工业飞机翼盒装配场景，精确构建了三维试验地图。在该场景中，随机选择机械臂的起始点和目标点，并采用1.2节中提出的碰撞检测模型。试验中，两种算法分别在机械臂构型空间中使用2000、3000和4000个采样点进行测试。对于改进PRM算法，控制点设置为（1.08，1.0，1.1），连接半径R为20 mm，每个采样点的近邻点数为10。每组试验重复50次以减少随机性，并统计路径长度、规划时间的均值，同时计算路径规划的成功率。试验结果见表3，规划结果如图13所示。

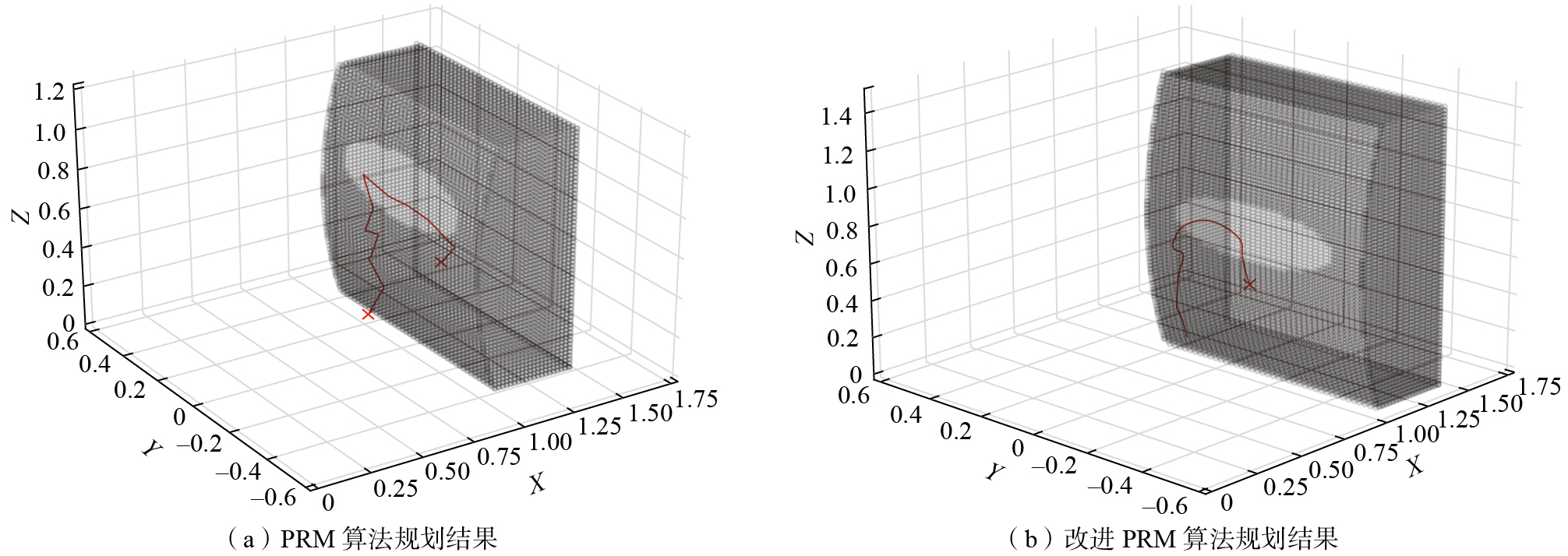
由表3和图13可知，在翼盒装配环境下，不管采样点数量大小，改进PRM算法在规划时间和成功率方面的表现显著优于传统PRM算法，其中，改进PRM算法的规划时间较传统PRM算法平均减少了68.43%。通过近似最近邻搜索和3次B样条曲线优化，尽管改进PRM算法的规划路径稍长于传统PRM算法，但路径更符合机械臂的运动需求且更平滑。综上所述，改进PRM算法在高维空间中的应用表现出更高的效率和更高的成功率，能够满足翼盒紧固件装配任务对路径规划精度和效率的要求。

本文阐述了翼盒装配机器人的结构及其碰撞检测模型，针对传统概率路线图（PRM）算法在应用中存在的各种问题，提出了一种改进的PRM路径规划方法。通过在二维和高维空间中的仿真试验，验证了该方法的有效性并得到以下结论。

（1）引入Halton序列改进采样策略，通过该伪随机采样序列提高采样质量，确保采样点在构型空间中的伪均匀分布。同时，提出基于控制点的椭圆区域冗余点优化策略，通过控制点、起始点和目标点构建椭圆区域，去除该区域外的冗余采样点，该策略既保留了起始点和目标点附近的采样点，确保路径规划的成功率，又有效减少了冗余点，节省了规划时间。

（2）采用局部敏感哈希（LSH）函数的连接策略，在牺牲一定搜索精度的条件下，提高了无向路径图的构建效率，缩短了规划时间，同时保证了较高的规划成功率。此外，使用B样条曲线对最终路径进行平滑处理，以确保路径更符合机械臂的运动要求。

（3）在Python环境中搭建试验平台对改进PRM算法的可行性进行了验证。在不同大小的测试地图上进行多次仿真试验后发现，相比传统PRM算法，改进PRM算法在二维空间中的规划时间平均减少约41.1%。在机械臂高维构型空间中，尽管改进PRM算法的规划路径稍长于传统PRM算法，但规划时间大幅减少，节省了计算资源，且最终生成的路径更平滑。