螺栓连接具有成本低、拆装方便、互换性强等优点，是航空、航天、风电、铁路等领域应用最广泛的装配连接方式^{[ [1]  齐艳华, 黄庆涛, 袁博, 等. 机械装备螺栓连接状态测试技术研究现状[J]. 航空制造技术, 2019, 62(5): 63–70.QI Yanhua, HUANG Qingtao, YUAN Bo, et al. Research status of testing technology for bolted state of mechanical equipment[J]. Aeronautical Manufacturing Technology, 2019, 62(5): 63–70.
[2]  张海兵, 温德宏. 航空螺栓超声检测中参数确定与波形分析[J]. 航空制造技术, 2020, 63(12): 97–101.ZHANG Haibing, WEN Dehong. Parameters setting and waveform analysis in ultrasonic inspection for aviation bolts[J]. Aeronautical Manufacturing Technology, 2020, 63(12): 97–101.
[3]  欧阳蔚瑾, 吴钊林, 赵兵. 航空发动机转子螺栓连接工艺评估与修正策略研究[J]. 航空制造技术, 2023, 66(22): 106–113.OUYANG Weijin, WU Zhaolin, ZHAO Bing. Evaluation and modification strategy of aero-engine rotor bolted connection process[J]. Aeronautical Manufacturing Technology, 2023, 66(22): 106–113.
1-3 ]}。螺栓预紧力直接影响螺栓连接质量和性能，预紧力过大，可能引起螺栓屈服断裂或被连接件压溃；预紧力太小，容易导致连接不可靠，服役时产生振动松弛、结构滑移等现象。

扭矩法是目前主流的螺栓预紧力控制方法，即对螺栓施加一个确定的扭矩值，间接控制预紧力的大小，但是在实际装配过程中，受摩擦系数不确定性和弹性相互作用的影响，即使施加相同的扭矩也可能导致±30%的预紧力偏差^{[ [4]  MIAO R S, SHEN R L, ZHANG S H, et al. A review of bolt tightening force measurement and loosening detection[J]. Sensors, 2020, 20(11): 3165.
[5]  LIU Z F, ZHENG M P, YAN X, et al. Changing behavior of friction coefficient for high strength bolts during repeated tightening[J]. Tribology International, 2020, 151: 106486.
[6]  GONG H, LIU J H, DING X Y. Calculation of the effective bearing contact radius for precision tightening of bolted joints[J]. Advances in Mechanical Engineering, 2016, 8(9): 1687814016668445.
4-6 ]}。螺栓预紧力直接测量方法包括光纤光栅、应变计、超声波等。

光纤光栅法主要根据布拉格波长的相对位移来测量螺栓预紧力^{[ [7]  REN L, FENG T Z, HO M, et al. A smart “shear sensing” bolt based on FBG sensors[J]. Measurement, 2018, 122: 240–246.
7 ]}，早在1999年，Hay^{[ [8]  HAY A D. Bolt, stud or fastener having an embedded fiber optic Bragg grating sensor for sensing tensioning strain: US5945665A[P]. 1999–08–31.
8 ]}首次提出将光纤光栅传感器嵌入螺栓内部以测量其应变，试验结果表明，在线弹性范围内该方法能够精确标定预紧力大小。此后，学者们通过研究将光纤光栅传感器嵌入螺栓体内，制成“智能螺栓”^{[ [9]  GUO Y X, HU Z, XIONG L, et al. Fiber Bragg grating based quasi-distributed bolt force sensor with torque resistance[J]. Measurement, 2022, 195: 111063.
[10]  LIANG M F, SONG Y, FANG X Q, et al. Structural design and application of desensitized FBG force-measuring bolt[J]. Sensors, 2022, 22(10): 3930.
[11]  DUAN C, ZHANG H Y, LI Z S, et al. FBG smart bolts and their application in power grids[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(5): 2515–2521.
9-11 ]}，或将光纤光栅传感器与垫圈结合，制成“智能垫圈”^{[ [12]  CHEN D D, HUO L S, LI H N, et al. A fiber Bragg grating (FBG)-enabled smart washer for bolt pre-load measurement: Design, analysis, calibration, and experimental validation[J]. Sensors, 2018, 18(8): 2586.
[13]  YEAGER M, WHITAKER A, TODD M. A method for monitoring bolt torque in a composite connection using an embedded fiber Bragg grating sensor[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(3): 335–344.
12-13 ]}等。应变计法是将应变计粘贴在螺杆表面或螺栓内孔表面，通过应变计在拉伸作用下的电阻变化测量预紧力大小^{[ [14]  NIKRAVESH S M Y, GOUDARZI M. A review paper on looseness detection methods in bolted structures[J]. Latin American Journal of Solids and Structures, 2017, 14(12): 2153–2176.
[15]  张忠伟, 王峻青, 史雄飞, 等. 植入应变片式智能螺栓预紧力测量系统的研究与应用[J]. 质量与可靠性, 2020(3): 31–34.ZHANG Zhongwei, WANG Junqing, SHI Xiongfei, et al. Research and application of inserted intelligent bolt pre-tightening force measurement system implanted with strain gauge[J]. Quality and Reliability, 2020(3): 31–34.
14-15 ]}。滕林斌等^{[ [16]  滕林斌, 雷浩帆, 饶春芳, 等. 基于结构振动–光纤声导波传感的无损检测系统: CN217980727U[P]. 2022–12–06.TENG Linbin, LEI Haofan, RAO Chunfang, et al. Nondestructive testing system based on structural vibration-‌guided-wave fiber acoustic sensing: CN217980727U[P]. 2022–12–06.
16 ]}研发悬挂式光纤光栅，测量小尺度轻量连接结构的预紧力；Wang等^{[ [17]  WANG T, TAN B H, LU G T, et al. Bolt pretightening force measurement based on strain distribution of bolt head surface[J]. Journal of Aerospace Engineering, 2020, 33(4): 04020034.
17 ]}应用有限元方法分析了应变计在不同预紧力作用下的应力–应变状态，仿真结果表明，径向应变和螺栓预紧力之间存在良好的线性关系，在此基础上，设计并制作了一种粘接在螺栓头表面的预紧力传感器。

为了获得高精度的预紧力测量，通常需要在螺栓内部开槽，并将光纤光栅和应变计粘贴在内孔表面，但这容易降低螺栓的疲劳强度。超声波法直接将超声探头粘贴在螺栓头表面，利用超声波飞行时间差和预紧力之间的线性关系，精确测量预紧力大小^{[ [18]  徐晓, 姜涛, 靳超, 等. 基于超声波的高强螺栓轴力检测技术研究[J]. 电子测量与仪器学报, 2024, 38(12): 163–172.XU Xiao, JIANG Tao, JIN Chao, et al. Research on ultrasonic-based axial force detection technology for high-strength bolts[J]. Journal of Electronic Measurement and Instrumentation, 2024, 38(12): 163–172.
[19]  LIU Y M, LIU E X, CHEN Y L, et al. Measurement of fastening force using dry-coupled ultrasonic waves[J]. Ultrasonics, 2020, 108: 106178.
[20]  HUANG J Y, LIU J H, GONG H, et al. A comprehensive review of loosening detection methods for threaded fasteners[J]. Mechanical Systems and Signal Processing, 2022, 168: 108652.
18-20 ]}。在实际应用时很多因素都可能影响预紧力的测量精度，相关学者进行了深入研究。其中，Pan等^{[ [21]  PAN Q X, PAN R P, CHANG M L, et al. A shape factor based ultrasonic measurement method for determination of bolt preload[J]. NDT & E International, 2020, 111: 102210.
21 ]}提出了形状因子模型，消除了非均匀轴向应力对测量结果的影响；Sun等^{[ [22]  SUN Q C, YUAN B, MU X K, et al. Bolt preload measurement based on the acoustoelastic effect using smart piezoelectric bolt[J]. Smart Material Structures, 2019, 28(5): 055005.
22 ]}提出了一种考虑理论误差和测量误差的超声预紧力测量模型，同时，开发的智能螺栓消除了耦合剂的影响；何宇琪等^{[ [23]  何宇琪, 涂莹谦, 芶俊轶, 等. 基于多频段加权能量衰减系数的螺栓轴向应力超声测量方法[J]. 无损检测, 2024, 46(12): 13–19, 33.HE Yuqi, TU Yingqian, GOU Junyi, et al. Ultrasonic measurement method for axial stress in bolts based on the multi-frequency weighted energy attenuation coefficient[J]. Nondestructive Testing, 2024, 46(12): 13–19, 33.
23 ]}提出了基于多频段加权能量衰减系数的螺栓轴向应力测量方法，显著提升了预紧力测量精度。

搭建超声波预紧力测量系统，实现工程应用是未来的发展趋势，当前，法国SOFRATEST公司、德国Kraut–Kramer公司在超声测量的应用方面处于先进水平^{[ [24]  PETROVIĆ I, SAMARDŽIĆ I, STOJKOV M. Determination of wagonaxels quality by NDT methods[J]. HDKBR INFO Magazin, 2017, 7(1): 8–12.
24 ]}。国内也做了相关探索，例如，刘家斌等^{[ [25]  刘家斌, 王雪梅, 倪文波. 螺栓轴向应力–超声波渡越时间自动标定系统研究[J]. 中国测试, 2020, 46(3): 91–96.LIU Jiabin, WANG Xuemei, NI Wenbo. Research on automatic calibration system of bolt axial stress–ultrasonic time of flight[J]. China Measurement & Test, 2020, 46(3): 91–96.
25 ]}研制了超声波飞行时间与螺栓轴向应力的自动化标定试验系统，可以快速实现螺栓的标定试验；庞松^{[ [26]  庞松. 基于超声波的风电机组多螺栓应力在线监测研究[D]. 成都: 西南交通大学, 2021.PANG Song. Research on on-line monitoring of multi-bolt stress of wind turbine based on ultrasonic wave[D]. Chengdu: Southwest Jiaotong University, 2021.
26 ]}开发了基于超声波的风电机组多螺栓应力在线监测系统。但是，目前仍然缺少将超声波生成、发射、接收、飞行时间差精确计算等过程进行集成的解决方案，尚无便携式螺栓预紧力测量系统。

本文基于声弹性理论，建立了螺栓预紧力精确测量模型，优化设计基于高压尖脉冲的超声波发射电路，提出通过时间数字转换芯片粗计算与精计算相结合对螺栓内超声波飞行时间进行精确测量的方法，并搭建超声波飞行时间测量的软硬件系统，最后，对搭建的超声波精确测量系统进行标定试验，分析并验证了该系统的测量精度。

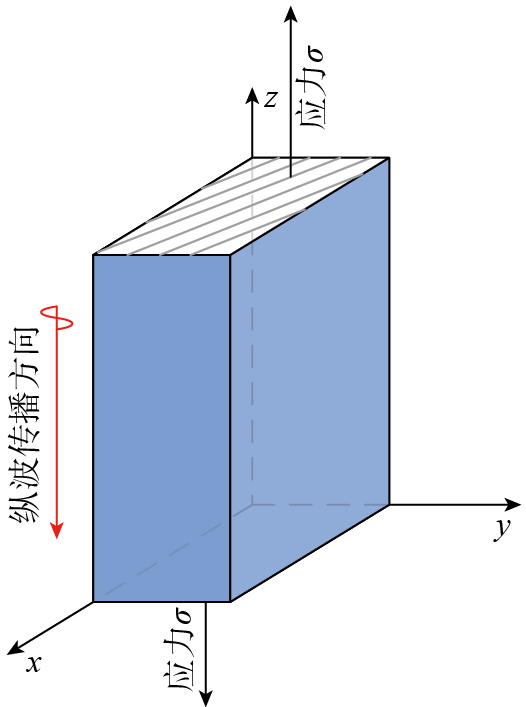
声弹性效应是指超声波在弹性介质中传播时，其声速等传播特性随介质应力、应变状态变化的现象，介质应力变化导致内部质点间的相互作用力和平衡位置改变，介质弹性常数变化，进而影响超声波的传播速度。以纵波为例，如图1所示，在材料内部z轴方向存在应力场，纵波沿z轴传播，其传播速度的计算如下^{[ [27]  SMITH R T. Stress-induced anisotropy in solids—The acousto-elastic effect[J]. Ultrasonics, 1963, 1(3): 135–147.
27 ]}。

式中，ρ₀为介质密度；V_Lσ为沿应力方向传播的纵波波速；σ为螺栓轴向应力；λ、μ为二阶弹性常数；l、m为三阶弹性常数。

无应力状态下的纵波波速V_L0可以表示为

将式（2）代入式（1）得到

在均匀各向同性介质中，超声纵波的传播路径与所受应力方向一致时，波速的一阶展开可以表示为

式中，A₁为声弹性系数，其数学表达式为

如图2所示，将超声波换能器通过耦合剂放置在螺栓头端面，产生超声波信号，并实现反射信号接收。在未施加预紧力时，超声波在螺栓内的传播路径总长L_h包括3个主要部分：螺栓头长度L₁、无应力夹紧长度L_σ0及无应力螺杆长度L_c0^{[ [28]  YUAN B, SUN W, WANG Y Q, et al. Study on bolt preload measurement: An error compensation model for ultrasonic detection based on solid coupling[J]. Measurement, 2023, 221: 113484.
28 ]}，即

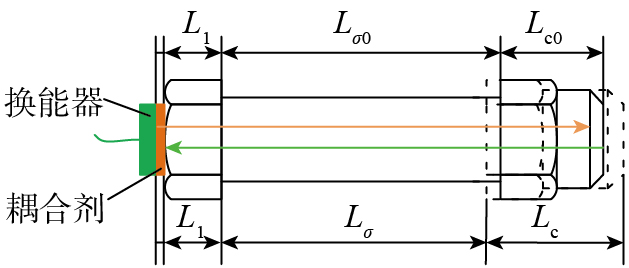
图2中，虚线表示施加预紧力后螺栓的伸长示意图，此时螺栓长度发生变化，超声波的传播路径L_H表示为

式中，L_σ为施加预紧力时的有应力夹紧长度；L_c为施加预紧力时的螺杆长度。

进一步地，根据胡可定律可以计算L_σ，即

式中，E为螺栓的弹性模量。

联立式（4）、（7）和（8），则超声波在有预紧力的螺栓中传播时，飞行时间t（σ）的计算如下。

对上式进行一阶泰勒展开，得到

初始无应力状态下的飞行时间为

因此，超声波在有无预紧力的螺栓内传播时，飞行时间的变化量Δt可以表示为

式中，F_S为螺栓预紧力；S_e为螺栓的有效面积；Δt₁为泰勒展开的高阶计算误差。当忽略高阶计算误差时，螺栓预紧力和飞行时间差近似呈线性关系，即

式中，k为标定系数，可以通过标定试验获得。因此可知，在假设温度和耦合剂厚度不变的情况下，标定系数与有效面积、夹持长度和材料的弹性模量等相关。

图3展示了超声波螺栓预紧力测量的整体方案设计。首先，为了满足超声波的高频要求，设计脉冲激励电路，通过控制电容充电后的瞬间放电来产生高压尖脉冲，激励超声波换能器，同时设计发射、接收切换电路来避免高压脉冲对后级电路的影响。其次，利用示波器观察微小回波信号质量，通过高带宽芯片AD603的二级级联，充分发挥每级的放大功能，将微弱信号放大。进行飞行时间的精确测量时，放大的回波信号仍无法有效触发时间数字转换芯片，设计高速比较电路将回波信号转化为标准电平信号以有效触发，通过时间数字转换芯片粗计算与精计算相结合的方法进行飞行时间的测量。最后，在万能拉伸机上进行飞行时间差和预紧力的标定试验，验证所提方法的可靠性，将飞行时间差转化为预紧力大小，并在显示屏上显示。

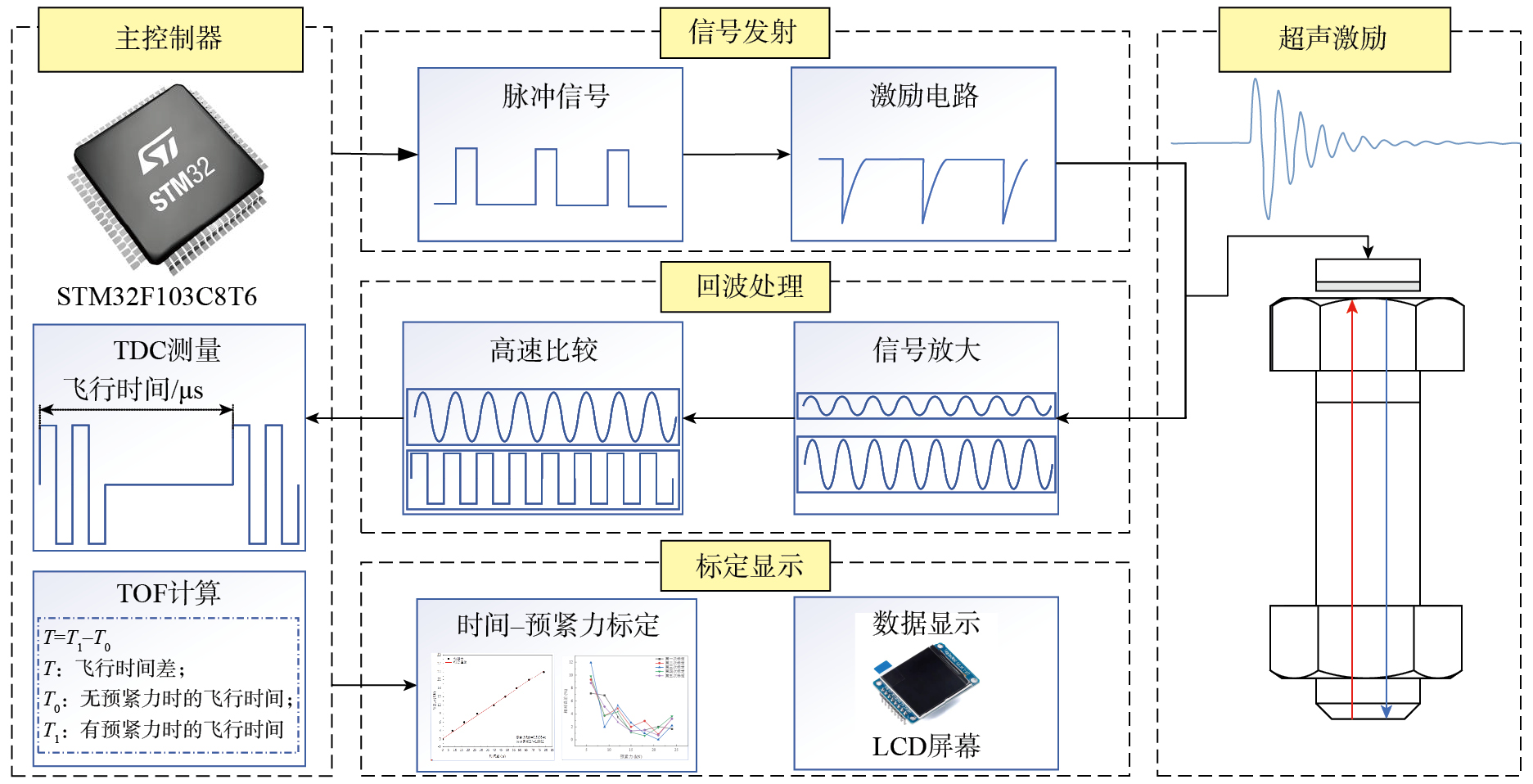
时间数字转换芯片广泛应用于超声流量计、超声燃气表等产品中，测量时间间隔的精度达到ps级。超声波在螺栓内的飞行时间为μs级，因此使用该芯片完全能满足精度要求。本文方案创新性地将时间数字转换技术应用在螺栓预紧力超声波飞行时间的测量中，经过高速比较的超声波信号触发TDC芯片完成超声波飞行时间测量，相比于传统方案（采集超声信号后再传输上位机，使用互相关算法计算超声波飞行时间），使用硬件级时间测量技术取代软件算法，无需高采样及高性能上位机传输，可直接求得超声波飞行时间，精度较高，具有成本低、体积小、便携性强等优点。

常见的换能器激励方式有方波脉冲和尖脉冲两种，方波脉冲激励可以获得较大的激发能量和较强的回波信号幅度，提高超声脉冲的幅度和穿透能力，而尖脉冲具有更好的分辨率^{[ [29]  詹绍正, 杨鹏飞, 王丹, 等. 超声波激发参数对检测结果的影响[J]. 环境技术, 2021, 39(5): 143–148.ZHAN Shaozheng, YANG Pengfei, WANG Dan, et al. The influence of ultrasonic excitation parameters on inspection results[J]. Environmental Technology, 2021, 39(5): 143–148.
29 ]}。螺栓为不锈钢金属材料，适合采用尖脉冲激励方式。本文所设计的超声波发射电路原理图如图4所示，包括高压电源、栅极驱动器等关键器件。其中，U1为栅极驱动器；U2为N型MOSFET；R1~R4为电阻；D1、D2为二极管。高压电源选用WRH12100，将锂电池的12 V电压转为系统所需的100 V高压，栅极驱动器选用UCC27517A，增强控制脉冲使达到完全驱动场效应管（MOSFET）的目的。发射电路工作过程分两阶段：第1阶段，MOSFET关断，外部电源经限流电阻给电容C0充电，电压升至近电源值，储备尖脉冲生成能量；第2阶段，控制信号高电平时，MOSFET导通，电容C0经MOSFET和换能器放电，在换能器两端产生负高压脉冲。单脉冲驱动电路靠电容的充放电实现能量转换与控制，而MOSFET快速开关特性可实现电容C0的短时间放电，产生高斜率、高幅值脉冲。

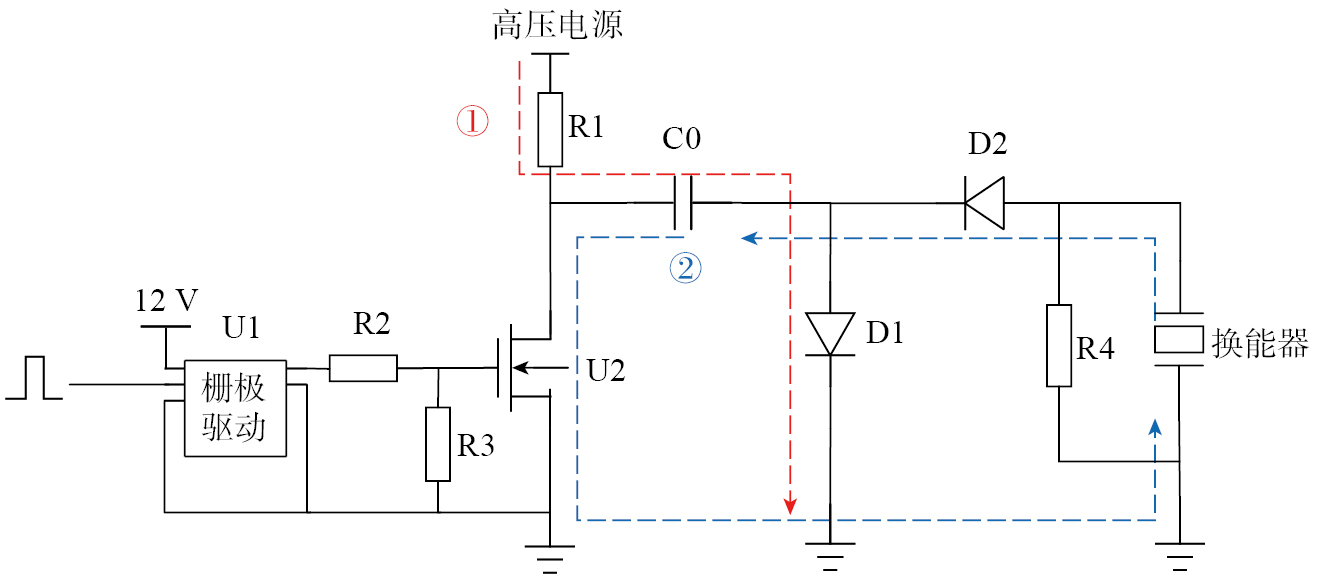
对控制脉冲作傅里叶变换，进行频域分析，其频谱能量分布存在0点，换能器谐振频率与零点频率相同时，会降低驱动效率。0点位置与脉冲宽度相关，信号能量集中于首个0点内，此时满足如下条件。

式中，f为压电换能器中心频率；τ为脉冲宽度。

当驱动脉冲的角频率低于首个0点对应的角频率时，驱动效果最佳。根据式（15）计算可知，脉冲宽度需控在0.1 μs内，但在实际实现时非常困难。因此，将中心频率对应的角频率取在偏离直流信号一定角频率的第一个峰值3π/τ处，即

式中，f₀为换能器中心频率。

对于5 MHz的换能器，按照上式计算出脉冲宽度为300 ns。在确保不造成回波信号混叠的情况下，重复频率应尽可能高，以提升测量效率，因此选择2 kHz的重复频率。在充电过程中，电容两端电压的变化由一阶电路理论得到，即

式中，U_C0为电容两端的电压；V_DC为电源电压。在电容放电过程中，其两端电压近似等于直流电源的供电电压。此时，放电电流的主要通路由阻尼电阻和超声换能器构成。改变阻尼电阻的阻值可以改变激励换能器的强度，从而改变测量的灵敏度，进一步有

式中，R_T为超声波换能器谐振时的等效阻抗。

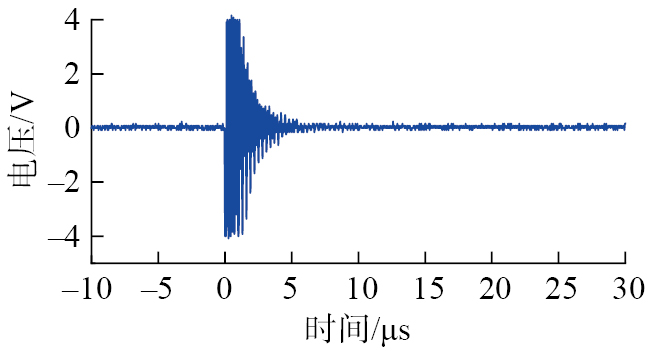
经上述理论推导，最终确定电容C₀为1 nF，取电阻R₄的阻值与换能器谐振阻抗相等（100 Ω）。对设计的超声波发射电路进行测试，如图5所示，可以看出，5 MHz换能器的激励效果良好。

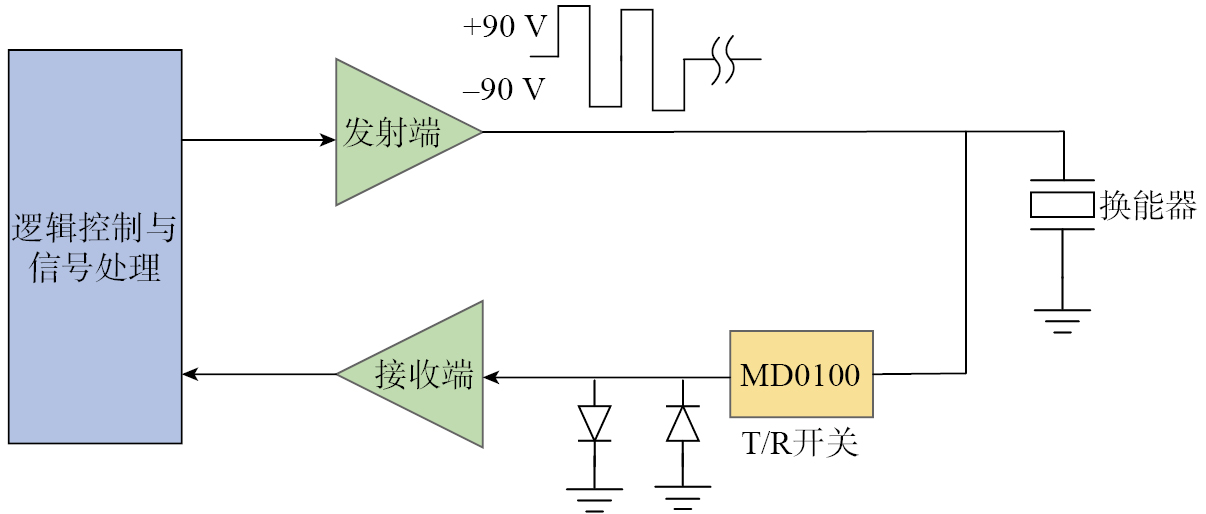
本文所用超声换能器可自发射、自接收，为防止发射信号干扰接收电路，设计了发射、接收切换电路，以保障回波信号顺利传输，隔离高压脉冲，并阻断负高压尖脉冲对后级放大电路的影响。传统的发射、接收切换电路抗干扰性能不足，常规模拟开关的导通电阻大、寄生电容高，容易导致回波信号畸变从而影响飞行时间测量。采用MD0100超声专用T/R开关（微芯公司），可承受±100 V电压。当压降超过±2.0 V时关闭，换能器激励尖脉冲峰值为80 V，在安全范围内，此条件下仅允许200 µA电流通过，避免了信号串扰，应用场景见图6。

超声波穿过螺栓反射回来以后，信号将大幅衰减，为了准确计算超声波飞行时间差，设计以AD603为核心搭建的放大电路，对微弱的回波信号进行放大。AD603是压控放大器，具有低噪声、高增益、宽带宽，且能线性调节增益等优点，有3种工作模式，本文采用–10~30 dB模式，增益计算如下。

式中，G为增益；V_G为GPOS引脚和GNEG引脚的电压差。

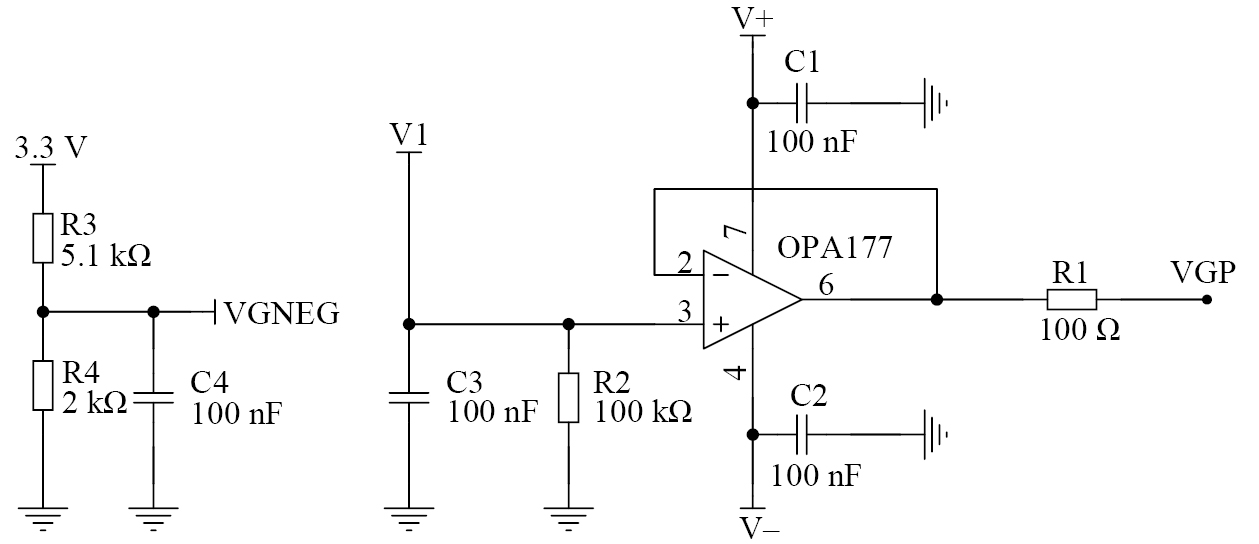
增益控制电路如图7所示，电阻R3和R4分压后接AD603的GNEG引脚，使得GNEG引脚电压保持在0.93 V，达到增益控制电压为正的目的，此时，0.43~1.43 V的控制电压对应–20~60 dB的增益。增益控制电压V1经OPA177缓冲后接GPOS引脚，AD603增益由两引脚的电压差控制。

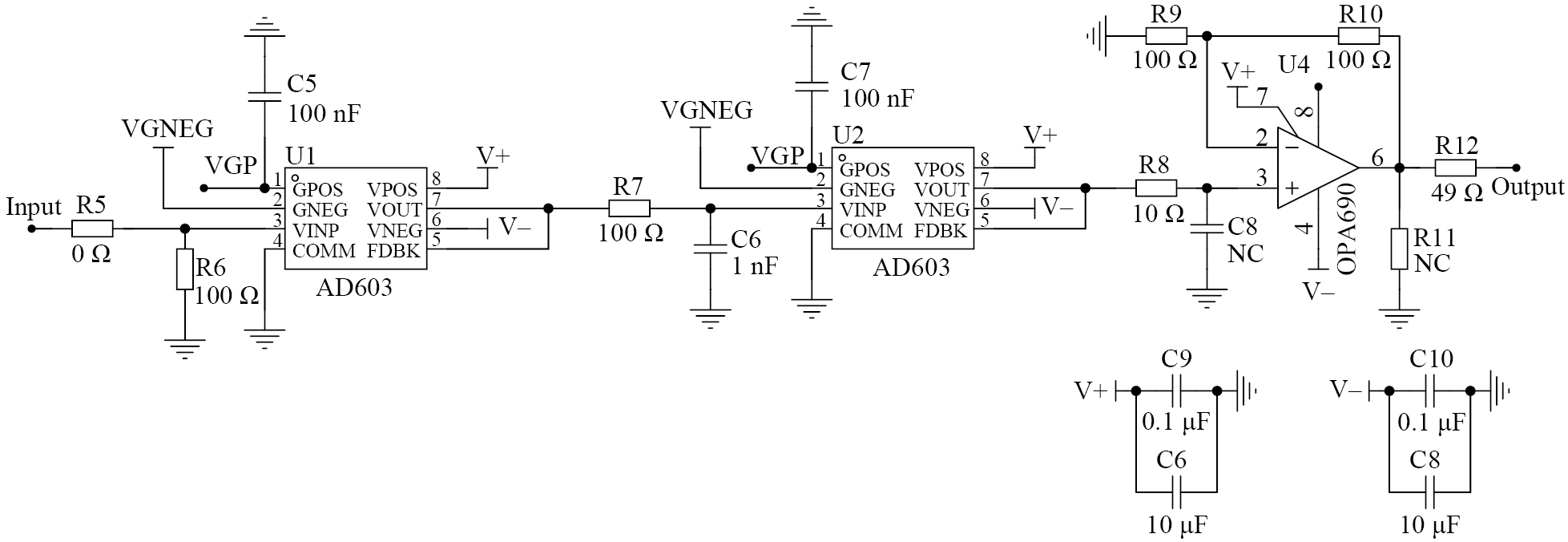
整个放大电路为三级架构，使用两片AD603级联构建信号放大电路，设计如图8所示，前两级采用AD603，工作范围为–10~30 dB。通过第1级VOUT输出接第2级VINP输入，级联提升性能，第3级采用OPA690，增益放大2倍，可抵消前面的衰减，此时电路增益的调节范围扩至–20~60 dB。

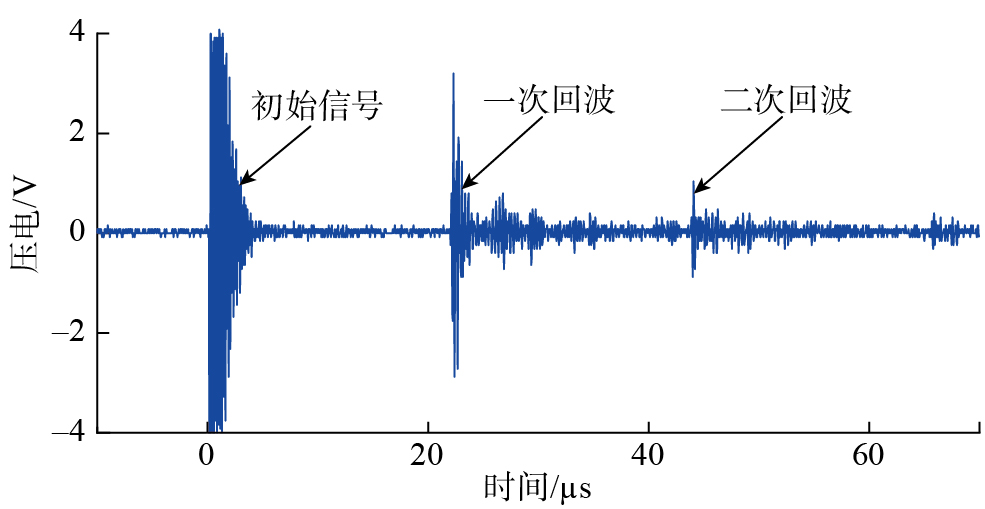
将放大电路应用在超声波发射电路中，在螺栓表面和换能器之间涂抹耦合剂，将换能器放置在螺栓表面，通过示波器观察回波信号，调节增益，并观察回波信号的变化，如图9所示，可以明显观察到一次回波与二次回波，而且增益越大，回波信号越明显。

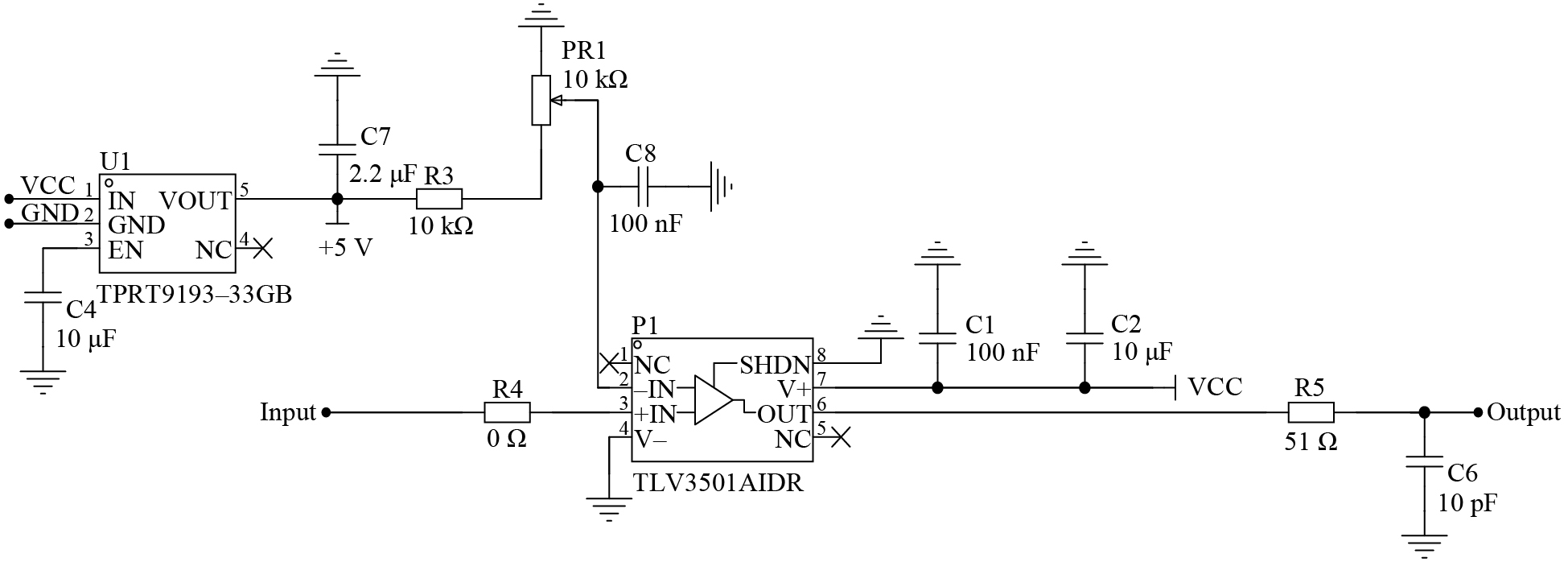
为了计算飞行时间，需要对信号发射和接收时刻进行计时，采用时间数字转换芯片，在开始计时与终止计时利用标准电平触发。但放大的回波信号无法触发停止计时，因此设计高速比较电路，如图10所示，将超声回波信号转换为TTL电平。选用TLV3501芯片（美国德州仪器），其轨至轨的推挽输出满足TTL接口要求，120 MHz的带宽远超超声信号频率，保证了信号处理的实时准确。比较器输出接TDC–GP22计时端口，工作电压为2.7~5.5 V，与5 V电源兼容。此外，本文采用同相比较模式，利用回波上升沿触发测量。

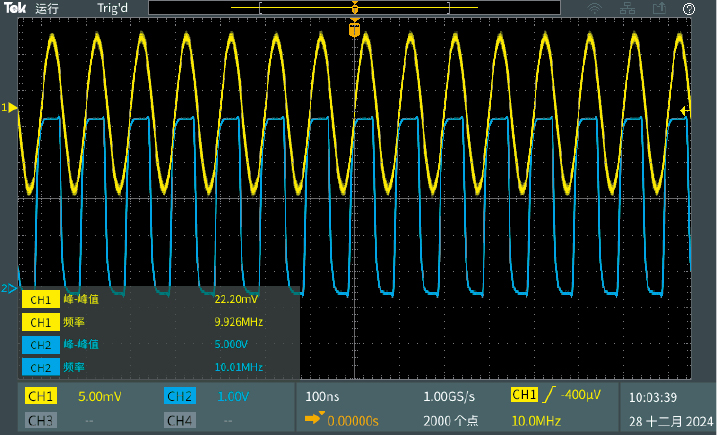
对高速比较电路进行超声信号测试，如图11所示。其中，通道1（CH1）为10 MHz的超声信号，通道2（CH2）为超声波信号经过高速比较后输出的信号，可以看出，超声波经过高速比较电路转换为标准电平信号的转换效果良好。

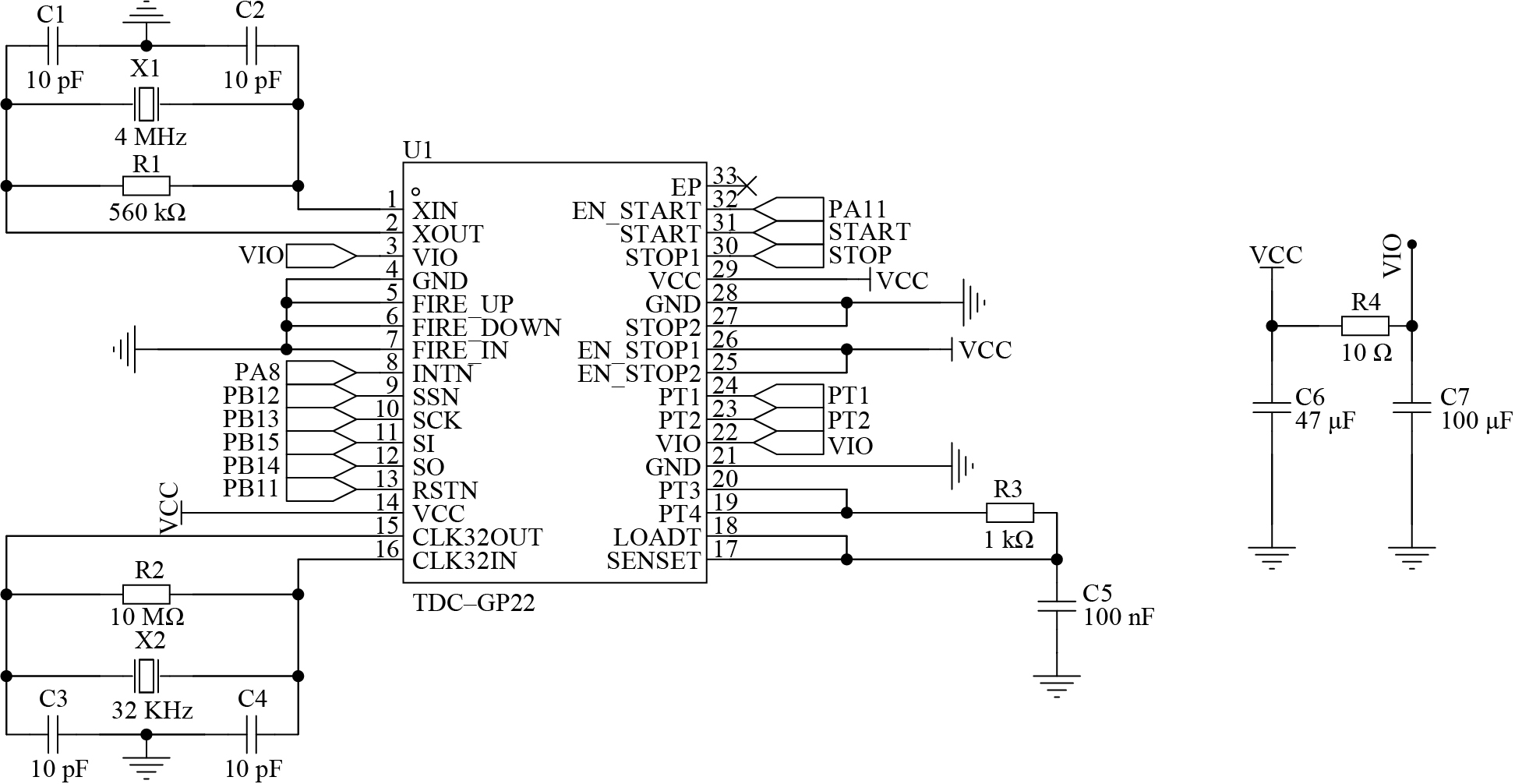
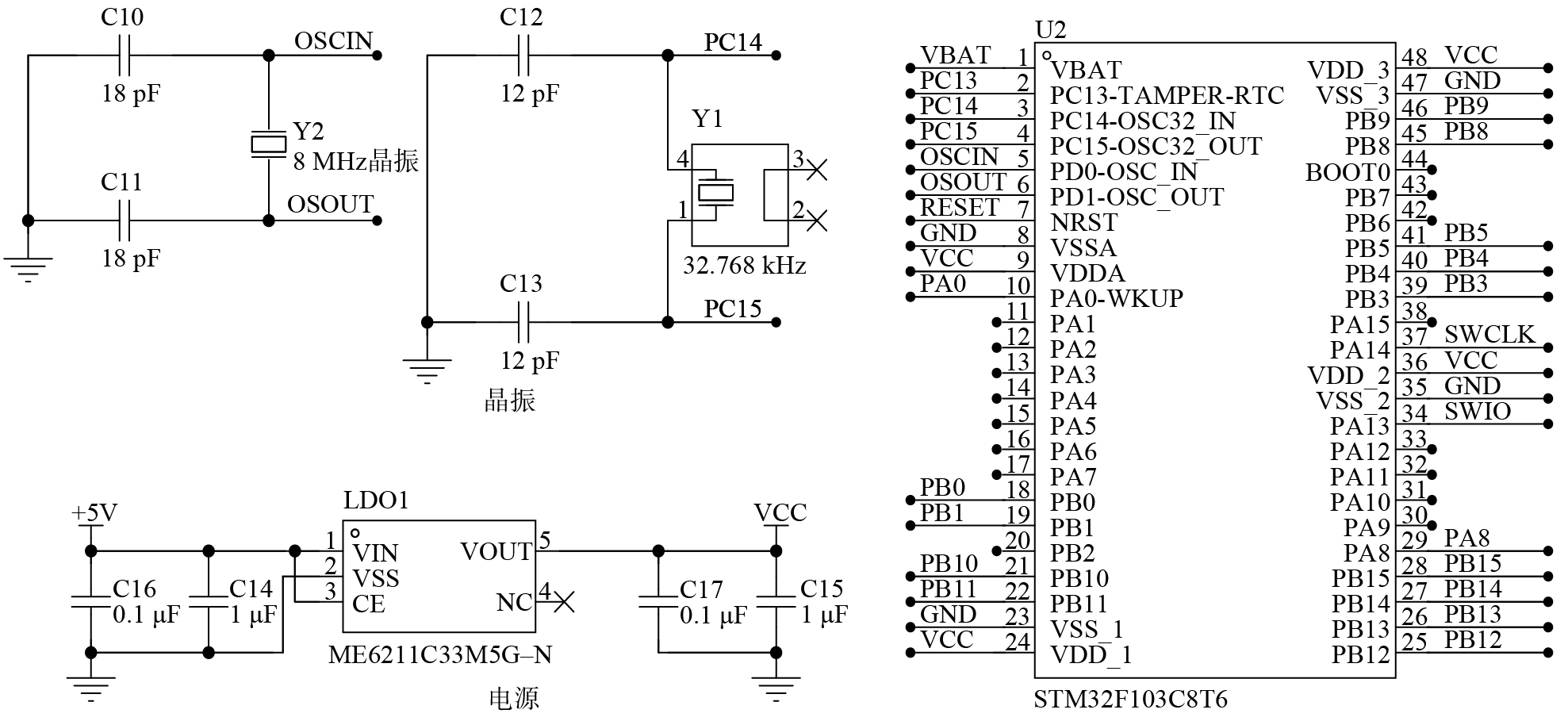
螺栓内超声波飞行时间的精确测量采用微处理器搭配时间数字转换芯片的方案，高精度时差测量芯片TDC–GP22的正常运行依赖两个外部晶振（4 MHz的高速时钟晶振），该晶振具有成本低廉和快速起振的优势，但存在0.3%~0.5%的误差，并且会受到温度漂移的影响。因此，为了实现精确的时钟校准测量，采用1个32.768 kHz的晶振作为测量基准。TDC–GP22的外围电路如图12所示。

STM32F103是意法半导体推出的基于ARM Cortex–M3内核的微处理器，具有丰富的外设接口和高速计算处理能力，将该微处理器与TDC–GP22进行搭配使用。STM32F103C8T6的外围电路如图13所示，通过GPIO引脚对TDC–GP22进行控制，通过SPI通信方式对TDC–GP22的内部寄存器进行读写。

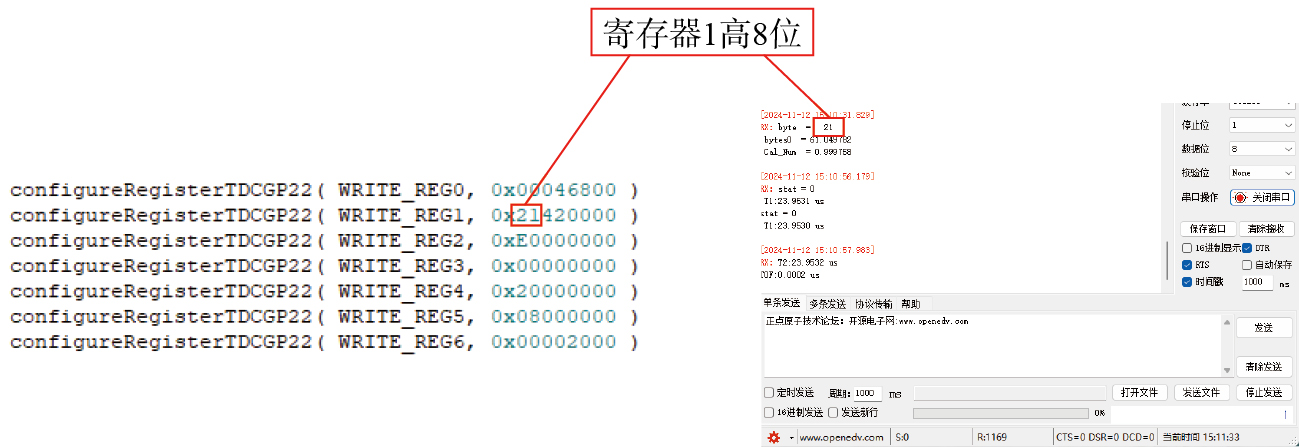
数字式TDC应用内部逻辑门延迟原理进行高精度时间间隔测量，其核心原理是将时间间隔转化为逻辑信号在电路中的传播延迟进行计算。TDC–GP22包含7组32位配置寄存器（表1），其中，高24位用于配置写入，低8位可读写ID。在测量超声波飞行时间时，还需要配置测量范围、时钟等功能。如表1所示，寄存器0关闭Fire端口脉冲功能，时钟不分频，校准周期数设置为0（代表61.035 µs），开启ALU校准，选择测量模式2并配置非反向输入；寄存器1设置HIT2为2，HIT1为1，STOP通道1的脉冲数比实际多1；寄存器2设置STOP屏蔽功能，屏蔽窗口从START信号起，精度为10 ns，使能引脚设置为1，屏蔽时间设置为20 μs，对应寄存器的十六进制值DELVAL1=500；其他寄存器则按需配置。

STM32F103微控制器与TDC–GP22时间数字转换器采用SPI协议通信，其中，STM32F103为主设备，TDC–GP22为从设备。SPI使用MOSI、MISO、SCK和CS四线通信，其中CS在低电平时激活通信。通信前，STM32F103进行SPI外设的初始化，配置参数与TDC–GP22匹配，设置SPI模式分别为0、8位的数据位宽。通信时，STM32F103拉低CS，经MOSI发出指令和数据，TDC–GP22经MISO返回数据，STM32F103可读取测量数据、写入配置数据，通信结束，STM32F103拉高CS。发送操作码0xB5读取REG_1（寄存器1）的测试通信，若读取值与配置寄存器1的高8位一致，表明通信成功，测试结果见图14。

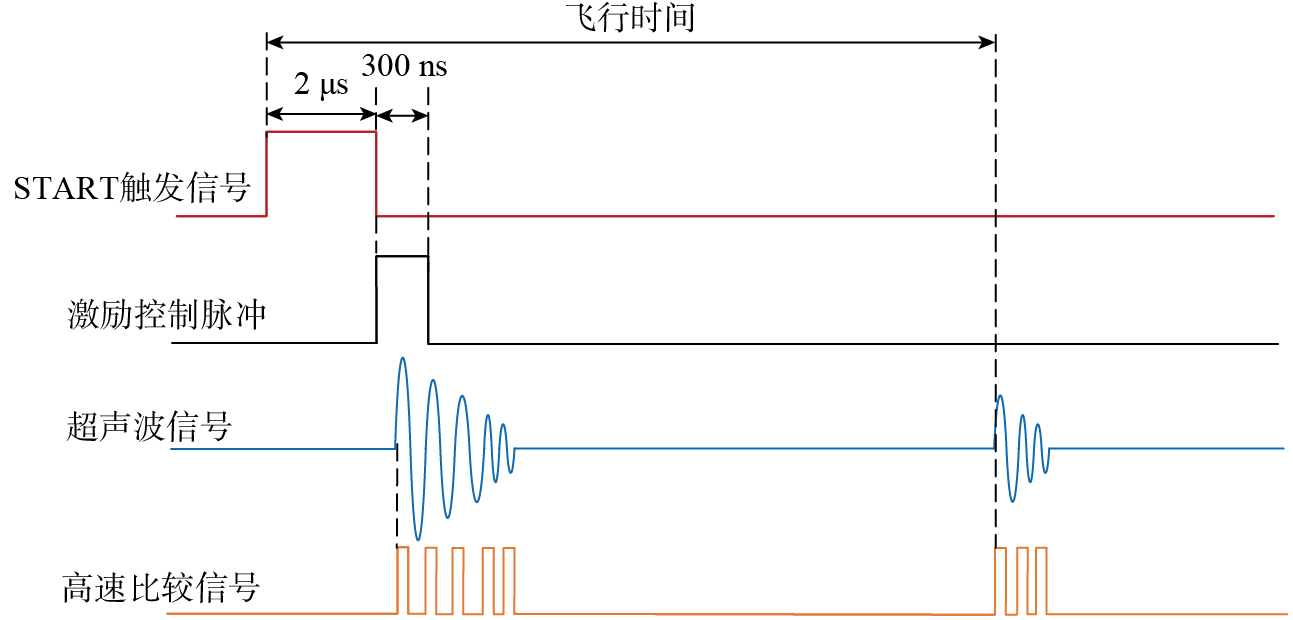
超声波飞行时间测量系统采用TDC–GP22芯片的STOP屏蔽功能提升精度与稳定性，为了实现抗干扰、防误触发的目的，芯片起始、终止引脚设置为上升沿触发，可屏蔽STOP1通道的触发，以START信号为起点，设置屏蔽时间为20 μs。系统寄存器的HIT数设置为2，即首个回波信号作为STOP的触发信号，启用STOP屏蔽功能，确保屏蔽时间之后的触发信号后才可以触发结束计时引脚。系统开始计时，引脚接外部脉冲，结束时，引脚接高速比较后的方波信号。启用STOP屏蔽功能需要3个时钟周期时间，因晶振为4 MHz，所以启动时间为750 ns，即750 ns内如有结束计时信号，仍会结束计时。

若以控制脉冲作为TDC的开始计时信号，此时STOP屏蔽功能未成功启用，则超声波初始信号经高速比较后会被误判为STOP信号，输入STOP1通道，使得计时提前停止。为了顺利启用STOP屏蔽功能，将START引脚启动信号提前2 μs至激励信号前，脉冲时序设计如图15所示。可以看出，虽然单次测量值会增加2 μs，但飞行时间差通过两次测量差值得到，并不影响最终时间差测量结果。

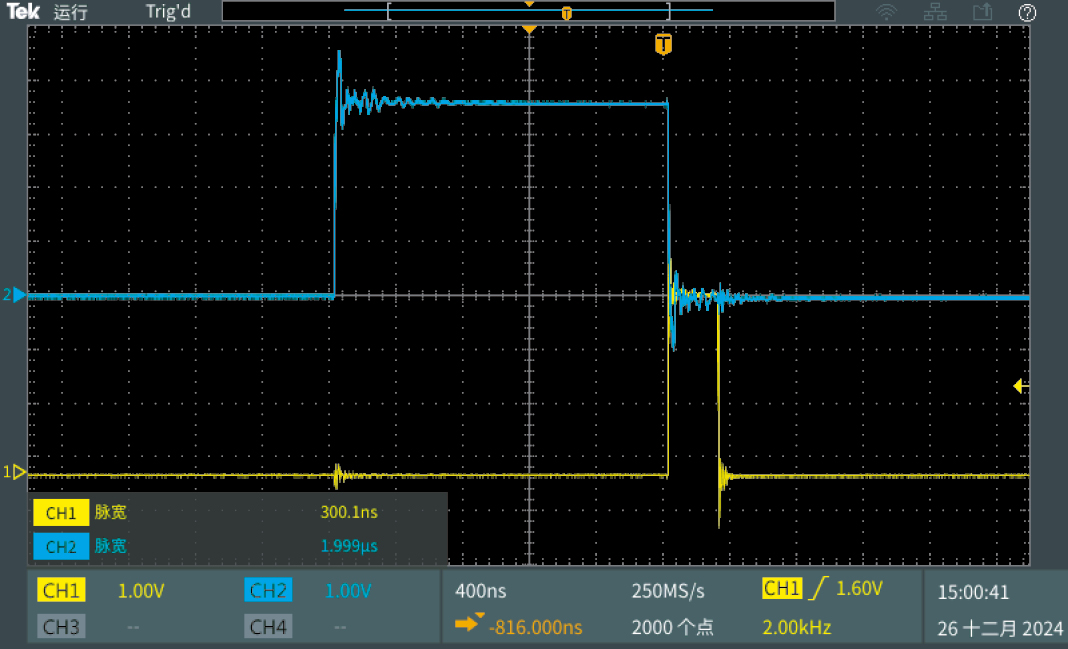
本文基于计数器原理实现脉冲时序控制，需生成300 ns和2 µs脉冲，2 µs脉冲下降沿与300 ns脉冲上升沿对齐，且二者重复频率相同。频率计数器负责生成2 μs可调频率方波，窄脉冲计数器控制生成300 ns方波，2 μs脉冲下降沿触发计数，开始生成300 ns脉冲，计数完成后信号拉低。生成的脉冲时序如图16所示，可以看出，通道1的脉冲宽度为300 ns，通道2的脉冲宽度为2 µs，且通道2上升沿对应通道1的下降沿，时序精准，高效同步。

预紧力测量系统由发射电路、回波信号处理电路（放大电路）、飞行时间测量电路及供电电源集成而成，如图17所示，将超声波发射电路与飞行时间测量模块独立布局，按照信号流向进行器件的拓扑排布，并对模拟/数字地平面实施分区隔离。发射电路使用12 V转100 V的升压电源提供高压；供电电源附近使用电解电容；放大电路通过零欧姆电阻构建低阻抗噪声抑制通道，降低共模干扰；飞行时间测量电路中使用高精度石英晶振，以提升测量系统的稳定性。

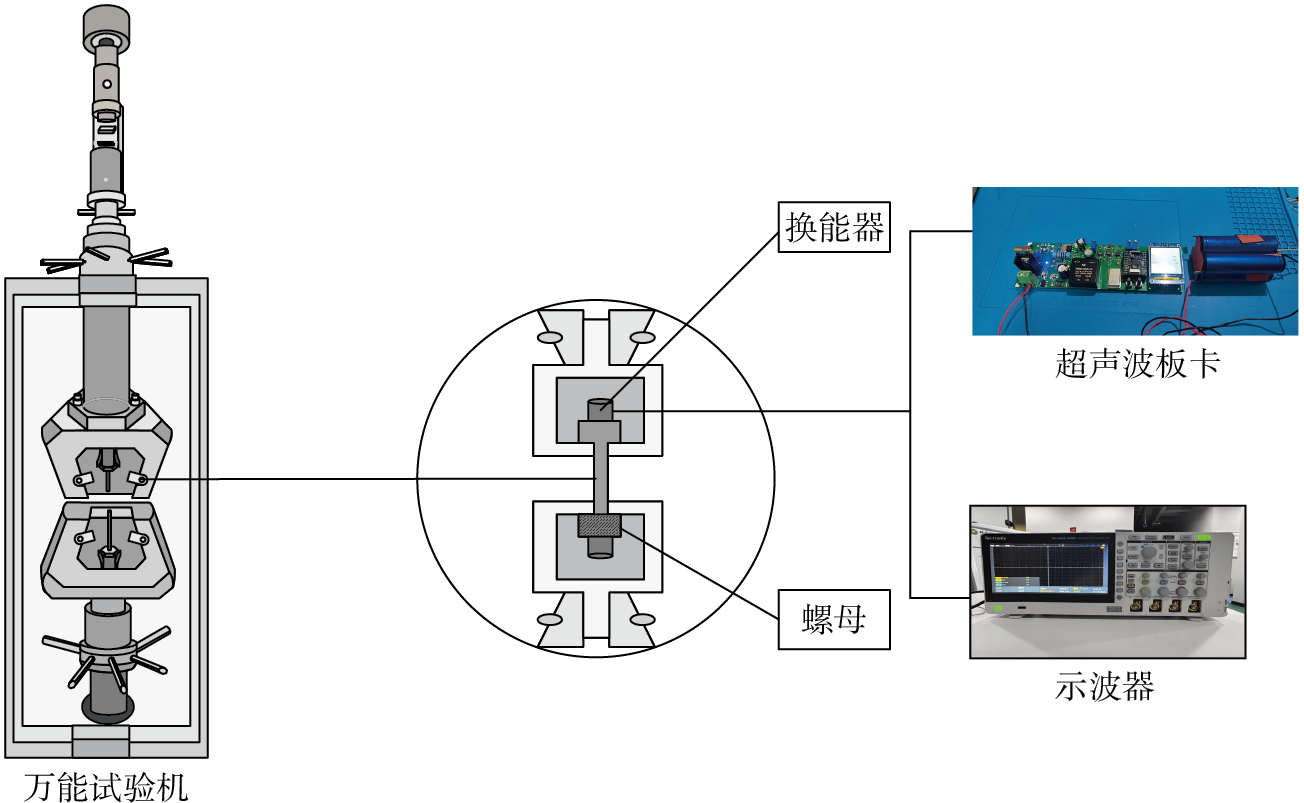
标定试验时各部分硬件连接如图18所示，首先超声波测量板卡由12 V锂电池供电，通过SMA接口连接超声波换能器，示波器通过引脚观察回波信号的稳定性，测得的超声波飞行时间和预紧力数值由LCD显示屏及电脑端串口调试助手显示，万能试验机控制电脑负责控制试验机的具体工作。

为了建立超声波飞行时间差与螺栓预紧力之间的定量关系，采用万能拉伸试验机进行标定试验（图19）。选用A2–70螺栓（M12×50、M14×60、M12×100）和12.9级35CrMo合金钢高强度螺栓（M12×100）作为试验对象。M12和M14属于中等尺寸螺栓，广泛应用于航空航天、车辆等关键连接部位，具有较高的工业普适性。M12不锈钢螺栓应用在通用机械紧固场景中时，标准预紧力为26.5 kN，一般应用场合要求预紧误差为21.2~31.8 kN，即最大不超过标准预紧力的20%；应用于航空内饰紧固时，需要精确预紧、防松，误差要求在24.4~28.6 kN（±8%）以内。M12不锈钢螺栓配套使用的中心频率为5 MHz，直径为8 mm（小于螺栓端面直径），侧方接口的是单晶超声换能器，黏附在螺栓端面的中间位置。采用TBS2074B型示波器（美国泰克）观察回波信号；加载装置选用UTM5504型拉伸试验机（中国三思纵横），量程为50 kN，试验力精度优于1%。

进行标定试验前专门设计并加工了适配工装，由40Cr板材电火花切割加工而成，其硬度指标优于被测螺栓材料，如图20所示，夹具中心孔轴线与拉伸载荷方向严格对中，确保螺栓轴向力的准确施加。选用680厌氧胶（德国乐泰）作为耦合介质，将耦合剂均匀涂覆在换能器表面，进行恒定压力加载直至完全固化，从而降低耦合状态波动引入的测量误差。

标定试验时要确保万能试验机的恒温箱干净整洁、温度稳定，标定环境如图21所示。在标定时，首先调节万能拉伸试验机归零，消除初始应力，采用示波器记录稳定的超声波初始回波信号；随后设置万能拉伸试验机的加载参数，拉伸试件，待拉力稳定60 s后，测量超声波飞行时间；最后，循环加载、测量并记录数据，直到拉力达到预设的总载荷。

使用M12（公称长度50 mm）和M14（公称长度60 mm）螺栓进行标定试验，试验过程中，拉伸机恒温箱温度控制在15 ℃，标定时夹持长度均为30 mm。首先，测量无应力状态下的超声波飞行时间，随后分别采用万能拉伸试验机进行3 kN和5 kN递进拉伸试验，得到超声波在不同拉伸力条件下的飞行时间，并计算飞行时间差，得到螺栓预紧力和飞行时间差的离散数据。M12螺栓分别以3 kN和5 kN递进标定的测量数据如表2和3所示，每个力值进行10次测量，结果取平均值，然后计算不同预紧力状态下与初始状态下的飞行时间差值。

由前述理论模型可知，螺栓预紧力和飞行时间差近似呈线性关系。将测量数据进行线性拟合，得到拟合曲线斜率，如图22和23所示，可以看出，M12和M14螺栓拟合直线的决定系数R²均大于0.99，充分验证了螺栓预紧力和飞行时间差之间的强线性相关性。

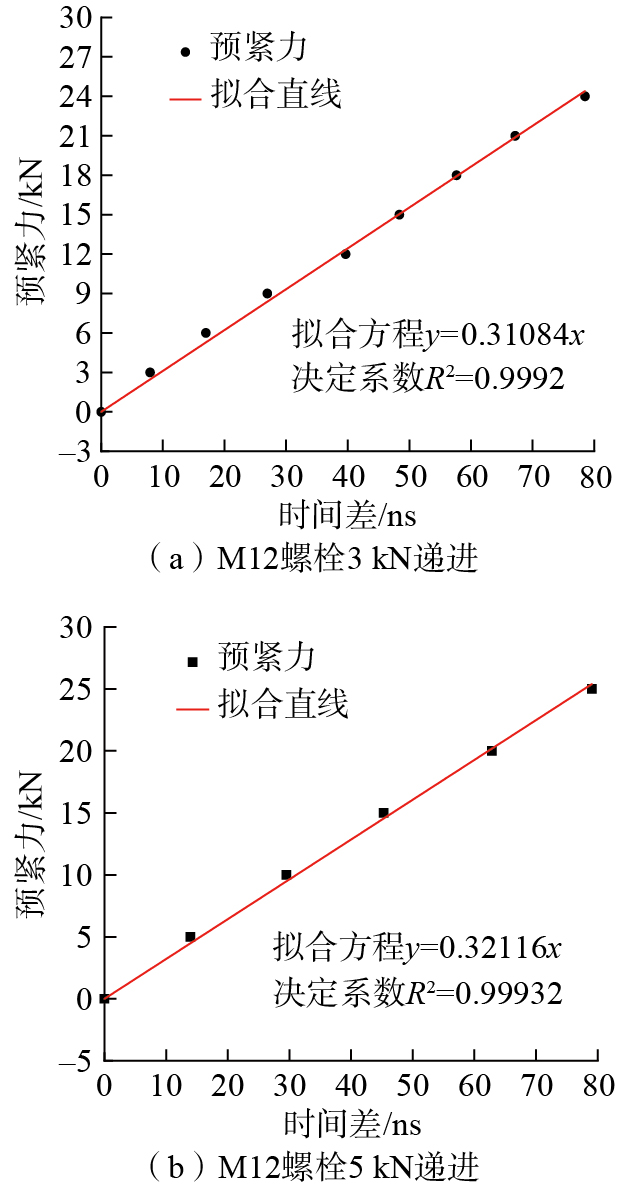
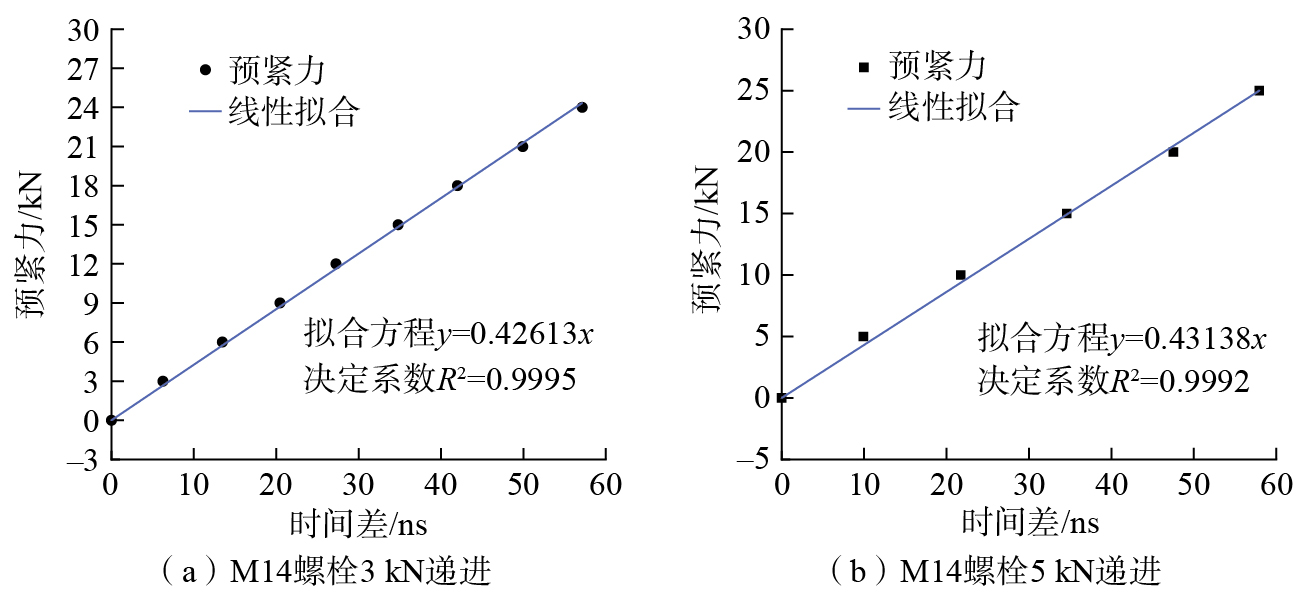
飞行时间测量结果表明，所设计的发射电路效果良好，换能器成功接收到高质量回波信号；经过高速比较电路的超声信号成功触发了时间数字转换芯片，设计的脉冲时序控制提升了系统稳定性，时间数字转换芯片在超声测量预紧力系统中应用良好。标定试验结果表明，相同夹持长度时，M12和M14螺栓的标定系数均值（由图22和23中拟合方程的斜率求得）分别为0.316 kN/ns和0.4288 kN/ns。同种材料的螺栓，在标定完成一种类型螺栓后，其标定系数可根据几何参数进行相互转换，这为批量螺栓的预紧力测量提供了条件。通过理论换算，将M12螺栓的参数转换为M14规格后，得到的标定系数为0.4313 kN/ns，与实测值具有良好的一致性。这一结果验证了标定系数在不同规格螺栓间的可转换性。基于这一特性，当获得某一规格螺栓的标定参数后，可推广应用于同材料系列的其他规格螺栓，扩展超声波预紧力测量技术的适用范围。

使用304不锈钢和12.9级强度35CrMo合金钢螺栓（规格为M12×100）进行标定试验，试验时螺栓夹持长度均为60 mm，标定结果如图24所示，可以看出，2种螺栓拟合直线的决定系数R²仍大于0.99，具有强线性相关性。

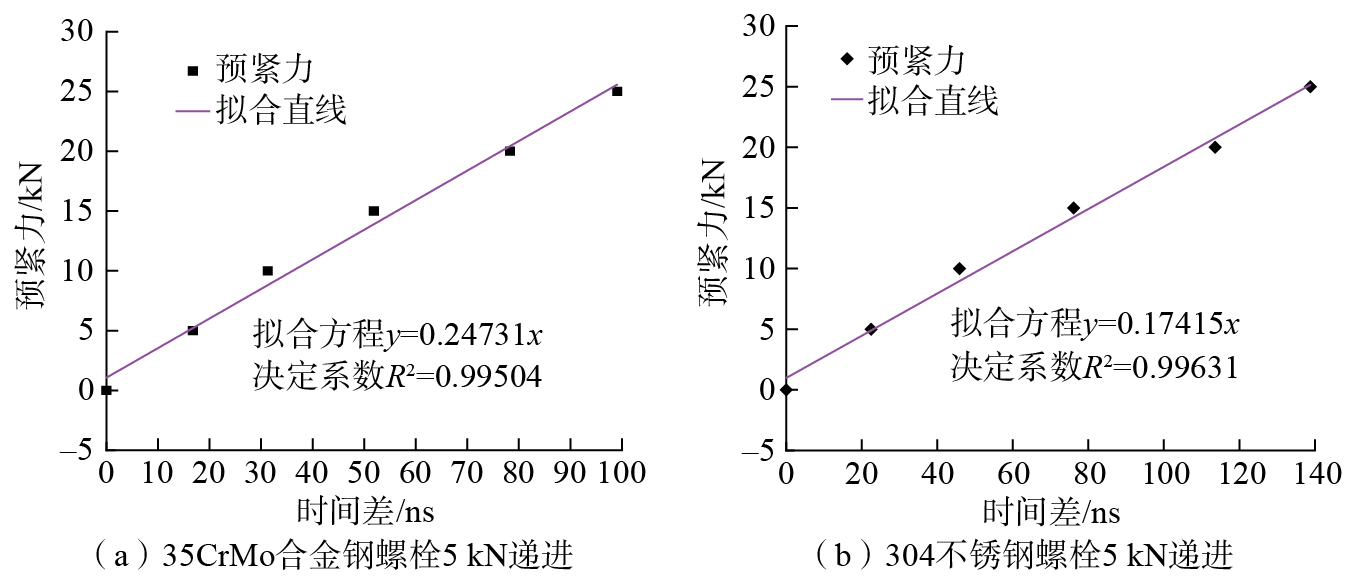
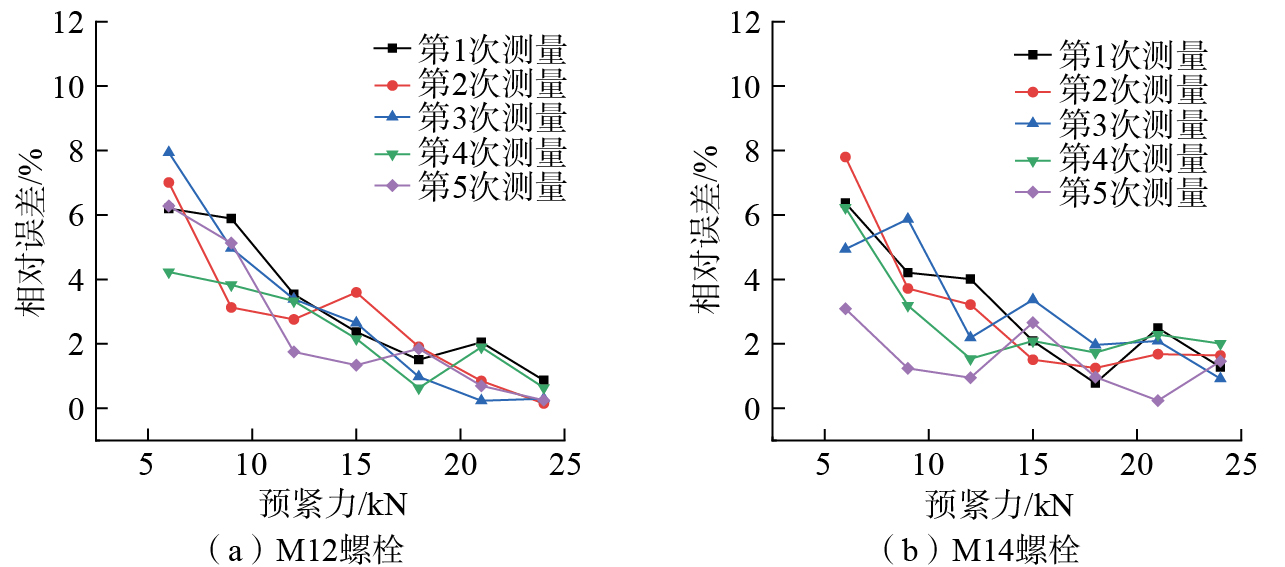
在万能拉伸试验机上对螺栓进行5次重复拉伸试验，采用超声波螺栓预紧力测量板卡测量预紧力，对比测量值与实际值结果，并分析测量结果的相对误差。如图25所示，随着施加预紧力的提升，测量误差范围降低，在预紧力较小时，螺栓拉伸小，测量得到的飞行时间差小，系统恒定的测量误差对实际飞行时间的影响比较显著；但随着预紧力增大，螺栓拉伸量增大，测量的飞行时间差也增大，恒定测量误差的影响变小，因此预紧力测量误差减小。当预紧力小于15 kN时，测量相对误差在2%~8%之间，当施加预紧力大于15 kN时，测量相对误差稳定在5%以下。大量研究结果表明，传统扭矩法的测量误差在10%~30%之间，本文所提超声波螺栓预紧力测量系统的测量误差（±5%）明显小于传统扭矩法的测量误差。

为了解决传统预紧力测量方法精度不高、破坏螺栓本身结构等问题，基于超声波声弹性效应，设计、开发了一套超声波螺栓预紧力精确测量系统，并对其测量精度进行了试验验证，主要结论如下。

（1）基于超声波声弹效应，建立螺栓预紧力和超声波飞行时间差之间的线性关系模型，万能拉伸试验表明二者拟合直线的决定系数大于0.99，充分验证了线性关系模型的可靠性。

（2）提出了使用时间数字转换芯片粗计算与精计算相结合以精确测量螺栓内超声波飞行时间的方法，搭建了超声波飞行时间测量的软硬件系统，设计了脉冲时序使用时间的屏蔽功能，通过提前触发的方式有效提升了系统稳定性，实现了飞行时间的精确测量，为螺栓预紧力精确测量系统小型化、集成化奠定基础。

（3）标定结果分析表明，相同材料M12与M14螺栓的标定系数可根据螺栓有效面积、夹持长度进行相互转换，为批量螺栓预紧力的测量提供了条件。预紧力测量结果的相对误差分析表明，预紧力小于15 kN时，测量相对误差在2%~8%之间，当施加预紧力大于15 kN时，测量相对误差稳定在5%以下。

（4）所研发的系统具有超声法高精度测量的效果，同时兼具小型化、集成化的优势，可为超声波测量螺栓预紧力系统的便携小型化提供参考。未来可针对不同材质（如复合材料、高温合金等）的螺栓预紧力测量开展深入研究，开发适用于特殊工况（如高温、高压、强腐蚀环境）的专用检测系统。