类V型复合材料薄壁件是优化飞机气动性能并保护机翼结构的重要部件。为了确保飞机的气动性能、结构完整性和飞行安全，类V型复合材料薄壁件的加工质量至关重要^{[ [1]  高丽敏, 王浩浩, 杨光, 等. 关于叶片前缘加工缺陷及气动合格性的探讨[J]. 推进技术, 2023, 44(1): 81–90.GAO Limin, WANG Haohao, YANG Guang, et al. Discussion on machining defects of blade leading edge and aerodynamic qualification[J]. Journal of Propulsion Technology, 2023, 44(1): 81–90.
1 ]}。类V型复合材料薄壁件通常是通过热压罐成型工艺制造的复合材料结构件，需要通过机械加工的方法去除多余的尺寸，即切边加工。

石英纤维增强树脂基复合材料具有耐高温、耐烧蚀、抗热震等特性，并具有优良的机械性能和耐恶劣环境能力，已被广泛应用于复合材料结构件的制造中^{[ [2]  王雅娜, 曾安民, 陈新文, 等. 2.5D机织石英纤维增强树脂复合材料不同方向力学性能测试与模量预测[J]. 复合材料学报, 2019, 36(6): 1364–1373.WANG Yana, ZENG Anmin, CHEN Xinwen, et al. Mechanical properties testing for 2.5D quartz fiber reinforced resin composites in different directions and module prediction[J]. Acta Materiae Compositae Sinica, 2019, 36(6): 1364–1373.
[3]  王强, 赵博研, 刘秋寒, 等. 曲面结构石英纤维增强树脂复合材料分层损伤缺陷太赫兹智能检测[J]. 复合材料学报, 2023, 40(3): 1785–1796.WANG Qiang, ZHAO Boyan, LIU Qiuhan, et al. Intelligent detection of delamination defect in curved structural quartz fiber reinforced polymer composites using terahertz technology[J]. Acta Materiae Compositae Sinica, 2023, 40(3): 1785–1796.
[4]  LI H L, LIN B, ZHANG C, et al. Mask-point: Automatic 3D surface defects detection network for fiber–reinforced resin matrix composites[J]. Polymers, 2022, 14(16): 3390.
2-4 ]}。由于类V型复合材料薄壁件属于薄壁零件，加工过程中极易产生振动和变形，影响加工质量。因此，亟须优化类V型复合材料薄壁件的切边加工参数，降低加工过程中的振动和变形，从而提高产品质量。

切削力和工件振动是评价加工系统稳定性的重要指标，间接反映了加工后的工件表面质量。国内外学者对薄壁零件加工过程中的切削力和工件振动进行了深入的研究。冯吕晨等^{[ [5]  冯吕晨, 赵文祥, 颜培, 等. 应用响应曲面法的机器人铣削工艺优化[J]. 制造业自动化, 2023, 45(1): 38–44.FENG Lyuchen, ZHAO Wenxiang, YAN Pei, et al. Optimization of robot milling process using response surface methodology[J]. Manufacturing Automation, 2023, 45(1): 38–44.
5 ]}通过试验研究了主轴转速、进给量、切削深度、铣削方式和走刀方向对切削力、振动加速度和表面粗糙度的影响规律，并建立了切削力、振动加速度和表面粗糙度的二阶预测模型。王建山等^{[ [6]  王建山, 何天宇, 肖聚亮, 等. 镜像铣加工过程中薄壁工件变形和振动的预测[J]. 天津大学学报（自然科学与工程技术版）, 2022, 55(3): 263–272.WNG Jianshan, HE Tianyu, XIAO Juliang, et al. Prediction of deflection and vibration of thin-walled workpiece during mirror-milling process[J]. Journal of Tianjin University (Science and Technology), 2022, 55(3): 263–272.
6 ]}通过仿真研究了大型薄壁工件镜像铣削中，支撑刚度、支撑阻尼、主轴转速和进给速度对薄壁工件变形和振动的影响规律。王荣华等^{[ [7]  王荣华, 汪振华. TC4钛合金铣削力及表面粗糙度分析[J]. 工具技术, 2021, 55(5): 30–33.WANG Ronghua, WANG Zhenhua. Analysis of milling force and surface roughness of TC4 titanium alloy[J]. Tool Engineering, 2021, 55(5): 30–33.
7 ]}通过多因素正交试验，研究了各铣削参数对铣削力及表面粗糙度的影响程度，并建立了铣削力及表面粗糙度的经验预测模型。为了抑制加工过程中的振动，王健等^{[ [8]  王健, 何立东, 杨建江. 基于主动阻尼技术的薄壁件铣削振动控制研究[J]. 机电工程, 2022, 39(2): 262–268.WANG Jian, HE Lidong, YANG Jianjiang. Vibration control of milling thin-walled workpieces based on active damping technology[J]. Journal of Mechanical & Electrical Engineering, 2022, 39(2): 262–268.
8 ]}提出了一种采用主动阻尼装置对带网格薄壁件铣削振动进行抑制的方法，对铣削振动抑制进行了理论推导、仿真分析与试验研究。

响应曲面法可有效寻找试验指标与各因子间的定量规律，找出各因子水平的最佳组合，被广泛应用于预测和优化机械加工中的切削参数^{[ [5]  冯吕晨, 赵文祥, 颜培, 等. 应用响应曲面法的机器人铣削工艺优化[J]. 制造业自动化, 2023, 45(1): 38–44.FENG Lyuchen, ZHAO Wenxiang, YAN Pei, et al. Optimization of robot milling process using response surface methodology[J]. Manufacturing Automation, 2023, 45(1): 38–44.
5 ]}。Li等^{[ [9]  LI R R, YANG F, WANG X D. Modeling and predicting the machined surface roughness and milling power in Scot’s pine helical milling process[J]. Machines, 2022, 10(5): 331.
9 ]}采用响应曲面法进行试验设计、数据处理分析和工艺参数优化，揭示了螺旋铣削加工过程中铣刀螺旋角、主轴转速、切削深度与表面粗糙度之间的关系。姜佳明等^{[ [10]  姜佳明, 刘战强, 王兵, 等. 基于响应曲面法的NOMEX蜂窝高速铣削参数优化[J]. 工具技术, 2020, 54(11): 8–13.JIANG Jiaming, LIU Zhanqiang, WANG Bing, et al. Optimization of high-speed milling parameters of NOMEX honeycomb based on response surface method[J]. Tool Engineering, 2020, 54(11): 8–13.
10 ]}基于响应曲面法设计试验方案，探究了NOMEX蜂窝铣削过程中切削速度、切削深度、切削宽度和进给速度对轴向切削力的影响，并建立了二阶切削力模型。Lu等^{[ [11]  LU X H, JIA Z Y, WANG H, et al. The effect of cutting parameters on micro-hardness and the prediction of Vickers hardness based on a response surface methodology for micro-milling Inconel 718[J]. Measurement, 2019, 140: 56–62.
11 ]}采用响应曲面法研究了Inconel718微铣削加工过程中，主轴转速、每齿进给量、轴向切削深度等因素对加工表面硬度的影响规律，并建立了硬度的预测模型，为合理选择切削参数提供了依据。

本文以类V型复合材料薄壁件为研究对象，基于响应曲面法，探究切边加工过程中主轴转速、进给速度和切削深度对切削力和振动加速度的影响规律，建立切削力和振动加速度的预测模型。以最小切削力和最小振动加速度为优化目标，得到类V型复合材料薄壁件切边加工过程中的最佳切削参数。

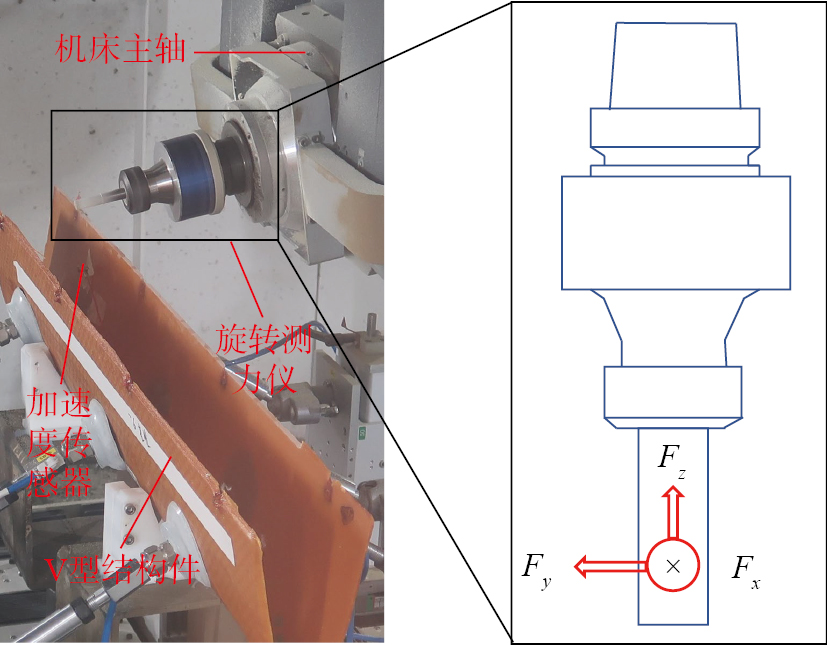
试验在罗威斯五轴龙门机床（最高转速24000 r/min）上进行，试验装置如图1所示。将工件放置在自制夹具上，对类V型复合材料薄壁件进行固定装夹。工件材料为石英纤维增强树脂基复合材料（工件厚度为2.4 mm），其物理力学性能参数如表1所示。

采用侧铣的方式对类V型复合材料薄壁件进行切边加工，其中因夹具的限制，主轴摆角为80°，因此切削宽度保持2.44 mm不变。试验刀具选用两刃PCD直齿铣刀，刀具直径为12 mm。采用9170B型Kistler旋转测力仪（采样频率10 kHz）和加速度传感器分别测量加工过程中的切削力信号和振动信号。因使用的是旋转测力仪，所以所测切削力分量为刀具坐标系下的切削力分量，旋转测力仪的力坐标系见图1（F_x，F_y，F_z）。

为了研究工艺参数对切削力和工件振动的影响规律，并预测加工过程中的工件振动和切削力，采用中心复合响应曲面法设计了试验方案，如表2所示。该试验方案中，以主轴转速n、进给速度f和切削深度a为输入变量；以切削力和振动作为响应变量。根据初步测试和实际加工需要，选择主轴转速7000 r/min、进给速度500 mm/min、切削深度1.5 mm作为零水平因素。根据三因素中心复合响应曲面法，选取臂值R=1.68，并按公式X_i=（x_i–x₀）/Δx_i对自变量进行编码。其中，X_i为自变量的编码值；x_i为自变量的真实值；x₀为试验中心点处自变量的真实值；Δx_i为自变量的变化步长。

根据中心复合响应曲面法的试验方案进行20组铣削试验，并测得每组试验切削分力F_x和振动加速度A，并选取平均切削力和振动加速度的峰值均值作为试验结果，如表3所示。

通过比较不同模型的相关系数（表4），选取二次模型来定量描述切削力及振动与工艺参数之间的关系，通过拟合得到了切削力和振动加速度关于切削参数的二次回归方程，分别如式（1）和（2）所示。式（1）为主轴转速n、进给速度f、切削深度a和切削力F_x之间的二次回归方程，式（2）为主轴转速n、进给速度f、切削深度a和振动加速度A之间的二次回归方程。切削力及振动模型的适用范围为：5318 r/min≤n≤8682 r/min，332 mm/min≤f≤668 mm/min，0.66 mm≤a≤2.34 mm。

切削力和振动加速度的预测值与实测值的关系（图2）表明，切削力的模型预测值与实测值非常接近，但是振动加速度的模型预测值与实测值之间存在一定的误差，这是因为在实际加工中，机床系统的稳定性、夹具的装夹效果等因素均会对工件的振动产生一定影响。

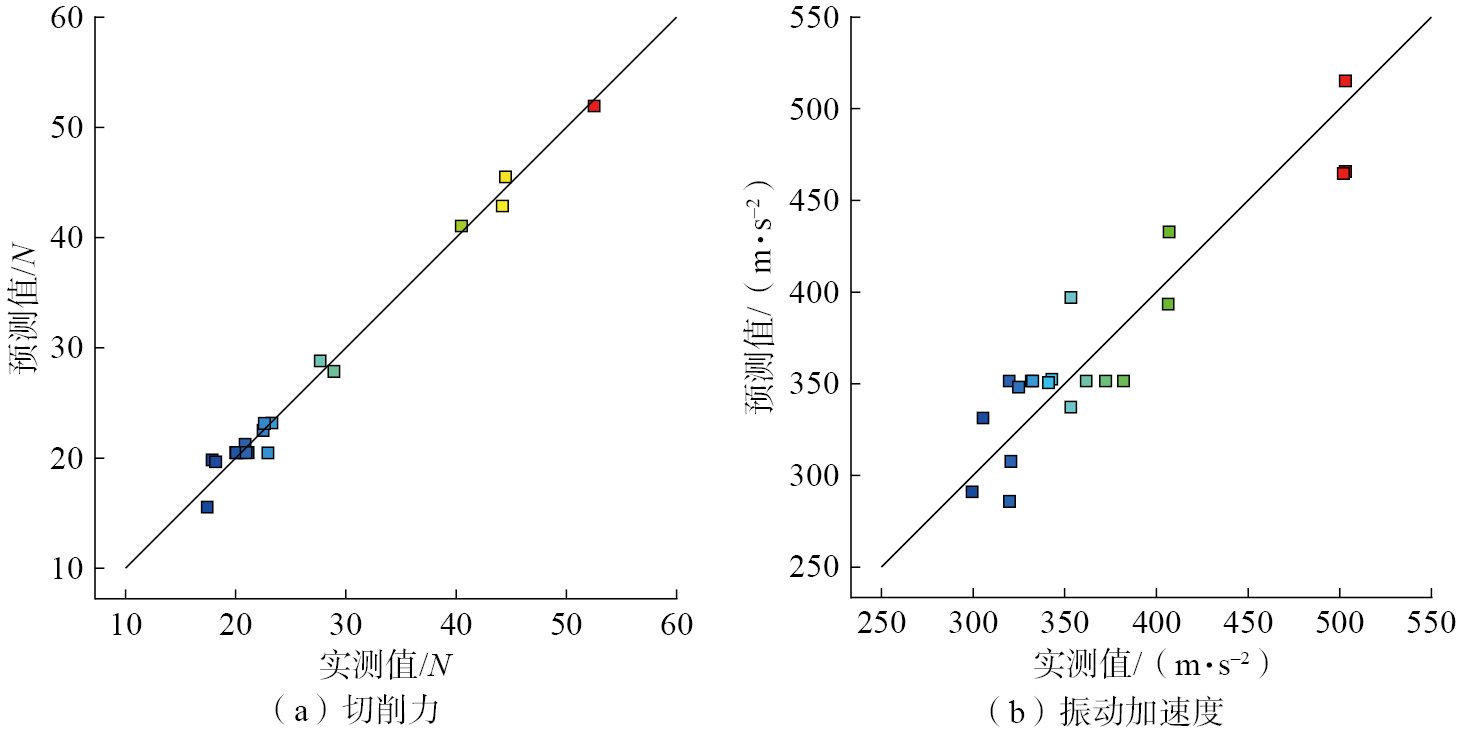
为了获得各切削参数对切削力和振动加速度的影响程度，对试验结果进行了方差分析，如表5和表6所示。其中，P值<0.05表示模型项是显著的，因此可知，n、f、a、fa、n²、f²、a²是切削力的有效模型项，f、a、nf和a²是振动加速度的有效模型项。F值分析表明，对于单因素作用，进给速度f是影响切削力和振动加速度的最重要因素，其次是切削深度a，最后是主轴转速n。在两因素交互作用对切削力的影响中，fa是最重要的因素，其次是nf，最后是na；在两因素交互作用对振动加速度的影响中，nf是最重要的因素，其次是fa，最后是na。在二次项因素对切削力的影响中，a²是最重要的因素，其次是f²，最后是n²；在二次项因素对振动加速度的影响中，a²是最重要的因素，其次是n²，最后是f²。

为了研究主轴转速、进给速度和切削深度对切削力和振动加速度的影响，保证其中2个切削参数为零水平，得到第3个切削参数对切削力和振动加速度的影响，如图3所示，其中A为主轴转速，B为进给速度，C为切削深度。可以看出，进给速度对切削力和振动加速度的影响最大，随着进给速度的增加，切削力和振动加速度持续增大。这是由于随着进给速度的增加，每齿进给量增加，单位时间内切削的材料增多，因此切削力和振动加速度增大。随着切削深度的增加，出现切削力和振动加速度先缓慢下降后急剧增大的现象。这是因为当切削深度小于临界切削厚度时，切削过程中存在犁耕现象，导致切削力较大，切削深度增加，耕犁现象逐渐消失，因而切削力逐渐减小；但是随着切削深度继续增加，单位时间内的材料去除量增多，因而切削力和振动加速度急剧增大。从表3和图3可以看出，当进给速度为500 mm/min，切削深度为1.5 mm时，随着主轴转速从5318 r/min增加到7000 r/min，切削力降低，这是因为随着主轴转速的增加，每齿进给量降低，因而切削力降低；随着主轴转速从7000 r/min增加到8632 r/min，切削力稳定性降低^{[ [12]  陈奎元. 中空铝合金结构铣削有限元仿真及加工参数优化[D]. 大连: 大连交通大学, 2019.CHEN Kuiyuan. Finite element simulation and cutting parameters optimization of hallow aluminum alloy structure milling[D]. Dalian: Dalian Jiaotong University, 2019.
12 ]}，因此逐渐增大至27.67 N。

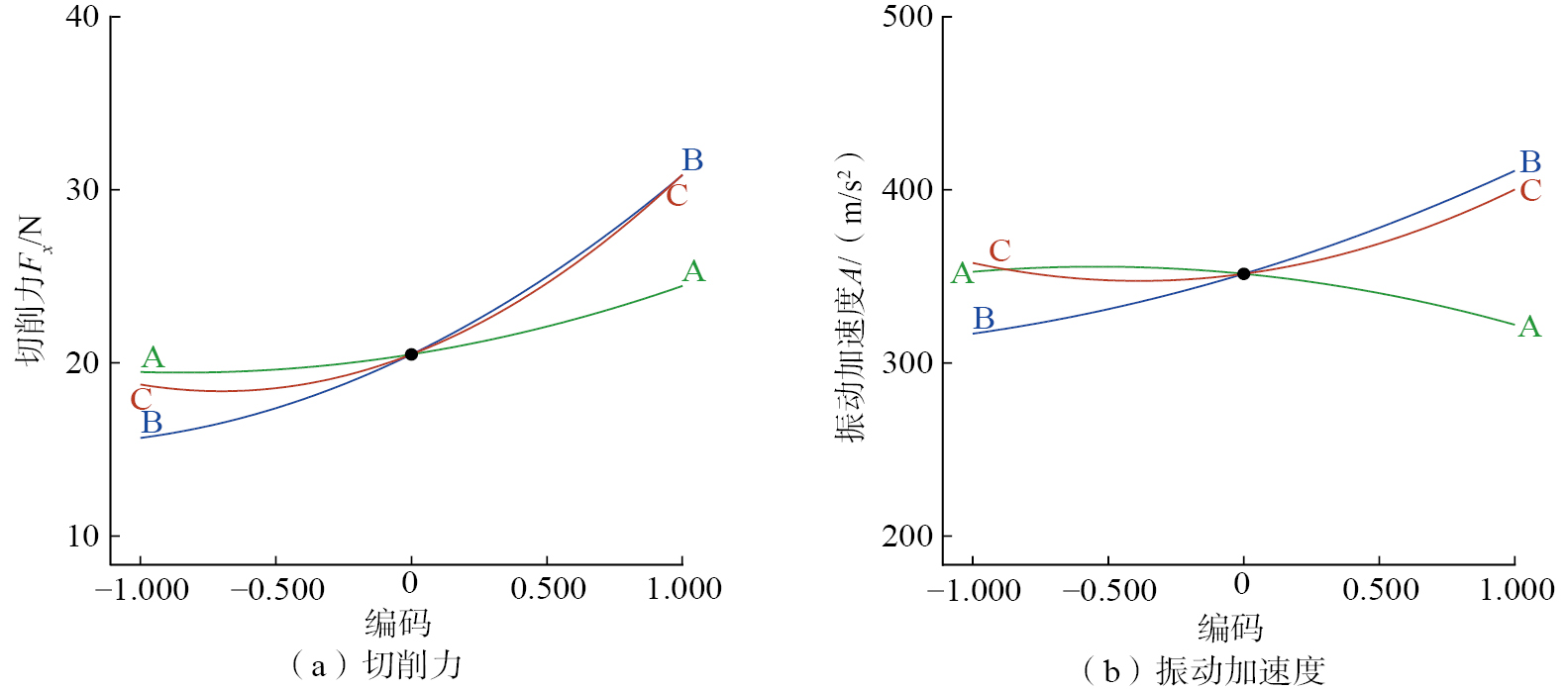
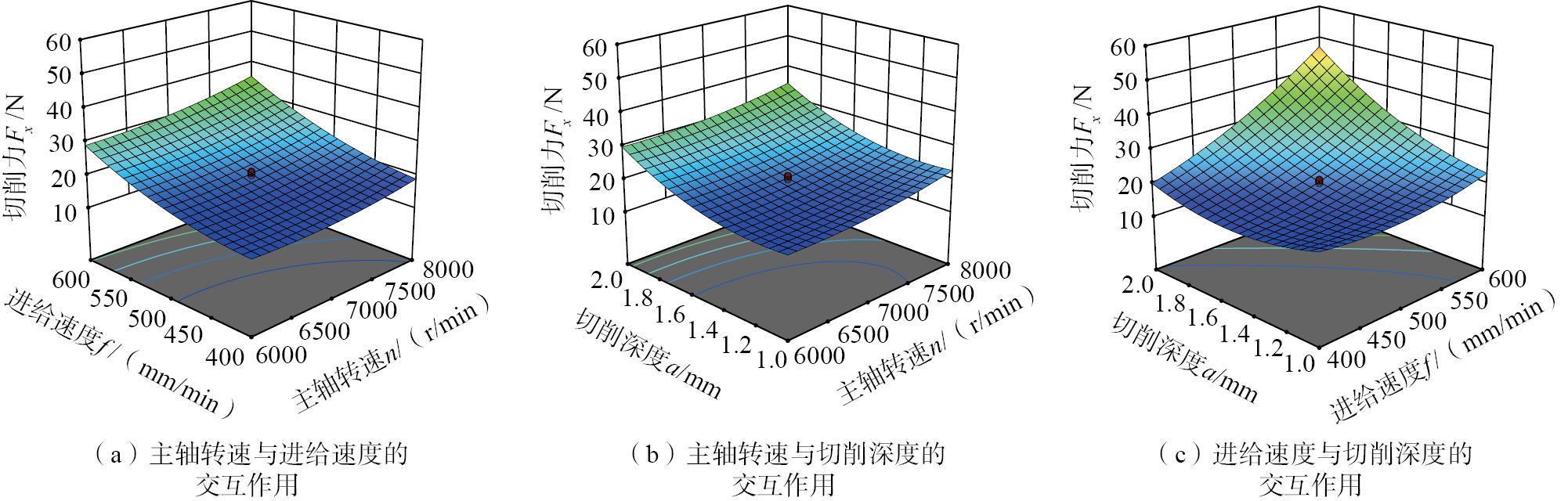
当保持其中1个切削参数为零水平时，探究其他切削参数之间的交互作用对切削力的影响，如图4所示。从图4（a）和（b）可以看出，在切削深度保持不变时，随着进给速度和主轴转速的增加，切削力逐渐增加。在进给速度保持不变时，随着主轴转速的增加和切削深度的增加，切削力逐渐增大。但是进给速度与主轴转速之间及主轴转速和切削深度之间的交互作用不太显著，这与表5和表6中的分析一致。从图4（c）可以看出，在保持零水平的主轴转速时，随着切削深度和进给速度的降低，切削力迅速减小，这是因为随着切削深度和进给速度的降低，刀具的每齿切削量减小，因此二者的交互作用减弱，使得切削力迅速减小。

切削参数之间的交互作用对振动加速度的影响如图5所示。从图5（a）可以看出，在保持切削深度为零水平时，进给速度对振动加速度的影响与主轴转速有很大的关系，随着主轴转速的降低，进给速度对振动加速度的影响增大。主轴转速对振动加速度的影响也与进给速度有很大的关系，随着进给速度的增加，主轴转速对振动加速度的影响增大。在较低主轴转速时，随着进给速度的增加，振动加速度迅速增大；但在较高主轴转速时，进给速度对振动加速度的影响很小。在较高进给速度时，随着主轴转速的增加，振动加速度迅速降低；但在较低进给速度时，随着主轴转速的增加，振动加速度变化不明显。这是因为主轴转速较低时，随着进给速度的增加，每齿进给量的增幅更大（与较高主轴转速时的每齿进给量增幅相比）。同样地，进给速度较高时，随着主轴转速的增加，每齿进给量的降幅更大（与低进给速度时的每齿进给量降幅相比）。从图5（b）可以看出，在进给速度和主轴转速不变的情况下，随着切削深度的增加，振动加速度先减小后增大；在进给速度和切削深度不变的情况下，随着主轴转速的增加，振动加速度逐渐减小。这是因为当切削深度小于临界切削厚度时，切削过程中出现犁耕现象，导致振动加速度增大，随着切削深度的增加，犁耕现象逐渐减少，因而振动加速度降低，但是随着切削深度的持续增加，单位时间内的材料去除量增加，因而振动加速度逐渐增大。从图5（c）可以看出，随着进给速度和切削深度的增加，振动加速度迅速增大，进给速度和切削深度越大，振动加速度越大。因为进给速度和切削深度的增加都会导致振动的增加，所以二者交互作用将导致振动加速度迅速增大。

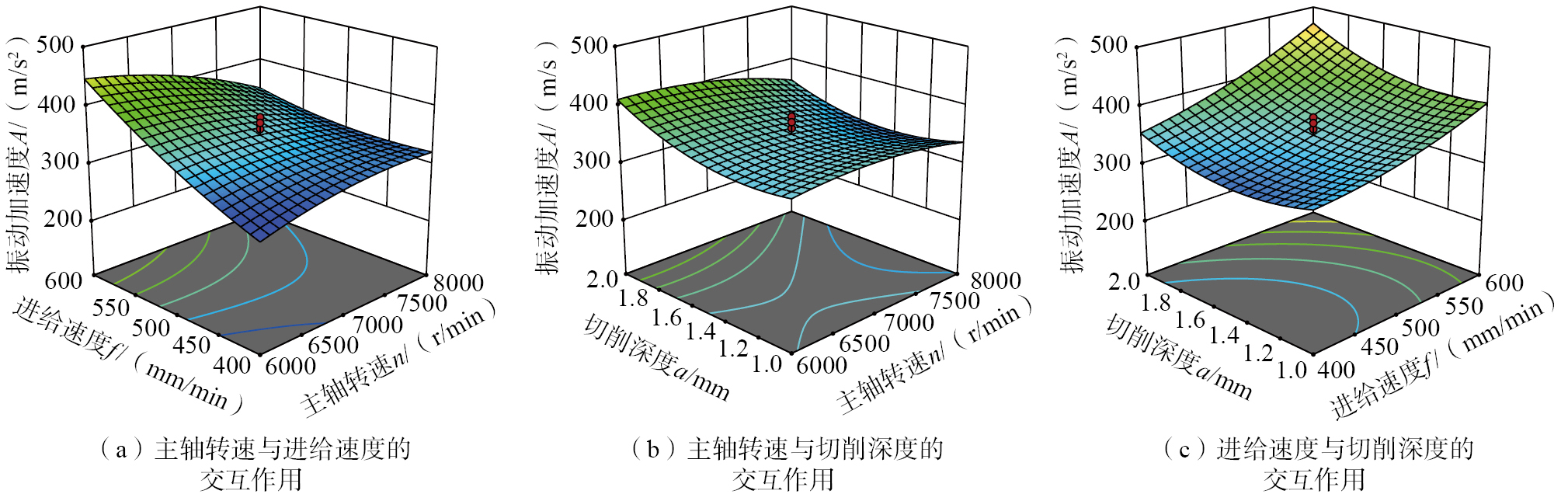
从切削参数对切削力和振动加速度的影响程度可知，nf、na对切削力的影响不显著，na、fa、n²、f²对振动加速度的影响不显著，因此在切削参数优化过程中忽略nf、na对切削力的影响及na、fa、n²、f²对振动加速度的影响，得到切削力和振动加速度的拟合方程，分别如式（3）和（4）所示。

在类V型复合材料薄壁件的切边加工过程中，更低的切削力和振动加速度往往会得到表面质量更好的产品。本研究中，切削参数优化条件为6000 r/min≤n≤8000 r/min、400 mm/min≤f≤600 mm/min、1 mm≤a≤2 mm，响应参数的目标为切削力最小和振动加速度最小。优化结果如图6所示，可以看出，主轴转速、进给速度和切削深度的优化组合为6000 r/min、400 mm/min和1.4 mm，此时切削力和振动加速度分别为14.82 N和281.13 m/s²。

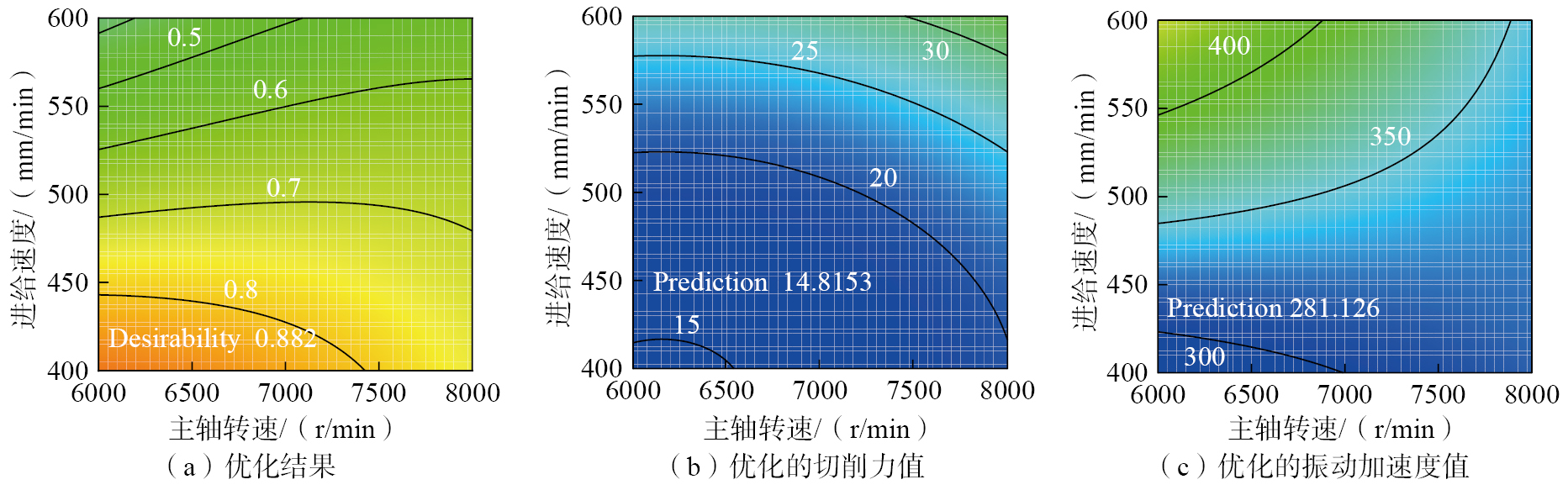
为验证本文优化结果的准确性，在相同的试验条件下，采用优化的切削参数（主轴转速6000 r/min、进给速度400 mm/min和切削深度1.4 mm）进行铣削试验，测得切削力为16.25 N，振动加速度为302.49 m/s²，如表7所示。将试验结果与模型预测结果进行对比，可以看出切削力和振动加速度幅值的预测误差均在10%以内，表明预测模型具有良好的精度，验证了模型及优化结果的准确性。

采用响应曲面法，研究了类V型复合材料薄壁件切边加工过程中切削参数对切削力和振动加速度的影响规律，建立了切削力和振动加速度的预测模型，以最小切削力和最小振动加速度为目标，对切削参数进行了优化，主要结论如下。

（1）通过响应曲面法建立的切削力和振动加速度模型是显著的，在试验范围内，可用于预测切削力和振动加速度。

（2）切削参数对切削力和振动加速度的影响程度由大到小为进给速度f>切削深度a>主轴转速n；交互项中fa对切削力有显著影响，nf对振动加速度有显著影响。

（3）以最小切削力和最小振动加速度为目标，优化得到类V型复合材料薄壁件切边加工过程中的最佳切削参数为主轴转速6000 r/min、进给速度400 mm/min、切削深度1.4 mm。

本文的研究结果将有助于指导类V型复合材料薄壁件切边加工参数的选择，以达到降低加工过程中振动、提高加工表面质量的目的。未来可以对类V型复合材料薄壁件切边加工的材料去除机理进行深入研究，建立切削力及振动加速度的理论预测模型，为切削参数的优化提供理论支撑。