复合材料是由聚合物基体与高强度纤维（碳纤维、玻璃纤维或芳纶纤维等）按照一定比例组合而成的新材料，具有比刚度高、比强度高、抗疲劳性好等优势，被广泛应用于航空航天、船舶、汽车、建筑等领域^{[ [1]  魏嘉兵, 邹礼洋, 杨浩然, 等. 复杂载荷下复合材料螺栓连接预紧力松弛试验研究[J]. 航空制造技术, 2024, 67(9): 98–105.WEI Jiabing, ZOU Liyang, YANG Haoran, et al. Experiment research of preload loss in composite bolted joint under complex loads[J]. Aeronautical Manufacturing Technology, 2024, 67(9): 98–105.
[2]  张桂书, 程胜, 万佳佳, 等. 民用飞机复合材料构件损伤失效分析在批产质量优化中的探索[J/OL]. 复合材料科学与工程, 2024: 1–9 [2024–06–28]. https://kns.cnki.net/KCMS/detail/detail.aspx?filename=BLGF20240627008&dbname=CJFD&dbcode=CJFQ.ZHANG Guishu, CHENG Sheng, WAN Jiajia, et al. Exploration of the process and method for damage failure analysis of civil aircraft composite components[J]. China Industrial Economics, 2024: 1–9 [2024–06–28]. https://kns.cnki.net/KCMS/detail/detail.aspx?filename=BLGF20240627008&dbname=CJFD&dbcode=CJFQ.
[3]  FERNANDES P, PINTO R, CORREIA N. Design and optimization of self-deployable damage tolerant composite structures: A review[J]. Composites Part B: Engineering, 2021, 221: 109029.
[4]  LI D H. Layerwise theories of laminated composite structures and their applications: A review[J]. Archives of Computational Methods in Engineering, 2021, 28(2): 577–600.
1-4 ]}。

混杂复合材料通过在聚合物基体中嵌入两种或两种以上的纤维，充分利用两种纤维的优势，而具有更强的可设计性^{[ [5]  WANG A N, YANG Y, ZHANG P X, et al. Effect of fiber volume fraction on hybrid effects of tensile properties of unidirectional aramid/carbon fiber hybrid composites[J]. Polymer Composites, 2024, 45(3): 2050–2062.
5 ]}。根据性能目标的设计需求，通过不同的混杂方式及不同的混杂区域，可实现单一材料所不具备的综合性能^{[ [6]  乌云其其格, 付宇彤, 高旭豪, 等. 中温固化环氧树脂混杂纤维复合材料性能研究[J]. 航空制造技术, 2020, 60(22):14–22.Wuyunqiqige, FU Yutong, GAO Xuhao, et al. Study on hybrid fiber composites properties of medium temperature curing epoxy resin matrix[J]. Aeronautical Manufacturing Technology, 2020, 60(22):14–22.
[7]  郑凯东, 曹东风, 胡海晓, 等. 厚/薄铺层混杂复合材料层合板低速冲击损伤及冲击后压缩特性研究[J]. 载人航天, 2024, 30(4): 469–477.ZHENG Kaidong, CAO Dongfeng, HU Haixiao, et al. Investigation on low-velocity impact damage and characteristics of compression after impact of thick-/thin-ply composite laminates[J]. Manned Spaceflight, 2024, 30(4): 469–477.
6-7 ]}，目前已有大量的相关研究。Kumar等^{[ [8]  KUMAR JESTHI D, NAYAK S, SAROJ S. Assessment of flexural and wear properties of carbon/glass fiber hybrid composite[J]. Materials Today: Proceedings, 2022, 49: 486–490.
8 ]}为了克服单种纤维的弱点，制备了具有不同堆叠顺序的碳/玻璃纤维增强聚合物，测试结果表明，碳/玻璃纤维混杂增强聚合物复合材料的弯曲应力和弹性模量比普通玻璃纤维增强聚合物分别高48%和76%。Dong等^{[ [9]  DONG C S. Flexural behaviour of carbon and glass reinforced hybrid composite pipes[J]. Composites Part C: Open Access, 2021, 4: 100090.
9 ]}对由碳纤维和玻璃纤维增强聚合物组成的混杂复合管的弯曲行为进行了研究，采用有限元分析模拟的方式，研究了层堆叠顺序、纤维体积分数与杂交对三点弯曲复合管渐进失效破坏的影响，结果表明，相较于全碳纤维或全玻璃纤维复合管，混杂复合管具有更高的破坏载荷。

多目标优化方法已在复合材料设计方面得到了广泛应用，在考虑复合材料的多目标优化设计时，性能指标包括屈曲载荷、结构重量、疲劳寿命、刚度、成本等^{[ [10]  王海艳, 付麒麟, 周秩同, 等. 基于NSGA–Ⅲ算法的碳纤维复合材料螺旋铣孔切削参数多目标优化[J]. 中国工程机械学报, 2024, 22(2): 208–213, 219.WANG Haiyan, FU Qilin, ZHOU Zhitong, et al. Multi-objective optimization of cutting parameters for helical milling of carbon fiber composites using NSGA–Ⅲ algorithm[J]. Chinese Journal of Construction Machinery, 2024, 22(2): 208–213, 219.
[11]  刘锐, 陈宏达, 胡海晓, 等. 再生碳纤维毛毡纤维取向与克重多目标优化研究[J]. 复合材料学报, 2024, 41(12): 6498–6517.LIU Rui, CHEN Hongda, HU Haixiao, et al. Multi-objective optimization of fiber orientation and grammage of recycled carbon fiber felt[J]. Acta Materiae Compositae Sinica, 2024, 41(12): 6498–6517.
10-11 ]}。崔勇江等^{[ [12]  崔勇江, 王斌团, 赵占文. 复合材料T型加筋壁板后屈曲承载能力研究[J]. 复合材料科学与工程, 2021(7): 22–27.CUI Yongjiang, WANG Bintuan, ZHAO Zhanwen. Research on the post-buckling bearing capacity of T-type composite stiffened panel[J]. Composites Science and Engineering, 2021(7): 22–27.
12 ]}研究了在轴压载荷下，飞机复合材料中T形加筋壁板结构的承载能力，将工程算法、有限元分析结果与轴压试验结果进行对比，证明了理论分析的有效性。Foroutan等^{[ [13]  FOROUTAN K, VAREDI-KOULAEI S M, DUC N D, et al. Non-linear static and dynamic buckling analysis of laminated composite cylindrical shell embedded in non-linear elastic foundation using the Swarm-based metaheuristic algorithms[J]. European Journal of Mechanics-A/Solids, 2022, 91: 104420.
13 ]}通过确定最大临界屈曲载荷的最佳纤维角度，研究了基于非线性弹性基础的层压复合圆柱壳在外载荷作用下的非线性静态和动态屈曲特性。但以上研究均没有考虑实际复杂环境工况下的多目标优化设计。

在实际工况条件下，由于设计和制造误差，涉及很多不确定性因素^{[ [14]  PENG X, JIANG H H, LI J Q, et al. Generation of two-level representative volume element model for uncertainty analysis of composite materials[J]. Polymer Composites, 2024, 45(16): 15211–15227.
[15]  SHARMA H, GANGULI R. Optimization of a higher-order sandwich composite beam under uncertainties[J]. Composite Structures, 2021, 269: 114003.
14-15 ]}。在现有的研究中，陶威等^{[ [16]  陶威, 刘钊, 许灿, 等. 三维正交机织复合材料翼子板多尺度可靠性优化设计[J]. 上海交通大学学报, 2021, 55(5): 615–623.TAO Wei, LIU Zhao, XU Can, et al. Multi-scale reliability-based design optimization of three-dimensional orthogonal woven composite fender[J]. Journal of Shanghai Jiao Tong University, 2021, 55(5): 615–623.
16 ]}考虑到材料和结构的不确定性因素，对复合材料翼子板进行不确定性优化设计，结果表明，翼子板在满足结构刚度和可靠性的要求之外，实现了结构轻量化的效果。宏观和微观尺度计算是典型的多尺度分析问题。Sun等^{[ [17]  SUN Q P, ZHOU G W, TANG H B, et al. In-situ effect in cross-ply laminates under various loading conditions analyzed with hybrid macro/micro-scale computational models[J]. Composite Structures, 2021, 261: 113592.
17 ]}使用混合宏观/微观计算模型，系统研究了交叉层层压板的破坏机制，结合计算、理论和试验研究，对层压复合材料中存在的原位效应进行了全面分析。Kormanikova等^{[ [18]  KORMANIKOVA E, KOTRASOVA K. Micro-macro modelling of laminated composite rectangular reservoir[J]. Composite Structures, 2022, 279: 114701.
18 ]}在微观层面上使用虚构的周期性微观结构模型计算材料特性，基于分析之后的参数，在宏观层面上解决了层压复合矩形储液罐的地震响应问题。微观结构的复杂性必然导致宏观性能的难以预料，虽然目前已经有大量的宏观参数不确定性分析，但很少有研究将微观参数视为不确定性变量，并通过多尺度分析得到宏观的不确定性。

本文将从微观层面确定不确定性参数，通过神经网络模型将不确定性参数传播到宏观层面，将宏观参数作为材料属性，并选取层间混杂复合材料加筋壁板作为主要的分析优化对象，使用多目标优化算法实现加筋壁板质量最小化和屈曲载荷最大化的协同优化。

在层间混杂复合材料的屈曲分析与结构优化中，主要考虑两类微观不确定性变量，分别是微观材料属性不确定性信息和微观几何参数不确定性信息。

（1）纤维的微观材料属性不确定性表征。

碳纤维和玻璃纤维的微观弹性属性参数（如弹性模量E₁、E₂，泊松比${\upsilon }_{12}$、${\upsilon }_{23}$，剪切模量G₁₂、G₂₃和密度ρ等）受制造过程、原材料类型、质量控制措施及测试方法等因素的影响，是典型的不确定性变量。假设这些不确定性变量为正态分布，且根据文献[ [19]  SANEI S H R, FERTIG R S. Length-scale dependence of variability in epoxy modulus extracted from composite prepreg[J]. Polymer Testing, 2016, 50: 297–300.
[20]  JI X, WANG C, FRANCIS B A P, et al. Mechanical and interfacial properties characterisation of single carbon fibres for composite applications[J]. Experimental Mechanics, 2015, 55(6): 1057–1065.
19-20 ]中的分析，选取变异系数为5%，从而进行碳纤维和玻璃纤维微观材料属性参数的不确定性表征，如表1所示。

（2）基体的微观材料属性不确定性表征。

基体中常出现气孔、结块、固化不足等缺陷，在基体的弹性模量E_m、泊松比${\upsilon }_{\text{m}}$、密度ρ_m等材料属性参数的不确定性量化中，假设其分布类型是变异系数为5%的正态分布，具体参数值如表2所示。

（3）微观几何参数的不确定性表征。

在不同的纤维体积分数下，相同的纤维和基体所表现的宏观材料属性存在巨大差异。因此，将基体分别与碳纤维和玻璃纤维进行组合，形成两种不同的复合材料结构。设置纤维体积分数V_f分别为0.4和0.6（均为平均值），标准偏差为0.03，根据纤维类型和体积分数的不同，得到4种含不同微观几何参数不确定性因素的备选材料（材料1~材料4），如表3所示。

为了得到宏观材料参数的不确定性状态，对微观材料进行多次采样，通过多尺度有限元分析获得多组宏观参数的基础数据，实现10种宏观材料参数（材料密度ρ、弹性模量E₁₁、E₂₂、E₃₃，泊松比${\upsilon }_{12}$、${\upsilon }_{13}$、${\upsilon }_{23}$，以及剪切模量G₁₂、G₁₃、G₂₃）的不确定性表征。

首先基于代表体积单元（RVE）均质化的理念，在ABAQUS软件中建立4种备选材料的微观RVE模型，通过使用约束方程并施加位移来满足周期性边界条件^{[ [21]  OMAIREY S L, DUNNING P D, SRIRAMULA S. Development of an ABAQUS plugin tool for periodic RVE homogenisation[J]. Engineering with Computers, 2019, 35(2): 567–577.
21 ]}，并计算有效的宏观弹性属性参数，RVE模型的几何尺度为1∶1∶1。考虑到分析精度和计算效率的相互协调^{[ [22]  OMAIREY S L, DUNNING P D, SRIRAMULA S. Influence of micro-scale uncertainties on the reliability of fibre-matrix composites[J]. Composite Structures, 2018, 203: 204–216.
22 ]}，将RVE模型的网格尺寸设置为4 μm，每个RVE模型中有20925个网格元素。选取4种纤维体积分数V_f，其对应的微观RVE模型如图1所示。

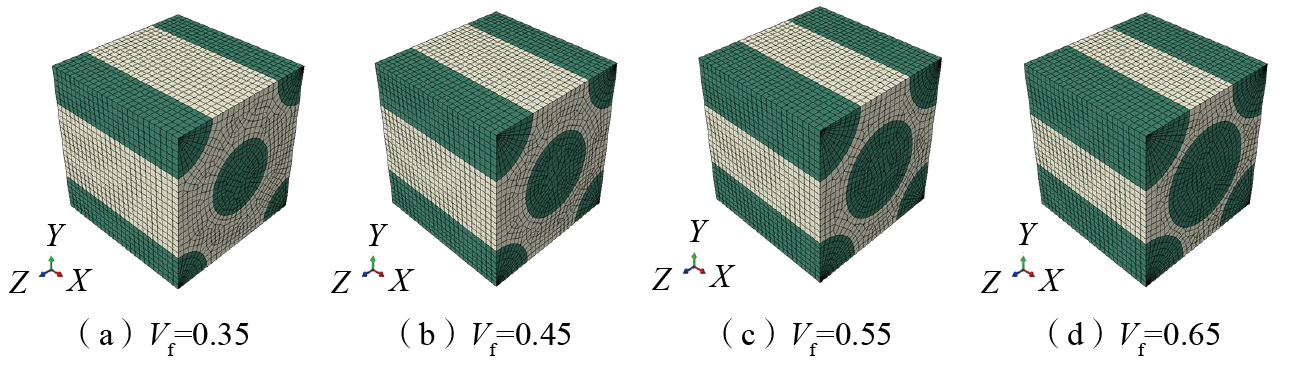
不同参数下的RVE模型能够计算出相应的宏观属性，取微观材料属性E₁为不确定状态，则其余微观变量为确定均值。例如材料1，在E₁=2.21×10⁵ MPa时，其宏观属性E₁₁=0.85×10⁵ MPa；对于材料2，在E₁=2.325×10⁵ MPa时，其宏观属性E₁₁=1.39×10⁵ MPa；对于材料3，在E₁=9.05×10⁴ MPa时，其宏观属性E₁₁=3.55×10⁴ MPa；对于材料4，在E₁=8.15×10⁴ MPa时，其宏观属性E₁₁=4.9×10⁴ MPa。

通过RVE模型进行多尺度分析时，计算过程非常耗时。因此，将神经网络模型应用于多尺度不确定性传播分析。对于每种备选材料，构建一个以sigmoid为激活函数的多层神经网络，如图2所示。其中，输入层为13个不确定的微观参数（E₂=E₃，${\upsilon }_{12}$=${\upsilon }_{13}$，G₁₂=G₁₃），输出层为10个宏观材料参数，2个隐藏层中各有11个神经元，该网络共有406个可训练参数。

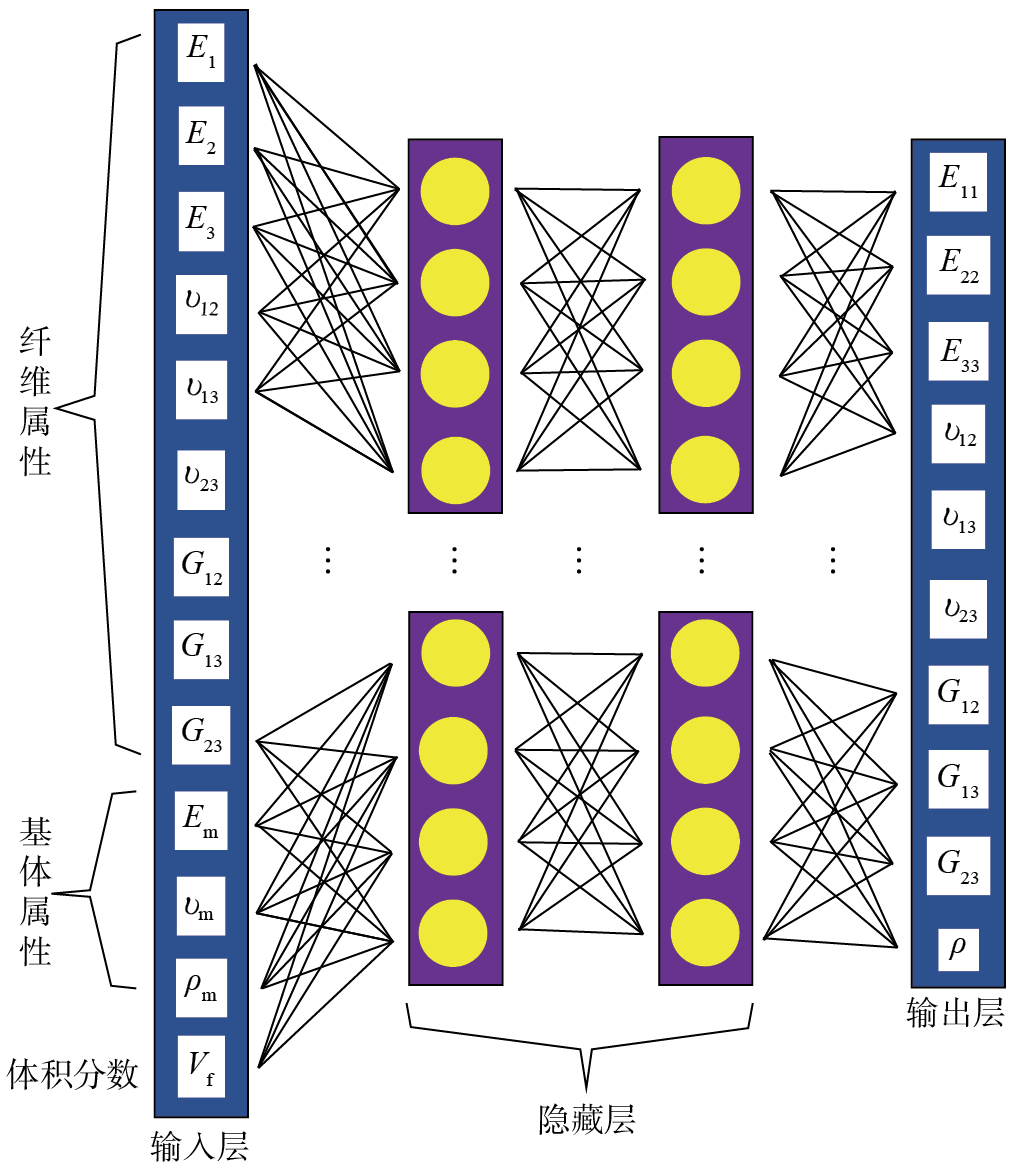
根据表2和3中13个不确定变量的微观尺度参数不确定性信息，通过拉丁超立方采样方法得到100个采样点，使用多尺度分析计算得到相应的宏观尺度材料参数。将70%的采样点作为训练集，15%的采样点作为验证集，剩下的15%作为测试集。该模型使用贝叶斯正则化算法进行参数训练，此算法是一种通过引入贝叶斯统计原理来增强神经网络泛化能力的正则化方法，在损失函数中加入了对权重的概率约束，将模型的复杂度作为正则化项，纳入优化过程，从而有效减少模型的过拟合。

针对4种备选材料分别构建了4个不同的神经网络模型，网络训练迭代了60个轮次，并且在第42轮迭代时开始收敛。在验证数据集中，4种备选材料的R值分别为0.9995（材料1）、0.99916（材料2）、0.99976（材料3）和0.99954（材料4），表明所构建的神经网络模型较准确。基于拟合后的神经网络模型，将复合材料微观属性变量的不确定性传播到宏观层面，得到了4种备选材料的宏观材料参数不确定性表征结果，如表4所示。

层间混杂复合材料是由不同类型材料在各个层之间交替排列而成的，其加筋壁板是将混杂状态的蒙皮与筋条按照特定要求固化而成。从制造角度来看，蒙皮和筋条均由单层层合板堆叠而成。在x方向上，将层合板划分为4个不同区域（Ⅰ~Ⅳ），每个区域铺设不同的备选材料；在z方向上，每一层的备选材料均一致。此外，不考虑区域划分问题，层合板每一层的角度均相同，如图3所示。

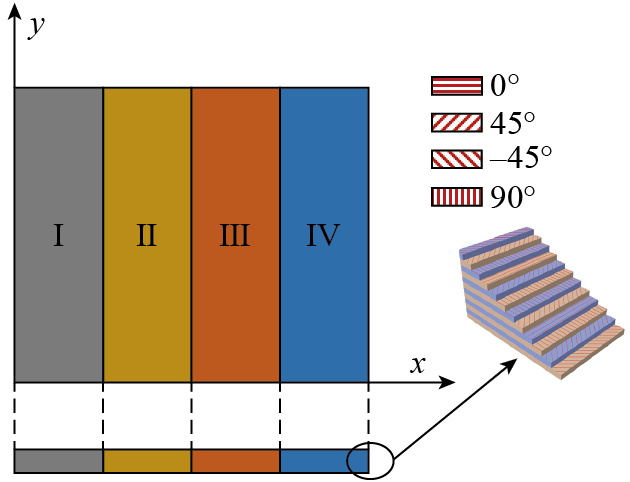
对于加筋壁板的蒙皮部分，在受到外界轴向压力载荷或剪切载荷时，不同区域的连接处会因为材料不连续等原因而发生屈曲失稳现象。因此，在不同区域的连接处添加筋条，提高壁板的屈曲稳定性。基于已有文献[ [23]  MORADI S, VOSOUGHI A R, ANJABIN N. Maximum buckling load of stiffened laminated composite panel by an improved hybrid PSO–GA optimization technique[J]. Thin-Walled Structures, 2021, 160: 107382.
23 ]中的相关数据和模型，构建了I形筋条、T形筋条和直形筋条，并将筋条以绑定约束的形式增加到层间混杂复合材料的蒙皮上，形成不同类型的加筋壁板，如图4所示。

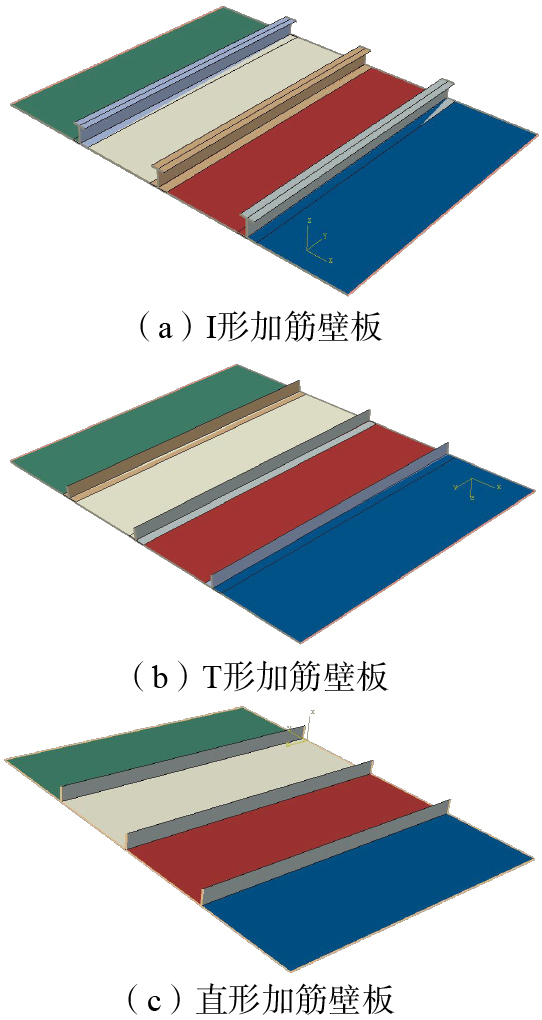
对蒙皮部分的不同区域赋予不同的层间混杂复合材料（图3），筋条部分铺设同一种材料。将蒙皮和筋条设置为完全连接关系，使蒙皮和筋条同时受到均匀轴压载荷作用，然后进行加筋壁板的屈曲稳定性及临界屈曲载荷的计算。使用S4R通用壳单元类型划分整个加筋壁板的网格，网格尺寸设置为10 mm，如图5所示。

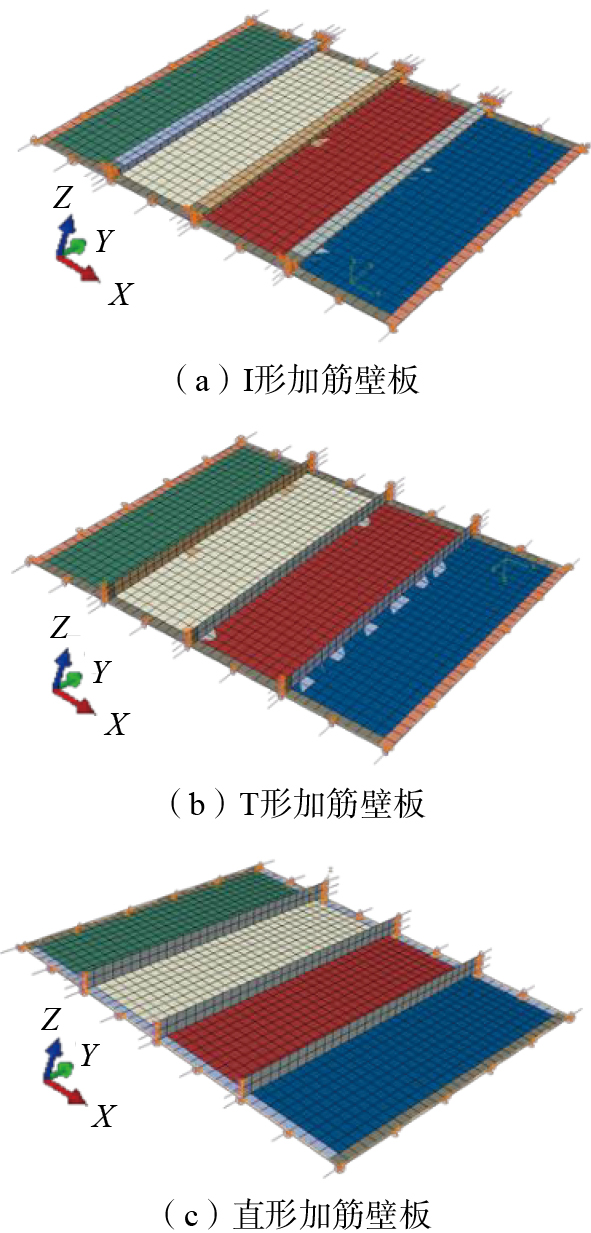
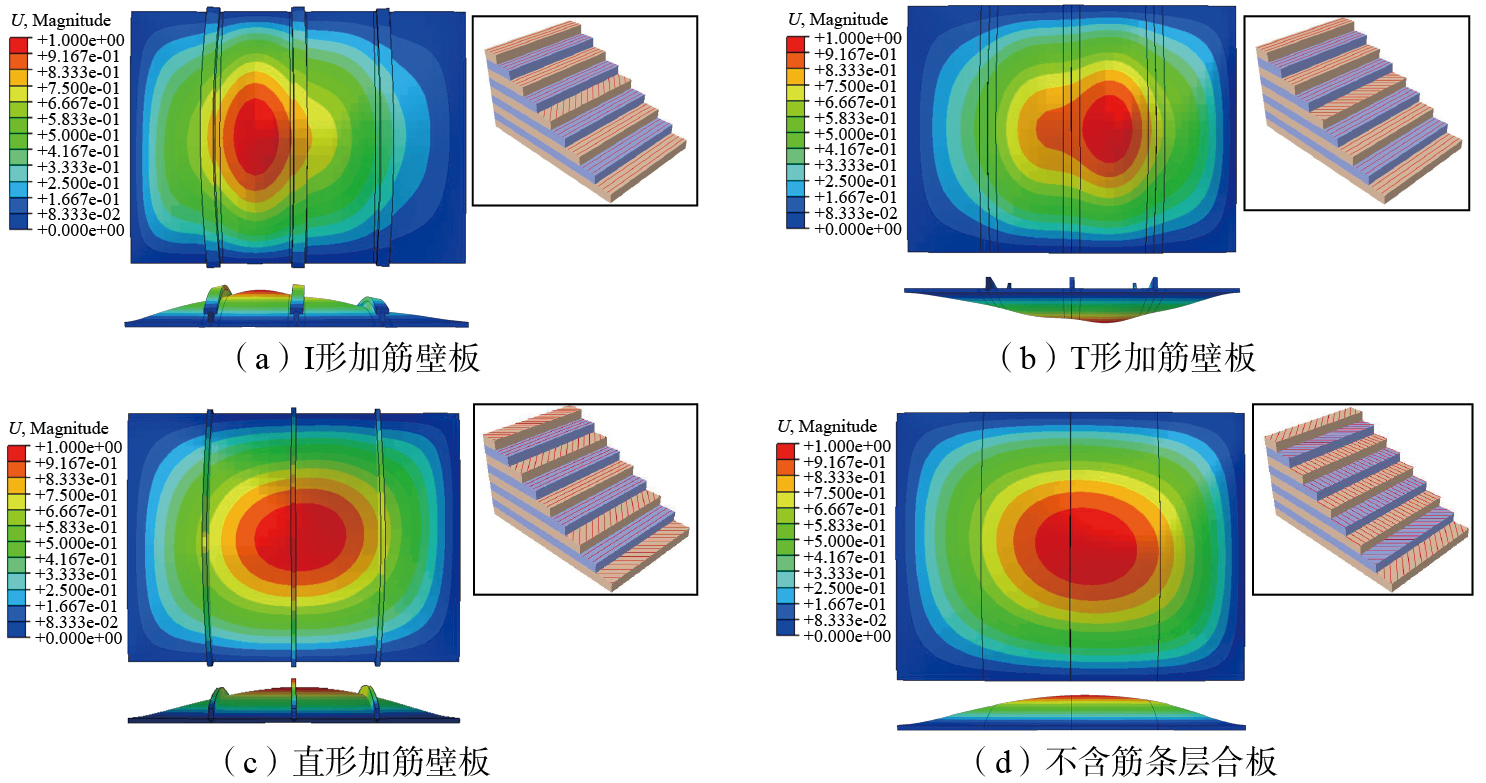
当对加筋壁板施加的载荷达到临界屈曲载荷时，层间混杂复合材料加筋壁板将从一个平衡状态转变为另一个平衡稳定状态。因此，使用ABAQUS中的Subspace特征值求解器，获得层间混杂复合材料加筋壁板临界屈曲载荷的特征值λ_i和相对应的屈曲模态{ψ}_i，进而得到第i阶临界屈曲载荷。对不同类型的加筋壁板进行分析，得到其临界屈曲模态云图，如图6所示。

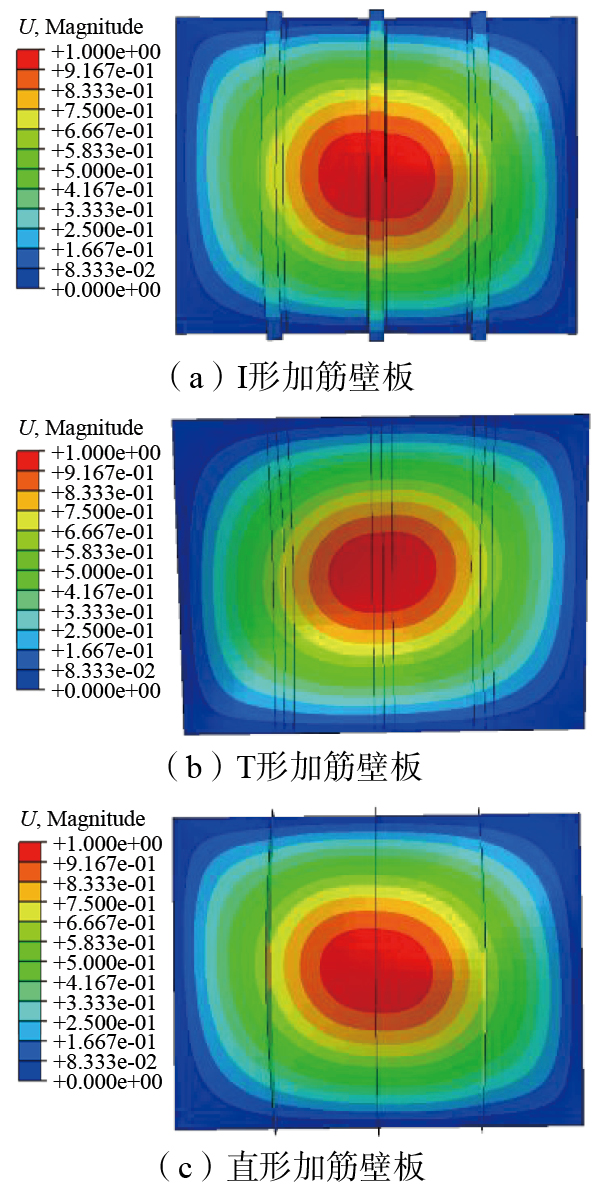
对于层间混杂复合材料层合板的屈曲稳定性而言，宏观材料的不确定性必然会导致屈曲稳定性表现出不稳定的状态。通过多尺度分析，将微观属性的不确定性传播到宏观层面，获得宏观材料属性的不确定分布状态。

为了分析3种不同类型加筋壁板临界屈曲载荷的稳健性，对屈曲稳定性分析结果进行取样，通过不断增加取样次数（样本点数）对响应目标进行统计分析，计算结果如图7所示。

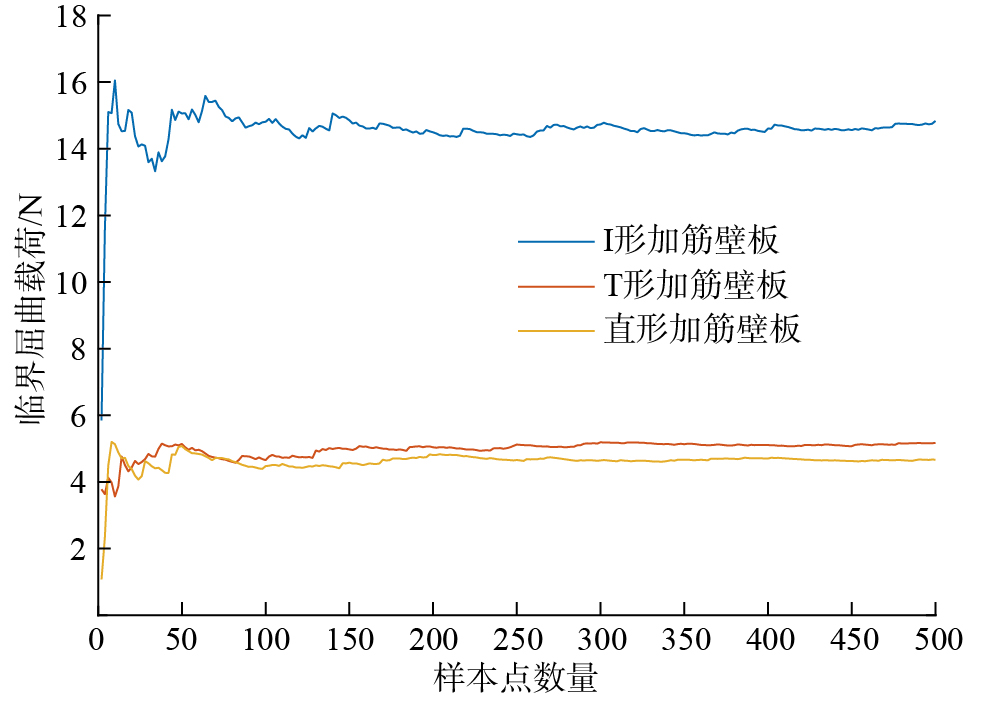
从图7可以看出，当样本点数达到150次左右时，3种加筋壁板的临界屈曲载荷基本达到稳定状态。在后续的优化设计中，将以150次分析之后得到的优化数据均值作为优化函数的目标值进行分析。

对于混杂复合材料加筋壁板而言，铺层顺序θ、材料混杂序列χ和单层厚度t均会对加筋壁板的屈曲稳定性产生影响。在开始优化之前，需要设置一个初始状态，其中铺层顺序为[–45°/0°/45°/90°/45°/90°/45°/0°/–45°]，层数n=9，单层厚度t=0.5 mm，混杂序列为[材料1，材料2，材料3，材料4，材料1]（前4位表示蒙皮部分的材料混杂方法，最后1位表示筋条的材料）。

优化模型以最大化屈曲载荷N和最小化结构总质量M为目标，并且以结构的总成本O为约束，进行铺层顺序θ、材料混杂序列χ和单层厚度t的优化设计，构建的多目标优化函数如下。

式中，θ的取值范围为0°、45°、–45°和90°；χ的取值范围为材料1、材料2、材料3和材料4；t的取值范围为0.4 mm、0.45 mm、0.5 mm、0.55 mm、0.6 mm、0.65 mm、0.7 mm、0.75 mm和0.8 mm；k=3为常数，表示目标函数N和M的置信度为99.6%；$\overline{O}$=7 USD（美元）是结构成本的最大值；N和M分别是加筋壁板临界屈曲载荷与结构总质量的稳健目标函数，其中mean（n（θ，χ，t））和std（n（θ，χ，t））是临界屈曲载荷n的均值和标准差，mean（m（θ，χ，t））和std（m（θ，χ，t））是加筋壁板结构总质量m的均值和标准差；碳纤维、玻璃纤维和基体的单位成本分别为c_fc=11 USD/kg、c_fg=2 USD/kg、c_m=2 USD/kg。

使用NSGA–II优化算法求解上述多目标优化问题，对不同类型的加筋壁板进行优化设计，同时分析了无加筋层间混杂复合材料层合板的屈曲稳定性与结构总质量。加筋壁板的优化设计中，属性参数来自于神经网络中获得的宏观不确定性参数。图8为3种不同加筋壁板和无加筋层合板的优化分析结果。

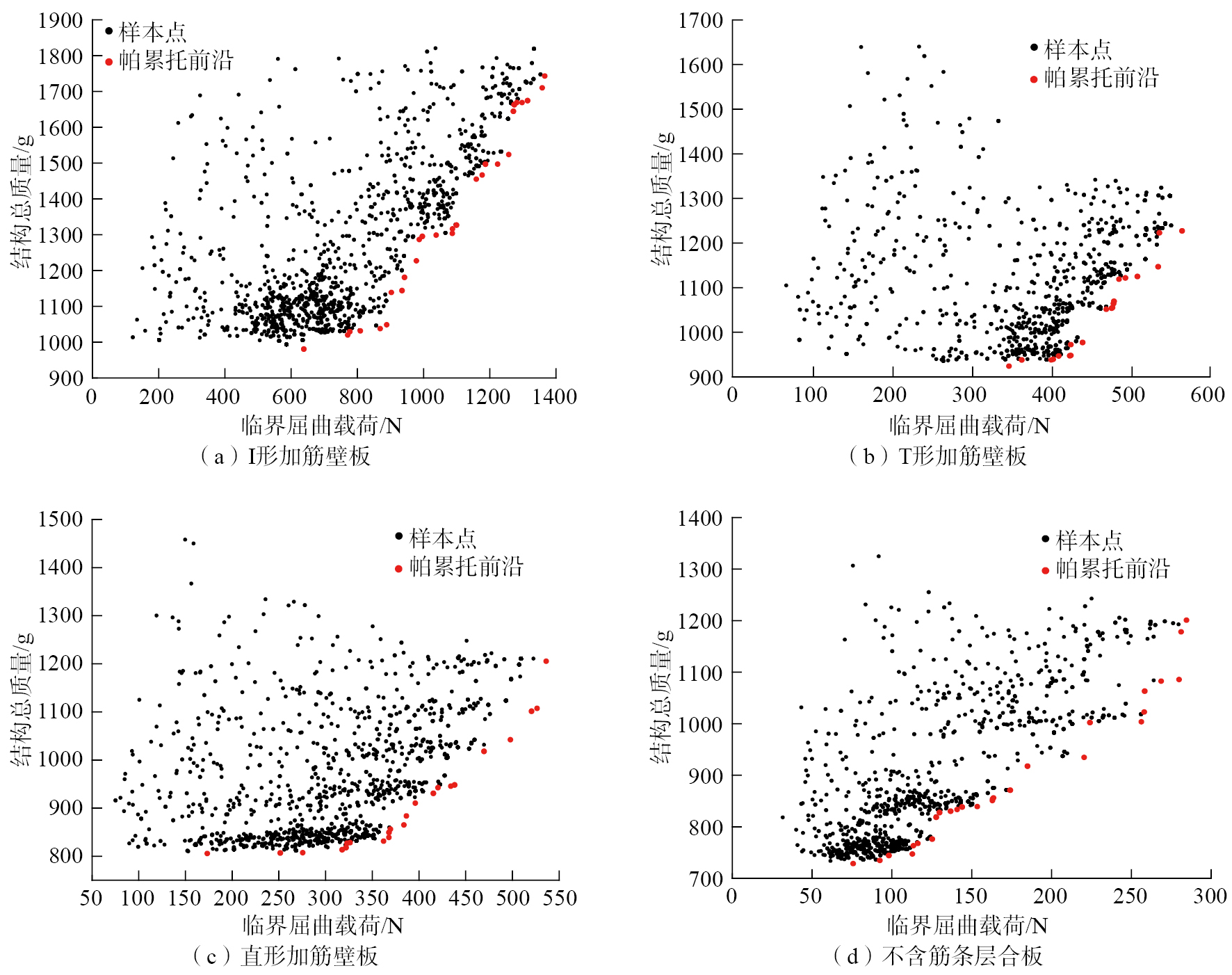
得到加筋壁板屈曲稳定性的优化分析结果之后，使用TOPSIS法对帕累托前沿进行处理和比较，获得相对最优解用以分析。在该方法中，首先对帕累托前沿中的优化目标进行规范化处理。通过式（2）构造优化目标的原始数据矩阵。

式中，i为帕累托前沿中的非劣解个数；j=2为加筋壁板优化中的两个优化目标。之后，采用式（3）和（4）对原始数据矩阵进行规范化处理，得到归一化处理后的决策矩阵Z。

在决策矩阵Z中分别获得两个目标函数值的正理想值Z⁺和负理想值Z^–，其中正理想值Z⁺由各列元素的最大值构成，Z^–由各列元素的最小值构成。基于理想值，采用式（5）和（6）分别获得非劣解与Z⁺和Z^–之间的接近程度；通过式（7）计算得到各非劣解的接近程度。

式中，$D_i^{+}$为非劣解和Z⁺的接近程度；$D_i^{-}$为非劣解和Z⁻的接近程度；C_i为各非劣解的接近程度；w_j为不同目标函数的权重，本研究将各目标的权重均定义为1，计算获得C_i的范围在0~1之间，越接近1表示该解更接近理想解，优先级更高。

根据上述优化方法，得到不同壁板帕累托解集中前5组非劣解的C_i值，如表5所示。

将3种不同类型加筋壁板的最优结果与各自的初始结果进行对比（#1表示优化结果，#2表示初始结果），如表6所示。可以看出，在满足成本约束的前提下，加筋壁板的临界屈曲载荷得到了一定程度的提高，且整体质量增幅不大。其中，直形加筋壁板的优化后屈曲载荷较初始值提高了164.8%，但结构总质量仅增加了8.19%，表明所提优化方法大幅提高了层间混杂复合材料的屈曲稳定性，且对结构总质量影响较小。图9为不同壁板最优结果的屈曲模态云图。

本文对多种层间混杂复合材料进行了多尺度研究分析，基于代表体积单元（RVE）模型将微观结构和材料属性的不确定性从微观传播到宏观层面，利用搭建的神经网格模型快速得到宏观材料属性的不确定性状态。然后将得到的宏观不确定性材料属性赋予层间混杂复合材料的优化过程中。

（1）针对层间混杂复合材料的模型优化，构建了3种不同类型加筋壁板，提出一种考虑多尺度不确定性的层间混杂复合结构的多目标优化设计方法。

（2）对构建的加筋板模型进行屈曲分析，通过稳健性分析发现，当样本点数量达到150时，加筋壁板的临界屈曲载荷基本稳定。

（3）相较于初始结果，优化后直形加筋壁板的屈曲载荷提高了164.8%，但结构总质量仅增加了8.19%。表明所提优化方法可大幅提高层间混杂复合材料的屈曲稳定性，且对结构总质量几乎无影响。