基于GPU并行计算的拓扑优化全流程加速设计方法
基金项目:
国家重点研发计划项目(2021YFB1715100);江苏省前沿引领技术基础专项(BK20202007)。
中图分类号:
V22
文献标识码:
A
引文格式:
张长东, 吴奕凡, 周铉华, 等. 基于GPU并行计算的拓扑优化全流程加速设计方法[J]. 航空制造技术, 2025, 68(12): 34-41, 67.
摘要
随着大尺寸航空航天装备的发展需求,高效高精度的大规模拓扑优化设计成为该领域关注的焦点。针对现有大规模拓扑优化设计存在的计算量巨大、计算效率低下等问题,基于GPU并行计算开展了拓扑优化全流程加速设计方法的研究。对网格划分、刚度矩阵计算与组装、有限元求解等过程进行了并行加速,实现了高效高精度的体素网格划分及有限元过程的高效求解。此外,该方法针对拓扑优化设计过程的加速需求,对灵敏度过滤过程进行了并行加速处理。以300万体素单元的姿态推力器模型为设计对象,发现相比于Abaqus 2022软件的拓扑优化并行加速计算,本文所提方法的加速比提高了1259%,且两种方法的相似度极高,验证了所提方法的有效性与实用性。
关键词
拓扑优化;并行计算;GPU加速;符号距离场;稀疏矩阵;网格划分;
GPU-Based Parallel Computing Topology Optimization Method for Full-Process Accelerating Design
Citations
ZHANG Changdong, WU Yifan, ZHOU Xuanhua, et al. GPU-based parallel computing topology optimization method for full-process accelerating design[J]. Aeronautical Manufacturing Technology, 2025, 68(12): 34-41, 67.
Abstract
With the growing demand of large-scale aerospace equipment, efficient and high-precision large-scale topology optimization design becomes focal point in this field. To address the issues of massive computational load and low efficiency in existing large-scale topology optimization design, study of full-process accelerating design of topology optimization based on GPU parallel computation is carried out. The proposed method accelerates the entire process including meshing, stiffness matrix computation and assembly, and solving of finite element linear systems, achieving efficient and precise voxel meshing and high-efficiency solutions to finite element process. Moreover, the proposed method parallel accelerates the sensitivity filtering process aiming at the accelerating demand by the topology-optimization design process. The design case of a 3-million-voxel attitude thruster model demonstrates that compared with the parallel speep-up ratio of topology optimization by the Abaqus 2022 software, that of the proposed method increased 1259%, and the similarities of the two methods are extremely high, verifying the validity and practicality of the proposed method.
Keywords
Topology optimization
近年来,随着增材制造(Additive manufacturing,AM)技术的深入发展及广泛应用,拓扑优化设计方法成为航空结构减重增效的高效方法[
朱继宏, 周涵, 王创, 等. 面向增材制造的拓扑优化技术发展现状与未来[J]. 航空制造技术, 2020, 63(10): 24–38.ZHU Jihong, ZHOU Han, WANG Chuang, et al. Status and future of topology optimization for additive manufacturing[J]. Aeronautical Manufacturing Technology, 2020, 63(10): 24–38.
白影春, 景文秀. 基于滤波/映射边界描述的壳–填充结构多尺度拓扑优化方法[J]. 机械工程学报, 2021, 57(4): 121–129.BAI Yingchun, JING Wenxiu. Multiscale topology optimization method for shell–infill structures based on filtering/projection boundary description[J]. Journal of Mechanical Engineering, 2021, 57(4): 121–129.
陈小前, 赵勇, 霍森林, 等. 多尺度结构拓扑优化设计方法综述[J]. 航空学报, 2023, 44(15): 528863.CHEN Xiaoqian, ZHAO Yong, HUO Senlin, et al. A review of topology optimization design methods for multi-scale structures[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(15): 528863.
1-4
对形状复杂的结构,为减少网格形状误差对计算精度的影响,通常需要将结构网格划分得十分精细。高保真的网格划分大幅提高了仿真计算的成本,尤其对于拓扑优化,每一步都伴随一次有限元计算过程。因此,拓扑优化的计算成本成为阻碍大型复杂结构优化设计的一大约束。为了降低拓扑优化的计算成本、提高大规模复杂结构的拓扑优化计算效率,研究人员提出了多种方法对拓扑优化进行加速,其中最重要的方法之一是并行计算。
Borrvall等[
5
6
然而随着计算机技术的发展,具有更多计算核心的图形处理器(Graphics processing unit multithreading,GPU)在多线程并行计算中展现出更大的优势。Wadbro等[
7
8
9
10
11
12
13
14
随着对拓扑优化方法的不断研究与计算机性能的不断提升,工程结构设计目标也逐渐从尺寸小、特征简单、工况单一的结构向着复杂结构转变。高自由度和复杂工况结构往往具有大规模网格数量,常规计算方法效率低,难以满足实际工程的需要。因此,研究并行计算等拓扑优化加速技术对结构设计具有重要意义。
为此,本文提出了基于GPU并行计算的拓扑优化全流程设计方法,以结构轻量化设计需求为目标,将有限元分析和拓扑优化设计理论作为支撑,开发高效率的拓扑优化设计方法,对典型航空航天结构开展轻量化设计及性能验证,为高效拓扑优化设计的需求提供技术支撑。
高性能计算的需求推动了并行处理技术的重大进步。随着计算机技术的发展,GPU已经从专用的图形渲染硬件发展为能够处理广泛并行计算的多功能处理器。CPU主要设计用于低延迟、执行复杂的单线程任务,具有少量高性能计算核心,适合处理依赖性强、逻辑复杂的计算。相比之下,GPU可设计用于高吞吐量执行的大量并行任务,GPU拥有成千上万个计算核心,能够同时处理大量数据并行任务。两者之间的架构对比如图1所示。
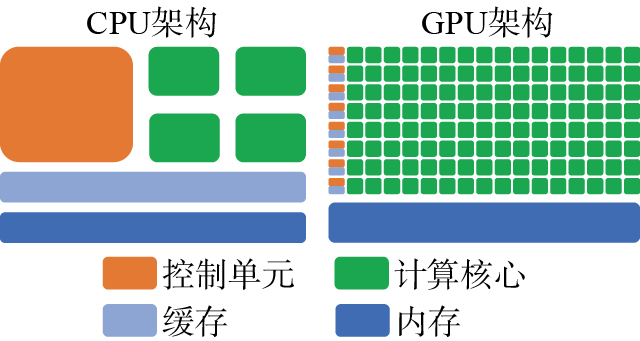
在将串行代码转化为并行代码的过程中,需要识别代码中可以并行执行的部分,该部分通常具有如下3个特性。(1)数据独立性:每个任务处理的数据是独立的,不依赖其他任务的数据。(2)计算密集型:任务主要涉及计算而非输入/输出操作。(3)高重复性:需要对大量数据重复执行相同的操作。
在拓扑优化过程中,网格划分、刚度矩阵组装与求解及灵敏度过滤等部分的数据处理均符合可并行的要求,识别各部分的并行性后,根据每个部分的数据要求将串行任务分解为可以并行执行的多个子任务,再将这些子任务映射到并行硬件上执行,从而实现GPU的并行加速。
网格划分是有限元分析前处理过程中的重要组成部分,网格质量直接影响有限元计算的效率及精确度。对于拓扑优化过程,为了实现后续的灵敏度过滤算法,需要使用均一、排列整齐的网格,因此,拓扑优化中常用体素六面体单元作为有限元网格单元。为加速网格划分效率,提出基于符号距离场(Signed distance field,SDF)的并行体素化网格划分方法,通过对模型设置体素包围盒,计算每个体素的符号距离并筛选获得体素网格,基于GPU加速实现该过程的并行化。
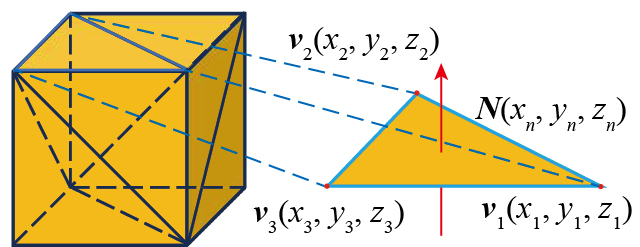
为了便于计算,采用STL(标准三角形网格模型,Stereo Lithography)格式的三维模型作为网格划分的输入。STL模型由多个三角面片组成,每个三角面片由3个顶点(v1、v2、v3)的坐标与面片方向的法向量组成,如图2所示。
并行体素化步骤如下。
(1)提取STL模型中所有三角面片的顶点坐标,并筛选出X、Y、Z方向的最大值与最小值,作为体素包围盒的对角线顶点vmax与vmin。
(2)根据设定的体素单元尺寸dx、dy、dz,计算3个方向的体素单元数量nx、ny、nz,以最小顶点vmin为起点进行节点阵列,获得体素包围盒网格,即
(3)每个GPU线程依次计算三角面片到包围盒中所有体素中心点的符号距离场,如下所示。
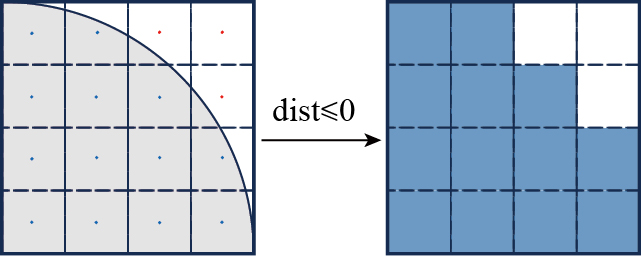
式中,p表示空间中的任意点;S表示集合模型的表面;M表示集合模型的内部;sign(p)表示点是否在集合模型中;dist(p)为点p到模型表面S的隐式距离,若dist > 0,说明该体素完全位于模型外,须删除该体素,若dist ≤ 0,则保留该体素。由此筛选出模型对应的体素网格,如图3所示。
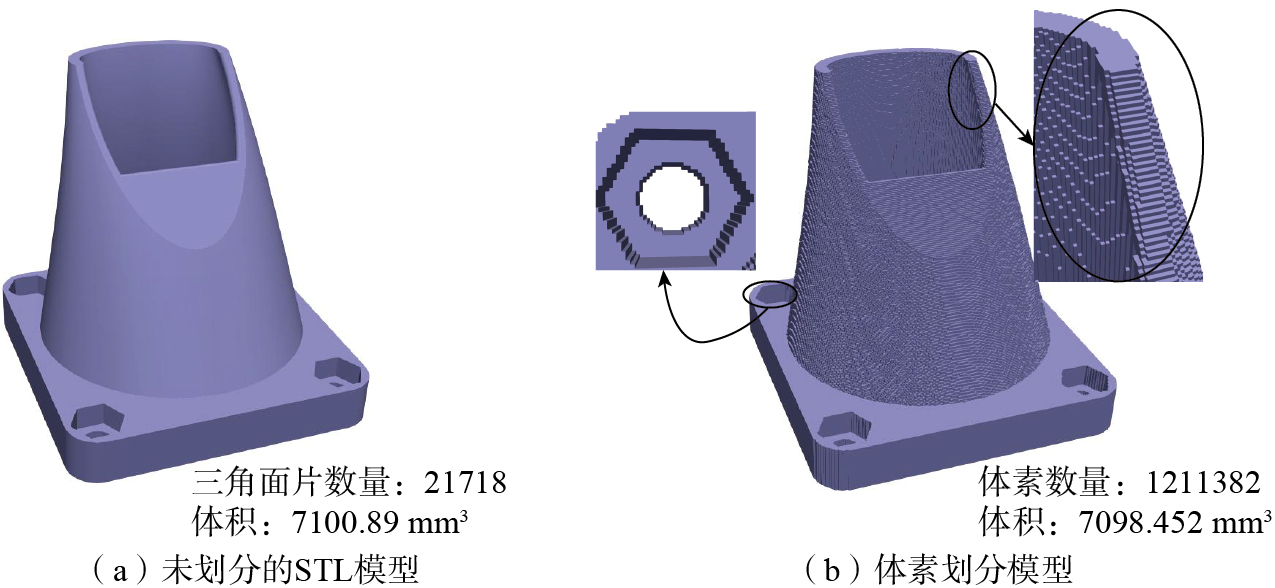
为了验证体素化方法的有效性,选取风扇管道模型进行网格划分验证,如图4所示,结果表明,两种模型的体积误差比为0.034%。
对于大规模网格数量的结构有限元计算问题,由于单元数量多、规模大,刚度矩阵求解和组装占用了拓扑优化全流程的大部分时间,因此采用基于GPU加速的并行刚度矩阵组装策略是提升计算效率的有效途径。刚度矩阵的组装过程中,涉及大量重复自由度数据的累加。对于六面体单元,总体刚度矩阵中的自由度由至少8个共用单元的合并而得。若直接采用并行组装方式,则容易产生大量的线程冲突,使得线程排队,增加计算时间,导致并行效果差。
为了解决并行组装中的写冲突问题,基于COO(Coordinate format)稀疏矩阵格式,提出了一种先计算矩阵索引,再执行压缩的并行刚度矩阵组装策略,主要步骤如下。
(1)根据COO稀疏矩阵格式,分别建立行索引向量Rows、列索引向量Cols,以及数据向量Data,其中Data由所有单元刚度矩阵合并后展开为一维而得。单个单元刚度矩阵为,其中M′为每个单元包含的节点数量,Dofs为单元的自由度数。将GPU线程按单元数量分成N组,每组中的GPU线程数量为N×(M′×Dofs)2,每个线程对应一个自由度,根据单元的节点编号数组nID分别计算行索引与列索引,如图5所示。

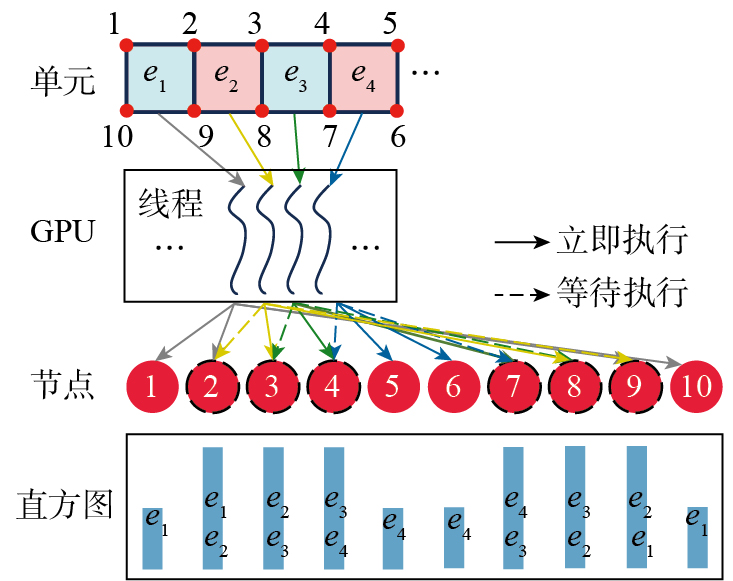
(2)由于共节点自由度单元的存在,不同刚度矩阵的值可能具有相同的行/列索引值,即写入线程会发生冲突。为了获得可用于计算的稀疏刚度矩阵结果,对上述矩阵进行去重操作。对于重复自由度,通过计算每个节点的对应单元进行去重。重复自由度在行/列上主要包含两种重复关系:相交节点处的自由度和相交线处的自由度。对于相交节点,只需计算每个节点被哪些单元使用,获得节点的单元编号eID,即可通过eID提取对应的单元自由度进行合并去重;而相交线处的自由度可以通过提取每两个节点的单元编号而得。其中节点的单元编号通过直方图算法(Histogram method)获得,重复节点的查找过程如图6所示。
(3)完成刚度矩阵K的组装后,根据平衡方程KU=F可以获得所有单元的位移场,其中,U为单元位移,F为载荷。求解该线性方程组是整个有限元计算中计算量最大、耗时最长的过程,因此使用基于GPU加速的PCG进行求解,相比于直接求解法,PCG法获得的迭代解在许用精度内所需的计算时间短、内存消耗低,且通常具有良好的可并行性,其核心思想是利用共轭方向加速收敛速度。
在求解线性方程组时,共轭梯度法通过迭代产生一系列逼近解,直到收敛到精确解或满足一定的收敛标准为止。每一步迭代中,使用前一步搜索方向的线性组合作为当前步的搜索方向,由此保证每一步都朝着最优解的方向前进,并且不会重复之前的搜索方向,从而提高收敛速度。对于一个线性方程组Ax=b,其计算流程如式(3)所示,其中初始搜索残差r0 = b – Ax0,初始搜索方向p0 = r0。
式中,k∈(0,1,2,…);αk为第k次迭代的搜索步长;xk为第k次迭代的解;βk为第k次迭代的共轭系数;pk为第k次迭代的搜索方向;b为已知条件,即F;A为已知的实对称正定矩阵,即K。
共轭梯度法的迭代次数主要取决于A的形状,若A = I + B,且rank(B)=r,则迭代次数的上限为r次。其中,I为单位矩阵;B为分解矩阵。当A的形状越接近单位矩阵,则收敛次数越少。而作为最常用的改进方法之一,PCG法通过添加预处理条件改进共轭梯度法,从而提高收敛速度。对于线性方程组Ax = b,选取A–1为近似矩阵M,则原方程组变为如下形式。
式中,M为预处理矩阵。若M=A–1,则rank(B)=1,此时共轭梯度法只需要一步即可收敛。但要获得这样的预处理矩阵,其计算量很大,因此预处理矩阵应选择尽可能接近A–1的矩阵,使得rank(B)的值尽可能小。对于线弹性问题的有限元稀疏刚度矩阵求解,使用雅克比预处理方法(即提取刚度矩阵的对角元素),该方法计算量小,处理过程简单。
拓扑优化方法旨在通过计算得到特定负载条件下,满足给定目标函数和一系列约束条件的最佳材料布局。优化过程中,需要将结构离散为有限个单元,并通过求解最优化问题来实现目标。本文所用的拓扑优化框架是以最小柔度为目标的变密度拓扑优化,该问题可以表示为
式中,x为结构的单元相对密度;c(x)为结构柔度函数,即优化问题中的目标函数;V(x)为单个单元的体积;Vfrac为最终规定的体积;p'为惩罚系数。
拓扑优化的均匀化理论引入了微观水平上的多孔复合材料作为实体材料和空材料(即没有材料)之间的过渡值。该理论将整个设计域定义为由无限多个周期性分布在基底材料中的带孔晶胞结构,其孔洞体积和数量可以由材料密度进行描述,由此可以将拓扑问题转化为尺寸问题,其中x=0对应于空材料,x=1对应于实体材料,0<x<1对应于微观水平上具有空隙的多孔复合材料。则单元材料的相关描述如下。
式中,Ei为通过插值后的单元弹性模量;Emin为空材料单元的弹性模量;E0为实体单元的弹性模量;xmin为空材料的相对密度;xi为单元的相对密度。为了保障计算的收敛性,空材料的弹性模量通常被定义为实体单元的10–9。
如果在拓扑优化中使用线性单元进行设计域的离散化,将使得灵敏度在单元之间不连续,在部分灵敏度变化较大的区域会出现“棋盘格”现象,这种结构不具有可制造性,该现象是由计算过程中对低阶单元的一阶项求导使得精度降低造成的,通常采用灵敏度过滤的方式解决这一问题。对于式(3)的拓扑优化问题,其灵敏度即为柔度对密度的一阶偏导,即
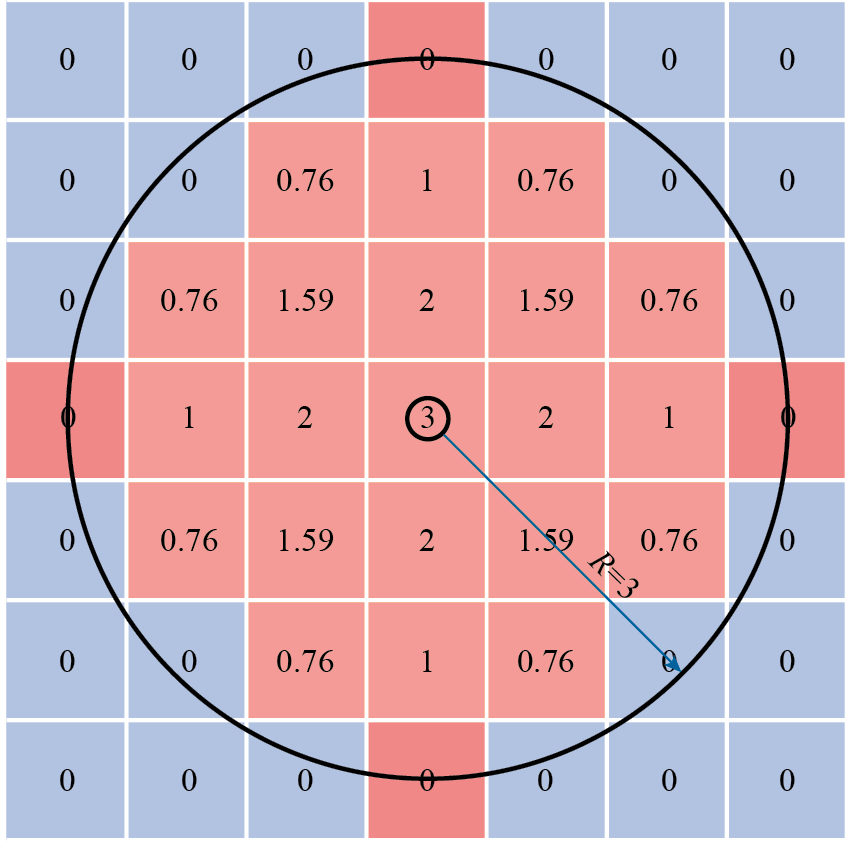
本文使用一种网格无关的灵敏度过滤方式,对过滤半径范围内的单元赋予距离权重因子,从而对单元灵敏度进行平均,该方法具有良好的过滤效果,如图7所示。
该方法的具体计算如下。
式中,ĉ为过滤后单元Ee的灵敏度;xe为单元Ee的密度;为距离权重,表示单元Ee过滤半径R范围内的邻近单元Ef对中心单元的影响值,与两单元的中心距离成反比,计算如下。
式中,Oe和Of分别为单元Ee与Ef的中心坐标,过滤前后效果如图8所示。

上述过滤方法中,过滤过程往往是经过单元遍历实现的,单元数量较多时遍历速度较慢,且并行效率低下。当过滤半径远小于整个设计域的尺寸时,大多数单元之间的距离权重为0。为了提高过滤过程的可并行性及压缩内存占用,通过构建稀疏矩阵的方式,在整个拓扑优化的开始阶段预处理每个单元与其邻近单元的距离权重稀疏矩阵H,每次迭代时使用矩阵H对灵敏度进行过滤,即
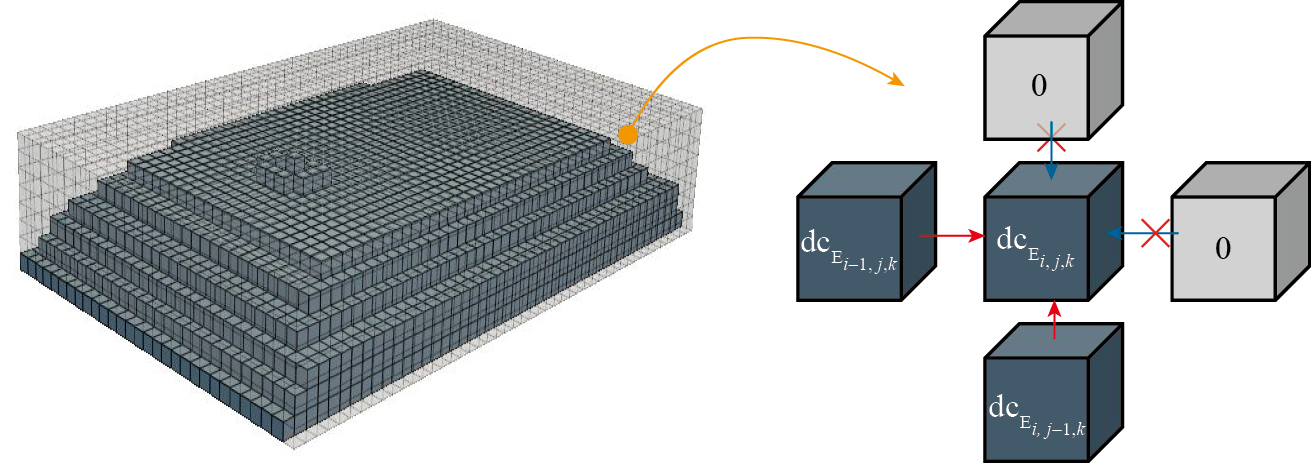
式中,Hs为每个单元的邻近单元距离权重和。对于N个单元的设计域,其权重矩阵的规模为N×N。在整个过滤过程中,每个单元灵敏度的过滤计算是独立的,因此具有良好的并行性。并行灵敏度过滤方法将GPU线程与单元对应,每条线程分别沿对应单元的X、Y、Z方向进行搜索,计算半径R范围内各个单元的距离权重因子hf与敏度dchf,并进行累加。
对于均匀分布的立方体结构,这一过程的实现较为容易;而对于非立方体模型,首先需要计算该模型的立方体包围盒,并对模型外的灵敏度与密度赋0,由此可以将模型的灵敏度与密度扩展为整个包围盒的灵敏度与密度。将距离权重因子与灵敏度绝对值的符号函数相乘,即可在过滤过程中排除包围盒外空材料单元的干扰,如图9所示。
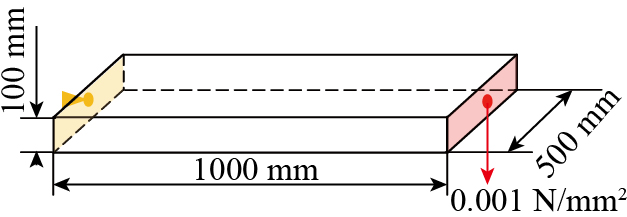
为了验证所建立的并行有限元计算框架的精度与计算性能,选取尺寸为1000 mm×500 mm ×100 mm的悬臂梁作为测试样件,工况条件为一端固定,一端施加0.001 N/mm2的面载荷,材料选择304钢,杨氏模量E为195 GPa,泊松比为0.29,测试样件尺寸与工况条件如图10所示。测试工作站配置为Intel Xeon Gold 6226R @2.9GHz 128G(英特尔),显卡为RTX 3090 24G(英伟达),所提出的方法基于Python编写,对比软件为Abaqus 2022,所有后续试验的软硬件条件均相同。
使用基于符号距离场的并行体素化网格划分样件,设置正六面体单元的尺寸为2.5 mm,划分后的六面体单元数量为106469,自由度数为352170。使用Abaqus 2022软件作为对比,单元类型选择C3D8,使用单精度计算,对比两种方法所得位移与Mises应力结果,如图11所示。
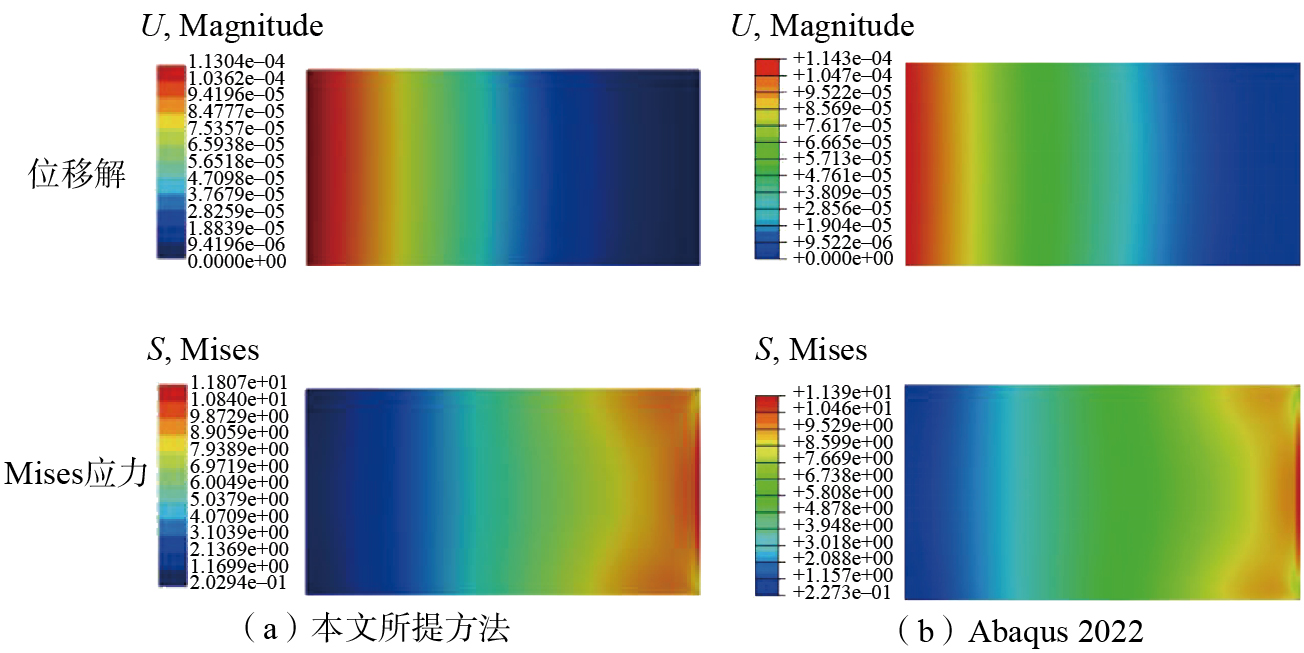
对比发现,对于正六面体单元,本文所提并行计算方法与Abaqus 2022方法所得最大位移解的差值为1.111%,最大Mises应力差值为3.532%。该误差来源于求解稀疏线性方程组时,PCG方法获得的是迭代解,而Abaqus 2022采用的是直接解法,在求解器的许用残差范围内(rtol<10–6),可以认为上述计算结果是准确的。
针对上述模型进行六面体网格划分,得到网格数量从10000到2281248不等的模型。对每种尺寸的网格模型分别计算10次,取10次计算时间的平均值作为平均计算时间。使用Abaqus 2022软件进行计算时间的对比,单元类型选择C3D8单元,分别在串行与并行计算模式下进行计算,其中并行计算模式选择20核+GPU。不同网格数量六面体的计算时间与加速比结果见图12。其中,Abaqus单核为Abaqus 2022的串行计算模式,Abaqus CPU+GPU并行为Abaqus 2022的并行计算模式,本文框架并行是指所建立的并行有限元计算框架,本文框架–Abaqus并行加速比则为本文框架与Abaqus并行加速计算速度的比值。
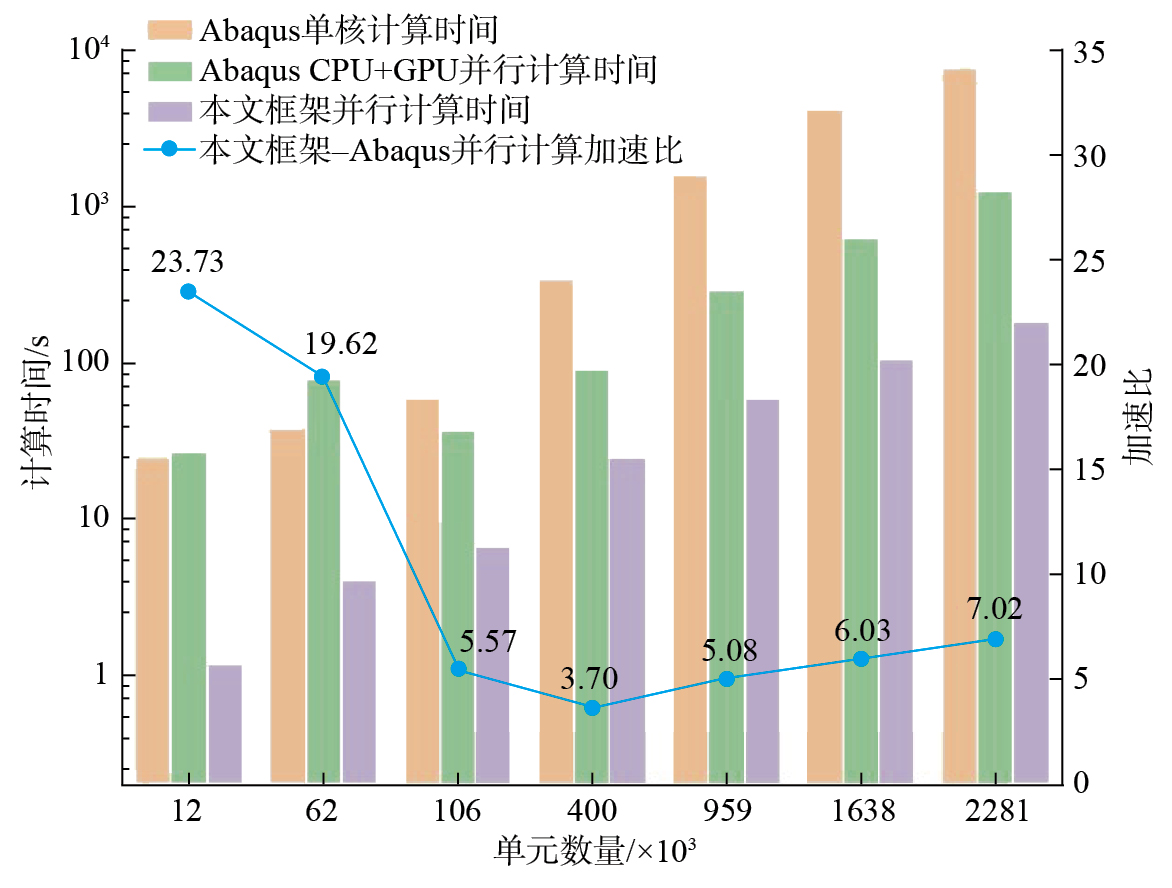
由图12可知,对于最大单元数量约为2000000的六面体单元有限元计算问题,本文框架并行的计算时间约为3 min,相比Abaqus 2022并行计算模式(约22 min),本文所提方法的加速比显著提高,且加速比随模型单元数量的增长逐渐提高。
卫星推力器是现代航天器中至关重要的组件之一,用于提供推力,控制卫星轨道、姿态及进行轨道修正。随着卫星在轨控制精度的提高和推进系统中推力器组件结构形式的多样化,其对应的轻量化需求也进一步提高。卫星总体和姿态推力器框架如图13所示。
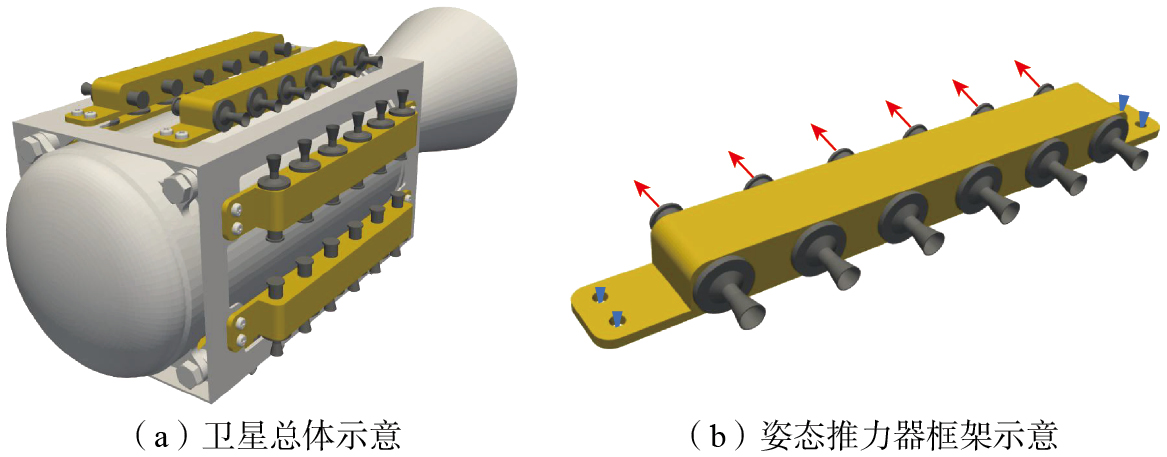
该卫星姿态推力器的框架尺寸为21.5 mm×210 mm×17.1 mm,材料为AlSi10Mg,性能如表1所示。单个姿态推力器框架的质量为0.128 kg,共8个,以对称形式围绕在主推力器框架周围。每个框架包含6个姿态推力器,相同时段内仅有1个推力器在工作状态,平均推力为250 N,超载情况下的最大推力为300 N。由于所有姿态推力器框架构型统一且呈对称分布,因此选择对单个框架进行拓扑优化。
| 弹性模量/GPa | 泊松比 | 密度/(kg/mm3) | 屈服强度/MPa |
|---|---|---|---|
| 60 | 0.33 | 2.6711×10–6 | 320 |
在实际工作过程中,考虑该结构的所有姿态推力器都产生推力的极限情况,对每个推力器的位置施加相同的均匀载荷,总计推力F为300 N。对模型进行拓扑优化预处理后,再进行网格划分。为保证优化结构的准确性,选取六面体单元的大小为0.25 mm,划分后单元数量为3238294,预处理后的模型如图14所示。

为验证本文拓扑优化方法的有效性,选择Abaqus 2022拓扑优化模块进行对比,并行计算模式选择20核+1 GPU,算法选择SIMP方法,选取优化目标的体积分数Vfrac=0.35。两种拓扑优化方法的结果如图15所示。

由图15(a)可知,利用本文方法进行拓扑优化后,被去除的低密度单元主要分布在各姿态推力器之间,使得框架中间形成数个空腔结构,且空腔四周包含细小的加强筋;两侧螺栓连接处应力较大,该部分低密度单元数量较少。对比Abaqus 2022优化结果(图15(b))可知,其整体结构与本文方法所得结果有一定相似性,在框架中间形成了空腔结构,主要区别在于,Abaqus 2022优化后的推力器末端附近产生了更多细小杆径,而上、下表面结构尚未形成加强肋条。
两种方法的迭代过程对比如图16所示。采用本文方法的优化过程经过49步迭代完成收敛,结构应变能由初始的12090.228 N·mm降至686.443 N·mm,每个迭代步的平均计算时间为368 s,共计用时18032 s;采用Abaqus 2022的优化过程经过63步迭代完成收敛,结构应变能由10753.959 N·mm降至632.111 N·mm,每个迭代步的平均计算时间为3890 s,共计用时245070 s。二者迭代步数的误差来源于使用了不同的求解器,本文方法与Abaqus 2022的数据对比如表2所示。可以看出,在计算时间上,本文方法具有较大优势,同样采用GPU并行计算的情况下,相比Abaqus 2022的拓扑优化全过程,本文所提方法的加速比提高了1259%。
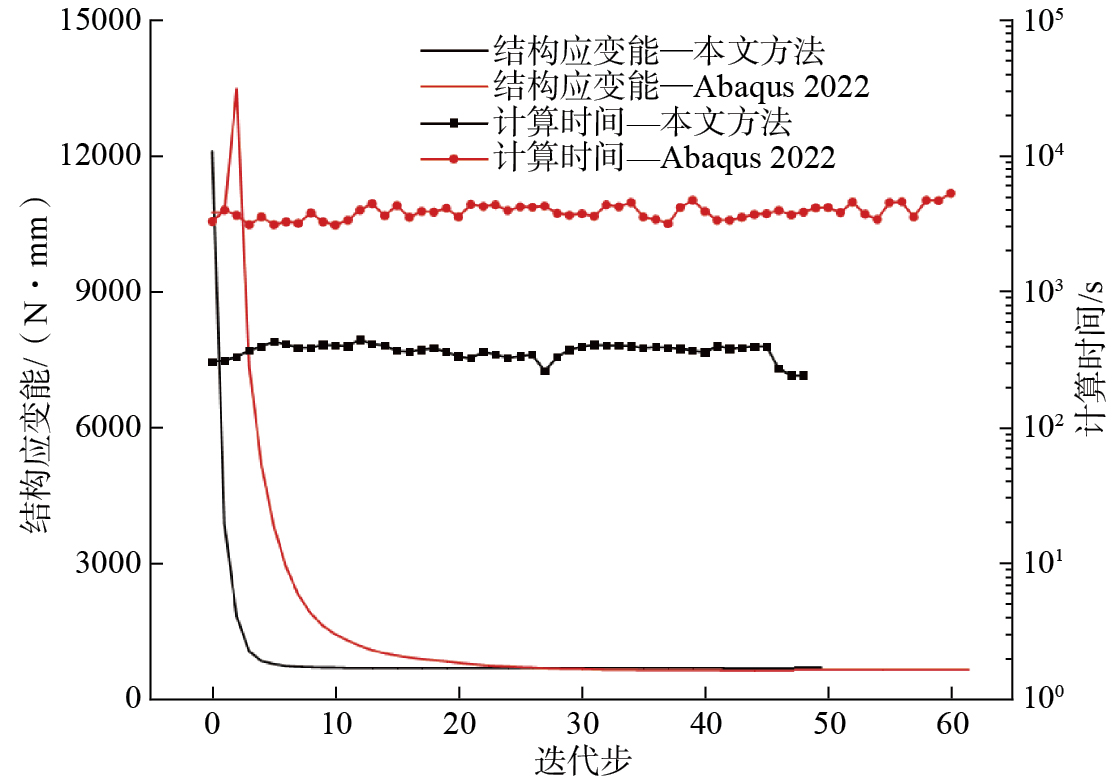
| 方法 | 收敛迭代步数 | 收敛时间/s | 原始结构应变能/(N·mm) | 优化后结构应变能/(N·mm) |
|---|---|---|---|---|
| 本文方法 | 49 | 18032 | 12090.228 | 686.443 |
| Abaqus 2022 | 63 | 245070 | 10753.959 | 632.111 |
(1)通过GPU并行计算方法对有限元计算过程进行加速,提出了基于符号距离场的并行体素网格划分方法,实现了高精度的体素网格划分。
(2)提出基于GPU并行的刚度矩阵计算与组装算法和预处理共轭梯度(PCG)求解算法,实现有限元过程的高效求解,在大规模的条件下,本文所提方法的计算效率较Abaqus 2022软件显著提高,加速效果明显。
(3)针对拓扑优化流程,提出基于GPU并行的灵敏度过滤策略,通过生成包围盒,实现对任意三维模型的高效灵敏度过滤。
(4)利用本文所提基于GPU并行计算的拓扑优化全流程设计方法对卫星姿态推力器框架结构进行拓扑优化设计,与Abaqus 2022软件的拓扑优化结果进行对比,本文方法所得的全过程加速比提高了1259%,且两种方法最后的优化结果相似度极高,验证了本文所提方法的有效性与实用性。
 | 张长东 教授,博士生导师,主要从事结构轻量化设计和增材制造技术研究。 |
参考文献
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |