TA18 钛合金具有密度小、比强度高、耐腐蚀、抗蠕变及抗疲劳性能好等优异特性,广泛应用于航空航天、汽车、造船等领域的燃油、液压和引气等管路系统[1]。TA18钛合金是一种近α型钛合金,名义成分Ti-3Al-2.5V,密度为4.47 g/cm3,室温弹性模量为118~123 GPa,硬度为15HRC~17HRC,相变点温度为925 ℃[2-4]。飞机发动机系统管路,特别是用于液压系统的高压管路,其性能和安全可靠性不仅影响飞机的操纵性,还直接影响飞机的安全[5]。
近年来,随着国内管材生产技术的进步,以及数字化自动弯管机的普及应用,管材成形的研究与行业应用已非常成熟,但其研究与应用主要集中于不锈钢导管和铝合金导管数控弯曲。
在国内钛合金管材领域,高强钛合金导管,尤其是TA18 型号的研制工作起步相对较晚。与之相应的工程化应用研究也是近些年才随着高强钛合金管制造工艺愈发成熟、稳定,而逐步开展起来的。相较于铝合金管与不锈钢管,钛合金管具备更高的强度,但延伸率欠佳。
在弯曲加工时,弯曲段外侧容易出现壁厚减薄的情况,严重时甚至会拉裂;弯曲段内侧则容易产生褶皱。同时,弯曲段的截面还会发生畸变,导致椭圆度增大,并且弯曲夹持力卸载后会引发严重回弹。上述这些难题给TA18 高强钛管的弯曲成形带来了极大挑战。
目前,导管数控弯曲成形是使用较为广泛的导管成形工艺,成形质量较高,成形效率也较为可观。国内各主机厂和高校针对导管数控弯曲开展的相关研究也取得了一定成果。靳舜尧等[6]应用PamStamp 仿真软件对5A02 铝合金管的数控弯曲过程进行了模拟仿真计算,研究了模具位置关系和导管弯曲角度对弯曲段外侧壁厚减薄率、椭圆度以及回弹的影响;同时进行数控弯曲成形试验,研究分析了芯棒伸长量与壁厚减薄、截面畸变之间关系;试验结果与有限元模拟结果一致,并在弯曲试验中获得理想的弯曲效果。李恒等[7]在获得高强TA18 钛管数控弯曲非线性回弹和伸长规律的基础上,针对回弹角度、回弹半径的补偿方式和导管轴向延长控制方法开展研究;同时通过模拟应用对成形控制方法进行验证,该方法能够满足多弯管件装配精度要求,证明所提出的成形精度控制方法是可靠的。
国内相关学者针对数控弯曲成形工艺做了大量研究,对铝合金管的研究已经相当成熟,但对于钛合金管,尤其TA18 高强钛合金薄壁管弯曲成形的研究较少。因此,针对TA18 钛合金管材开展数控弯曲性能研究是很有必要的。
目前在企业生产中,TA18 钛合金管材的弯曲成形一般采用数控绕弯工艺。但由于绕弯过程中存在多种影响因素耦合作用,弯曲后结果差强人意,较难控制成形质量。基于企业实际生产情况,结合国内管材绕弯的研究现状,本文采用单向拉伸试验与有限元仿真相结合的方法进行研究,主要涉及的参数有各模具与管材之间的摩擦系数、间隙和弯曲速度等。
管材力学性能是影响管材数控绕弯成形行为的关键因素之一。不同材料、不同轧制方向、不同截面的管材试样,其力学性能差别较大。目前钛合金管材的评价标准主要是针对轴向性能进行评价[8]。本文旨在通过单向拉伸试验研究TA18 钛合金管材的拉伸力学性能,获得拉伸变形阶段的应力-应变曲线,对试验数据进行拟合处理,计算出TA18 钛合金管材的真实应力、应变和基本力学性能参数。利用ABAQUS 软件对TA18 钛合金管材绕弯过程进行有限元分析,模拟不同参数对管材成形后壁厚减薄程度及椭圆畸变率的影响情况。
1 纵向拉伸试验
1.1 试样准备
如图1所示,本试验采用规格Φ8 mm、壁厚0.6 mm的TA18 钛合金管材为研究对象。纵向拉伸试验中同种规格选取3 种不同的拉伸速率,每种拉伸速率下测试3 个样品,保证3 个重复样,共计9 个试样,试验结果取其平均值。
图1 试样规格图(mm)
Fig.1 Specimen specification diagram (mm)
1.2 试验方法及设备
纵向拉伸试验及操作方法按照GB/T 228.1—2021执行[9]。拉伸试验在MTS Exceed E45.305 电子万能试验机上进行,如图2所示,在样品上夹持标距为50 mm的纵向引伸计来记录拉伸应变。

图2 电子万能试验机
Fig.2 Electromechanical universal testing machine
随着电子万能试验机对TA18 钛合金管试样施加的轴向拉力不断增大,试样最终会发生失效断裂,图3为TA18 钛合金部分试样拉伸断裂的形貌图。

图3 部分试样拉伸断裂形貌图
Fig.3 Morphological images of some samples after tensile fracture
1.3 不同速率下试样真实应力–应变曲线
拉伸试验中,拉伸速率分别为5 mm/min、10 mm/min、15 mm/min,具体测试结果如表1和图4所示。可以看出,拉伸速率为15 mm/min 时屈服强度和抗拉强度最大,但延伸率最小;拉伸速率为5 mm/min 时延伸率最大;拉伸速率为10 mm/min 时屈服强度和抗拉强度最低。各速率下测得的屈服强度平均值为855.38 MPa,延伸率平均值为15.63%,抗拉强度平均值为1068.45 MPa。
表1 拉伸试验参数
Table 1 Tensile test parameters

拉伸速率/(mm/min) 屈服强度/MPa 延伸率/% 抗拉强度/MPa 5 852.59 16.52 1068.45 10 837.92 15.31 1044.43 15 875.62 15.06 1092.48
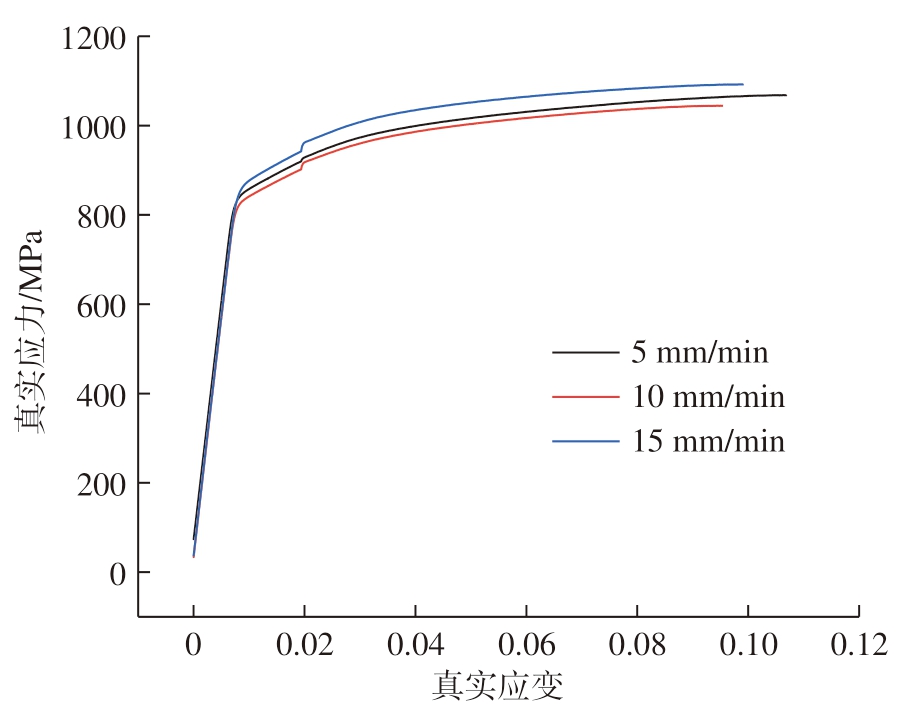
图4 Φ8 mm 试样真实应力–应变曲线
Fig.4 True stress – strain curve of Φ8 mm sample
2 TA18 钛合金导管成形仿真模型的建立
2.1 拉伸材料模型的构建
通过单向拉伸试验得到的数据,以工程应力σ 取代轴向载荷F,即
式中,A0 为管材截面积。以工程应变ε 取代伸长量Δl,即
式中,l0 为标距长度。
材料真实应力由式(3)计算获得。
以Φ8 mm 的管材为例,弹性阶段材料参数由式(4)拟合获得。
式中,E 为斜率,即弹性模量,MPa。拟合范围从应力初始点到屈服点。塑性阶段材料参数由式(5)拟合获得。
式中,K为强化系数;ε0为塑性应变;b为材料常数;n为硬化指数。屈服点至强度极限之间为拟合数据范围。
将真实应力-应变试验数据导入Origin 软件进行处理,与式(4)和(5)拟合并得到所需的参数,图5 为管材弹性和塑性部分拟合图。
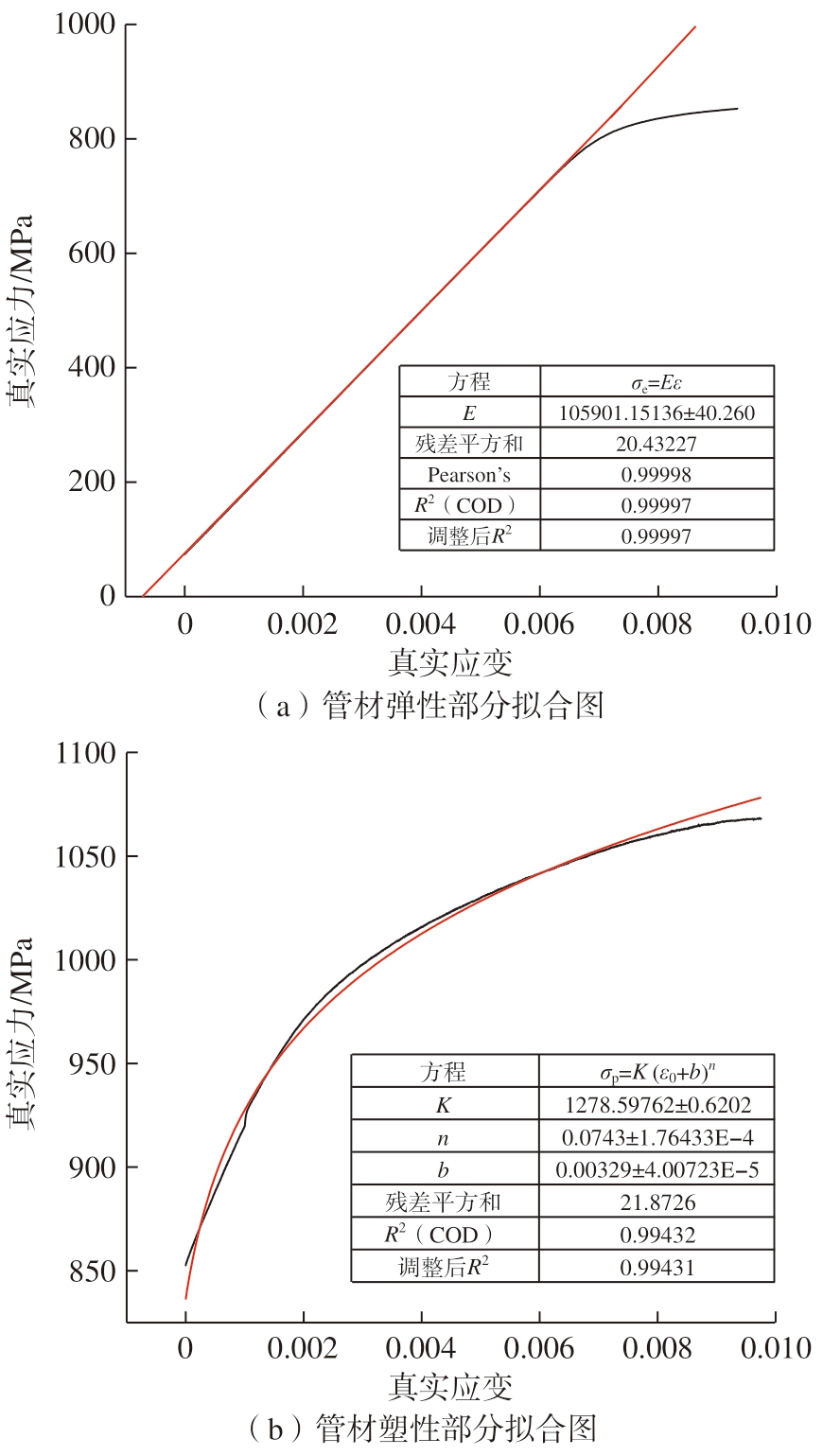
图5 Φ8 mm 管材弹性和塑性的部分拟合图
Fig.5 Partial fitting diagrams of the elasticity and plasticity of the Φ8 mm pipes
由Φ8 mm 管材试验数据得到的应力-应变曲线拟合出的弹塑性材料模型分别为
式(6)模型处于弹性阶段,材料变形可逆,变形趋势为线性;式(7)为塑性材料模型,材料变形不可逆,塑性阶段通常发生在弹性极限之后,当应力超过屈服强度时,材料进入塑性变形阶段。
2.2 几何模型的建立
由于圆管弯曲是一个集几何非线性、材料非线性和边界条件非线性等特征于一体的复杂塑性变形过程,建立既符合实际又能兼顾计算精度和效率的圆管弯曲三维有限元模型是实现圆管弯曲成形模拟的关键。几何模型的建立(生成模具及管坯的几何模型)为有限元划分网格提供载体。基于ABAQUS 软件平台,建立钛合金典型件绕弯全过程模拟有限元模型[10]。零件加工参数:TA18 钛合金、零件规格Φ8 mm×0.6 mm×140 mm、弯曲角度45°。
2.2.1 圆管坯几何模型的建立
在弯曲过程中,采用壳单元对模型进行计算分析,比采用实体单元所得到的计算结果精度更高,而且计算量更小,所以管坯单元的属性选为壳单元,并设定其厚度。本文研究的是管坯的变形情况,因此将管坯定义为变形体,在弯曲过程中,管坯既有随弯曲模的转动,又有自身的变形,因此,在模拟中以管坯为基准建立局部坐标,生成的管材模型如图6所示。

图6 管件几何模型
Fig.6 Pipe fitting geometric model
2.2.2 数控绕弯模具几何模型的建立
数控弯曲成形是多模具耦合的复杂非线性成形过程,因此,管与模具间的接触设置是准确建模的关键因素之一[11]。加工时将管坯的一端置于夹模,弯曲模在数控程序的驱动下实现管材弯曲成形。数控绕弯不仅能提高管材弯曲的成形质量,还可以通过程序控制实现连续弯曲,完成复杂的空间弯管[12]。圆管绕弯成形过程的模具由弯曲模、压块、夹块、防皱块、芯模等组成,各模具尺寸根据管坯的尺寸设计,在考虑管坯壁厚的同时,还需要根据装配时的间隙要求来设计模具的合理尺寸。在ABAQUS 中,刚体的自由度完全由各自的参考点确定,即各个参考点的自由度代表各成形模具的自由度。根据各模具的实际尺寸,建立简化后的模型,假设弯曲模、压块、夹块、防皱块与管坯之间的间隙值均设置为0,只有芯模与管坯之间的间隙值为0.2 mm,各模具的具体几何属性及设定原则见表2。
表2 弯曲模具主要参数
Table 2 Main parameters of the bending die mm
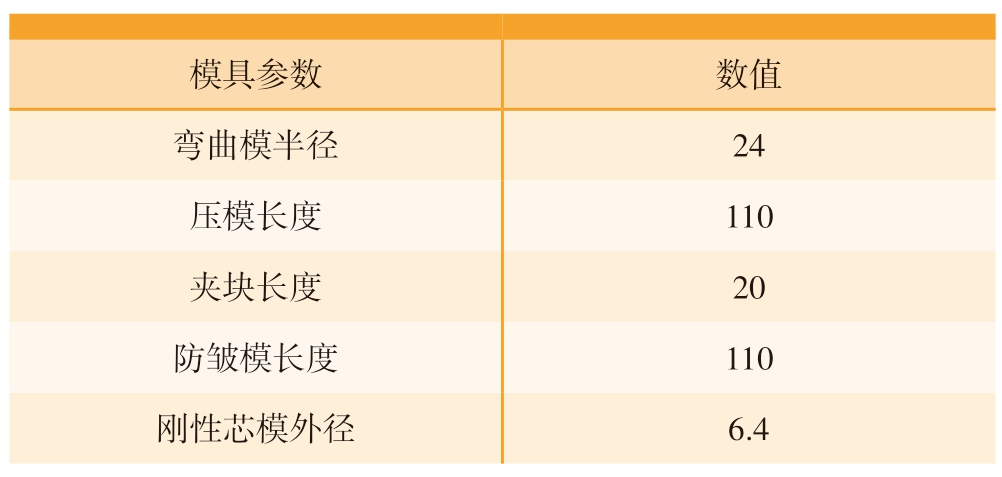
模具参数 数值弯曲模半径 24压模长度 110夹块长度 20防皱模长度 110刚性芯模外径 6.4
(1)弯曲模。
设计弯曲模的弯曲半径为24 mm,根据管坯的尺寸,弯曲模设计如图7所示。管材的弯曲角度为45°,因此在设计弯曲模时,弯曲部分的角度应大于45°,将弯曲模的几何中心点设置为参考点。
图7 弯曲模的几何模型
Fig.7 Geometric model of bending die
(2)压模。
压模也称为助推块,在弯曲过程中起到控制管材变形及助推作用。根据管坯的尺寸,压模设计如图8所示,在压模上定义一个参考点。

图8 压模的几何模型
Fig.8 Geometric model of the stamper
(3)夹块。
夹块在弯曲过程中起到控制管材变形及辅助弯曲的作用。根据管坯的尺寸,夹块设计为图9所示的结构,在夹块上定义一个参考点。由于夹模要在弯曲过程中始终控制管坯的成形,因此夹块的参考点须与弯曲模的参考点重合,以保证在绕弯成形过程中管坯、夹块与弯曲模能够保持同步运动。
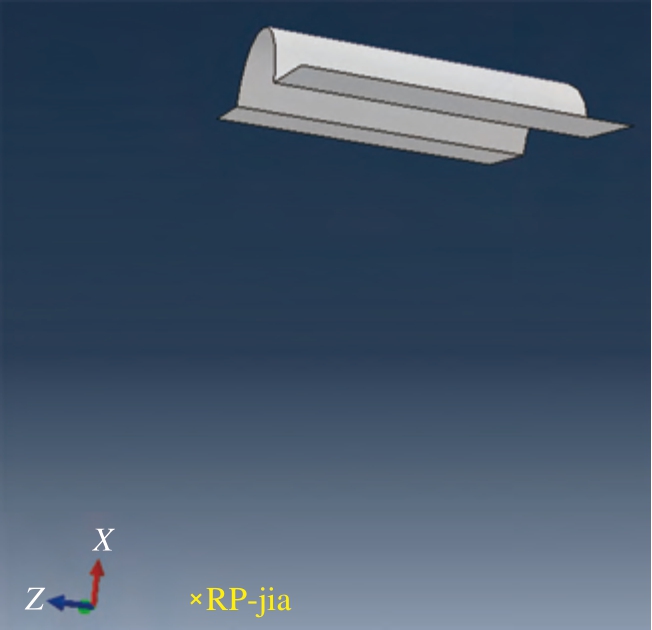
图9 夹块的几何模型
Fig.9 Geometric model of clamping block
(4)防皱模。
防皱模在弯曲过程中起到抑制管材起皱的作用。根据管坯的尺寸,防皱模设计为图10所示的结构,在防皱模上定义一个参考点。

图10 防皱模的几何模型
Fig.10 Geometric model of anti-wrinkle die
(5)刚性芯模。
刚性芯模包括芯棒与芯球,芯模的形状与圆管的截面形状一致。有限元建模时,为减少芯棒对管坯表面造成痕迹,芯棒的周边棱角处应采用圆角处理,并将实际芯棒和芯球进行简化,因此将芯棒设计为图11(a)所示的结构,在芯棒上定义一个参考点。在本文的模拟研究中,芯棒伸出量为1 mm。
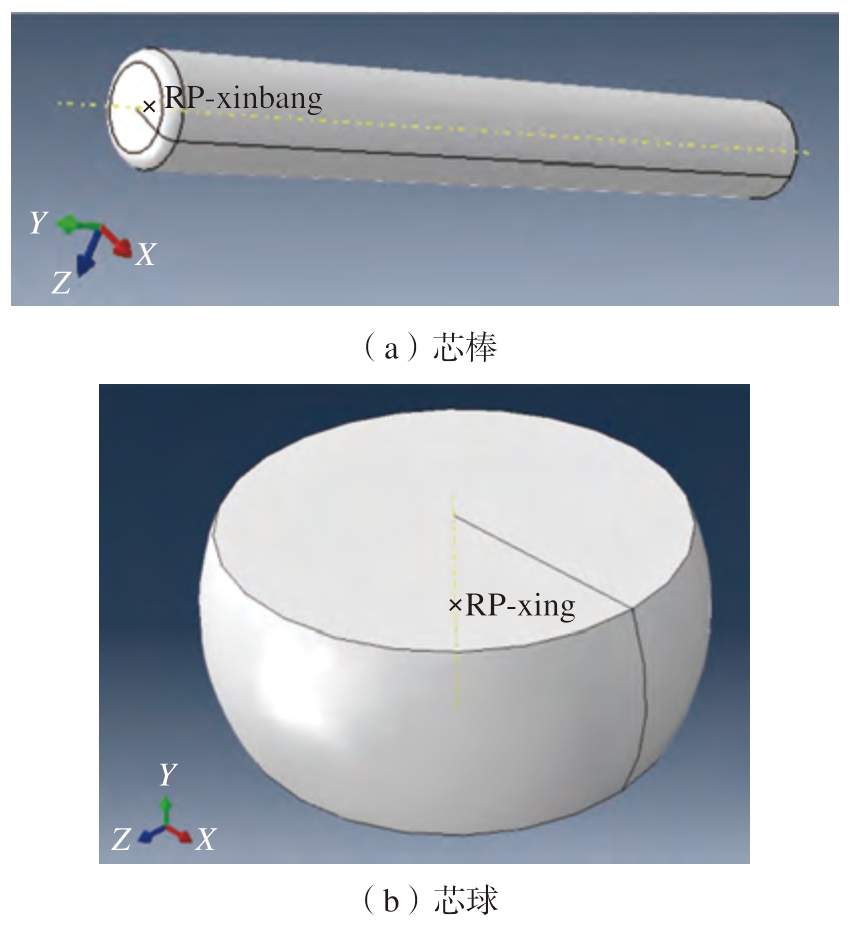
图11 刚性芯模的简化模型
Fig.11 Simplified models of the rigid mandrel
为提高管坯弯曲质量,采用芯棒的同时,也应采用与之结构和尺寸相适应的芯球。将芯球进行简化,芯球的各属性设置与芯棒相同,在芯球的几何中心处定义一个参考点,如图11(b)所示。
由于在模拟过程中,芯球也要随弯曲模运动而发生运动,因此要在芯球上定义一个转动惯量。建立的简化模型将芯棒与芯球之间,以及芯球与芯球之间定义为连接属性。在创建连接属性时,在基本属性中,定义平移类型为链接,旋转类型为弯-扭,如图12所示。再分别做芯球与芯棒,以及芯球与芯球间的连接线,将连接赋予到线上。
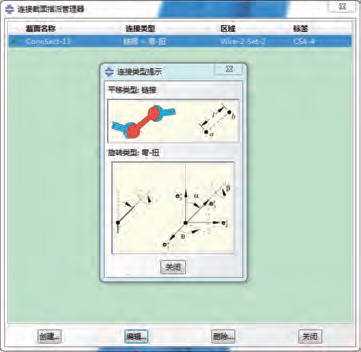
图12 选取的连接方式
Fig.12 Selected connection method
2.2.3 材料属性的定义
由于刚体不需要定义材料属性,因此在TA18 钛合金管绕弯模型中只需定义管坯的材料属性,根据不同规格的管径选取不同材料属性。
2.2.4 模型装配
在各部件建立过程中,每个几何构件都有独立的坐标且均独立于其他部件。装配模型的建立基于各部件间的联系及相互的作用关系,并定义在一个整体坐标下,圆管绕弯成形装配模型如图13所示。

图13 圆管绕弯成形装配模型
Fig.13 Assembly model of round tube rotary draw bending
2.2.5 接触的定义
首先确定各个接触平面间的接触属性,各模具与管坯接触对摩擦系数选择如下:弯曲模弯曲部分、压块、防皱块与管坯间的摩擦系数均为0.2;带有柔性芯球的刚性芯模与管坯间的摩擦系数为0.02;为防止在弯曲过程中发生打滑,将夹块、弯曲模镶块部分与管坯间的摩擦系数设置为粗糙无穷大。将各模具与管坯的接触定义为几个接触对,所定义的接触对之间的摩擦条件如表3所示,同时刚体一般被设为主面,而变形体被设为从面。
表3 接触对之间的摩擦条件
Table 3 Friction conditions between contact pairs
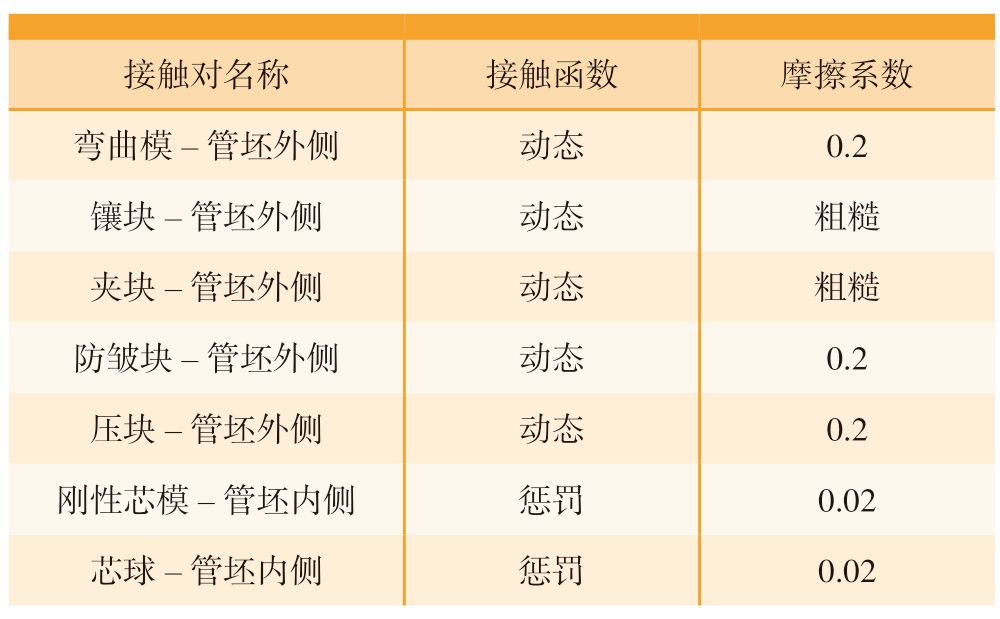
接触对名称 接触函数 摩擦系数弯曲模-管坯外侧 动态 0.2镶块-管坯外侧 动态 粗糙夹块-管坯外侧 动态 粗糙防皱块-管坯外侧 动态 0.2压块-管坯外侧 动态 0.2刚性芯模-管坯内侧 惩罚 0.02芯球-管坯内侧 惩罚 0.02
2.2.6 边界条件的处理
夹块与弯曲模连同管坯一起绕着弯曲模中心轴以角速度(ω = 0.471 rad/s)做旋转运动,它们的刚体运动边界载荷和约束都定义在各自的参考点上,管坯的绕弯过程需要动力,所以在压块上赋予一个指向绕弯方向的轴向速度(ν = 12 mm/s),用以推动绕弯过程的进行,压块助推速度取管坯外侧的最大切线速度。添加防皱块防止管坯在弯曲过程中起皱,运动方式设置为固定。
在边界处理这一步中,除了以上定义的载荷及约束外,弯曲模、夹块、压块、防皱块及弹性芯模的其他自由度均为0。
2.2.7 单元的选取及网格的划分
管材绕弯过程大多为不可变形的几何体,因此需采用三维、离散型刚体模型,单元类型选用4 节点四边形壳单元。其中弯曲模、夹块和防皱块划分为1.5×1.5的网格,压块划分为1.5×1.5 的网格,刚性芯棒划分为2×2 的网格,芯球划分为1×1 的网格。管坯在绕弯成形过程中发生变形,所以将管坯定义为变形体。管坯单元属性为壳单元,管坯单元类型选用可变形的4 节点四边形壳单元,该单元类型具有沙漏控制和缩减积分功能,将管坯划分成1.5×1.5 的网格,如图14所示。

图14 模型网格划分
Fig.14 Model meshing
2.2.8 有限元模型的建立
基于上述对管坯与模具的单元属性、结构与基本尺寸、接触摩擦系数与边界条件等建模过程关键问题的处理,所建立的TA18 钛合金管有限元模型如图15所示。

图15 管材绕弯成形有限元模型
Fig.15 Finite element model of pipe bending forming
3 工艺参数对TA18 钛合金导管弯曲成形的影响分析
截面椭圆畸变率为
式中,D1为变形后的管材截面长轴距离;D2为变形后的管材截面短轴距离;D0为未变形的管材外径。
壁厚减薄率为
式中,t1为变形后的壁厚;t0为未变形的壁厚[13]。
3.1 摩擦系数对成形质量的影响
保持其他工艺参数不变的情况下,分别改变管材与弯曲模的摩擦系数、管材与防皱块的摩擦系数、管材与压紧块的摩擦系数,研究管材与模具摩擦对TA18 钛合金管数控绕弯成形最大截面畸变和最大外侧壁厚减薄的影响规律。
3.1.1 弯曲模与管材之间摩擦系数对成形质量的影响
图16所示为45°弯曲角度下,管材与弯曲模摩擦系数对TA18 钛合金管材数控绕弯成形最大截面畸变率和最大外侧壁厚减薄率的影响规律,此时压模和防皱块与管材之间的摩擦系数固定为0.2。可以看出,当摩擦系数从0.05 增加到0.1 时,管材最大截面椭圆畸变率保持平稳,摩擦系数从0.1 到0.25 时,管材最大截面椭圆畸变率呈现大幅下降趋势;而最大外侧壁厚减薄率曲线呈波动趋势,但整体变化较小。这是因为管材在成形过程中,弯曲模对管材外表面产生切向摩擦,同时防皱块也给予摩擦力,二者合力向下,可以抵消一部分引起该表面凹陷变形的压应力,增加弯曲模与管材之间摩擦系数,增强了弯曲模对管材的切向摩擦作用。因此,更大的摩擦系数导致管材弯曲变形区域的截面畸变程度较为轻微,畸变率变小。
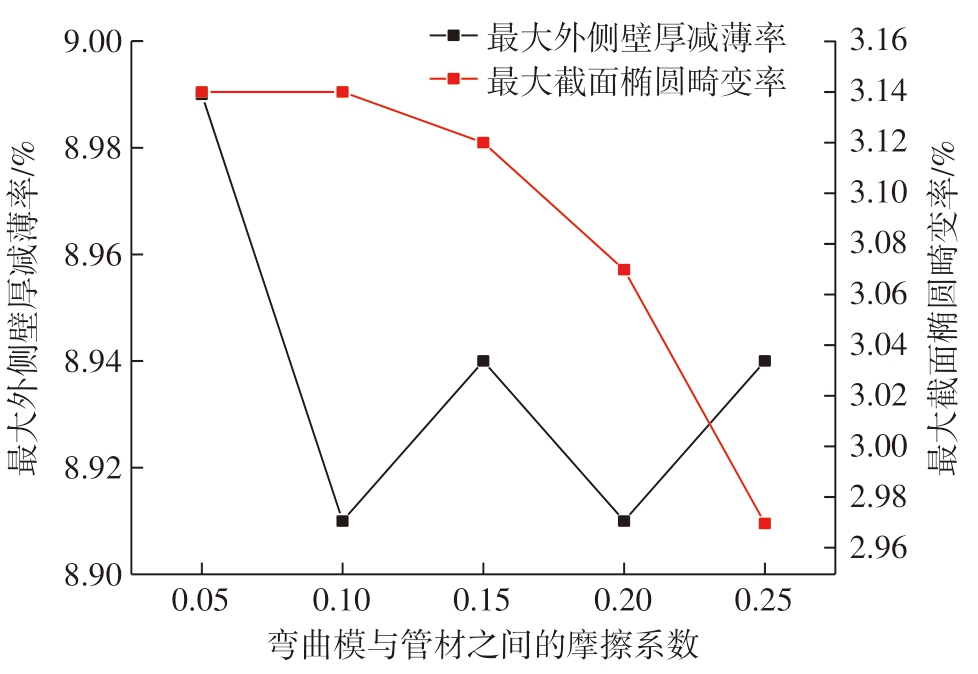
图16 弯曲模与管材之间摩擦系数对成形质量的影响
Fig.16 Effect of friction coefficient between bending die and pipe on forming quality
3.1.2 压模与管材之间摩擦系数对成形质量的影响
图17所示为45°弯曲角度下,管材与压模之间的摩擦系数对TA18 钛合金管数控绕弯成形最大截面椭圆畸变率和最大外侧壁厚减薄率的影响规律,此时弯曲模、防皱块与管材之间的摩擦系数固定为0.2。可以看出,最大截面椭圆畸变率先上升后略微下降,然后上升再下降,但整体变化并不大。最大外侧壁厚减薄率在摩擦系数0.05 到0.1 时略微下降,然后呈现一直上升的趋势,说明压模与管材之间的摩擦系数应选择一个合适的值。
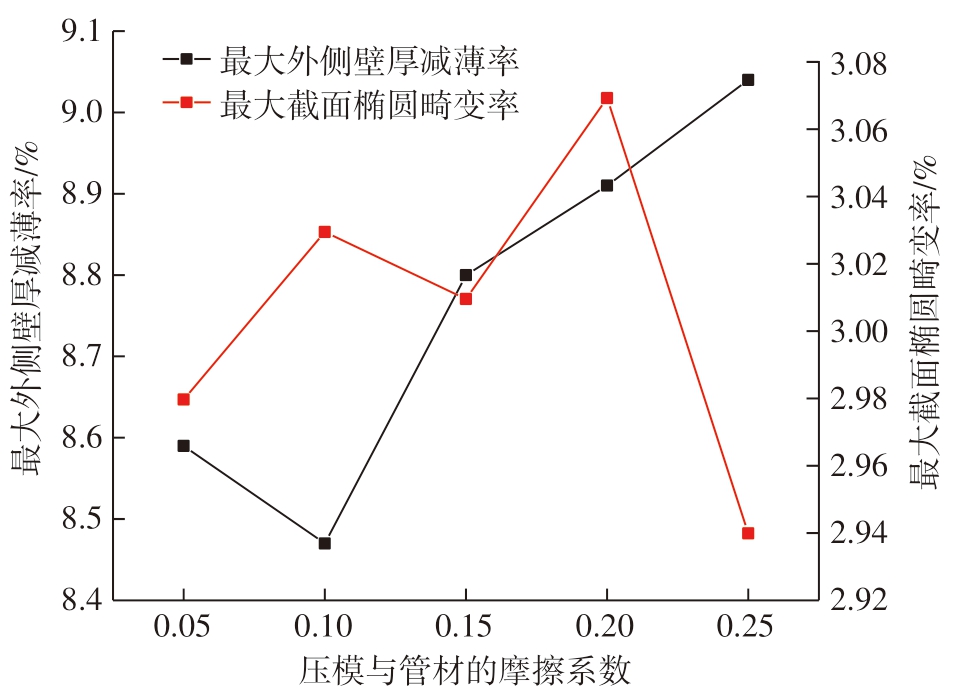
图17 压模与管材之间摩擦系数对成形质量的影响
Fig.17 Effect of friction coefficient between pressing die and pipe on forming quality
3.1.3 防皱块与管材之间摩擦系数对成形质量的影响
图18所示为45°弯曲角度下,管材与防皱模之间的摩擦系数对TA18 钛合金管数控绕弯成形最大截面椭圆畸变率和最大外侧壁厚减薄率的影响规律,此时弯曲模和压模与管材之间的摩擦系数固定为0.2。可以看出,随着摩擦系数增加,最大外侧壁厚减薄率呈现出先上升后下降再上升的趋势;而最大截面椭圆畸变率总体较为平稳,差距不大。
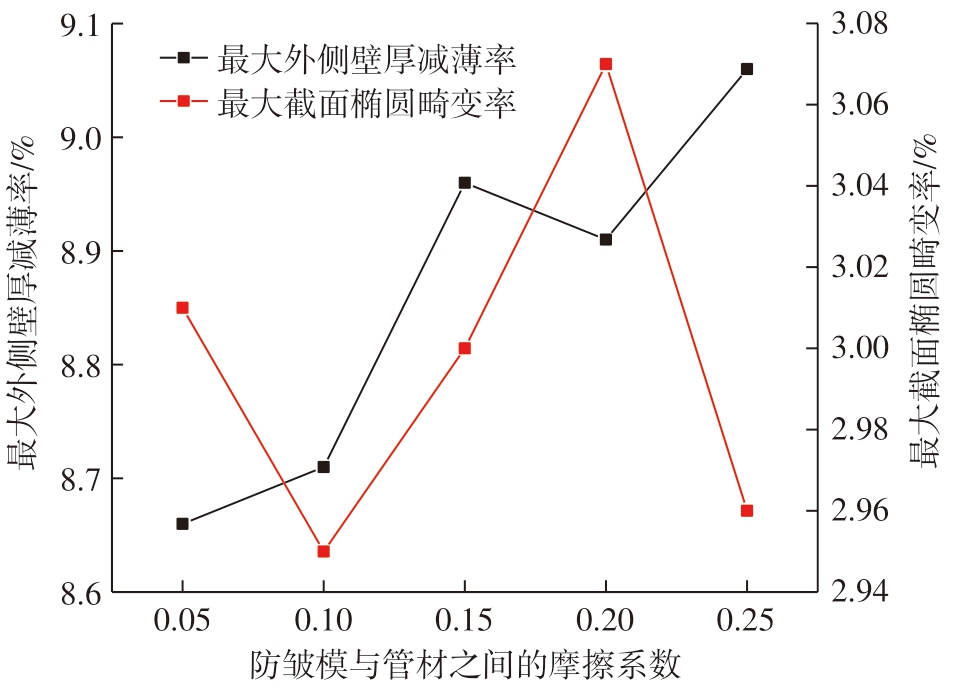
图18 防皱模与管材之间摩擦系数对成形质量的影响
Fig.18 Effect of friction coefficient between anti-wrinkle die and pipe on forming quality
3.2 管材与模具间隙对成形质量的影响
管材与模具之间的间隙影响管材变形时的材料流动,合理选取管材与模具间隙对提高管材弯曲成形质量具有重要意义。
压模是数控绕弯成形的重要模具之一,压模与管材之间的间隙大小对于管材弯曲的成形质量也有重要影响。图19所示为管材与压模之间的间隙示意图。管材与压模之间的间隙对管材最大截面椭圆畸变率和最大外侧壁厚减薄率的影响如图20所示。其中弯曲角度为45°,管材与压模的间隙分别为- 0.01 mm、0、0.01 mm、0.02 mm、0.03 mm,此时弯曲模和防皱模与管材之间的间隙固定为0。随着间隙值的增加,当间隙从- 0.01 mm增加到0.01 mm 时,管材外侧减薄率先略微增大,然后大幅度减小;间隙值从0.01 mm 增加至0.03 mm 时,最大外侧减薄率先增加后下降,原因为随着间隙值的增大,压模的助推作用减弱,导致减薄率有所增加;而最大截面椭圆畸变率整体呈先下降后平稳的趋势,特别是当间隙从- 0.01 mm增加至0时,管材截面畸变程度降低较明显,当间隙进一步增大时,管材的截面畸变率较为平稳。
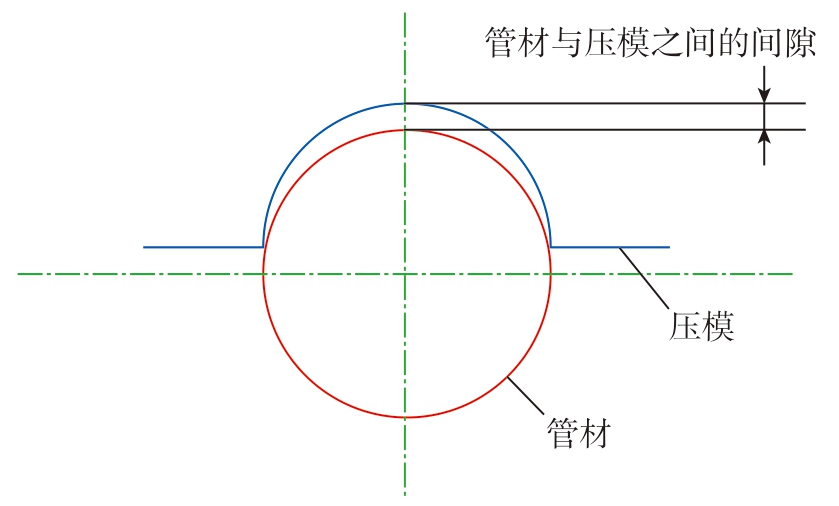
图19 管材与压模之间的间隙示意图
Fig.19 Schematic diagram of the gap between the pipe and the pressing die
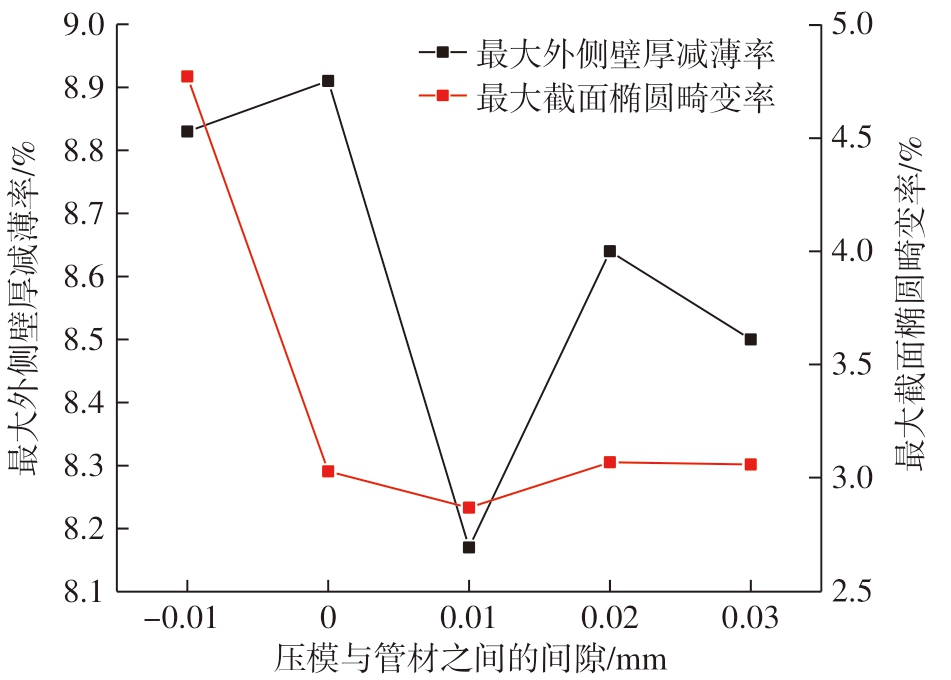
图20 压模与管材之间的间隙对成形质量的影响
Fig.20 Effect of the gap between the pressing die and the pipe on the forming quality
3.3 弯管机加工参数对成形质量的影响
3.3.1 弯曲速度对成形质量的影响
图21所示为弯曲速度对TA18 钛合金管45°数控绕弯最大截面椭圆畸变率和最大外侧壁厚减薄率的影响,这里选取9(°)/s 到45(°)/s(0.157 rad/s 到0.785 rad/s),此时压模助推速度设为与弯曲速度相同以保证助推作用不变。可以看到,随着弯曲速度的增加,管材的最大外侧壁厚减薄率呈现出先平缓后上升的趋势,管材的最大截面椭圆畸变率呈现先缓慢下降后快速上升的趋势。这是因为弯曲速度的增加会使变形过程中材料的流动速度增大,流动速度过快使得管材的截面畸变率和外侧减薄率增大,因此适当减小弯曲速度有利于减小管材弯曲成形时的最大截面椭圆畸变率和最大外侧壁厚减薄率,从而提高管材绕弯时的成形质量。
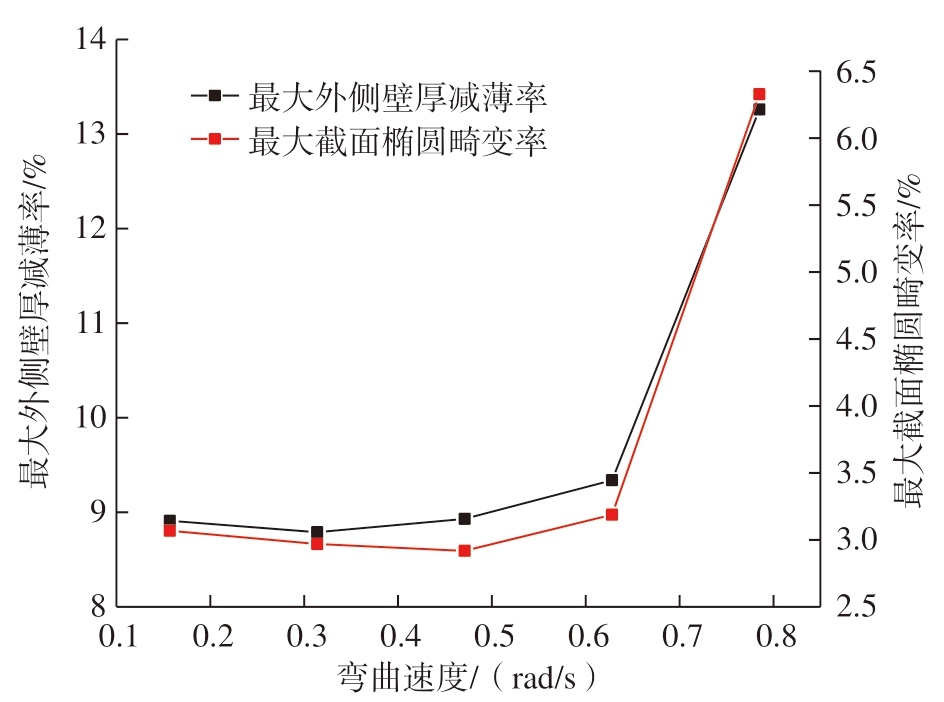
图21 弯曲速度对管材成形质量的影响
Fig.21 Effect of bending speed on pipe forming quality
3.3.2 压模推进速度对成形质量的影响
轴向推进速度会影响管材弯曲部位的材料流动性能,进给速度不变的情况下,取不同推进速度与固定弯曲速度下的管材成形质量进行对比。
图22 为TA18 钛合金管45°数控绕弯最大截面椭圆畸变率和最大外侧壁厚减薄率随推进速度的变化曲线,此时采用的弯曲速度为0.157 rad/s。可以看出,随着推进速度的增加,最大截面椭圆畸变率和最大外侧壁厚减薄率呈波动状态,但整体处于下降趋势。这是因为在TA18 钛合金管数控弯曲过程中,压模助推会沿着轴向给管材外侧施加轴向摩擦力。当推进速度小于弯曲速度时候,轴向摩擦力方向与弯曲方向相反,此时摩擦力阻碍管材绕弯成形,随着推进速度减小,摩擦力增大,导致外侧拉应力增加,因此截面畸变增加;当推进速度大于弯曲速度时,轴线摩擦力方向与弯曲方向相同,此时有利于管材绕弯成形,随着推进速度的增加,使得外侧拉应力减小,因此最大截面椭圆畸变率也减小。
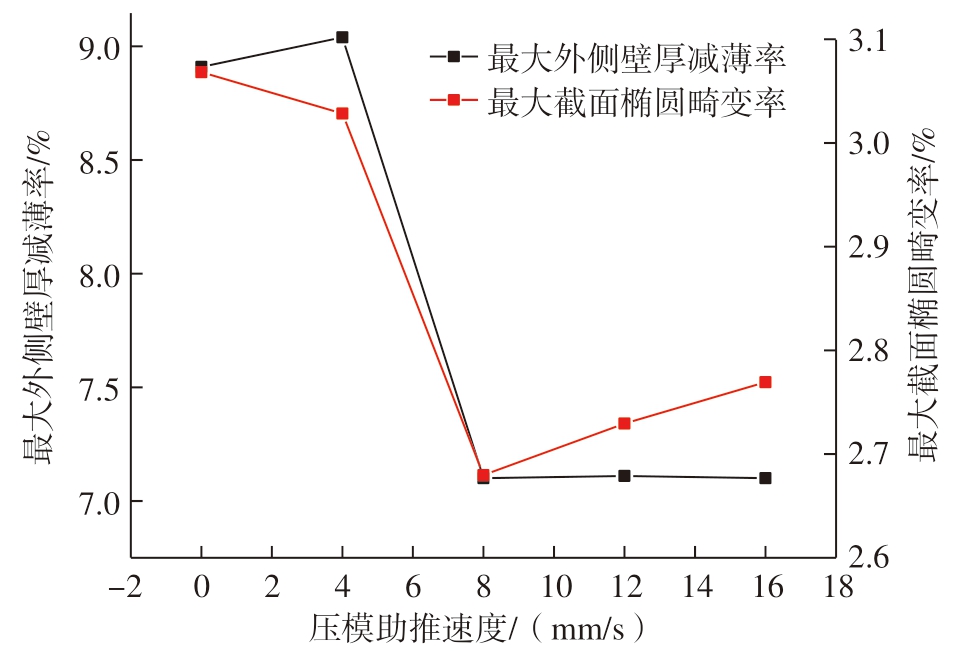
图22 压模推进速度对管材成形质量的影响
Fig.22 Effect of pressing die advancement speed on pipe forming quality
3.3.3 轴向进给速度对成形质量的影响
弯曲成形过程中,管材外侧受到拉应力作用,外侧壁厚发生减薄,通过改变轴向进给的速度可以改变轴向的进给力,有利于削弱外侧的拉应力作用,减少弯曲成形过程中外侧壁厚的减薄率以及截面畸变程度。压模推进速度不变的情况下,取不同进给速度与固定弯曲速度的比值,即轴向进给速度比作为参数,本文分别取0.8、0.9、1.0、1.1、1.2 共5 种进给速度比进行成形质量的对比。
轴向进给速度对成形角度为45°的管材最大截面椭圆畸变率和最大外侧壁厚减薄率的影响如图23所示。可以看出,随着轴向进给速度比的逐渐增加,最大外侧壁厚减薄率逐渐减小,从14.17%降低至4.53%;最大截面椭圆畸变率也随着轴向进给速度比的增加而减小,从6.62%降低至2.2%,说明轴向进给速度比的增加既可以很大程度地减少外侧壁厚的减薄率,也可以减少截面椭圆畸变率。但从有限元模拟结果来看,轴向进给速度增加也会使管材的尾部截面增厚并发生畸变,因此,要合理选用轴向进给速度。

图23 轴向进给速度对管材成形质量的影响
Fig.23 Effect of axial feed speed on pipe forming quality
4 模型试验验证
为了确定有限元模型的准确性,通过对试验件表面质量、最大截面椭圆畸变率和最大外侧壁厚减薄率的测量,分析与有限元模型结果的差异,以此判断模型准确性。
选取表4所示的模型试验参数进行有限元模拟,使用伊顿伦纳德VB19 弯管机进行角度45°弯曲试验,模拟结果与试验件对比如图24所示。
表4 模型试验参数
Table 4 Model test parameters

验证参数 试验摩擦介质及试验值 仿真模拟值弯曲模与管材间摩擦系数 干摩擦 0.25压模与管材间摩擦系数 润滑油 0.05防皱模与管材间摩擦系数 润滑油 0.1压模与管材间间隙/mm 0.01 0.01弯曲速度/(rad/s) 0.2 0.2压模推进速度/(mm/s) 10 10轴向进给速度比 1.1 1.1

图24 有限元模拟结果与试验件
Fig.24 Finite element simulation results and test pieces
对试验件弯曲段进行测量,对比有限元仿真值与试验件实测值差异,结果如表5所示。通过差异分析可以看出,模拟与实测误差控制在3%以内,说明使用有限元模型仿真确定的弯曲成形工艺参数是准确可靠的。
表5 模型验证结果
Table 5 Model validation results %
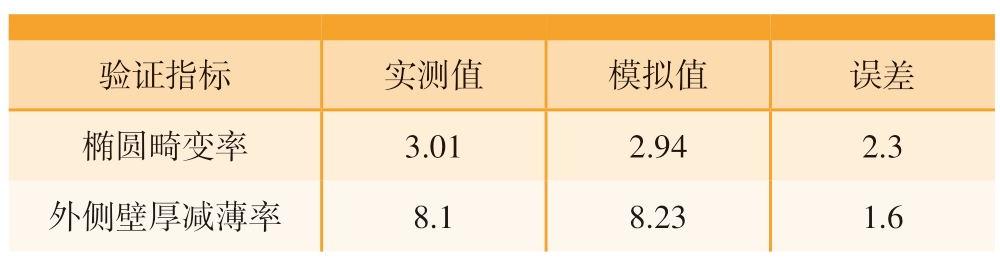
验证指标 实测值 模拟值 误差椭圆畸变率 3.01 2.94 2.3外侧壁厚减薄率 8.1 8.23 1.6
5 结论
本文通过调整管材与弯曲模具(弯曲模、压模、防皱模)之间的摩擦系数和间隙,阐述了二者对最大截面椭圆畸变率和最大外侧壁厚减薄率的影响,并得出了理想的摩擦系数和间隙数值。通过调整管材绕弯时的弯曲速度、推进速度、进给速度,总结出数控弯曲工艺参数规律。
在导管弯曲加工中,最大外侧壁厚减薄率和最大截面椭圆畸变率是衡量导管弯曲段质量的两大关键指标。基于此,分别从摩擦系数、导管与模具之间的间隙以及设备加工参数这3 个维度展开影响性分析,以此深入探究各因素对导管弯曲质量的作用机制。结果表明,在TA18 钛管数控弯曲成形过程中,为获得较理想的最大截面椭圆畸变率和最大外侧壁厚减薄率,推荐选择较大的弯曲模与管材间的摩擦系数,以及较小的压模、防皱模与管材间的摩擦系数。压模与管材之间间隙设置在0.01 mm;加工参数弯曲速度设置为0.15 ~ 0.5 rad/s,压模推进速度设置为8 ~ 16 mm/s,相对于固定弯曲线速度,弯管机轴向进给速度比设置为1.1~1.2。
[1] 江志强, 杨合, 詹梅, 等. 钛合金管材研制及其在航空领域应用的现状与前景[J]. 塑性工程学报, 2009, 16(4): 44-50, 84.
JIANG Zhiqiang, YANG He, ZHAN Mei, et al. State-of-the-arts and prospectives of manufacturing and application of titanium alloy tube in aviation industry[J]. Journal of Plasticity Engineering, 2009, 16(4): 44-50,84.
[2] 房永强, 余泽利, 白新房, 等. TA18 钛合金管收缩应变比的测量不确定度评定[J]. 塑性工程学报, 2021, 28(12): 230-236.
FANG Yongqiang, YU Zeli, BAI Xinfang, et al. Evaluation of measurement uncertainty of contractile strain ratio of TA18 titanium alloy pipe[J]. Journal of Plasticity Engineering, 2021, 28(12): 230-236.
[3] 庞君保, 唐寿全, 王立昌. TA18钛合金管收缩应变比的测定及其影响因素[J]. 理化检验(物理分册), 2016, 52(12): 864-867.
PANG Junbao, TANG Shouquan, WANG Lichang. Contraction strain ratio determination and its influencing factors of TA18 titanium alloy tube[J]. Physical Testing and Chemical Analysis (Part A: Physical Testing), 2016, 52(12): 864-867.
[4] 石科学, 常波涛, 刘竟艳, 等. TA18钛合金管材残余应力分析[J]. 世界有色金属, 2020(16): 145-147.
SHI Kexue, CHANG Botao, LIU Jingyan, et al. Analysis of the residual stress in TA18 titanium tubes[J]. World Nonferrous Metals, 2020(16): 145-147.
[5] 张旺峰, 张晖, 颜孟奇, 等. 飞机液压系统用TA18钛合金管材性能特殊性研究[J]. 钛工业进展, 2018, 35(4): 22-25.
ZHANG Wangfeng, ZHANG Hui, YAN Mengqi, et al. Performance specialty of TA18 titanium alloy tube used for aircraft hydraulic system[J].Titanium Industry Progress, 2018, 35(4): 22-25.
[6] 靳舜尧, 唐振宇, 黄重国, 等. 5A02铝合金薄壁管绕弯成形数值模拟及试验[J]. 热加工工艺, 2018, 47(21): 122-127.
JIN Shunyao, TANG Zhenyu, HUANG Chongguo, et al. Numerical simulation and experiments of 5A02 aluminum alloy thin-walled tube rotary-draw-bending forming[J]. Hot Working Technology, 2018, 47(21):122-127.
[7] 李恒, 杨合, 张志勇, 等. 高强TA18钛管连续整体多弯成形精度控制[J].精密成形工程, 2014, 6(5): 25-30, 44.
LI Heng, YANG He, ZHANG Zhiyong, et al. Precision control strategies of high strength TA18 titanium alloy tube in multi-bending[J].Journal of Netshape Forming Engineering, 2014, 6(5): 25-30, 44.
[8] 刘凡, 李赟, 王文睿, 等. TA18钛合金管材织构对环向拉伸性能的影响[J]. 稀有金属材料与工程, 2020, 49(6): 2011-2016.
LIU Fan, LI Yun, WANG Wenrui, et al. Effect of texture on circumferential tensile properties of TA18 titanium alloy tubing[J]. Rare Metal Materials and Engineering, 2020, 49(6): 2011-2016.
[9] 李恒,杨合,宋飞飞,等. 材料性能波动下TA18钛管绕弯回弹行为[J]. 稀有金属材料与工程, 2014, 43(1): 64-71.
LI Heng, YANG He, SONG Feifei, et al. Springback rules of TA18 titanium tube upon rotary draw bending under variations of material properties[J]. Rare Metal Materials and Engineering, 2014, 43(1): 64-71.
[10] 闫晶, 张荣霞, 吴为, 等. 航空液压钛合金导管组件制造关键技术应用[J]. 航空制造技术, 2022, 65(10): 44-51, 60.
YAN Jing, ZHANG Rongxia, WU Wei, et al. Application of key technologies on manufacturing process of titanium alloy tube assembly for aeronautic hydraulic pressure system[J]. Aeronautical Manufacturing Technology, 2022, 65(10): 44-51, 60.
[11] 刘大海, 陈劲东, 李波, 等. TA18中强钛合金管数控弯曲成形工艺与结构参数显著性分析[J]. 锻压技术, 2021, 46(4): 156-165.
LIU Dahai, CHEN Jindong, LI Bo, et al. NC bending process and significance analysis on structural parameters of TA18 medium strength titanium alloy tube[J]. Forging & Stamping Technology, 2021, 46(4): 156-165.
[12] 李毅, 贺韡. 航空用TA18高强钛合金管材弯曲成形技术及研究进展[J]. 内燃机与配件, 2021(22): 38-39.
LI Yi, HE Wei. The bending technology and research progress of TA18 high-strength titanium pipe for aviation[J]. Internal Combustion Engine & Parts, 2021(22): 38-39.
[13] 江志强, 杨合, 詹梅, 等. 模具与管材不同配合条件下中强TA18厚壁钛管数控弯曲变形行为[J]. 塑性工程学报, 2011, 18(1): 21-27.
JIANG Zhiqiang, YANG He, ZHAN Mei, et al. Deformation behaviors of medium-strength TA18 thick-walled tubes during NC bending under various contact conditions between tube and dies[J]. Journal of Plasticity Engineering, 2011, 18(1): 21-27.