纺织结构高性能纤维增强复合材料,如编织复合材料、机织复合材料、缝合复合材料等兼具轻量化、高强度、抗疲劳等特性,可代替传统金属材料制造航空航天领域的大型承力结构件,达到减轻重量,提升使用寿命的目的。
空天领域大部分主承力结构件和次承力结构件存在非圆截面、变截面、大曲率和变曲率等复杂几何特征,使用铺放、缠绕等成型工艺难以实现高效、精确成型。三维编织工艺根据芯模几何形状实时改变编织姿态,可实现大规模纱线同时成型为整体网状预成型体,成为最适合异型结构件的成型方法之一。然而,复杂的结构特征增加了建立高精度织物模型的难度,更难以实现三维编织的工艺参数的模拟验证与性能仿真。因此,模拟异型结构件的编织过程成为当前的研究热点,根据芯模几何形状可以快速、准确地生成预成型体中织物的编织结构,提高复合材料构件成型质量,缩短复合材料产品研发周期。
编织过程的模拟方法主要分为三大类。第一类为基于有限元的方法[1–3],对纱线的编织过程进行跨尺度分析,通过建立虚拟纤维等方法,精确模拟编织过程中的行为和响应[4–6]。Hans 等[7]使用商用显式有限元软件模拟编织过程,提取纱线的编织角度和轴向间距;Del Rosso 等[5]通过定义锭子在编织机底盘上的解析函数确定模拟边界,建立纱线的虚拟纤维微观模型对编织过程进行模拟;Li等[8]使用基于有限元方法的虚拟纤维进行编织过程模拟,表征纱线编织过程的介观行为。第二类为基于纺织过程几何模型的解析求解法,对芯模形状的几何函数与纱线的位置建立确定的非线性方程组。邵将等[9]以数学关系模拟编织运动,采用Bézier 曲线对编织织物结构进行高精度拟合;Du 等[10]通过解析法对变截面芯模进行编织角与覆盖率的分析预测,并在试验中验证了此方法的精度。然而,有限元法耗时长、解析法对于异型结构件的模拟精度较低,因此,提出第三类运动学方法[11],这也是当前相关研究中应用最为广泛的方法。运动学方法通过运动学分析,提供编织复合材料的实时编织状态详细信息, Akkerman 等[12]首次提出用纱线沉积模型对编织过程进行模拟,并对异型结构件进行了模拟与试验验证;Gondran 等[13]基于纱线沉积法对大尺寸异型结构件进行工艺设计与模拟仿真试验;Monnot 等[14]对飞机隔框进行运动学求解;Van Ravenhorst等[15]对于等截面圆管进一步分析纱线相互作用在编织模拟中的影响;Li等[16–17]提出一种考虑纱线间沉积与提前沉积现象的预测模型;Vu 等[18–19]对纱线间摩擦力进行深入分析并耦合进轨迹预测模型中。然而,由于运动学方法对芯模表面网格有依赖性,在芯模存在孔洞、空心等与编织无关的特征时,此方法对纱线轨迹预测的精准度和效率影响较大。
本文针对异型结构件编织过程模拟耗时长,传统算法对复杂几何特征的预测精度低、算法鲁棒性差等问题,提出一种快速、适用性强、通用于复杂异型芯模的编织模拟方法。首先,对芯模特征进行提取,优化异型结构件芯模中的编织冗余几何特征,重构异型结构件三维模型;其次,基于重构网格预测纱线在芯模表面的轨迹,分析编织过程的纱线交织状态,提出预成型体中纱线的交织关系矩阵;最后,基于试验分析,验证了本文提出的编织模拟方法的有效性,有效提升了工艺验证与调整的效率,降低了编织试制的次数。
1 异型结构件模型重构算法
优化芯模网格的孔洞、法兰、凹角、空心等复杂冗余特征是有限元仿真、运动学求解、动力学求解必要的预处理过程。中心线是重构网格的中心参考依据,其长度区间对应芯模的长度分段。本节基于芯模的端面坐标系xoz、xoy 平面的投影轮廓边界求解并合成中心线及牵引轨迹,所用的芯轴三维模型建模基准和姿态统一沿原点向x 轴延伸。首先,将芯轴的轮廓边界投影至xoy、xoz 平面上,通过三次曲线插值算法和曲线拟合算法拟合求解轮廓边界的曲线,如图所示;然后,取上、下边界曲线上的某点,沿各自法向相交,当两点连线长度相等则为中心线的离散点Ci;最后,按照牵引步长取值xi,以xoz、xoy 平面曲线方程合成中心线空间曲线方程![]() 为
为
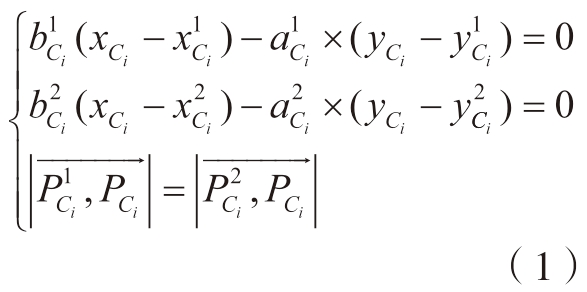
式中,正交平面上的映射轮廓![]() 以及其法向量
以及其法向量![]() 对应坐标为
对应坐标为![]()
![]() ,用作二维直线点向式求交点
,用作二维直线点向式求交点![]() 。判断线段
。判断线段![]() 与
与![]() 两者长度相等且夹角为钝角,此时
两者长度相等且夹角为钝角,此时![]() 点在中心线上,记作中心线的无序离散点Ci。
点在中心线上,记作中心线的无序离散点Ci。
重构网格结构如图2所示,其表面拓扑结构均匀地围绕中心线切向分布,其排列顺序与面片索引号对应,可通过面片索引号直接调用相邻面片,是工艺设计快速迭代方法的关键;重构网格去除了STL(STereoLithography)原生网格孔洞、棱角、空心等冗余特征,克服了面片分布无序、不均匀,无法直接调用相邻面片的缺点,纱线轨迹预测算法的迭代效率提升;下列方程组使用图1中心线法平面ηcl 与原网格面片ηp 的交集作为稠密截面点集;然后提取最外侧轮廓点形成有序轮廓点集,过滤孔洞、凹角、空心等冗余特征,形成重构网格的关键截面,构建重构面片的角点、数量及位姿。
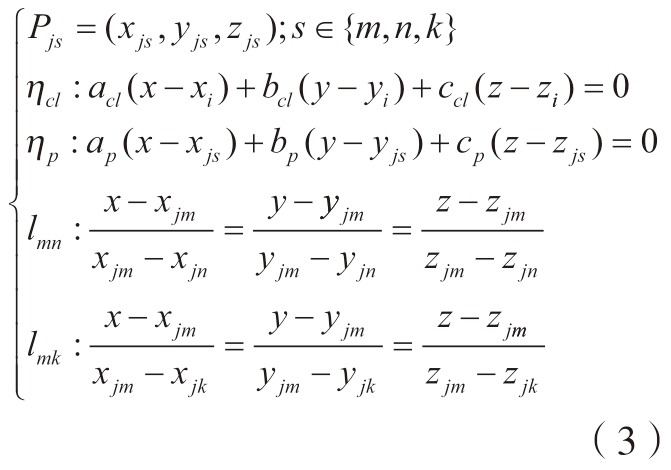
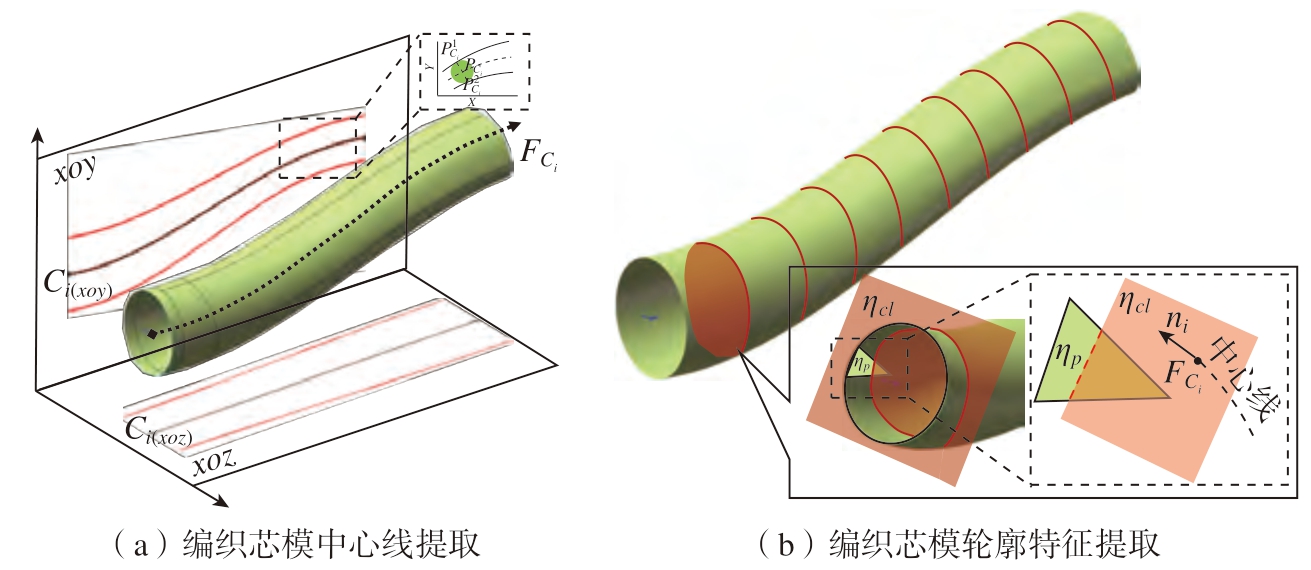
图1 芯模特征过滤过程
Fig.1 Mandrel feature filtering process

图2 重构网格结构
Fig.2 Reconstructed mesh
式中,m,n,k 分别代表三角面片上的3 个点;x、y、z、a、b、c 分别对应平面点法式的点坐标与法向量坐标; lmn、lmk 分别代表三角面片上与中心线法平面相交的两条边的空间直线方程;Pjs 代表三角面片上的任意角点。
关键截面有序轮廓点集组成了重构网格的面片角点,将相邻关键截面对应序号的点依次组合,形成多组面片的角点序列及法线。其中A1.7 面片索引号为奇数,其角点序列为(P1.6,P 1.5,P 2.5);A1.8 面片索引号为偶数,其角点序列为(P 1.6,P 2.5,P 2.6);面片按照索引号A0.0,A0.1,A0.2,…,A1.0,A1.1,A1.2…在每个分段中沿顺时针分布。设定每段网格段(如S1~S2之间的面片集合)共有48 个面片,每个关键截面有24 个面片角点,并以txt 静态数据的形式保存,方便后续工作中按顺序调用三角面片。
2 编织工艺模拟方法
如图3所示,在使用径向编织机编织过程中,两组锭子携带线轴分别被放在拨盘上相应的槽口处,并且齿轮带动拨盘,拨盘带动锭子沿编织机的底盘上蛇形轨道做顺时针和逆时针运动[20–21],纱线不断相互交织形成网状结构。同时,芯模姿态调节系统中的机器人夹持芯模通过导向环,纱线经过收敛距离在成型平面与芯模表面相切[22],最终高度交织的大规模纱线逐步在芯模表面构建网状增强结构。
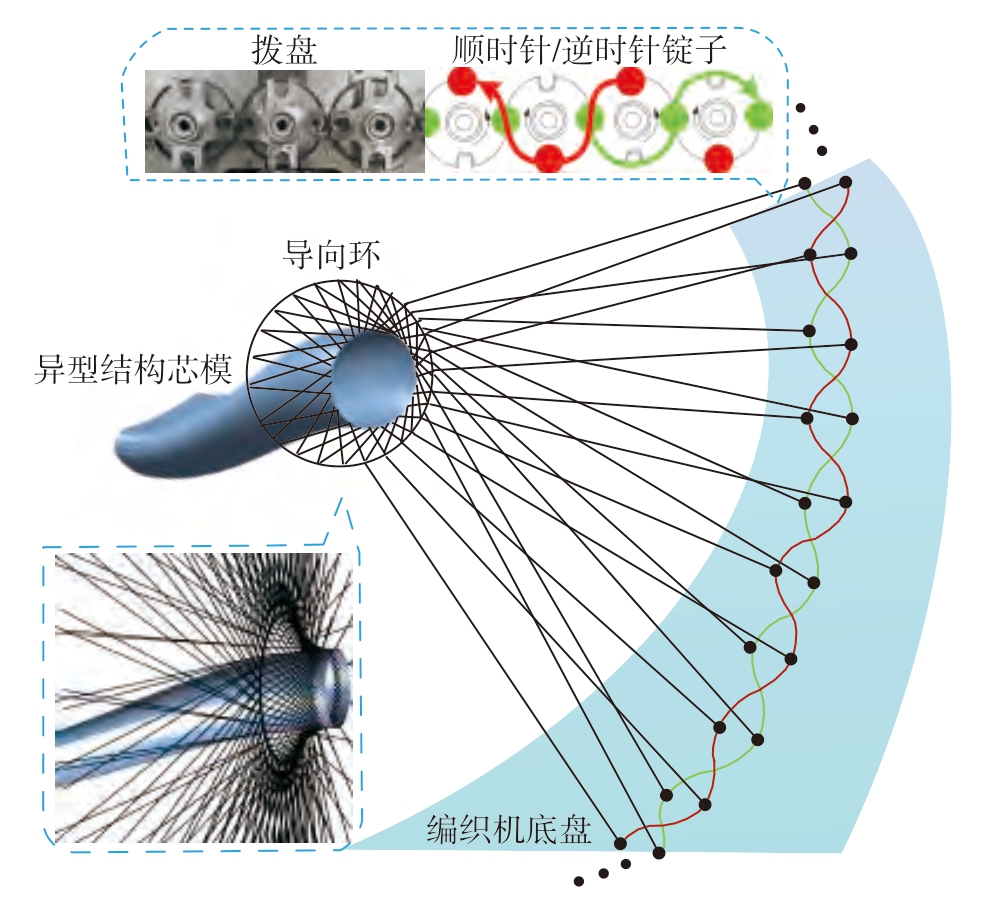
图3 编织工艺示意图
Fig.3 Schematic diagram of the braiding process
为简化模拟编织过程所需的边界条件,以达到提高运算效率的目的,本文忽略纱线间相互作用关系与锭子的蜿蜒运动,将导向环描述为半径为Rg 的圆形线圈,将编织设备描述为半径为Rsp 的圆形线圈。同时为降低每次编织姿态变换后更新模型数据所带来的庞大计算量,通过读取重构芯模模型的表面网格数据,本文将芯模设置为固定参考系,底盘上的锭子根据牵引轨迹做螺旋运动,螺旋线表达式为
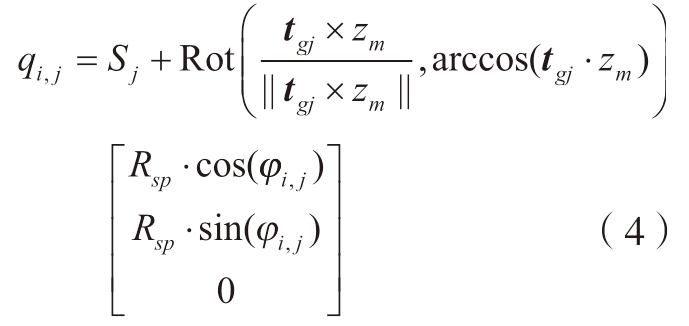
式中,qi,j 为j 时刻下第i 个锭子在螺旋线上的空间位置信息,顺时针与逆时针锭子的数量均用nc 表示;Sj 为j时刻下编织机底盘中心点位置信息,其中导向环中心点被定义为与编织机底盘中心点相同;tgj 为j 时刻下编织机底盘平面的法向量;zm 为芯模端面坐标系中z 轴,方向为指向芯模内部方向;φ 为锭子在底盘上的角度位置信息,如图4所示。

图4 相对运动转换后的编织模拟示意图
Fig.4 Schematic diagram of the braiding simulation after the relative motion conversion
对编织纱线在芯模表面的沉积过程进行数学描述,纱线从出纱口出发,经过导向环时,纱线方向被迫发生弯折后形成收敛区域。由于在编织非圆形芯模的过程中纱线不均匀分布的原因,纱线在导向环上圆周方向的运动速度不等于编织速度,因此需要根据几何关系确定纱线与导向环的交点g,表达式如下:
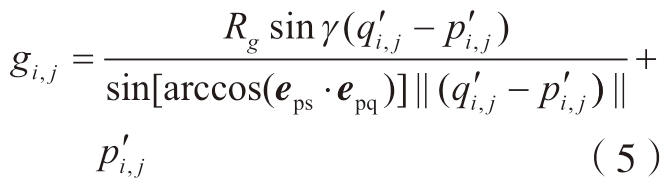
式中,![]() 为纱线落点在导向环所在平面的投影点位置信息;
为纱线落点在导向环所在平面的投影点位置信息;![]() 为锭子在导向环所在平面的投影点位置信息;eps 为描述纱线落点与底盘中点所组成的向量在导向环平面的投影;epq 为纱线落点与锭子所组成的向量在导向环平面的投影;γ 为导向环坐标系中xy 平面内接触点、导向环中点与落点之间所形成的夹角,表达式为
为锭子在导向环所在平面的投影点位置信息;eps 为描述纱线落点与底盘中点所组成的向量在导向环平面的投影;epq 为纱线落点与锭子所组成的向量在导向环平面的投影;γ 为导向环坐标系中xy 平面内接触点、导向环中点与落点之间所形成的夹角,表达式为
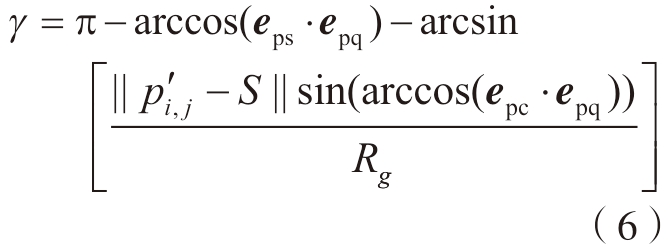
为更新纱线落点位置,需要使用沉积判据对每一条纱线的沉积状态进行判断,根据纱线与导向环的交点gi,j、纱线落点pi,j、落点所在芯模表面的三角网格法向量nM 对纱线状态进行分析,当纱线位于所在三角网格下时,定义此刻纱线沉积在芯模表面形成织物,判断表达式为
为实现编织复合材料的高保真建模与性能分析,基于上述编织成型模拟方法,在芯模表面生成纱线拓扑轨迹,建立织物覆盖在芯模外面的交织结构。编织的交织结构主要分为两种,即菱形编织结构与常规编织结构,编织结构与锭子的排布方式有着密切联系。两种织物结构与锭子排布的关系如图5所示。

图5 不同锭子排布下的织物结构
Fig.5 Fabric structure with different spindle arrangements
在菱形编织结构的锭子排布中,顺时针锭子与逆时针锭子的交织情况单一、周期性强。基于单根纱线的拓扑周期性,表现为每两个相邻交织点的空间相位重复,通过拨盘机构的运动学分析可知,奇偶序列差异导致顺/逆时针锭子组合生成相同的交织几何构型,本文定义为:顺时针纱线在上,逆时针纱线在下。相反,相同奇偶序列的顺时针锭子与逆时针锭子所形成的交织点为另一种相同形式的交织几何构型,本文定义为顺时针在下,逆时针在上。为建立量化分析模型,采用nc×nc 的矩阵对交织点的空间分布进行系统表征。顺时针纱线在上,逆时针纱线在下的交织状态在矩阵中定义为1;顺时针纱线在下,逆时针纱线在上的交织状态在矩阵中定义为0。此矩阵表征方法有效捕捉了纱线路径中每间隔两个交织点,重复出现的周期性规律。编织关系矩阵表达式为
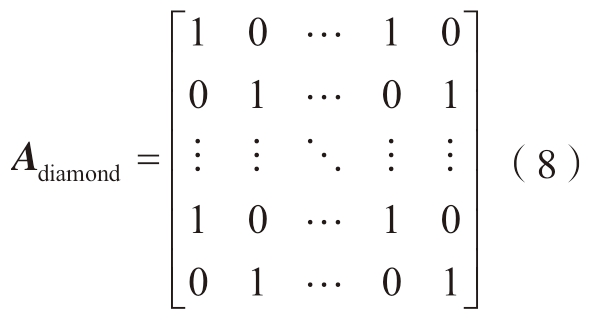
在常规编织结构的锭子排布中,顺时针锭子与逆时针锭子的交织规律相比于菱形编织结构较为复杂,同一根纱线上出现相同交织情况的周期为4 个交织点。因此,需要分别对4 种序号的锭子进行讨论。常规编织下交织形式为两上两下,因此根据锭子排布顺序可知,常规编织下的交织关系矩阵表达式为

基于纱线轨迹与交织形态,对芯模表面每个交织点进行二次处理,形成纱线的空间拓扑。在矩阵内容为1 的交织点处,将顺时针纱线沿所在芯模表面的法向量偏移两倍纱线厚度,逆时针偏移一倍纱线厚度;对矩阵内容为0 的交织点,将逆时针纱线偏移两倍纱线厚度,顺时针偏移一倍纱线厚度。使用椭圆形截面与纱线的空间拓扑生成单根纱线的实体单元,如图6所示。
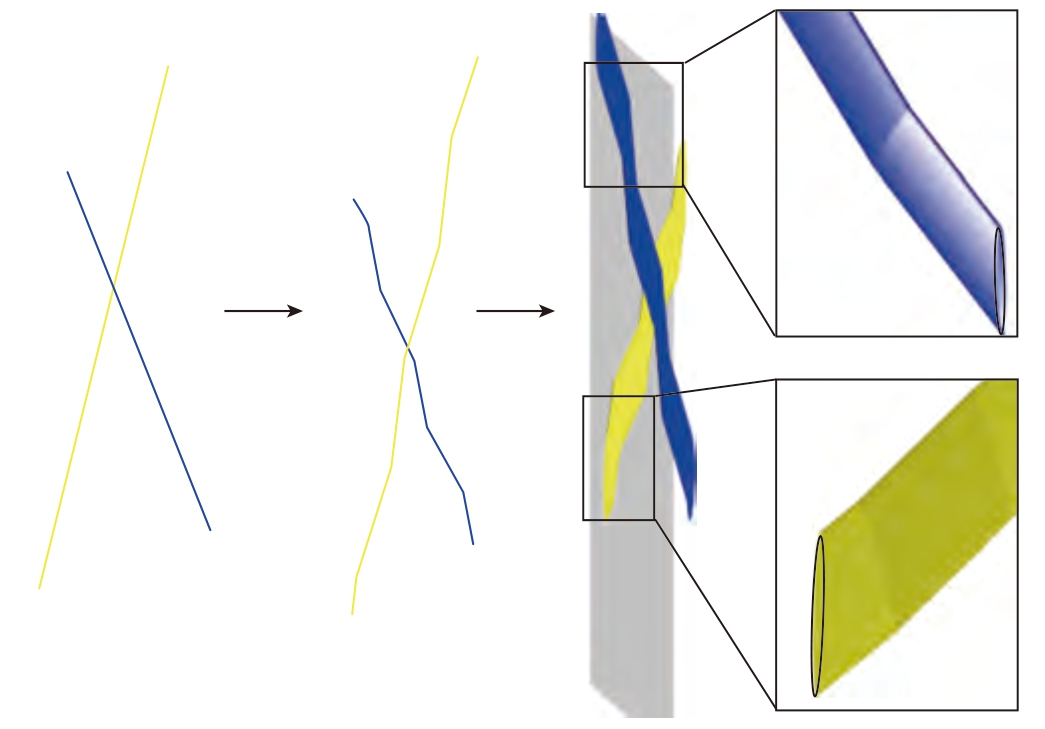
图6 织物空间结构生成
Fig.6 Fabric spatial structure generation
3 试验
仿真模拟试验使用Matlab R2023b软件进行数值分析,计算在配备Intel(R) Core(TM) i9–14900HX 的处理器、NVIDIA GeForce RTX4070 的显卡,32 GB 的RAM 与Windows 11 操作系统下进行。在实际编织过程中对3 种尺寸的芯模进行编织作业,纱线在芯模起始段使用绑带扎紧,所以纱线的起始点在芯模端面上均匀分布,因此仿真模型中纱线初始落点为锭子和芯模端面中点的连线与轮廓线的交点,3 种芯模几何尺寸如图7所示。
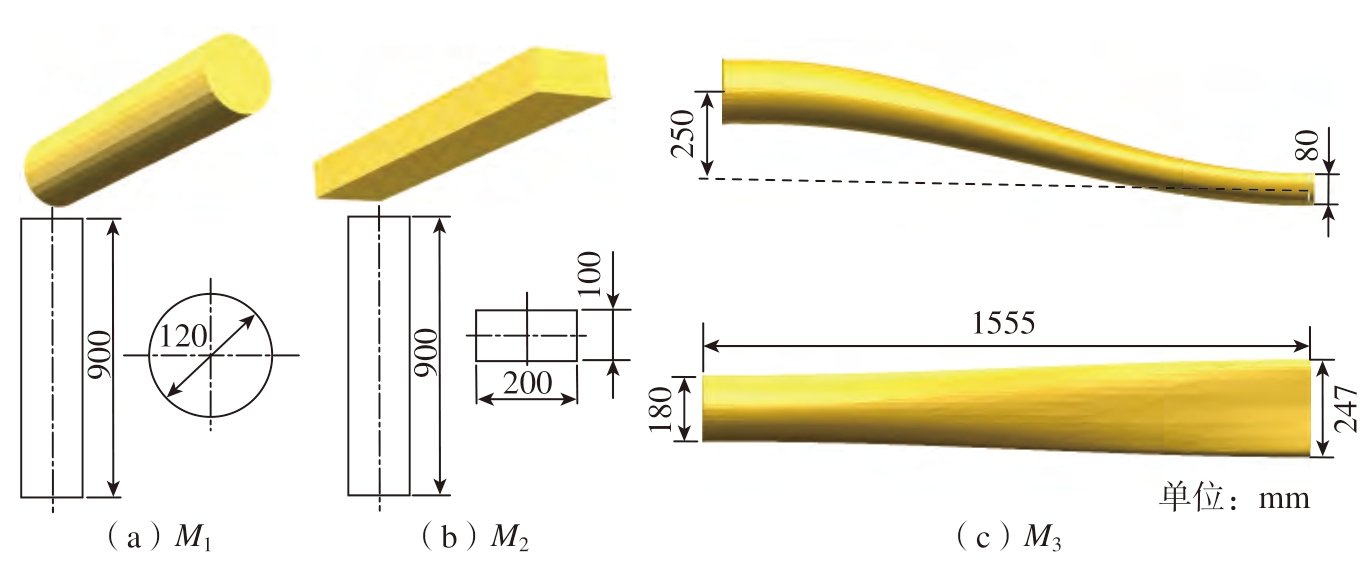
图7 芯模几何尺寸示意图
Fig.7 Schematic diagram of the geometric dimensions of the mandrel mold
编织试验中,采用云路复材176锭径向编织机与安装在线性导轨上的六自由度工业机器人进行编织作业。径向编织机中每个锭子按照编织机底盘的轨道前行,通过安装在锭子上面的纱筒携带纱线进行编织,同时,编织机的运动系统包括4 个伺服电机、2 个振动电机和控制器组成,3 种芯模的编织过程如图8所示,编织装备参数见表1。在编织角等参数的测量过程中,针对M1 与M2 芯模,由于芯模不存在变截面变曲率等几何特征,因此选择预成型体中的一根纱线在芯模表面的轨迹进行测量。针对M3 芯模,由于其形状复杂,因此在如图9所示的黄色测量区域内取编织角进行测量,在测量区域内,对每个测量单元进行编织角测量,测量单元宽度为测量区域宽度,长度为30 mm,每个测量区域内测量5 组数据,取得试验数据与误差棒上下限。
表1 编织装备参数
Table 1 Weaving equipment parameters

芯模编号 锭子数量/个锭子运动速度ω/(r/s)牵引速度V/(mm/s)导向环半径Rg/mm底盘半径Rsp/mm M1 176 0.1332 4 150 1821 M2 176 0.1332 4 200 1821 M3 176 0.1332 2 250 1821

图8 编织试验
Fig.8 Braiding experiments

图9 模拟编织与实际编织的织物对比
Fig.9 Comparison of simulated and actual braided fabrics
4 结果与讨论
4.1 芯模截面形状对预测结果的影响
为验证算法对不同截面形状芯模的适用性,采用圆形 M1)与矩形(M2)芯模进行试验分析。如图10(a)所示,圆形截面芯模的编织角预测值与实测值高度吻合,结果显示平均误差<0.5°。这一现象可通过几何约束理论解释,圆形截面的轴对称特性使纱线始终沿芯模表面法向相切,编织角仅受宏观参数,如牵引速度、锭子角速度、芯模形状的影响,而纱线间相互作用因均匀分布被弱化。此结果与Hans 等[7]基于有限元的圆管编织模拟结论一致,表明运动学模型在对称几何中的普适性。
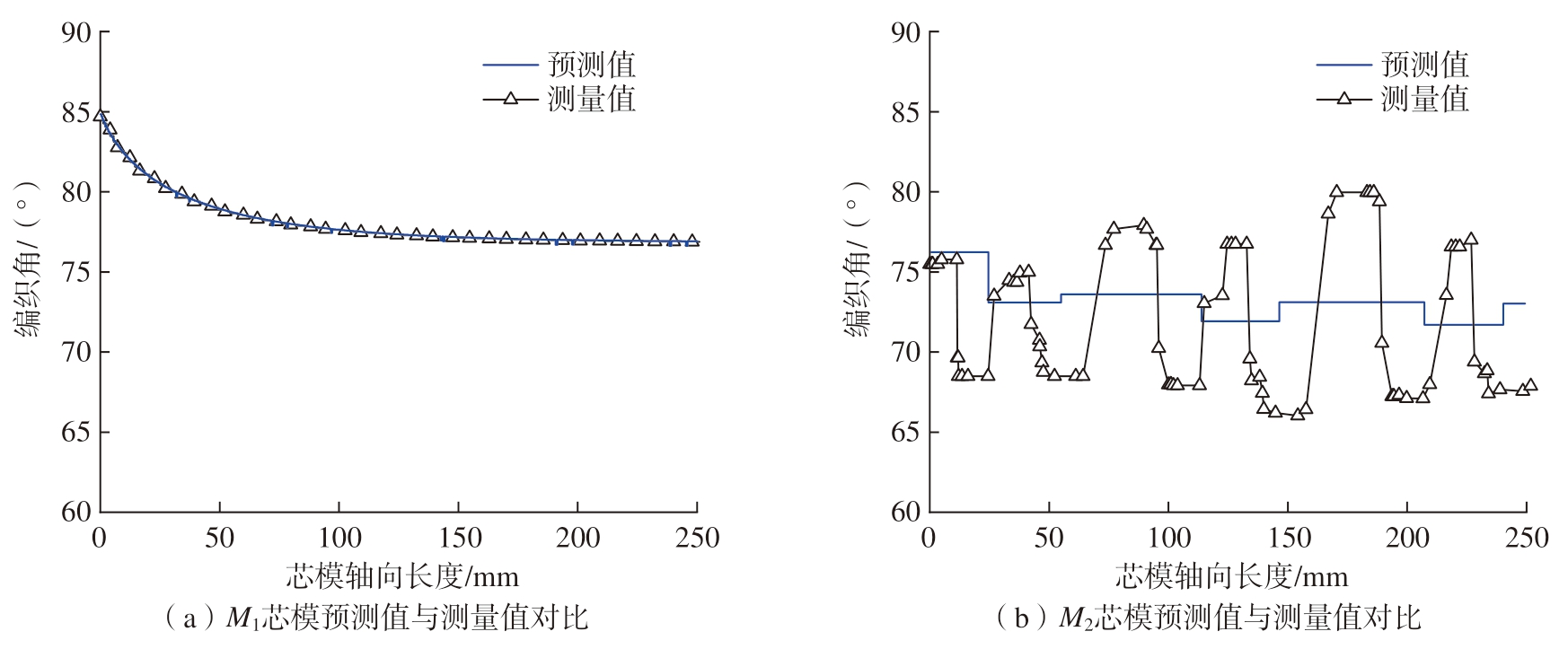
图10 不同形状芯模预测结果
Fig.10 Predicted results for different mandrels
相比之下,矩形截面芯模(M2)的预测结果在平坦面棱边处出现显著偏差如图10(b)所示。这一误差源于纱线沉积机制的复杂性,当任意方向纱线组未达到相切状态时,由于与异向运动纱线组的高度交织特性,使得在棱边处形成局部沉积。根据Del Rosso 等[5]的有限元分析,此类区域易产生纱线分布的变化与挤压滑移等介观行为,而本文模型未考虑纱线间摩擦力的动态耦合,导致预测值滞后于实际沉积位置。尽管如此,模型仍能准确捕捉不同平坦面之间的编织角变化趋势,验证了算法对非对称截面的适应性,证明了运动学模型在复杂几何特征中的优势。
4.2 异型结构件芯模预测精度分析
针对同时具有变截面与变曲率几何特征的M3 芯模,模拟编织与实际编织的织物结构对比显示高度一致性(图 9)。图11 进一步量化了编织角误差分布,在初始段(0~100 mm),因收敛距离的延迟效应,编织角呈现先减小后稳定的非线性特征;而变截面段误差逐渐增大至4.9°,主要源于纱线间摩擦力未考虑进模型。在近似棱边处因纱线间相互作用关系织物提前成型,导致实测编织角较预测值偏大。此现象与Vu 等[18]的摩擦耦合模型结论一致,表明引入纱线相互作用力可进一步压缩误差。

图11 模拟编织与实际编织的编织角对比
Fig.11 Comparison of the braiding corners of the simulated braiding with the actual braiding
值得注意的是,尽管存在局部偏差,整体误差范围仍可以保证在5°以内,证明该方法在工程应用中的可靠性。此外,模型在变曲率区域的表现优于传统解析法,因为通过重构网格精确捕捉了曲率梯度对纱线轨迹的影响。
4.3 异型结构件网格重构对模拟时间的影响
网格重构算法通过优化数据结构显著提升了计算效率。如图12所示,重构后的有序网格通过预定义面片索引与相邻关系,将纱线轨迹预测时间从0.32 h 缩短至0.05 h(M5 芯模),时间缩短了84%,核心机制在于避免了传统STL 网格的全局遍历,传统方法需对每个面片进行搜索,而重构网格通过分段映射将复杂度大幅度降低。剩余计算时间主要用于导向环交点迭代,其耗时与锭子数量呈线性关系,适用于大规模编织仿真。
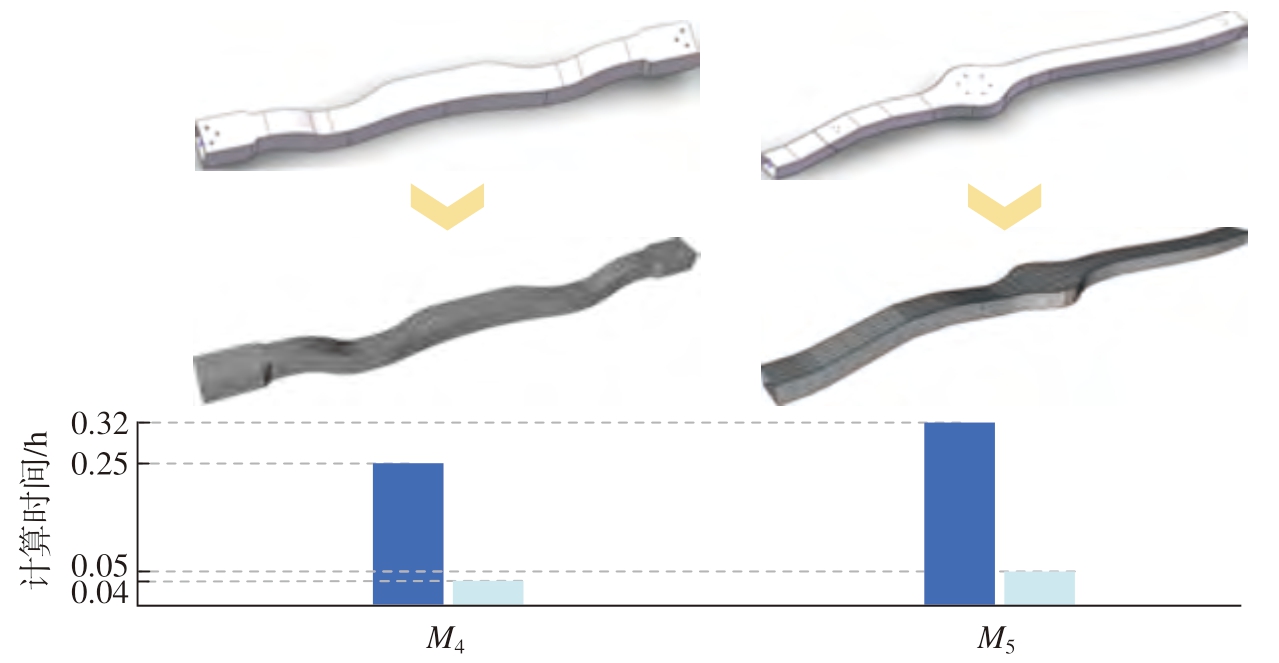
图12 不同异型结构件芯模网格重构示意图及编织模拟所需时间
Fig.12 Restructured mesh of mandrels for different shaped structural parts and time required for braiding simulations
相比之下,商业有限元软件因为需要求解纱线接触非线性问题,计算时间随锭子数量呈指数增长。本文方法在保证精度的前提下,将M4 与M5 等复杂芯模的总仿真时间控制在0.1 h 内。效率提升使得该方法可集成至CAE 系统,支持多参数实时优化,为复杂构件的工艺设计提供了可扩展的解决方案。此效率优势为工艺参数的实时优化(如牵引速度自适应调整)提供了技术基础。未来可通过并行计算进一步压缩时间,满足航空构件多工况迭代需求。
5 结论
本文针对任意形状的异型编织结构件提出了一种新颖的、基于网格重构算法的编织过程模拟方法,可有效解决复杂构件的工艺数字化难题。网格重构算法可以自动识别并消除芯模的通孔、凸台等影响织物预测精度的冗余特征,保证编织模拟精度与效率。同时基于重构网格与纱线轨迹建立参数化纱线结构重建模型,基于优化网格,自动生成三维交织空间构型。为提高计算效率,本文提出的模拟方法以运动学为基础,在保证精度的基础上实现异型结构件的模拟计算时间远小于商业有限元软件。通过某型飞机进气道进行试验验证,在圆截面部分模拟方法提取的编织角与实测值误差较小,在变截面部分由于本文没有考虑纱线间的相互作用关系,误差值明显增大,但仍能保证在5°以内。本文提出的基于网格重构算法的编织模拟方法满足实际生产精度,可用于验证实际生产中的工艺设计方案,降低样件试制所带来的高额成本。
[1] BÖHLER P, PICKETT A,MIDDENDORF P. Finite element method (FEM)modeling of overbraiding[M]//Advances in Braiding Technology. Amsterdam: Elsevier, 2016:457–475.
[2] VAN RAVENHORST J H. Design tools for circular overbraiding of complex mandrels [D].Enschede: TWENTE University, 2018.
[3] 马莹, 向卫宏, 赵洋, 等. 三维正交织物织造过程模拟及其微观几何结构预测[J].纺织学报, 2023, 44(6): 105–113.
MA Ying, XIANG Weihong, ZHAO Yang, et al. Weaving process modeling and micro-geometry prediction of three-dimensional orthogonal woven fabrics[J]. Journal of Textile Research, 2023,44(6): 105–113.
[4] SWERY E E, HANS T, BULTEZ M, et al. Complete simulation process chain for the manufacturing of braided composite parts[J]. Composites Part A: Applied Science and Manufacturing, 2017, 102: 378–390.
[5] DEL ROSSO S, IANNUCCI L, CURTIS P T. Finite element simulation of the braiding process[J]. Mechanics of Advanced Materials and Modern Processes, 2019, 5(1): 1–11.
[6] 刘岳岩, 马莹, 禄盛, 等. 不同纱线张力下的三维正交织物微观几何结构建模[J].复合材料科学与工程, 2021(1): 19–27.
LIU Yueyan, MA Ying, LU Sheng, et al. Micro-geometry of 3D orthogonal woven fabric modeling under different yarn tension[J].Composites Science and Engineering, 2021(1):19–27.
[7] HANS T, CICHOSZ J, BRAND M, et al. Finite element simulation of the braiding process for arbitrary mandrel shapes[J]. Composites Part A: Applied Science and Manufacturing, 2015, 77:124–132.
[8] LI Y D, YAN S B, YAN Y, et al. Highfidelity modeling of the braiding process for generating the realistic mesostructure of preforms in braided composites[J]. Polymer Composites,2023, 44(5): 2898–2909.
[9] 邵将, 温卫东, 崔海涛. 三维纵横步进编织预成型件的计算机仿真[J]. 纺织学报,2008, 29(9): 129–132, 136.
SHAO Jiang, WEN Weidong, CUI Haitao.Computer simulation of three-dimensional preforms using track and column braiding[J].Journal of Textile Research, 2008, 29(9): 129–132,136.
[10] DU G W, POPPER P. Analysis of a circular braiding process for complex shapes[J].The Journal of the Textile Institute, 1994, 85(3):316–337.
[11] VAN RAVENHORST J H,AKKERMAN R. Circular braiding take-up speed generation using inverse kinematics[J]. Composites Part A: Applied Science and Manufacturing, 2014,64: 147–158.
[12] AKKERMAN R, RODRíGUEZ B V. Braiding simulation for RTM preforms[C]. 8th International conference on textile composties(Texcomp 8). Nottingham, 2006.
[13] GONDRAN M, ABDIN Y,GENDREAU Y, et al. Automated braiding of nonaxisymmetric structures using an iterative inverse solution with angle control[J]. Composites Part A:Applied Science and Manufacturing, 2021, 143:106288.
[14] MONNOT P, LÉVESQUE J,LABERGE LEBEL L. Automated braiding of a complex aircraft fuselage frame using a non-circular braiding model[J]. Composites Part A: Applied Science and Manufacturing, 2017, 102: 48–63.
[15] VAN RAVENHORST J H, AKKERMAN R. A yarn interaction model for circular braiding[J]. Composites Part A: Applied Science and Manufacturing, 2016, 81: 254 – 263.
[16] LI Q Y, JI C C, LI S Y, et al. Predicting the topology of braided structures in arbitrarily composite preforms based on yarn interactions[J].Textile Research Journal, 2024, 94(19–20): 2201–2219.
[17] LI C E, LI Q Y, CHI X F, et al. Design of fast braiding process based on reconstructing mesh with complex and irregular mandrels[J].Textile Research Journal, 2024, 94(13–14): 1527–1542.
[18] VU A N, GROUVE W J B,AKKERMAN R. Modeling of yarn interactions for non-axisymmetric biaxial overbraiding simulations[J]. Composites Part A: Applied Science and Manufacturing, 2023, 167: 107421.
[19] VU A N, GROUVE W J B, DEROOIJ M B, et al. A mesoscopic model for interyarn friction[J]. Composites Part A: Applied Science and Manufacturing, 2024, 180: 108070.
[20] LI Q Y, CHI X F, JI C C, et al. Offcenter braiding process for complex composite preforms based on analysis of the geometric contour model of the mandrel[J]. Textile Research Journal, 2022, 92(23–24): 4845–4859.
[21] 杨金, 李麒阳, 季霞, 等. 复合材料编织–缠绕–拉挤系统建模及其控制策略[J].纺织学报, 2023, 44(7): 199–206.
YANG Jin, LI Qiyang, JI Xia, et al. Modeling and control strategy of composite braidingwinding-pultrusion system[J]. Journal of Textile Research, 2023, 44(7): 199–206.
[22] CHI X F, LI Q Y, YAN H X, et al.Robot trajectory optimization control of braiding for three-dimensional complex preforms[J].Journal of Engineered Fibers and Fabrics, 2021,16: 15589250211043226.
