复合材料薄壁构件广泛应用于制造业相关领域。由于应用场景的需要，这些构件通常具有明显的薄壁特征，导致构件刚性差，在加工过程中极易产生加工振动及变形；同时复合材料为典型的难加工材料，加工时容易产生分层、毛刺等问题，严重影响加工质量，两种因素将共同导致复合材料薄壁构件的加工质量难以得到保证。因此，对薄壁构件加工过程中的振动、变形控制要求也日益严苛。此外，不同铺层的存在和材料各向异性导致了所成型构件在物理特性（如振动模态等）上会与相同几何外形的均质材料构件有所差异，加工过程中的振动控制也需要考虑更多的因素。因此，抑制复合材料薄壁构件加工变形及振动一直是加工领域的重要课题。

在抑制薄壁构件加工振动及变形方面，学者们已经开展了大量研究。其中，通过增加辅助支撑来增大系统刚度以减小振动或变形^{[ [1]  WANG L, QIAO F, LI Y J, et al. Optimization of clamping for thin-walled rotational conical aluminum alloy with large diameter: Modal simulation and experimental verification[J]. The International Journal of Advanced Manufacturing Technology, 2021, 114(7): 2387–2396.
[2]  WANG X, MA P J, PENG X L, et al. Study on vibration suppression performance of a flexible fixture for a thin-walled casing[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106(9): 4281–4291.
[3]  GAO P X, LI J W, ZHAI J Y, et al. A novel optimization layout method for clamps in a pipeline system[J]. Applied Sciences, 2020, 10(1): 390.
1-3 ]}是常用的方法。对于辅助支撑而言，支承点的支撑刚度和支撑位置在工程应用中非常重要，支撑刚度或位置的微小变化都将显著影响结构的动态特性^{[ [4]  AYDIN E, DUTKIEWICZ M, ÖZTÜRK B, et al. Optimization of elastic spring supports for cantilever beams[J]. Structural and Multidisciplinary Optimization, 2020, 62(1): 55–81.
[5]  HAUSER B R, WANG B P. Optimal design of a parallel beam system with elastic supports to minimize flexural response to harmonic loading using a combined optimization algorithm[J]. Structural and Multidisciplinary Optimization, 2018, 58(4): 1453–1465.
[6]  FRISWELL M I, WANG D. The minimum support stiffness required to raise the fundamental natural frequency of plate structures[J]. Journal of Sound and Vibration, 2007, 301(3–5): 665–677.
4-6 ]}。因此，支撑布局设计是保证薄壁构件制造质量的重要方法^{[ [7]  LIU C H, WANG J, ZHOU B H, et al. Development of fixture layout optimization for thin-walled parts: A review[J]. Chinese Journal of Mechanical Engineering, 2024, 37(1): 17.
[8]  王张浩, 李东升, 翟雨农. 弱刚性薄壁件夹具布局优化方法研究概述[J]. 航空制造技术, 2023, 66(14): 118–135.WANG Zhanghao, LI Dongsheng, ZHAI Yunong. A review of fixture layout optimization method for weakly-rigid thin-walled workpieces[J]. Aeronautical Manufacturing Technology, 2023, 66(14): 118–135.
7-8 ]}，已有许多学者针对不同工件类型和工况开展了支撑布局优化研究，其中将进化算法与有限元/代理模型结合是常用且有效的方法。

王壮^{[ [9]  王壮. 弱刚性薄壁环形工件装夹布局优化与振动控制[D]. 大连: 大连理工大学, 2020.WANG Zhuang. Optimization of clamping layout and vibration control of weakly rigid thin-walled annular workpiece[D]. Dalian: Dalian University of Technology, 2020.
9 ]}针对弱刚性薄壁环形工件，根据主振型确定了初始支撑点数量，并通过遗传算法结合有限元进行了最佳支撑位置的优化，减小了工件加工振动。Li等^{[ [10]  LI C, WANG Z Q, TONG H, et al. Optimization of the number and positions of fixture locators for curved thin-walled parts by whale optimization algorithm[J]. Journal of Physics: Conference Series, 2022, 2174(1): 012013.
10 ]}提出一种基于鲸鱼优化算法的夹具布局优化方法，对弯曲薄壁零件的夹具数量和位置进行了优化，并通过飞机蒙皮定位布局优化验证了该方法的有效性。Meng等^{[ [11]  MENG S, ZHENG L Y, FAN W, et al. Intelligent layout optimization of reconfigurable flexible fixture for assembling multiple aircraft panels[J]. The International Journal of Advanced Manufacturing Technology, 2023, 126(3): 1261–1278.
11 ]}针对飞机壁板的装夹问题，建立了考虑铆接、面板自重和弹力绷带拉力的面板夹具系统有限元模型，并创建了基于卷积神经网络的夹具布局优化代理模型，结合遗传算法获得代理模型的最优解。Ramesh等^{[ [12]  RAMESH M, SUNDARARAMAN K A, SABAREESWARAN M, et al. Development of hybrid artificial neural network–particle swarm optimization model and comparison of genetic and particle swarm algorithms for optimization of machining fixture layout[J]. International Journal of Precision Engineering and Manufacturing, 2022, 23(12): 1411–1430.
12 ]}建立了预测二维工件最大变形的混合神经网络–粒子群优化算法预测模型，并利用粒子群优化算法优化了网络的权值和偏差，最后对比了遗传算法和粒子群算法的优化结果。Xie等^{[ [13]  XIE W S, DENG Z P, DING B H, et al. Fixture layout optimization in multi-station assembly processes using augmented ant colony algorithm[J]. Journal of Manufacturing Systems, 2015, 37: 277–289.
13 ]}开发了一种基于连续优化方法的增强蚁群算法，用于优化多工位装配过程中二维刚性零件的装夹布局，并通过三工位汽车侧孔装配验证了优化方法的有效性。Alshameri等^{[ [14]  ALSHAMERI T, DING H, DONG Y D, et al. Multi-objective approach to automated fixture synthesis incorporating deep neural network for deformation evaluation[J]. Robotics and Computer-Integrated Manufacturing, 2023, 84: 102579.
14 ]}考虑了定位精度、工件变形等因素，提出了一种在离散域中进行夹具布局的多目标优化方法，使用改进的模拟退火算法进行优化，并通过深度神经网络来估计变形。Yang等^{[ [15]  YANG B, WANG Z Q, YANG Y, et al. Multi-objective optimization of fixture locating layout for sheet metal part sing Kriging and MOBA[J]. Procedia CIRP, 2022, 112: 418–423.
15 ]}针对夹具定位布局优化过程中存在的多目标属性和有限元分析计算量大的问题，提出了一种基于Kriging代理模型和多目标优化算法的钣金夹具多目标优化设计方法，以工件在自重作用下的整体变形和最大变形为目标进行布局设计。

上述研究只考虑了单一的工件振动或变形，而在实际加工过程中，薄壁工件的加工振动、变形通常都是不容忽略的问题，只考虑单一因素有时难以达到预期的效果。同时在实际的薄壁构件支撑中，由于加工需求等因素，经常将带有刚性定位点的真空吸盘作为夹紧和支撑结构。但在基于有限元的薄壁构件支撑布局优化中，为了简化计算，很多时候直接将工件与吸盘支撑点的接触位置固定或约束其法向自由度，而忽略了吸盘吸附带来的变形和在切削力作用下可能存在的微小滑移。虽然上述情况在多数工况中可被视为合理，但当吸盘尺寸相对于工件尺寸来说不能被忽略或者工件足够薄时，可能会导致变形计算结果与实际有较大偏差。此外，对于一些结构复杂的工件，为了满足加工质量要求，有时还需要在无法放置吸盘的位置额外增加辅助支撑结构，这些结构的布局同样需要进行设计优化。

本文提出一种粒子群优化算法（PSO）与有限元融合驱动的薄壁构件支撑布局优化方法，综合考虑了工件吸附变形、支撑后工件固有频率与刀具激励频率有效分离、额外辅助支撑等因素，并针对复合材料薄壁构件进行了支撑布局优化计算与试验，验证了所提出方法的有效性。

以工件加工路径上最大变形量最小化为目标，采用吸盘对工件可吸附区域进行夹紧和支撑，同时采用辅助支撑对吸盘不可达区域进行支撑，约束条件为：（1）支撑点（吸盘吸附点、辅助支撑点）位于工件指定区域内；（2）任意两个支撑点之间满足最小间距要求；（3）支撑后工件任意一阶固有频率与刀具激励频率之间都满足最小安全系数的要求；（4）支撑点数量为满足上述要求时的最小值。具体可表示为

式中，F（x）表示加工路径上的最大变形量；f_p（x，u）表示第p条路径上的最大变形量；V=（v₁，…，v_i，…，v_j，…，v_n）为待求解的支撑布局；x=（x₁，…，$x_{n_1}$）为吸盘布局，其中，n₁为吸盘个数，$x_{n_1}$为第n₁个吸盘的位置向量；$u=(u_1，\cdots ，u_{n_2})$为辅助支撑布局，其中，n₂为辅助支撑个数，$u_{n_2}$为第n₂个辅助支撑点的位置向量，n为总的支撑点个数；v_ik为第i个支撑点位置向量的第k个坐标；d为两个支撑点间的最小间距；f_s为支撑后工件第s阶固有频率；f_d为第d个加工参数引起的激振频率；t₁、t₂分别为固有频率阶数和激振频率个数；{N₁，N₂，…，N_m}为满足其他约束条件的支撑点个数的集合。

采用PSO与有限元融合驱动的方式进行薄壁构件的支撑布局优化，先通过PSO生成满足几何约束条件的支撑布局相关参数，再结合参数化建模方法实现Abaqus仿真建模，求解对应变形及模态参数，并根据结果和优化算法生成下一步支撑布局方案，直到满足求解终止条件，获得优化结果。基于Python实现上述优化方法，整体优化思路如图1所示。

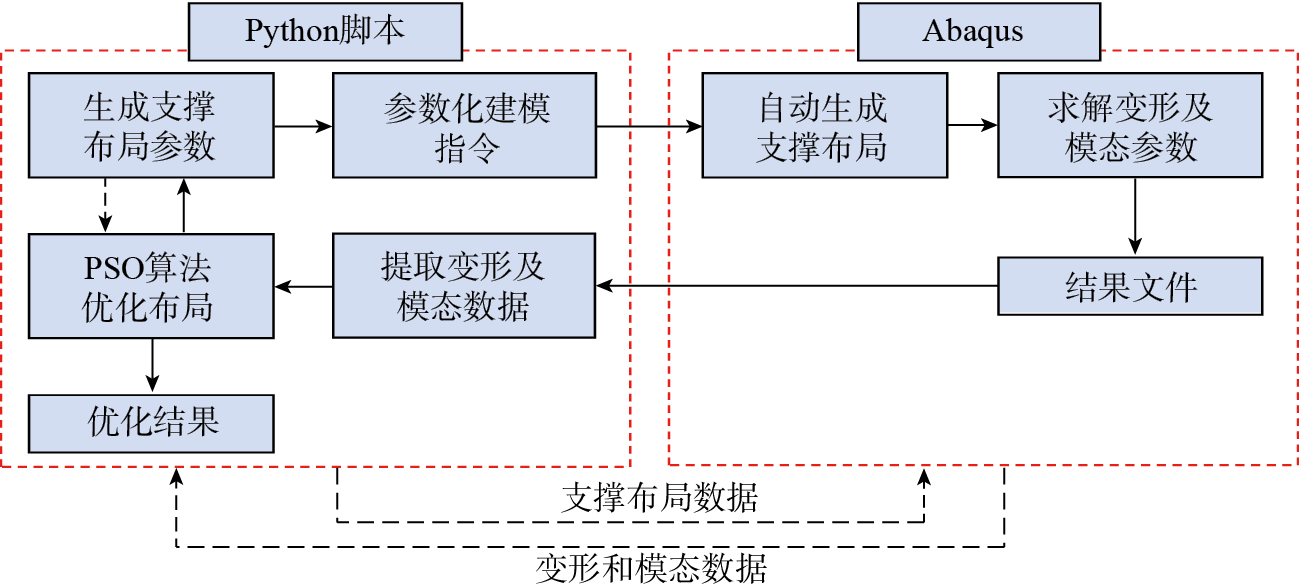
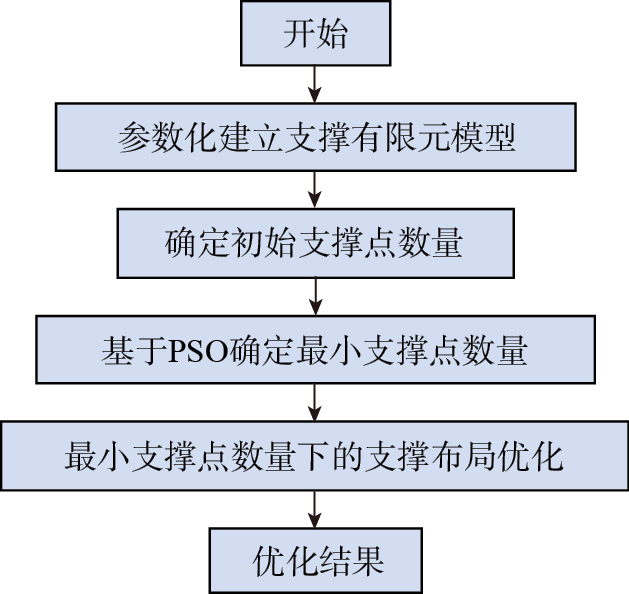
本文提出的支撑布局优化方法主要包括以下4个步骤：（1）基于有限元进行支撑仿真参数化建模；（2）初步确定能满足要求的支撑点个数；（3）基于PSO进行支撑点数量优化；（4）在最小支撑点数量下进行支撑点位置优化。整体优化步骤如图2所示。

在将PSO算法及有限元结合进行支撑布局优化之前，需要先实现有限元的参数化建模，以实现模拟支撑、生成指定中心点的吸附面集合两个功能。为了便于后续实现指定区域内施加面载荷、在节点上建立连接器等操作，本文所用有限元模型为孤立网格模型。

（1）模拟支撑。连接器主要用于模拟吸盘、辅助支撑的支撑效果，为了与实际的支撑情况相符，考虑了连接器作用于接触面时的刚度和摩擦，选用Cartesian型连接器进行支撑约束的模拟，并给每个连接器建立Z轴垂直于工件接触面的坐标系，用于指定连接器刚度方向，此外连接器的滑移方向设置为X、Y方向。

（2）生成吸附面集合。为了考虑吸盘吸附工件的实际状态，需要在以吸盘中心点为中心，吸盘半径为半径的吸附区域内施加与吸盘吸附力一致的面压力。采用的方法为，在已知支撑点编号x₀的前提下，计算支撑区域内任意节点x_i（i为≤节点总数的整数）到x₀的距离，记录距离在吸盘半径r以内的节点编号，形成集合N，然后遍历每个网格e_j（j为≤总网格数的整数）所包含的节点编号，记录所有节点均在N中的网格，形成面集合E，在此面集合上施加等同于吸盘吸附力的面载荷，完成吸盘吸附模拟。

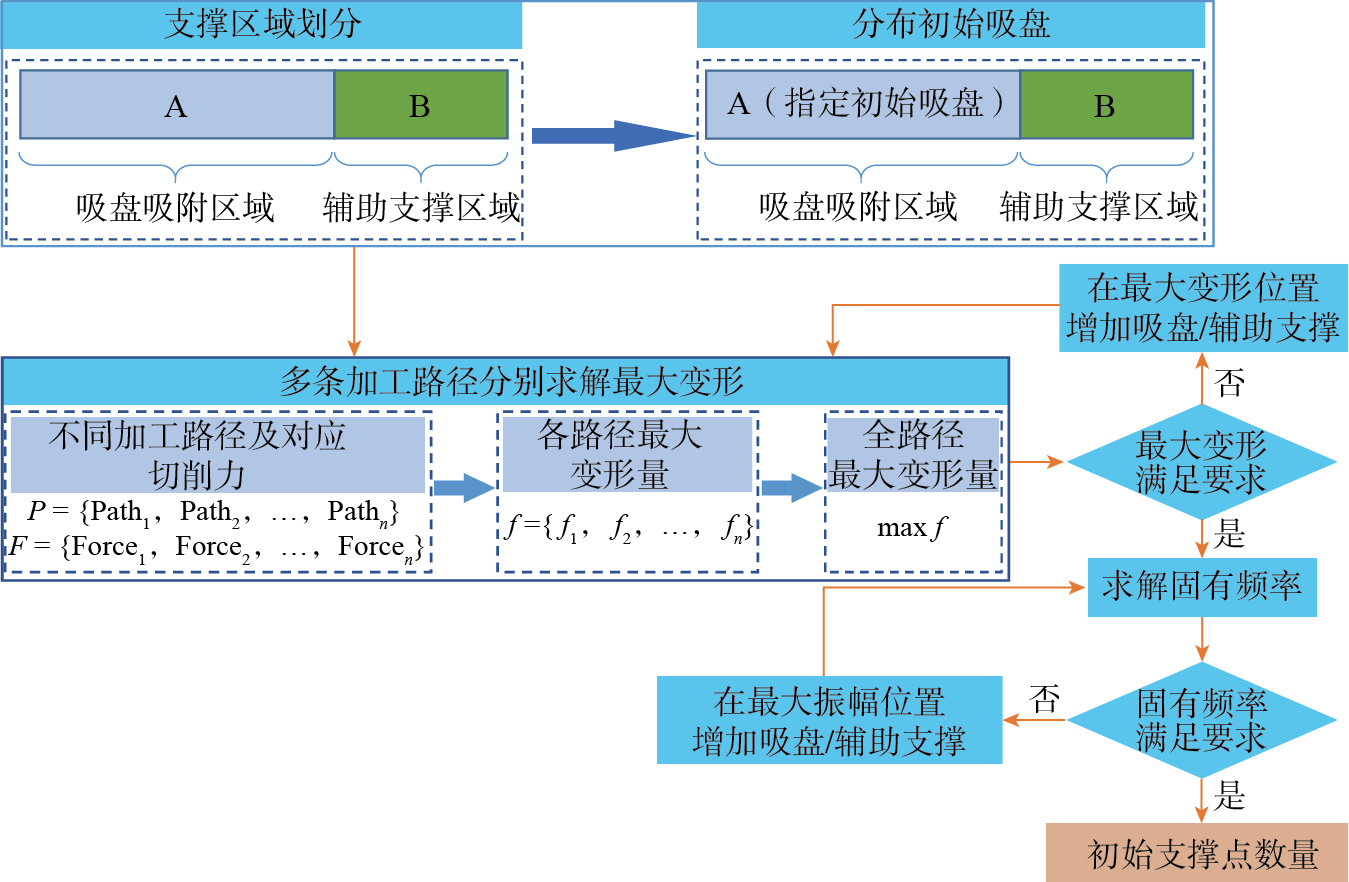
在进行支撑点数量及位置优化之前，需要先找到一个满足约束条件的支撑点数量。本文采用的方法为先任意指定初始吸盘使工件稳定支撑，再逐条路径求解最大变形量，在最大变形点增加吸盘/辅助支撑，直至所有路径下的变形均满足要求。然后计算工件固有频率，在工件不满足要求的固有频率所对应的模态振型振幅最大处增加吸盘/辅助支撑，直至所有固有频率均满足要求，从而获得满足约束条件的初始支撑点数量，整体流程如图3所示。

PSO算法中重要参数的取值均选用常用值，如表1所示，种群数量和最大迭代次数基于前期优化测试结果和时间成本的综合考虑进行取值。基于PSO和有限元的支撑点数量优化流程如图4所示，具体步骤如下。

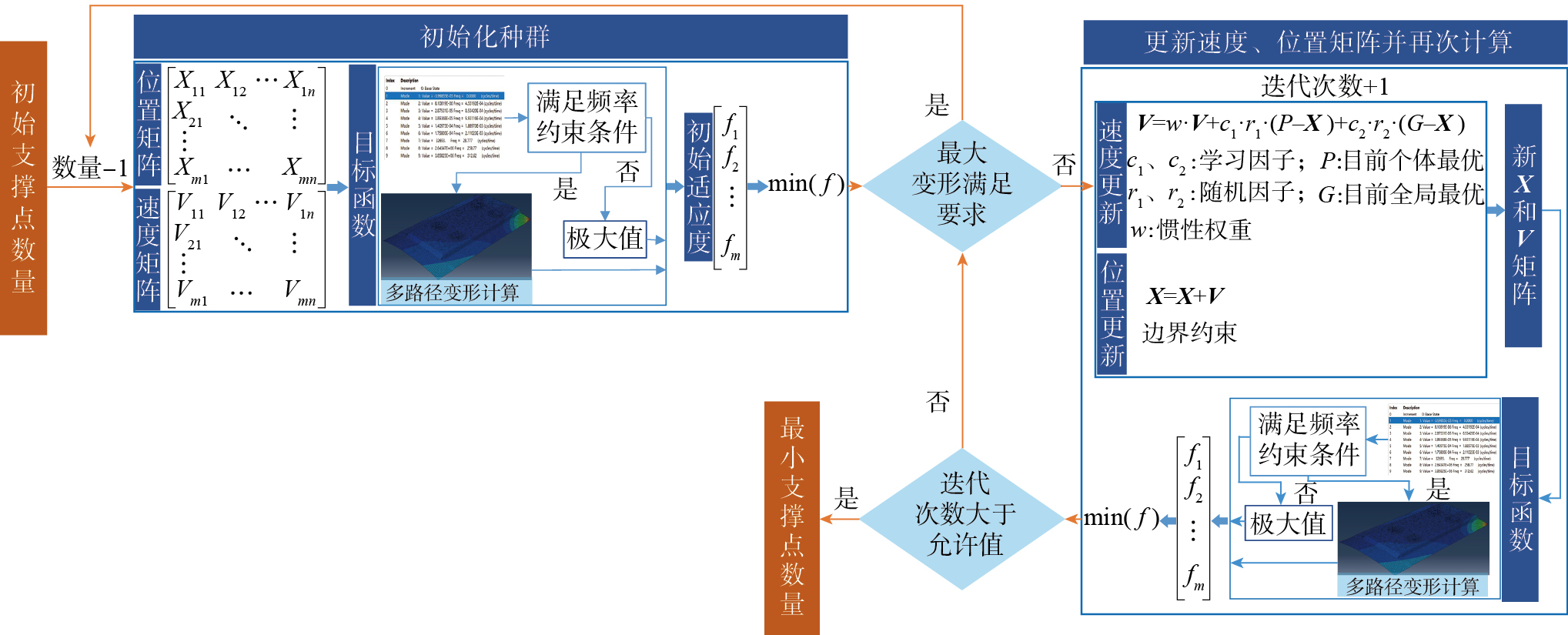
（1）初始支撑布局生成。在支撑区域随机选取满足几何限制的D个节点编号（D为初始支撑点数量减1），组成初始布局。根据前述参数化建模方法，建立每种布局下的有限元模型。

（2）配置载荷条件并求解。由于在支撑布局的约束条件中，要求固有频率与刀具激励频率分离良好，因此在求解时先计算工件固有频率，满足要求后再计算各路径的加工变形。先依次根据第i条加工路径下加工所用的刀具刃数$F_{t_i}$和刀具转速n_i确定刀具激励频率$F_{{\text{d}}_i}$，获得加工危险频率序列$F_{\text{d}}=\left\{F_{{\text{d}}_1}，F_{{\text{d}}_2}，\cdots F_{{\text{d}}_{t2}}\right\}$；再进行模态分析，获得工件固有频率序列$F_{\text{s}}=\left\{F_{{\text{s}}_1}，F_{{\text{s}}_2}，\cdots F_{{\text{s}}_{t1}}\right\}$。按照数学模型中的频率约束条件判定是否满足要求，如果不满足要求则舍去该方案。如果均满足要求则逐条路径求解变形量，获得全路径最大变形量。

（3）更新速度、位置信息。完成适应度的获取后，按照下式对各种支撑布局下的支撑点进行更新迭代。

式中，$P_{\text{ pbest}}^k$、$P_{\text{ gbest}}^k$分别为前k次迭代中个体最优布局和全局最优布局；V^k+1、V^k分别为第k+1次迭代和第k次迭代中粒子速度向量；X^k+1、X^k分别为第k+1次迭代和第k次迭代时的支撑布局方案；然后对更新后的各种支撑布局进行参数化建模，不断重复步骤（2）和（3），直至迭代次数到达设定的最大值。

（4）减少支撑点数量。按照步骤（3）所述，如果迭代次数达到设定的最大值时，仍未找到满足变形要求的布局方案，则在此时的支撑点数量上加1，作为最小支撑点数量。如果在达到最大迭代次数之前就找到了满足最大变形要求的布局方案，则对支撑点数量减1。然后重新执行步骤（1）~（4），直至出现达到最大迭代次数限制的情况，再将支撑点数量加1，作为最小支撑点数量。

得到最小支撑点数量之后，将该值作为最终的支撑点数量，按照支撑点数量优化中的方法，重新执行步骤（1）~（3），直到达到最大迭代次数，此过程不再赘述，至此完成了支撑点数量及位置的协同优化。

基于Abaqus开发了实现上述功能的专用模块，包含了基本模型参数、加工参数、支撑参数和算法参数4个部分，模块界面如图5所示。

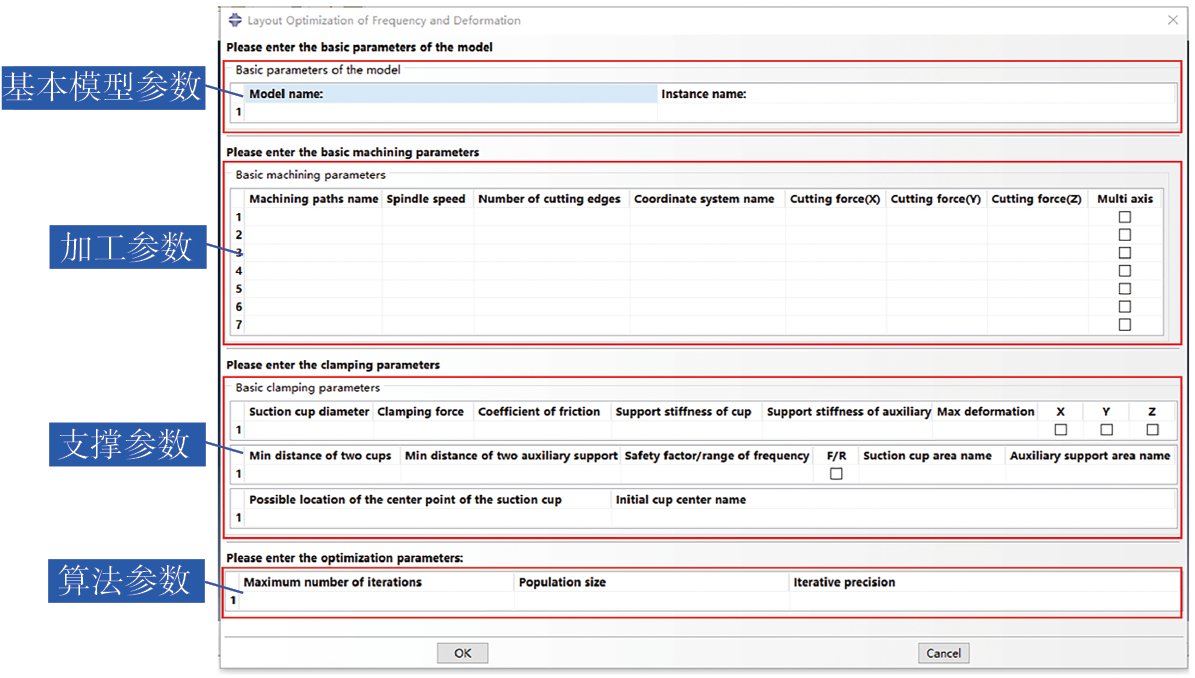
基本模型参数部分包含了2个相关参数，分别为模型名称（Model name）和实例名称（Instance name）。

加工参数部分包含了8个相关参数，分别为加工路径名（Machining paths name）、主轴转速（Spindle speed）、刀具刃数（Number of cutting edges）、坐标系名称（Coordinate system name）、X方向切削力（Cutting force X）、Y方向切削力（Cutting force Y）、Z方向切削力（Cutting force Z）、多轴加工（Multi axis）。此部分可配置多条加工路径，每条加工路径可以具有不同的工艺参数和刀具参数，主轴转速和刀具刃数主要用于确定刀具激励频率。多轴加工参数为可选项，如果不选中，则每条加工路径计算变形时将只在单个节点上施加切削力，选中后将对路径上的离散节点同时施加切削力来求解最大变形。

支撑参数部分包括17个相关参数，分别为吸盘直径（Suction cup diameter）、吸附力（Clamping force）、摩擦系数（Coefficient of friction）、吸盘支承刚度（Support stiffness of cup）、辅助支撑刚度（Support stiffness of auxiliary）、最大允许变形量（Max deformation）、最大变形方向（X、Y、Z）、吸盘间的最小间距（Min distance of two cup）、辅助支撑间的最小间距（Min distance of two auxiliary support）、频率安全系数（Safety factor of frequency）、系数或绝对值（F/R）、吸附区域名称（Suction cup area name）、辅助支撑区域名称（Auxiliary support area name）、吸盘中心吸附区域名称（Possible location of the center point of the suction cup）及初始吸盘中心位置（Initial cup center name）。

算法参数部分包括3个相关参数，分别为最大迭代次数（Maximum number of iterations）、种群数量（Population size）、迭代精度（Iterative precision）。

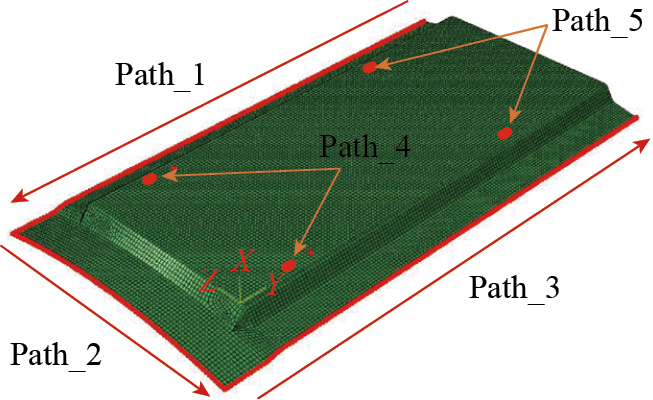
基于上述开发的模块进行典型复合材料薄壁构件的支撑布局优化，该薄壁构件需要进行3条边缘铣边及4个长条孔加工，工件边缘凸沿区域为辅助支撑区域，其余为吸盘吸附区域（排除了加工位置），工件模型及加工路径定义如图6所示，其中Path_4和Path_5分别包含了2个长条孔，需同时加工。

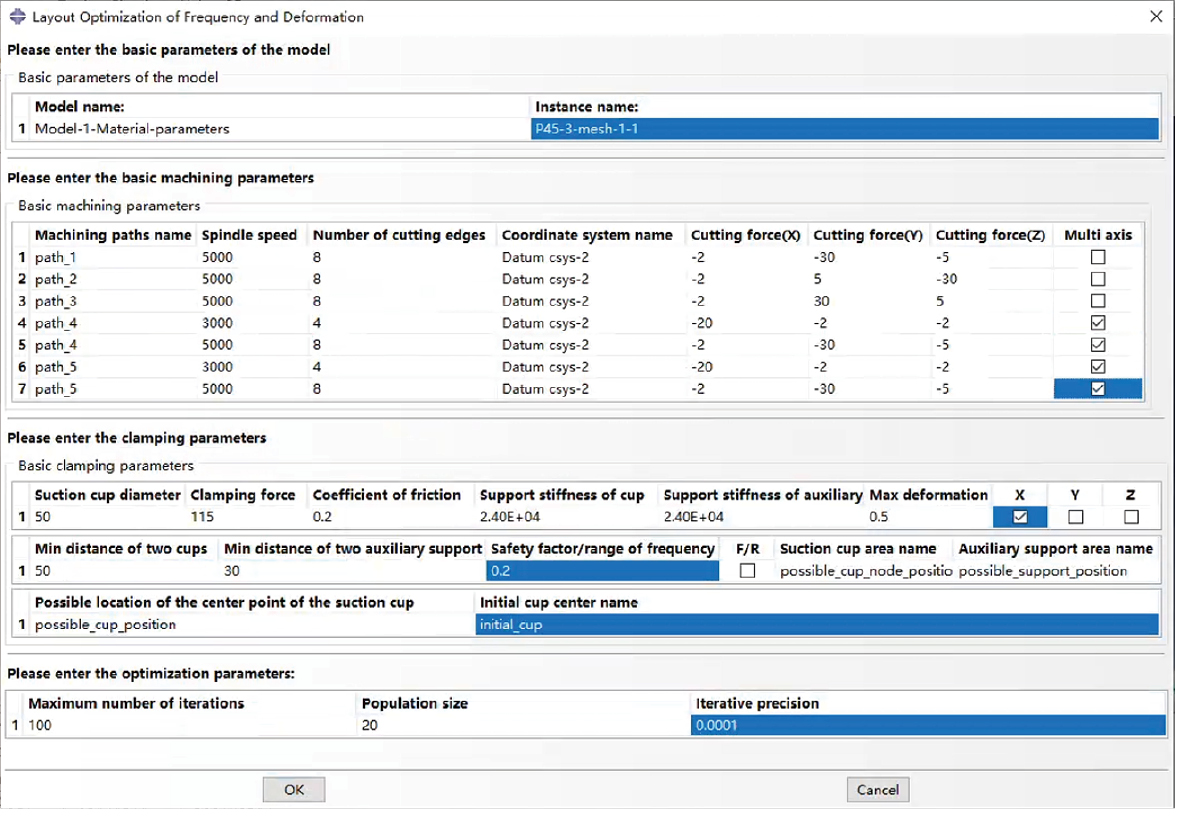
优化所需的所有参数设置如图7所示，其中各加工路径切削力为试验所得，由于长条孔实际加工时包含垂直进给和水平进给两个阶段，切削力明显不同，因此对两个阶段分别进行计算。

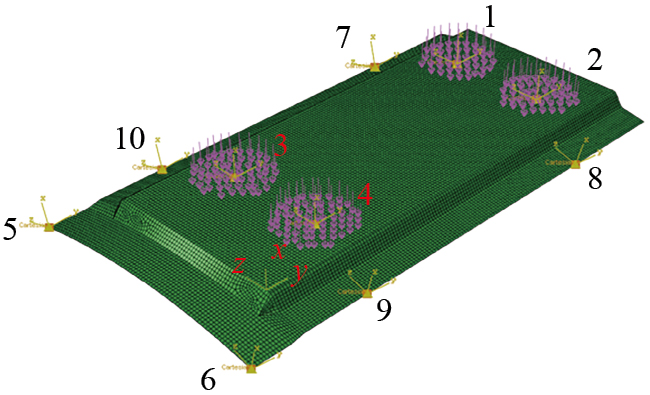
任选4个初始吸盘位置，保证支撑稳定性，吸盘位置如图8所示。逐次在最大变形/振幅位置附近增加支撑点，以完成初始布局，支撑点数量及最大变形量如表2所示。当支撑点数量为10时，最大变形量小于设定的0.5 mm，即初始支撑点数量为10，初始支撑布局如图9所示。获得初始支撑布局后，逐次减少支撑点并进行优化计算，每种情况下的计算结果如表3所示。

由表3可知，当支撑点数量为7时，达到最大迭代次数后仍未能满足变形要求，因此确定最小支撑点数量为8。需要说明的是，此处的最大变形量并非对应支撑点数量下所能达到的最小值。在进行支撑点数量优化时，只要在迭代过程中首次找到了小于最大允许变形量（0.5 mm）的支撑方案，便不再寻找更小的变形量，而是减少支撑点数量，由于算法本身在寻优过程中具有一定随机性，首次找到的、满足要求的值和支撑点数量并无直接关系。用8个支撑点进行最终的支撑布局优化，迭代曲线和最终布局（即优化后支撑布局）如图10所示。当迭代次数达到66次时，后续最大变形量不再减小，此时支撑点由4个吸盘和4个辅助支撑点组成，最大变形量为0.357 mm。

采用加工中心及自研阶梯微齿刀具进行试验。根据支撑布局优化前后的支撑方案（10个支撑点和8个支撑点）设计了专用夹具，吸盘直径为50 mm，辅助支撑为一端带有半球的圆杆结构，并在工件4个边角位置布置了CL–L030型激光位移传感器（基恩士），测量两种支撑方案加工过程中的变形量，测量点的选取通过前期工艺试验进行确定。考虑到工件的薄壁特征（壁厚仅1 mm），以及实际加工时工件厚度方向的变形最显著，因此只测量工件Z轴方向的变形量作为参考结果。同时，在试验前通过3225F型力锤和加速度传感器（Dytran公司）测量工件支撑后模态参数，并使用MI–7008型模态采集设备（ECON公司）进行数据分析。试验布置如图11所示，试验参数设置如表4所示。

通过支撑布局优化前后的试验对比，验证仿真及优化方法的可行性。两种情况下工件固有频率及4个典型位置（工件4个边角位置，如图10所示）的变形量结果如图12所示。

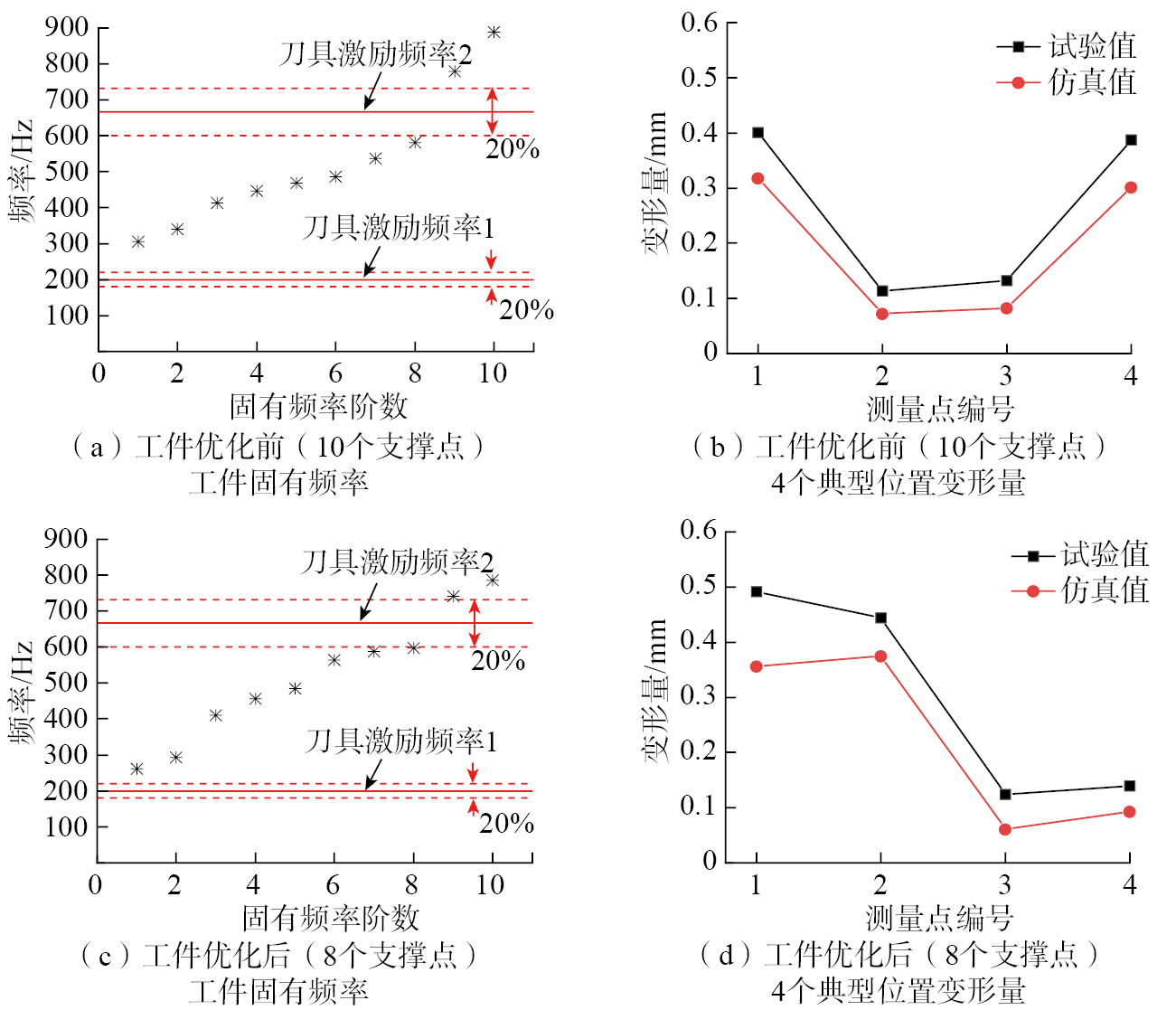
从工件固有频率来看，由工艺参数1（主轴转速为3000 r/min，刀具刃数为4）确定的刀具激励频率1比工件优化前后的第一阶固有频率小，由工艺参数2（主轴转速为5000 r/min，刀具刃数为8）确定的刀具激励频率2均位于工件优化前后的第8阶和第9阶固有频率之间，所有固有频率均满足优化时设定的频率要求，即在激励频率的±10%区间内（其中红色虚线所示）没有出现工件的固有频率。从工件4个典型位置的变形量来看，仿真中的变形量均小于试验测得的变形量，优化前（10个支撑点）工件试验测得的最大变形量为0.401 mm，对应点的仿真变形量为0.318 mm，仿真误差为20.7%；优化后（8个支撑点）工件试验测得的最大变形量为0.492 mm，对应点的仿真变形量为0.357 mm，仿真误差为27.4%。

由图12可知，仿真值与试验值有一定偏差，从试验角度分析，主要原因在于试验时只能手动对准传感器测点位置，实际测点和仿真中的理论位置有一定偏差，而且测量位置区域为倾斜的曲面结构，因此测点的较小位置区别会导致测量结果出现较大差异。从仿真模型本身来看，由于网格的存在，对吸盘吸附区域施加面载荷时，加载区域并非理想的圆形，且本文选取加载区域的算法为仅当1个单元的4个节点均在吸盘吸附区域内时，才将该单元列入加载区域，使得仿真中的加载区域面积略小于实际吸盘吸附面积，这也在一定程度上导致变形的仿真值偏小。从整体来看，优化前后的工件变形量均小于所设定的0.5 mm最大变形量要求，优化后支撑点数量从10个减少到8个，且满足频率要求，验证了所提支撑布局优化方法的有效性。

（1）提出了一种粒子群优化算法和有限元融合驱动的薄壁构件支撑布局优化方法，综合考虑了工件吸附变形、支撑后工件固有频率与刀具激励频率有效分离、额外辅助支撑等因素，能够在保证最大变形量满足要求的前提下实现支撑点数量及位置的优化，为薄壁构件的支撑布局设计提供了参考。

（2）针对提出的薄壁构件支撑布局优化方法进行了算法实现，并基于Abaqus开发了薄壁构件支撑布局优化的专用模块，提供了参数配置界面，实现了优化所需参数的便捷配置。

（3）典型复合材料薄壁构件优化计算与试验结果表明，所提出的支撑布局优化方法能够较好地实现支撑后工件固有频率与刀具激励频率的分离，并且在保证加工路径最大变形量满足要求的情况下，将支撑点数量从10个减少到8个。