钛合金具有比强度高、耐高温、耐腐蚀等特点[1],广泛应用于飞机[1]、发动机[2]和导弹[3]等航空装备。在航空器高速化的发展趋势下,气动生热引发的热累积效应使蒙皮表面温度急剧升高,对航空装备的耐高温性能提出进一步提升的要求,TA15、TA32、Ti65 等耐高温钛合金在高温下具有优异的抗氧化性能、组织稳定性和长时抗蠕变性能,可以满足不同温度区间服役性能的要求[4]。TA32 钛合金是一种在TA12 合金基础上改进的典型近α型高温钛合金,具有优异的高温抗蠕变性能,已应用于航空发动机加力燃烧室筒体和巡航导弹弹体结构[5]。
TA32 钛合金在常温下成形存在变形抗力大、回弹严重和局部破裂等问题,通常采用热成形工艺实现零件的成形[6]。TA32 钛合金零件热成形工艺为:将模具和毛坯加热至700~800 ℃,在恒温条件下利用材料高温软化冲压成形,保压一段时间使材料应力松弛后取出零件。热成形后的TA32 钛合金零件成形精度较好,但仍存在一定的回弹现象。由于新一代航空装备对隐身性能的高要求,对零件的型面精度和装配阶差要求越来越高,精确的回弹预测和模面补偿是提高钛合金零件型面精度的可靠方法。
钛合金在热成形保压阶段发生应力松弛行为,其本质为金属材料在保持恒定变形时内部弹性应变不断转化为永久的塑性应变[7]。部分学者对钛合金的应力松弛行为进行了研究。Xiao 等[8]研究了TC4 钛合金的应力松弛行为,并构建了描述应力松弛行为的蠕变本构模型。杨晓明[9]将TC4 钛合金高温短时蠕变本构模型应用于U 型件叠层冷模热冲压工艺及回弹模拟研究,并通过试验验证了模拟的准确性。对于耐高温的TA32钛合金,Wu 等[10]研究了TA32 钛合金高温应力松弛行为并构建了蠕变本构方程;陈灿[11]则研究了TA32 钛合金复杂蒙皮热成形的成形性问题,但并未将TA32 钛合金应力松弛行为与热成形数值模拟结合。基于应力松弛行为构建更为准确的热成形回弹预测模型,对于实现复杂耐高温航空钣金零件的精确成形具有重要意义。
本文研究了TA32 钛合金在不同温度 (650 ℃、700 ℃、750 ℃、800 ℃)和预应变 (2%、4%、8%)条件下的应力松弛行为,构建了基于应力松弛行为的Arrhenius 高温蠕变本构方程,将构建的蠕变本构模型应用于加强框这一典型热成形零件的热成形模拟中,分析保压参数对加强框回弹的影响规律,并通过试验验证模拟结果的准确性。
1 试验及方法
试验材料为宝钛公司提供的M 态TA32 钛合金板材,厚度为2.0 mm,化学成分如表1 所示。试验设备为电子蠕变松弛试验机RDL50(图1),包括数据监控记录装置、加热保温炉、温度和位移控制器等。试样尺寸如图2 所示,参照GB/T 10120—2013《金属材料拉伸应力松弛试验方法》,在不同温度 (650 ℃、700 ℃、750℃、800 ℃)和预应变 (2%、4%、8%)下进行应力松弛试验,松弛时间为1 h。

图1 应力松弛试验装置
Fig.1 Stress relaxation testing equipment
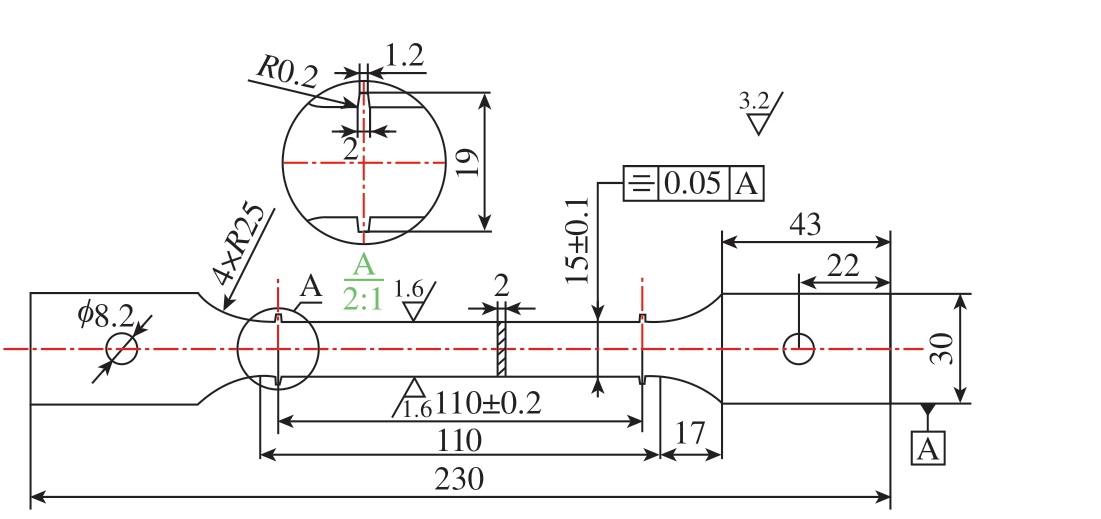
图2 应力松弛试样几何尺寸
Fig.2 Dimensional size of the stress relaxation sample
表1 TA32 钛合金化学成分( 质量分数)
Table 1 Chemical compositions of TA32 titanium alloy(mass fraction) %

Al Sn Zr Mo Si Nb Ta Ti 5.5 3.5 3.0 0.7 0.3 0.4 0.4 余量
2 结果与讨论
2.1 应力松弛行为分析
不同温度下的应力松弛曲线如图3 所示,整体来看,TA32 钛合金的应力松弛行为分为两个阶段,第一阶段残余应力在很短的时间内迅速下降,第二阶段残余应力缓慢下降,且逐渐趋近于某一常数,即应力松弛极限。刘坡等[12]的研究指出,对于应力松弛第二阶段,随着应力松弛的进行,弹性应变不断转化为塑性应变,材料内应力减小,位错滑移驱动力降低,最终硬化与回复趋于平衡。温度对应力松弛行为影响显著,在同一预应变下,温度越高,TA32 钛合金应力松弛速率越快,最终所达到的应力松弛极限越小,温度从650 ℃升高到800 ℃,应力松弛极限从28.3 MPa 下降至0.76 MPa。
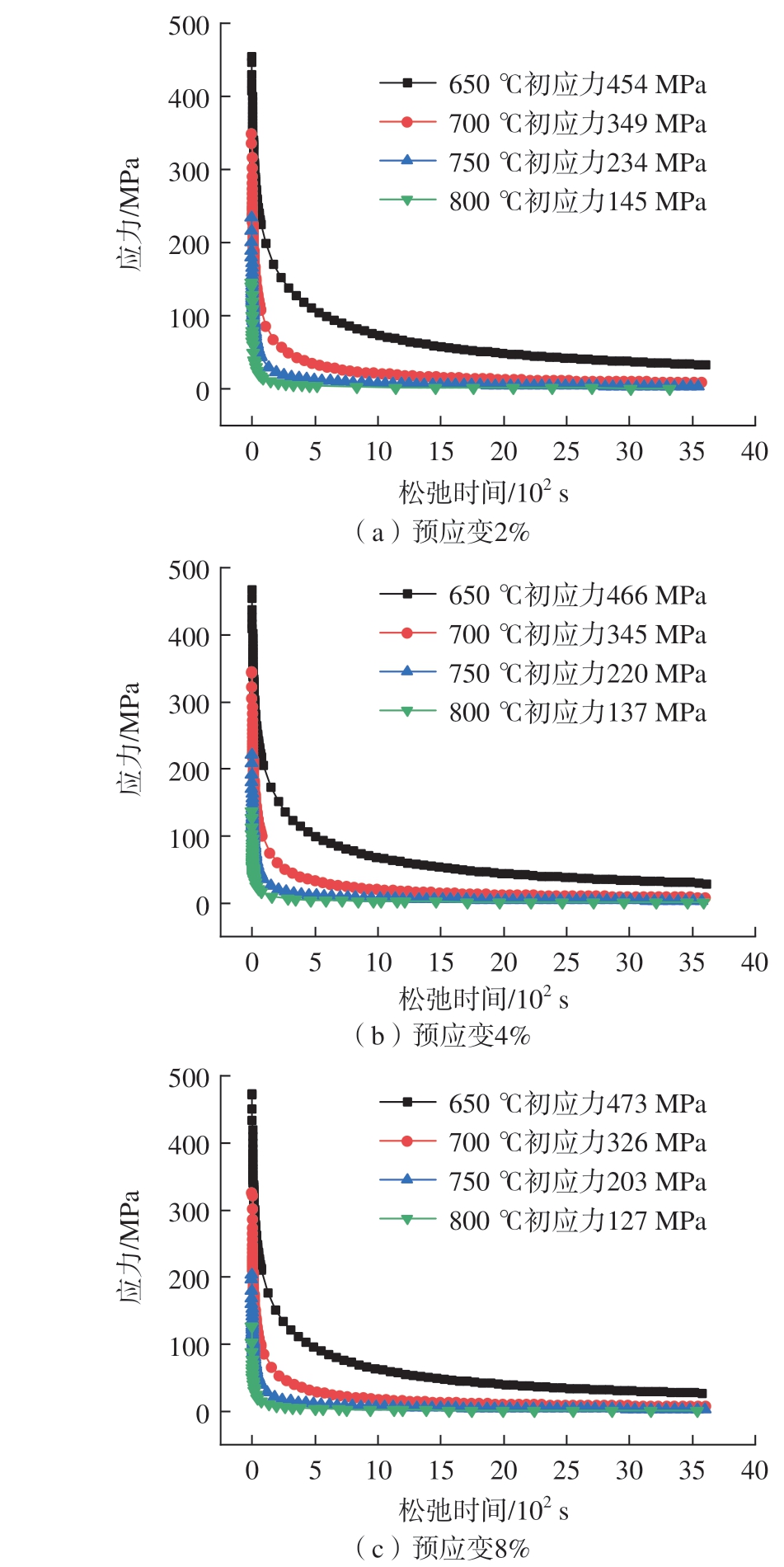
图3 不同预应变下的应力松弛行为
Fig.3 Stress relaxation behaviors under different pre-strains
650 ℃、800 ℃下,不同预应变的应力松弛曲线如图4 所示。可以看出,预应变对应力松弛行为的影响受温度的限制,在650 ℃时,预应变对TA32 钛合金应力松弛行为第一阶段影响较大,预应变越大,第一阶段松弛速率越快;在800 ℃时,不同预应变下的应力松弛行为几乎一样,这是由于温度对应力松弛速率的影响远大于预应变对应力松弛速率的影响,温度越高,材料内部位错驱动的热能越高,且原子扩散激活能降低,位错运动速率更高,从而应力松弛速率提高[13],这也反映了TA32钛合金应力松弛行为主要受温度的影响。Zong 等[14]的研究指出,在650 ℃下,应力松弛机理以位错滑移为主,伴随少量的位错攀升,而在800 ℃下,应力松弛机理为位错滑移和亚晶界迁移。此外,在同一温度下,预应变对应力松弛极限几乎没有影响,在松弛时间足够长的情况下,不同预应变下的应力松弛极限相同,应力松弛极限只与温度有关[15]。

图4 不同温度下的应力松弛行为
Fig.4 Stress relaxation behaviors at different temperatures
2.2 基于应力松弛行为的蠕变本构建模
目前,通常采用自然对数方程、指数方程、延迟函数方程等经验公式来表征材料的应力松弛行为。其中,通过延迟函数表征的应力松弛曲线具有较高的精度,并且随着延迟函数次数的增加,其结果精度越高,本文拟采用五次延迟函数对TA32 钛合金的高温应力松弛行为进行拟合描述,其表达式如式 (1)[9]所示。
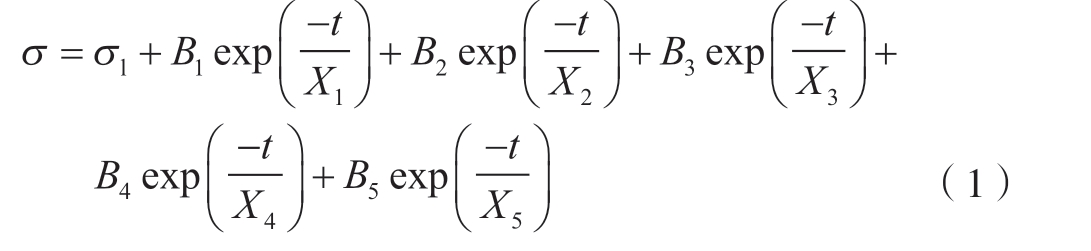
式中,σl 为材料极限松弛应力;B1~B5、X1~X5 为材料参数;t 为应力松弛时间。
采用回归拟合的方法拟合五次延迟函数参数,五次延迟函数描述了TA32 钛合金在应力松弛过程中的瞬时应力与时间的关系,可以通过现有的蠕变本构模型来描述材料的应力松弛行为。
在整个应力松弛过程中,弹性应变、塑性应变与总应变关系满足式 (2)。
式中,ε总为总应变;ε弹性为弹性应变;ε塑性为塑性应变。
在总应变一定的情况下,弹性应变不断转化为塑性应变,弹性应变向塑性应变转化的过程可认为是应力不断减小的蠕变,则有
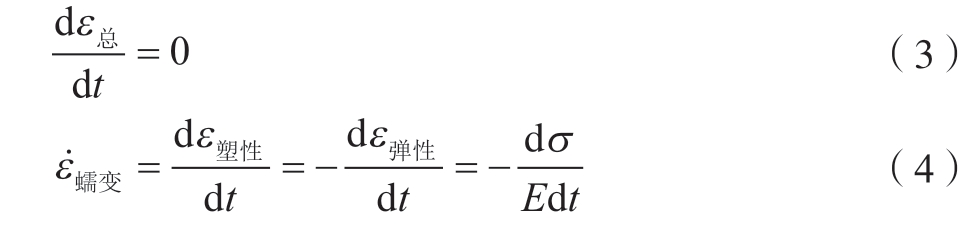
式中,ε蠕变为蠕变应变速率;E 为弹性模量。
由式 (4)可知,在宏观上材料的应力松弛行为可以认为是在一定时间内,材料部分弹性应变的减小量与蠕变应变的增加量相等。
联立式 (1)和 (4)可得TA32 钛合金蠕变应变速率与时间的关系式,即
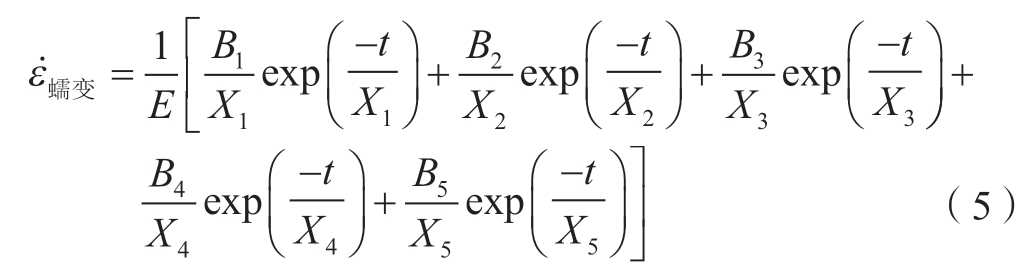
由此可以通过时间将蠕变应变速率与应力联系起来,构建蠕变应变速率与应力关系曲线,如图5 所示。
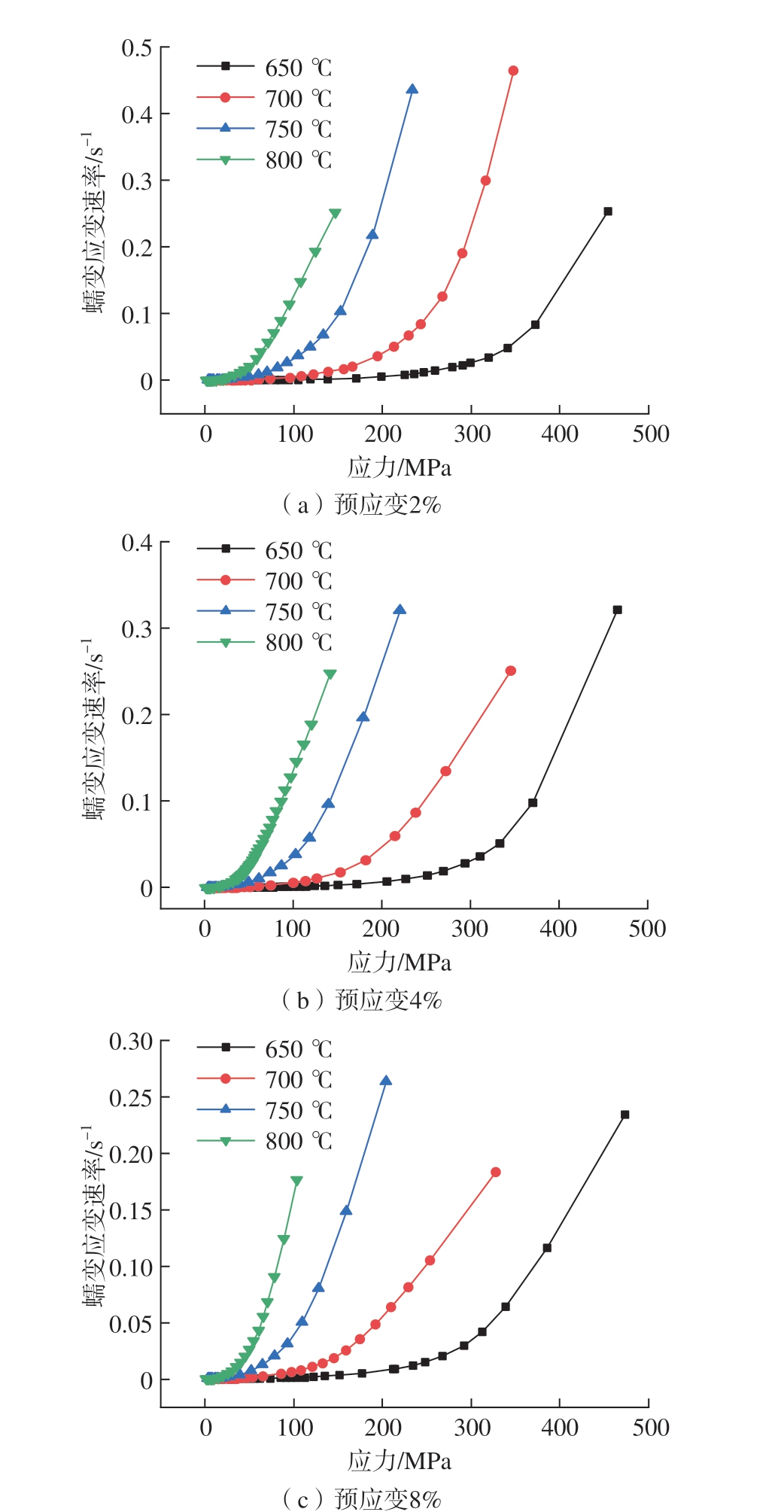
图5 不同预应变下的蠕变应变速率–应力曲线
Fig.5 Creep strain rate - stress curves under different pre-strains
由图5 可知,应力对蠕变应变速率的影响随温度的升高而增强,温度越高,到达相同蠕变应变所需的应力越小,随着应力的增加,材料的蠕变应变速率先基本保持不变,后快速增长。
目前常用Garofalo 和Arrhenius 方程相结合的形式来描述材料应变率与应力之间的关系[9],即
式中,ε为应变速率;σ为材料应力;R为摩尔气体常数,其数值为8.31 J/(mol·K);Q 为热变形激活能;T 为材料变形温度;A 为材料常数;n 为应变速率敏感指数;α 为应力水平指数。
Arrhenius 本构方程表达式[16]为

式中,C1、n1、C2 和β 为材料常数, α = β/n1。
由式 (7)~ (9)求得Arrhenius 本构方程各个参数,如表2 所示。
表2 Arrhenius 本构方程参数
Table 2 Parameters of the Arrhenius constitutive equation
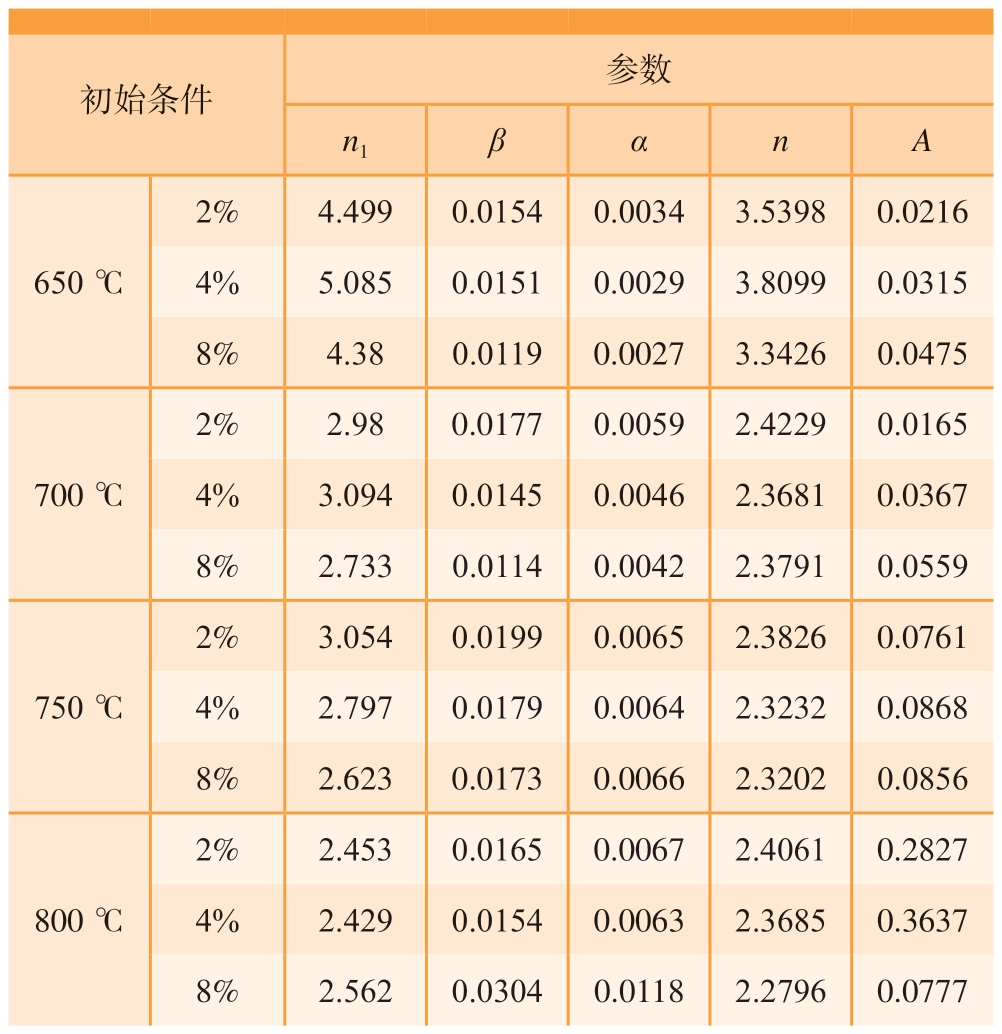
初始条件 参数n1βαnA 650 ℃2% 4.499 0.0154 0.0034 3.5398 0.0216 4% 5.085 0.0151 0.0029 3.8099 0.0315 8% 4.38 0.0119 0.0027 3.3426 0.0475 700 ℃2% 2.98 0.0177 0.0059 2.4229 0.0165 4% 3.094 0.0145 0.0046 2.3681 0.0367 8% 2.733 0.0114 0.0042 2.3791 0.0559 750 ℃2% 3.054 0.0199 0.0065 2.3826 0.0761 4% 2.797 0.0179 0.0064 2.3232 0.0868 8% 2.623 0.0173 0.0066 2.3202 0.0856 800 ℃2% 2.453 0.0165 0.0067 2.4061 0.2827 4% 2.429 0.0154 0.0063 2.3685 0.3637 8% 2.562 0.0304 0.0118 2.2796 0.0777
将表2 中的参数拟合结果代入式 (11),得到蠕变应变率与应力的关系曲线、试验数据与预测曲线对比,如图6 所示。

图6 不同预应变下试验数据与预测曲线对比
Fig.6 Comparison between experimental and predicted curves under different pre-stains
通过相关系数r 与平均相对误差AARE 衡量试验值与预测值之间的偏差,如图7 所示,可以看出,试验值与预测值之间的相关系数r 值为0.9868,平均相对误差AARE 为14.1%,所构建的蠕变本构模型能较好地预测TA32 钛合金的蠕变应变率与应力的关系。
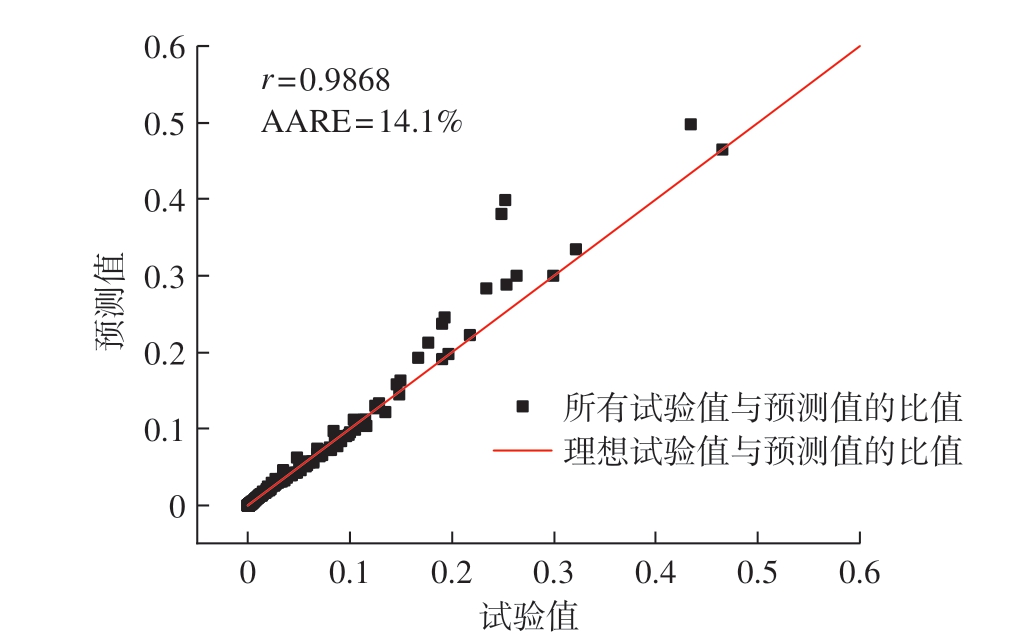
图7 Arrhenius 型蠕变本构方程拟合精度分析
Fig.7 Fitting accuracy of Arrhenius type creep constitutive equation
2.3 有限元模拟与试验验证
加强框为航空典型零部件,如图8 所示,零件厚度为1.5 mm,中心圆弧面半径91.5 mm,成形精度要求±0.1 mm。采用等温热成形工艺成形的零件仍存在一定的回弹现象,本文基于构建的蠕变本构模型,通过有限元精确模拟探究工艺参数对热成形回弹的影响规律,为回弹修正奠定基础。
图8 加强框零件模型
Fig.8 Reinforced frame model
使用ABAQUS 软件构建的加强框零件热成形有限元模型如图9 所示,毛坯尺寸为 150 mm×70 mm×1.5 mm,成形环境为800 ℃等温,不考虑板料和模具的换热,毛坯采用实体单元C3D8R;模具设置刚体耦合,网格类型为S4R。定义板料与上、下模具的切向接触行为为罚函数接触,采用石墨作为润滑剂,摩擦系数取0.3[17–18]。成形模拟包括冲压、保压和回弹3 个阶段。冲压分析步中,凹模设置固定约束,凸模沿冲压方向运动;保压分析步中,保持凹凸模不动,施加一定的保压力;回弹分析步中去除所有约束和接触,只保留板料模型,采用无模法计算回弹。

图9 加强框热成形有限元模型
Fig.9 Finite element model of the reinforced frame hot forming
在冲压分析步与回弹分析步采用TA32 钛合金真应力–真应变曲线数据 (图10),在保压分析步中采用本文构建的基于应力松弛行为的Arrhenius 蠕变本构模型。
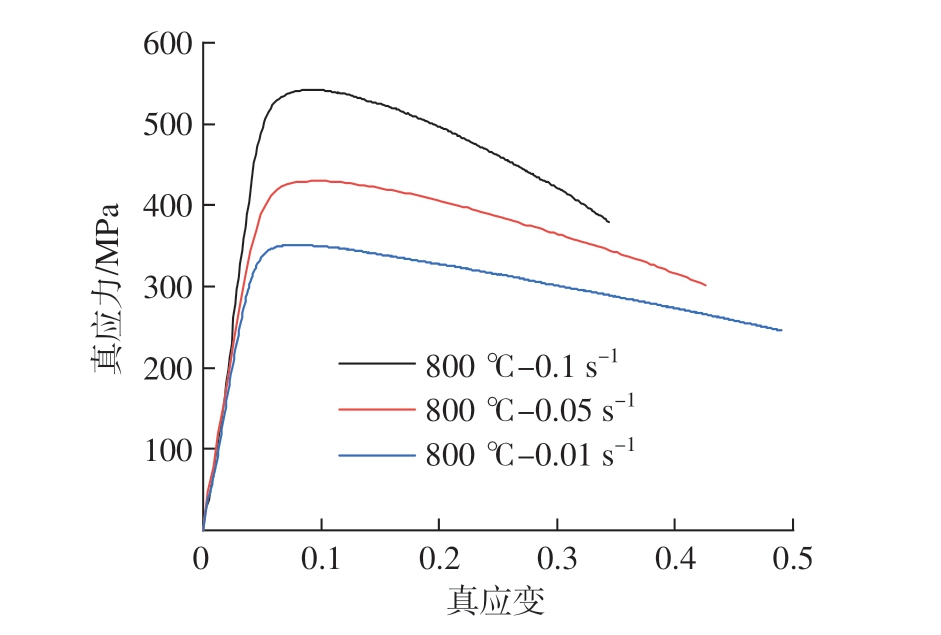
图10 800 ℃下TA32 钛合金真应力–真应变曲线
Fig.10 True stress – strain curves of the TA32 titanium alloy at 800 ℃
800 ℃下,TA32 钛合金冲压结束后的应力分布如图11(a)所示,可以看出,整体轮廓呈圆弧状,主要发生弯曲变形,应力主要集中在加强框外侧带有圆角特征的位置。保压10 s、60 s 和300 s 的应力分布变化如图11(b)~(d)所示,随着保压时间的延长,零件内部应力逐渐松弛,最大应力由504.320 MPa 减少至87.997 MPa,且应力分布更均匀。图12 显示了加强框某节点在800 ℃时应力随时间变化曲线,可以看出,在前100 s内应力迅速下降,随后缓慢下降并趋于平缓,在保压时间300 s 时,应力松弛基本完成。
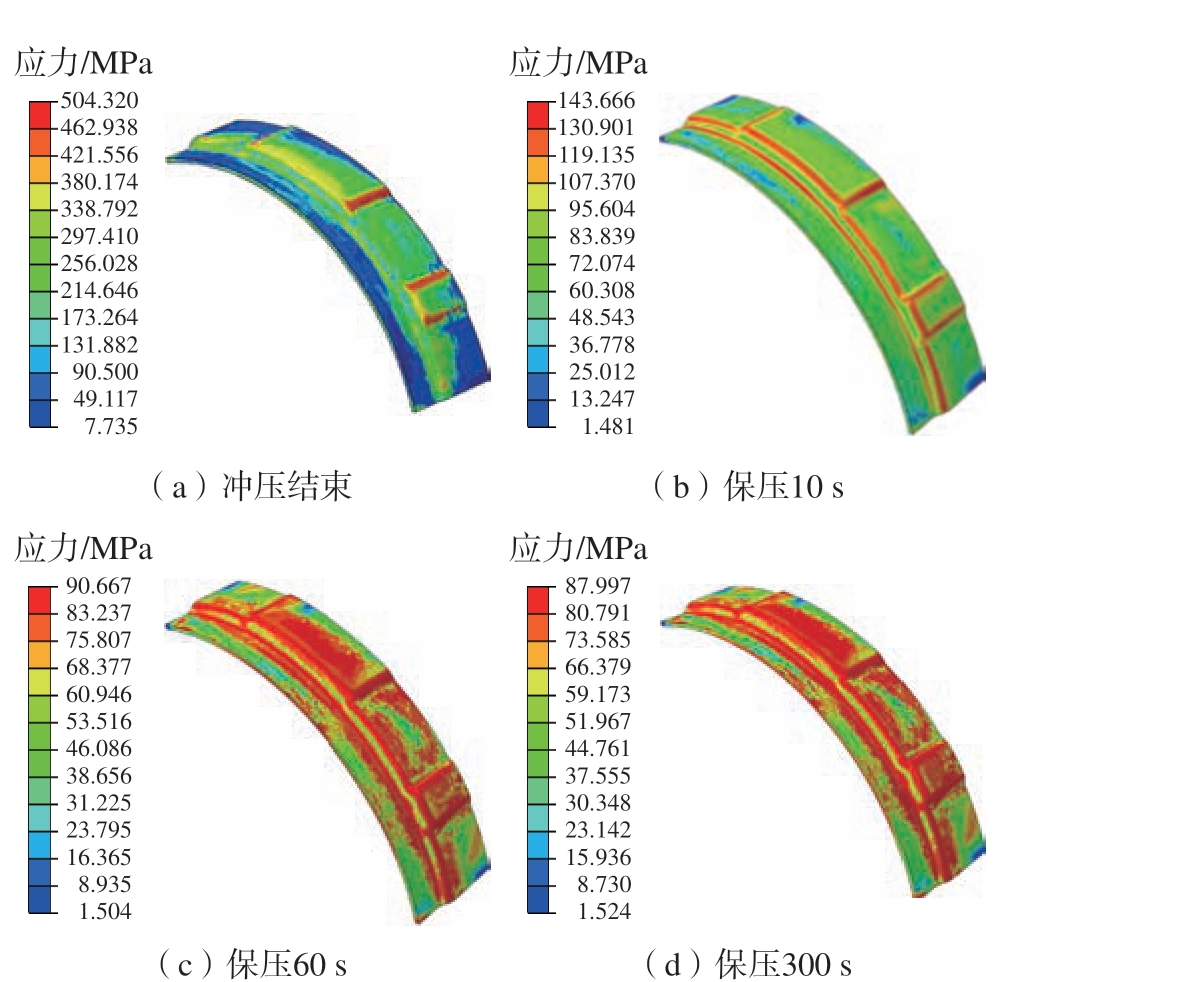
图11 热成形不同时刻应力分布云图
Fig.11 Stress distribution cloud map of the part at different forming periods
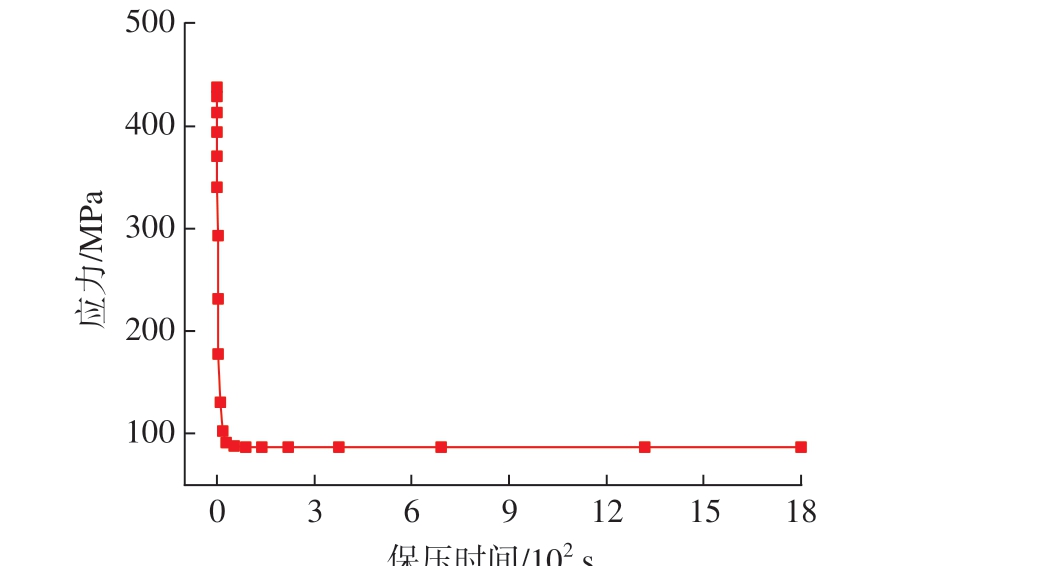
图12 某节点应力随时间变化曲线
Fig.12 Relationship curve between the stress and holding time at one node
TA32 钛合金在成形保压卸载后发生了回弹,如图13(a)所示,零件回弹主要表现在弯曲半径的变化,由于加强框外侧轮廓带有特征,不便测量,内侧为完整的弯曲圆弧,可以通过测量弯曲半径评价回弹结果。通过CAD 软件绘制外形轮廓,测量加强框内侧弯曲半径变化作为回弹计算结果。在热成形压力机上开展加强框热成形试验,热成形模具示意图如图13(b)所示,试验过程如图13(c)所示,温度选取800 ℃,保压时间分别选取10 s、60 s、300 s、1800 s。成形后零件如图13(d)所示,采用GOM 三维光学扫描仪扫描成形后零件轮廓,以800℃、保压时间1800 s 为例,在原始模型上选取固定3 点,基于投影算法,反射到扫描曲面同样位置的3 点上,根据三点确定一个圆的准则,计算圆弧处的弯曲半径,实际零件半径与理想半径的差值为回弹量,如图14 所示。

图13 加强框零件热成形过程
Fig.13 Hot forming process of the reinforced frame part
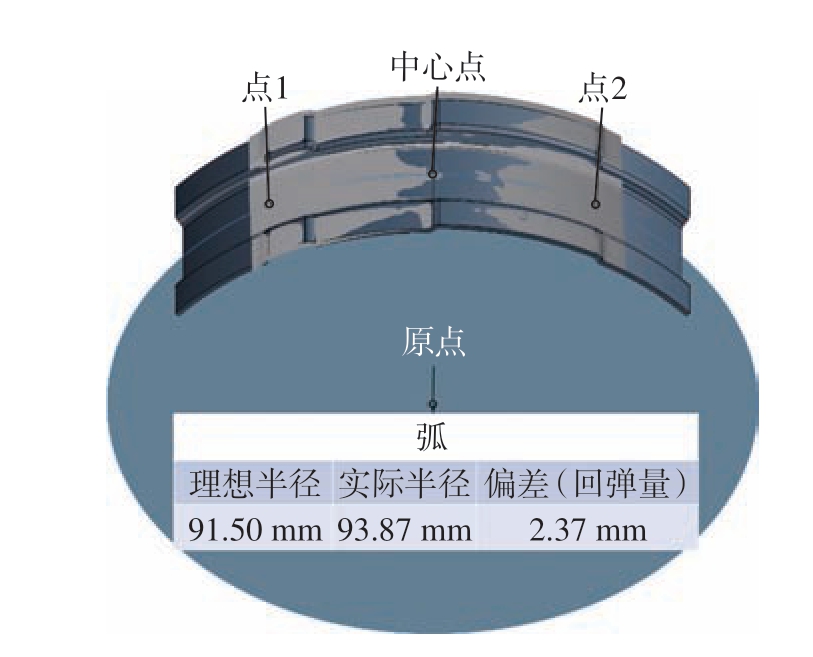
图14 回弹计算方法
Fig.14 Calculation method of springback
模拟结果与工艺试验回弹结果对比如图15 所示。可以看出,模拟结果与试验结果趋势基本一致,有限元模拟预测精度为93.85%。说明所构建的基于应力松弛行为的Arrhenius 蠕变本构模型能够用于TA32 钛合金热成形数值模拟,提高回弹预测能力。试验过程中,零件在成形和保压结束后,冷却至室温测量回弹,有限元模型未考虑冷却过程对回弹的影响,导致模拟结果与试验结果存在一定偏差。随着保压时间的延长,回弹量减小且减小幅度越来越小。当保压时间由10 s 增加到1800 s 时,模拟获得的回弹由3.15 mm 减小到2.55 mm,试验获得的回弹量由3.39 mm 减小到了2.37 mm。由于应力松弛极限的存在,零件内部应力无法完全降为0,回弹无法完全消除,在实际生产中选取合适的保压时间需考虑生产效率及成本等因素。
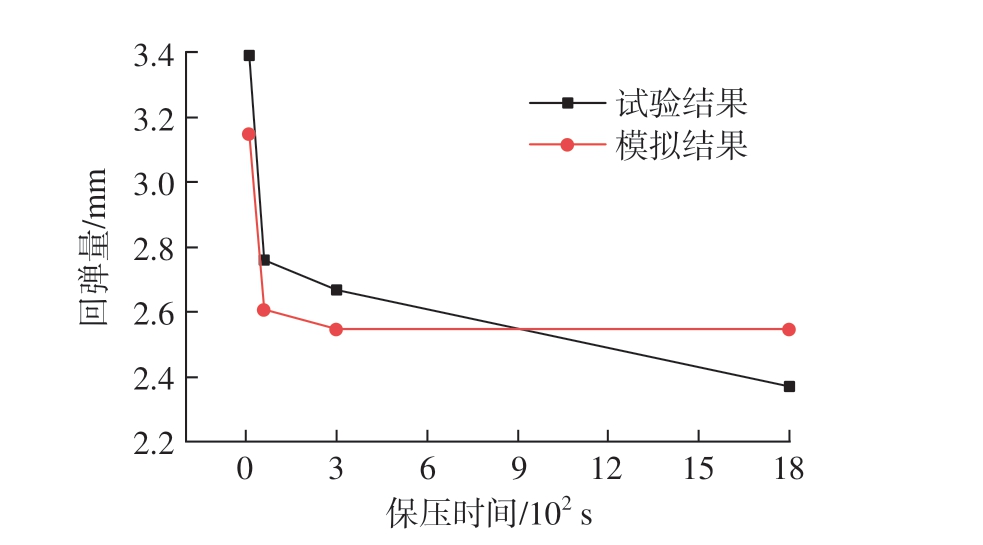
图15 模拟与试验回弹结果对比
Fig.15 Comparison of simulated and experimental springback results
3 结论
(1)温度对应力松弛行为影响显著,温度越高,应力松弛极限越低,在650 ℃时,应力松弛极限为28.3 MPa,而在800 ℃时,应力松弛极限为0.76 MPa,材料内部应力基本释放完成;预应变对应力松弛行为的影响受温度限制,在650 ℃下,预应变越大,第一阶段应力松弛速率越快,在800 ℃下,预应变对应力松弛行为几乎没有影响。
(2)基于TA32 钛合金应力松弛行为,采用五次延迟函数构建了TA32 钛合金应力松弛显式本构方程,通过时间关联蠕变应变速率与应力,建立了基于应力松弛行为的Arrhenius 蠕变本构模型,能较好描述TA32 钛合金蠕变应变率与应力的关系,所获得的试验值与预测值之间的相关系数为0.9868,平均相对误差为14.1%。
(3)用Arrhenius 型蠕变本构模型对加强框零件进行了热成形有限元模拟,预测精度可达93.85%;保压阶段能有效降低零件成形后的回弹,随着保压时间的延长,零件回弹量减小。
[1]赵丹丹.钛合金在航空领域的发展与应用[J].铸造, 2014,63(11): 1114-1117.ZHAO Dandan.Development and application of titanium alloys in the aviation[J].Foundry, 2014, 63(11): 1114-1117.
[2]李亚江, 刘坤.钛合金在航空领域的应用及其先进连接技术[J].航空制造技术, 2015, 58(16): 34-37.LI Yajiang, LIU Kun.Application and advanced bonding technology of titanium alloy in aviation industry[J].Aeronautical Manufacturing Technology, 2015, 58(16): 34-37.
[3]张绪虎, 单群, 陈永来, 等.钛合金在航天飞行器上的应用和发展[J].中国材料进展, 2011, 30(6): 28-32, 63.ZHANG Xuhu, SHAN Qun, CHEN Yonglai, et al.Application and development of titanium alloys for aircrafts[J].Materials China, 2011,30(6): 28-32, 63.
[4]蔡建明, 弭光宝, 高帆, 等.航空发动机用先进高温钛合金材料技术研究与发展[J].材料工程, 2016, 44(8): 1-10.CAI Jianming, MI Guangbao, GAO Fan, et al.Research and development of some advanced high temperature titanium alloys for aeroengine[J].Journal of Materials Engineering, 2016, 44(8): 1-10.
[5]王清江, 刘建荣, 杨锐.高温钛合金的现状与前景[J].航空材料学报, 2014, 34(4): 1-26.WANG Qingjiang, LIU Jianrong, YANG Rui.High temperature titanium alloys: Status and perspective[J].Journal of Aeronautical Materials,2014, 34(4): 1-26.
[6]武永, 陈明和.钛合金薄壁件热塑性成形工艺研究进展[J].航空制造技术, 2021, 64(20): 78-87.WU Yong, CHEN Minghe.Progress of hot metal plastic forming technology for titanium alloy thin-walled parts[J].Aeronautical Manufacturing Technology, 2021, 64(20): 78-87.
[7]熊志卿, 林兆荣.钛板热校形及其高温力学性质的研究[J].南京航空航天大学学报, 1983, 15(3): 159-179.XIONG Zhiqing, LIN Zhaorong.A study of the hot sizing and high temperature mechanical behavior of titanium sheet[J].Journal of Nanjing University of Aeronautics & Astronautics, 1983, 15(3): 159-179.
[8]XIAO J J, LI D S, LI X Q.Modeling and simulation for the stress relaxation behavior of Ti-6Al-4V at medium temperature[J].Rare Metal Materials and Engineering, 2015, 44(5): 1046-1051.
[9]杨晓明.TC4 钛合金冷模叠层热冲压工艺及回弹研究[D].北京: 北京科技大学, 2022.YANG Xiaoming.Study on hot stamping process and springback of TC4 titanium alloy by cold die stacking[D].Beijing: University of Science and Technology Beijing, 2022.
[10]WU R H, CHEN M H, XIE L S, et al.Stress relaxation behavior and corresponding constitutive relation of TA32 titanium alloy at high temperature[J].Rare Metal Materials and Engineering, 2019, 48(10): 3142-3148.
[11]陈灿.TA32 高温钛合金复杂飞机蒙皮零件热成形工艺研究[D].南京: 南京航空航天大学, 2018.CHEN Can.Study on hot forming process of TA32 high temperature titanium alloy complex aircraft skin parts[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2018.
[12]刘坡, 宗影影, 郭斌, 等.钛合金高温短时蠕变与应力松弛的关系研究[J].材料研究学报, 2014, 28(5): 339-345.LIU Po, ZONG Yingying, GUO Bin, et al.Relation between short-term creep and stress relaxation of titanium alloy at high temperature[J].Chinese Journal of Materials Research, 2014, 28(5): 339-345.
[13]陈源, 李淑慧, 李永丰, 等.TA15钛合金应力松弛行为宏微耦合本构建模[J].机械工程学报, 2022, 58(12): 64-74.CHEN Yuan, LI Shuhui, LI Yongfeng, et al.Macro-micro coupled constitutive modeling for stress relaxation behavior of TA15 alloy sheet[J].Journal of Mechanical Engineering, 2022, 58(12): 64-74.
[14]ZONG Y Y, LIU P, GUO B, et al.Investigation on high temperature short-term creep and stress relaxation of titanium alloy[J].Materials Science and Engineering: A, 2015, 620: 172-180.
[15]王明伟, 王春燕, 杨继新, 等.BT20钛合金高温应力松弛行为研究[J].稀有金属材料与工程, 2012, 41(3): 502-505.WANG Mingwei, WANG Chunyan, YANG Jixin, et al.Study of high temperature stress relaxation behavior of BT20 alloy[J].Rare Metal Materials and Engineering, 2012, 41(3): 502-505.
[16]SELLARS C M, MCTEGART W J.On the mechanism of hot deformation[J].Acta Metallurgica, 1966, 14(9): 1136-1138.
[17]CUI J J, SUN G Y, XU J R, et al.A method to evaluate the formability of high-strength steel in hot stamping[J].Materials & Design,2015, 77: 95-109.
[18]WU Y, FAN R L, QIN Z H, et al.Shape controlling and property optimization of TA32 titanium alloy thin-walled part prepared by hot forming[J].Transactions of Nonferrous Metals Society of China, 2021, 31(8):2336-2357.