加工精度是衡量数控机床性能的重要指标,通常采用误差防止法和误差补偿法来提高[1]。误差防止法是对机床硬件设施进行改进,由于存在难度大、成本高等问题,目前不适用于机床的设施改进,因此主要采用误差补偿法。误差补偿法包括误差测量、误差建模、误差补偿等多个方面,多用激光干涉仪进行直接测量或者综合误差测量以获得机床各项误差[2],并以此建立综合误差模型对机床进行误差补偿。误差补偿法主要有硬件静态、NC 代码、系统参数、快速刀具伺服机构、位置环反馈和坐标偏置补偿法[3]。Fu 等[4]利用鸡群优化算法自适应修正所有轴的运动位置,获得修正后的NC代码,实现了五轴机床闭环模式下的几何误差补偿,将误差从0.1863 mm 减少到0.1149 mm。Wu 等[5]基于螺距误差补偿改进方法,将A 轴正向和反向角度定位误差减少了79.8%和81.4%,极大提高了机床回转轴定位精度。Li等[6]基于快速刀具伺服系统,克服了弱刚度反射镜的夹持误差,显著降低了加工过程中的切削误差。冯文龙等[7]提出了基于热特性分析的光栅定位热误差建模理论,采用偏置补偿法进行实时补偿,将定位精度提升了90%以上。
上述补偿方式均可提高机床加工精度,且具有较好的补偿效果。但这些方法都是在静态或者准静态下测量的机床误差,不能很好地反映机床在高速或不同进给速度下的误差,导致其在实际加工状态下补偿效果不理想。大量研究表明,机床加工精度不仅受几何误差、热误差等静态/准静态误差的影响[8],还受伺服环外动态误差影响[9],其中进给轴伺服系统的动态特性是造成加工误差的一个重要原因[10]。动态误差依赖于进给轴的速度和加速度[11],在进给速度较低时,静态/准静态误差是产生加工误差的主要因素,但在复杂零件高速加工中,数控机床的动态误差远超静态/准静态误差[12]。杨泽青 [13]和孙慧娟[14]等利用球杆仪进行圆度误差检测,发现当进给速度增大到6000 mm/min 和10000 mm/min 时伺服动态误差占总误差的50%和75%左右。Schmitz 等[15]的研究得出误差源对加工误差的贡献值,发现当进给速度由150 mm/min 提高到8000 mm/min 时,动态误差几乎增大1 倍。孙兴伟等[16]推导出三维空间中机床加工圆弧轮廓时的轮廓误差表达式,表明适当降低进给速度可以减小轮廓误差。虽然,学者们已在机床进给速度研究领域取得一定的成果,但主要集中在对误差的影响分析上,对于机床误差补偿效果的研究相对较少。
因此,本文主要开展了不同进给速度对误差补偿效果影响的研究。对数控机床的螺距误差和反向间隙进行补偿,测量其在静态和不同进给速度下误差补偿前后的误差值,从而得到静态和不同进给速度下的误差补偿效果,对比获得进给速度对误差补偿效果的影响。最后进行的切削试验验证,为静、动态结合误差补偿提供了一定的理论依据。
1 进给速度与轮廓误差关系分析
数控机床通过多轴联动进行曲面零件轮廓加工,设理想状态下刀具刀尖点指令位置为M(x,y),如图1 所示,但由于各个进给轴存在跟随误差,导致实际位置N(x',y')总是滞后于指令位置,因此在加工曲面轮廓时会产生轮廓误差,结合本文试验情况,推导出数控机床中X、Y 两轴联动时进给速度对轮廓误差的影响。其中,点M、N 到圆心的距离计算公式为
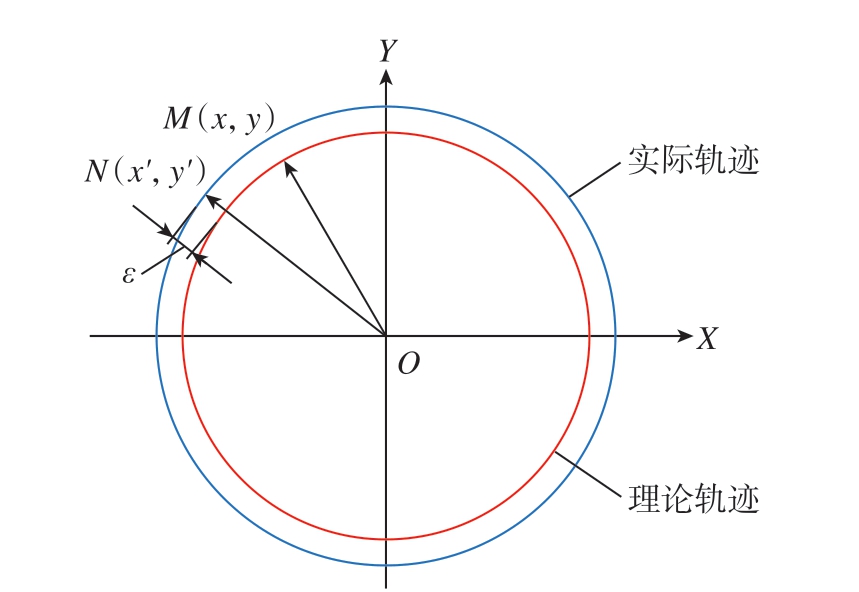
图1 跟随误差对轮廓误差的影响
Fig.1 Influence of tracking error on contour error
式中,R 为圆弧半径;ε 为轮廓误差。
点M、N 坐标关系为
式中,evx、evy 分别为X 轴和Y 轴的跟随误差;v 为进给速度。因此,X 轴和Y 轴的跟随误差计算公式为
式中,vx、vy 分别为X 轴和Y 轴的进给速度,mm/min;kvx、kvy 分别为X 轴和Y 轴的速度增益,mm /(mm ·min)。
对式(4)求导,可以得到X 轴和Y 轴的进给速度,即

由式(8)可知,进给速度会影响轮廓误差的大小,在保证伺服系统稳定的前提下,增大速度增益kv 可以减小轮廓误差,在kv 不变情况下,轮廓误差与进给速度平方成正比。
2 试验与讨论
2.1 试验设备
为了研究数控机床进给速度对机床误差补偿效果的影响,可采用球杆仪和平面光栅进行测量,基于课题组试验条件,选用QC–20 无线球杆仪 (Renishaw 公司),在1 台五轴机床上测量圆轨迹轮廓误差,同时使用XL–80 激光干涉仪测量机床进给轴定位误差,即可获得误差补偿数据。测量仪器部分参数如表1 所示。
表1 测量仪器部分参数
Table 1 Part parameters of measuring instrument
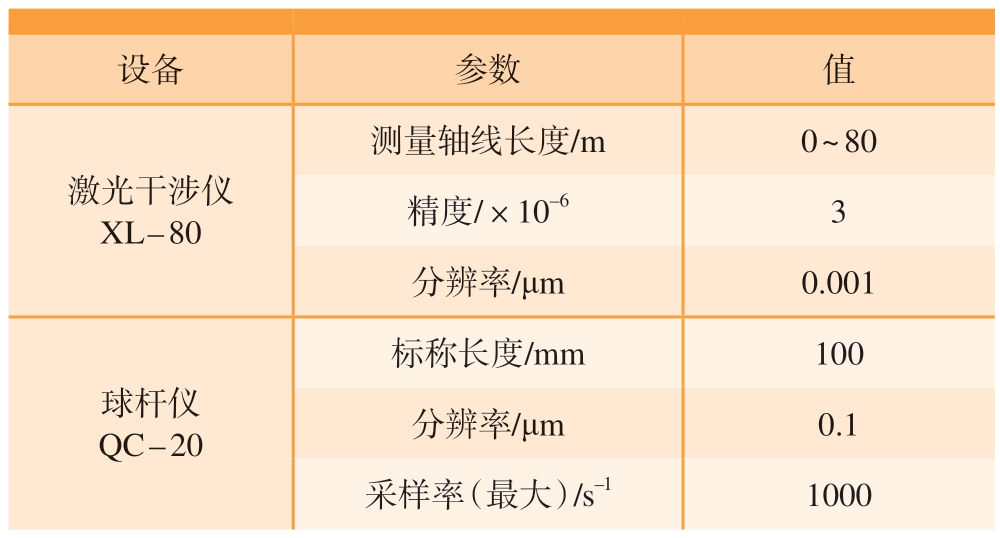
设备 参数 值激光干涉仪XL – 80测量轴线长度/m 0 ~ 80精度/×10–6 3分辨率/μm 0.001球杆仪QC – 20标称长度/mm 100分辨率/μm 0.1采样率(最大)/s–1 1000
本次试验所用五轴机床为TTTRR 型双摆台机床V545 - 5AXⅢ,其数控系统为SINUMERIK 840D SL。试验时A、C 两轴不动,因此认定为两旋转轴对测量结果没有影响,机床的X 轴行程为820 mm;Y 轴行程为520 mm;Z 轴行程为460 mm。
2.2 试验方案
试验主要分为4 步: (1)对球杆仪中心偏置进行去除,获得精确的杆长变化量; (2)测量静态误差补偿效果,主要使用激光干涉仪测量X、Y 两轴的定位误差,获得其螺距误差和反向间隙值并进行补偿,再用球杆仪手动测量圆轨迹获得静态误差补偿效果; (3)测量不同进给速度对误差补偿效果的影响,主要使用球杆仪自动测量圆轨迹轮廓误差,对数据进行处理,获得进给速度对补偿效果的影响; (4)进行实际切削与测量,验证球杆仪测量结果。
2.2.1 球杆仪中心偏置去除
轮廓误差由球杆仪进行测量,安装时将球杆仪中心座固定在机床工作台上,与装在主轴上的工具杯对齐即可,但在对齐过程中,工具杯与中心座不可能完全对齐,会存在中心偏置,如图2 所示。
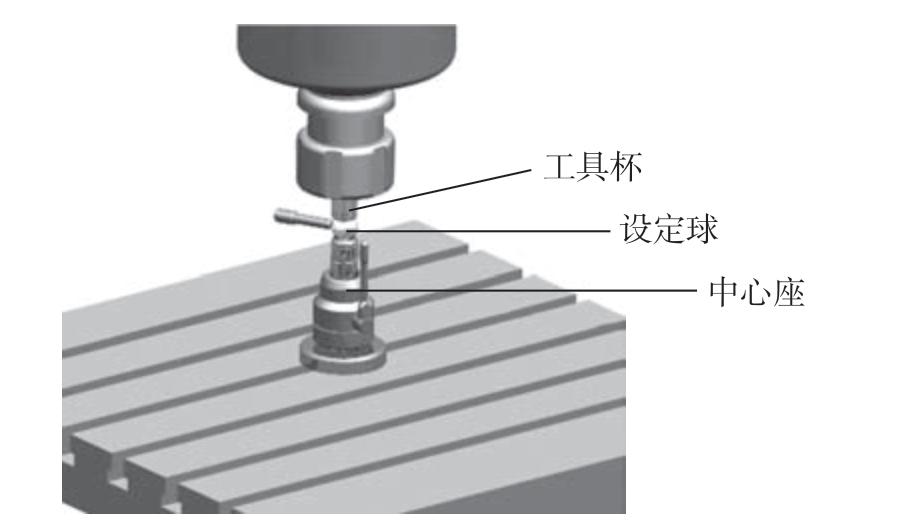
图2 球杆仪对中
Fig.2 Double ball bar centering
球杆仪测量过程中,机床误差与球杆仪本身的安装误差一起作用,导致球杆仪杆长发生变化。因此,在处理球杆仪杆长变化数据时,必须对球杆仪数据去除中心偏置,进而获得更精确的球杆仪杆长变化量。根据球杆仪配套软件提供的中心偏置值,推导出球杆仪精确杆长变化量。如图3 所示,Pa(xi,yi)为实际圆轨迹中第i个点的坐标。
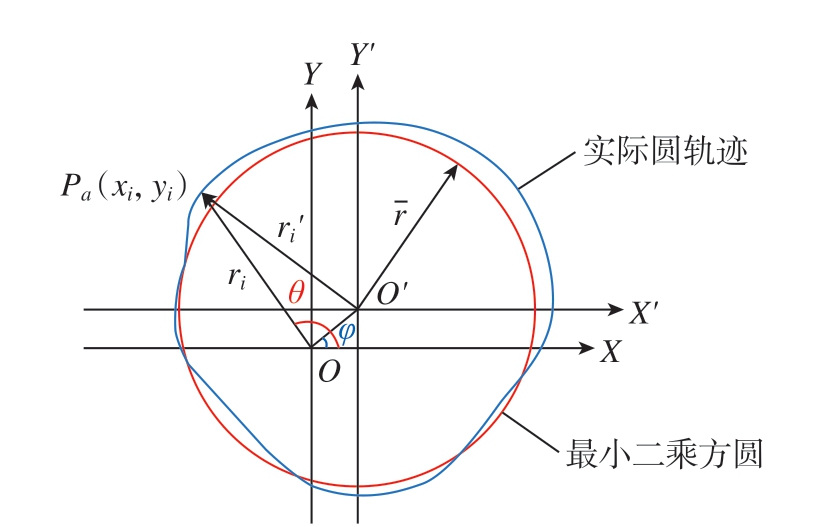
图3 圆轨迹偏心
Fig.3 Eccentricity of circular trajectory
在三角形O'OP 中,由余弦定理可得
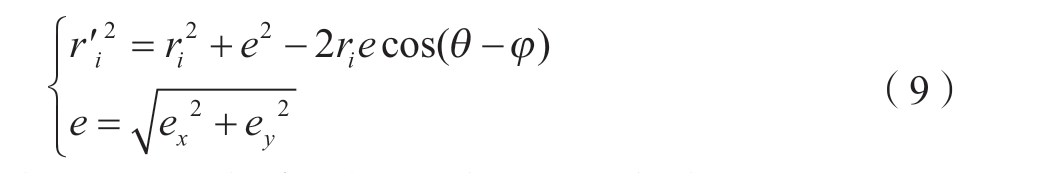
式中,ri'和ri 分别为实际圆轨迹到坐标中心O'和O 的距离;e 为中心偏置;ex 和ey 分别为X 和Y 方向的中心偏置;θ 为球杆仪转动角度;φ 为偏心角度,则实际圆轨迹到坐标中心O 的距离ri 为
考虑到中心偏置e 远小于半径,可以通过去除高阶项化简得到

由式(12)可求得去除中心偏置后的球杆仪杆长变化量。
2.2.2 静态误差补偿效果的测量
在本次试验中,五轴机床处于密闭恒温环境,外部环境温度保持在20 ℃。五轴机床X、Y 轴的测量行程分别为780 mm、700 mm,按照国际标准ISO 230—2 的要求,其X、Y 轴的定位误差测量中两个测量点的测量间隔为20 mm。在测量定位误差之前,需将机床上原有补偿数据清除并对机床进行预热使其达到热平衡。图4 所示为五轴机床Y 轴定位误差测量过程,X 轴与Y 轴定位误差测量结果如图5 所示。

图4 Y 轴定位误差测量示意图
Fig.4 Measurement of Y-axis positioning error
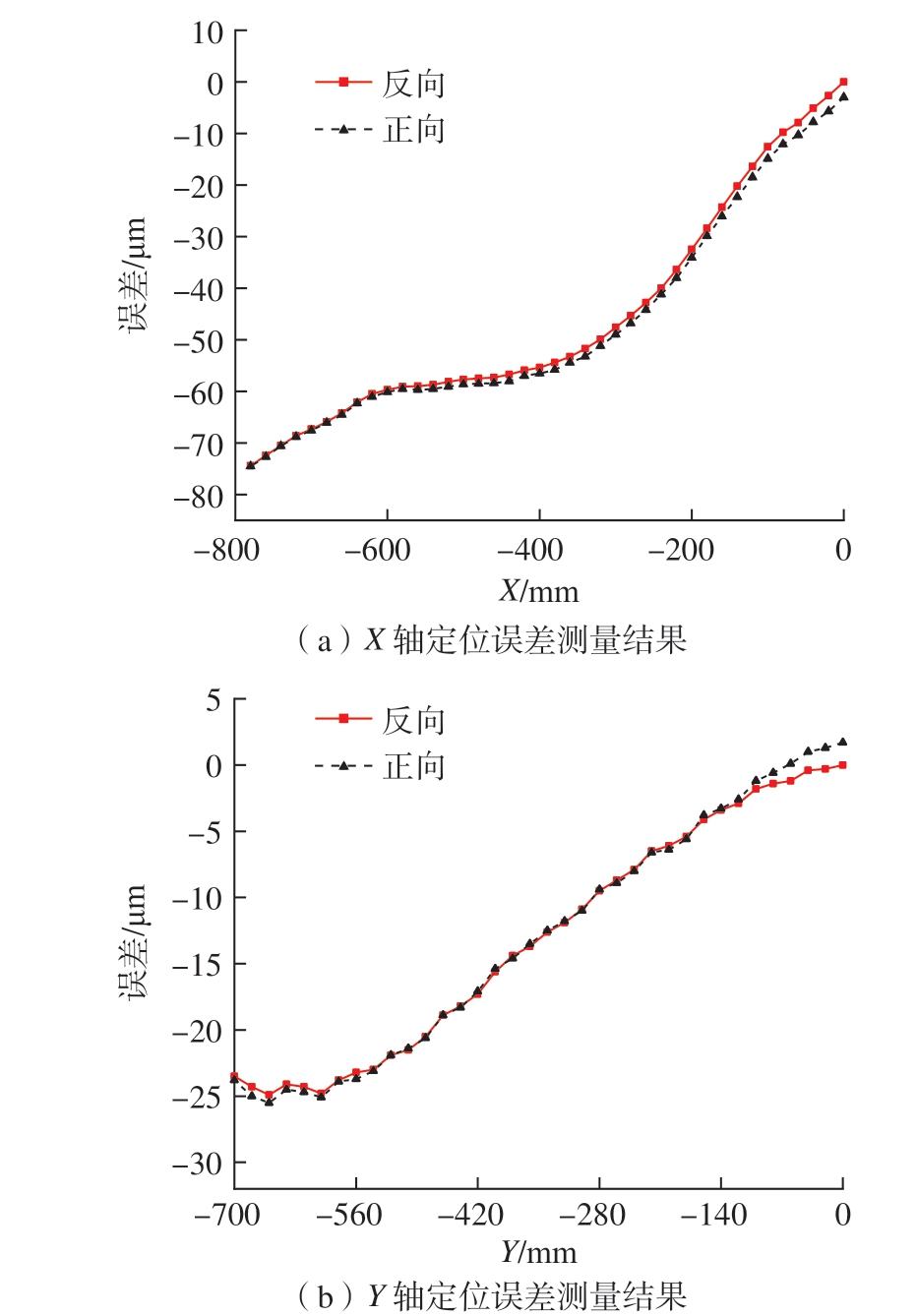
图5 机床X 轴与Y 轴定位误差测量结果
Fig.5 Measurement results of positioning error of X-axis and Y-axis of machine tool
依据激光干涉仪配套软件获得X、Y 轴螺距误差补偿值与反向间隙补偿值,在进行螺距误差、反向间隙补偿后,X 轴和Y 轴的定位误差情况如图6 所示。由图5和6 可知,五轴机床XY 轴系统偏差分别从74.6 μm 和27.3 μm 降为2.2 μm 和3.2 μm,可见补偿效果显著。
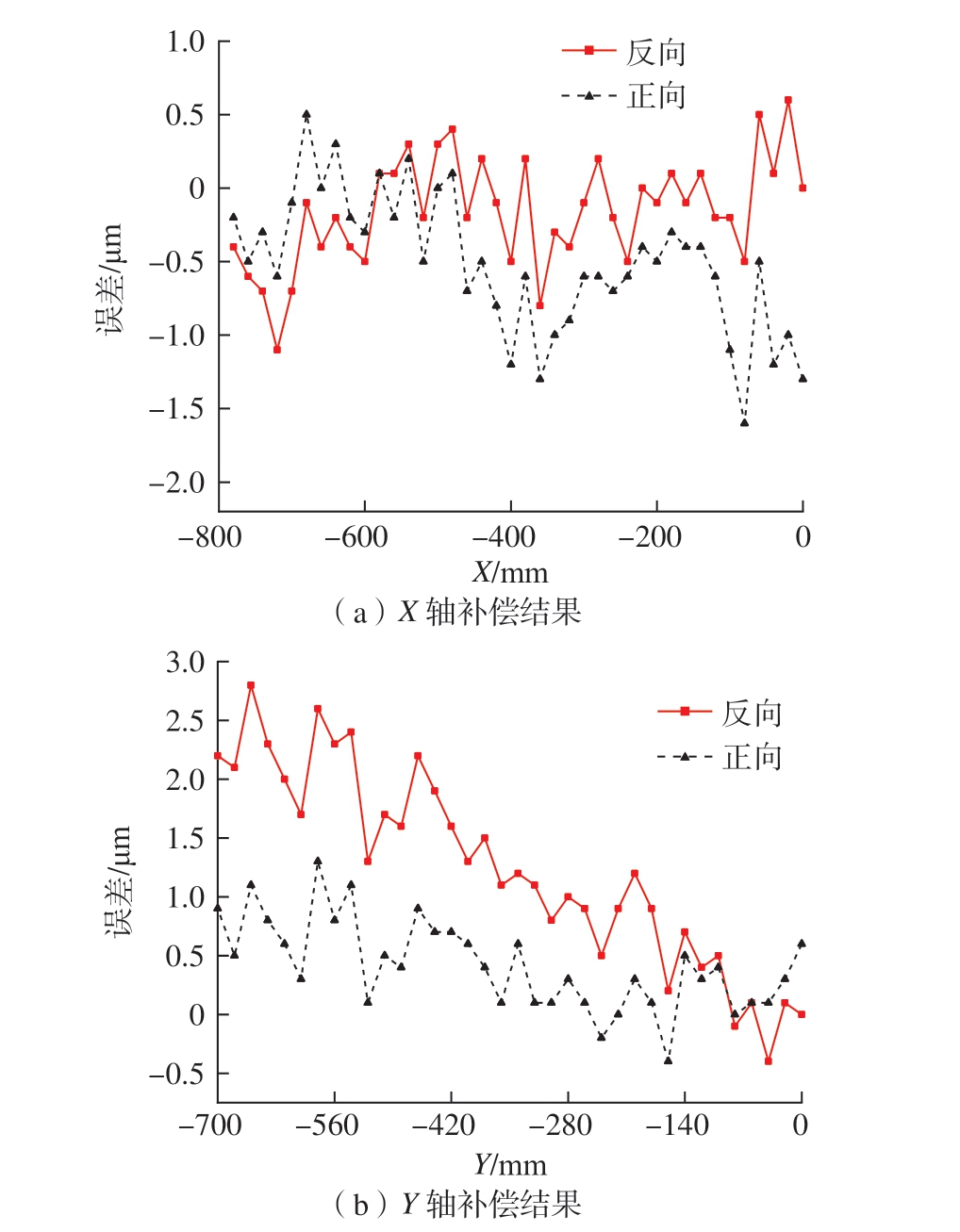
图6 机床X 轴与Y 轴误差补偿结果
Fig.6 Compensation results of machine tool X-axis and Y-axis error
为了对比不同进给速度下的误差补偿效果,在静态下的补偿效果同样需采用球杆仪测量圆轨迹轮廓误差。在圆轨迹上均匀选取360 个坐标点将其分割成359 段直线,手动将球杆仪运动到坐标点并记录杆长变化量,杆长变化量即为轮廓误差。
手动测量数据前,需使用球杆仪自动进行圆轨迹运动,获得其中心偏置值,分别将手动测量的补偿和无补偿状态下的球杆仪杆长变化量代入式 (12)中,以去除中心偏置的影响并对数据取极差值,从而获得圆轨迹圆度误差。同时通过对有补偿和无补偿的圆度误差进行比较来评价静态补偿效果,结果如表2 所示。
表2 静态补偿效果
Table 2 Effect of static compensation
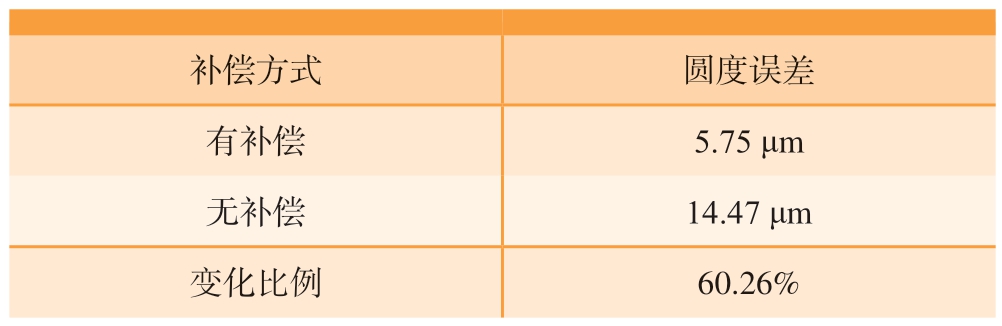
补偿方式 圆度误差有补偿 5.75 μm无补偿 14.47 μm变化比例 60.26%
从表2 可知,对机床进行螺距误差和反向间隙补偿,可减少静态圆轨迹轮廓误差变化范围,使其圆度误差降低了60.26%,证明补偿效果显著。
2.2.3 不同进给速度下补偿效果的测量
由前文中对进给速度和轮廓误差关系分析可知,进给速度对轮廓误差存在影响。为更好地反映进给速度对轮廓误差的影响情况,进给速度取值范围应尽可能大,结合仪器设备情况分别取500 mm/min、1000 mm/min、1500 mm/min、2000 mm/min、3000 mm/min、4000 mm/min、5000 mm/min 和6000 mm/min 共8 个不同进给速度进行试验。
由于球杆仪自带软件处理的图形不能直观呈现出不同进给速度下球杆仪杆长变化量情况,因此需要对球杆仪采集的原始数据进行处理。在球杆仪测量过程中,球杆仪运动一周大概采集1500 个数据,从这些数据中均匀选取360 个数据的测量结果如图7 所示。
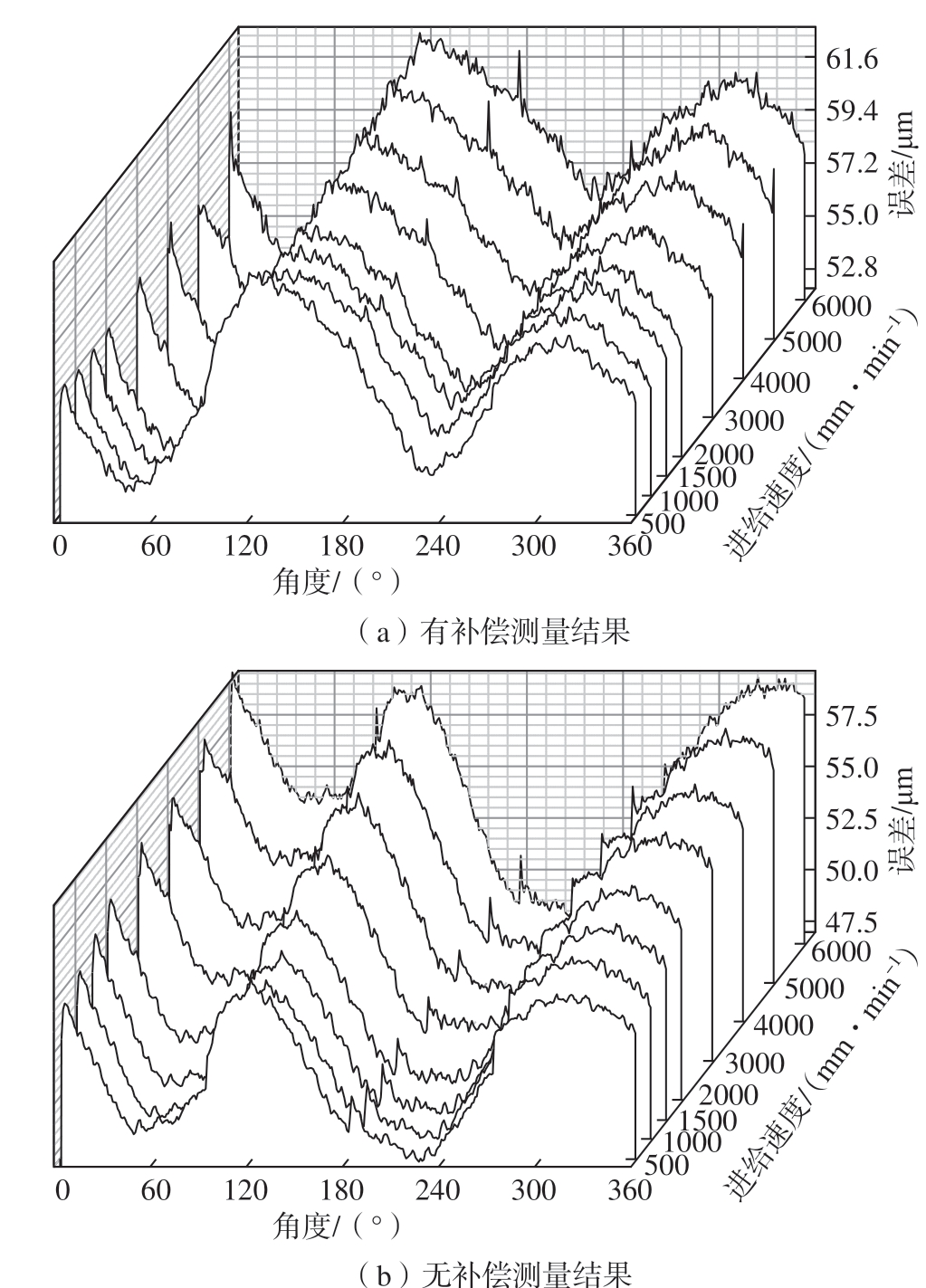
图7 球杆仪测量结果
Fig.7 Measurement results of double ball bar
为了更好地呈现出轮廓误差随进给速度的变化情况,对每个进给速度下测量的数据,分别提取出球杆仪杆长变化量最大值和圆轨迹圆度误差,结果如图8 所示。由图7 和8 可知,在8 个不同进给速度中,五轴机床轮廓误差随进给速度的增加呈递增趋势且在低速时变化小,高速时变化大。
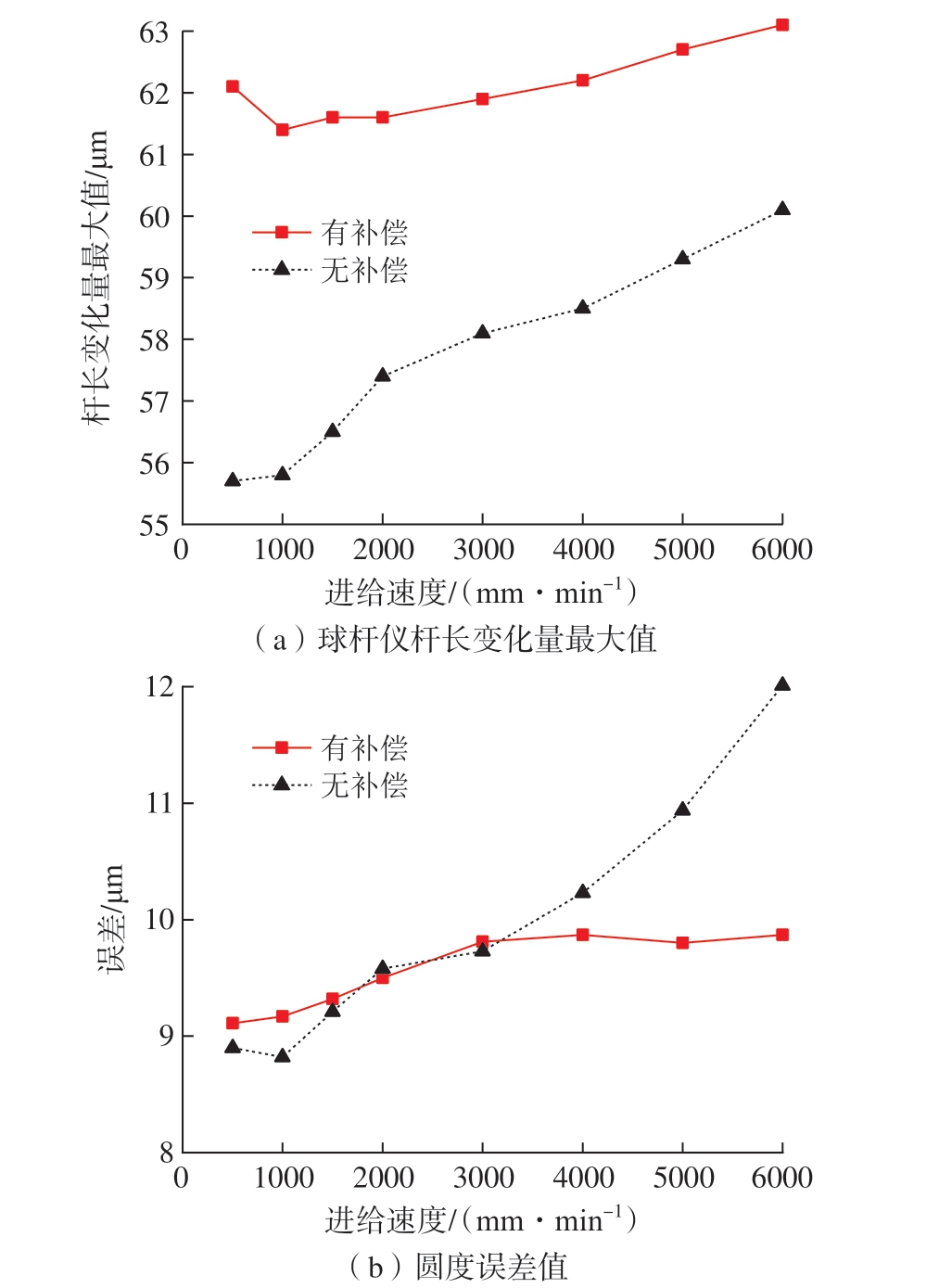
图8 五轴机床测量数据
Fig.8 Five-axis machine tool measurement data
对球杆仪杆长变化量最大值与进给速度平方进行线性相关分析及显著性检验,可得有补偿和无补偿的皮尔逊相关系数分别为r = 0.93 和r = 0.95;显著性检验结果分别为p = 9.15×10-4< 0.01 和p = 3.43×10-4<0.01,表明最大值与速度平方之间呈显著正相关,验证了前文中关于轮廓误差与进给速度成正比的结论。
为了评价进给速度对机床误差补偿效果的影响,根据图7 和8 的分析结果,以500 mm/min 的进给速度测得的圆度误差为基准,其余7 个进给速度测得的圆度误差相对基准的变化情况如图9 所示,相对变化比例越大,表明误差补偿效果越差。

图9 不同进给速度下补偿效果
Fig.9 Compensation effect under different feed rates
从图9 中可得,圆度误差在有补偿状态下最小变化比例为0.66%,最大为8.34%;在无补偿状态下最小变化比例为- 0.9%,最大为34.94%。当进给速度从500 mm/min增加到6000 mm/min 时,机床误差补偿仅将圆轨迹圆度误差减少26.6%,相对于静止状态下60.26%的误差补偿效果,不同进给速度下的补偿效果明显降低。
2.2.4 切削和测量验证
为了验证误差补偿下,球杆仪测量得到的圆度误差随进给速度变化比例情况,进行实际圆试件试切和检测。本次试验采用五轴机床加工长×宽为102 mm×102 mm 的5052 铝合金块,机床主轴转速8000 r/min、切深5 mm,分别在进给速度为500 mm/min、1500 mm/min 和3000 mm/min 的条件下切削,如图10 所示。对于切削完成的圆试件,采用德国温泽LH65 三坐标测量机的扫描模式测量其圆度,如图11 所示。

图10 圆试件切削
Fig.10 Circular specimen cutting

图11 三坐标测量机测量
Fig.11 CMM measurement
由三坐标测量机测量得到3 个不同进给速度加工的圆试件圆度测量结果分别为5.4 μm、5.8 μm 和6.5 μm,以500 mm/min 进给速度下切削的圆试件圆度为基准,1500 mm/min 和3000 mm/min 进给速度下圆试件圆度变化比例分别为7.41%和20.37%。在实际加工中,一半误差来自于加工过程误差和检测误差;另一半来自于几何误差和热误差。但由于几何误差和热误差在热平衡时变化小甚至不发生变化,因此造成圆试件圆度变化的原因一半来自加工过程误差和检测误差;另一半来自于进给速度变化导致的伺服动态误差。因此,由进给速度造成的圆试件圆度误差变化比例分别为3.70%和10.19%,与球杆仪测量的圆度误差变化比例2.31%和7.68%较接近 (图9),说明实际加工中进给速度影响补偿误差效果且呈现一定的变化规律,但由于存在振动、刀具磨损、温度变化等因素的影响,使得圆试件圆度变化比例与球杆仪测量结果不同。
3 结论
(1)通过在不同进给速度下进行球杆仪试验,可得数控机床的轮廓误差随着进给速度的增大呈递增趋势,且进给速度低时变化小,进给速度高时变化大,证实了轮廓误差与进给速度的平方成正比。
(2)数控机床进行螺距误差和反向间隙补偿时,在静止状态下补偿效果显著,但在不同进给速度下补偿效果明显降低,表明进给速度严重影响机床误差补偿效果,且数控机床自带补偿模块对于动态误差抑制作用不足。通过圆试件切削和检测,发现实际加工过程和空载球杆仪测量的圆度变化比例呈现一定的变化规律,因此对于高速或不同进给速度的轮廓加工,需采取基于不同进给速度的综合误差建模,并进行实时补偿才能更好地抑制轮廓误差变化,为机床综合误差建模提供一定的理论依据。
[1]吕学祜, 郭前建, 王昊天, 等.数控机床误差补偿关键技术综述[J].航空制造技术, 2022, 65(11): 104-111, 119.LÜ Xuehu, GUO Qianjian, WANG Haotian, et al.Summary of key technologies for error compensation of CNC machine tools[J].Aeronautical Manufacturing Technology, 2022, 65(11): 104-111, 119.
[2]季泽平, 田春苗, 郭世杰.数控机床几何误差研究现状与展望[J].航空制造技术, 2021, 64(22): 65-77.JI Zeping, TIAN Chunmiao, GUO Shijie.Research status and prospect of geometric error of CNC machine tools[J].Aeronautical Manufacturing Technology, 2021, 64(22): 65-77.
[3]张恩忠.多轴精密数控机床误差测量、综合建模及补偿技术的研究[D].长春: 吉林大学, 2017.ZHANG Enzhong.Research on error measurement, comprehensive modeling and compensation technology for multi-axis precision CNC machine tools[D].Changchun: Jilin University, 2017.
[4]FU G Q, SHI J H, XIE Y P, et al.Closed-loop mode geometric error compensation of five-axis machine tools based on the correction of axes movements[J].The International Journal of Advanced Manufacturing Technology, 2020, 110(1): 365-382.
[5]WU Y C, SHEN J X.Analysis and improvement of the positioning accuracy of rotary axes of compound machine tools based on pitch error compensation[J].Measurement Science and Technology, 2020,31(11): 115003.
[6]LI Z L, DAI Y F, GUAN C L, et al.High-precision machining method of weak-stiffness mirror based on fast tool servo error compensation strategy[J].Micromachines, 2021, 12(6): 607.
[7]冯文龙, 黄奕乔, 拓占宇, 等.基于温度积分方法的大型数控机床光栅定位热误差建模及实时补偿[J].上海交通大学学报, 2016,50(5): 710-715.FENG Wenlong, HUANG Yiqiao, TUO Zhanyu, et al.Modeling of thermally induced grating positioning error of large machine tools based on temperature integral method and real-time compensation[J].Journal of Shanghai Jiao Tong University, 2016, 50(5): 710-715.
[8]SHEN H Y, FUN J Z, HE Y, et al.On-line asynchronous compensation methods for static/quasi-static error implemented on CNC machine tools[J].International Journal of Machine Tools and Manufacture,2012, 60: 14-26.
[9]LYU D, LIU Q, LUO S Y, et al.The influence of dynamic error outside servo-loop on the trajectory error[J].The International Journal of Advanced Manufacturing Technology, 2021, 113(5): 1517-1525.
[10]KATO N, TSUISUMI M, SATO R.Analysis of circular trajectory equivalent to cone-frustum milling in five-axis machining centers using motion simulator[J].International Journal of Machine Tools and Manufacture, 2013, 64: 1-11.
[11]李杰, 刘辛军, 谢福贵, 等.基于时变特性的数控机床综合误差建模方法[J].科技导报, 2016, 34(2): 65-70.LI Jie, LIU Xinjun, XIE Fugui, et al.A comprehensive error modeling method for numerical control machine tools based on time-varying characteristics[J].Science & Technology Review, 2016, 34(2): 65-70.
[12]吕盾, 张佳辉, 王大伟, 等.国产数控机床动态精度技术现状与对策[J].航空制造技术, 2022, 65(6): 22-33.LÜ Dun, ZHANG Jiahui, WANG Dawei, et al.Technical status and countermeasures of dynamic accuracy of domestic CNC machine tools[J].Aeronautical Manufacturing Technology, 2022, 65(6): 22-33.
[13]杨泽青, 李增强, 刘奇, 等.立式加工中心综合误差建模及实验分析[J].现代制造工程, 2019(10): 6-13.YANG Zeqing, LI Zengqiang, LIU Qi, et al.Comprehensive error modeling and experimental analysis of vertical machining center[J].Modern Manufacturing Engineering, 2019(10): 6-13.
[14]孙惠娟, 殷国富, 方辉, 等.五轴数控机床综合误差建模评价方法研究[J].四川大学学报(工程科学版), 2012, 44(6): 197-202.SUN Huijuan, YIN Guofu, FANG Hui, et al.Research on integrated error modeling and evaluation method of five-axis machine tools[J].Journal of Sichuan University (Engineering Science Edition), 2012, 44(6): 197-202.
[15]SCHMITZ T L, ZIEGERT J C, CANNING J S, et al.Case study: A comparison of error sources in high-speed milling[J].Precision Engineering, 2008, 32(2): 126 - 133.
[16]孙兴伟, 董蔚, 王可, 等.数控机床伺服系统跟随误差对加工轮廓的影响[J].制造技术与机床, 2010(6): 76 - 78.SUN Xingwei, DONG Wei, WANG Ke, et al.Influence of follow error of servo system of CNC machine tool on processing contour[J].Manufacturing Technology & Machine Tool, 2010(6): 76 - 78.