钛合金材料被广泛应用于航空航天零件的制造中,并且在航空航天深腔类零件占有很大的比重,然而现有的深腔加工过程中刀具长径比大,动态特性差,极易发生颤振 (颤振是一种有害的自激振动[1]),对工件加工质量和刀具寿命造成极大的影响[2],是影响加工效率和质量的关键因素[3],因此,钛合金材料加工过程中的颤振抑制具有重要的研究意义和工程意义。
颤振问题的解决策略有3 种:优化切削参数、主动控制和被动控制[4]。优化切削参数的方法,通常指采用稳定波瓣图和颤振检测方法来指导加工参数的选择,尤其是稳定波瓣图具有高精度和实时性,能够检测出在加工过程中的颤振[5]。然而对于识别出的颤振只能在加工完成后针对加工中的问题进行切削参数的优化,并不能增强加工系统的稳定[6],而且额外的监测装置增加了机床操作者的负担,从而限制了主动控制方法在实际生产中的应用[7]。
被动控制在实际的工程应用中更易实现,可以通过对刀具或者工件添加特殊材料或添加一定的装置实现加工系统的稳定性,因此也是最常用的减振方法,目前已经被广泛研究[8]。高硬度材料是提升振动稳定性的方法之一。Razak 等[9]采用碳化钨代替传统钢制备刀杆,虽然碳化钨和钢的阻尼比近似,但由于碳化钨的静刚度大,因此相较于钢质刀杆具有更大的动刚度,但固有频率相对较低,更容易诱发颤振现象。动力吸振器作为一种被动减振方式,同样能够获得较好的减振效果。Sandvik Coromant 公司生产各类减振刀杆时,在刀杆前部增加动力吸振器以提高加工质量,所生产的工具已经广泛应用于工程生产[10]。Li 等[11]通过优化动力吸振器的参数,使得新型减振刀杆的动态特性有了一定的提升。章伟等[12]通过优化吸振器结构,设计了一种结构简单的内置吸振器的减振刀杆,有效提高了零件表面加工质量。Van Zyl 等[13]利用调谐质量阻尼器对细长单点镗削刀具进行阻尼,以提高其抗颤振能力。动力吸振器的减振方式虽然具有优良的减振效果,但存在制备复杂、价格昂贵等问题,普适性较差。
近年来,阻尼材料被广泛应用于刀杆以抑制加工振动。唐志雄等[14]设计了一种基于动力减振法与阻尼材料减振法相结合的复合减振铣刀,对比分析结果表明,复合减振铣刀的动态性能优于普通硬质合金铣刀。Lee等[15]采用碳纤维增强复合材料作为阻尼层,设计出新型旋转镗杆,试验结果表明,复合镗杆的动刚度比碳化钨镗杆提高了28%,固有频率提高了72%,阻尼比提高了168%。Song 等[16]采用泡沫铝合金作为减振镗杆的阻尼层,有效提高了杆体的固有频率、静刚度和阻尼比。与普通镗杆相比,该镗杆具有更大的阻尼,在相同的激励下振幅减小34%,表面粗糙度值降低50%以上。Liu 等[17]设计了一款阻尼立铣刀,通过改变阻尼层的材料解析求解了最优立铣刀设计几何参数,结果表明,所研制的阻尼刀杆的动刚度和固有频率都有一定的提高。Xia 等[18]开发了一种用于卧式加工的长悬伸变截面铣刀,可以实现稳定高效的加工。Yuvaraju 等[19]使用碳/碳化硅–环氧树脂和317 不锈钢作为减振刀杆的阻尼层和约束层,试验表明,在给定的切削范围内,该镗杆可以避免强迫振动,有效抑制颤振。Zhang 等[20]研究了具有约束阻尼层的复合镗杆在深孔镗削过程中的振动稳定性,提出了复合材料镗杆稳定性计算模型。Ma 等[21]采用碳纤维复合材料设计变截面镗杆,数值计算结果表明,在低阻尼比下,随着锥度比的增大,一阶固有频率和镗削稳定性都有所提高。采用新材料更加容易实现刀杆的制备,并且通过结构的合理设计能够在兼顾刚度的同时提升刀杆的阻尼特性,从而具备优异的动态特性。
在当前的研究中,所设计的减振刀杆多数为镗杆,加工对象多面向于铝合金和钢材加工,然而钛合金材料属于难切削材料,其加工特性复杂,尚未有专用于钛合金材料加工的减振立铣刀杆。因此,本文基于被动控制方法开发了一种用于钛合金深腔加工的复合减振刀杆,基于Euler-Bernoulli 梁理论建立了刀杆的动力学模型。通过有限元分析比较了4 种不同的芯轴对刀杆动态特性造成的影响,基于仿真数据选择最佳的芯轴,通过对普通刀杆和减振刀杆进行静态和动态性能分析及对比,并进行铣削试验,验证加工后的表面粗糙度。
1 复合减振刀杆动态模型与设计
1.1 刀杆动态特性模型
现有的刀具动态特性较弱,当进行深腔零件材料加工时通常会出现颤振现象,因此最好的解决办法就是通过优化铣刀刀杆结构提高动态特性来减少颤振现象的发生。为更好地进行结构优化,需要建立刀杆工作时的动态特性模型,用以分析刀杆结构设计时的考虑因素。为了更好地研究铣刀在加工时的动力学特性,可以将铣刀等效为悬臂梁,采用Euler-Bernoulli 梁理论近似模拟刀杆的低阶弯曲模式[22],选取铣刀刀杆的一段微元如图1 所示。

图1 刀杆动力学模型
Fig.1 Dynamic model of toolholder
通过牛顿第二定律和微元平衡定理可得
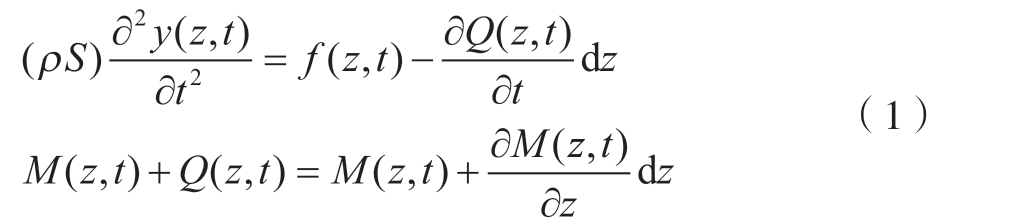
式中,ρ 为材料体密度;S 为截面横截面积;Q(z,t)为截面受到的剪切力;M(z,t)为截面受到的弯矩;y(z,t)为y 方向的挠度;f(z,t)为外部激励力;t 为任意瞬时时间;z 为所取微元部分距离刀杆上端距离。
基于扩展的Hamilton 原理,经过整理式 (1)可以得到刀杆的运动的控制方程,为

式中,L 为刀杆长度;βn 为第n 阶振动模式的特征值;n为第n 阶固有频率。
当系统达到共振频率 (w)时,wn= w,则刀杆的最大振动幅值为
式中,|H(w)|max 为共振时的最大振幅;ξ 为阻尼。
通过式(3)和 (4)可知,刀杆振动时的幅值和固有频率受到刚度和阻尼的直接影响,在其他参数不变的情况下,增加刚度可以有效地降低稳态响应时的幅值,若增加系统的阻尼系数,刀杆的响应幅值也会降低,其三者的变化关系如图2 所示,可以看出,随着阻尼比和刚度的提高,共振时的稳态响应幅值逐渐减小。意味着,可以通过改变刀杆的阻尼系数和刚度来改善刀杆的动态性能,增加铣削加工时的刀杆稳定性。
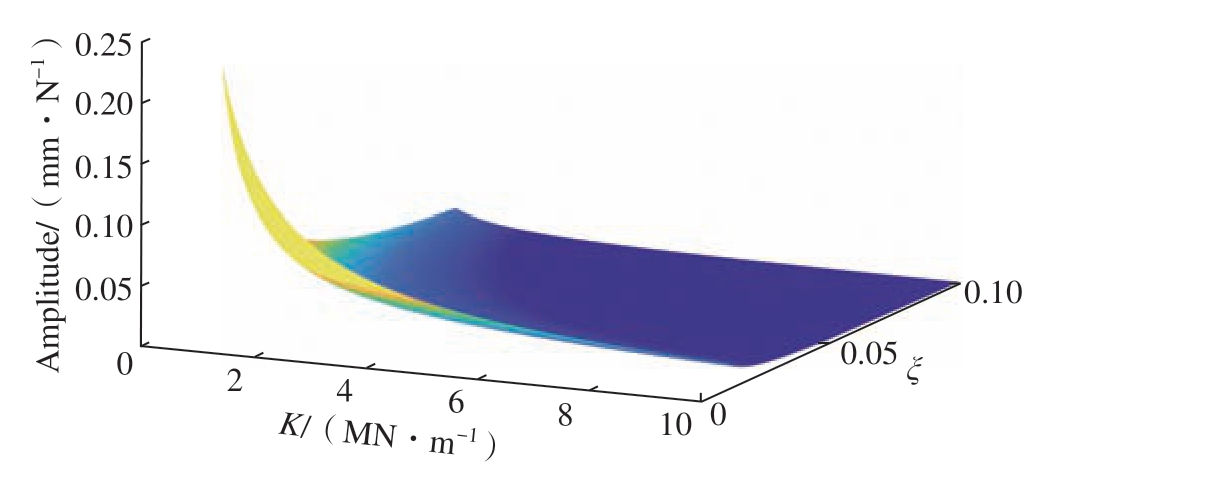
图2 刚度和阻尼对振幅的影响
Fig.2 Effect of stiffness and damping on amplitude
1.2 复合减振刀杆结构设计
为了保证所设计的铣刀能够具有更好的普适性,外形采用等截面设计,刀头可替换,整体采用强力刀柄夹持。刀杆的本体部分所用材料为硬质合金、聚氨酯橡胶和碳纤维材料,整体结构如图3 所示,刀杆外径为25 mm,芯轴尺寸为6 mm,其他部分为碳纤维缠绕。所用材料的机械性能如表1 所示。
表1 材料机械性能
Table 1 Mechanical properties of materials
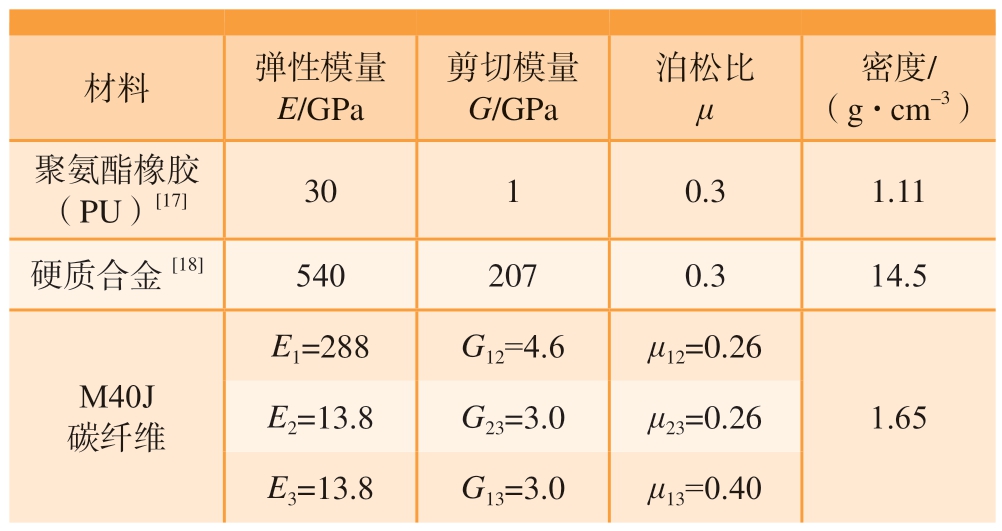
材料 弹性模量E/GPa剪切模量G/GPa泊松比μ密度/(g·cm–3)聚氨酯橡胶(PU)[17] 30 1 0.3 1.11硬质合金[18] 540 207 0.3 14.5 E1=288 G12=4.6 μ12=0.26 M40J碳纤维E2=13.8 G23=3.0 μ23=0.26 E3=13.8 G13=3.0 μ13=0.40 1.65
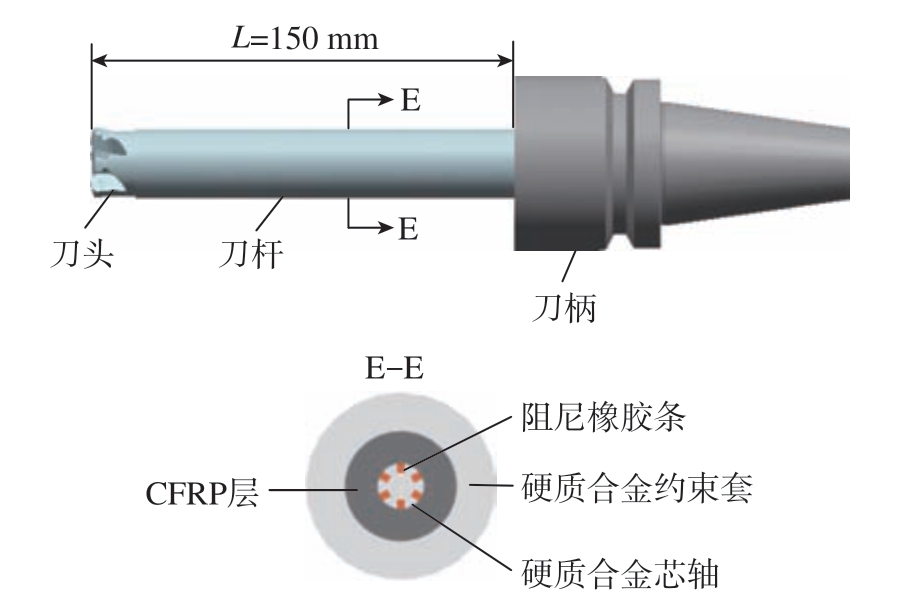
图3 铣刀结构
Fig.3 Structure of tool
在芯轴外缠绕高强度、高刚度的M40J 碳纤维环氧复合材料,碳纤维层具有3 个作用: (1)能够补偿由于橡胶条损失的静刚度; (2)作为阻尼层并能同时提高阻尼能力; (3)碳纤维作为轻量化材料,能够减轻刀杆的质量,降低对机床结构的负载,同时减小刀杆端头的变形。
1.3 复合刀杆芯轴结构设计
黏弹性高分子聚合物材料是目前应用最多的阻尼材料,由于黏弹性材料的材料特性,在发生振动时材料本身会发生变形吸收振动能量,因此可用于振动系统增加结构阻尼、减少振动现象。在制备过程中,金属芯轴采用线切割方式切割出凹槽,将聚氨酯阻尼橡胶制备成条带,通过胶黏剂粘接在刀杆的芯轴中,以增加阻尼特性。阻尼材料的分布和占比会影响刀杆的振动特性,为确定阻尼材料在何种分布和占比下可以得到更好的阻尼效果,设计了4 种形式的芯轴结构,如图4 所示。
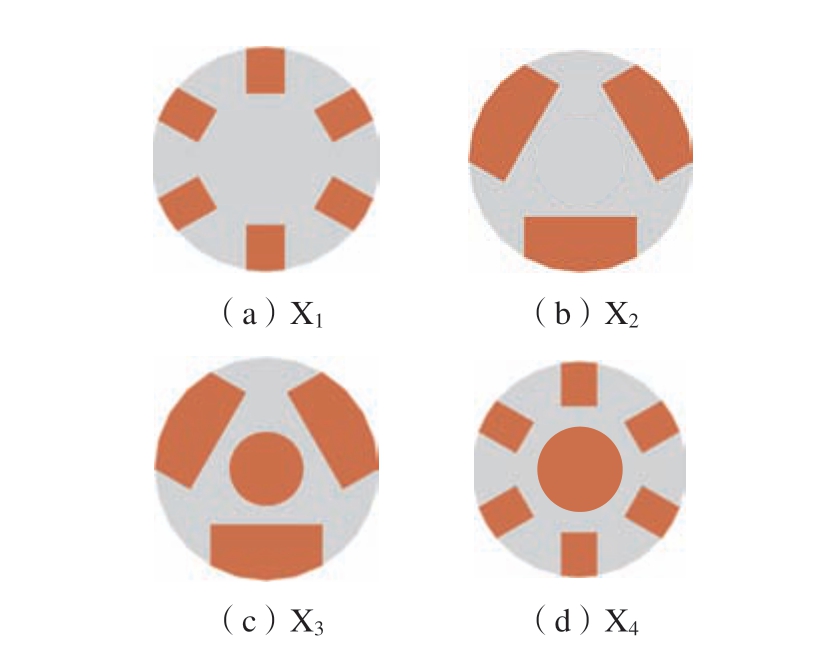
图4 4 种形式的芯轴结构
Fig.4 Four forms of core shaft structures
2 复合减振刀杆性能分析
2.1 芯轴有限元优化分析
引入有限元法对设计的4 种芯轴模型进行有限元分析,使用ABAQUS(2022)商业软件生成有限元模型。由于线性缩减积分单元C3D8R 需要精密的网格配置才能获得较为精确的收敛解,考虑到复合减振刀杆的结构由多部分结合而成,因此考虑在获得较为精确的收敛解的前提下,采用非线性协调单元C3D8I 单元,可以在不降低计算精度的前提下降低计算量,使用较少的网格数量快速获得收敛解。将表1 中的材料属性参数导入有限元计算模型中,计算时首先通过模态分析获得各阶的固有频率、模态振型等;随后采用模态叠加法进行稳态动力学分析,获得刀杆的稳态振动幅值曲线[23]。4 种轴芯的共振幅值响应结果如图5 所示。
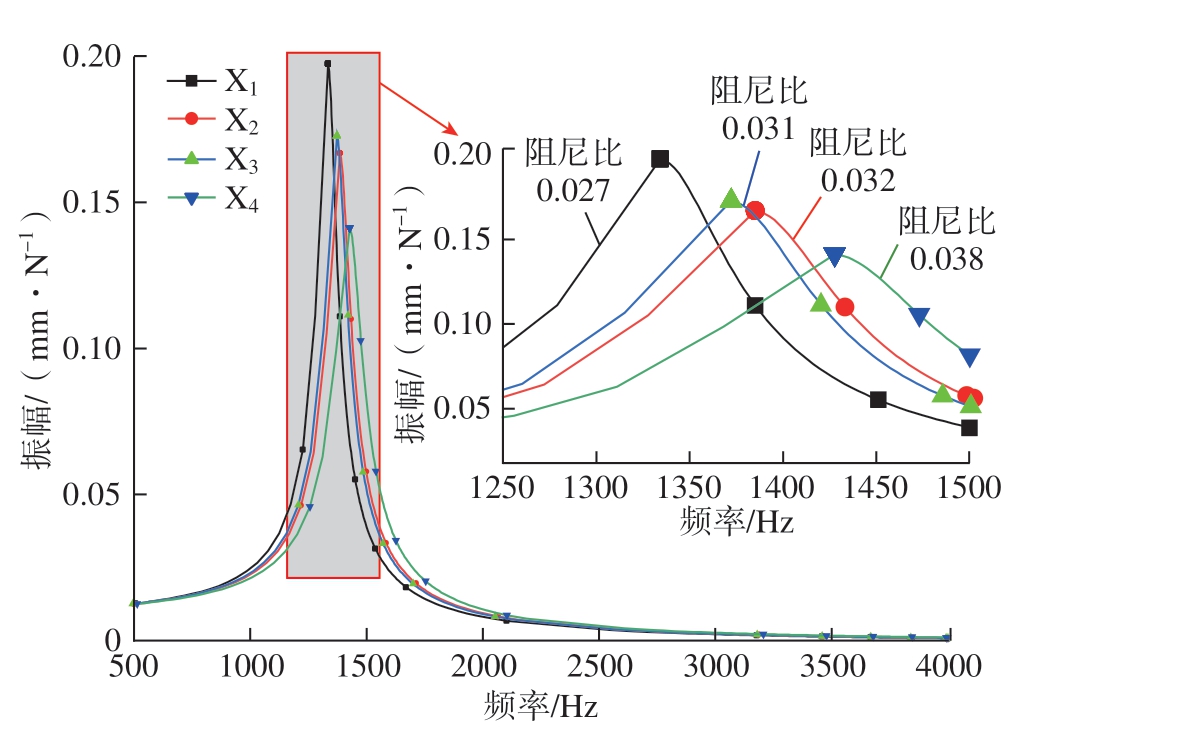
图5 4 种芯轴共振幅值响应
Fig.5 Resonance amplitude response of four core shafts
从图5 可以看出,橡胶部分在芯轴中所占的比例很大程度上影响了发生颤振时的振幅和阻尼,橡胶部分所占比例越大,芯轴的阻尼越大,越能够更好地降低振动幅值。因此,在后续的工作中同时考虑加工性能和共振响应的要求,最终选择X4 作为芯轴进行刀杆整体有限元分析和实物加工。
2.2 刀杆整体有限元建模
对加工现场现有的硬质合金刀杆 (刀杆A)和设计的复合结构减振刀杆 (刀杆B)进行对比分析。为降低有限元计算量,进行有限元建模前需要对模型进行合理的简化和假设:
(1)刀杆夹持在刀柄中,仅对刀杆的悬伸部分进行建模分析,且刀头连接部分视为实心材料;
(2)各部分之间视为刚性连接。
有限元建模步骤包括材料属性的定义、网格划分和边界条件的定义。具体而言,将材料属性分别定义到每个部分,其中碳纤维的缠绕角度设置为±5°[24],单层材料厚度为0.125 mm。在网格划分的阶段,由于对模型进行了简化,将全面采用高质量的六面体结构化网格进行网格划分,单元仍选用C3D8I 非线性协调单元,网格划分完成后的有限元模型如图6 所示。

图6 刀杆网格划分
Fig.6 Toolholder grid partition
2.3 刀杆静刚度验证
静刚度是刀杆设计时需要考虑的重要因素,刀杆设计时首先要在满足静刚度的基础上提升动力学性能,需要对刀杆的静刚度进行分析。在进行静态刚度分析时,仅对悬伸部分进行分析,因此将右端面进行全约束,左端面进行耦合约束,参考点为左端面的圆心位置,沿着y轴负方向在耦合点上施加100 N 的切削力,计算出端头的挠度,如图7 所示。
图7 静态分析边界条件设置
Fig.7 Boundary condition settings for static analysis
刀杆A 和B 的端头最大挠度分别为6.9 μm 和2.6 μm,可以看出在同等切削力的作用下,复合刀杆B 的静刚度相比原始刀杆A 提升了62%,意味着设计的复合刀杆具有更好的刚性,能够允许加工时使用更快的进给速度,从而实现高效加工。
2.4 刀杆模态分析
刀杆的结构对振动特性有重要的影响,模态分析为动态特性分析的基础。因此,在ABAQUS(2022)软件中进行模态分析时,同样将其右端进行约束,计算出两种刀杆在约束状态下的一阶固有频率,计算结果如表2所示。
表2 刀杆的一阶固有频率
Table 2 First natural frequency of toolholders
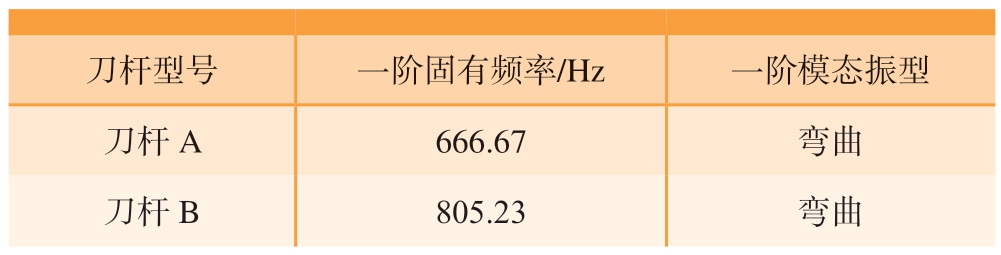
刀杆型号 一阶固有频率/Hz 一阶模态振型刀杆A 666.67 弯曲刀杆B 805.23 弯曲
从表2 可以看出,复合减振刀杆的一阶固有频率值相较于传统金属刀杆提高了21%,这是因为在复合减振刀杆的材料配置中橡胶和碳纤维材料的密度较低,可以产生更大的固有频率,表明设计的复合减振刀杆在工作时共振现象更难被激发,可以承受加工中更高的转速。由于刀杆的对称性,弯曲振型也具有对称性,复合刀杆一、三、五、七阶振型 (二、四、六、八为对称振型)如图8所示,可以看出,刀杆的主要模态振型为弯曲振型和扭转振型,在实际加工中,被激发的一般为前两阶振型,而复合减振刀杆具有固有频率高、刚度高的特点,可以更好抵抗弯曲变形。

图8 复合刀杆模态振型
Fig.8 Modal vibration mode of composite toolholder
2.5 刀杆谐响应分析
通过谐响应分析可以更好地分析刀杆的动态性能,通过施加y 方向的单位正弦载荷激励,取频率为0~1500 Hz 的样本,观察y 方向的共振响应幅值来判断刀杆本身的动态特性,共振响应分析如图9 所示。
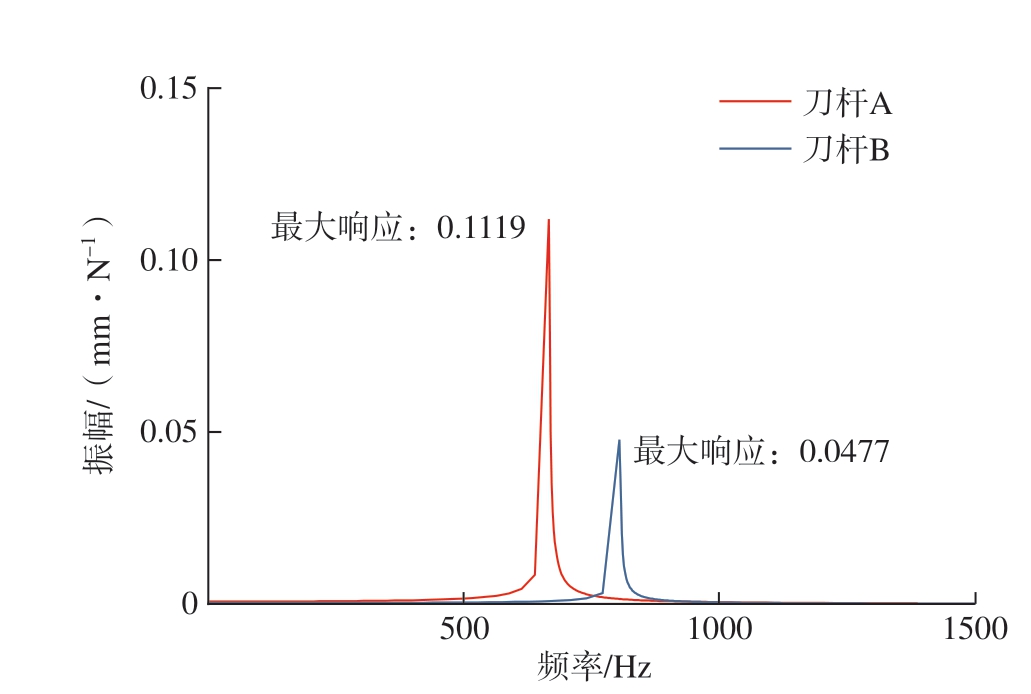
图9 刀杆谐响应分析
Fig.9 Harmonic response analysis of toolholder
在单位正弦载荷的激励下,减振刀杆B 的动刚度相较于传统刀杆A 提高了135%,也就意味着刀杆在工作时更加的稳定,在极端共振情况下的刀具跳动更小,刀具加工对工件的影响更小,可以保证零件的加工精度。
3 复合减振刀杆铣削试验测试
在大悬伸的加工中,常常会出现振动现象,致使零件加工表面粗糙度大,严重影响加工精度。采用复合减振刀杆可以大大降低加工后的表面粗糙度,提升零件加工精度。因此,为体现所设计的减振刀杆在加工中的作用,在相同的切削参数下对现有金属刀杆A 和复合减振刀杆B 进行加工验证,使用表面粗糙度测试仪测试加工后零件表面的粗糙度。
3.1 试验系统
采用TC4 材料的零件进行切削测试,其机械性能如表3 所示。采用三轴加工中心进行平面铣削试验,所采用的刀具为安装有刀头的现场用原始刀杆A 和减振刀杆B,整体的铣削加工系统如图10 所示,将加工好的深腔零件采用表面粗糙度仪进行粗糙度对比测试。
表3 TC4 材料性能
Table 3 TC4 material properties
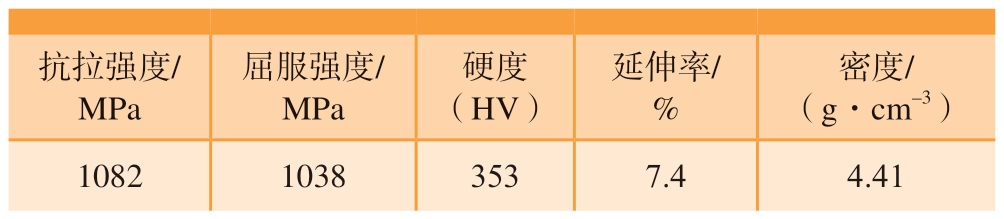
抗拉强度/MPa屈服强度/MPa硬度(HV)延伸率/%密度/(g·cm–3)1082 1038 353 7.4 4.41
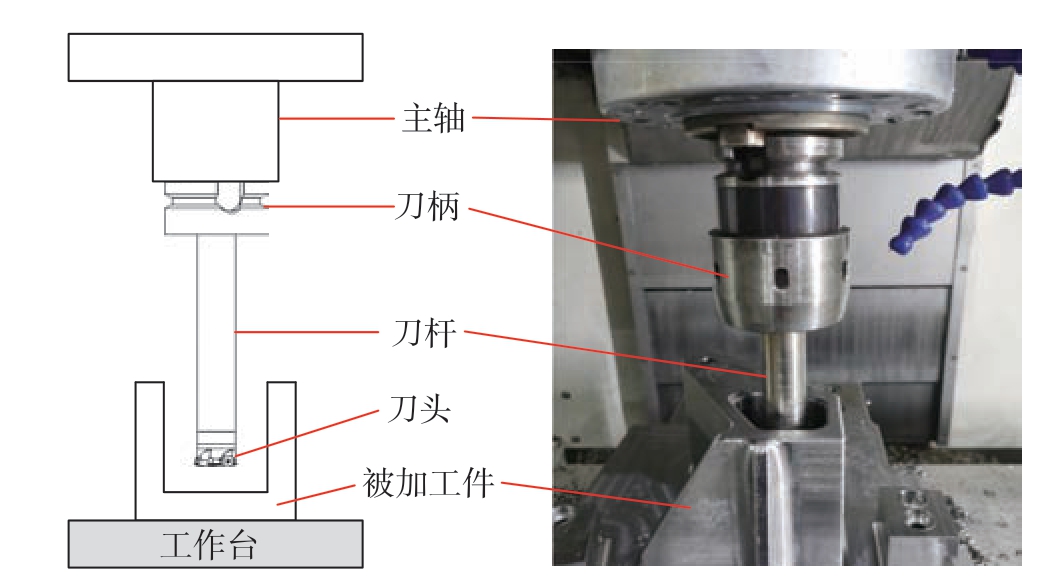
图10 铣削加工系统
Fig.10 Milling machining system
3.2 试验结果分析
图11 展示了传统刀杆A(图11(a))和复合减振刀杆B(图11(b))在相同的加工参数下进行平面铣削加工后的表面形貌。使用传统刀杆A 加工后的零件表面粗糙,表面粗糙度为2.084 μm,而使用复合减振刀杆加工后的零件表面相对光滑,表面粗糙度降低到1.140 μm,加工精度能够达到较高的水平。采用复合减振刀杆进行钛合金细小加工后表面质量提升45.3%,表明所设计的复合减振刀杆在零件加工上具有优异的减振性能,在实际的加工中能明显提升零件质量。

图11 零件粗糙度测试结果
Fig.11 Roughness test results of parts
4 结论
在钛合金深腔加工中,大长径比刀具极易产生振动现象,相较于传统刀杆,复合减振刀杆具有良好的静态和动态特性,被用于钛合金深腔加工,可以有效抑制加工振动。
(1)采用Euler-Bernoulli 梁理论近似模拟刀杆的低阶弯曲模式,得出阻尼和刚度是影响刀杆动态性能的关键参数。
(2)建立复合减振刀杆模型,并通过有限元分析进行了4 种芯轴动态性能的比较,根据谐响应分析结果得出X4 芯轴具有更大的阻尼。
(3)通过有限元分析对复合减振刀杆和传统金属刀杆进行静态和动态性能仿真。复合减振刀杆的静态刚度提升62%,一阶固有频率提升21%,动刚度提升135%,相较于传统金属刀杆,复合减振刀杆具有优异的动静态性能。
(4)通过切削试验,对比复合减振刀杆和传统金属刀杆的加工性能,通过表面粗糙度测试得出,复合减振刀杆加工后的零件表面质量提升45.3%。
[1]王民, 刘保钟, 秦鹏, 等.多层堆叠式永磁动力减振刀杆设计与仿真分析[J].振动与冲击, 2022, 41(3): 8-17.WANG Min, LIU Baozhong, QIN Peng, et al.Design and simulation analysis for multilayer stacked permanent magnet dynamic vibration absorber cutter bar[J].Journal of Vibration and Shock, 2022, 41(3): 8-17.
[2]QIN Y, BROCKETT A, MA Y, et al.Micro-manufacturing:Research, technology outcomes and development issues[J].The International Journal of Advanced Manufacturing Technology, 2010,47(9): 821-837.
[3]YUE C X, GAO H N, LIU X L, et al.A review of chatter vibration research in milling[J].Chinese Journal of Aeronautics, 2019,32(2): 215-242.
[4]JIANG G Q, WANG Y, LI F M, et al.An integrated nonlinear passive vibration control system and its vibration reduction properties[J].Journal of Sound and Vibration, 2021, 509: 116231.
[5]LIU C F, ZHU L D, NI C B.Chatter detection in milling process based on VMD and energy entropy[J].Mechanical Systems and Signal Processing, 2018, 105: 169-182.
[6]YU G, WANG L P, WU J, et al.Milling stability prediction of a hybrid machine tool considering low-frequency dynamic characteristics[J].Mechanical Systems and Signal Processing, 2020, 135:106364.
[7]XIA Y, WAN Y, LUO X C, et al.Chatter suppression in large overhang face milling using a toolholder with high dynamic performance[J].The International Journal of Advanced Manufacturing Technology, 2020, 108(5-6): 1713-1724.
[8]BIJU C V, SHUNMUGAM M S.Performance of magnetorheological fluid based tunable frequency boring bar in chatter control[J].Measurement, 2019, 140: 407-415.
[9]RAZAK N H, CHEN Z W, PASANG T.Progression of tool deterioration and related cutting force during milling of 718Plus superalloy using cemented tungsten carbide tools[J].The International Journal of Advanced Manufacturing Technology, 2016, 86(9): 3203-3216.
[10]SANDVIK COROMANT.Silent tools application guide[EB/OL].(2012-06-17) [2022-09-21].http://www.sandvik.coromant.cn.
[11]LI L, SUN B B, HUA H T.Nonlinear system modeling and damping implementation of a boring bar[J].The International Journal of Advanced Manufacturing Technology, 2019, 104(1-4): 921-930.
[12]章伟, 李季飞, 付秉鑫, 等.内置式镗孔用减振刀杆的结构优化[J].硬质合金, 2022, 39(4): 260-267.ZHANG Wei, LI Jifei, FU Bingxin, et al.Structural optimization of built-in damping tool holder for boring[J].Cemented Carbides, 2022,39(4): 260-267.
[13]VAN ZYL D, ALTINTAS Y, OSTLING D.Parametric design of boring bars with adaptive tuned mass dampers[J].CIRP Journal of Manufacturing Science and Technology, 2022, 38: 491-499.
[14]唐志雄, 黄晓斌, 闫宁, 等.大长径比铣刀复合减振技术研究[J].工具技术, 2021, 55(12): 86-89.TANG Zhixiong, HUANG Xiaobin, YAN Ning, et al.Study on compound damping technology of large long diameter ratio milling cutter[J].Tool Engineering, 2021, 55(12): 86-89.
[15]LEE D G, HWANG H Y, KIM J K.Design and manufacture of a carbon fiber epoxy rotating boring bar[J].Composite Structures,2003, 60(1): 115-124.
[16]SONG Q H, SHI J H, LIU Z Q, et al.Boring bar with constrained layer damper for improving process stability[J].The International Journal of Advanced Manufacturing Technology, 2016,83(9): 1951-1966.
[17]LIU Y, LIU Z Q, SONG Q H, et al.Development of constrained layer damping toolholder to improve chatter stability in end milling[J].International Journal of Mechanical Sciences, 2016, 117:299-308.
[18]XIA Y, WAN Y, LUO X C, et al.Development of a toolholder with high dynamic stiffness for mitigating chatter and improving machining efficiency in face milling[J].Mechanical Systems and Signal Processing, 2020, 145: 106928.
[19]YUVARAJU B A G, NANDA B K, SRINIVAS J.Investigation of stability in internal turning using a boring bar with a passive constrained layer damping[J].FME Transactions, 2021, 49(2):384-394.
[20]ZHANG J F, WANG H, REN Y S, et al.Chatter and stability analysis of the slender composite boring bar with constrained damping layer[J].Applied Sciences, 2020, 10(13): 4537.
[21]MA J M, XU J F, LI L F, et al.Analysis of cutting stability of a composite variable-section boring bar with a large length-to-diameter ratio considering internal damping[J].Materials, 2022, 15(15): 5465.
[22]QI L L, LI C H, YU X D, et al.Effect of reinforced fibers on the vibration characteristics of fibers reinforced composite shaft tubes with metal flanges[J].Composite Structures, 2021, 275: 114460.
[23]王鹏, 张振伟, 骆海涛, 等.空间桁架复合结构的阻尼减振分析与试验研究[J].机械设计与制造, 2020(6): 121-124.WANG Peng, ZHANG Zhenwei, LUO Haitao, et al.Simulation analysis of the application of viscoelastic damping in truss and space load[J].Machinery Design & Manufacture, 2020(6): 121-124.
[24]郭海伟.复合材料减振镗杆参数设计与加工精度试验研究[D].徐州: 中国矿业大学, 2020.GUO Haiwei.Parametric design and machining accuracy test of composite damping boring bar[D].Xuzhou: China University of Mining and Technology, 2020.