复合材料因其可设计性、耐腐蚀性、轻质、高强等优点已大量应用于飞机制造中,且使用部位越来越重要[1]。然而,在复合材料固化成型过程中,由于纤维与基体之间的热不匹配、基体树脂化学反应收缩,以及材料与固化模具之间的温度梯度导致固化成型后复合材料内部存在大量的残余应力,脱模后应力释放使复合材料的形状与理论形状不完全匹配,产生固化变形[2]。因此,在装配过程中常出现复材零件与金属骨架结构间存在间隙或干涉等问题。特别是对于飞机进气道蒙皮等大曲率U 型复合材料结构,该类问题尤为明显。
针对固化变形较大的复合材料零件装配问题,工艺上常采用加垫补偿的方式消除间隙。加垫补偿间隙可极大地减小构件表面的应变幅值和范围[3]。然而在飞机生产制造中,对于一些不允许加垫或加垫后仍不能消除间隙的位置,工艺上必须采取强迫装配的方式保证复合材料零件与骨架相贴合。复合材料是一种典型的各向异性脆性材料,其层间强度较弱,若在强迫装配过程中引入较大的装配载荷,则会削弱其力学性能,容易导致在服役过程中引起复合材料分层、裂纹扩展等损失[4]。F/A–18、AV–8B 和UK-5B 等国外军机都曾因为装配引入过大载荷而导致蒙皮产生裂纹和分层[5-7]。因此,在复合材料强迫装配过程中控制装配载荷是至关重要的。目前,国内外对于复合材料强迫装配并没有统一的标准,但大体上分为基于力控制的装配策略和基于应变控制的装配策略。如波音公司对复合材料结构强迫装配给出了45 1b/ft (约200 N/300 mm)的装配力限值,但出于技术保密等原因,具体研究细节和详细资料均未见公开报道[8]。
在此背景下,国内外学者及飞机制造商针对复合材料结构强迫装配开展了大量的研究。岳烜德等[9]基于一种简化装配模型,通过试验和有限元分析方法研究了液体垫片对复合材料装配结构应力和应变的影响,结果表明,强迫装配时,处在装配间隙边缘的区域受间隙影响相对严重,液体垫片的引入使应变分布趋于均匀。王世杰等[10]通过试验和数值分析,研究了装配应力对加筋壁板破坏行为的影响,研究结果为复合材料壁板的装配作业规范和铺层设计方案设计验证提供了一定的参考。朱生茂[11]在容差分析的基础上分析了蒙皮与长桁装配后的变形和装配力,并提出采用残余间隙评价装配质量的计算方法。蒋麒麟等[12]以复合材料层合板机械连接中典型的单螺栓连接为对象,研究了间隙补偿及不同液体垫片参数下层合板的单层面内应力与层间应力的变化。
综上所述,目前对于复合材料结构强迫装配问题的研究多集中于通过加垫改善间隙、控制复材装配应力应变,而缺少铆接顺序对复合材料装配应力、应变的研究。实际飞机生产制造中,铆接过程涉及成百上千的铆钉,铆接顺序是影响复合材料应力、应变的主要因素之一。现阶段对于铆接顺序的研究均是针对不同铆接顺序对结构变形的影响开展,如王仲奇等[13]针对飞机壁板外形装配精度差的问题,以壁板自动钻铆为对象,以铆接变形最大值最小为目标,采用遗传算法进行铆接顺序优化,实现了对壁板铆接变形的有效控制;殷俊清[14]分别以三钉、四钉、十钉结构为对象,采用数值计算方法研究了不同铆接顺序对薄壁结构变形的影响,基于PSOSVR 智能算法对多钉薄壁结构铆接顺序进行了优化,解决了壁板铆接变形大的问题。在复合材料结构铆接装配过程中,不同的铆接顺序其核心是不断地改变各铆接点所受的约束作用,从而使不同铆接顺序下零件中产生不同的应力、应变及变形。由于复合材料层合板应变分布是线性的,而应力分布与各层刚度特性相关,是沿厚度方向非连续分布的[15],所以目前各大飞机制造商常根据应变对复合材料进行结构设计和工艺控制。然而,目前尚未发现有基于复合材料应变进行铆接顺序优化的研究。
本文以某大曲率U 型碳纤维复合材料蒙皮为研究对象,首先测量蒙皮待铆接点与骨架之间的间隙,然后构建复合材料蒙皮铆接数值计算模型,并以铆接时复合材料蒙皮中最大应变最小为目标,以加载点、约束点处支反力小于临界值为约束条件建立优化模型,基于遗传算法及ABAQUS 二次开发求解优化模型,搜索最优铆接顺序,实现复合材料结构大批量铆钉铆接顺序智能规划。
1 大曲率碳纤维蒙皮预装配
本研究所用大曲率碳纤维U 型复合材料蒙皮如图1 所示,固化成型后蒙皮变形为开口端两条长边向内凹,蒙皮中间部分能够与骨架贴合。根据大曲率U 型复合材料蒙皮装配工艺要求,先调整蒙皮,使中间部位与骨架贴合,并使用穿心夹将该区域所有铆接孔与骨架连接,保证该区域蒙皮与骨架之间无间隙、无相对滑动或转动,实现蒙皮预装配。预装配后使用塞尺测量有间隙区域蒙皮上铆接孔与骨架之间的间隙值,如表1 所示(本文以10 个铆接点为例)。
表1 待铆接点与骨架间隙
Table 1 Gap between the riveting point and the skeleton
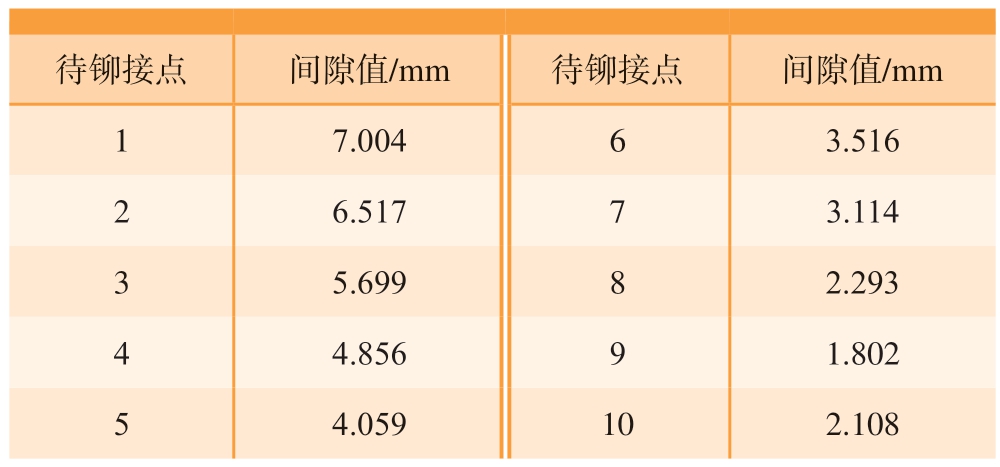
待铆接点 间隙值/mm 待铆接点 间隙值/mm 1 7.004 6 3.516 2 6.517 7 3.114 3 5.699 8 2.293 4 4.856 9 1.802 5 4.059 10 2.108
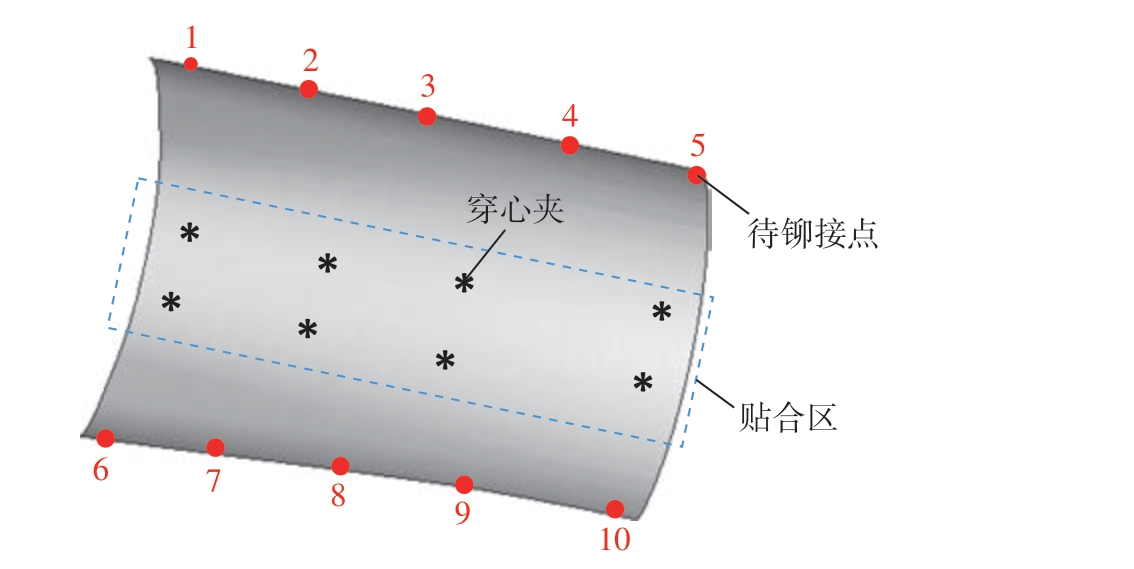
图1 大曲率U 型复合材料蒙皮
Fig.1 Skin of U-shaped composite with large curvature
2 大曲率碳纤维蒙皮铆接数值模型
2.1 数值模型
大曲率碳纤维蒙皮尺寸较大,且实际铆接过程中往往会涉及成百上千的铆钉铆接,不适合采用全三维实体模型进行全过程的弹塑性计算。本文采用壳单元模拟大曲率碳纤维蒙皮,单元类型为四节点减缩积分单元S4R,有限元模型如图2 所示,共计18930 个单元。
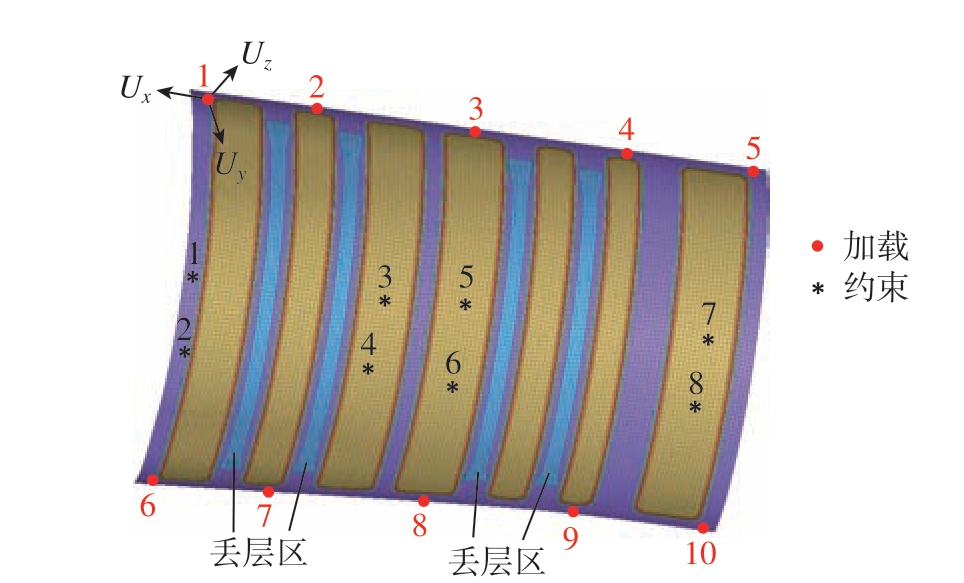
图2 有限元模型
Fig.2 Finite element model
大曲率碳纤维蒙皮材料为ZT7H/QY9611 碳纤维增强树脂基材料,材料属性如表2 所示;单层名义厚度为0.125 mm,共28 层,总厚度为3.5 mm;蒙皮存在4 个丢层区域,由于厚度变化,在丢层区域易产生应力集中,因此,为提高计算精度设置每一层积分点个数为7。
表2 ZT7H/QY9611 的材料参数
Table 2 Material parameters of ZT7H/QY9611
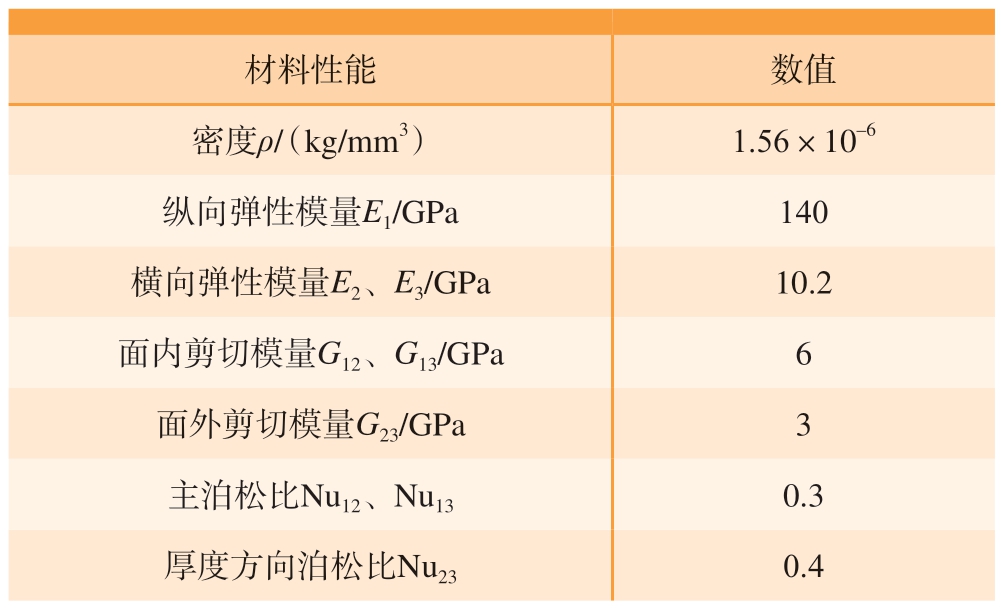
材料性能 数值密度ρ/(kg/mm3) 1.56×10–6纵向弹性模量E1/GPa 140横向弹性模量E2、E3/GPa 10.2面内剪切模量G12、G13/GPa 6面外剪切模量G23/GPa 3主泊松比Nu12、Nu13 0.3厚度方向泊松比Nu23 0.4
大曲率碳纤维蒙皮实际装配过程中,首先调整蒙皮,使中间部位与骨架贴合并连接贴合区域的铆钉,数值模型的约束位置即为图1 所示穿心夹位置,加载点即为待铆接点,该模型共10 个待铆接点。各加载点处均建立局部坐标系,其中局部坐标系Z 轴沿加载点处蒙皮型面法线方向,见图2。
铆接过程通过在各加载点处施加位移边界条件实现,各加载点处位移载荷方向均沿局部坐标系Z 向,位移量即为加载点与骨架之间的间隙值,见表1。铆接顺序通过在不同的分析步中对不同加载点施加位移载荷实现,如铆接顺序为[3/4/5/10/9/8/7/6/1/2]则表示第一个分析步中在3 号加载点施加位移载荷、第2 个分析步中在4 号加载点施加位移载荷,以此类推。
2.2 模型校核
通过比较数值计算得到的加载点处支反力与实测得到的待铆接点压紧力验证模型正确性。有限元数值计算实现方法为在各加载点处依次分别施加相应间隙值的位移载荷,计算完成后统计各个加载点处节点的支反力。实际测量时,在蒙皮预装配状态下采用手持式压力计依次将各待铆接点压紧至与骨架贴合,并读取压力值。
有限元数值计算得到的加载点处支反力云图如图3 所示。数值计算得到的支反力与实测待铆接点处压紧力对比如图4 所示。由图4 可知,仿真所得加载点处支反力与实测压紧力大小较吻合,最大误差仅为13%,说明有限元模型可信。误差主要源于手持式压力计压紧时操作空间有限,且压紧力较大不易控制蒙皮与骨架之间的贴合程度,易导致过压,从而使得测量值偏大。
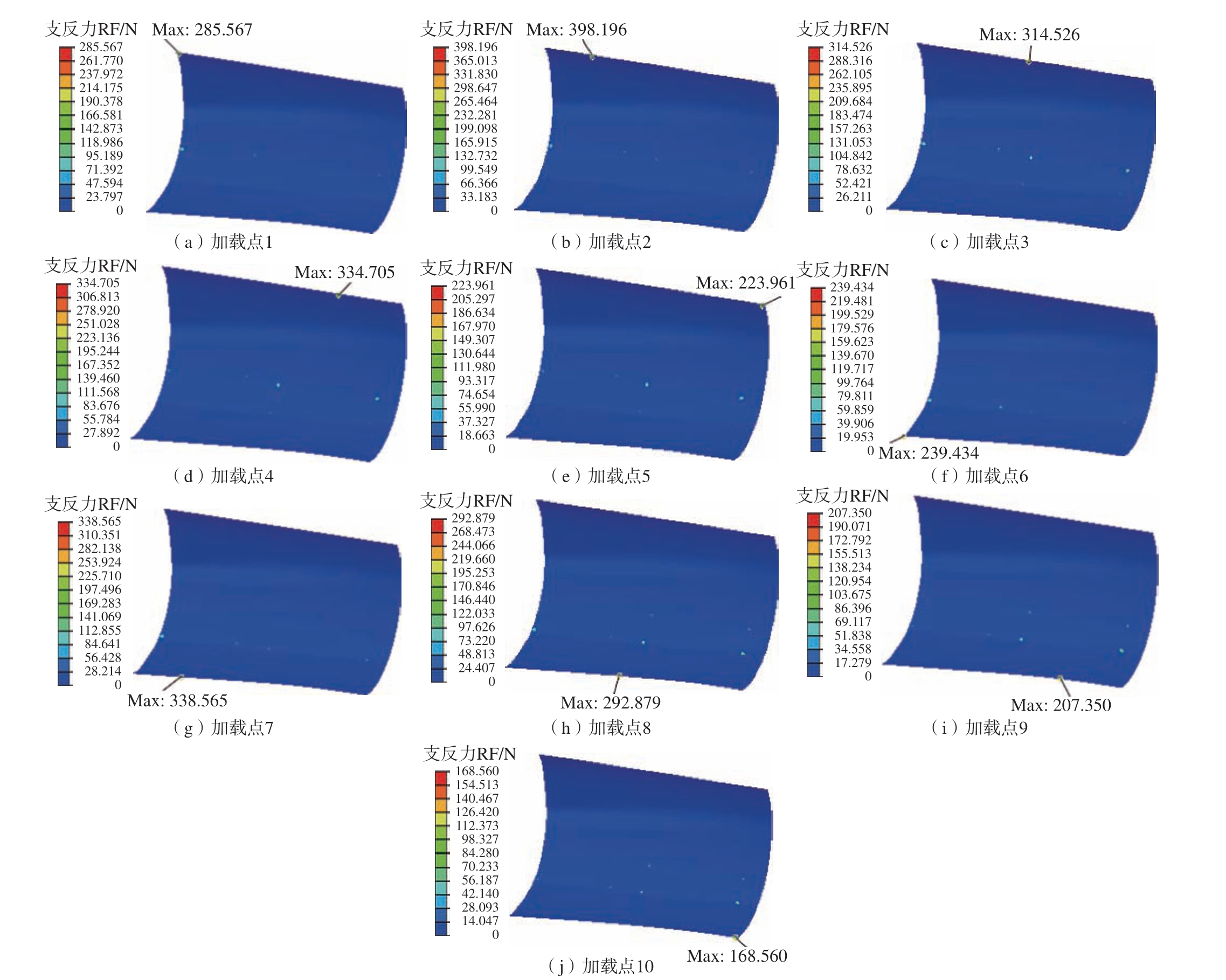
图3 支反力云图
Fig.3 Cloud map of support reaction force
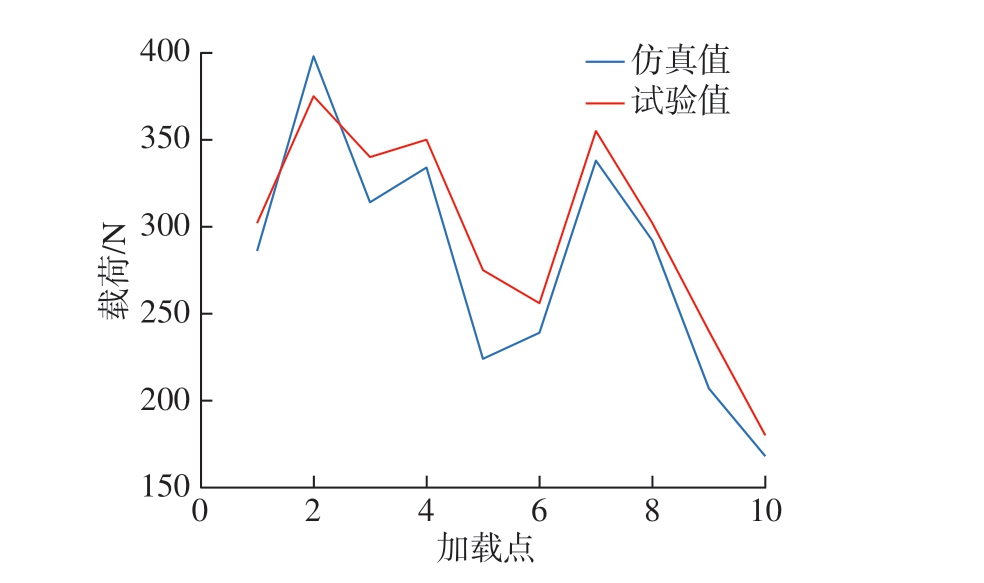
图4 压紧力实测值与计算值
Fig.4 Measured and calculated values of compaction force
2.3 基于Python 语言的参数化模型
为了便于与遗传算法主程序集成运算,需要建立参数化的有限元数值计算模型。本文以Python 为脚本语言对ABAQUS 进行二次开发,在ABAQUS CAE 界面操作时,采用宏录制的方式记录相应的代码并将其中多余的语句删除并保存,将其作为ABAQUS 数值计算主程序 (.py)。针对大曲率碳纤维蒙皮铆接顺序问题,需要将脚本中的分析步、加载位置、加载顺序等可变参数用关键字代替,该关键字通过读取Matlab 生成的shunxu.dat 文件 (用于存储每一次计算的铆接顺序)获得具体值。
在ABAQUS 计算完成后,同样利用Python 语言进行后处理,遍历搜索读取每一种铆接顺序下模型中的最大应变及加载点、约束点处的最大支反力,并将其分别写入E.dat 文件及RF.dat 文件供Matlab 遗传算法主程序读取。
3 基于遗传算法的铆接顺序优化
遗传算法 (Genetic algorithm,GA)是模拟生物在自然环境中的遗传和进化过程而形成的自适应全局优化搜索算法[16]。它借用了生物遗传学的观点,通过自然选择、遗传和变异等作用机制,实现各个个体适应性的提高,其本质是一种并行、高效、全局搜索的方法,能够在搜索过程中自适应地控制搜索过程以求得最优解。本文采用遗传算法与有限元数值计算相结合的方法,以遗传算法为主优化程序,通过有限元数值计算求解各铆接顺序下的最大应变及最大支反力,计算个体适应度值,在此基础上通过遗传算法 (选择、交叉、变异)对铆接顺序进行优化,具体优化流程如图5 所示。
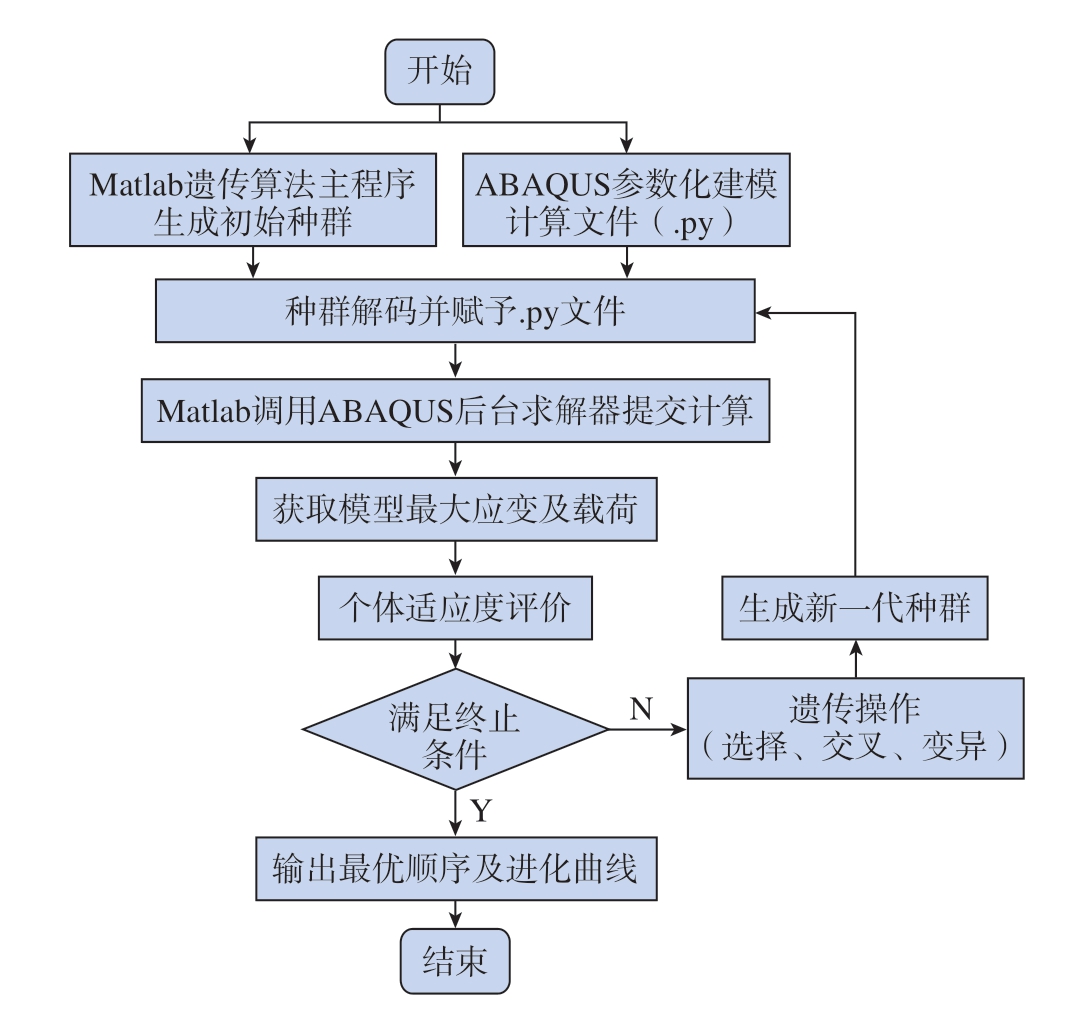
图5 基于遗传算法的铆接顺序优化流程
Fig.5 Optimization process of riveting sequence based on genetic algorithm
3.1 优化模型
不同于金属材料,复合材料蒙皮铆接装配过程中,通常以零件中应变水平及载荷水平衡量铆接质量,而不同铆接顺序下零件中最大应变及载荷均有所差异。为了获得一种优化的铆接装配顺序从而降低复合材料零件中的最大应力及载荷水平,本文以复合材料零件中最大应变最小为优化目标,以加载点、约束点处最大支反力小于工艺要求的压紧力临界值为约束条件,数学模型为
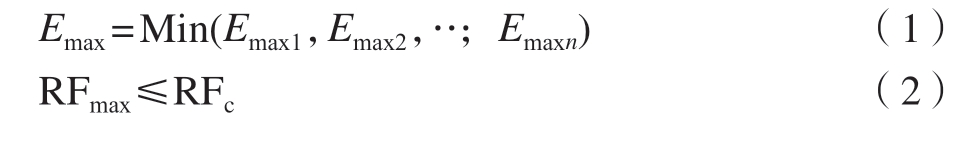
式中,Emaxn 表示n 种铆接顺序下复合材料中的最大应变;RFmax 表示n 种铆接顺序下加载点、约束点处最大支反力;RFc 表示工艺要求的压紧力临界值。
3.2 遗传算法
采用遗传算法对大曲率碳纤维蒙皮铆接顺序进行优化时,首先需要将铆接顺序进行编码,转化成遗传算法能够识别的参数[17],然后对个体选取合适的适应度函数,并通过选择、交叉、变异等操作更新种群,进一步通过迭代进化确定最优顺序。
(1)编码及初始种群。
编码就是将优化变量转化为基因的组合表示形式,遗传算法的编码方式包括二进制、十进制 (整数编码)等[15]。针对大曲率碳纤维蒙皮大量铆钉铆接顺序问题,采用计算精度高、解码简单的整数编码方式。如图2 所示的有限元模型,共有10 个铆钉,对每一个铆钉进行唯一的整数编号。
种群即为存储铆接顺序的一个集合,种群规模即是该种群中铆接顺序的个数。种群规模需根据特定的问题进行选择,种群规模太小会影响搜索效果,种群规模太大则会降低搜索效率。初始种群采用随机数的方式产生,根据铆钉孔的整数编号,随机生成一种序列即为一种铆接顺序,如[3,6,7,8,1,10,2,4,9,5]。
为了与大曲率碳纤维蒙皮实际铆接装配过程更加吻合,规定所有铆接顺序中第一个铆接的孔不能为1、5、6、10 号铆钉。
(2)适应度函数。
适应度函数是用于评价个体优劣的数学函数,其构造方式一般有目标函数映射成适应度函数、基于序的适应度函数等[16]。在大曲率碳纤维蒙皮铆接装配过程中,要求复合材料零件中的最大应变最小,即以最大应变为优化目标求其最小值。因此,本文以有限元数值计算得到的各铆接顺序下复合材料蒙皮中的最大应变为目标,构造归一化的适应度函数,即
式中,Fitness(i)表示当前种群里第i 个个体的适应度,该值越大则个体适应度越好;Emin、Ei 分别表示当前种群中的最小应变及第i 个个体对应的最大应变。
(3)选择算子。
选择即根据个体的适应度,按照一定的规则或方法,从第t 代群体P(t)中选择出一些优良的个体遗传到下一代群体P(t+1)中[13]。本文采用随机遍历抽样选择算子,并且对每一个个体规定:若该个体对应的加载点、约束点最大支反力大于工艺要求的临界值 (RFmax > RFc)则直接剔除该个体。
(4)交叉算子。
交叉是提高遗传算法搜索能力的主要操作,本文采用部分匹配交叉法。该方法的基本思路是首先从群体中随机抽取要交叉的一对个体,然后选取交叉点个数及交叉区域,最后根据交叉概率Pc 实施交叉操作,互换两个交叉个体之间的部分基因,从而形成一对新的个体。
例如,对于10 个铆钉铆接顺序的一对待交叉个体P1:[3,6,7,8,1,10,2,4,9,5] 和P2:[2,5,10,4,6,1,7,3,8,9],选择交叉点个数为3,交叉区域为2/5,即将两个个体中第3~5 个基因互换,互换后形成两个新个体P1':[3,6,10,4,6,10,2,4,9,5]和P2':[2,5,7,8,1,1,7,3,8,9],且两者之间的映射关系为7–10、8-4、1–6。互换后新个体中出现重复编号,需保持交换区域的基因不变,并根据映射关系变更其他位置处的重复编号,变更后形成的新个体为Q1:[3,1,10,4,6,7,2,8,9,5]和Q2:[2,5,7,8,1,6,10,3,4,9]。
(5)变异算子。
变异属于遗传算法中的辅助性操作,主要目的是保持种群多样性。变异的基本思想是对于选中的个体,以某一概率 (变异概率Pm)将某一个或某一些基因值改变为其他的等位基因。
例如,对于10 个铆钉铆接顺序的一个待交叉个体P1:[3,6,7,8,1,10,2,4,9,5],交换第2 位基因与第7 位基因,得到新个体Q1:[3,2,7,8,1,10,6,4,9,5]。
(6)终止条件。
针对大曲率碳纤维蒙皮铆接装配问题,在计算之前无法预测目标函数的收敛值,因此设置最大迭代次数作为终止条件,达到最大迭代次数后计算终止并输出此进化过程中具有最大适应度值的个体作为最优铆接顺序。
4 实例分析
针对图2 所示的具有10 个铆钉的大曲率碳纤维蒙皮铆接装配问题,以模型中最大应变最小为目标,以加载点、约束点处的支反力小于400 N 为约束条件,设置种群规模为20,最大遗传代数为40,交叉概率Pc 为0.8,变异概率Pm 为0.1。
编写Matlab 程序并根据图5 所示的流程进行遗传算法搜索,得到的适应度进化曲线如图6 所示。由图6可知,经过7 次迭代后适应度进化曲线达到收敛,最大应变为7.76×10–8,对应的铆接顺序为[7,4,6,9,8,1,2,3,5,10]。
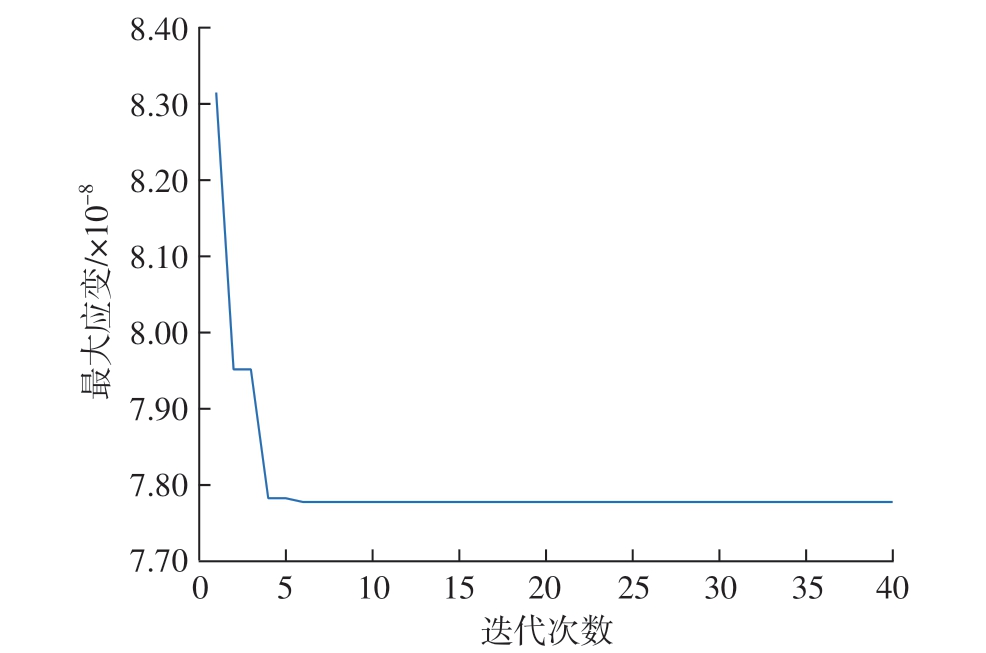
图6 适应度进化曲线
Fig.6 Curve of fitness evolution
将4 种经验铆接顺序下的最大应变与遗传算法搜索得到的结果进行对比。4 种经验铆接顺序如表3 所示。
表3 4 种经验铆接顺序
Table 3 Four empirical riveting sequences
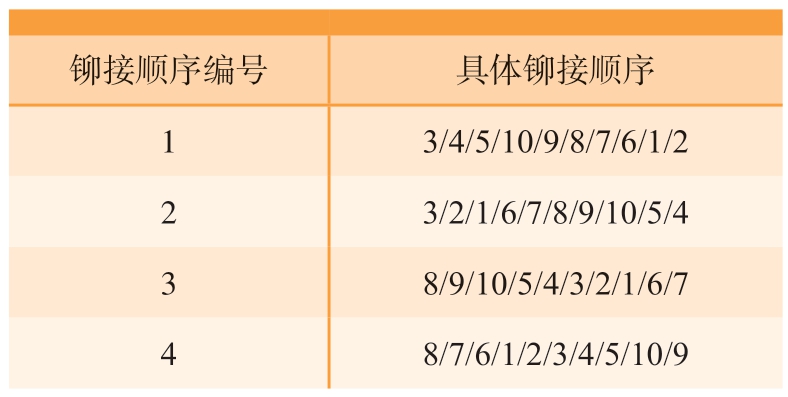
铆接顺序编号 具体铆接顺序1 3/4/5/10/9/8/7/6/1/2 2 3/2/1/6/7/8/9/10/5/4 3 8/9/10/5/4/3/2/1/6/7 4 8/7/6/1/2/3/4/5/10/9
大曲率碳纤维蒙皮4 种经验铆接顺序下的最大应变如图7 所示。由图7 可知,第3 种经验铆接顺序下复合材料零件中最大应变为8.15×10–8,其余3 种经验铆接顺序下复合材料零件中最大应变均接近8.40×10–8。显然,铆接顺序下通过遗传算法搜索得到的最大应变明显小于经验铆接顺序下的最大应变。
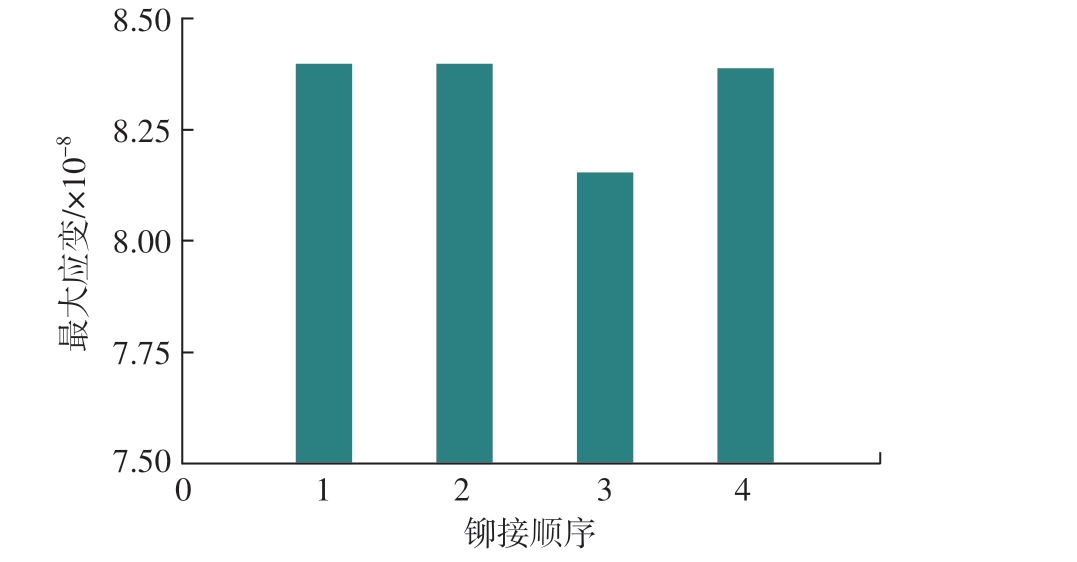
图7 经验铆接顺序下零件最大应变
Fig.7 Maximum strain of parts under empirical riveting sequence
经验铆接顺序1、3 及遗传算法搜索得到的最优铆接顺序下,零件中最大应变云图如图8 所示。对比图8可知,经验铆接顺序1 下零件最大应变出现在铆接点3,经验铆接顺序3 下零件最大应变出现在铆接点2,遗传算法搜索到的最优铆接顺序下零件最大应变出现在铆接点4。因此,不同的铆接顺序既能影响零件中的最大应变值又能影响最大应变出现的位置。
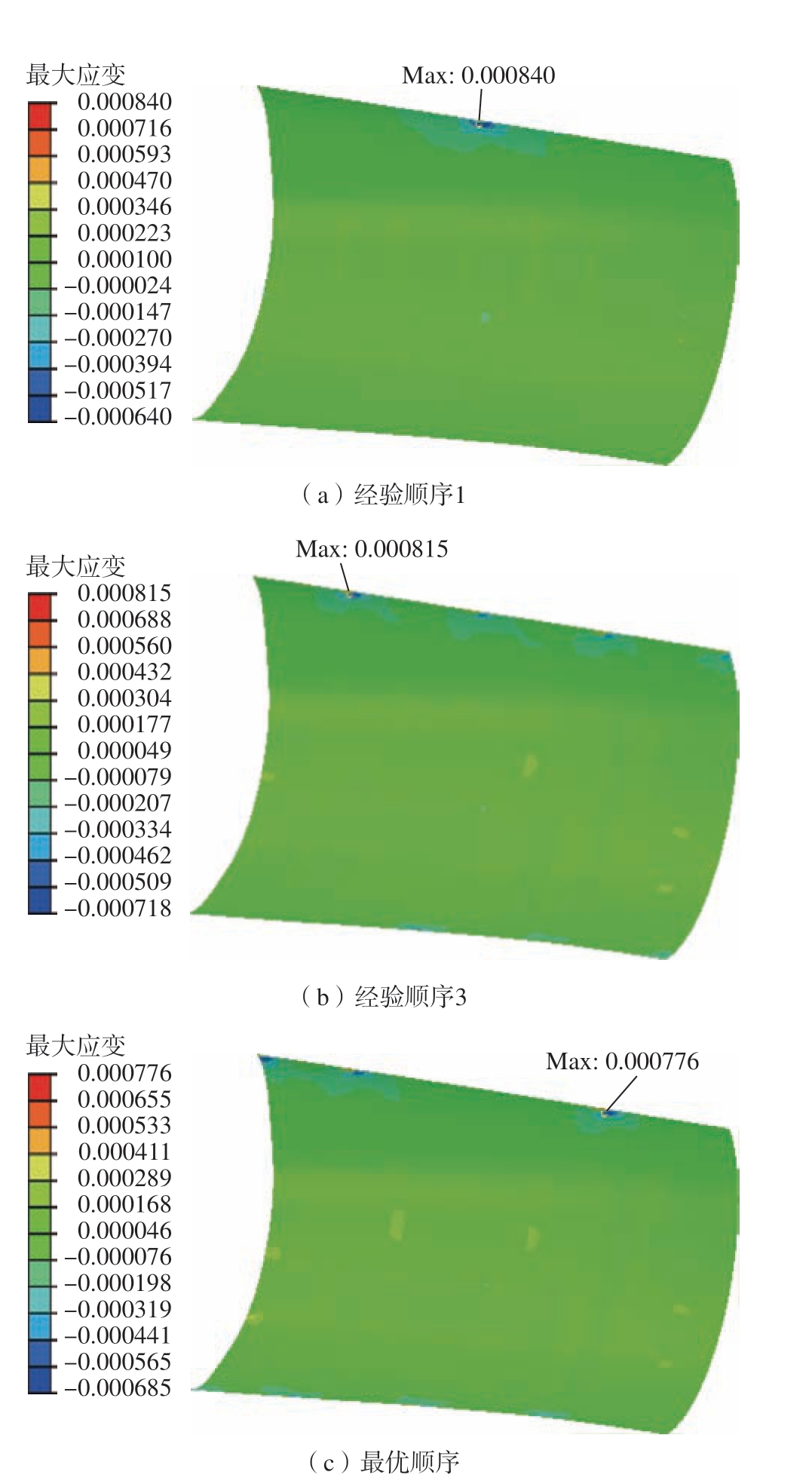
图8 不同铆接顺序下零件最大应变云图
Fig.8 Maximum strain nephogram of parts under different riveting sequences
5 结论
为控制大曲率碳纤维蒙皮铆接装配过程中的装配载荷,建立了蒙皮铆接过程有限元数值计算模型;通过压紧力的实测值与计算值验证了模型的正确性,以铆接过程中蒙皮最大应变最小为目标,以加载点、约束点处的支反力小于临界值为约束条件,构建大曲率碳纤维蒙皮铆接顺序优化模型;通过遗传算法及ABAQUS 二次开发实现优化模型求解,搜索最优铆接顺序。结果表明,按工艺经验顺序铆接后复合材料蒙皮的最大应变为8.40×10–8,而通过遗传算法优选的铆接顺序下复合材料蒙皮最大应变仅为7.76×10–8,证明该方法有效可行。
利用该方法可实现大曲率碳纤维蒙皮大批量铆钉铆接顺序智能规划,也可推广应用至其他类似的工艺问题。
[1]李西宁, 王悦舜, 周新房.复合材料层合板分层损伤数值模拟方法研究现状[J].复合材料学报, 2021, 38(4): 1076-1086.LI Xining, WANG Yueshun, ZHOU Xinfang.Status of numerical simulation methods for delamination damage of composite laminates[J].Acta Materiae Compositae Sinica, 2021, 38(4): 1076-1086.
[2]周洪, 李宁, 李阔, 等.固化工艺影响L形复合材料制件固化变形研究[J].航空精密制造技术, 2021, 57(1): 17-22.ZHOU Hong, LI Ning, LI Kuo, et al.Influences of curing process on geometrical deformation of L-shaped composite component[J].Aviation Precision Manufacturing Technology, 2021, 57(1): 17-22.
[3]叶鑫, 安鲁陵, 岳烜德, 等.间隙与垫片补偿下复材 – 铝合金结构表面应变的研究[J].机械制造与自动化, 2020, 49(6): 18-20, 35.YE Xin, AN Luling, YUE Xuande, et al.Research on surface strain of composite-aluminum alloy structures with gap and shim compensation[J].Machine Building & Automation, 2020, 49(6): 18-20, 35.
[4]叶鑫, 安鲁陵, 岳烜德, 等.填隙补偿对碳纤维/环氧树脂复合材料 – 铝合金装配结构力学性能的影响[J].复合材料学报, 2020,37(9): 2183-2199.YE Xin, AN Luling, YUE Xuande, et al.Effect of gap-filling compensation on mechanical properties of carbon fiber/epoxy compositealuminum assembly structure[J].Acta Materiae Compositae Sinica, 2020,37(9): 2183-2199.
[5]PAUL D, KELLY L, VENKAYYA V, et al.Evolution of U.S.military aircraft structures technology[J].Journal of Aircraft, 2002, 39(1):18-29.
[6]GOERING J, BOHLMANN R, WANTHAL S, et al.Assembly induced delaminations in composite structures[R]//FAA, Ninth DOD(NASA)FAA Conference on Fibrous Composites in Structural Design: NASA- CR-198722.1992.
[7]CAMPONESCHI E T Jr, BOHLMANN R E, FOGARTY J H.Composite to metal joints for the ARPA man-rated demonstration article[J].Journal of Thermoplastic Composite Materials, 1995, 8(1): 56-79.
[8]李东升, 翟雨农, 李小强.飞机复合材料结构少无应力装配方法研究与应用进展[J].航空制造技术, 2017, 60(9): 30-34.LI Dongsheng, ZHAI Yunong, LI Xiaoqiang.Research and application advances of stress-less assembly methods for composite airframe[J].Aeronautical Manufacturing Technology, 2017, 60(9): 30-34.
[9]岳烜德, 安鲁陵, 云一珅, 等.液体垫片对复合材料装配结构应力和应变的影响[J].复合材料学报, 2018, 35(10): 2665-2677.YUE Xuande, AN Luling, YUN Yishen, et al.Effect of liquid shim on stress and strain of composite assembly structure[J].Acta Materiae Compositae Sinica, 2018, 35(10): 2665-2677.
[10]王世杰, 陈振, 徐鹏, 等.复合材料加筋壁板装配应力对结构失效影响的试验与数值分析[J].复合材料科学与工程, 2021(4):96-101.WANG Shijie, CHEN Zhen, XU Peng, et al.Experimental and numerical analysis of the effect of assembly stress on the composite stiffened panel failure[J].Composites Science and Engineering, 2021(4): 96-101.
[11]朱生茂.壁板柔性零件装配过程分析与研究[D].杭州: 浙江大学, 2013.ZHU Shengmao.Analysis and research on assembly process of flexible parts of wallboard[D].Hangzhou: Zhejiang University, 2013.
[12]蒋麒麟, 安鲁陵, 云一珅, 等.间隙补偿及液体垫片参数对层合板单层与层间应力的影响[J].机械科学与技术, 2017, 36(10):1633-1640.JIANG Qilin, AN Luling, YUN Yishen, et al.Effect of gap compensation and parameters of liquid shim on composite laminate internal stress and interlayer stress[J].Mechanical Science and Technology, 2017,36(10): 1633-1640.
[13]王仲奇, 张津铭, 常正平, 等.壁板铆接变形分析及铆接顺序规划研究[J].航空制造技术, 2017, 60(22): 16-23.WANG Zhongqi, ZHANG Jinming, CHANG Zhengping, et al.Research on deformation analysis and sequence planning of aircraft panel in riveting process[J].Aeronautical Manufacturing Technology, 2017,60(22): 16-23.
[14]殷俊清.航空薄壁件铆接变形分析及预测研究[D].西安:西北工业大学, 2015.YIN Junqing.Study on riveting deformation analysis and prediction of aviation thin-walled parts[D].Xi’an: Northwestern Polytechnical University,2015.
[15]曹景斌, 郝钢凝, 章强.某型机复合材料机翼盒段设计许用值确定技术研究[J].中文科技期刊数据库(文摘版)工程技术, 2015(8): 256.CAO Jingbin, HAO Gangning, ZHANG Qiang.Study on the determination technology of allowable design value of composite wing box section of a certain aircraft[J].Engineering Technology of Chinese Sci Tech Journal Database (Abstract Edition), 2015(8): 256.
[16]包子阳, 余继周.智能优化算法及其MATLAB 实例[M].北京: 电子工业出版社, 2016.BAO Ziyang, YU Jizhou.Intelligent optimization algorithm and its MATLAB example[M].Beijing: Publishing House of Electronics Industry, 2016.
[17]张秋月, 安鲁陵, 岳烜德, 等.基于遗传算法的飞机复合材料结构装配压紧力大小与布局的优化[J].复合材料学报, 2019, 36(6): 1546-1557.ZHANG Qiuyue, AN Luling, YUE Xuande, et al.Optimization of size and layout of pressing force for composite airframe structure assembly based on genetic algorithm[J].Acta Materiae Compositae Sinica, 2019, 36(6):1546-1557.