喷丸成形是一种利用大量刚性球形弹丸喷射薄壁零件表面从而使零件成形的工艺方法,被广泛应用于航空航天领域的大型金属整体壁板成形[1-2]。预应力喷丸是喷丸成形工艺中经常被采用且十分重要的技术手段,其原理是通过在某个方向上预先施加一定的应力场 (简称预应力)来达到提高被加工零件在某个方向上变形的目的[3]。然而到目前为止,如何对预应力进行表征,不同的学者所采用的方法各不相同。
在早期研究中,学者采用预弯试片外层纤维的延伸量来表征预应力,并以此作为参数来描述不同喷丸条件下预应力对喷丸变形的影响[4],此方法的优点是表层应变易于测量。张懃[5]在进行预应力喷丸夹具研究时,采用预弯半径来表征所施加的预应力,用以提高壁板件喷丸变形的效果并克服球面变形的趋势。彭月友[6]通过板件的预弯曲率来表征所施加的预应力,并将其应用于复杂弯折形状壁板件预应力状态的描述。Wang 等[7]进一步以试件的预弯曲率半径作为表征预应力水平的参数,通过试验研究了不同预应力水平下三点预弯厚板件喷丸变形与喷丸次数之间的量化关系。相较于表层纤维的延伸量,用预弯半径或预弯曲率来描述预应力相对更直观一些。在一些新型喷丸成形方法研究中,也可以看到以预弯曲率或预弯曲率半径表征预应力的应用。周圳等[8-9]在薄壁板预应力超声喷丸成形中,采用试件的预弯曲率、曲率半径等物理量作为预应力的表征来研究预应力和超声喷丸参数对试件变形的影响。王治业[10]以试件的预弯曲率半径来表征预应力,研究预应力和超声波喷丸参数对带筋板件的变形作用规律等。
在弧高仪等测量工具被引入工程应用后,尚建勤[11]采用预变形区的预弧高来表征预应力,并以此来定量化地研究受喷板件沿预应变和垂直于预应变方向的喷丸变形与预弯弧高之间的关系。这种表征方法的优点是作为表征参数的预弯弧高在测量上更方便一些,但仍难以反映在预应力喷丸中对喷丸变形有重要影响的材料厚度、弹性模量等信息。Miao 等[12]采用预弯弯矩来表征预应力,用于综合反映材料厚度和弹性模量等参数,并以此来研究预应力对板件喷丸变形的影响。Miao 等[13]进一步将预弯弯矩引入喷丸变形有限元模型中以表征预应力场,研究预应力对受喷板件变形的影响。Xiao 等[14]引入了预应力参数的概念来表征预应力水平,但这一应用局限于预应力对静态和动态弹丸压痕的影响。
综上所述,如何对预应力喷丸成形中的预应力这一重要的力学参数进行表征,目前已有测量外层纤维延伸量、预弯半径、预弯弧高、预弯弯矩等多种方法,但目前这些方法仍不能反映所加载的预应力距离屈服点的远近程度,而且对于不同的材料采用这些方法表征的预应力并不具备可比性,从而限制了预应力喷丸变形规律在不同材料、不同喷丸条件之间的可推广性。本文针对该问题,建立了预应力状态表征的归一化模型,提出采用归一化的预应力参数来表征预应力状态,用以规范化地描述预应力对板件喷丸变形的影响规律,最后设计实施了预应力喷丸成形试验对表征模型进行验证,并建立了以预应力参数表述的预应力弯曲喷丸变形规律模型。
1 归一化预应力模型
在喷丸成形实际工程中,常用的预应力施加方法有三点压弯法 (图1(a)[7])和模具型面法 (图1(b)[3])。
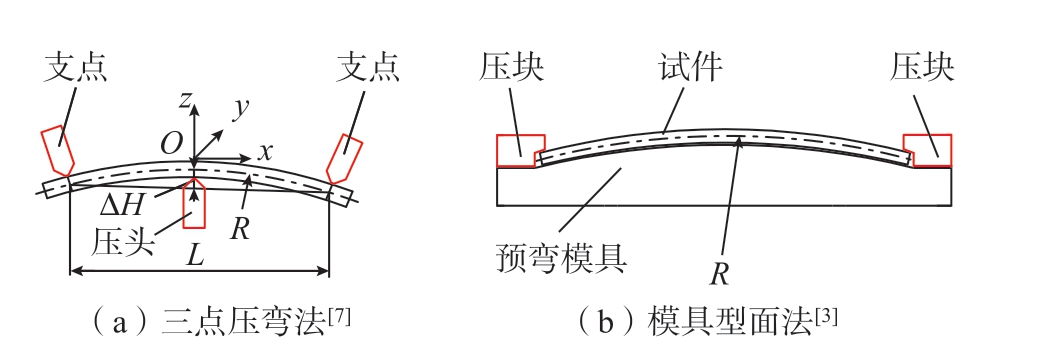
图1 常用的预应力施加方法
Fig.1 Common pre-stress application methods
为了避免截面形状和厚度分布等复杂因素对喷丸变形的影响,本文采用具有均匀厚度的矩形板件作为研究对象。假设板件在弯曲过程中,其中性层不发生厚度方向的偏移,同时由于在工程实践中一般将预弯变形限定在弹性范围内,因此当板件在某点处的中性层预弯半径为R 时,在预弯方向上的预应力σ 的分布可表示为[15]
式中,z∈[- t/2,t/2]表示沿厚度t 方向偏离中性层的位移;E、v 分别为材料的弹性模量和泊松比;R 为板件的弯曲半径。当z = ± t/ 2 时,预弯板件的预应力在上、下表面分别达到的最大值σ*为
由此可见,在相同的喷丸参数作用下,相同尺寸规格的预应力喷丸板件与自由喷丸板件在变形上存在差异,这是由预应力喷丸板件的预应力状态所导致的,即预应力喷丸件的变形是喷丸参数和预应力状态两组参数的函数。对于图1(a)所示的三点压弯预应力施加方式,在以板件的中间位置为原点的坐标系下,试件在原点处的预弯曲率可由式(3)计算得出,即三点压弯板件在各处的弯曲半径是其坐标的函数。
式中,L 为两支点之间的距离;ΔH 为板件中性面在两支点之间的弧高。相应地,将式 (3)代入式 (2)得出三点压弯板件在其上下表面处的最大预应力为
将式 (3)代入式 (1)得
式 (4)和 (5)表明,在三点压弯作用下,板件外表面上的预弯应力状态随着x 向的改变而变化,同时在给定的x 向位置处板件沿厚度的应力也随着纵向坐标z的变化而变化。因此,采用三点压弯的方式来表征预弯应力状态是困难的。而式 (2)表明,在弯曲半径为定值的模具型面的预弯作用下,板件在其外表面上各处的预应力状态是恒定的。因此,以曲率半径为定值的模具型面预弯板件的应力状态作为参数对预应力状态进行表征存在影响因素单一的问题。
考虑到不同牌号的铝合金的弹性模量、屈服应力水平并不相同,即使在相同预弯半径下,由式 (2)得到的板件预应力水平也并不相同,不能反映该表面预应力水平距离相应材料屈服点的远近,因此,定义归一化的预应力参数ξ 如下。
式中,σs 为材料的屈服应力,在本文中对于铝合金取σs = σ0.2,即塑性应变达到0.2%时,材料的真实应力为-1≤ξ≤1。如果仅取外凸表面上的预应力,则0≤ξ≤1。当ξ = 0 时,对应无预应力状态;当ξ = 1 时,对应最大预应力状态。将式 (2)代入式 (6)得出
由式 (1)、 (2)和 (6)可得
从而得出预应力参数ξ 可以表征预弯半径为定值的板件的预应力状态。由此,对于预弯半径在各处为定值的板件,在喷丸参数给定的情况下,其受预应力的影响也可以表述为ξ 的函数,其一般形式为
式中,r 为预应力喷丸作用后板件在自由状态下沿预弯方向的半径,即板件的预应力喷丸成形半径。
2 试验方法
试验所用材料为2024-T351 和7055-T7751 铝合金,经单向拉伸试验测得有关力学参数如表1 所示[16]。
表1 材料力学参数[16]
Table 1 Mechanical parameters of materials[16]
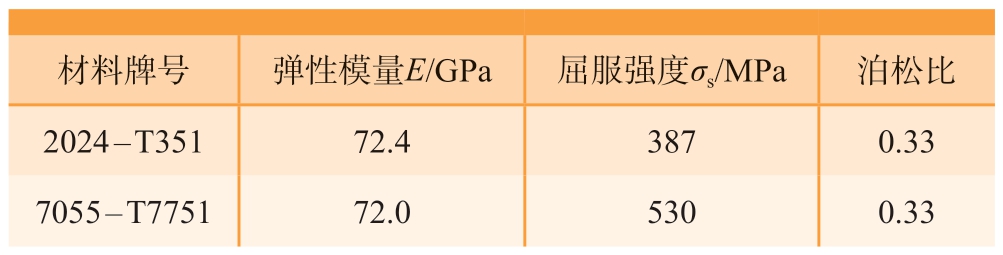
材料牌号 弹性模量E/GPa 屈服强度σs/MPa 泊松比2024 - T351 72.4 387 0.33 7055 - T7751 72.0 530 0.33
参考工程中常用的Almen 试片的长宽比[17],所有试件均加工成矩形板件,板件的面内尺寸均为长200 mm×宽50 mm,均由轧制的铝合金厚板加工而成且板件的长度方向与原材料的轧制方向保持一致,如图2所示。板件厚度t 有4 mm、6 mm、8 mm、12 mm 和16 mm,共5 种规格。
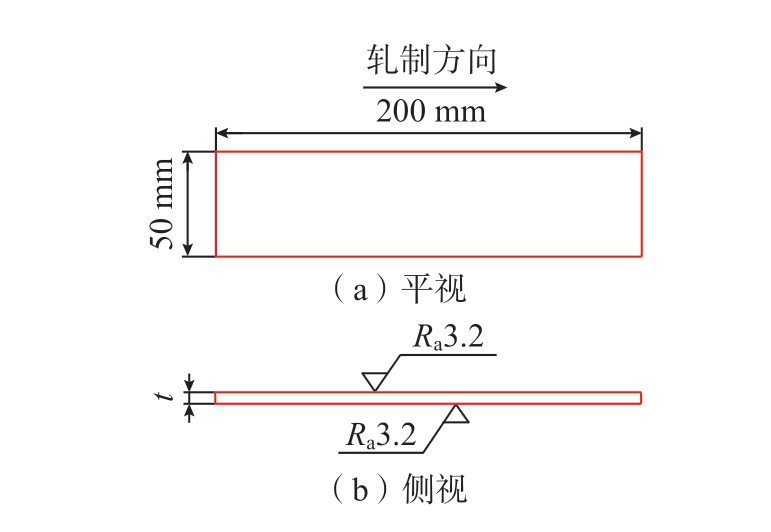
图2 试验用板件尺寸
Fig.2 Dimensions of experimental specimens
试验所采用的喷丸设备为MPPF20000/2500 数控喷丸机,所采用的喷丸气压分别为0.15 MPa、0.20 MPa、0.25 MPa、0.30 MPa、0.35 MPa。喷丸速度 (即喷嘴相对于板件在长度方向上的相对运动速度)分别取2 m/min、4 m/min、6 m/min、8 m/min。弹丸采用APB1/8 铸钢弹丸,弹丸直径3.18 mm,弹丸流量均为12 kg/min,单喷嘴喷丸 (喷嘴直径10 mm),喷丸距离 (即喷嘴到板件受喷表面的距离)均为500 mm,喷丸角度90°。采用不同半径的模具按图1(b)所示的方式施加板件预应力,按式 (2)试算板件外凸表面上的应力水平,所得值分别为相应材料屈服强度σs 的20%、40%、60%、80%和100%,所有板件均按以下步骤进行试验。
(1)用丙酮清洁板件表面。
(2)画线并编号。
(3)测量原始弧高。
(4)对板件按图1(b)所示的方式进行有 (或无)预应力装夹并按照试验参数进行喷丸。
(5)卸载并用丙酮清洁板件表面。
(6)测量并记录板件变形。
3 结果与讨论
3.1 预应力参数对变形曲率的影响
图3 所示为8 mm 厚的7055-T7751 铝合金板件在弹丸流量12 kg/min、喷丸速度4.0 m/min,以及喷丸气压分别为0.15 MPa、0.20 MPa、0.25 MPa、0.30 MPa、0.35 MPa 时的变形曲率随预应力参数ξ 的变化情况。
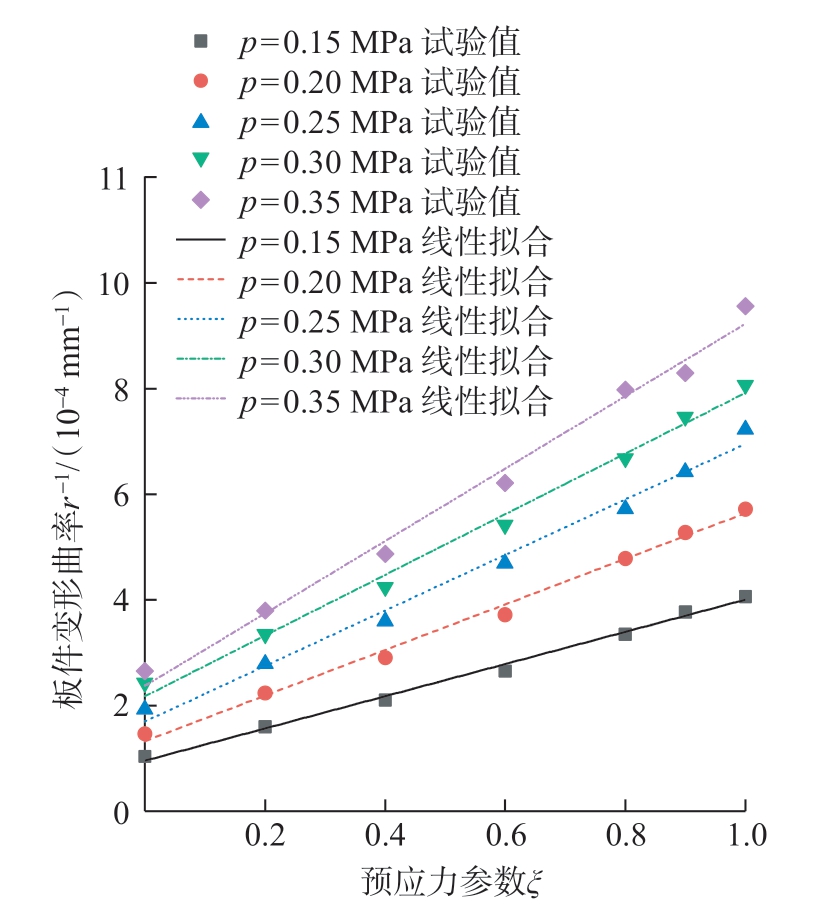
图3 预应力参数对板件喷丸变形曲率的影响
Fig.3 Influence of pre-stress parameter on the deformation curvature of shot peened plates
在不同的喷丸气压下,受喷板件沿预弯方向的变形曲率1/r 与预应力参数ξ 之间均为线性关系,即在弹性预弯范围内,预应力参数ξ 的增大将引起预应力方向上变形曲率1/r 的线性增加。该线性关系为
式中,α、β 分别为与喷丸气压有关的常数和比例系数。α为预应力为0时相应喷丸参数作用下试件的变形曲率;β 为相应喷丸气压下预应力参数ξ 对应的喷丸变形增进效率。在试验给定的喷丸条件下,分别由式 (11)得出α、β,其中,p 为喷丸气压。
图3 和式 (10)表明,当喷丸气压增大时,试件在无预应力条件下的变形曲率1/r 将增大,同时在施加预应力时,预应力对沿预弯方向的喷丸变形增进效率,即比例系数β 也随之增大。
由式( 10)进一步可得ξ 与1/r 之间的增量关系为
在喷丸参数保持不变以及弹性预弯的条件下,当变形曲率的目标变化量Δ(1/r)给定时,所需的预应力参数调整量Δξ 可通过以上增量关系得出。
3.2 喷丸速度对变形曲率的影响
图4 所示为不同预应力参数下喷丸速度对厚度为6 mm 的2024-T351 受喷板件变形曲率的影响。当弹丸流量、喷丸气压等喷丸参数保持不变时,在不同的预应力水平下,板件沿预应力方向的喷丸变形曲率均随着喷丸速度v 的增大而减小,但这些变化趋势均受预应力参数的影响,可用式 (13)中的函数关系进行量化描述。
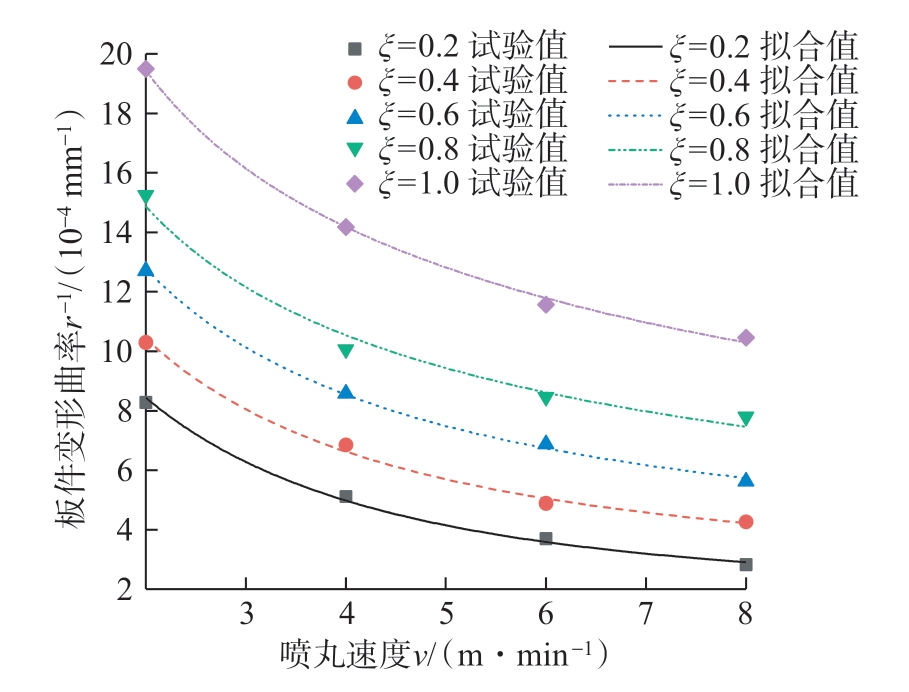
图4 不同预应力参数下喷丸速度对2024-T351板件变形曲率的影响
Fig.4 Influence of shot peening speed on the deformation curvature of 2024-T351 plates under different pre-stress parameters
式中,比例常数A、B 均为ξ 的函数,有
式 (13)表明,喷丸板件的1/r 与喷丸速度v 之间并不是简单的反比关系,这一结论与文献[18]中对无预应力喷丸模型的修正是一致的,本文将其称为拟反比关系。当ξ 增大时,1/r 与v 之间的拟反比关系将提升到更高的变形水平上。如图4 所示,在v 相同的情况下,ξ越大,1/r 也越大。
受试验条件的限制,本文采用的喷丸速度仅限于工程常用的范围内。试验采用MPPF20000/2500 数控喷丸机,当v << 2 m/min 时,弹丸分布趋于饱和,此时式(13)所给出的数量关系将不再成立,而是应采用饱和喷丸条件下的数量关系[18],本文暂不考虑这一特殊情况。
3.3 喷丸气压对变形曲率的影响
图5 为弹丸流量在12 kg/min 时喷丸气压在不同预应力参数下对厚度为8 mm 的7055-T7751 板件沿预弯方向变形曲率的影响。在工程常用的喷丸气压范围内和一定的预应力参数下,受喷板件沿预弯方向的1/r 与p 之间成正比关系,即
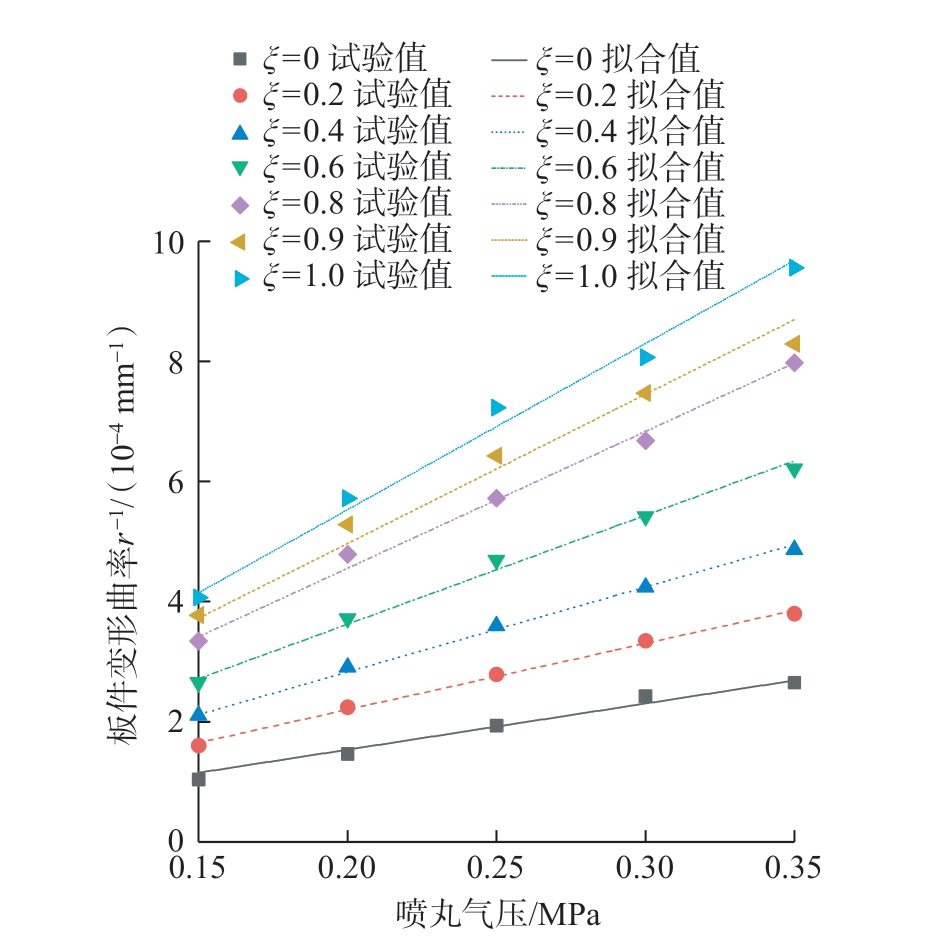
图5 不同预应力参数下喷丸气压对7055-T7751 板件喷丸变形曲率的影响
Fig.5 Influence of shot peening air pressure on the deformation curvature of 7055-T7751 plates under different pre-stress parameters
式中,比例系数M 由ξ 确定。
上述关系表明,当板件厚度、弹丸类型、弹丸流量和喷丸速度等喷丸参数给定时,试件弯曲喷丸的1/r 与p之间的比例系数M 由预应力参数ξ 决定。当ξ 增大时,M 也相应地线性增大。同时,这一比例关系也受到喷丸机自身设备特性的影响,关于喷丸机设备特性的影响不在本文的探讨范围之内。
3.4 厚度对喷丸变形的影响
图6 为不同预应力参数下厚度对2024-T351 板件变形曲率的影响。试验参数为喷丸速度4.0 m/min、弹丸流量12 kg/min、喷丸气压0.2 MPa。
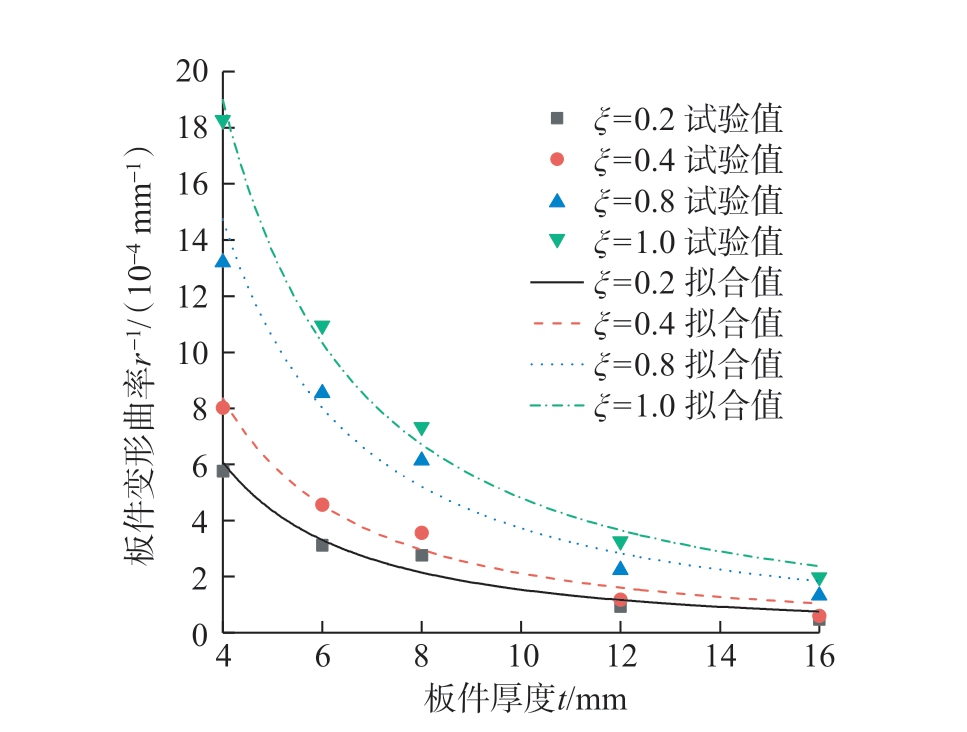
图6 不同预应力参数下厚度对2024-T351 板件变形曲率的影响
Fig.6 Influence of thickness on the deformation curvature of 2024-T351 plates under different pre-stress parameters
在一定的预应力参数下,受喷丸板件的1/r 可近似视为与其厚度t 的3/2 次幂成反比,即
式中,Q 为与ξ 有关的比例常数,即
式 (17)与经典板件纯弯曲理论[19]中当弯矩固定时1/r ∝t-3 的关系不同,在本文喷丸条件下,当喷丸参数,即弯曲喷丸变形作用保持不变时,板件的喷丸1/r 与其厚度t 之间的关系为1/r ∝t -3/2。这一条件使本文的结论与文献[18]接近,Q 是ξ 的线性函数,当ξ 增大时,Q 线性增大。
3.5 预应力参数的归一化
不同牌号的铝合金的屈服强度往往相差很大,导致不同牌号的铝合金之间以实际应力表征的预弯状态不具备可比性。图7 为厚度8 mm 的2024-T351 和7055-T7751 铝合金板件在不同预应力水平σ*下沿预弯方向的喷丸变形曲率。外凸表面上的预应力均通过式(2)得出。所采用的喷丸参数为弹丸流量12 kg/min、喷丸气压0.2 MPa、喷丸速度4 m/min。
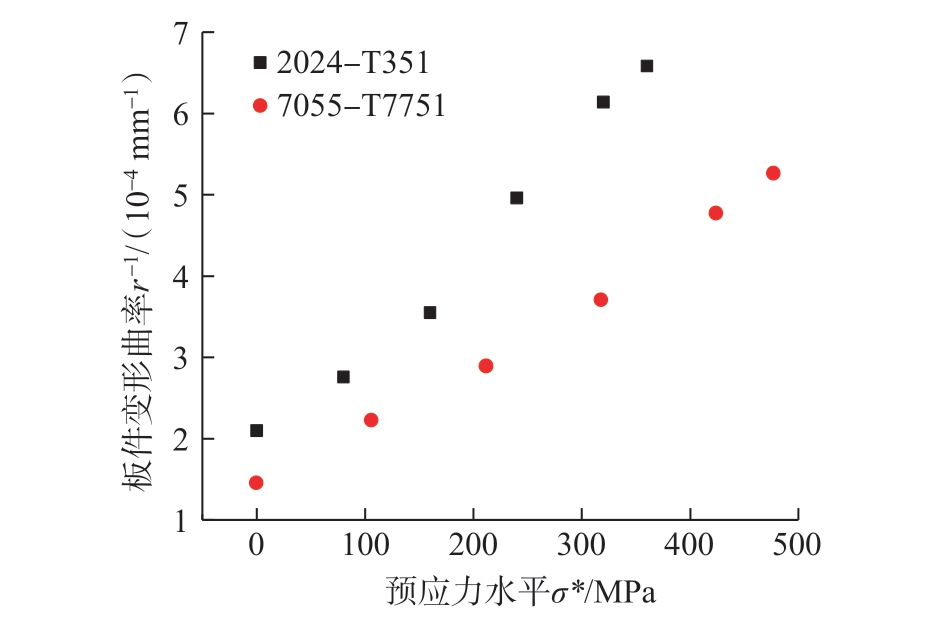
图7 预应力对2024-T351 和7055-T7751 喷丸变形曲率的影响
Fig.7 Influence of pre-stress on the deformation curvature of shot peened 2024-T351 and 7055-T7751 plates
图7 表明,当喷丸参数保持不变时,随着板件外凸预弯表面上σ*的增大,两种铝合金板件在预弯方向上的弯曲1/r 均呈线性增长。然而,对于两种不同的铝合金,相同的预应力水平所产生的喷丸变形量并不相同,如果要产生相同的弯曲变形量,7055-T7751 铝合金需要更高的预应力水平,其本质原因是铝合金7055-T7751 比2024-T351 的屈服强度更高 (表1)。因此并不能根据图7 所示的试验数据直接对预应力和喷丸参数作用于不同铝合金时的喷丸变形作用效果进行比较。而当对预应力水平进行归一化处理后,则可以避免屈服强度差异导致的问题。
图8 为以预应力参数ξ 为自变量描述的2024-T351 和7055-T7751 两种铝合金板件在预弯方向上的弯曲1/r 与ξ 之间的关系。两种材料的预应力均通过归一化ξ 将其取值限定在规范化的[0,1]范围之内,不同材料在预弯方向上的变形均采用式 (10)形式建立的1/r 与ξ 之间的规范化函数关系。
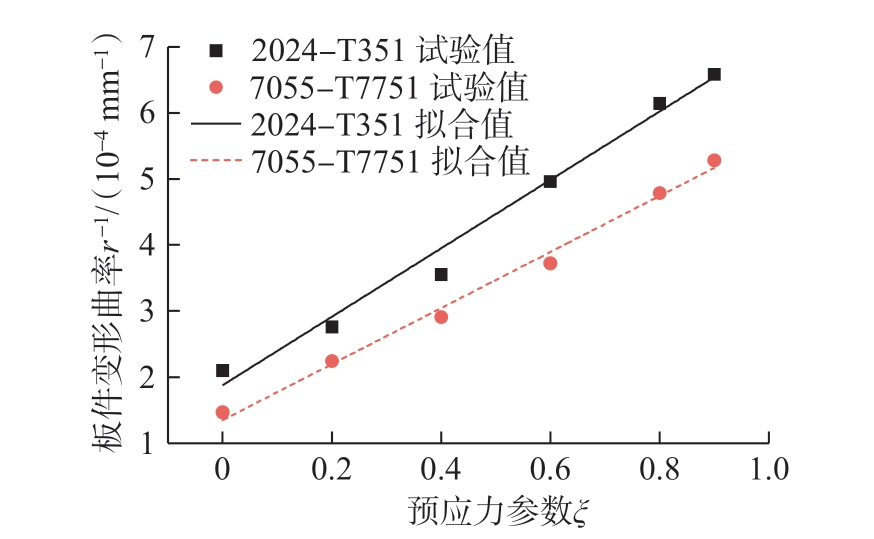
图8 归一化预应力参数对2024-T351 和7055-T7751 喷丸变形曲率的影响
Fig.8 Influence of unitized pre-stress parameter on the defermation curvature of shot peened 2024-T351 and 7055-T7751 plates
对于2024-T351 铝合金:
对于7055-T7751 铝合金:
即2024-T351 和7055-T7751 两种材料对应的α值分别为1.88 和1.35,β 值分别为5.18 和4.24。根据式 (10)对α 和β 物理意义的定义,式 (19)和 (20)的归一化表述形式表明,在相同的喷丸参数和相同的尺寸规格下,在无预应力时2024-T351 试件比7055-T7751试件的弯曲喷丸变形曲率大;当施加预应力时,预应力对2024-T351 试件弯曲喷丸变形曲率增进的效率高于对7055-T7751 试件的增进效率;当ξ=1,即预应力达到相应材料的屈服强度时,2024-T351 试件最大预应力弯曲喷丸的1/r 也相应地大于7055-T7751 试件。因此,在将预应力采用归一化的预应力参数ξ 进行表征后,不同材料的预应力喷丸变形行为可以规范化到一致的预应力参数区间[0,1]上进行比较分析。
4 结论
(1)以预弯板件表面应力与材料屈服强度的比值作为预应力参数来表征预弯喷丸变形的预应力状态,可以实现对预应力喷丸变形行为在[0,1]预应力参数区间上的归一化描述。
(2)板件沿预弯方向的喷丸变形曲率与预应力参数之间呈线性关系,当喷丸参数给定时,预应力参数的增大将导致板件沿预弯方向的喷丸变形曲率线性增大。
(3)板件沿预弯方向的喷丸变形曲率与喷丸速度之间成拟反比关系,当喷丸参数给定时,比例系数由预应力参数决定。
(4)板件沿预弯方向的喷丸变形曲率与喷丸气压之间成正比,比例系数是预应力参数的线性函数。当预应力参数增大时,比例系数线性增大。
(5)板件沿预弯方向的喷丸变形曲率与板件厚度的3/2 次幂成反比,比例常数是预应力参数的线性函数。当预应力参数增大时,比例常数线性增大。
[1] 赵安安, 张贤杰, 高国强, 等. 大型机翼整体壁板系统化喷丸成形技术[J]. 航空学报, 2019, 40(2): 522635.ZHAO An’an, ZHANG Xianjie, GAO Guoqiang, et al. A systematic method of shot peen forming of large integral wing skin panels[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(2): 522635.
[2] 曾元松, 黄遐. 大型整体壁板成形技术[J]. 航空学报, 2008,29(3): 721-727.ZENG Yuansong, HUANG Xia. Forming technologies of large integral panel[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3):721-727.
[3] 曾元松, 黄遐, 李志强. 先进喷丸成形技术及其应用与发展[J]. 塑性工程学报, 2006, 13(3): 23-29, 39.ZENG Yuansong, HUANG Xia, LI Zhiqiang. The application and development of advanced shot peen forming technologies[J]. Journal of Plasticity Engineering, 2006, 13(3): 23-29, 39.
[4] 六二五研究所七三二八四课题组. 歼击机机翼整体壁板的喷丸成形[J]. 航空制造技术, 1976, 19(8): 5-13.625 Research Institute 73284 Project Team. Shot peening forming of integral panel of fighter wing[J]. Aeronautical Manufacturing Technology,1976, 19(8): 5-13.
[5] 张懃. 预应力喷丸夹具[J]. 航空制造技术, 1984, 27(4): 18-21.ZHANG Qin. Prestressed shot peening fixture[J]. Aeronautical Manufacturing Technology, 1984, 27(4): 18-21.
[6] 彭月友. 三叉戟飞机8 号肋加强板的喷丸成形[J]. 航空制造技术, 1984, 27(6): 13-15.PENG Yueyou. Shot peening forming of trident No.8 rib stiffener[J].Aeronautical Manufacturing Technology, 1984, 27(6): 13-15.
[7] WANG M T, ZENG Y S, BAI X P, et al. Deformation rule of 7150 aluminum alloy thick plate by pre-stress shot peen forming[J].Advanced Materials Research, 2014, 1052: 477-481.
[8] 周圳. 薄壁板预应力超声波喷丸成形实验研究与数值分析[D]. 南京: 南京航空航天大学, 2017.ZHOU Zhen. Experimental and numerical research of stressing ultrasonic peening forming on thin plate[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017.
[9] 周圳, 鲁世红, 张涛, 等. 铝合金弹性预应力超声喷丸成形试验[J]. 中国表面工程, 2017, 30(3): 31-39.ZHOU Zhen, LU Shihong, ZHANG Tao, et al. Experimental study of elastic prestressed ultrasonic peen forming on aluminum alloy[J].China Surface Engineering, 2017, 30(3): 31-39.
[10] 王治业. 加筋板预应力超声波喷丸成形工艺研究[D]. 南京:南京航空航天大学, 2018.WANG Zhiye. Research of stressing ultrasonic peening forming technology in stiffened plate[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018.
[11] 尚建勤. 预应力对喷丸成形的影响[J]. 锻压技术, 2000, 25(1):42-43.SHANG Jianqin. Effect of pre-stress on peen-forming[J]. Forging &Stamping Technology, 2000, 25(1): 42-43.
[12] MIAO H Y, DEMERS D, LAROSE S, et al. Experimental study of shot peening and stress peen forming[J]. Journal of Materials Processing Technology, 2010, 210(15): 2089-2102.
[13] MIAO H Y, LAROSE S, PERRON C, et al. Numerical simulation of the stress peen forming process and experimental validation[J].Advances in Engineering Software, 2011, 42(11): 963-975.
[14] XIAO X D, WANG Y J, ZHANG W, et al. Numerical research on stress peen forming with prestressed regular model[J]. Journal of Materials Processing Technology, 2016, 229: 501-513.
[15] TIMOSHENKO S, WOINOWSKY-KRIEGER S. Theory of Plates and Shells[M]. 2nd ed. New York: McGraw-Hill Book Company,1959.
[16] 国家钢铁材料测试中心,中国标准出版社第五编辑室. 金属力学及工艺性能试验方法标准汇编—上[M]. 第4版. 北京: 中国标准出版社, 2014.National Analysis Center for Iron and Steel, The Fifth Editorial Office Standards Press of China . Standard compilation of test methods for mechanical and technological properties of metals—Part I[M]. 4th ed.Beijing: Standards Press of China, 2014.
[17] CHAMPAIGNE J. Almen strip specifications[J]. The Shot Peener, 1997, 11(3): 6-13.
[18] ZHANG X J, WANG T, WANG J B, et al. Analytical modeling of shot peen forming process using cross-sectional linear indentation coverage method[J]. International Journal of Mechanical Sciences, 2017, 133: 838-845.
[19] MARCINIAK Z, DUNCAN J L, HU S J. Mechanics of Sheet Metal Forming[M]. 2nd ed. Oxford: Butterworth-Heinemann, 2002:86-87.