| 航空制造技术 第68卷 第3期 76-82 2025-02-01 出版 | Aeronautical Manufacturing Techinology, Vol.68, No.3: 76-82 |
| DOI: 10.16080/j.issn1671-833x.2025.03.076 |
论坛 >> 高性能特种陶瓷(FORUM >> High-Performance Special Ceramics)
大尺寸空心涡轮叶片一体化陶瓷铸型冷冻干燥应力仿真分析
2.长安大学工程机械学院,西安 710064
3.中国船舶集团有限公司第七〇三研究所,哈尔滨 150007
[摘要] 大尺寸空心涡轮叶片一体化陶瓷铸型在冷冻干燥过程中容易产生裂纹,针对该问题进行了铸型应力分布规律的研究。通过有限元仿真建立了铸型收缩受阻产生应力的理论模型,分析了不同冻干收缩率、铸型壁厚和曲率对铸型冷冻干燥应力的影响,采用变壁厚对铸型尾缘进行了结构优化。研究发现,在冷冻干燥过程中,一体化陶瓷铸型所受应力随着收缩率增大而线性增大,且铸型尾缘曲率最大处承受的应力最大。通过尾缘变壁厚的结构优化设计增大了尾缘处铸型冷冻干燥过程中的抗弯强度,当试样厚度从4 mm增至7 mm时,坯体平均强度从8.32 MPa提升至11.81 MPa。本研究制备了结构完整的一体化陶瓷铸型并进行浇铸验证,得到了陶瓷铸型冷冻干燥的应力分布规律,并提出了尾缘变壁厚结构优化设计的方法,成功解决了一体化陶瓷铸型冷冻干燥过程中产生裂纹的问题。
关键词:空心涡轮叶片;一体化铸型;冷冻干燥;变壁厚;应力
Simulation Analysis of Freeze-Drying Stress in Integrated Ceramic Casting Mold of Large-Sized Hollow Turbine Blade
2.School of Construction Machinery, Chang’an University, Xi’an 710064, China
3.No. 703 Research Institute, China State Shipbuilding Corporation Limited, Harbin 150007, China
[ABSTRACT] This study focuses on the problem of cracks generated during freeze-drying in the integrated ceramic casting mold of large-sized hollow turbine blade, and studies the stress distribution law of the casting mold. A theoretical model of stress generated by mold shrinkage obstruction was established through finite element simulation. Effects of various freeze-drying shrinkage rates, mold wall thicknesses, and curvatures on mold freeze-drying stress were analyzed. Structural optimization was carried out on trailing edge of the mold using variable wall thickness. It is found that during the freeze-drying process of integrated casting, the stress increases linearly with increase of shrinkage rate, and the stress is the highest at the position with the maximum curvature of the mold trailing edge. By increasing wall thickness at the trailing edge, bending strength of the mold during freeze-drying process is enhanced. When sample thickness increases from 4 mm to 7 mm, average strength of the base substrate increases from 8.32 MPa to 11.81 MPa. The integrated mold with structural integrity is successfully manufactured and verified by casting in this study, stress distribution law of ceramic casting mold and various wall thickness of trailing edge are obtained and proposed, which help to solve the issue of cracks generated during freeze drying for integrated ceramic casting mold.
Keywords: Hollow turbine blade; Integrated casting mold; Freeze drying; Variable thickness; Stress
引文格式:刘岩, 周子明, 艾子超, 等. 大尺寸空心涡轮叶片一体化陶瓷铸型冷冻干燥应力仿真分析[J]. 航空制造技术, 2025, 68(3): 76–82.
LIU Yan, ZHOU Ziming, AI Zichao, et al. Simulation analysis of freeze-drying stress in integrated ceramic casting mold of large-sized hollow turbine blade[J]. Aeronautical Manufacturing Technology, 2025, 68(3): 76–82.
通信作者:鲁中良,教授,研究方向为航机/燃机关键热端零部件设计和增材制造技术。
基金项目:国家科技重大专项(J2019–Ⅱ–0018–0039)。
涡轮叶片是工业燃气轮机和航空发动机中涡轮段的热端关键部件。在发动机的工作过程中,涡轮叶片需要承受高温、高压的高速气流冲击,工作环境极为恶劣[1–3],其失效故障将严重影响燃气轮机和航空发动机的工作可靠性[4]。涡轮叶片的研制是制约我国热端动力装备发展的关键,要想提高航空发动机和燃气轮机的热力循环效率和推重比,必须提高涡轮的进口温度,这是两机装备设计时极为关键的技术要点。随着叶片冷却技术的发展,其冷却系统也越来越复杂,这对涡轮叶片的制造提出了更高的要求。西安交通大学将目前增材制造(AM)技术中成形精度最高的光固化成型(Stereo lithography,SL)技术和凝胶注模技术相结合,提出了型芯/型壳一体化的涡轮叶片快速制造技术,并将冷冻干燥技术成功应用于涡轮叶片一体化陶瓷铸型坯体的干燥,在脱除陶瓷铸型水分的同时,较大程度上保证了铸型的完整性[5]。
冷冻干燥技术可在低温下将待干燥物料的水分以升华的形式去除,干燥后的产品质量好,最大程度上保留了产品的原有特性,因此广泛应用于食品和制药领域[6–7]。在陶瓷材料方面,冷冻干燥技术主要用于多孔陶瓷的制备,在相同气孔率条件下,通过冷冻干燥制备的多孔陶瓷具有更优异的机械性能[8–10]。该技术从原理上降低了待干燥物料产生干燥缺陷的概率,然而在铸型制备阶段经常发现,凝胶注模后的坯体结构完整,冷冻干燥后却产生了型芯断裂、型壳开裂等缺陷,这些缺陷会在后续的工艺中延展甚至变大,导致叶片制造流程终止。
目前,仅有少量研究涉及冷冻干燥物料的开裂问题,如英国剑桥大学的Zhai等[11]在柠檬酸盐缓冲剂块的冷冻干燥过程中发现,当物料温度高于冰晶融化点温度时,缓冲剂块发生了开裂,而物料温度低于冰晶融化点温度时,缓冲剂块不发生开裂。西安交通大学吴海华等[12]首次应用冷冻干燥技术脱除一体化铸型中的水分,初步确定了冻干工艺,总结了铸型坯体的冻干收缩规律,建立了气膜孔坯体收缩受阻模型,但是该模型仅适用于分析气膜孔型芯的开裂问题。刘飞等[13]发现凝胶注模成型的陶瓷坯体在干燥失水率为20%~60%时易产生裂纹,并通过降低隔板温度和设计坯体穿孔结构避免冻干裂纹的产生,但未能从根本上解决铸型的冷冻干燥开裂问题。庞师坤[14]测试了陶瓷铸型冷冻及干燥过程中的应变和弹性模量,发现铸型冷冻和干燥过程中的应力远小于铸型冷冻坯体和干燥坯体的强度,即坯体收缩或膨胀引起的宏观干燥内应力不会导致裂纹的产生,但该研究未针对裂纹的产生进行深入探讨,也未能揭示裂纹形成机理和制定冻干裂纹的控制工艺。Tian等[15]针对冷冻干燥过程中铸型坯体内部的裂纹缺陷进行研究,揭示了裂纹形成机理,制定了冻干裂纹控制工艺,但其试验对象为柱状陶瓷坯体,未能描述一体化陶瓷铸型在干燥过程中收缩受SL树脂原型阻碍的作用机理。Pinches等[16]提出了不同冻干速率下陶瓷冻干裂纹形成的机理模型,发现裂纹虽然形成于干燥阶段,但是冻结速率会影响裂纹的形成,慢速冷冻可以最大限度地减少干燥阶段的裂纹,但该冷冻干燥开裂机理模型并不适用于凝胶注模成型的陶瓷铸型。
对于陶瓷坯体的干燥开裂问题,国内外主流观点认为,干燥过程中坯体收缩不均导致的内应力是引起坯体变形和开裂的主要原因[17]。而冷冻干燥过程中水分脱除较为均匀,从根本上降低了干燥收缩不均造成的不利影响,但一体式陶瓷铸型的冷冻干燥阶段仍不时出现铸型开裂的问题。目前国内外鲜有针对凝胶注模成型陶瓷铸型冻干裂纹的研究,现有的技术和理论不能完全解决实际制造过程中的问题。因此,本文基于凝胶注模快速成型的型芯/型壳一体化陶瓷铸型技术,对大尺寸一体化陶瓷铸型在冷冻干燥过程中的收缩率、曲率及铸型所受应力进行了分析,并对铸型结构进行了变壁厚优化,确保陶瓷铸型在冷冻干燥完成后完整、无裂纹。
1
1.1
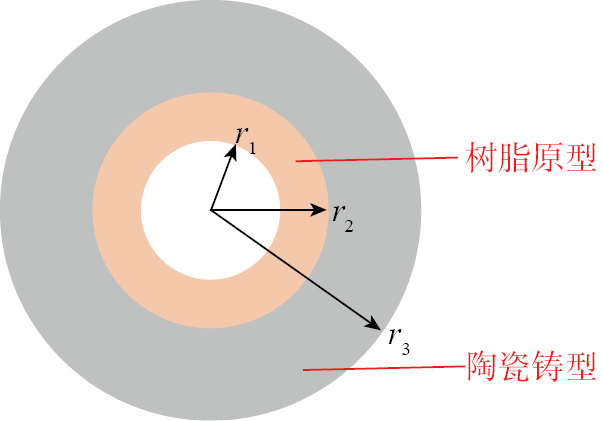
在一体化陶瓷铸型的制造过程中,树脂原型与陶瓷铸型间的相互作用可以简化为两个圆环间的作用,其中内部圆环为树脂原型,外部圆环为陶瓷铸型,位置关系如图1所示。假设上述两种材料只发生弹性形变,且沿轴向的弹性形变不受限制;树脂原型内径为r1,外径为r2,陶瓷铸型内径(即树脂原型的外径)也为r2,外径为r3。

图1
Fig.1
圆环模型中,两种不同热膨胀系数的材料因升温过程膨胀不一致而导致的径向相对变形[18]为
| (1) |
式中,δ为径向相对变形量;ΔT为相对于初始温度的升温温差;α1为树脂原型的热膨胀系数;α2为陶瓷铸型的热膨胀系数。
将该模型应用到冷冻干燥过程中,忽略树脂在干燥过程中的细微变形,则干燥过程中树脂原型与陶瓷铸型收缩不一致造成的径向相对变形δ′可用收缩率η表示,即
| (2) |
根据弹性力学中平面应力问题的解法[19],δ′引起的树脂原型与陶瓷铸型接触面上的压强为
| (3) |
式中,P为树脂原型与陶瓷铸型接触面上的压强;E1为树脂原型的弹性模量;E2为陶瓷铸型的弹性模量;λ1为树脂原型的泊松比;λ2为陶瓷铸型的泊松比。
因此陶瓷铸型受到的应力为
| (4) |
| (5) |
式中,σr为径向应力;σθ为周向应力。
由上述分析可知,影响陶瓷铸型冷冻干燥应力的主要因素有陶瓷铸型的收缩率、树脂原型和陶瓷铸型的弹性模量、树脂原型和陶瓷铸型的壁厚。其中,铸型的收缩率可通过冻干工艺的优化和材料配方的设计进行调控,但陶瓷铸型的冻干收缩无法完全避免;树脂原型和陶瓷铸型的弹性模量由材料本身属性决定,也难以进行调控。因此有必要对铸型的结构进行优化设计,从而降低陶瓷铸型受到的径向和周向应力。
1.2
选取某型号双层叶片陶瓷铸型作为研究对象进行仿真分析,双层叶片的上层小叶片为空心叶片,下层大叶片为实心叶片,双层叶片及其陶瓷铸型的三维模型如图2所示。
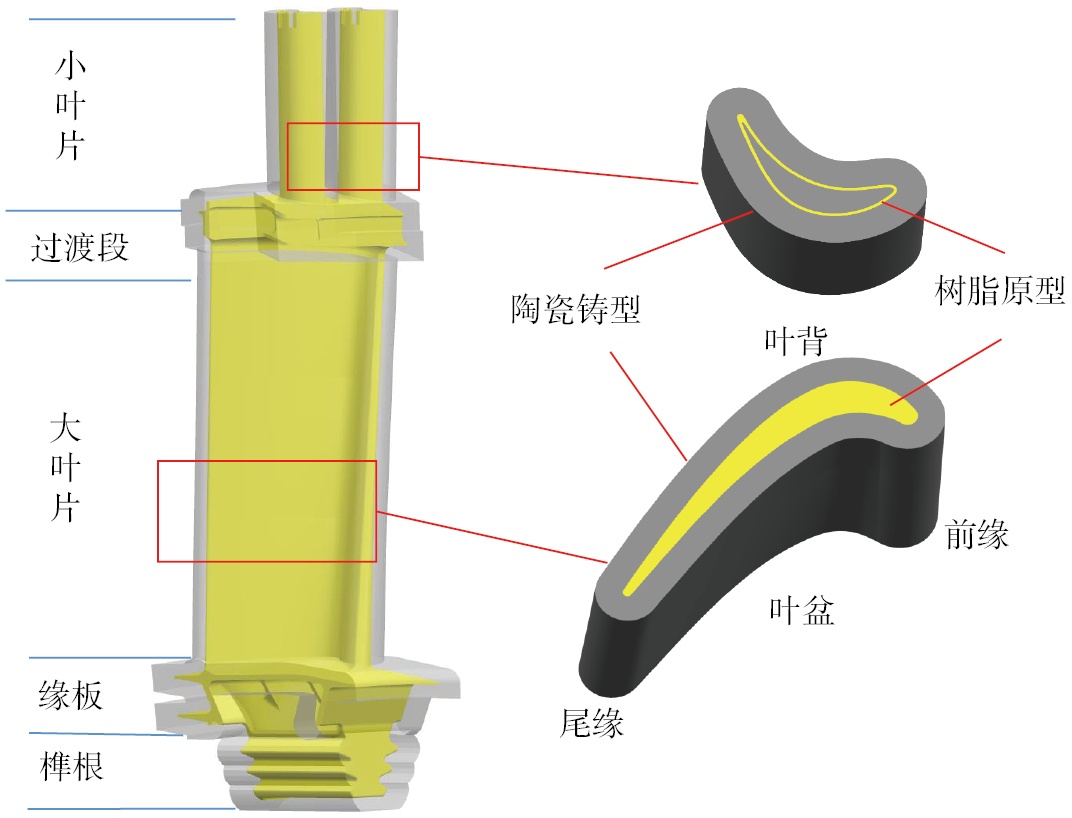
图2
Fig.2
采用ANSYS Workbench自带的网格划分平台(Mesh)进行网格划分,并根据计算需要对关键区域进行网格加密,降低网格划分难度的同时保证了计算精度。在模型网格划分中,对树脂原型和陶瓷铸型的接触面进行局部网格细化以提高运算精度,划分后的网格共有1780032个节点和1187760个网格单元。采用Mesh自带的网格质量度量指标对网格进行质量分析,测得平均网格质量为0.80739,大于0.8,满足有限元分析的要求。
1.3
采用ANSYS Workbench为计算平台进行稳态热力耦合分析。通过试验测算并结合光敏树脂原料的出厂参数,在材料库中定义陶瓷铸型和光敏树脂的材料属性,主要性能参数如表1所示。
表1
Table 1
| 材料 | 杨氏模量E/MPa | 导热系数K/(W·m–1·K–1) | 比热容C/(J·kg–1·K–1) | 密度ρ/(g·cm–3) |
|---|---|---|---|---|
| 树脂 | 2399 | 0.132 | 1050 | 1.12 |
| 陶瓷 | 1050 | 2.358 | 784 | 2.3 |
2
对陶瓷铸型的整体结构进行求解分析,得到壁厚6 mm一体化陶瓷铸型所受的Von–Mises应力,如图3所示。可以看出,大叶片叶身与下缘板连接处应力高达12.987 MPa;大叶片叶身尾缘处所受应力较大,其次是前缘部分,叶盆和叶背处所受应力较小;小叶片处所受应力小于大叶片,这是因为小叶片为空心叶片,内部型芯的收缩一定程度上引起了与其粘连的树脂原型收缩,降低了外部型壳收缩所受到的阻力。

图3
Fig.3
从应力的总体分布情况来看,仅有叶身与缘板连接处等少数几个部位的应力较大处出现在外型面,大部分应力集中出现在铸型内型面,且大叶片叶身所受应力大于小叶片叶身。双层叶片陶瓷铸型的应力仿真结果与实际冷冻干燥的开裂情况较为一致:裂纹出现在铸型内部并向外扩展,铸型尾缘处的开裂概率较大。从叶身处铸型的应力仿真结果及冷冻干燥过程中陶瓷铸型开裂的位置来看,铸型所受应力与相应部位的曲率有较强的关联性,尾缘曲率最大处最容易产生冻干裂纹。
选取均匀壁厚的大叶片叶身处陶瓷铸型的某截面进行平面仿真,分析变曲率结构对应力的影响。从图4(a)的仿真结果来看,应力最大点出现在铸型内侧的尾缘上。通过UG自带的曲率梳分析工具对铸型内型面曲率进行分析,得到内型面的曲率极点(图4(b))。将曲率最大点的坐标与应力最大点的坐标进行对比,发现二者几乎重合。
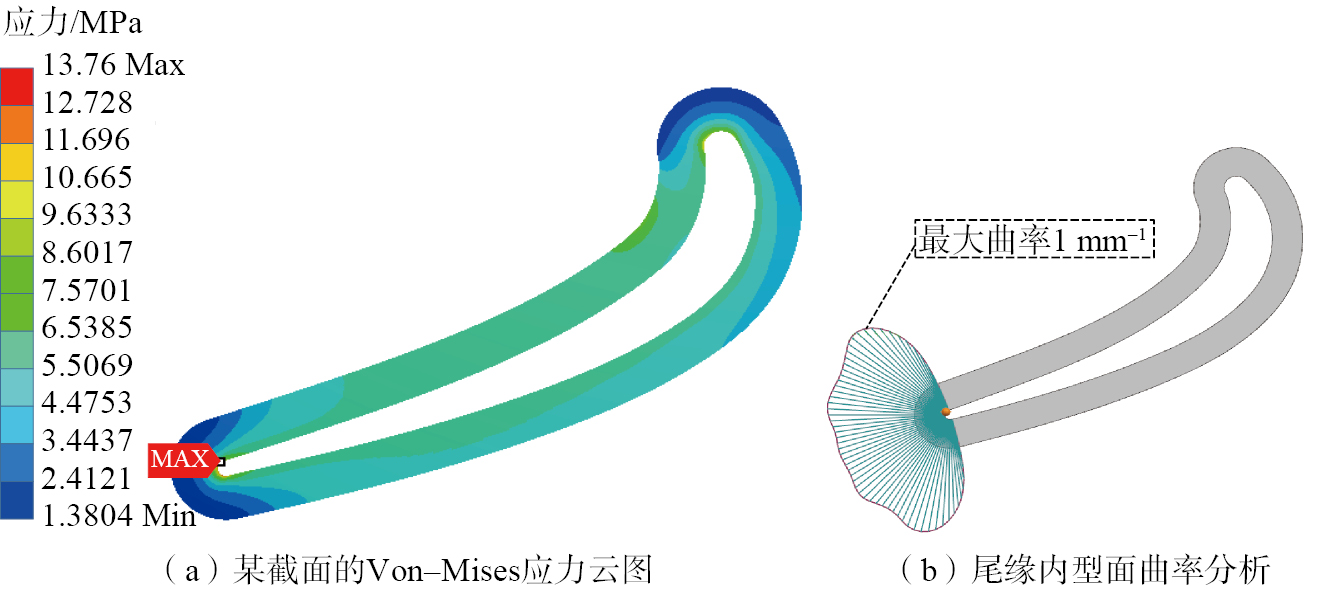
图4
Fig.4
进一步分析图4(a)可知,陶瓷铸型内型面的前缘和尾缘处所受应力较大,有较明显的应力集中,在型面曲率极点处尤为明显。在曲率变化较为均匀的叶盆和叶背处,应力过渡均匀,且远小于前缘和尾缘。陶瓷铸型外型面所受应力情况则恰好相反,前缘和尾缘处的应力很小,大部分应力被内型面的曲率较大处,特别是曲率极点处所承担。
2.1
为避免支撑设计造成的应力集中和人为选点造成的数值误差,截取陶瓷铸型中部的6个等距截面,通过软件读取不同收缩率下每个截面的应力最大值,得到陶瓷铸型冻干收缩率与最大应力的关系,如图5所示。
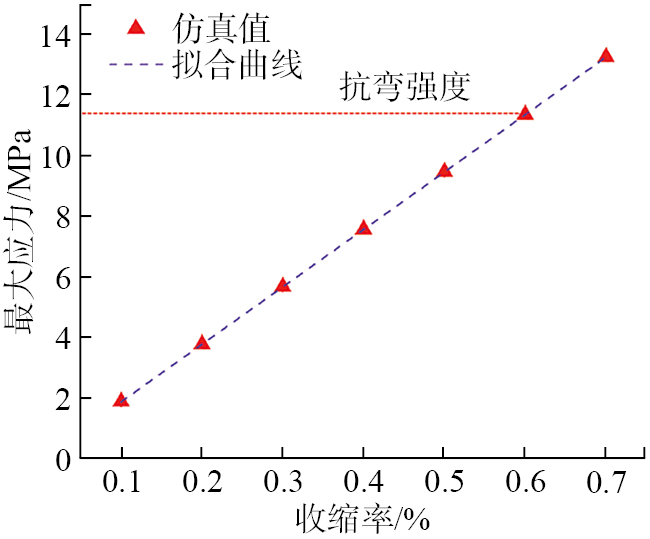
图5
Fig.5
可以看出,随着陶瓷铸型冻干收缩率的增大,其本身所受的最大应力也增大,最大应力随冻干收缩率的变化几乎呈线性。对于选定的壁厚6 mm陶瓷铸型,冻干收缩率每增加0.1%,最大应力增大1.89 MPa。当收缩率增大至0.6%时,最大应力为11.36 MPa,略大于陶瓷铸型的抗弯强度。因此壁厚6 mm陶瓷铸型的冻干收缩率不应超过0.6%,否则,在不对铸型进行任何结构优化的前提下,冷冻干燥期间铸型将产生裂纹缺陷。
2.2
对截取的带树脂原型的大叶片叶身处陶瓷铸型进行有限元分析,改变铸型壁厚得到不同壁厚铸型所受的Von–Mises应力云图(图6)。铸型的前缘和尾缘在冷冻干燥过程中受到的应力较大,其中尾缘曲率最大处所受应力最大,前缘曲率较大处也承受了较大的应力。陶瓷铸型前缘和尾缘的应力主要集中在内型面,外型面所受应力很小,而叶盆和叶背处所受的应力则比较均匀。随着壁厚从5 mm增至8 mm,铸型内腔受到的最大应力分别为10.09 MPa、10.39 MPa、10.66 MPa、10.45 MPa,未发生明显波动,说明铸型所受应力大小主要与叶片本身结构有关,与铸型整体设计厚度无明显关系。
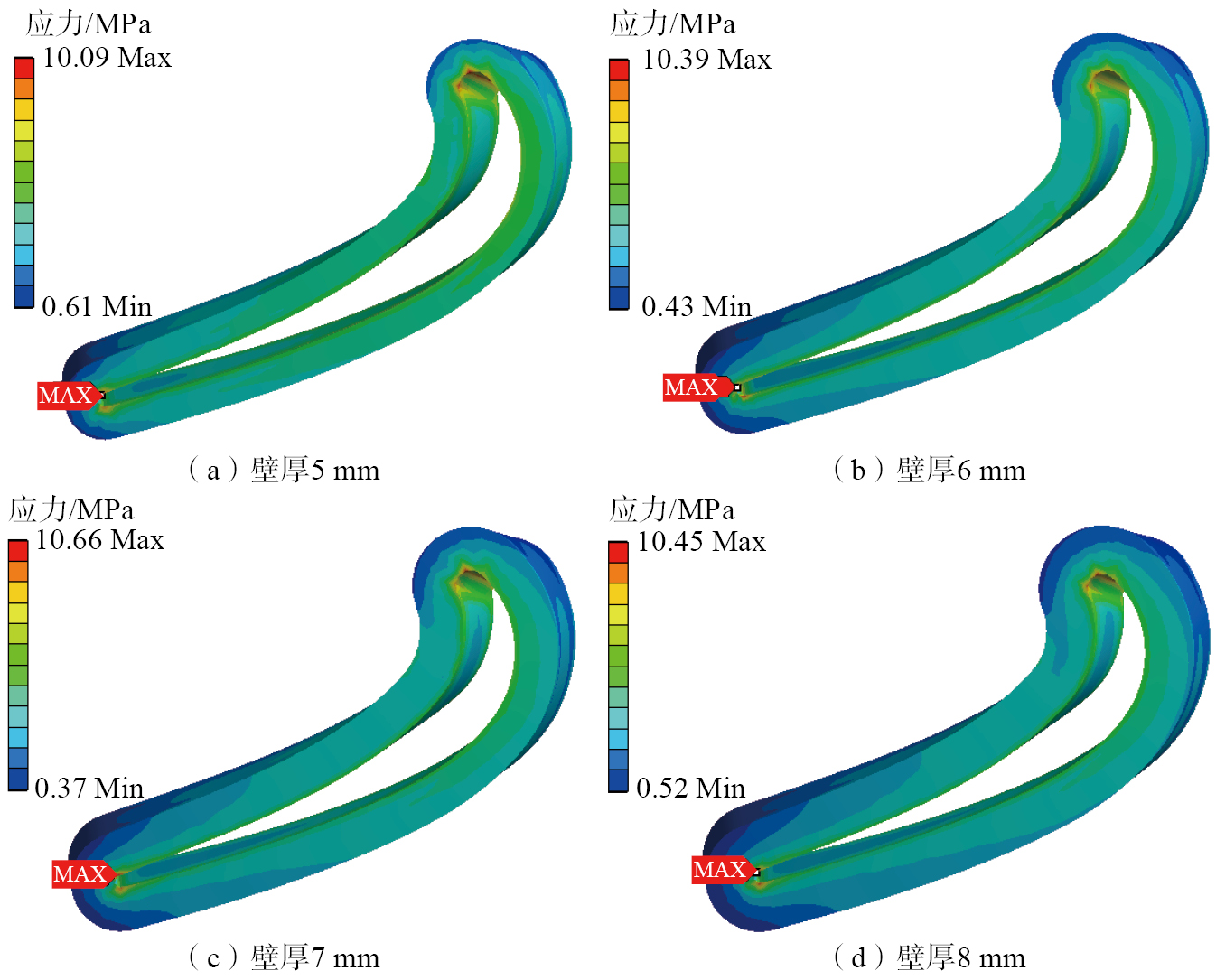
图6
Fig.6
根据涡轮叶片叶身处的型面曲率,设计不同外型面曲率的陶瓷铸型柱状坯体(带树脂原型,壁厚6 mm),探究变曲率结构铸型与均匀曲率铸型在相同条件下所受应力的差别。如图7(a)~(f)所示,柱状坯体的应力分布呈环状,由外环向内环不断增大,陶瓷铸型与树脂原型的接触面上应力最大。随着曲率的减小,陶瓷铸型所受最大应力减小,陶瓷铸型所受最小应力有所增大,应力分布更均匀。
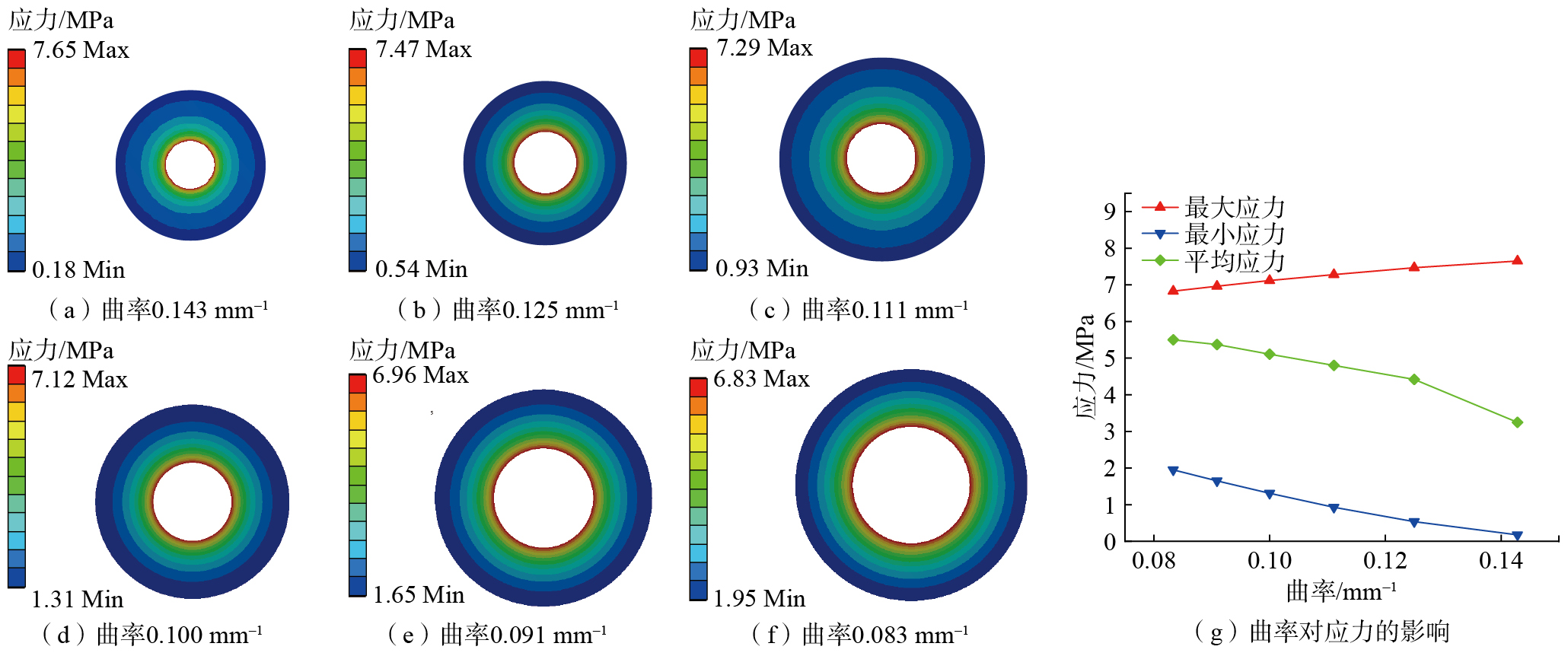
图7
Fig.7
图7(g)为曲率与应力的关系图。可以看出,增大曲率会增加铸型承受的最大应力,而平均应力和最小应力的变化趋势则恰好相反。随着曲率的增加,平均应力和最小应力有所降低,当曲率较大时,平均应力的降低尤为明显。减小曲率对最大应力的降低效果比较有限,但显著提高了应力分布的均匀性。
图3中陶瓷铸型内外型面的最大曲率与图7(a)中的设定一致,但前者的最大应力10.111 MPa远大于后者的7.65 MPa,说明涡轮叶片叶身的变曲率结构会造成相应陶瓷铸型在冷冻干燥过程中的应力集中,导致变曲率陶瓷铸型最大曲率处的应力高于相应均匀曲率下陶瓷铸型所受的应力。
基于以上仿真结果可知,陶瓷铸型叶身部位的曲率最大处承受了最大的应力。陶瓷铸型冷冻干燥过程中尾缘的最大应力不仅与此处曲率最大有关,还源于应力会从曲率较小处向曲率较大处集中。
2.3
对大叶片叶身铸型尾缘部位进行变壁厚设计优化,一般情况下,陶瓷铸型壁厚为5~7 mm即可满足涡轮叶片的铸造散热性能要求,因此在变壁厚设计时,叶盆、叶背最薄处壁厚不低于5 mm,尾缘最大壁厚不超过7 mm。
对设计好的变壁厚大叶片叶身陶瓷铸型进行求解分析,得到尾缘变壁厚铸型的Von–Mises应力云图,如图8所示。截取铸型内部6个等距截面,统计各截面的应力最大值,得到铸型尾缘变壁厚设计与应力的关系(图9)。当尾缘壁厚从5.5 mm增至7 mm,铸型最大应力均产生于尾缘处,且应力大小无明显变化,保持在10 MPa左右,说明铸型所受应力主要与其曲率及冷冻干燥过程中的收缩率有关,增加铸型型壳的厚度不会导致铸型所受应力增大,因此可适当提高铸型型壳厚度以提升其强度。
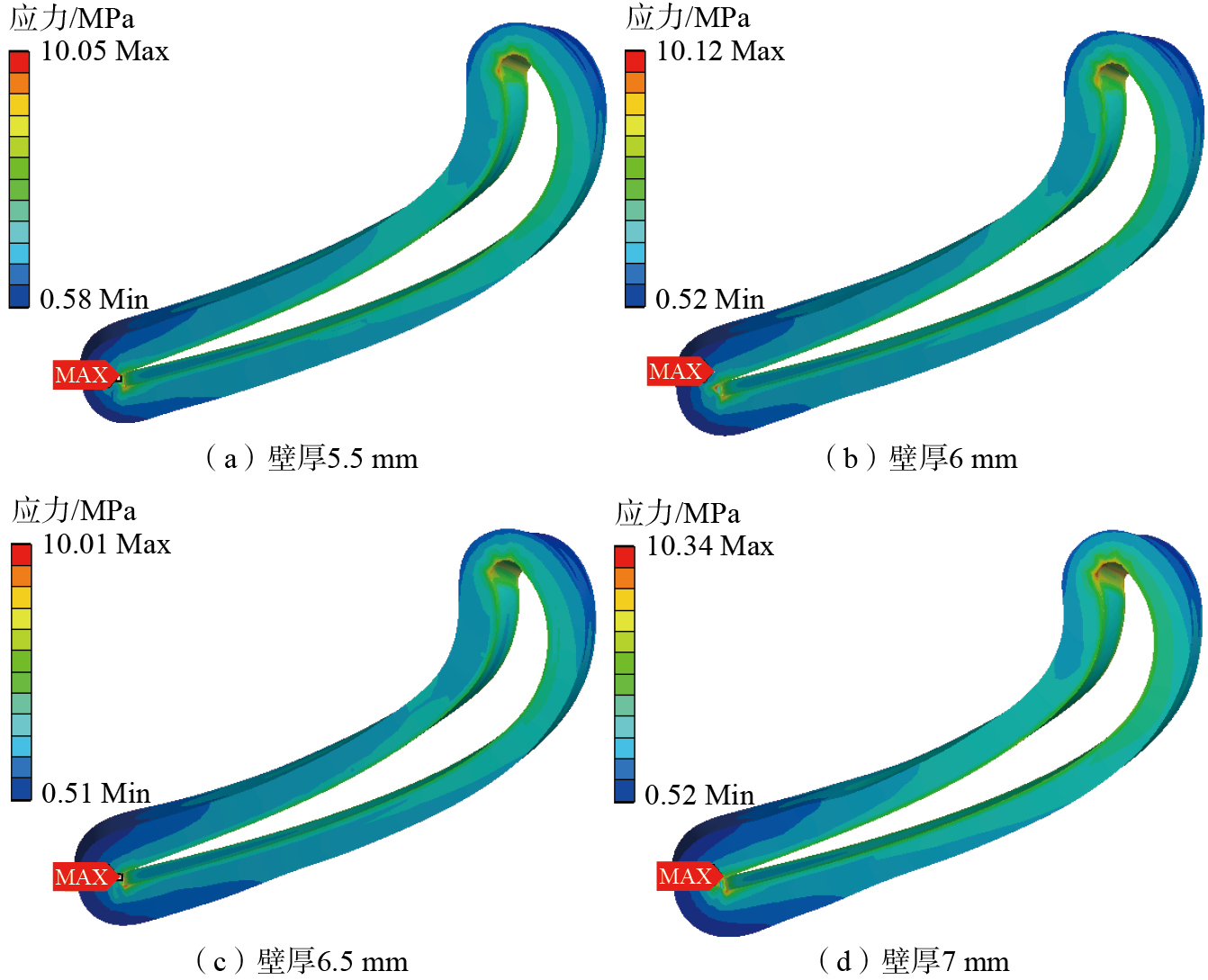
图8
Fig.8
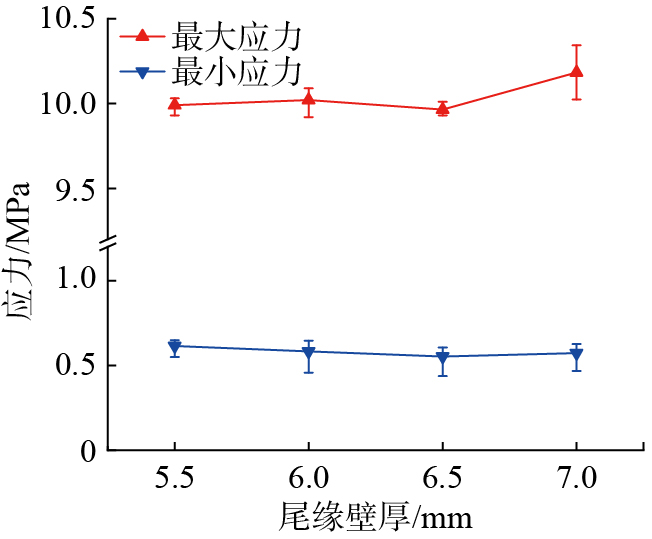
图9
Fig.9
为分析尾缘变壁厚设计对铸型抗弯强度的影响,分别制备不同尾缘厚度的坯体试样进行抗弯测试试验,结果如图10所示。可以看出,试样抗弯强度随尾缘厚度的增大而增大,当尾缘厚度从4 mm增至7 mm,坯体的抗弯强度由8.32 MPa提升至11.81 MPa。当尾缘厚度为6 mm时,坯体抗弯强度大于叶片尾缘处的最大应力(10.12 MPa)。因此,可以将尾缘处的局部型壳加厚至6 mm以防止尾缘部分的型壳开裂。
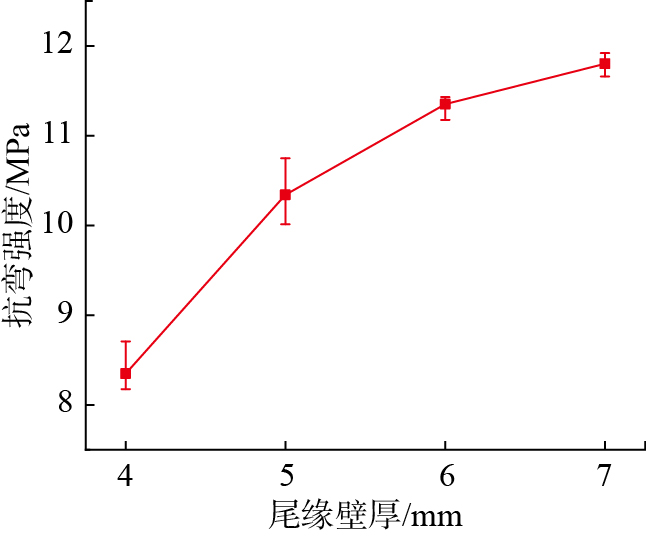
图10
Fig.10
虽然变壁厚设计不能降低陶瓷铸型承受的最大应力,但该设计方法可以提升危险区域的强度。对于部分区域最大应力超过其抗弯强度的铸型,采用变壁厚设计可以解决铸型产生冻干裂纹缺陷的问题。
2.4
根据仿真计算结果,采用变壁厚结构优化设计,将铸型尾缘壁厚设计为6 mm,对外壳的尖角位置倒2.5 mm圆角,使一体式陶瓷铸型所受应力小于其抗弯强度。采用凝胶注模工艺制备一体化铸型,待铸型完全固化后进行冷冻干燥,冷冻温度为–40 ℃,干燥期间隔板温度为–3.5 ℃,真空度为1~10 Pa。冷冻干燥后的陶瓷铸型结构完整,无开裂迹象。将冷冻干燥后的陶瓷素胚脱脂烧结并进行高温合金浇铸验证,得到的金属叶片尾缘处无残余飞边,说明所制备的变壁厚陶瓷铸型在冷冻干燥及后续处理过程中均未出现开裂问题,成功验证了变壁厚优化设计方法的可行性。试验所制备的陶瓷铸型和金属叶片如图11所示。

图11
Fig.11
3
基于铸型收缩受阻理论,通过ANSYS Workbench对某型号双层涡轮叶片的大尺寸一体化陶瓷铸型的冷冻干燥过程进行应力分析,得到了应力分布规律并采用变壁厚结构优化的方法进行了试验验证,主要结论如下。
(1)铸型在冷冻干燥过程中产生的应力主要与铸型的冻干收缩率有关,冻干收缩率每增加0.1%,铸型所受最大应力增加1.89 MPa。
(2)陶瓷铸型大叶片叶身尾缘处所受应力最大,最大值出现在内型面曲率最大处。此处应力值最大不仅与“曲率越大应力越大”的规律有关,还因为应力会从曲率较小处向曲率较大处集中。变曲率结构曲率最大处所受的应力(10.111 MPa)是对应均匀曲率下柱状铸型所受应力(7.65 MPa)的1.32倍。
(3)通过对铸型尾缘进行局部加厚的变壁厚设计方法,可以在几乎不提高铸型所受应力的情况下提高铸型的局部强度。当铸型尾缘壁厚从4 mm增至7 mm,坯体抗弯强度由8.32 MPa提升至11.81 MPa。浇铸试验发现,铸型在冷冻干燥过程中不产生裂纹。本文所提尾缘变壁厚的设计方法可以有效解决一体化铸型在冷冻干燥过程中产生裂纹的问题。
 刘岩 博士研究生,研究方向为空心涡轮叶片型芯/型壳一体化铸型。
刘岩 博士研究生,研究方向为空心涡轮叶片型芯/型壳一体化铸型。
参考文献