减重增推是发动机不断追求的目标,航空发动机常用的镍基高温合金密度在8.24 g/cm3 左右,而钛基高温合金密度在4.52 g/cm3 左右,长纤维增强钛基复合材料(Titanium matrix composites,TMCs)的密度更低,因此使用钛基复合材料替代镍基合金等传统材料是实现发动机轻量化、提高推重比的有效途径。据报道,在相同服役条件下,使用连续SiC 纤维 (长纤维)增强的钛基复合材料制备的部件相较于传统材料制备的部件减重在50%以上[1–4]。将SiC 纤维作为增强相的长纤维增强TMCs 还具有高比强度、高比模量的优势,与镍基合金相比,长纤维增强TMCs 在500~1000 ℃温度区间内的抗蠕变能力和比疲劳强度同样有明显优势[5]。由于上述诸多良好性能,连续SiC 纤维增强的TMCs 在航空航天领域具有广泛的应用前景,美国怀特实验室及美国空军就将连续SiC 纤维增强钛基复合材料应用于宇航飞机和先进战斗机的涡轮部件,国内使用该材料试制了航空发动机压气机的叶环[6–7]。
连续SiC 纤维增强钛基复合材料的制备工艺流程是,钨芯CVD 制作SiC 纤维→CVD 或PVD 制备涂层→PVD 制成先驱丝→缠绕或铺放制成预制体→HIP 或VHP 制备毛坯件,其中预成型体的致密化过程对复合材料的使用性能有着重要作用[8]。因异种材料的热匹配差异,致密化过程中产生较大的热残余应力,影响材料的缺陷控制、疲劳性能、断裂强度等一系列性能[9–10]。黄浩等[11]利用拉曼光谱测定了SiCf /Ti17 中的热残余应力,其中基体的轴向残余拉应力为701.3 MPa。在SiCf /Ti 复合材料体系下的热残余应力相关报道表明,复合材料的热残余应力能达到基体材料拉伸强度的30%~80%[12]。此外,复合材料在复杂工况下发生的热机械疲劳 (Thermal mechanical fatigue,TMF)同样会受到热残余应力的影响。在TMF 过程中,热残余应力与机械载荷的叠加会影响纤维和基体对加载载荷的响应[13]。因此,复合材料热压致密化过程中应力形成与分布特征是国内外研究人员重点关注内容之一。
相较于试验研究方法,有限元模拟方法在系统评价复合材料残余应力和致密度等方面更经济和方便,尤其可以对界面层附近复杂的应力状态进行分析描述,数值模拟分析逐渐成为研究复合材料的重要手段。在复合材料细观研究中,常用的模型包括同心圆柱模型、桥连模型、代表性体积单元 (RVE)模型等,其中RVE 模型由于可根据工况灵活设置纤维排列方式、部件间的约束、边界条件和工艺参数等,得到了广泛的应用。姚泉等[14]使用ABAQUS 建立了长纤维增强TMCs 的无界面层的RVE 模型,并根据致密度随时间的变化规律,将复合材料致密化过程分为缓慢致密化阶段、加速致密化阶段、快速致密化阶段和减速致密化阶段。在复合材料RVE 模型中,无界面层的RVE 模型仅有纤维和基体两种成分,这种模型主要用于研究复合材料在高温高压状态下的变形过程;有界面层的RVE 模型主要用于表征复合材料在降温降压状态受温度变化影响而产生的热应力,但这种模型是致密化完成后的模型,没有塑性变形的过程[15]。为了适应快速、准确及多参数影响研究的需要,建立考虑界面层的RVE 模型,研究在整个热压过程中HIP 工艺对应力分布的影响。本文利用ABAQUS仿真软件建立了基于界面特征的有限元模型,分析了SiCf /Ti60 复合材料的应力分布规律,并研究了界面层厚度和HIP 温度对应力分布的影响,模拟分析结果为TMCs 的先驱丝制备、HIP 工艺设计等提供技术依据。
1 有限元模型的建立
在SiCf /Ti60 复合材料制备过程中,首先在钨芯SiC纤维表面沉积C 涂层,之后再沉积Ti60 基体,涂层会促进纤维和基体间的结合。扫描电镜 (SEM)观察结果如图1 所示,存在两个界面层,能谱分析结果表明,靠近纤维的界面层成分是C,厚度约为1.7 μm,靠近基体的界面层成分是TiC,厚度约为1.3 μm,与其他研究者的分析结果相符合[16–17]。
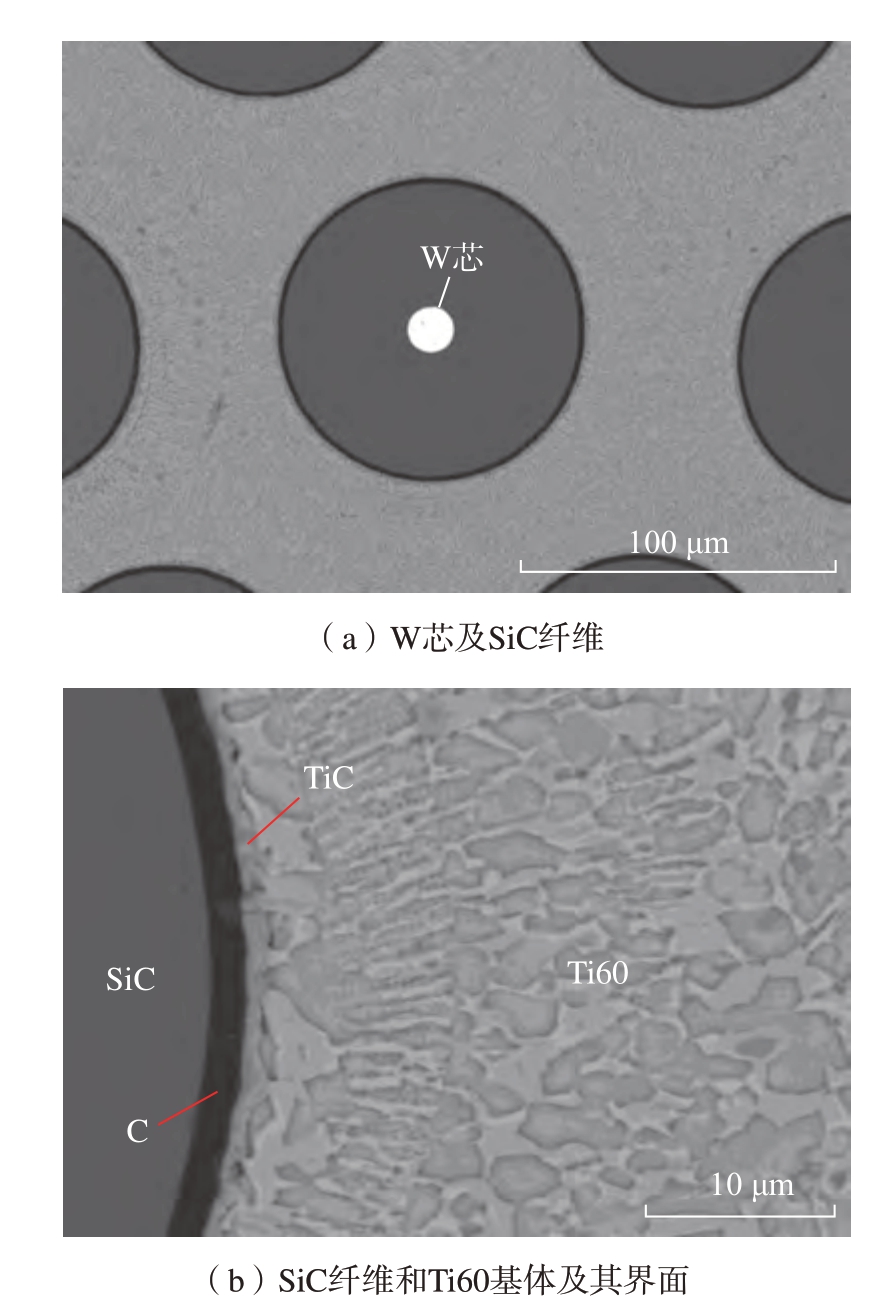
图1 SiC/Ti60 复合材料的微观形貌
Fig.1 Micromorphology of SiC/Ti60 composites materials
考虑到连续SiC 纤维增强的Ti 基复合材料在纤维方向上的尺寸 (即轴向尺寸)远大于截面上的尺寸,变形过程可视为平面应变状态,因此可将复合材料三维变形模型简化为截面上的二维模型。由于SiC 纤维中心的W 芯对复合材料力学性能的影响很小,因此在建模过程中将SiC 纤维视为整体进行仿真,另外SiC、C、TiC和Ti60 之间均视为完美结合。本文选取预制体中先驱丝的堆垛排布方式为六方排布,建立RVE 模型进行研究,如图2 所示。
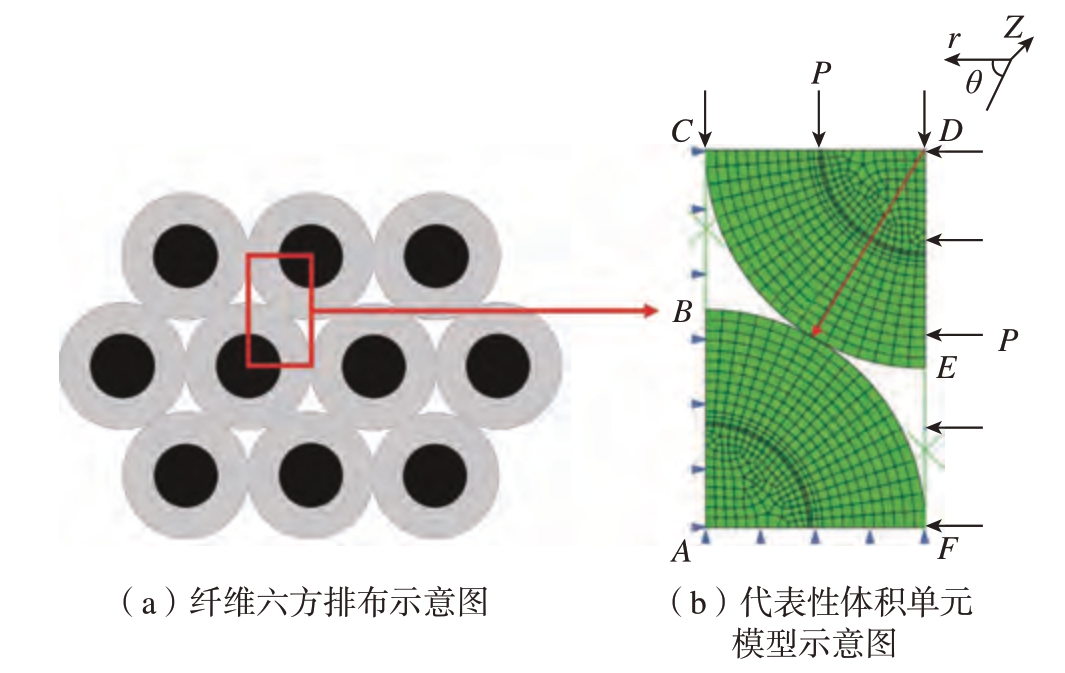
图2 SiCf /Ti60 复合材料模型结构图
Fig.2 Structural diagram of SiCf /Ti60 composites material model
建立六方RVE 仿真模型 (图2(b)),定义各区域组分从内向外分别为SiC、C、TiC、Ti60,厚度分别设置为50 μm、1.7 μm、1.3 μm 和50 μm,模型中的纤维体积分数为25%。在AC 边和AF 边上施加固定约束,通过耦合约束将CD 边的y 方向自由度和DF 边的x 方向自由度约束到点D。BC 和EF 两个刚性边界与先驱丝之间设置无摩擦条件,两个先驱丝之间则设置常摩擦条件,摩擦系数为0.8。在BF 和CE 圆弧边上 (即先驱丝表面)施加温度载荷,在CD 边和DF 边上施加压强载荷P,温度和压强按图3 中的HIP 工艺曲线变化。根据工艺曲线变化特点,在HIP 过程中选择6 个特征时刻进行分析:升温升压阶段中段7200 s、保温保压阶段开始14400 s、保温保压阶段中段19800 s、保温保压阶段结束25200 s、降温降压阶段拐点32400 s 和降温降压阶段结束68400 s。以图2(b)上方先驱丝中心为起点,在模型的60°方向设置预定路径,在后处理步骤中提取应力数据。
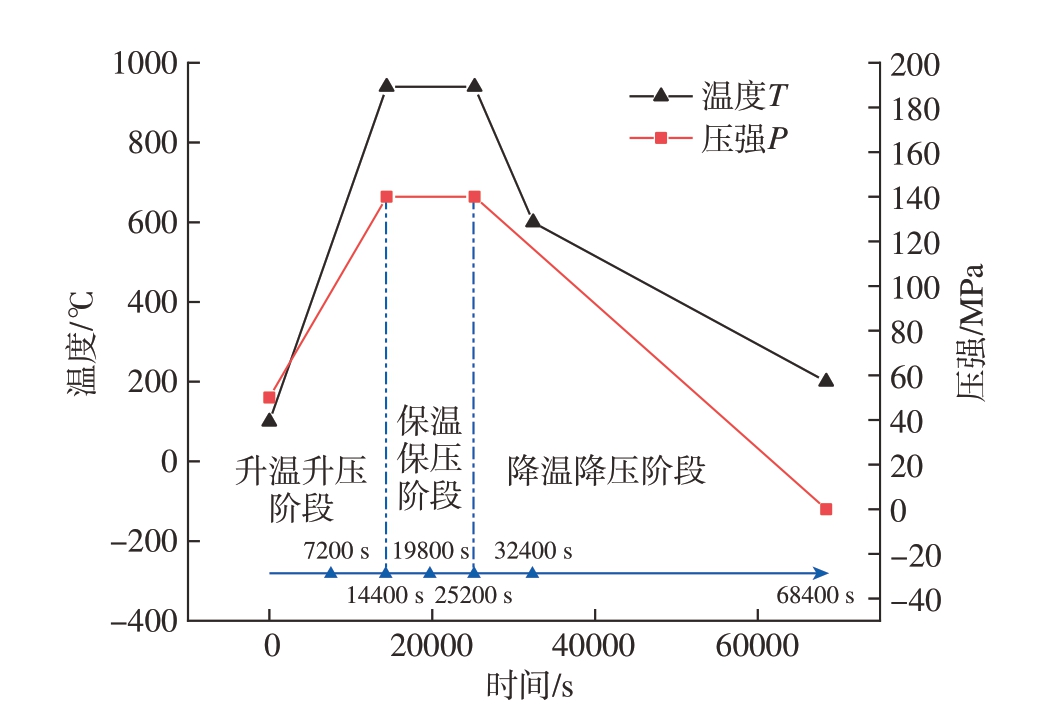
图3 热等静压工艺过程中的温度和压力变化曲线
Fig.3 Temperature and pressure curves during hot isostatic pressing process
复合材料HIP 制备过程中变形温度范围为600~980℃,Ti60 合金不同温度下的压缩真应力–真应变数据来自参考文献[18],根据该数据在ABAQUS 中建立Ti60合金的塑性参数。Ti60 合金的其他材料参数如表1 所示。表2 中列出了SiC 在不同温度下的材料参数,C 和TiC的材料参数在表3 中列出。
表1 Ti60 合金在不同温度下的材料参数
Table 1 Material parameters of Ti60 alloy at different temperatures
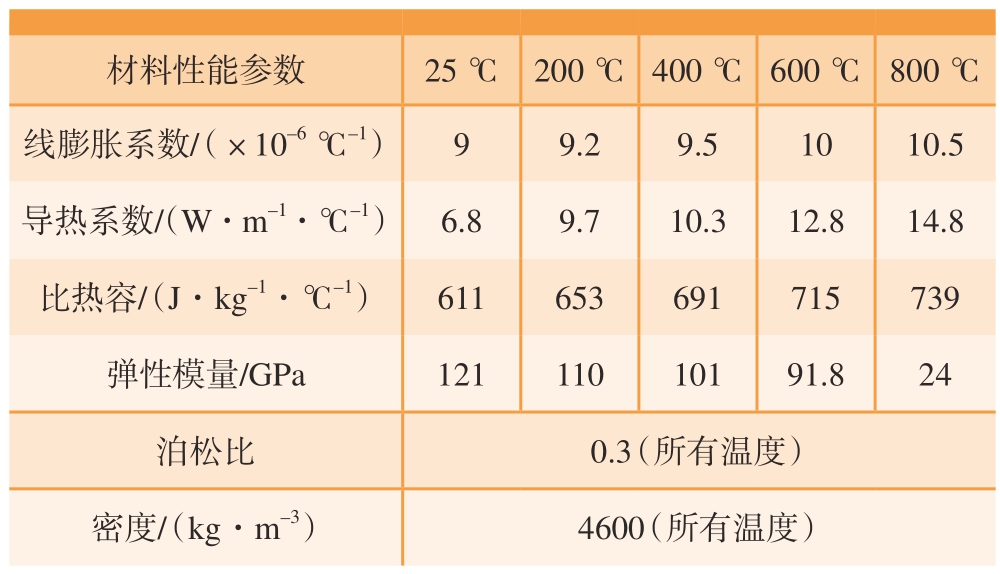
材料性能参数25 ℃ 200 ℃ 400 ℃ 600 ℃ 800 ℃线膨胀系数/(×10–6 ℃–1)99.29.51010.5导热系数/(W·m–1·℃–1) 6.89.710.312.814.8比热容/(J·kg–1·℃–1)611653691715739弹性模量/GPa12111010191.824泊松比0.3(所有温度)密度/(kg·m–3)4600(所有温度)
表2 SiC 在不同温度下的材料参数
Table 2 Material parameters of SiC at different temperatures
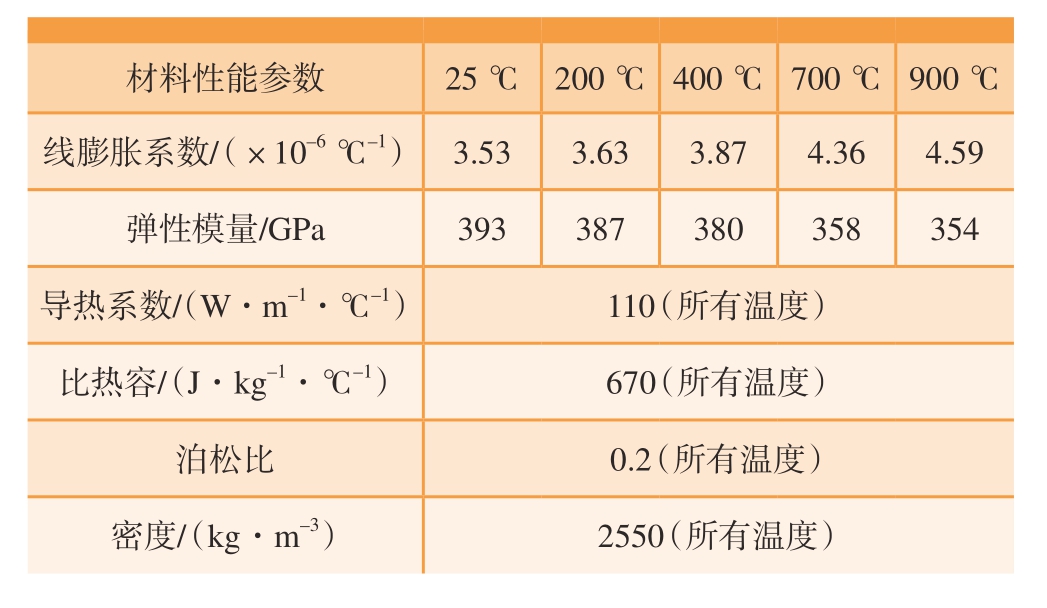
材料性能参数25 ℃ 200 ℃ 400 ℃ 700 ℃ 900 ℃线膨胀系数/(×10–6 ℃–1) 3.533.633.874.364.59弹性模量/GPa393387380358354导热系数/(W·m–1·℃–1)110(所有温度)比热容/(J·kg–1·℃–1)670(所有温度)泊松比0.2(所有温度)密度/(kg·m–3)2550(所有温度)
表3 C 和TiC 的材料参数
Table 3 Material parameters of C and TiC
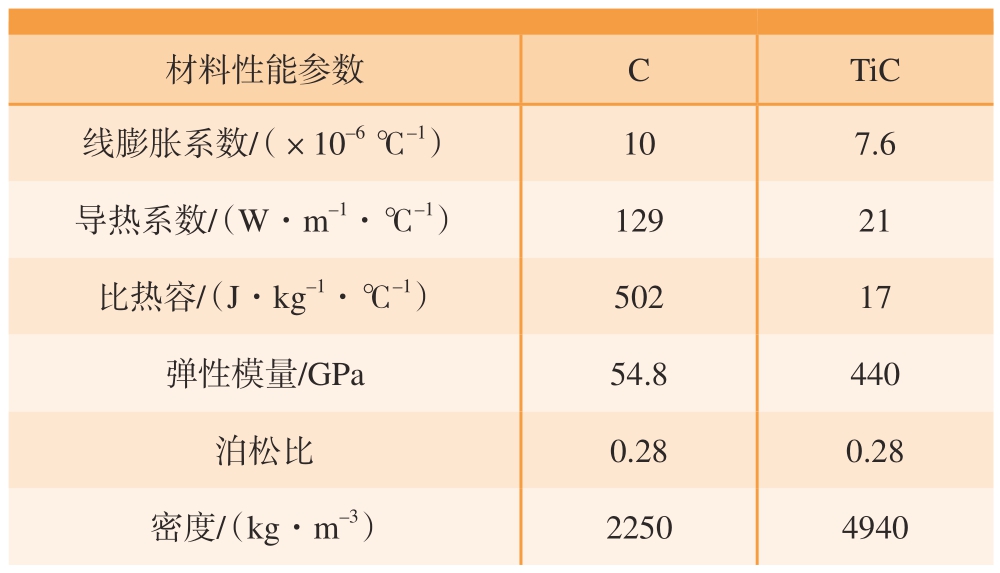
材料性能参数CTiC线膨胀系数/(×10–6 ℃–1)107.6导热系数/(W·m–1·℃–1)12921比热容/(J·kg–1·℃–1)50217弹性模量/GPa54.8440泊松比0.280.28密度/(kg·m–3)22504940
2 模拟结果及分析
2.1 RVE 模型中三向应力的分布
在仿真模拟的后处理部分利用柱坐标系提取三向残余应力,即径向应力S11、周向应力S22、轴向应力S33。坐标系原点设置在上方纤维中心,z 轴为纤维轴向,r 方向为纤维径向,θ 方向为纤维周向。在ABAQUS 软件的后处理模块将1/4 先驱丝模拟结果还原成完整先驱丝结果,先驱丝在HIP 过程中的等效塑性应变 (PEEQ)变化情况如图4 所示。
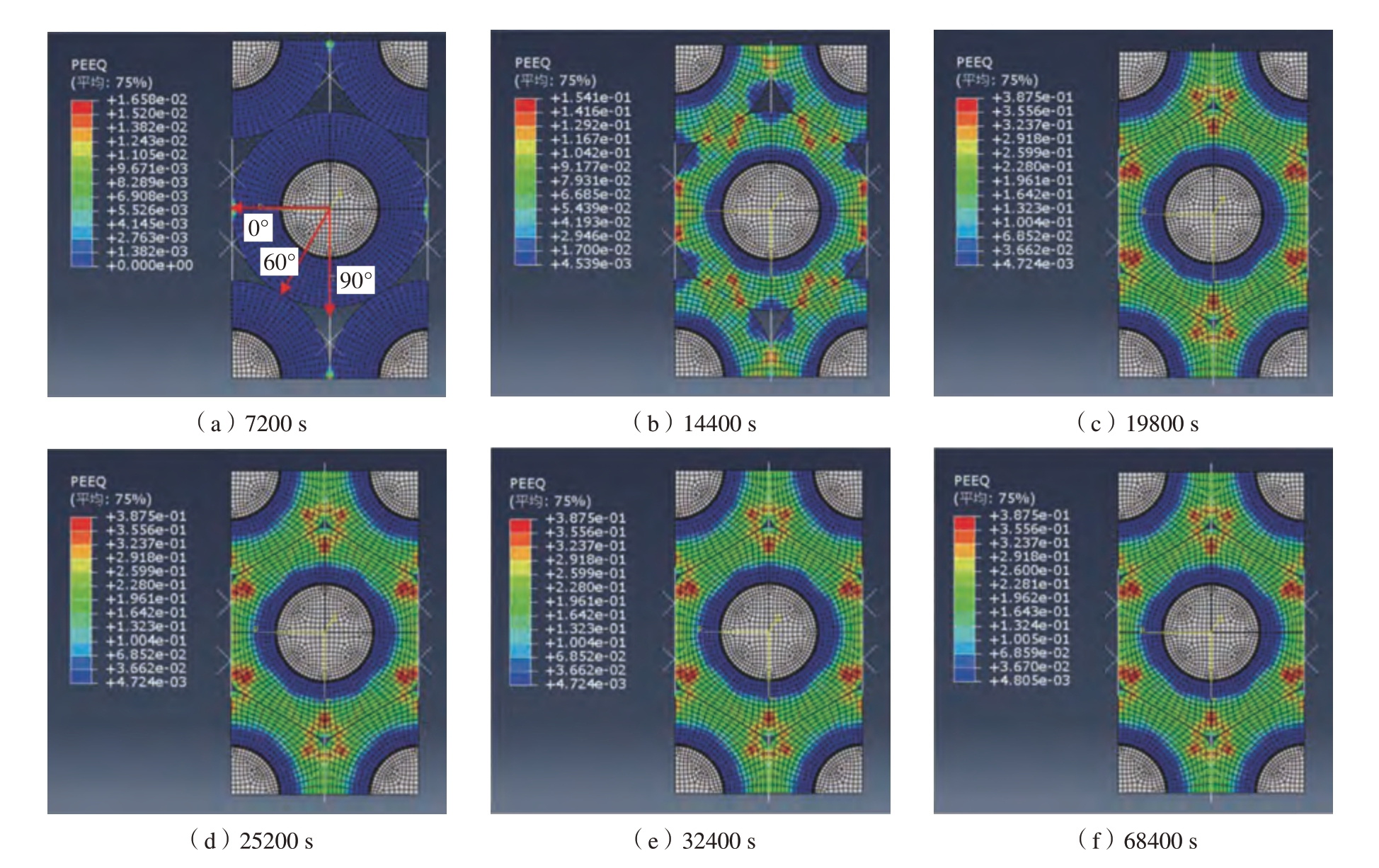
图4 复合材料在HIP 过程中的等效塑性应变PEEQ 云图
Fig.4 PEEQ nephogram of composite material during HIP process
等效塑性应变PEEQ 可以反映模型在HIP 过程中发生的塑性变形大小。图4(a)是升温升压阶段的PEEQ 分布,RVE 模型中的塑性应变很少,因为此时温度和压强比较低,Ti60 基体塑性流动能力差。在保温保压阶段 (图4(b)~(d)),RVE 模型中的空腔迅速缩小直至湮灭,并且最大的塑性变形正是位于空腔最后湮灭的位置。保温保压阶段结束时,致密化程度接近100%,在此之后模型中的塑性应变分布不再变化,表明致密化变形过程主要发生在保温保压阶段。RVE 模型在空腔湮灭位置不能达成完全的致密化 (30°和90°方向),因为有限元仿真过程中有限的网格和节点在最终空隙弥合的位置不能达成完全致密化的效果。考察模拟仿真结果可见,模型在受压方向上 (60°方向)可以完全结合,因此选择在60°方向提取三向应力,分析完全致密化后的应力分布情况。
HIP 过程中径向应力的变化云图如图5 所示。在图5(a)所示的升温升压阶段,Ti60 基体在0°和60°方向上的径向应力为压应力,在其他方向则为拉应力。当HIP 过程进行到保温保压阶段 (图5(b)~(d)),整个模型都受到径向压应力作用,数值大小也十分接近,说明在保温保压阶段应力分布规律保持一致。最先受压的方向 (0°和60°方向)压应力最大,越晚受压的部分其所受压应力越小。60°方向的径向压应力保持到HIP 工艺结束,产生了残余径向压应力,如图5(e)和 (f)所示。

图5 RVE 模型中的径向应力S11 随时间的变化
Fig.5 Variation of radial stress S11 in RVE model with time
在HIP 升温升压阶段,随着温度和压强的升高,纤维所受到的径向压应力增大。纤维处的径向压应力在保温保压阶段保持不变。当HIP 进行到降温降压阶段,纤维上的径向应力继续增大,在HIP 过程结束后产生了残余径向压应力。
HIP 过程结束后在界面层附近的径向应力云图如图6(a)所示。其中,各组分区域的径向残余应力均为压应力。提取预设路径上的径向应力,结果如图6(b)所示,径向应力分布曲线没有明显突变,说明界面层对径向应力的分布影响较小。SiC 纤维上的残余径向应力在–160 MPa 左右,基体上的残余径向应力在–140 ~ –155 MPa 之间。界面层上的应力与基体、纤维间的应力差距不大,C 涂层上的残余径向应力为–154 MPa,TiC 界面层上的压力比C 涂层略大,最大为–164 MPa。
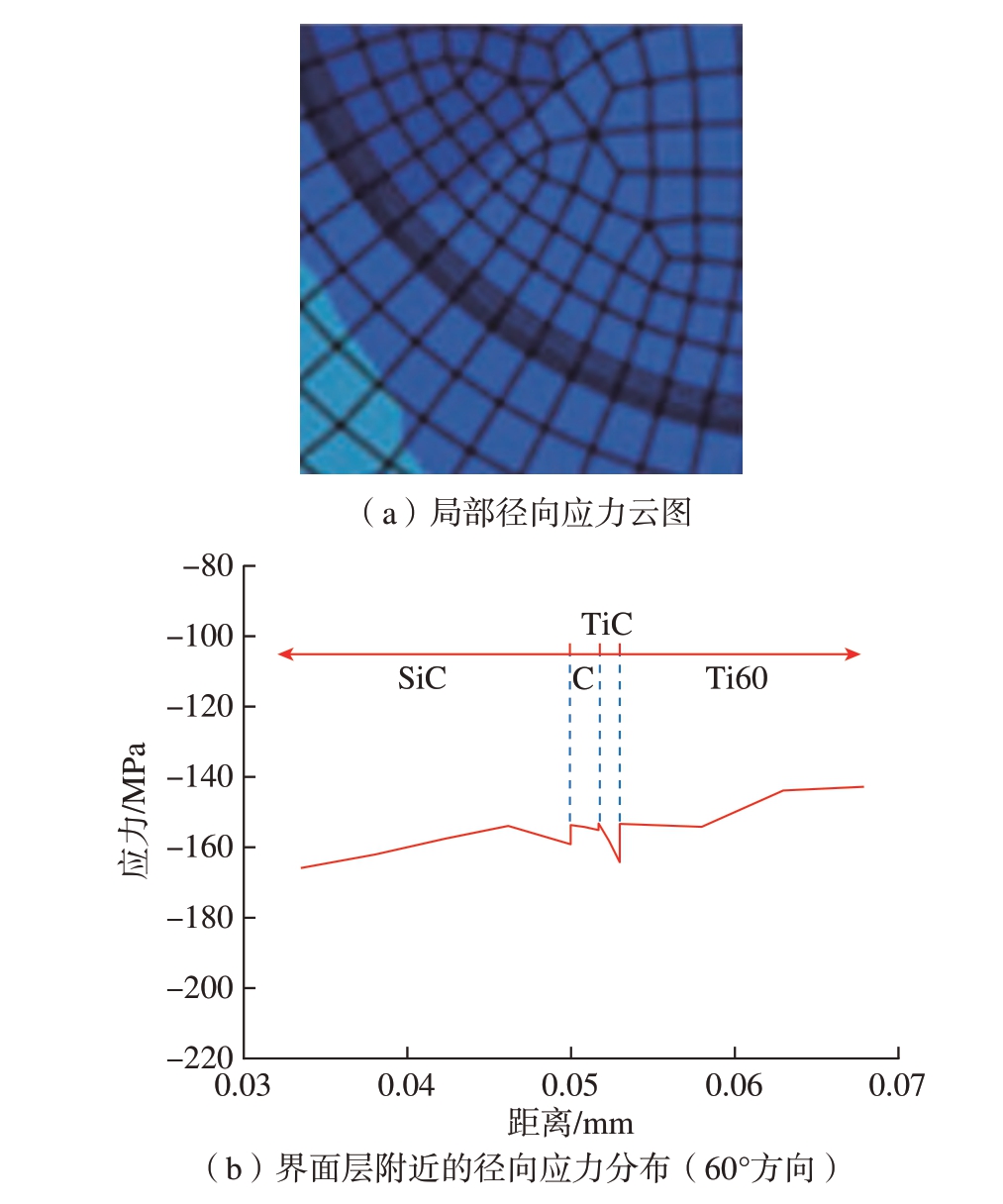
图6 RVE 模型HIP 过程完成后的径向应力分布
Fig.6 Radial stress distribution of the RVE model after HIP process
HIP 过程结束后周向应力云图和周向应力分布曲线如图7 所示。基体上的残余周向应力为拉应力,应力值在120~216 MPa之间。纤维上的残余周向应力在–185 MPa 左右,C 涂层上的周向应力略小于纤维,约为–125 MPa。TiC 界面层上的周向应力有明显突变,最大应力为–390MPa。Shaw 等[19]的研究结果同样指出了这种界面层处的周向压缩状态。
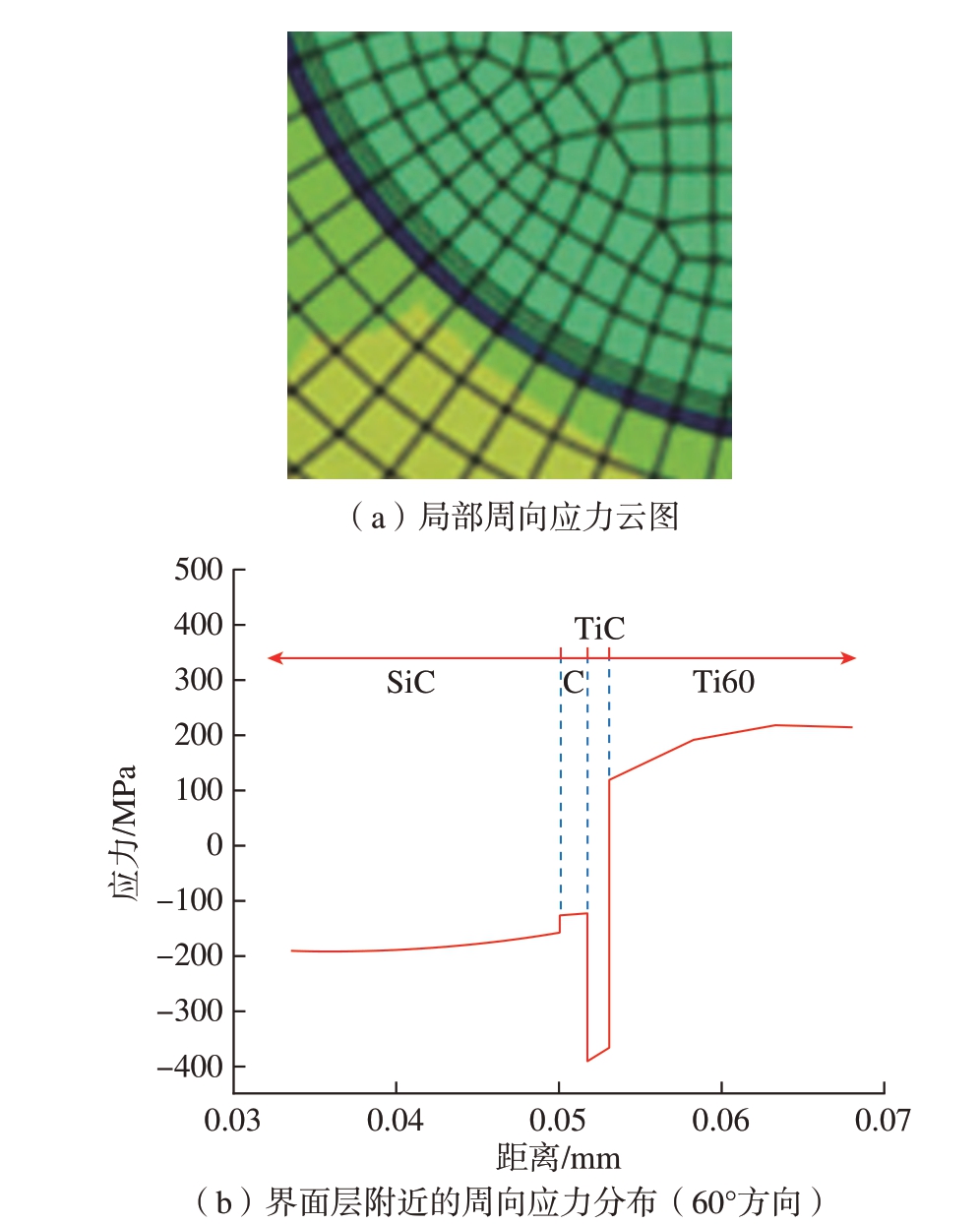
图7 RVE 模型HIP 过程完成后的周向应力分布
Fig.7 Circumferential stress distribution of the RVE model after HIP process
HIP 过程结束后轴向应力云图和轴向应力分布曲线如图8 所示,通过建立相同设置的三维模型以得到轴向应力。图8 中基体上的残余轴向应力为拉应力,而纤维的残余轴向应力为压应力。一般认为轴向应力产生于温度变化导致的纤维、基体间的热失配。SiC 纤维和Ti60 基体的热膨胀系数存在差异,在温度降低的过程中,热膨胀系数大的基体合金体积收缩趋势更大。基体的变形趋势被纤维限制而受到拉应力作用,纤维受到压应力的作用。从图8(b)的S33 分布曲线得知,SiC 纤维上的残余轴向应力在–959 MPa 左右,基体上的轴向拉应力在230 MPa 左右。C 涂层和TiC 界面层处残余应力较小,分别为45 MPa 和35 MPa。界面层为基体和纤维间的应力变化起到了过渡作用。
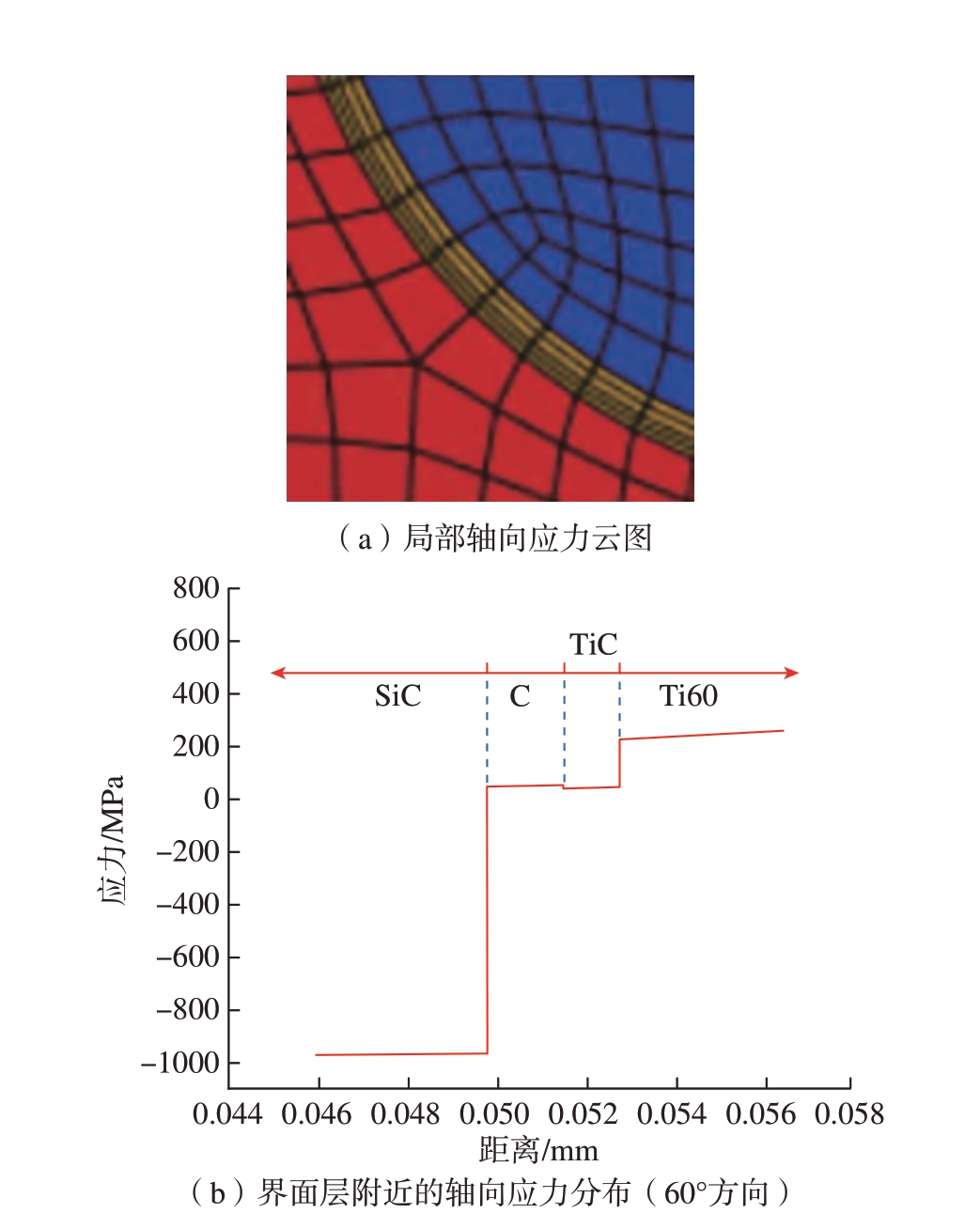
图8 RVE 模型HIP 过程完成后的轴向应力分布
Fig.8 Axial stress distribution of the RVE model after HIP process
由于复合材料中增强体尺寸极小,TMCs 的径向和周向应力测定十分困难。为了验证模型的有效性,依据李建康等[20]的研究,采用基体腐蚀法测定SiCf /Ti60 复合材料的轴向残余应力。基体腐蚀法是将复合材料中的部分Ti60 基体腐蚀去除,通过腐蚀前后纤维轴向的长度变化计算纤维的轴向残余应变 (式(1)),然后通过胡克定律计算释放出的应力 (式(2))[20]。

式中,εfr 为纤维轴向残余应变;L'为复合材料基体腐蚀后的总长度;L0 为复合材料基体腐蚀前的总长度;X 为腐蚀后残余基体的轴向长度;Ef 为纤维的弹性模量,计算得到纤维的轴向残余应力σfr 为–840.5 MPa。本研究模型中得到SiC 纤维上的应力为–959 MPa,与试验测定结果的误差约为14%,说明本文模型的模拟结果可以视为有效。
2.2 C 涂层厚度变化对残余应力分布的影响
本文选择SiCf /Ti60 复合材料的C 涂层厚度范围为1.5~2.5 μm,采用六方RVE 模型研究该范围内C 涂层厚度对残余应力分布的影响。固定TiC 界面层的厚度为1.3 μm,设置3 种C 涂层厚度: 1.5 μm、2.0 μm、2.5 μm。模拟获得复合材料的径向应力和周向应力分布,如图9 所示。
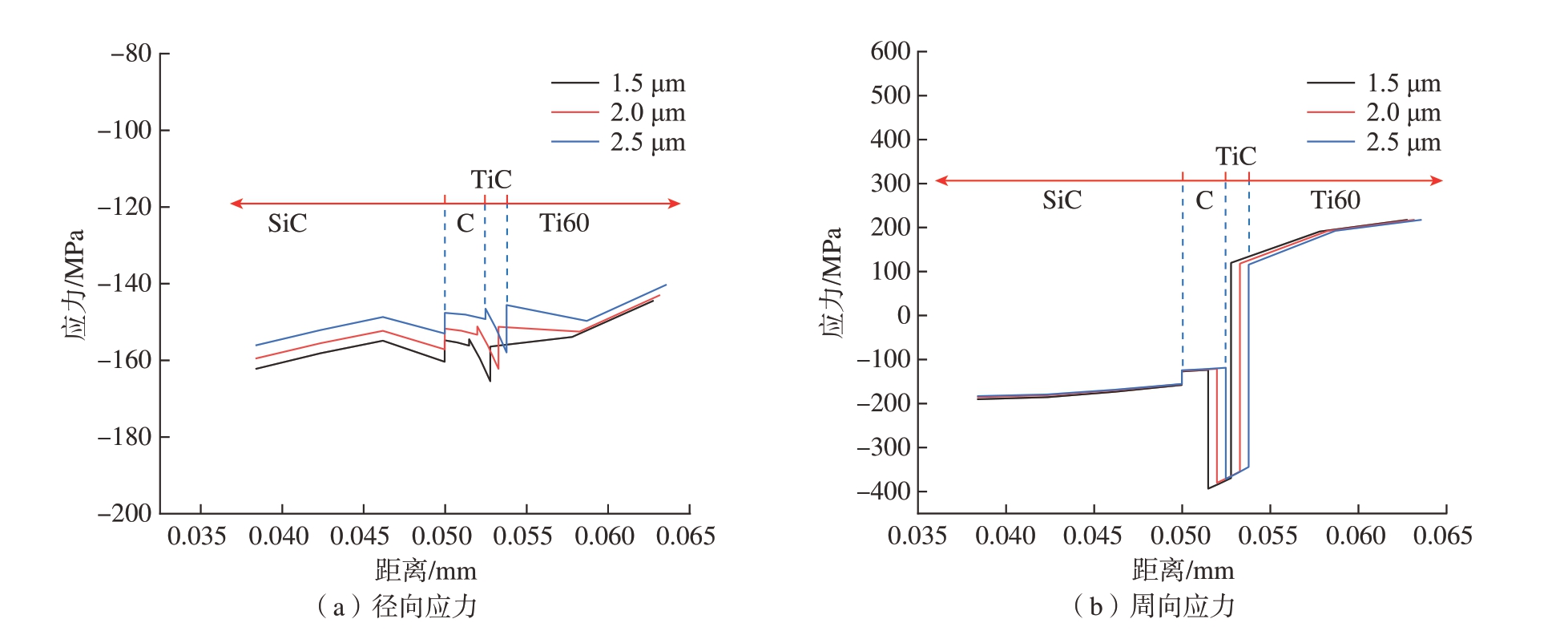
图9 不同C 涂层厚度模型的应力分布
Fig.9 Stress distribution of models with different C-coating thicknesses
径向应力分布受C 涂层厚度增大的影响较明显,随着C 涂层厚度的增加,界面层本身及周边区域的径向应力均有减小趋势。C 涂层厚度从1.5 μm 增大到2.5 μm,径向残余应力减小了7 MPa 左右。C 涂层厚度增大使TiC 界面层上的周向应力减小了20 MPa 左右,但是对其他区域上的周向应力分布影响很小。
2.3 HIP 保温温度对残余应力分布的影响
根据前文分析,致密化过程主要发生在保温保压阶段,为了研究工艺参数中保温温度对复合材料残余应力的影响,使保温温度和压强同步变化,设置940 ℃、960℃、980 ℃ 3 个温度,对应的压强为140 MPa、142 MPa、144 MPa。不同保温温度的仿真模拟结果如图10 所示。

图10 不同HIP 保温温度下模型的致密化
Fig.10 Densification of the model at different HIP holding temperatures
从图10 中可以观察到,随着保温温度上升,最大PEEQ 增大,残余空腔变小。说明保温温度越高,模型的致密化程度越好,反之保温温度越低,致密化程度则越差。较低的保温温度使基体塑性流动能力变差、致密化程度降低。在HIP 结束后可能会产生空洞等缺陷,这些缺陷对复合材料的影响是灾难性的[21–22],提高保温温度有利于避免相关缺陷的产生。
模型的径向应力和周向应力分布曲线如图11 所示。径向应力分布 (图11(a))显示,随着保温温度升高,界面层及附近区域的径向应力有所增大,C 涂层上的径向压应力从153 MPa 增大到159 MPa,TiC 界面层上的径向压应力则从164 MPa 增大到170 MPa。模拟结果说明保温温度的提高,不会改善界面层处的应力分布状态,反而会小幅增大界面层处的径向应力。周向应力分布如图11(b)所示,各模型间的周向应力差距很小,在纤维和C 涂层上周向应力分布基本一致。在TiC界面层上,其周向应力随保温温度升高而小幅增大,应力值从–388 MPa 增大到– 412 MPa。
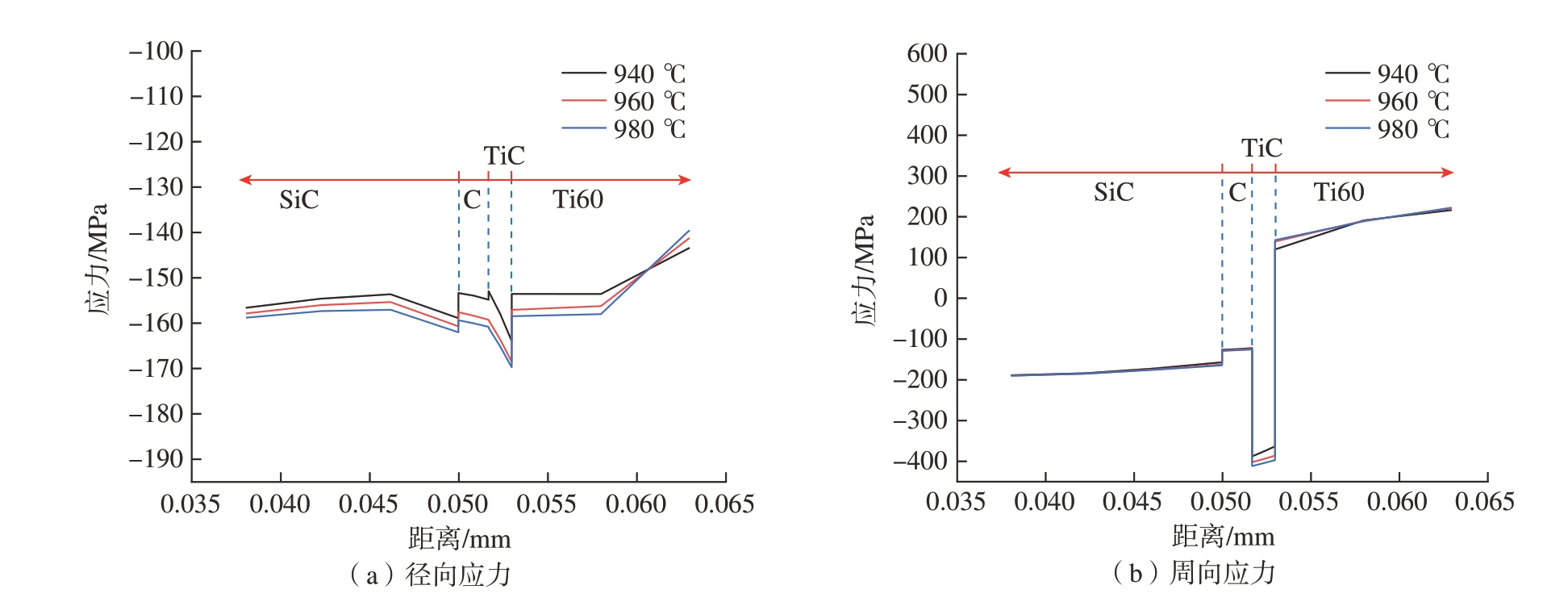
图11 不同保温温度模型的应力分布
Fig.11 Stress distribution of models with different insulation temperatures
综上所述,高温高压状态利于基体的塑性流动,有效提高最终致密度,但会使界面层处的应力增大。
3 结论
针对SiCf /Ti60 复合材料中纤维–界面层–基体的组分分布特点,建立了纤维体积分数为25%的六方RVE 模型,对复合材料热等静压成型过程进行了仿真。
(1)界面层的热残余应力特征与钛合金基体或SiC纤维存在显著差异且呈方向性。在纤维径向,界面层、纤维和基体的径向应力差距很小;在纤维周向,界面层中TiC 反应层的周向应力有明显应力突变,相较于SiC纤维其压应力值增加了205 MPa。
(2)在纤维轴向,界面层降低了纤维和基体间的残余应力梯度。基体轴向残余拉应力为230 MPa;纤维轴向残余压应力为–959 MPa。C 涂层和TiC 界面层上的轴向应力接近于0,对纤维和基体应力有过渡作用。
(3)增大复合材料中的C 涂层厚度会减小界面层的热残余应力。随着C 涂层厚度从1.5 μm 增大到2.5 μm,界面层及周边区域的径向应力减小了7 MPa,TiC界面层的周向应力减小了20 MPa。
[1] MIRACLE D B. Metal matrix composites–From science to technological significance[J]. Composites Science and Technology, 2005,65(15–16): 2526–2540.
[2] 巢青, 孙剑芬, 孙志刚, 等. 金属基复合材料力学性能研究进展[J]. 航空发动机, 2018, 44(4): 91–98.CHAO Qing, SUN Jianfen, SUN Zhigang, et al. Research progress in mechanical properties of metal matrix composites[J]. Aeroengine,2018, 44(4): 91–98.
[3] 陈际伟, 黄浩, 刘湘斌. SiCf /Ti 复合材料在航空发动机中的应用进展[J]. 高科技纤维与应用, 2015, 40(3): 29–32, 60.CHEN Jiwei, HUANG Hao, LIU Xiangbin. Application progress of SiC fiber reinforced titanium matrix composites in aero Engine[J]. Hi-Tech Fiber & Application, 2015, 40(3): 29–32, 60.
[4] 蔡建明, 弭光宝, 高帆, 等. 航空发动机用先进高温钛合金材料技术研究与发展[J]. 材料工程, 2016, 44(8): 1–10.CAI Jianming, MI Guangbao, GAO Fan, et al. Research and development of some advanced high temperature titanium alloys for aeroengine[J]. Journal of Materials Engineering, 2016, 44(8): 1–10.
[5] 黄旭, 李臻熙, 黄浩. 高推重比航空发动机用新型高温钛合金研究进展[J]. 中国材料进展, 2011, 30(6): 21–27, 62–63.HUANG Xu, LI Zhenxi, HUANG Hao. Recent development of new high-temperature titanium alloys for high thrust-weight ratio aeroengines[J]. Materials China, 2011, 30(6): 21–27, 62–63.
[6] 梁春华. 连续纤维增强的金属基复合材料部件在航空涡扇发动机上的应用[J]. 航空制造技术, 2009, 52(15): 32–35.LIANG Chunhua. Application of continuous fiber reinforced metal matrix composite component on turbofan aeroengine[J]. Aeronautical Manufacturing Technology, 2009, 52(15): 32–35.
[7] 张红园, 杨延清, 罗贤, 等. 钛基复合材料压气机叶环应力的数值模拟[J]. 燃气涡轮试验与研究, 2014, 27(6): 41–48.ZHANG Hongyuan, YANG Yanqing, LUO Xian, et al. Numerical simulation on stress distribution of Ti-matrix composite ring[J]. Gas Turbine Experiment and Research, 2014, 27(6): 41–48.
[8] 黄浩, 王敏涓, 李虎, 等. 连续SiC纤维增强钛基复合材料研制[J]. 航空制造技术, 2018, 61(14): 26–36.HUANG Hao, WANG Minjuan, LI Hu, et al. Preparation of SiC fibers reinforced titanium matrix composites[J]. Aeronautical Manufacturing Technology, 2018, 61(14): 26–36.
[9] MA Z J, YANG Y Q, WANG H Y, et al. Numerical simulation of densification during consolidation of titanium-matrix coated fibers[J].Composites Part A: Applied Science and Manufacturing, 2006, 37(10):1587–1590.
[10] 罗恒军, 杨延清, 黄斌, 等. SiCf /Ti–6Al–4V复合材料的界面反应及其影响[J]. 机械工程材料, 2009, 33(3): 1–4.LUO Hengjun, YANG Yanqing, HUANG Bin, et al. Interfacial reaction and effect of SiCf/Ti–6Al–4V composites[J]. Materials for Mechanical Engineering, 2009, 33(3): 1–4.
[11] 黄浩, 张侃, 吴明, 等. SiC纤维增强Ti17合金复合材料轴向残余应力的拉曼光谱和X 射线衍射法对比研究[J]. 物理学报, 2018,67(19): 288–296.HUANG Hao, ZHANG Kan, WU Ming, et al. Comparison between axial residual stresses measured by Raman spectroscopy and X-ray diffraction in SiC fiber reinforced titanium matrix composite[J]. Acta Physica Sinica, 2018, 67(19): 288–296.
[12] HUANG B, YANG Y Q, LUO H J, et al. Effect of the interfacial reaction layer thickness on the thermal residual stresses in SiCf /Ti–6Al–4V composites[J]. Materials Science and Engineering: A, 2008, 489(1–2): 178–186.
[13] 牛莉莎, 郑岩, 胡齐阳, 等. 金属基复合材料热机械疲劳加载模型的数值解法和应用[J]. 机械强度, 2004, 26(S1): 115–120.NIU Lisha, ZHENG Yan, HU Qiyang, et al. Numerical solution of mechanical model of fiber reinfoced MMCs under cyclic thermomechanical loading[J]. Journal of Mechanical Strength, 2004,26(S1): 115–120.
[14] 姚泉, 鲁世强, 王克鲁, 等. SiCf /Ti60 复合材料预制体热等静压致密化过程数值模拟[J]. 塑性工程学报, 2021, 28(1): 60–68.YAO Quan, LU Shiqiang, WANG Kelu, et al. Numerical simulation of hot isostatic pressing densification process of SiCf /Ti60 composites prefabricated body[J]. Journal of Plasticity Engineering, 2021, 28(1):60–68.
[15] 秦琳, 杨延清, 罗贤, 等. SiC纤维增强钛基复合材料中涂层性能对残余热应力的影响[J]. 热加工工艺, 2014, 43(24): 171–173.QIN Lin, YANG Yanqing, LUO Xian, et al. Effects of interfacial coating on thermal residual stress in SiC/Ti–6Al–4V composite[J]. Hot Working Technology, 2014, 43(24): 171–173.
[16] 原梅妮, 杨延清, 马志军, 等. SiC纤维增强钛基复合材料界面强度研究进展[J]. 稀有金属材料与工程, 2007, 36(6): 1115–1118.YUAN Meini, YANG Yanqing, MA Zhijun, et al. Research progresses on interfacial bonding strength of SiC fiber reinforced titantium matrix composites[J]. Rare Metal Materials and Engineering, 2007, 36(6): 1115–1118.
[17] 王玉敏, 张国兴, 张旭, 等. 连续SiC纤维增强钛基复合材料研究进展[J]. 金属学报, 2016, 52(10): 1153–1170.WANG Yumin, ZHANG Guoxing, ZHANG Xu, et al. Advances in SiC fiber reinforced titanium matrix composites[J]. Acta Metallurgica Sinica, 2016, 52(10): 1153–1170.
[18] 王天祥, 鲁世强, 王克鲁, 等. Ti60合金的热变形行为及加工工艺参数优化[J]. 稀有金属材料与工程, 2020, 49(10): 3552–3561.WANG Tianxiang, LU Shiqiang, WANG Kelu, et al. Hot deformation behavior and processing parameter optimization of Ti60 alloy[J]. Rare Metal Materials and Engineering, 2020, 49(10): 3552–3561.
[19] SHAW L L, MIRACLE D B. Effects of an interfacial region on the transverse behavior of metal-matrix composites—a finite element analysis[J]. Acta Materialia, 1996, 44(5): 2043–2055.
[20] 李建康, 杨延清, 罗贤, 等. 连续SiC纤维增强Ti基复合材料中的纵向残余热应力分析[J]. 金属热处理, 2007, 32(11): 65–69.LI Jiankang, YANG Yanqing, LUO Xian, et al. Measurement of the longitudinal thermal residual stress in continuous SiC fiber reinforced titanium matrix composites[J]. Heat Treatment of Metals, 2007, 32(11):65–69.
[21] HU C Y, LIU J H, XU L, et al. Effect of sintering temperature on properties of carbon fiber-reinforced titanium matrix composites[J].ACS Omega, 2022, 7(34): 30087–30092.
[22] BORDERE S, MAGNY C, MARCHAL K, et al. Prediction of the pore-closing kinetics during the consolidation stage of SiC unidirectional long fibers: Titanuum alloy matrix composites[J]. Journal of Materials Processing Technology, 1996, 62(1–3): 100–107.