Ti–6Al–4V（TC4）合金具有良好的综合力学性能，比强度高、耐蚀性好，是目前应用最广泛的钛合金之一，其优异的性能可以充分发挥增材制造技术中设计制造一体化方面的优势。采用TC4制成的薄壁件在航空航天领域被广泛应用，但薄壁结构在加工过程中易变形，且残余应力的存在限制了其装配与使用，因此对其进行变形控制十分必要。
在激光粉末床熔融 （Laser powder bed fusion，L-PBF）成形过程中，相比于已凝固层，激光焦点及其热影响区面积较小，从而产生显著的、方向相关的温度梯度，导致热应力和残余应力积累。这些应力影响L-PBF所制备工件的力学性能[1]，并在加工过程中或加工后造成几何变形和开裂，借助计算机模拟技术对成形件进行预测，并调整工艺参数可有效降低生产成本。对L-PBF过程进行仿真，可根据精细度分为3个尺度，即微米级微观尺度、毫米级细观尺度、宏观尺度。微观模型通过考虑熔池内的流体动力学及相变过程来探究熔池内部流场和组织结构的变化，这一层面的模型有着较高的精细度，但受限于计算量只能对微小区域的演化进行模拟；而毫米级的细观模拟和基于真实工件模型的宏观模拟通过一些简化方法，可在更大尺度上预测成形结果，并考虑扫描路径、层间停留时间等微尺度模型不包含的参数。目前，有限单元法在工件成形温度场和应力场方面的宏观尺度模拟已经受到国内外研究人员的关注[2]，通过模拟手段进行工艺优化已发展为解决增材制造过程中缺陷、变形、开裂等瓶颈问题的核心方法。
针对宏观尺度下的热过程，现有研究一般侧重于热历史和残余应力的仿真，揭示成形工艺参数与成形质量之间的关系。Fu等[3]采用表面移动热通量对Ti–6Al–4V在激光增材多层堆积过程中的温度梯度和热历史进行了模拟，评估了工艺参数和材料对熔化过程的影响。Masoomi等[4]建立了多激光同时扫描的有限元模型来计算温度场，结果表明多激光成形不仅可以提高成形效率和热影响区域，还可以减小局部温度梯度和冷却速率。Li 等[5]建立了多层多道次激光增材过程的三维热–力耦合有限元模型，模拟加工过程中加热、熔化、蒸发、凝固、收缩及冷却等现象，研究结果表明，残余应力随着扫描层数的增加而增大，揭示了残余应力累积效应。Wang等[6]采用逐层模拟的方法对电子束粉末床熔融的热过程进行了计算预测，分析了热历史对材料微观结构的影响。Li等[7]模拟了不同长度薄板的应力分布，发现一定范围内变形程度与板长成正比。
综上，薄壁结构在加工过程中易产生变形且精度控制较为困难，目前国内针对于增材成型薄壁结构的报道多集中于残余应力和毫米级平直样条的变形，L-PBF过程动态热应力的研究报道较少，亦缺乏整体工件的成形模拟及变形补偿的研究。本文分别在细观和宏观尺度下对TC4合金的L-PBF过程进行热–力耦合仿真，采用两种不同尺度下的有限元计算方法，得到各工序的温度场、应力场和整体变形结果及特定位置变形量，并基于宏观模拟结果构建变形补偿模型。细观尺度模拟结果可为打印参数优化提供指导，并为后续的介观模拟提供温度、应力等参数，宏观模拟及所构建的补偿模型可在打印前对模型进行优化，改善预期结果。
1 试验及方法
L-PBF过程涉及参数众多，根据本工作所涉及的熔池仿真和工件成形过程仿真的特点，并考虑将计算过程简化，本文建立的模型包括以下5个假设： （1）基材和金属粉末属于各向同性[8]；（2）忽略粉末熔化过程中形成的微熔池内部流动作用的影响；（3）不考虑基材和金属粉末之间的汽化作用；（4）基材和金属粉末的屈服准则都采用Von Mises准则；（5）材料的塑性区段遵循流动准则和硬化准则。
1.1 热–弹塑性有限元模型及理论
1.1.1 温度场控制方程
在L-PBF过程中随激光的移动，金属粉末在极短的时间内受热熔化又快速冷却，并包含热传导、热对流和热辐射过程，属于非线性瞬态热传导过程。基于热力学第一定律和傅立叶定理，所得到的三维瞬态温度场热传导控制微分方程为[9]
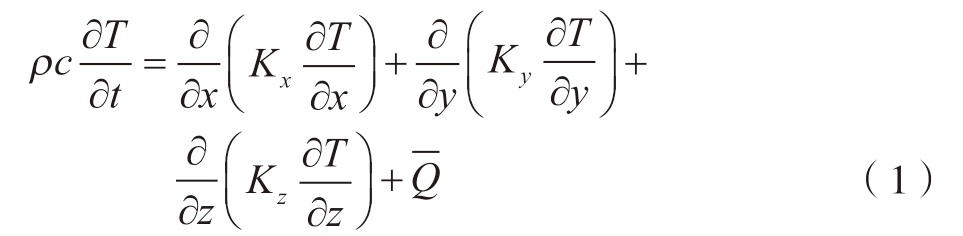
式中，ρ为材料密度；c为材料比热容；T为温度；t为时间；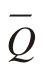
为内部热源密度；Kx、Ky、Kz是沿x、y、z方向导热系数，即公式右侧前3项为导热项，第4项为潜热项。
通过给出的初始状态和边界条件，可求出上述微分方程的唯一解，即温度场分布。初始状态为加工开始时粉床所处的环境温度T0，即
L-PBF加工过程中，根据所设定的热源模式，考虑工件内部和环境中的对流换热，涉及的3类边界条件如下。
第1类：给定边界温度T *，即
第2类：给定边界热流密度q，即
第3类[10]：边界进行热对流与热辐射，即
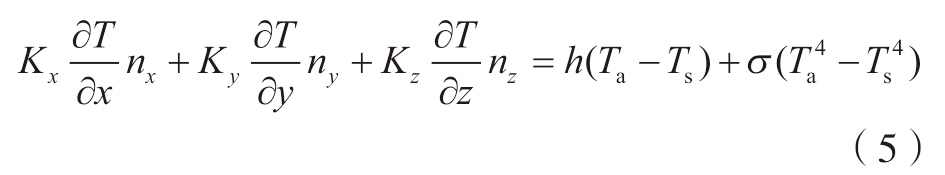
式中，nx、ny、nz分别是边界外法线的方向余弦；h为工件外表面热对流系数；Ta – Ts为工件表面温度与外界温度差。
1.1.2 相变潜热
金属材料在受热时出现固液相转变的现象，在转变过程中会吸附并放出潜热，这会对冷却作用的持续时间以及微观组织结构产生影响，因此温度场模拟中需要考虑到相变潜热对计算结果的影响。ANSYS中采用热焓法来计算潜热，是密度与比热的乘积对温度的积分。
式中，H为热焓值。文中所用材料热物性的变化规律如图1所示[11]。
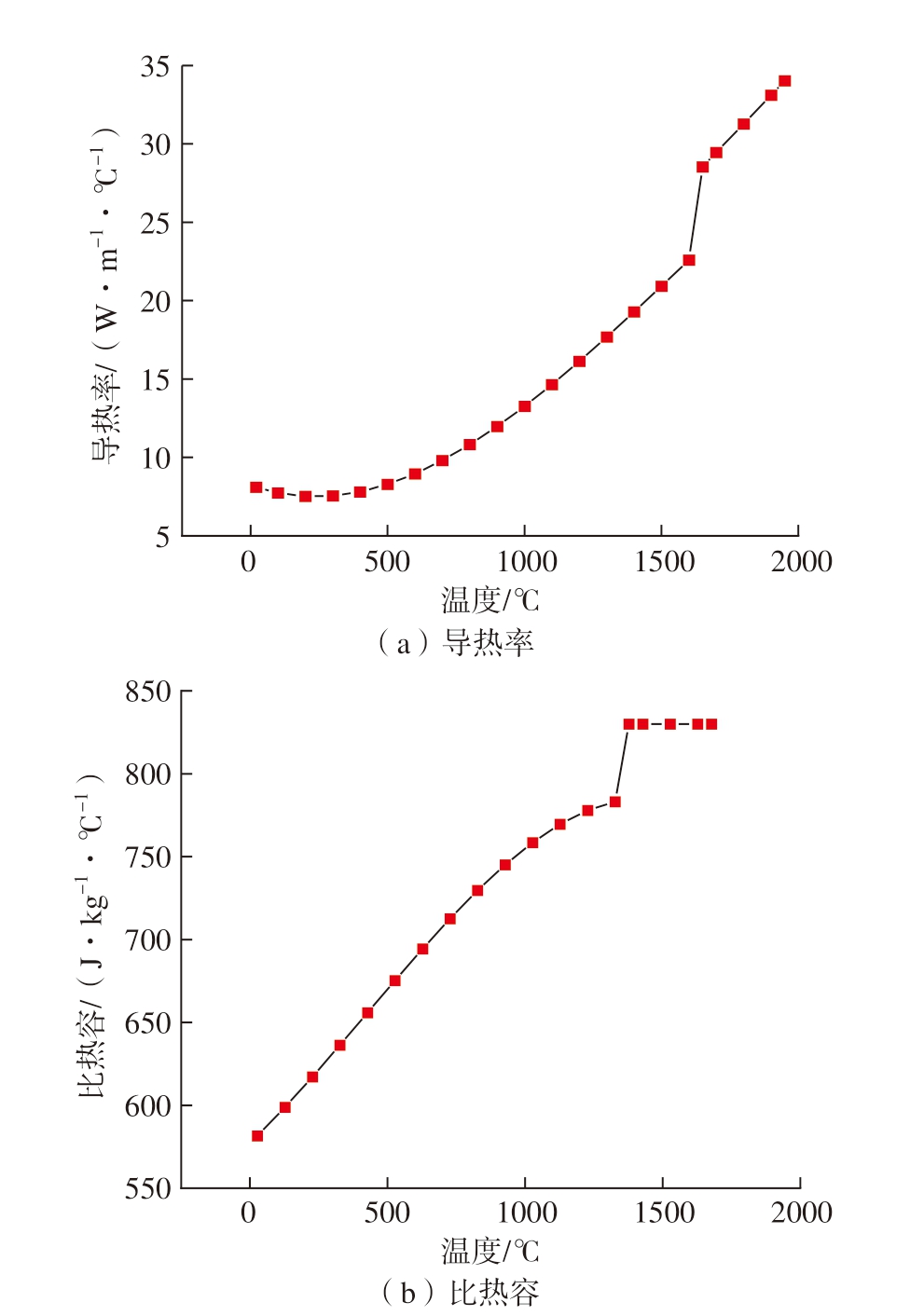
图1 TC4材料热物性参数[11]
Fig.1 Thermophysical parameters of TC4 titanium materials[11]
1.1.3 应力场分析理论
在ANSYS Mechanical中先求解出全过程中各节点的温度值，再将温度场结果作为体载荷赋予到瞬态结构中，求解热应力和变形。在此热力耦合过程中，热应力是由分布不均匀的温度场造成的，而由此产生的应力场对温度的分布则几乎没有影响，因此忽略结构变化对热过程的影响，即采用热–结构间接耦合的方法。
在L-PBF过程中，由于高输入能量集中在一个小区域，产生了较大的温度梯度，从而导致高残余应力和应变，二者关系为
式中，{σ}为应力矢量；[D]为单元弹性矩阵；{εe}为应变矢量，其中{εe}由以下3部分组成。
式中，{ε}、{εp}、{εt}分别表示总应变向量、塑性应变向量和热应变向量。将式 （8）代入式 （7）得
对于本文所用的各向同性材料，上述关系式可由笛卡尔坐标系表示为[12]
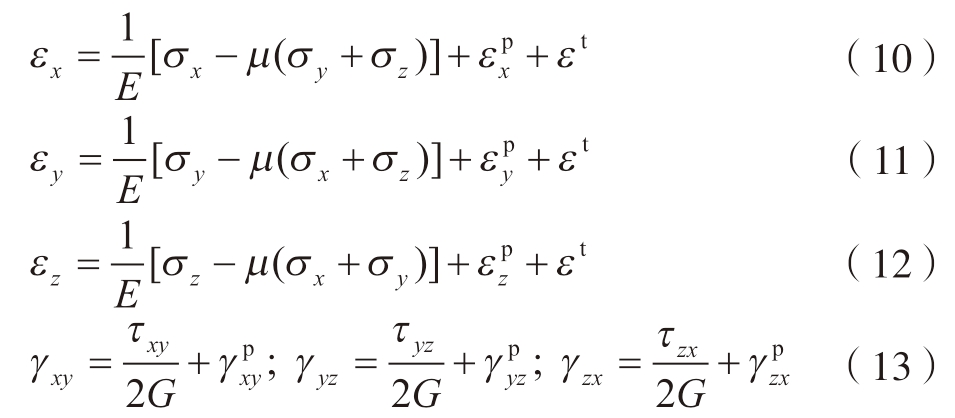
式中，E、G、μ分别表示弹性模量、剪切模量和泊松比，热应变εt可通过式 （14）计算。
式中，Tref为初始参考温度；αe为材料热膨胀系数。
本文通过Von Mises屈服准则来判断材料是否发生屈服，其等效应力为
式中，σ1、σ2、σ3分别为第一、第二、第三主应力，当材料内部的等效应力超过最大屈服强度σ0后，便会发生塑性变形，其增量大小及方向则由流动准则判断。随着塑性变形的增加，屈服强度也增加，从而对初始屈服准则产生影响的过程有各向同性强化和随动强化两类主要模型，本文采用各向同性的双线性随动强化模型 （BKIN）。TC4材料力学参数如表1所示[13]。
表1 TC4材料力学参数[13]
Table 1 TC4 material mechanical parameters[13]
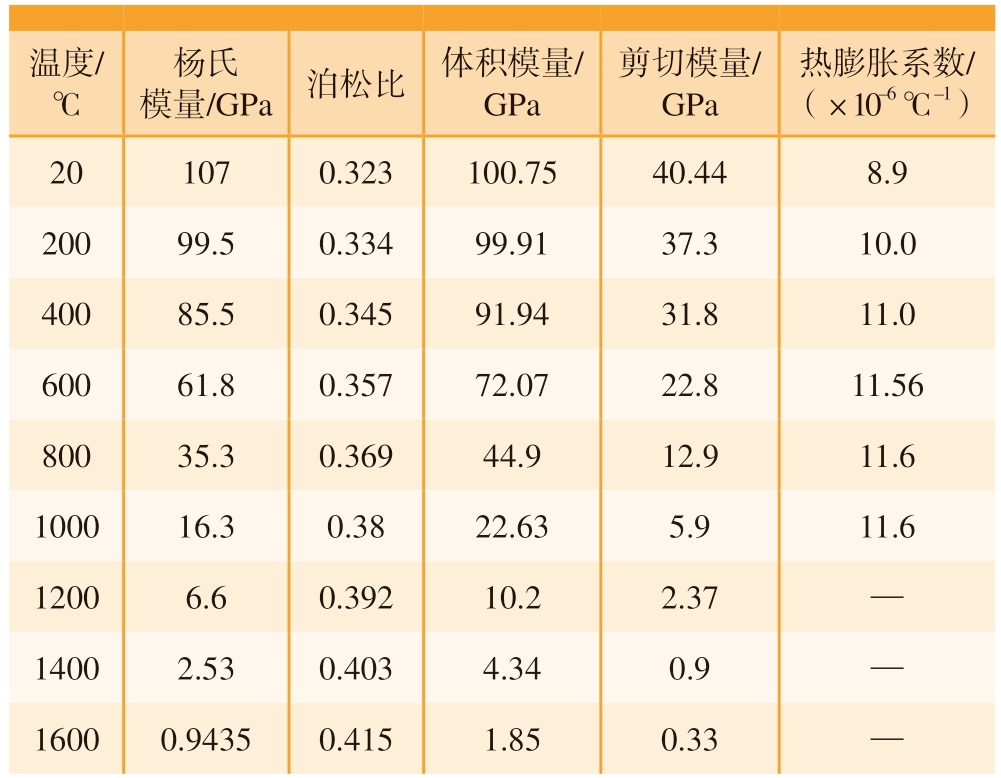
温度/℃模量/GPa泊松比体积模量/GPa杨氏剪切模量/GPa热膨胀系数/（×10–6 ℃–1）201070.323100.7540.448.9 20099.50.33499.9137.310.0 40085.50.34591.9431.811.0 60061.80.35772.0722.811.56 80035.30.36944.912.911.6 100016.30.3822.635.911.6 12006.60.39210.22.37—14002.530.4034.340.9—16000.94350.4151.850.33—
1.2 模型
本文中多尺度模拟的计算流程如图2所示，其中有限元模拟分为细观与宏观两部分，通过细观模拟为宏观模拟提供了较优的工艺参数，并对二者应力场分布和变形量等结果进行验证。
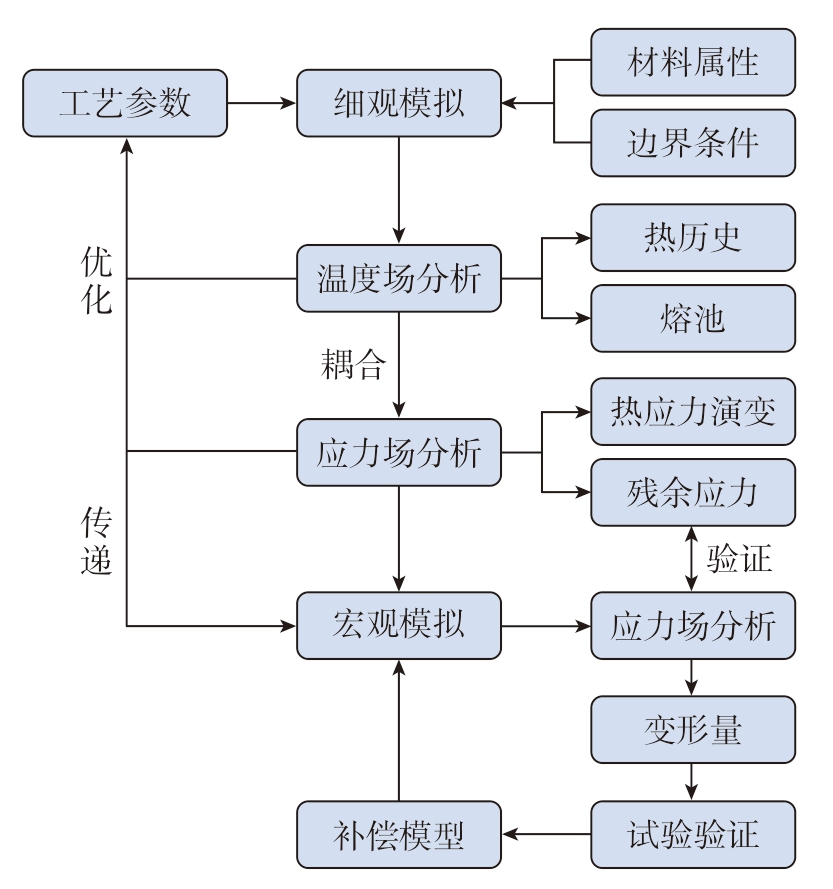
图2 计算流程图
Fig.2 Calculation flow chart
1.2.1 薄壁件模型
如图3（a）所示，薄壁件模型基板尺寸为8 mm×3 mm×0.5 mm，在薄壁件上构建5 mm×0.5 mm×30 μm的3层矩形模型。对模型进行网格划分，为保证精度的同时减少计算量，基板采用上密下疏、中心加密的网格划分方法，熔覆层采用较小的网格划分，每个单元的尺寸为0.02 mm，如图3（b）所示，标记网格节点A，位于扫描起始点后0.5 mm处。
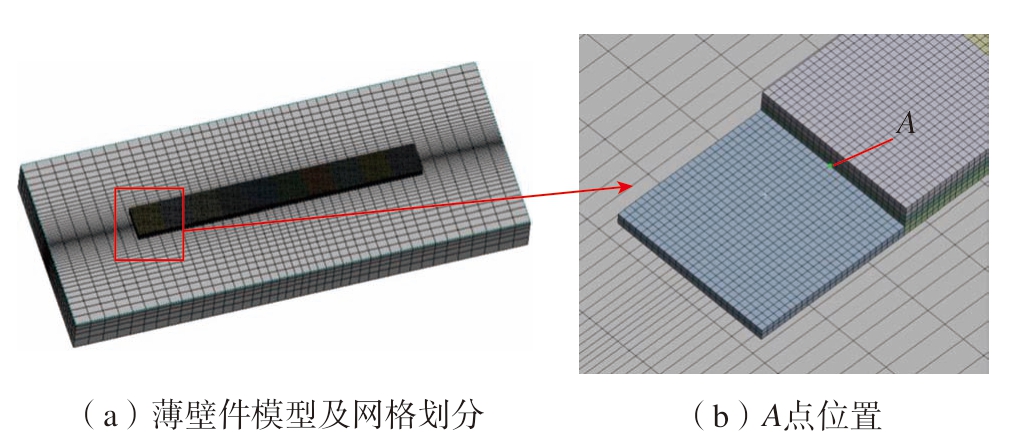
图3 薄壁件模型及局部放大图
Fig.3 Thin-walled model and partial enlarged view
对熔化熔覆行为的模拟采用“生死单元”方法，将未熔化区域内的单元附加一个极小的缩减因子，使其不参与计算也不对其他单元产生影响，即“杀死单元”，随着激光热源的移动来逐步激活照射区域的粉末单元，从而模拟粉末逐步融化的过程。
1.2.2 热源模型
由于激光器产生的光源照射到工件表面时，其热流密度呈现出正态高斯分布状态，故本工作中使用对应的移动高斯热源模型，表达式为[14]
式中，A'是粉末吸收率；P是激光输出功率；r是光斑半径；R是表面上任意点距光斑中心的距离。由于光斑中心随时间在工件表面快速移动，因此先定义中心点坐标（x0 = 0，y0 = vs），其中v、s分别为激光扫描速度与历时。由此熔覆层表面上任意点 （x，y）与 （x0，y0）之间的距离为
将式 （17）代入式 （16）即可设定热源方程。其中，激光功率分别设为130 W、160 W、180 W，3组记为E1、E2、E3，仿真工艺参数如表2所示。
表2 仿真工艺参数
Table 2 Simulation process parameters
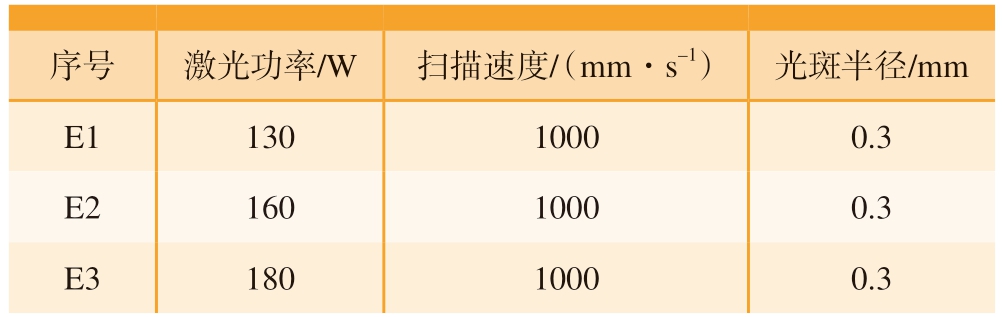
序号激光功率/W扫描速度/（mm·s–1）光斑半径/mm E113010000.3 E216010000.3 E318010000.3
1.2.3 宏观模型
由于激光增材制造过程中受到多重因素的影响，受限于模型复杂程度和计算量，难以实现对每个成形层详细的热–力耦合模拟。为了提高计算效率，在细观模型采用的5点假设基础上，还包含宏观成形过程的3个简化模型。
（1）在使用标准生死单元技术的同时采用超层模拟，将20个成形层构建为一个计算层，金属粉末以计算层为单位进行构建。
（2）在构建过程中通过施加一个面积、深度与目标层一致的瞬间体热源，使目标层粉末全部熔化，从而规避具体扫描矢量，且加大时间步长，使其能够捕捉到导致扭曲的热应变和塑性应变。
（3）在L-PBF工艺过程中，不对成形件周围的粉末进行显式建模。
图4（a）是成形工件的有限元模型，尺寸为70 mm×74 mm×51 mm，基板尺寸为100 mm×100 mm×15 mm。对其使用分层四面体网格进行划分，部件采用较小的网格进行划分，每个单元的尺寸为0.8 mm，层高0.8 mm；基板采用较大的网格进行划分，每个单元的尺寸为5 mm，如图4（b）所示。
图4 成形工件的有限元模型及网格划分
Fig.4 Finite element model and meshing of formed workpiece
根据模型设置基板预热温度为100 ℃，舱室环境温度22 ℃，激光扫描速度为1000 mm/s，扫描间距为0.11 mm，粉末层厚为0.03 mm，层旋转角度为66.67°，两次扫描的时间间隔10 s。试验采用苏州倍丰激光科技有限公司SP101设备进行L-PBF的样品成形，打印试验参数与上述仿真保持一致。
1.2.4 计算效率
仿真计算均在主频3.2 GHz、8核16线程的计算机上完成，采用移动高斯热源的细观模型共用时9.65 h。根据前3道的所用计算时间可以做出推测，整体工件模型共有700成形层，如每层都采用热力耦合模型来计算热应力，所需计算时间约为2252 h，而通过超层模拟技术配合瞬态热源后，计算共耗时5.6 h。从计算效率方面看，采用全尺寸的移动热源模型的时间成本无法接受，本工作中所构建的宏观模型可以用于实际工业生产中对应力场分布趋势及变形量的预测和修正。
2 结果与讨论
2.1 细观模拟结果
2.1.1 温度场
温度场结果如图5所示，图5（a）为E1条件下的熔池轮廓，显示出在此L-PBF过程中，最高温度达2166.8 ℃，位于光斑中心处，周围出现高温度梯度，且光斑前方等温线分布更密集，整体呈椭圆状，后部有较长“拖尾”，这主要是因为随着扫描位置的移动，后端熔融后的实体材料导热率显著高于前方的粉末状材料，热量在已成形区和基板上快速传导，进而使后部温度梯度分布较为缓和。
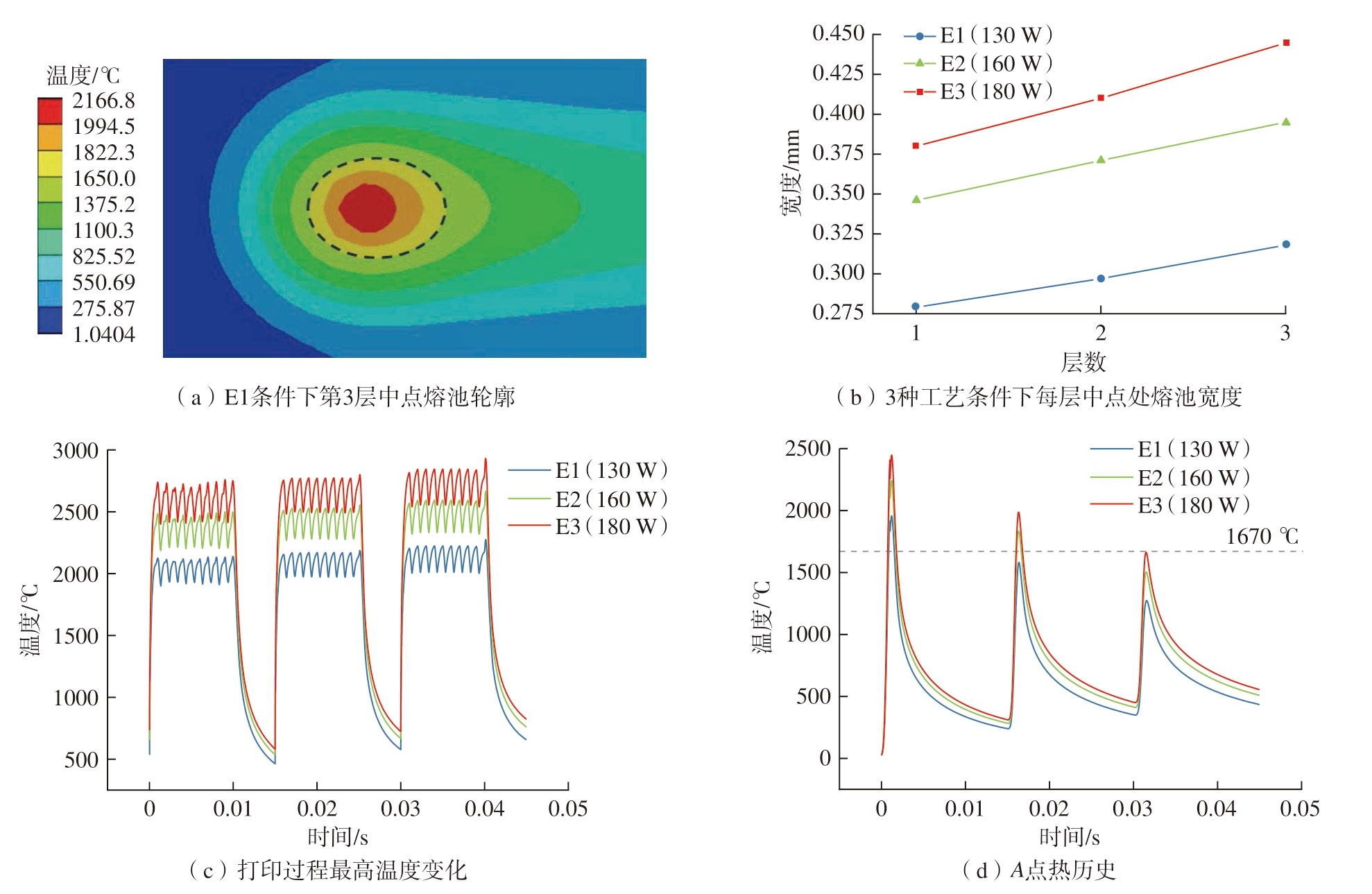
图5 温度场结果
Fig.5 Temperature field results
图5（b）和 （c）中，E2条件下第3层中点处熔池宽度0.386 mm，相比第2层的宽度0.364 mm、第1层的0.343 mm，分别增大了6%和12.5%；第3层最高温度2583.8 ℃也略高于前两层的2547.9 ℃、2512.1 ℃。可以看出，随扫描层数增加，同功率下每道次最高温度及熔池尺寸均在增加，原因是下层成形过程中的热积累效应对上层产生影响。在L-PBF加工中，热量散失的主要途径是热传导，通过表面与环境热辐射/热对流散失的热量较少，随着成形层数的增加，通过基板热传导散热的能力逐渐下降，激光积累的能量密度升高，使上层的温度更高且熔池更大。同时，熔池尺寸随功率增长而增大的趋势更为明显，即熔池尺寸对功率更敏感。
图5（d）为不同激光功率下A点 （图3（b））处温度随成形时间的变化图，曲线的3个峰值代表激光照射至A点及其正上方，此时温度达到最高后快速冷却，冷却速率即为曲线的斜率。在0.005 s的层间冷却时间下，E1、E2、E3工艺参数的冷却速率分别为1.234×105 ℃/s、1.411×105 ℃/s、1.54×105 ℃/s。由此可见，更高的功率会带来更大的冷却速率，导致出现更大的温度梯度，使内部的残余应力增大，但由于过小的冷却速率不利于晶粒尺寸的细化，同样不利于成形件机械性能的提高，因此要控制冷却速率处于合理区间。E2、E3曲线的第2个峰值均超过TC4熔点温度 （1670 ℃），说明在这两种功率下激光扫描第2层时前一层均出现了重熔，使层与层之间发生较好的冶金结合。
2.1.2 应力场
基于上述温度场计算结果，进行热–结构间接耦合的热应力分布计算。在基板左侧施加固定面约束以模拟L-PBF过程中的固定夹具，固定端及变形示意见图6。由于打印过程中材料高温区域受热膨胀的过程被低温区域的实体限制，整体表现出压应力及向下变形。
图6 材料受热应力变形示意图
Fig.6 Schematic diagram of material deformation by heat stress
图7为130 W功率下Von Mises等效应力分布及x、y、z方向应力。可以看出，主要等效应力分布呈哑铃形集中在熔覆层首尾两端和熔覆层表面，存在固定约束的一段分布更广；x方向的残余拉应力主要集中在熔覆层两侧，而靠近熔覆层的基板中部到熔覆层左端表面则出现压应力，熔覆层右端未冷却区域仍表现为拉应力；由于大部分热应力由熔池凝固时局部不均匀收缩引起，而熔池在沿扫描方向上的尺寸比垂直方向更大，因此y、z方向热应力数值总体较小，熔覆层与基板接触区分布压应力，两端尤其是固定端则表现为拉应力。
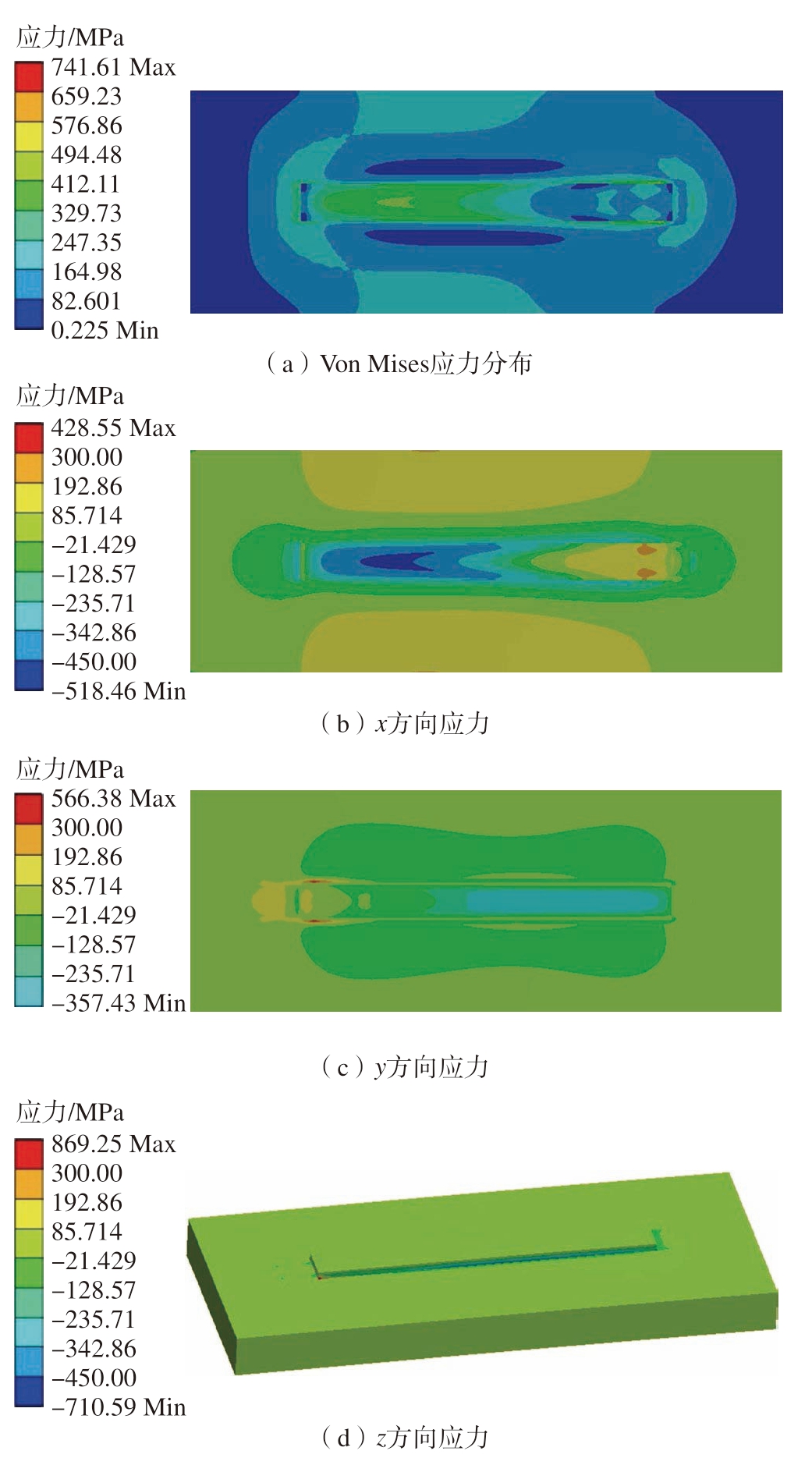
图7 E1组打印结束时Von Mises应力分布及x、y、z方向应力（130 W）
Fig.7 Von Mises stress distribution and x, y, z direction stress at the end of E1 group printing (130 W)
图8为采用E3工艺参数扫描过程中热应力的演变。图8（a）、（c）、（e）对应时间分别为0.01 s、0.025 s、0.04 s，此时光斑中心移动至每道次末端，右端材料被熔融，应力基本为0，左端材料已经凝固冷却，其变形受基板与已成形区的约束，应力较大。在温度场分析中，已知由于热积累效应，高温影响区域随着层数升高而变大，未完全冷却的已打印层起到基板加热的效果，层间温度梯度减小，因此高层打印过程中的整体热应力较小。由图8（b）、（d）、（f）可知，随着层间冷却过程的进行，凝固冷却区域扩大，每道次平均应力均上升。
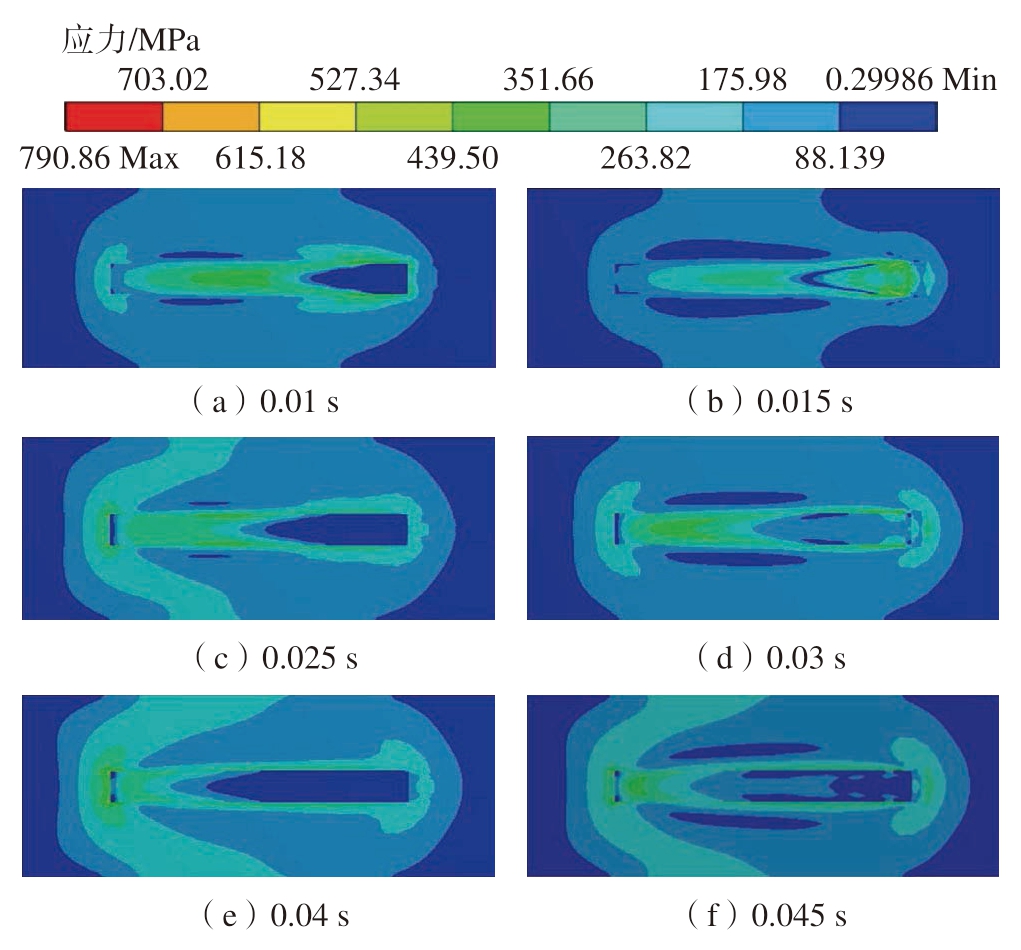
图8 E3工艺下不同时间点的Von Mises应力分布
Fig.8 Von Mises stress distribution at different time points under E3 process
细观模型应力分析如图9所示，可以看出在第1道次打印中，面对相同的散热条件，高功率组具有更高的热应力，这与温度场分析中高功率组温度梯度大，致使应力更大的推断相符，且热应力的变化稍滞后于温度梯度（图9（a））。结合图5（d）可知，0.015 s后随着第2道次打印的进行，E1组无法使已成形层发生重熔，应力释放效果较小，而E2、E3两组对第1道次有重熔效果，使平均热应力值降低，且高功率组降幅更大。但同时层间冷却过程中E3组更快的冷却速度也使其应力增长速率更高，整个打印过程中的最大热应力也超过E2。图9（b）中E2、E3最大应力显著小于E1，同样说明高层扫描时对底层的重熔作用可以释放积累的热应力，这符合Xiao等[15]的结论，即重熔作用相当于瞬间的非均匀退火致使局部应力消除。
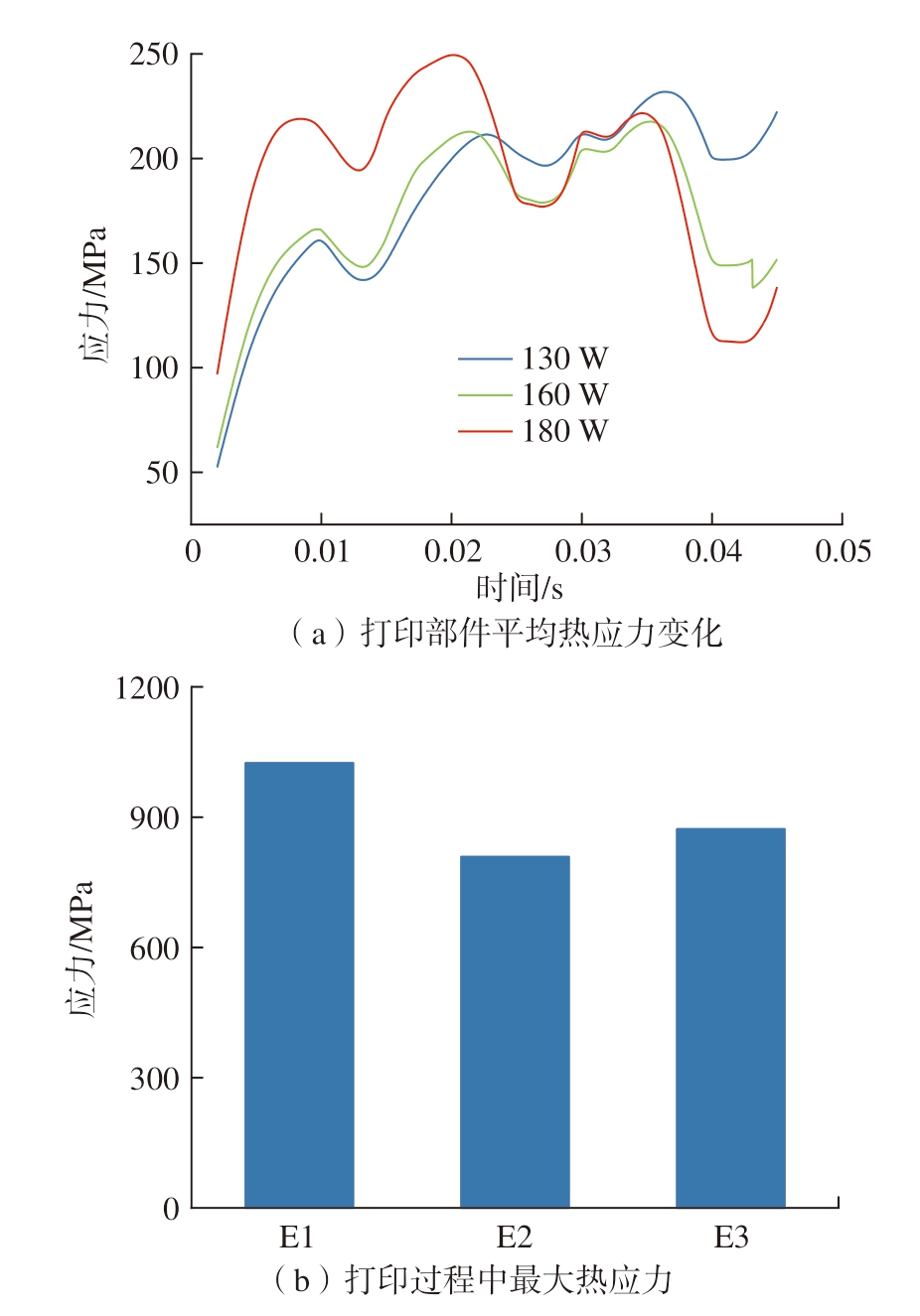
图9 细观模型应力分析
Fig.9 Stress analysis of mesoscopic model
2.2 宏观模拟
熔池模拟结果表明，高功率激光的重熔效果在保持良好冶金结合的同时可以释放下层累积的热应力，使打印过程中部件整体热应力水平降低。而E2、E3的结果表明，熔池的冷却速率随激光功率增加而增加，进而产生较大的温度梯度，引起热应力更快增长，容易导致L-PBF过程产生微裂纹或缺陷。综合考虑应力与温度梯度，薄壁件打印仿真采用E2对应的工艺参数，打印仿真结果如图10和11所示。
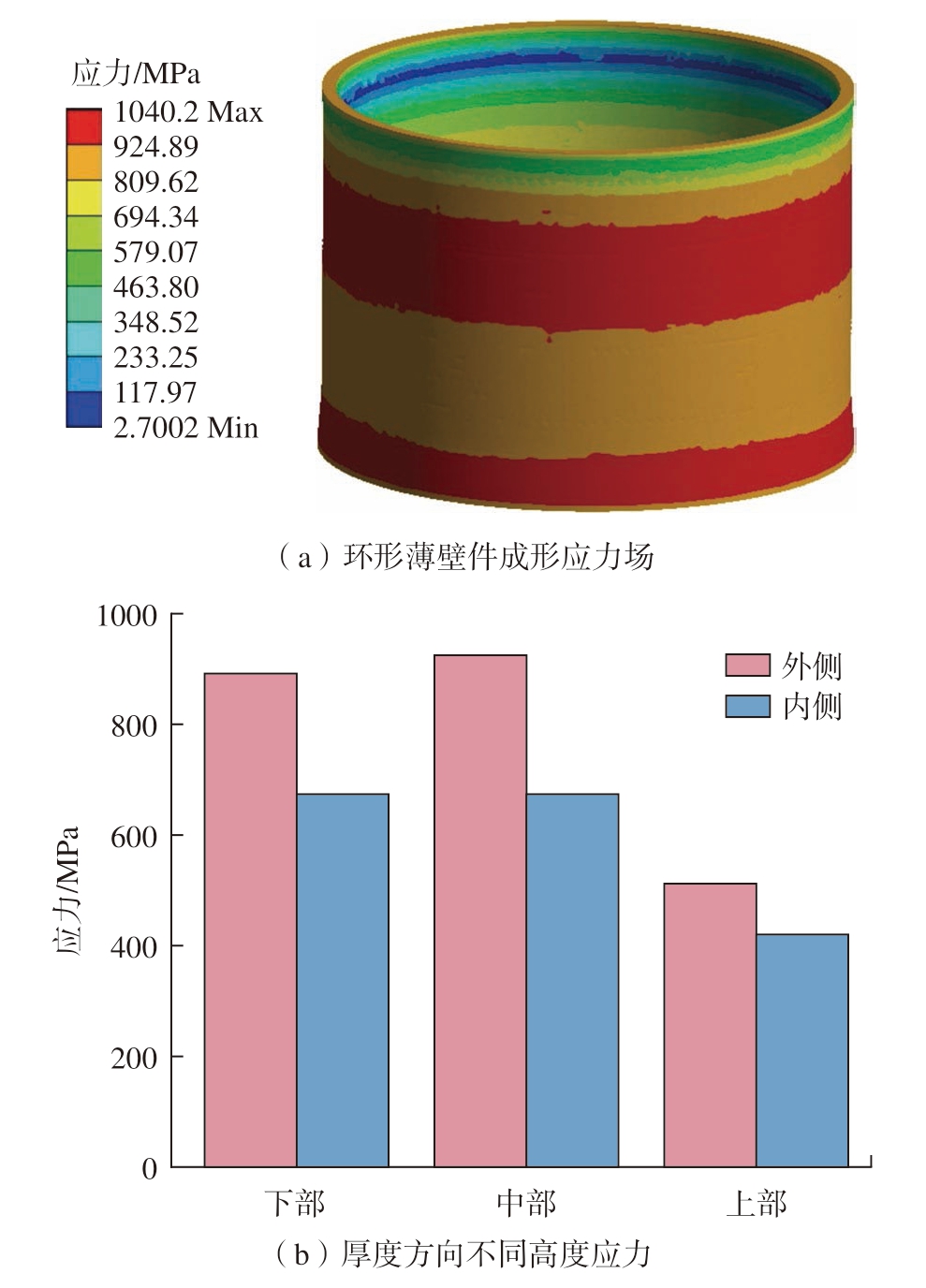
图10 宏观仿真应力结果
Fig.10 Macroscopic simulation stress results
图10显示了打印态的应力分布。残余应力主要分布于环形件的中上部，在厚度方向上由外侧向内，不同高度的残余应力均出现下降趋势。由于基板采用的钢材质，导热系数高于部件，因此成形件下部的热量可以及时导出，且基板加热也缩小了下层区域的温度梯度，使下层残余应力较小，残余应力随层高上涨出现累积效果，与Wang等[16]研究得到的研究结果相符。
图11为打印态变形量分布，工件底部由于基板的限制，变形量几乎为0，上部随应力场的增大而增大，由于对应点阵因热应力影响出现向内凹陷的位移，后续材料在按预定位置打印过程中与已成形层之间出现向外的相对位移，因此顶部总体变形量有所下降。与图10对比，显示出变形量与应力场之间的强相关性。
图11 仿真结果变形分布
Fig.11 Deformation distribution of simulation results
2.3 试验结果
打印成形的样品见图12（a），通过蓝光扫描对样品表面进行测量，绘制样品三维模型并与初始数字模型对比，得到变形量分布 （图12（b））。可以看出，样品呈现中部向内凹陷的形态，且两端较小，中上部较大的变形分布趋势与仿真结果高度吻合。变形量绝对值的差异可能是由于仿真未考虑到的因素，如粉末颗粒度、扫描路径等，以及打印过程中的不稳定因素 （如氧含量、不同设备的误差等）导致的[17]，后期可以通过针对具体设备进行参数标定来改善。
图12 模型打印结果及对比
Fig.12 Model printing results and comparison
2.4 基于宏观模型结果的变形补偿模型输出
通过对宏观模型中工件变形区域进行反向补偿的方法构建新模型，通过ANSYS Workbench平台导出成形件各点变形量数据并与静力学分析进行耦合。采用取值为–1的矫正因子对初始模型进行变形补偿 （图13），计算并导出补偿模型，作为该工件实际打印时的最终模型。图 13（a）为变形量放大10倍后的补偿模型，以表现补偿区域向外凸出。
图13 补偿模型变形量
Fig.13 Deformation of compensation model
使用补偿模型进行成形模拟后，采用初始模型变形最显著的35 mm高度区域进行变形量评判。由图 13（b）可知，补偿模型与初始模型在该高度的位移量大小与分布基本一致，经过补偿矫正后，各方向的位移偏差控制在0.03 mm之内，相比原模型的最大位移量由0.626 mm减小至0.027 mm，降低约95.7%；平均位移量由0.595 mm减小至0.024 mm，降低约95.97%。
3 结论
（1）在L-PBF过程中随功率和扫描道次层数的增加，熔池尺寸与最高温度均增大，其中受功率的影响更显著，且高功率可以带来重熔效果。
（2）由应力分析可知，激光的重熔效果在保持良好冶金结合的同时可以释放下层累积的热应力，但更高的冷却速度也使最大热应力有所增大。
（3）对宏观模型打印过程的模拟验证了残余应力的累积效果，应力分布与变形分布趋势基本匹配，与原模型的成形结果相比，本文所构建的补偿模型平均变形量下降了95.97%，各方向变形均控制在30 μm以内。所采用的超层模拟方法可以高效预估大尺寸工件的变形结果，为实际打印提供预测。
[1] FU J, LI H, SONG X, et al.Multi-scale defects in powderbased additively manufactured metals and alloys[J].Journal of Materials Science & Technology, 2022, 122: 165–199.
[2] 魏雷, 林鑫, 王猛, 等.金属激光增材制造过程数值模拟[J].航空制造技术, 2017, 60(13): 16–25.
WEI Lei, LIN Xin, WANG Meng, et al.Numerical simulation on laser additive manufacturing process for metal components[J].Aeronautical Manufacturing Technology, 2017, 60(13): 16–25.
[3] FU C H, GUO Y B.Three-dimensional temperature gradient mechanism in selective laser melting of Ti–6Al–4V[J].Journal of Manufacturing Science and Engineering, 2014, 136(6): 061004.
[4] MASOOMI M, THOMPSON S M, SHAMSAEI N.Laser powder bed fusion of Ti–6Al–4V parts: Thermal modeling and mechanical implications[J].International Journal of Machine Tools and Manufacture, 2017, 118–119: 73–90.
[5] LI Y L, ZHOU K, TAN P F, et al.Modeling temperature and residual stress fields in selective laser melting[J].International Journal of Mechanical Sciences, 2018, 136: 24–35.
[6] WANG Q S, ZHANG W Y, LI S J, et al.Material characterisation and computational thermal modelling of electron beam powder bed fusion additive manufacturing of Ti2448 titanium alloy[J].Materials, 2021, 14(23): 7359.
[7] LI Z H, XU R J, ZHANG Z W, et al.The influence of scan length on fabricating thin-walled components in selective laser melting[J].International Journal of Machine Tools and Manufacture, 2018, 126:1–12.
[8] 王丽芳, 孙亚新, 朱刚贤, 等.激光熔覆316L不锈钢残余应力工艺参数的优化模拟[J].应用激光, 2019, 39(3): 376.
WANG Lifang, SUN Yaxin, ZHU Gangxian, et al.Optimization simulation of process parameters on the residual stress in 316L stainless steel by laser cladding[J].Applied Laser, 2019, 39(3): 376.
[9] 傅广.钛合金选择性激光熔化成形热过程数值模拟及实验研究[D].重庆: 重庆大学, 2019.
FU Guang.Numerical simulation and experimental study on thermal process of selective laser melting forming of titanium alloy[D].Chongqing: Chongqing University, 2019.
[10] 孙成, 孙亦璋, 刘金, 等.激光增材制造TC4/TC11钛合金梯度结构温度场预测与显微组织分析[J].航空制造技术, 2018, 61(4):96–101.
SUN Cheng, SUN Yizhang, LIU Jin, et al.Temperature field prediction and microstructure analysis of gradient TC4/TC11 titanium alloy deposited by laser additive manufacturing[J].Aeronautical Manufacturing Technology, 2018, 61(4): 96–101.
[11] 冯庆晓, 李多生, 叶寅, 等.层间停留时间对SLM成形Ti6Al4V应力场模拟研究[J].应用激光, 2021, 41(6): 1249–1256.
FENG Qingxiao, LI Duosheng, YE Yin, et al.Numerical simulation on the effect of inter layer idle time on stress field of Ti6Al4V fabricated by SLM[J].Applied Laser, 2021, 41(6): 1249–1256.
[12] LI Y L, GU D D.Thermal behavior during selective laser melting of commercially pure titanium powder: Numerical simulation and experimental study[J].Additive Manufacturing, 2014, 1–4: 99–109.
[13] SHIPLEY H, MCDONNELL D, CULLETON M, et al.Optimisation of process parameters to address fundamental challenges during selective laser melting of Ti–6Al–4V: A review[J].International Journal of Machine Tools and Manufacture, 2018, 128: 1–20.
[14] YIN J, ZHU H H, KE L D, et al.Simulation of temperature distribution in single metallic powder layer for laser micro-sintering[J].Computational Materials Science, 2012, 53(1): 333–339.
[15] XIAO Z, CHEN C, ZHU H, et al.Study of residual stress in selective laser melting of Ti6Al4V[J].Materials and Design, 2020, 193:108846.
[16] WANG L F, JIANG X H, ZHU Y H, et al.An approach to predict the residual stress and distortion during the selective laser melting of AlSi10Mg parts[J].The International Journal of Advanced Manufacturing Technology, 2018, 97(9): 3535–3546.
[17] KING W E, ANDERSON A T, FERENCZ R M, et al.Laser powder bed fusion additive manufacturing of metals: Physics,computational, and materials challenges[J].Applied Physics Reviews,2015, 2(4): 041304.