随着全球工业化水平的不断提高,提升企业的生产效率、降低生产成本成为制造业发展的方向,车间调度问题作为关键问题也越来越受到人们的关注[1]。传统的作业车间调度本质上属于组合优化问题,是NP-hard(非确定性多项式)问题。在作业车间调度的定义中,工件的每道工序仅能被同一台机床加工一次,因此需要解决工序的加工顺序问题。但是随着生产技术水平的不断提高,传统的作业车间调度问题已经不符合现在的生产环境,这使得引入柔性作业车间调度问题成为必然,相较于作业车间调度问题,柔性作业车间调度问题的每道工序既可以在同一台机床加工多次,也允许在多台机床上进行加工,而且不同机床的加工时间通常存在差异,这增加了求解的难度。在求解过程中,机床选择序列和工序选择序列的细微变化都会对结果产生较大的影响,但这更符合实际生产要求,同时也更具有研究意义。目前解决车间调度问题的主要方法有两类[2],分别为最优化方法和近似方法。最优化方法可以求得全局最优解,但是求解速度无法保证;近似方法可以在短时间得到满意解,但是无法适应车间的动态扰动。
针对深度强化学习算法在调度问题中的应用,国内外诸多学者进行了大量研究。对于调度问题的执行方案主要分为两种,第1种是对于组合调度规则进行选取,第2种是对于机床编号进行选取。Bouazza等[3]将部分柔性作业车间分解成分配机床和分配工序两种子问题,针对这两种子问题各采用4种调度规则,利用Q学习算法对规则的选择概率进行计算。Luo[4]利用深度Q网络,将车间状态信息作为神经网络的输入,提出了6种复合调度规则,在工件加工完成和新工件到达时将待加工工件分配到可行的机床上。Liu等[5]考虑了环境中的突发事件,将车间调度视为贯序决策问题,利用Actor–Critic算法构建出演员网络和评论家网络,将状态矩阵作为输入,简单调度规则作为输出。Han等[6]对DQN算法进行改进,加入了优势网络和优先经验回放,并基于析取图模型对车间约束进行建模。Zhou等[7]在DQN算法的基础上提出一种复合奖励机制,构造新型价值网络,以高维度状态数据作为输入,借助学习状态动作值函数,实现精准高效的实时决策。Zhou等[8]针对动态车间,在强化学习算法中使用预测网络和目标网络分别学习预测值和目标值,以当前时刻最大等待时间为优化目标,用两种不同任务间隔概率的案例来说明所提出方法的有效性。Wang等[9]将作业车间调度问题建模为马尔可夫决策过程 (Markov decision process,MDP),利用近端策略优化 (Proximal policy optimization,PPO)算法来解决作业车间动态调度问题,考虑了机床故障、工件再加工等动态及不确定因素,以最小化最大完工时间为优化目标。Kardos等[10]利用多Agent Q学习算法将每个产品作为一个Agent,当到达决策点时选择合适的机床进行加工,同时将产品和机床的状态作为输入。Zhou等[11]针对小批量在线调度问题,将车间中的设备实体作为Agent,利用多Agent强化学习算法,使每个设备都可以通过学习以往调度经验来与其他Agent进行协作。
本文同时训练两种Agent对每个决策点的机床和工件进行评分,分别解决柔性作业车间调度问题中的工序排序子问题和机床排序子问题。通过设计通用的车间环境状态空间,将对工件和机床的评分值离散化后作为动作输出,根据优化目标设定奖励值函数,训练工件Agent和机床Agent,在每个决策点选取评分值最高的工件和机床作为当前调度方案。利用Agent与环境的不断交互,使Agent可以根据环境的变化即时做出反应,且同时具备一定的抗干扰能力。
1 柔性作业车间调度模型的构建
1.1 柔性作业车间调度约束模型
对于柔性作业车间调度问题的描述如下。假设有n个工件 (J1,J2,…,Jn)要在m台机床 (M1,M2,…,Mm)上加工,对于每一个工件,包含hi道工序 (Oi1,Oi2,…,Oihi);其中每道工序可以在多台同种类型的机床上加工;由于机器之间的差异性,每道工序在不同机床上的完工时间互不相同;为了使整个系统的特定性能指标达到最佳,需要完成机床和工件工序的安排,将每道工序放置在当前最适宜加工的机床上,并确定机床上每一道工序的加工序列和开始加工的时间。所以柔性作业车间包含两个子问题:确定工件的加工机床 (机床选择子问题)和各机床上工件的加工顺序 (工序排序子问题)。而对于作业车间调度问题,工件每道工序仅可以安排在一台机床上,所以柔性作业车间调度问题更加复杂,但更符合实际车间加工环境。
柔性作业车间加工过程中的约束条件: (1)每台机床在每一时刻只能加工一个工件;(2)每一个工件的每一个工序在同一时刻只能被一台机床加工;(3)每个工件一旦开始加工,到此道工序结束,中间不能暂停;(4)不同的工件之间的优先级相同;(5)同一个工件的工序先后顺序不能改变,只有当前一道工序加工完成后方可加工下一道工序;(6)在开始时刻,所有的工件都可以被加工。具体约束条件公式如下。
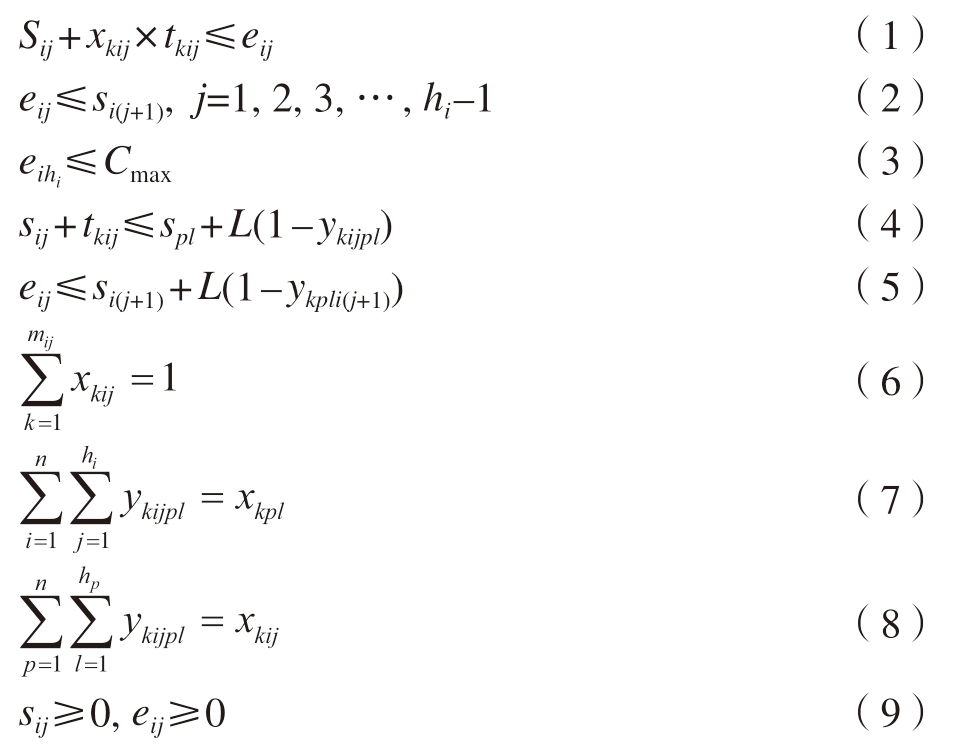
各变量符号含义见表1。式(1)和 (2)表示同一个工件的后一道工序必须在前一道工序加工完成后才可以开始;式 (3)表示所有工件完成加工的时间要小于等于总工件的最大完工时间;式 (4)和 (5)表示每台机床在每一时刻只能加工一个工件的其中一道工序;式 (6)表示同一时刻同一道工序仅可以被一台机床加工;式(7)和 (8)表示每一台机床有循环排列的操作;式 (9)表示参数变量的值必须为非负数。
表1 变量符号含义
Table 1 Variable sign meaning
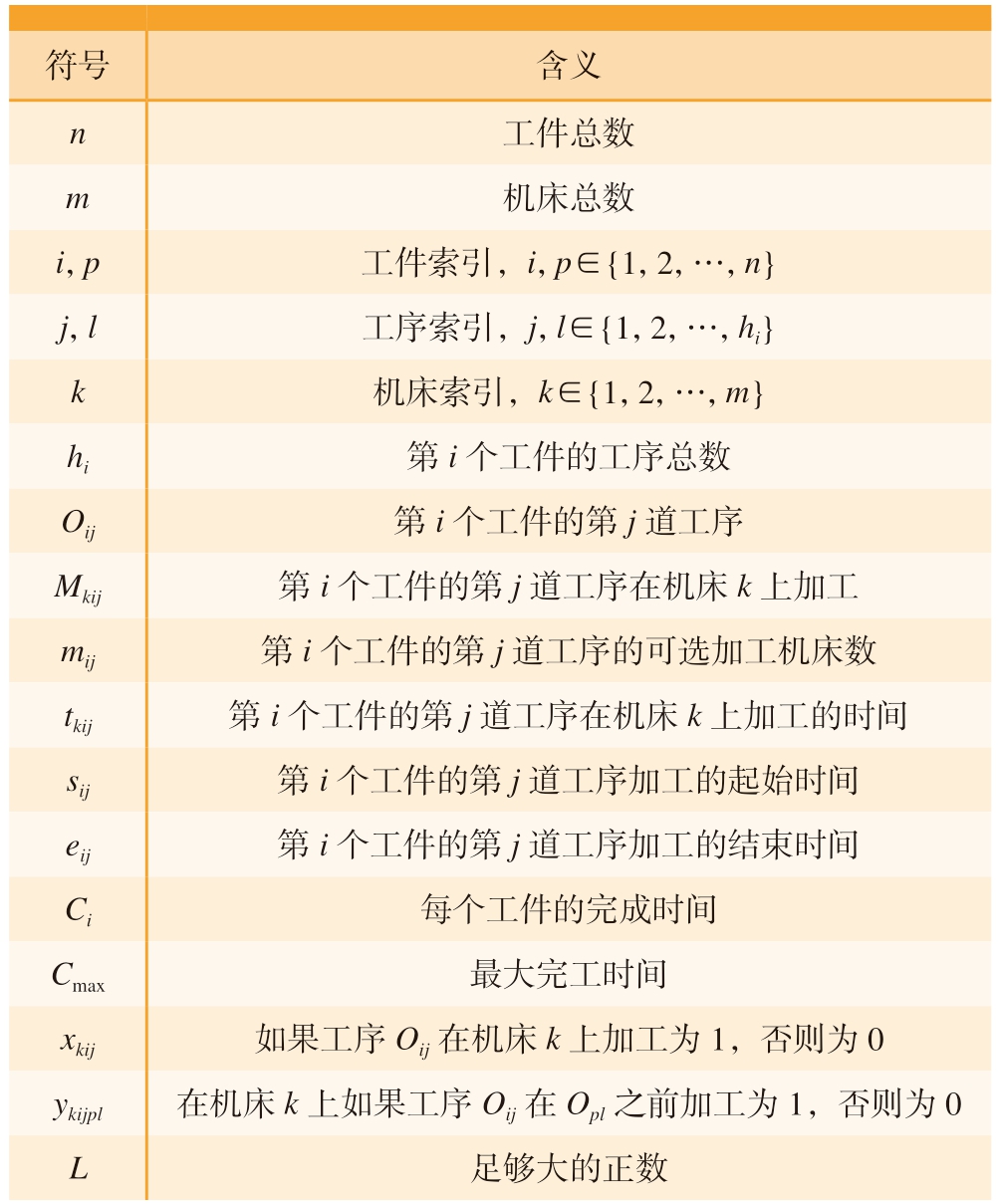
符号含义n 工件总数m机床总数i,p工件索引,i,p∈{1,2,…,n}j,l工序索引,j,l∈{1,2,…,hi}k机床索引,k∈{1,2,…,m}hi第i个工件的工序总数Oij第i个工件的第j道工序Mkij第i个工件的第j道工序在机床k上加工mij第i个工件的第j道工序的可选加工机床数tkij第i个工件的第j道工序在机床k上加工的时间sij第i个工件的第j道工序加工的起始时间eij第i个工件的第j道工序加工的结束时间Ci每个工件的完成时间Cmax最大完工时间xkij如果工序Oij在机床k上加工为1,否则为0 ykijpl在机床k上如果工序Oij在Opl之前加工为1,否则为0 L足够大的正数
1.2 强化学习与马尔可夫决策过程
本文将作业车间调度问题抽象成MDP并进行数学建模。一个MDP一般由状态空间、动作空间、状态转移函数、奖励值函数等组成,由一个四元组来表示 (S,As,P,R),其中S表示环境中状态空间的集合;As表示Agent可以采用的动作空间集合;P表示状态转移函数,当一个Agent对当前所观测到的环境采取动作a后,状态从s变到s+1的状态转移概率;R则表示动作执行后环境反馈的奖励值。
在强化学习中,本文将Agent动作执行后得到的奖励值定义为 (r1,r2,…,rn),将折扣回报定义为各时刻奖励值的折扣累加和,即
式中,γ为折扣率;rt为时间差分目标;rk为执行动作后得到的奖励值。
定义动作价值函数和最优动作价值函数为
式中,St、st为t时刻的状态及其观测值;At、at为t时刻的动作及其观测值。
通过以上公式可以推导出最优贝尔曼方程:
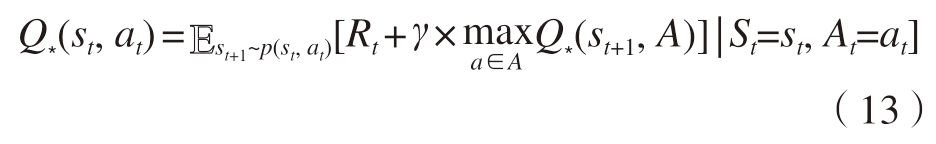
Agent在执行动作at后,环境将根据p(st+1 | st,at)计算新状态st+1,并且观测到这次动作的奖励值rt,将结果记录到四元组中 (st,at,rt,st+1),于是可得近似结果为
将式 (14)中得到的最优动作价值函数替换成神经网络的形式,得到
式中,ω为神经网络参数。
本文采取的是基于DQN的强化学习算法,需要考虑算法存在的高估问题,这种高估对Agent的所有动作是非均匀的,会严重影响算法的性能,所以通过使用Double DQN加上Dueling network来进一步提高算法的准确性。Agent的第1步是进行选择 (式 (15)),第2步计算求值时使用目标网络 (式 (16))。
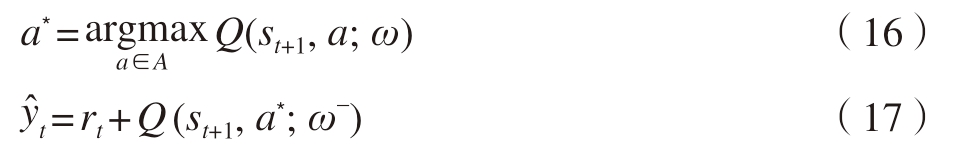
同时使用D(s,a;ωD)作为最优优势函数D*(s,a)的近似,V(s;ωV)作为最优状态价值函数V*(s)的近似,可以将最优动作函数进一步写为
Q(s,a;ωD)和V(s;ωV)共享部分全连接层,先将输出分为每个动作的优势值和状态的价值,最终合并输出每个动作的动作价值。
2 基于Dueling double DQN(D3QN)的车间调度算法设计
2.1 状态空间
对于车间状态来说,需要从总体和局部两方面综合考虑,以便Agent能够全面地观测到车间的所有状态。本文综合考虑了18种状态,涉及工件、机床、订单队列和缓冲区的状态信息,由于这些状态之间的数据范围和量纲都不相同,如果不加处理直接作为算法输入可能会不适用于未经过训练的数据。所以为了提高算法的泛化性和通用性,采用归一化的方式将这些状态信息映射到[0,1]的区间,将这些状态信息组合成状态向量s=[s1,s2,…,s18],具体状态信息如表2所示。
表2 车间环境的状态特征
Table 2 State characteristics of job-shop environment
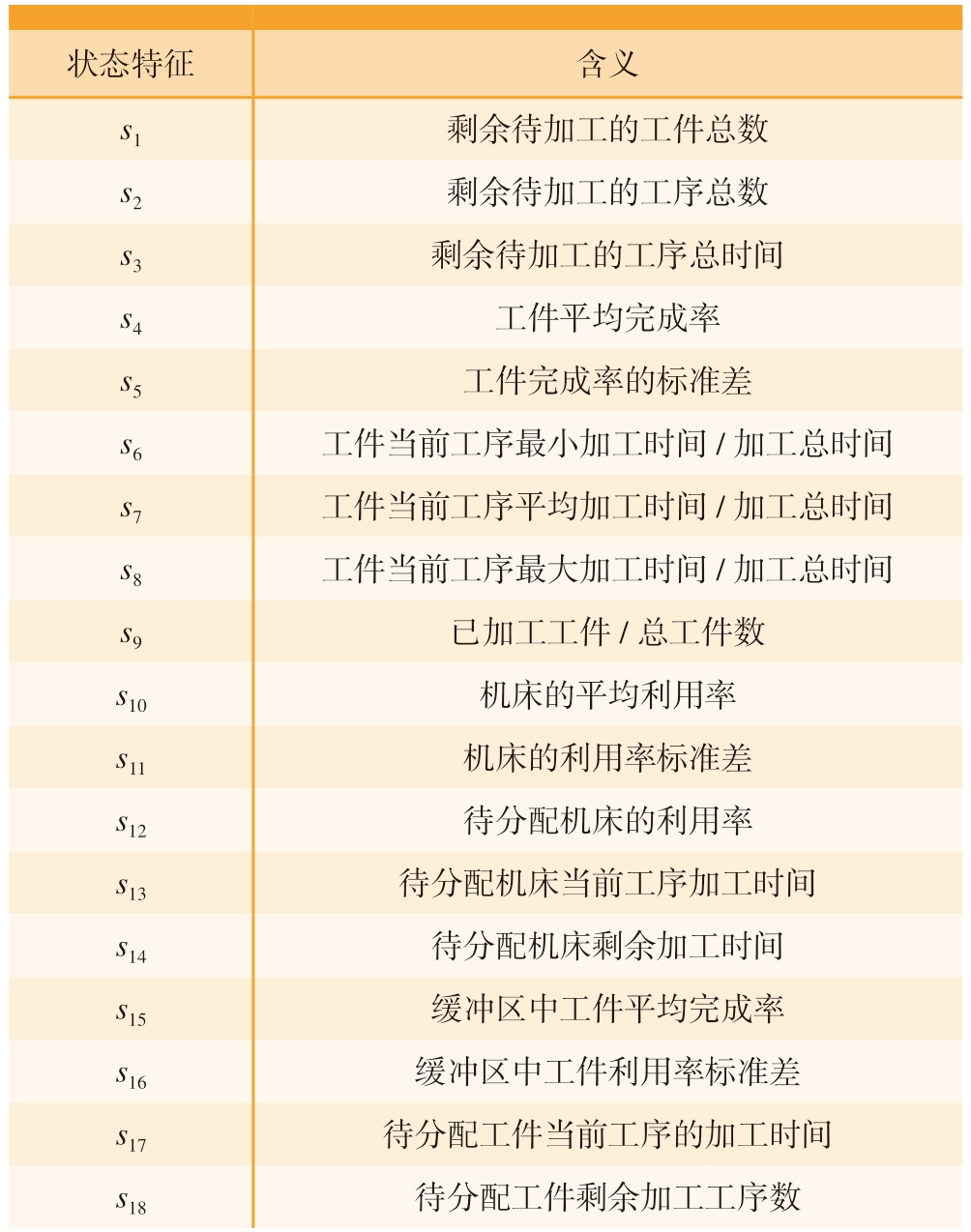
状态特征含义s1剩余待加工的工件总数s2剩余待加工的工序总数s3剩余待加工的工序总时间s4工件平均完成率s5工件完成率的标准差s6工件当前工序最小加工时间/加工总时间s7工件当前工序平均加工时间/加工总时间s8工件当前工序最大加工时间/加工总时间s9已加工工件/总工件数s10机床的平均利用率s11机床的利用率标准差s12待分配机床的利用率s13待分配机床当前工序加工时间s14待分配机床剩余加工时间s15缓冲区中工件平均完成率s16缓冲区中工件利用率标准差s17待分配工件当前工序的加工时间s18待分配工件剩余加工工序数
2.2 动作空间
动作空间为Agent可选的动作集合,本文将整个调度问题分解为两个子问题,工件选择当前工序可以加工的机床和最早可用的机床选择缓冲区内的工件。本文算法的训练目的是对待选择机床和工件分别进行评分,从候选结果中选择得分较高的机床和工件作为下一步要执行的动作。设定分值都为正数,将分值从10~90平均分成9段,每隔10分为一段,划分出9个动作,a=[a1,a2,a3,…,a9],分值作为对待选择机床或工件的评分值,分值越高代表选择当前机床或工件的调度结果越好,越能满足调度指标。
2.3 奖励值函数
奖励函数的设定与算法最终的优化目标有着密切的关联,本文要优化的调度目标为最小化最大完工时间,是衡量调度性能的最根本指标,可以体现车间的生产效率,可表示为
在解决两个子问题时,需要采取不同的奖励函数,首先在工件选择待加工机床时,要充分考虑各台机床的负荷情况,瓶颈设备就是负荷最大的机床,要使机床的负荷平衡且尽量小,即时奖励值为
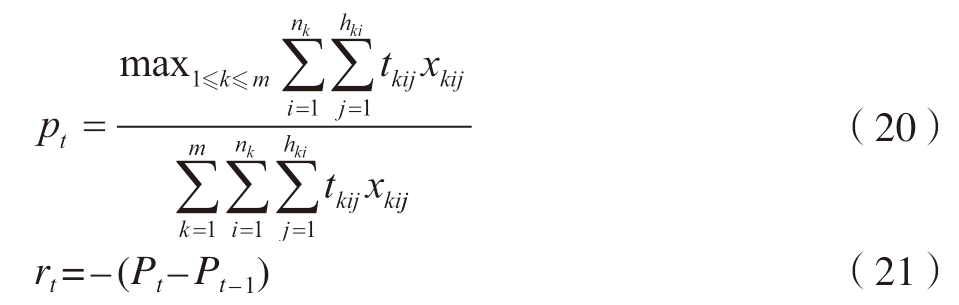
式中,nk表示已加工的工件数;hki表示已加工工件的工序数。
在机床选择缓冲区内的工件时,采用动作执行之后的平均机床利用率之差来计算[12],平均机床利用率为

式中,tmax表示到达当前决策时间点的最长时间,则即时奖励函数定义为
2.4 探索和利用
在强化学习中不仅要利用已经学习到的经验,从已知动作中选择下一步动作,最大限度地提高累计回报值,还要尝试探索更多的环境信息,尝试未试过的行为,以免陷入局部最优结果。大多数的强化学习算法中会使用ε-greedy算法,即
式中,p为在0 ~ 1之间生成的随机数值,以ε(探索的概率)的概率选取当前价值最大的动作,以1– ε(利用的概率)的概率从动作空间中随机选取动作,作为当前Agent的动作。
2.5 车间调度框架设计及模型更新流程
本文使用Dueling double DQN算法对车间调度问题进行求解,同时训练两个Agent,分别对待选工件和机床进行评分,在所有候选集中选择分值最高的机床和工件,作为下一步的调度方案,从而完成工件和机床的资源分配任务,算法的更新流程如下。


车间调度流程如图1所示,在流程开始后,首先初始化车间状态和其他超参数,将机床加工记录清除,并把订单中的工件加入生产订单队列,等待分配加工设备。然后判断是否达到迭代设定阈值,如果达到则算法流程结束,保存训练模型,否则继续执行训练流程。在车间调度过程中,算法的核心是如何同时训练工件评分和机床评分两个Agent,两个Agent同时参与执行调度任务,如果各自没有达到决策点,Agent会阻塞当前进程,直到出现下一个决策点。当机床前的缓冲区有空余的位置时,唤醒阻塞的机床Agent对订单队列里下一个工件当前工序的所有可加工机床进行评分,选出动作at,比较所有候选机床的分值,选定分值最大的机床,将工件分配到该机床上,将当前经验值 (st,at,rt,st+1)存储到经验回放池中,如果出现分数相同的情况,则随机选取。当机床结束当前工序的加工任务时,唤醒工件Agent,对机床缓冲区前的工件进行评分,同样选取分值最大的工件进行下一步加工,将经验值存入回放池中。最后当经验池达到足够多的样本后,从中随机抽取出固定批量的样本,计算样本的时序差分误差,对神经网络参数执行梯度下降法更新,当达到设定的C步后,重设Target网络的参数值。本文使用经验回放的方式来打破序列之间的相关性,因为在训练Agent对工件和机床进行评分的过程中,搜集到的两个相邻四元组 (st,at,rt,st+1)和 (st+1,at+1,rt+1,st+2)之间有很强的相关性,所以加入经验回放来消除相关性对算法训练结果的影响。
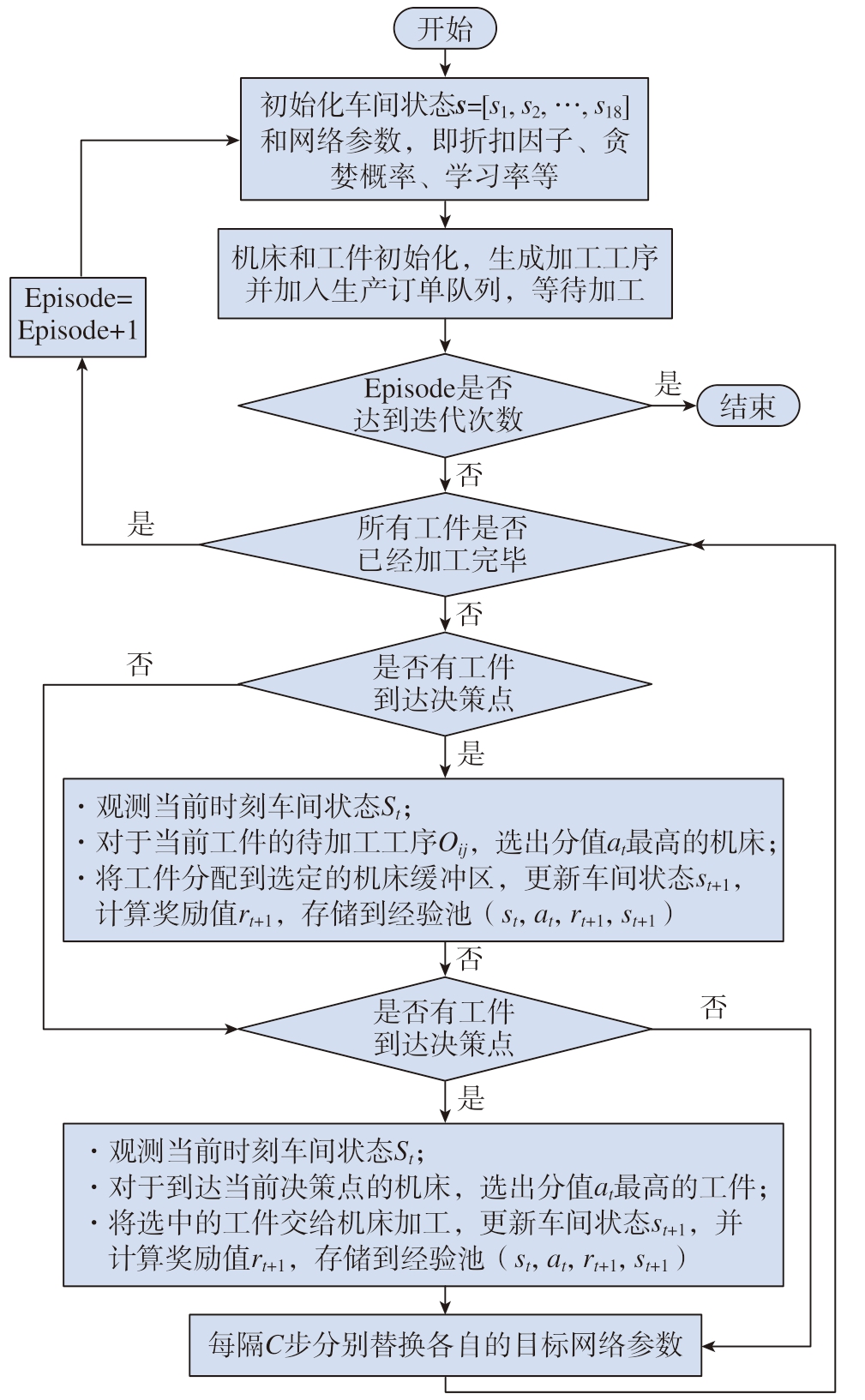
图1 调度算法流程图
Fig.1 Flow chart of scheduling algorithm
3 实例验证
3.1 算法参数设置
本文使用Python 3.6与Tensorflow 2.0框架作为深度强化学习算法试验环境,硬件配置为Intel(R) Core(TM) i5–6300HQ CPU @2.30 GHz,RAM 16 GB,NVDIA GeForce GTX 960 M,部分算法参数见表3。
表3 算法参数设置(部分)
Table 3 Algorithm parameters setting (partly)
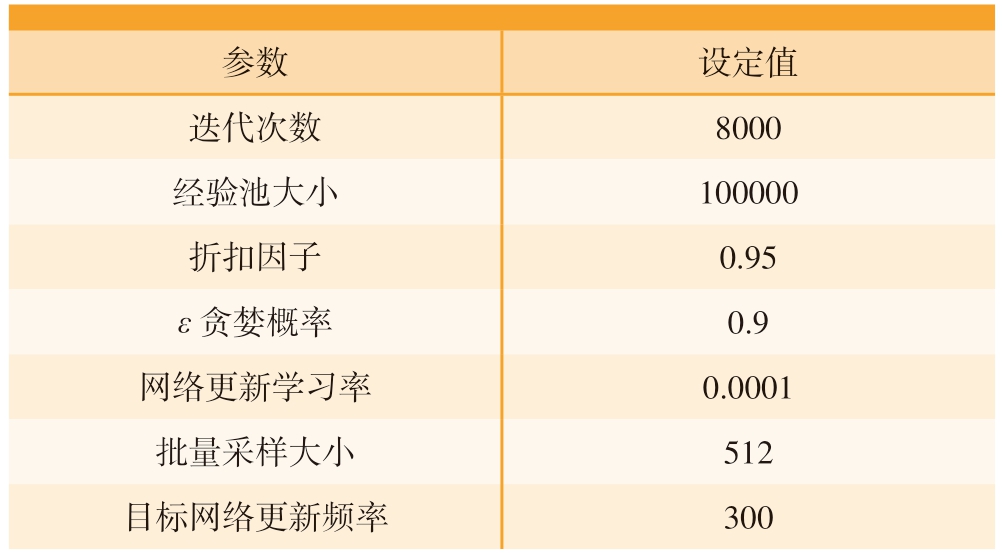
参数设定值迭代次数8000经验池大小100000折扣因子0.95 ε贪婪概率0.9网络更新学习率0.0001批量采样大小512目标网络更新频率300
本文的神经网络使用了全连接神经网络,包含3个隐藏层,节点数为100、50、30,在第1层输出后加入Sigmoid激活函数,后两层的输出都加入Relu激活函数,价值网络和优势动作网络共享相同的全连接神经网络层,神经网络结构图如图2所示。
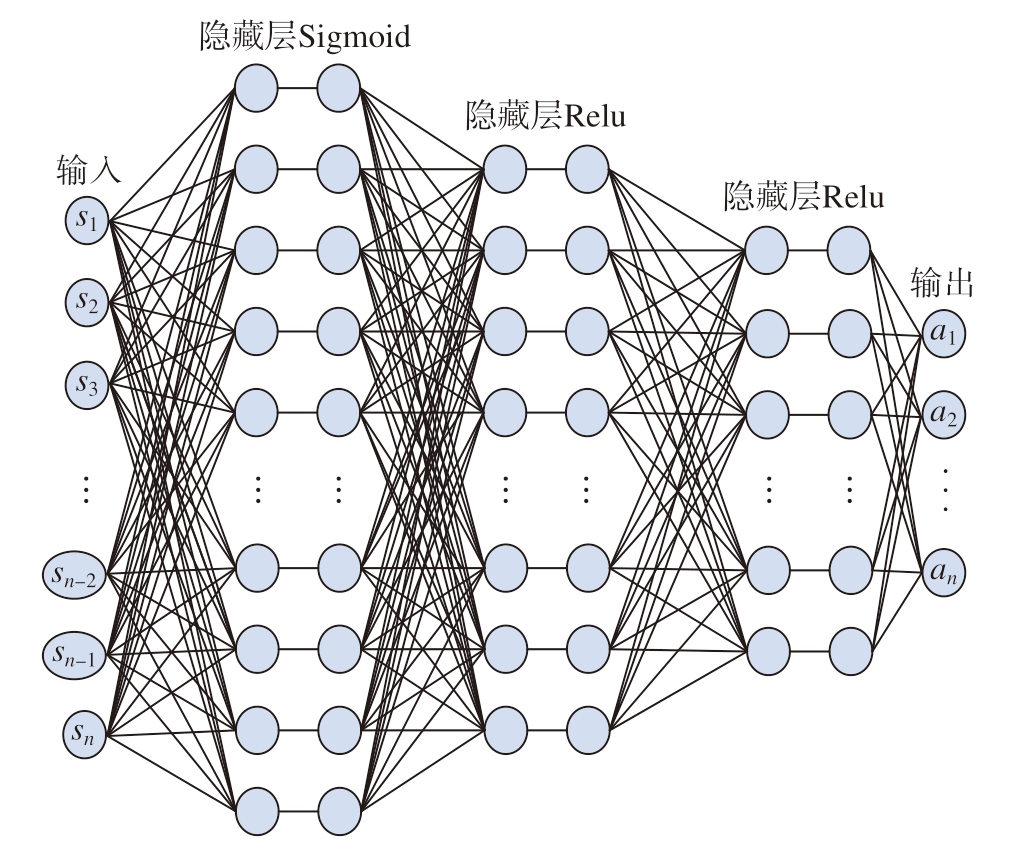
图2 神经网络结构图
Fig.2 Structure diagram of neural network
3.2 案例分析和试验对比
本文使用的车间试验环境包含3种加工设备,分别为车床、铣床和钻床,每种机床各4台,共12台机床,工件的同种工序在不同机床上的加工时间各不相同,设定工序额定加工时间乘以加工系数为机床实际加工时间。加工的工件种类有3种,每种工件有3种或4种工序,设定工件的到达时间相同,且各机床的缓冲区容量都为4。车间环境参数如表4所示,算法的迭代次数设定为1000次,3种工件个数分别随机生成,共30个工件进行初步训练,机床Agent和工件Agent的累计回报值的结果平滑曲线如图3所示。可以看出,机床评分Agent在大约750次迭代之后达到稳定,工件评分Agent在大约700次迭代后收敛。由于训练过程中的贪婪概率始终存在,在Agent做选择时有一定概率会随机从动作空间中选择,所以后期的迭代依然存在波动,但并不影响算法整体的收敛性能。最大完工时间的收敛结果如图4所示,在600次迭代后趋于平缓,说明两个Agent都学习到了如何有效分配车间的资源,验证了本文算法的有效性。
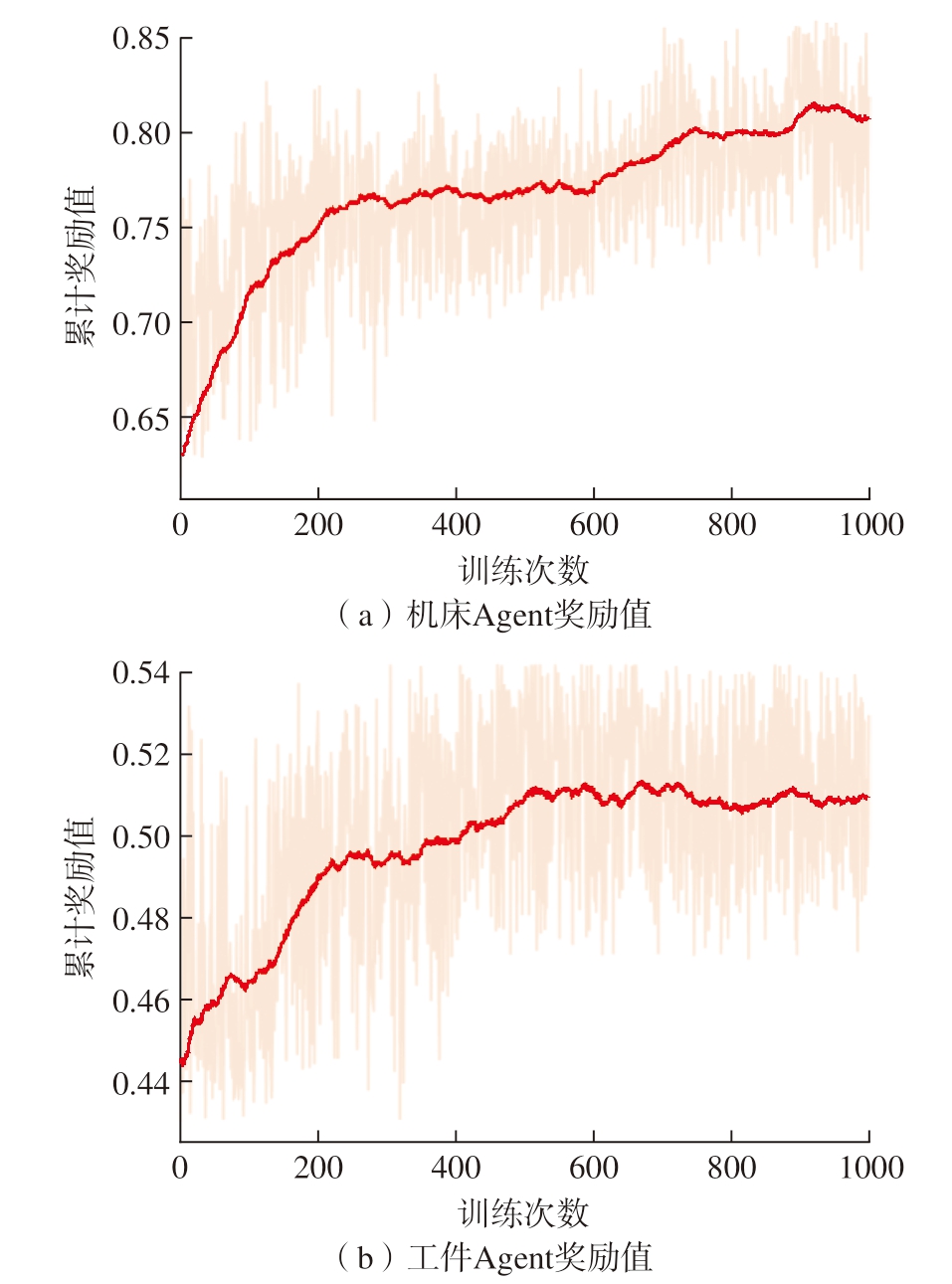
图3 机床Agent和工件Agent奖励值曲线
Fig.3 Reward value curves of machine tool Agent and workpiece Agent
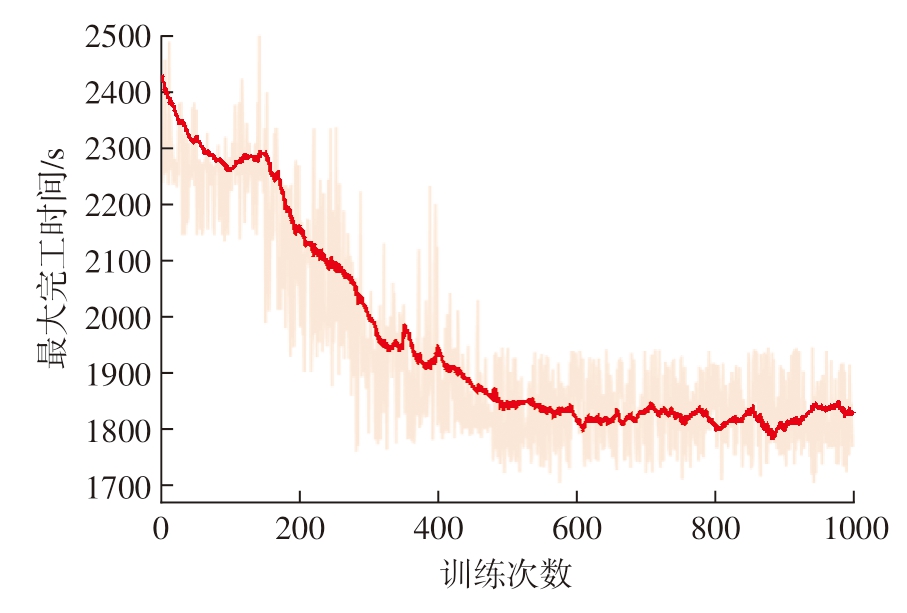
图4 最大完工时间收敛曲线
Fig.4 Convergence curve of maximum completion time
表4 车间环境参数
Table 4 Job-shop environment parameters
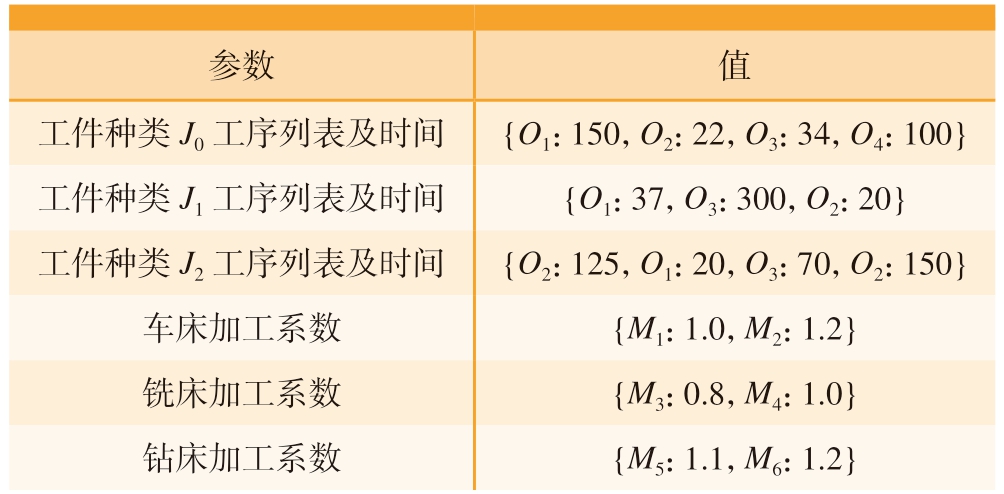
参数值工件种类J0工序列表及时间{O1:150,O2:22,O3:34,O4:100}工件种类J1工序列表及时间{O1:37,O3:300,O2:20}工件种类J2工序列表及时间{O2:125,O1:20,O3:70,O2:150}车床加工系数{M1:1.0,M2:1.2}铣床加工系数{M3:0.8,M4:1.0}钻床加工系数{M5:1.1,M6:1.2}
为了分析算法在不同规模订单下的求解情况,在上述工件的工序数量和种类不变的情况下,将工件的规模设定为10个、20个、30个、50个、100个和200个并分别进行10次独立的仿真试验,对最终的完工时间取平均值,并与其他两种基于DQN算法的调度方案进行对比。其中,方法1对于组合调度规则进行 (SDR):选取SPT、LPT、FIFO、LIFO、SRPT、LRPT 6种调度规则作为动作空间;方法2对于机床编号进行选取 (SMN),将机床的编号作为动作空间,通过选取编号完成机床分配工件,机床则采取先进先出的规则来选择要加工的工件。最终得到的结果如图5所示,可以看出在相同的试验环境中,本文算法通过对工件和机床的组合分配,可以达到更优的解,在不同规模的问题上都表现较好。
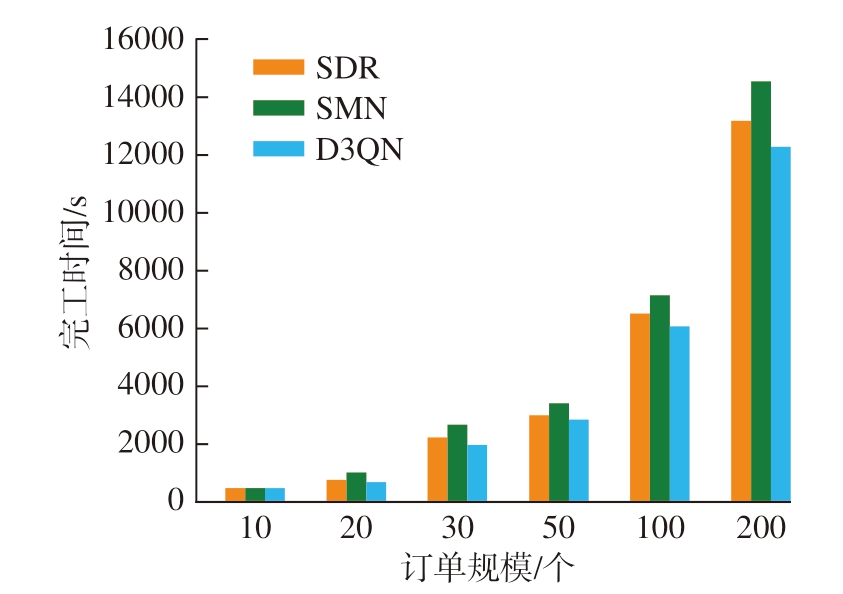
图5 不同订单规模下的完工时间
Fig.5 Completion time under different order sizes
本文的算法考虑到在工件调度到机床后,并不一定立刻开始加工,而是先放到缓冲区,然后根据当前车间环境状态选择此刻适宜加工的工件,这样就会有更灵活的选择方案,从而得到更优的调度结果。同时本文也考虑到车间中会出现机床故障,导致加工无法进行的情况,同样在机床发生故障概率为10% ~ 60%的情况下进行10次试验,选定工件的数量为30个,并设定机床的恢复时间相同,一旦恢复即可开始加工,得到的结果取平均值,如图6所示。结果表明本文算法在车间发生动态扰动的情况下可以快速产生反应并得到一个较优的结果。
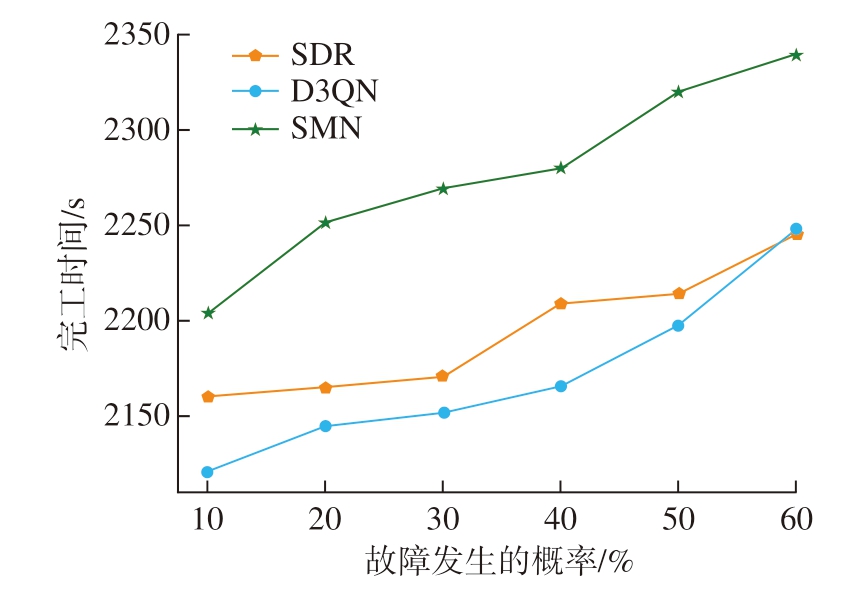
图6 不同故障概率下的完工时间
Fig.6 Completion time under different failure probabilities
4 结论
本文针对柔性作业车间提出了基于Dueling double DQN的强化学习车间调度算法,将调度问题转化为马尔可夫决策过程,同时训练机床Agent和工件Agent对当前待选工件和机床进行评分,从而完成机床和工件的分配。设计了18种通用的车间环境状态并归一化处理,评分值作为动作空间,以最小化最大完工时间作为最终目标来设计奖励函数。经过多次试验表明,本文算法在不同规模的订单下都可以取得很好的效果,结果都优于选择组合调度规则和直接选择加工机床两种调度方式。进一步的研究工作主要集中在对分值进行更细粒度地划分、采用基于策略的强化学习算法 (如A– C、PPO)等;本文以最小化工件的最大完工时间作为优化目标,可以针对多种目标和动态调度等方面进行下一步的研究。
[1] 罗梓珲, 江呈羚, 刘亮, 等.基于深度强化学习的智能车间调度方法研究[J].物联网学报, 2022(1): 53–64.
LUO Zihui, JIANG Chengling, LIU Liang, et al.Research on deep reinforcement learning based intelligent shop scheduling method[J].Chinese Journal on Internet of Things, 2022(1): 53–64.
[2] 钟敬伟, 石宇强.基于DQN的智能工厂作业车间调度[J].现代制造工程, 2021(9): 17–23, 93.
ZHONG Jingwei, SHI Yuqiang.Job shop scheduling based on DQN algorithm in intelligent factory[J].Modern Manufacturing Engineering,2021(9): 17–23, 93.
[3] BOUAZZA W, SALLEZ Y, BELDJILALI B.A distributed approach solving partially flexible job-shop scheduling problem with a Q-learning effect[J].IFAC-PapersOnLine, 2017, 50(1): 15890-15895.
[4] LUO S.Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning[J].Applied Soft Computing,2020, 91: 106208.
[5] LIU C L, CHANG C C, TSENG C J.Actor–Critic deep reinforcement learning for solving job shop scheduling problems[J].IEEE Access, 2020, 8: 71752–71762.
[6] HAN B A, YANG J J.Research on adaptive job shop scheduling problems based on dueling double DQN[J].IEEE Access, 2020, 8: 186474–186495.
[7] ZHOU T, TANG D B, ZHU H H, et al.Reinforcement learning with composite rewards for production scheduling in a smart factory[J].IEEE Access, 2020, 9: 752–766.
[8] ZHOU L F, ZHANG L, HORN B K P.Deep reinforcement learning-based dynamic scheduling in smart manufacturing[J].Procedia CIRP, 2020, 93: 383–388.
[9] WANG L B, HU X, WANG Y, et al.Dynamic job-shop scheduling in smart manufacturing using deep reinforcement learning[J].Computer Networks, 2021, 190: 107969.
[10] KARDOS C, LAFLAMME C, GALLINA V, et al.Dynamic scheduling in a job-shop production system with reinforcement learning[J].Procedia CIRP, 2021, 97: 104–109.
[11] ZHOU T, TANG D B, ZHU H H, et al.Multi-agent reinforcement learning for online scheduling in smart factories[J].Robotics and Computer-Integrated Manufacturing, 2021, 72: 102202.
[12] 李宝帅, 叶春明.深度强化学习算法求解作业车间调度问题[J].计算机工程与应用, 2021, 57(23): 248–254.
LI Baoshuai, YE Chunming.Job shop scheduling problem based on deep reinforcement learning[J].Computer Engineering and Applications,2021, 57(23): 248–254.