铝合金有轻质、耐腐蚀性、可加工、低成本等特点，广泛应用于航空航天、轨道交通、汽车等领域。然而，铝合金在铸造过程中会不可避免地出现气孔、缩孔等缺陷，严重影响合金的力学性能[1]，因此优化成形工艺的前提条件是对三维微观组织缺陷的预测。
当前，模拟计算凝固过程显微结构的方法主要有元胞自动机 （Cellular automaton，CA）[2–3]、相场法 （Phase field，PF）[4–5]、前沿跟踪法 （Front tracking，FT）等。其中CA模型能够清晰直观地展现凝固过程中孔洞和枝晶等微观组织复杂的形核和长大的过程，是一种高效的计算方法，因此CA模型在凝固过程中的模拟得到广泛的应用。对于铝合金来说，氢在固、液两相中的溶解度相差数十倍，因此氢气孔是铝合金最常见的缺陷之一。为此，Lee等[6]对2001年以前的铝合金孔隙模拟方法进行了系统地综述，对比了解析解、判据函数、达西定律、气体扩散模型和连续–随机模型5种孔隙模拟方法的优点和局限性。为了研究凝固过程孔隙的形核和生长的演化过程，Lee[7]和Atwood[8]等建立了针对于二元铝合金中氢的扩散，以及孔隙的形核、生长与晶粒形核生长相耦合的CA模型，系统分析了不同冷速下形核温度与孔隙尺寸分布。Wang[9]在Lee等[7]的模型基础上模拟了不同铸造工艺的Al–Cu、Al–Si和Al–Si–Cu合金的孔洞，还采用球形度和弯曲度来描述孔洞三维形貌。此外，Wang[10]和Li[11]等分别采用三维CA模型对Al–Si–Cu和Al–Li合金在不同冷却速率下的微孔尺寸进行量化分析。进一步地，Sun等[12]建立的CA–格子玻尔兹曼 （CA–LB）模型可以模拟流场作用下枝晶和微孔的生长。Hu等[13]建立了二维多相CA–FD–LB耦合模型 （FD为有限差分），对亚共晶Al–Si合金中枝晶和共晶凝固过程中氢气孔的形成进行精确预测。Gu等[14]在之前模型的基础上考虑了凝固过程中液相收缩压力，不仅能预测气孔，而且能预测凝固后期的缩孔。
上述CA模型仅能在微观尺度上进行预测，存在一定的限制。当前现有的铸造铝合金的多尺度预测模型也存在耦合成本过高[15–17]，在实际应用中受限等问题，无法满足工业需求[18–19]。为此，本文基于ProCAST有限元模拟软件，与CA模型进行耦合程序开发，能够高效预测整个轮毂的孔洞缺陷。为了验证模型的准确性，使用X射线计算机断层扫描技术 （X-CT）根据合金内部灰度值差异准确地量化三维空间的微孔分布，X-CT比二维表征更有优势。Zhang[20]和Li[11]等也利用X-CT技术验证了Al–Li合金微孔模拟的预测精度。
综上所述，本文基于ProCAST有限元软件和CA模型的耦合，系统地介绍了多尺度预测模型中冷却速率计算、微孔演变等过程，通过X-CT技术三维表征轮毂不同区域的孔洞分布，从孔洞当量直径、几何长度等多个特征参数入手，对比并评估该模型的准确性，为铸造铝合金一体化成形工艺优化奠定基础。
1 试验及方法
1.1 基于有限元和CA的耦合模型建立
1.1.1 耦合模型的整体框架
首先基于传统的铸造仿真模拟软件ProCAST（2018）进行二次开发，可以获得低压铸造的铸件宏观缩孔，以及有限元网格上各节点的物理信息，主要包括平均冷却速率，同时将各节点的坐标与编号一同输入到数据库中。进一步地，以铸造仿真的平均冷却速率作为输入，使用CA模型模拟铸造仿真有限元网格上所有节点处的微观组织生长，获得微观孔洞的形貌和尺寸数据。最后将CA仿真结果输入到数据库相应节点处保存，主要包括节点处微孔当量直径和微孔长度等。等待运行，完成整个程序，即可以得到轮毂各个位置节点的孔洞参数，实现从介观到宏观的多尺度仿真模拟。图1展示了耦合模型的整体框架。
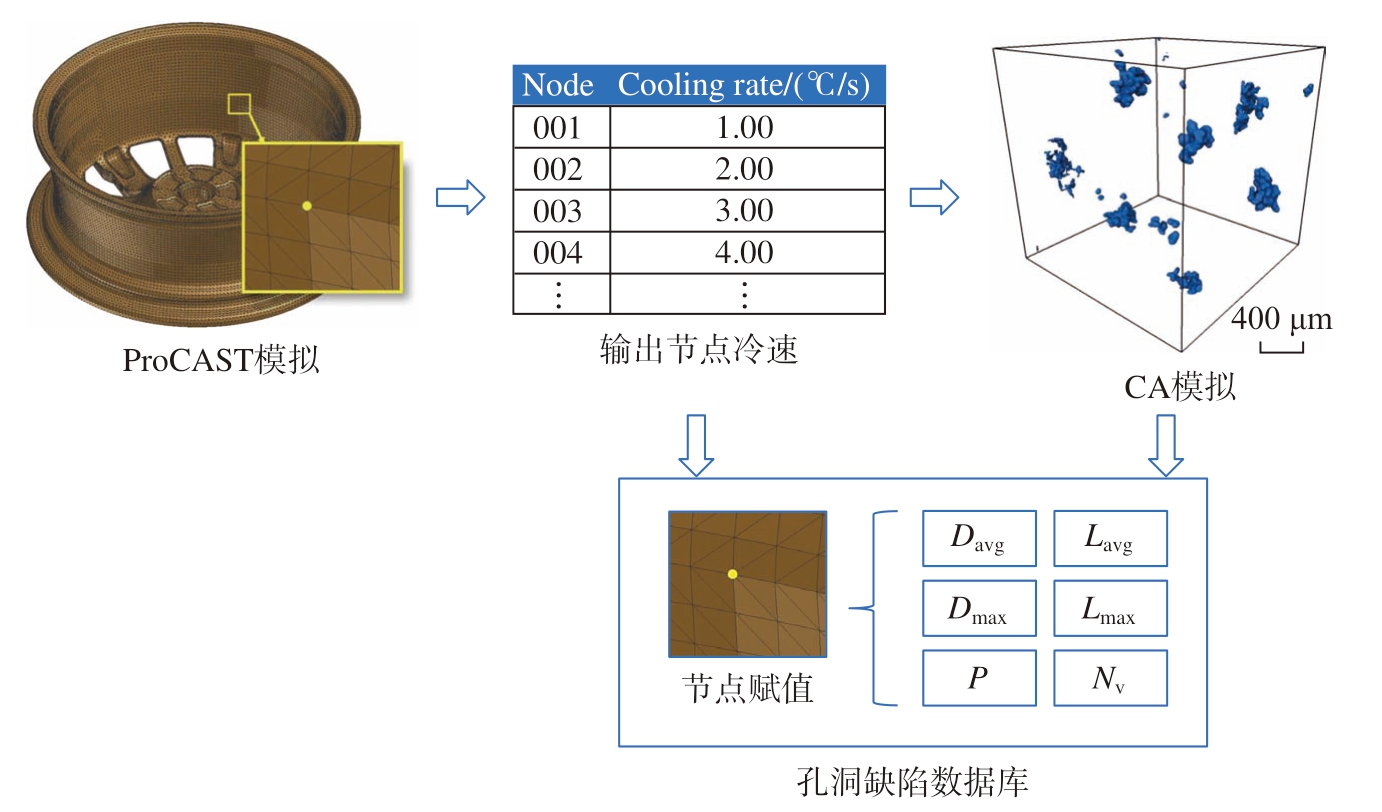
图1 多尺度耦合预测模型的流程图
Fig.1 Flow chart of multi-scale coupling prediction model
注：Davg为孔洞当量直径；Dmax为孔洞最大当量直径；P为孔隙率；Lavg为孔隙的平均几何长度；Lmax为孔隙的最大几何长度；Nv为孔洞数量密度，即单位体积内的孔洞数量。
1.1.2 基础理论
本研究使用的CA模型是基于Lee等[9，21]在帝国理工学院开发的Al–Cu–Si多组分扩散模型。计算域中气孔的成核是通过随机分配成核点来模拟的，成核的可能性由局部临界过饱和度SS决定，即
式中，CH为元胞内实际氢浓度，通过求解氢的质量守恒方程得到；
为局部平衡氢浓度，通过式（2）获得，该方程基于Sievert定律和经验方程得到[22]。
式中，Pg为孔隙内部压力；Patm为参考压力；T为绝对温度；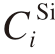
为Si的质量分数。孔隙的成核由高斯函数控制[23]，即
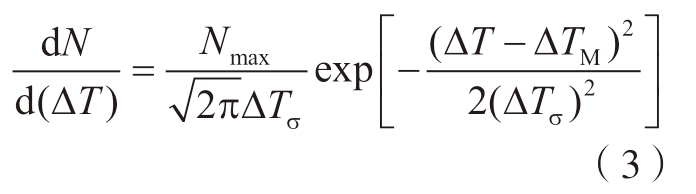
式中，N为原子核数；ΔT为过冷度；ΔTM为所有成核元胞的平均过冷度；ΔTσ为过冷度的标准偏差；Nmax为原子核的最大数密度。一旦克服成核势垒，气孔就会形成，其半径遵循理想气体定律和Sievert定律，即
式中，ri为气孔的初始半径；γGL为气、液界面的界面能。成核之后，局部压力的变化是影响气孔生长或者消失的主要因素，气孔生长的评价标准为
式中，Pm是金属静压；Pγ是由于表面张力和气孔曲率造成的压力，在本模型中可描述为Pγ=2γGL/ri。孔隙的生长由气体扩散控制。假设周围没有枝晶的限制，气孔则按照理想气体定律呈球形生长，气孔半径rp由Young-Laplace方程计算得出[21]。
式中，n是气体物质的量；R是摩尔气体常数。在实际情况下，孔隙的形状是复杂多变的，因此本模型考虑了枝晶限制孔隙生长的规则。结合相图计算方法 （Pandat，2021，Compu Therm LLC）和文献[24–25]，得到CA模型中Al–Si合金的热力学参数，如表1所示。
表1 Al–Si合金在CA模型中的物理参数
Table 1 Physical parameters of Al–Si alloy in CA model
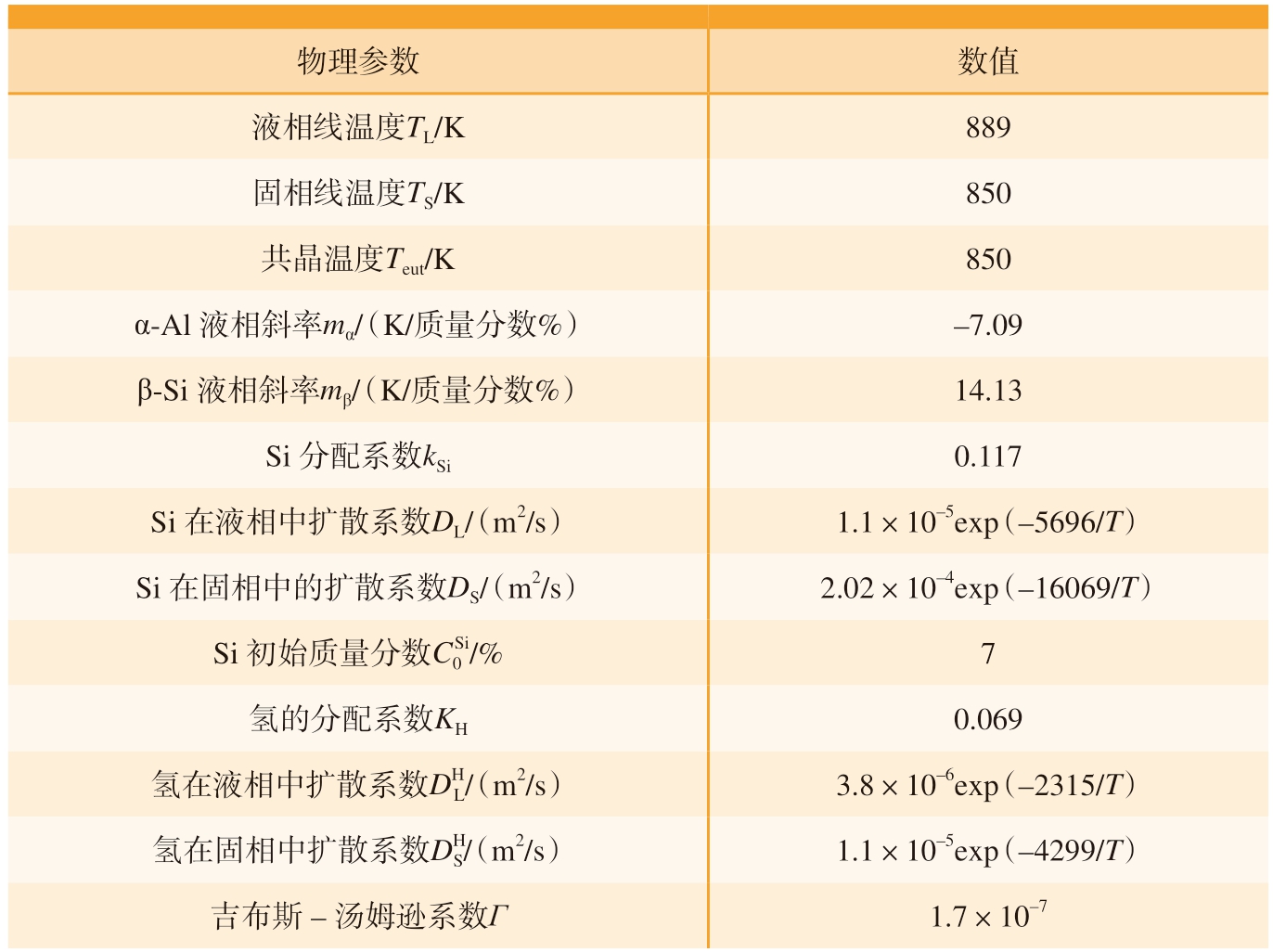
物理参数数值液相线温度TL/K889固相线温度TS/K850共晶温度Teut/K850 α-Al液相斜率mα/（K/质量分数%）–7.09 β-Si液相斜率mβ/（K/质量分数%）14.13 Si分配系数kSi0.117 Si在液相中扩散系数DL/（m2/s）1.1×10–5exp（–5696/T）Si在固相中的扩散系数DS/（m2/s）2.02×10–4exp（–16069/T）Si初始质量分数C0Si/%7氢的分配系数KH0.069氢在液相中扩散系数DH L/（m2/s）3.8×10–6exp（–2315/T）氢在固相中扩散系数DH S/（m2/s）1.1×10–5exp（–4299/T）吉布斯–汤姆逊系数Γ1.7×10–7
为了获得孔隙的生长动力学，并考虑到预测精度与计算效率，本文将元胞尺寸设为12.5 μm，计算域为1.25 mm×1.25 mm×1.25 mm的立方体单元，根据Wang等[26]的研究，初始氢浓度设为0.15 mL/100 g（STP），初始压力为1 atm。
1.2 材料和取样位置
利用多尺度耦合模型得到轮毂6个位置的冷却速率和对应的孔洞参数，每个位置分别选取5个节点，以5个节点冷却速率的平均值作为该位置的冷却速率。为了验证该模型的准确性，以T6热处理状态下的低压铸造Al–Si铝合金轮毂作为试验对象。该合金的化学成分为Al – 0.26Mg – 6.62Si（质量分数，%）。在轮毂对应的6个位置分别取1个试样，如图2（a）所示，S1～S6分别代表轮辐、轮心、内轮缘、轮辋中部、外轮缘以及轮辋与轮辐交界处。试样的具体尺寸如图2（b）所示，其中红色方框区域为X-CT扫描区域，具体尺寸为Φ4 mm×4 mm。
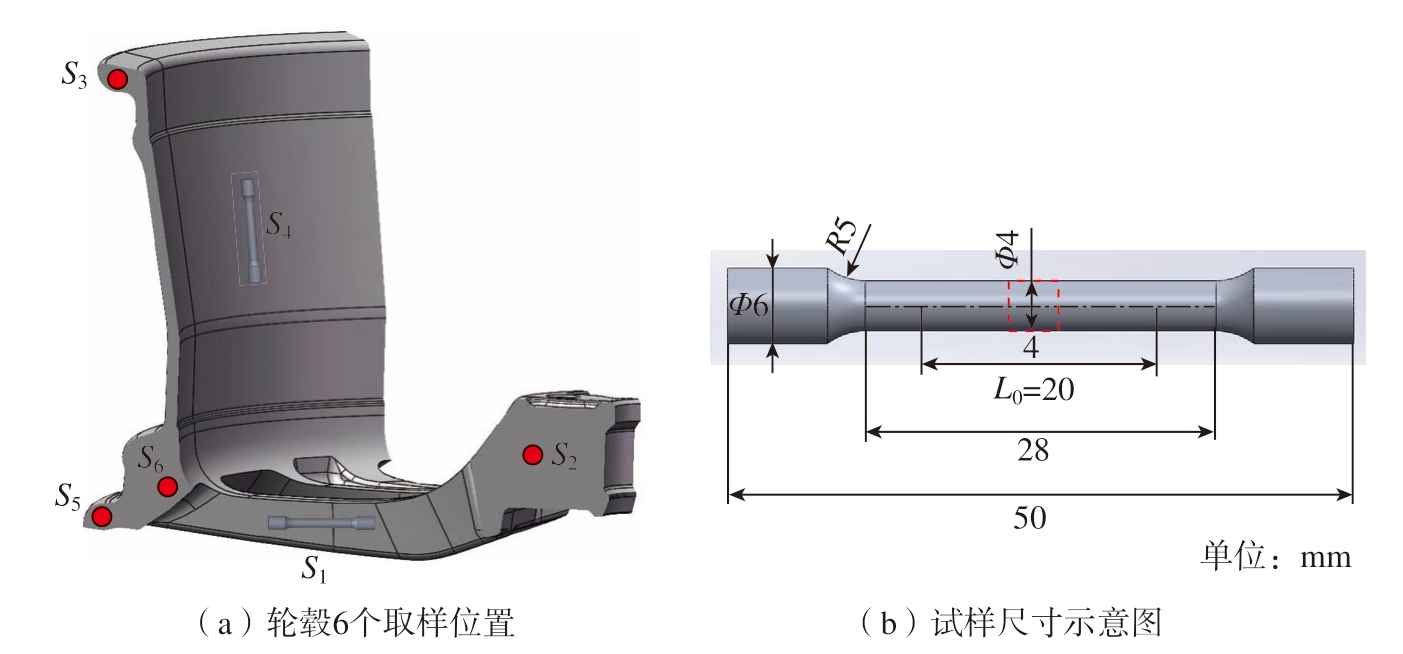
图2 取样位点及试样尺寸
Fig.2 Sampling site and sample size
1.3 X射线计算机断层扫描技术
采用蔡司Xradia 520 Versa对6个位置进行高空间分辨率的孔洞缺陷三维表征。X-CT是由X射线源、探测器、可旋转的样品台及计算机图像处理系统构成[27]。试验中X-CT的加速电压为70 kV，目标功率为6 W，以180°扫描方式采集了1001张图像，构建体素尺寸为4.0018 μm×4.0018 μm×4.0018 μm的三维结构。根据灰度值的不同，对孔洞缺陷进行分割和提取，最后使用商业软件Avizo（ThermoFisher Scientific）进行系列化的图像处理和3D渲染，定量表征孔洞的形态、大小、数量和空间分布。
为了精确排除噪音的干扰，选取当量直径在15 μm以上的微孔隙进行定量表征。假设不规则孔隙的体积与球体的体积相同，则孔洞可以用平均当量直径Davg和最大当量直径Dmax来表征，即
式中，D表示当量直径；V表示孔隙的体积。孔隙的平均几何长度Lavg和最大几何长度Lmax是孔隙缺陷在三维空间或者平面中距离最远的两点之间的距离。为了精确预测大尺寸孔洞对轮毂的影响，本文选取长度≥50 μm的孔洞进行量化表征。
2 结果与讨论
2.1 冷却速率的计算
基于该模型的数据库可以导出不同位置的温度曲线及对应的平均冷却速率，如图3所示。图3（a）是S1和S3部位节点处的温度变化曲线及瞬时冷却速率。图3（b）是轮毂6个位置S1 ～ S6的平均冷却速率，分别为（2.95±0.13） ℃/s、（0.85±0.01） ℃/s、（6.85±0.52） ℃/s、（3.93±0.14） ℃/s、（6.15±0.64）℃/s、（2.46±0.52） ℃/s。可以发现S3部位的冷却速率最大，为6.85 ℃/s，而S2部位的冷却速率最小。
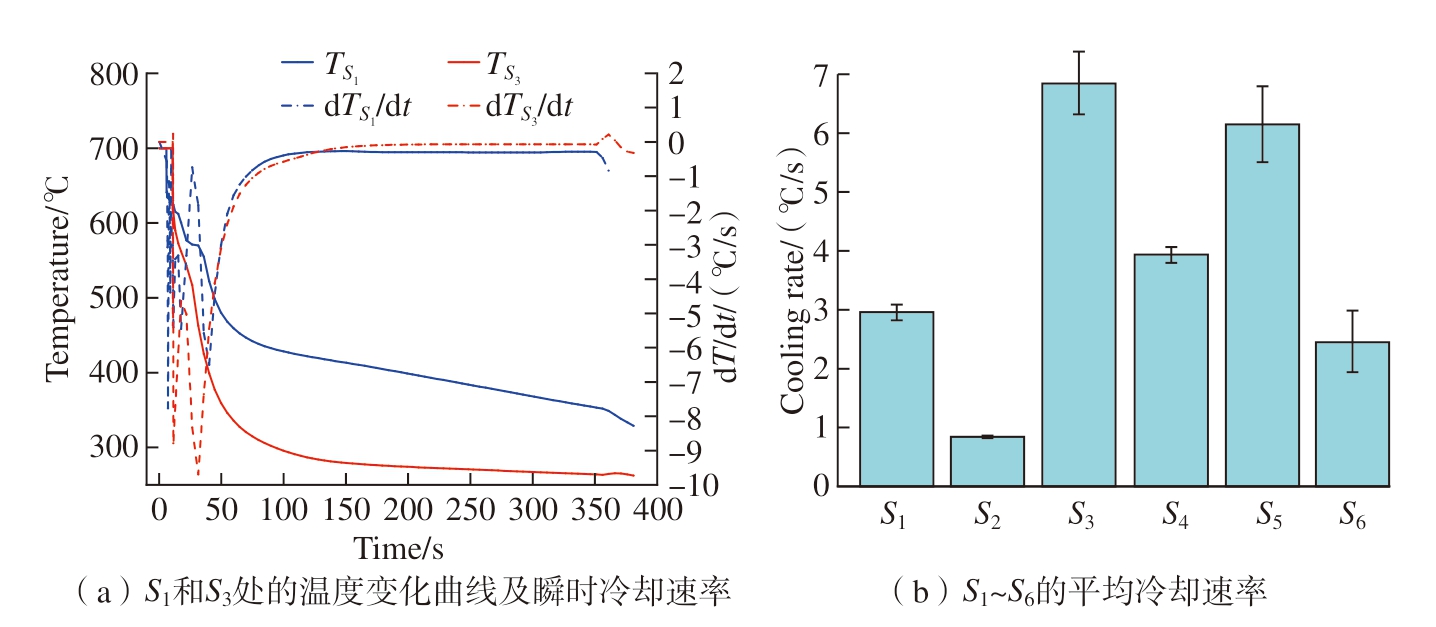
图3 轮毂温度曲线和平均冷却速率
Fig.3 Wheel hub temperature curves and average cooling rates
2.2 CA模拟
将上述6个位置的冷却速率输入到CA模型中，结合合金的热力学参数，可以得到轮毂6个位置的三维孔洞形貌特征，如图4所示 （蓝色区域代表孔洞，橙色方框代表一个计算区域）。可以发现，冷却速率的变化会影响孔洞的尺寸以及数量分布。进一步地，从数据库中导出6个位置处的孔洞平均当量直径Davg、最大当量直径Dmax、平均长度Lavg、最大长度Lmax、孔隙率P和数量密度Nv，如表2所示。随着冷却速率从0.85 ℃/s增长到6.85 ℃/s，孔洞平均当量直径Davg从 （51.31±25.07） μm降低到（26.03±10.25） μm，孔洞数量密度Nv从5.02 mm–3增加到20.92 mm–3，仅在冷却速率相差不大的时候存在微小波动。这主要是由于冷却速率影响铝液中氢扩散，进而影响微孔的生长[10，28]。在低冷速下，氢元素从固相的析出速率较慢，微孔的生长速率相对较慢，一旦孔隙成核，它们就有足够的时间吸收氢气进行生长，此时，气孔吸收氢气的速率高于氢气从固相析出的速率，这种情况下合金内部的微孔具有大尺寸。在高冷速下，氢元素从固相析出的速率较快，微孔的生长速率相对较快，但生长时间缩短。同时，液相中氢的浓度瞬间增加，气孔的成核速率增加，加剧了微孔之间的竞争，减少了微孔生长时间并限制了其尺寸。另外，代表性地选择不同冷速S1和S3位置，量化孔洞当量直径D的频数分布情况，如图5所示。结合图3（a），进一步证明冷却速率对孔洞尺寸和数量的影响。
表2 基于CA模型量化S1～S6的孔洞特征参数
Table 2 Quantification of microporosity characteristic parameters of S1–S6 based on CA model
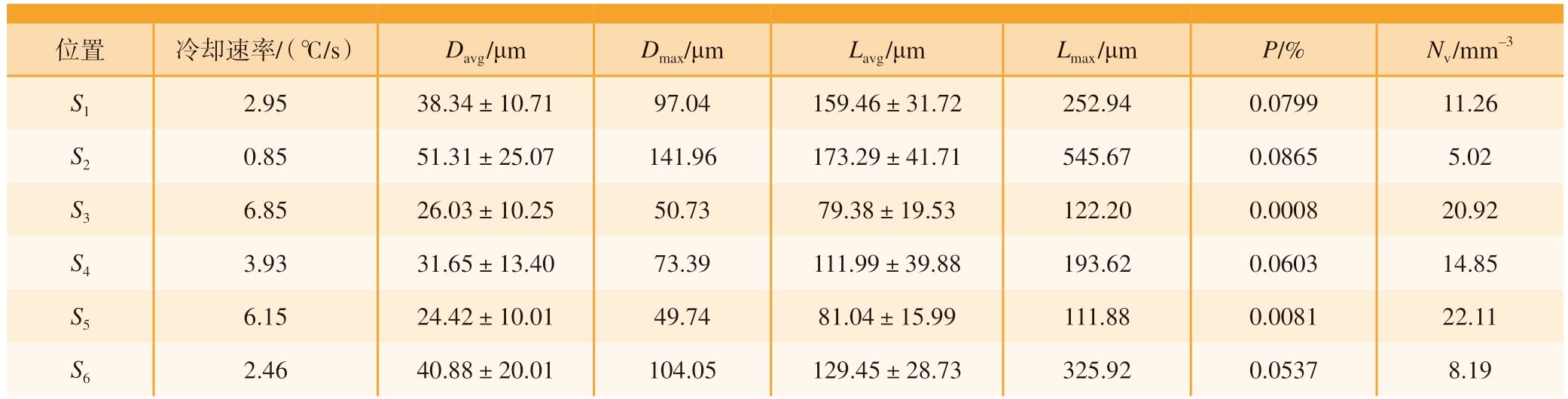
位置冷却速率/（℃/s）Davg /μmDmax/μmLavg /μmLmax /μmP/%Nv /mm–3 S12.9538.34±10.7197.04159.46±31.72252.940.079911.26 S20.8551.31±25.07141.96173.29±41.71545.670.08655.02 S36.8526.03±10.2550.7379.38±19.53122.200.000820.92 S43.9331.65±13.4073.39111.99±39.88193.620.060314.85 S56.1524.42±10.0149.7481.04±15.99111.880.008122.11 S62.4640.88±20.01104.05129.45±28.73325.920.05378.19
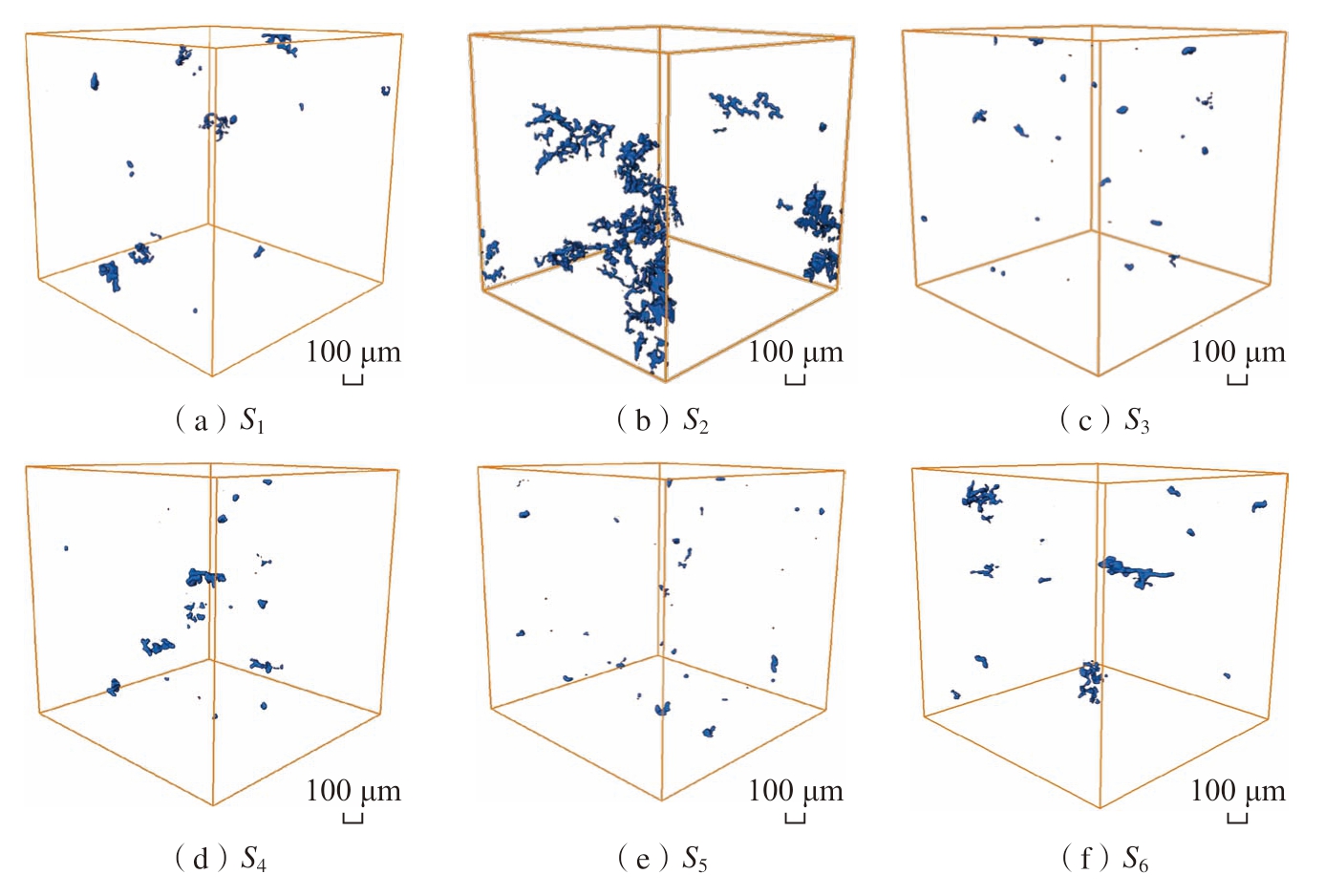
图4 CA模拟三维孔隙形貌
Fig.4 CA simulation of 3D microporosity morphology
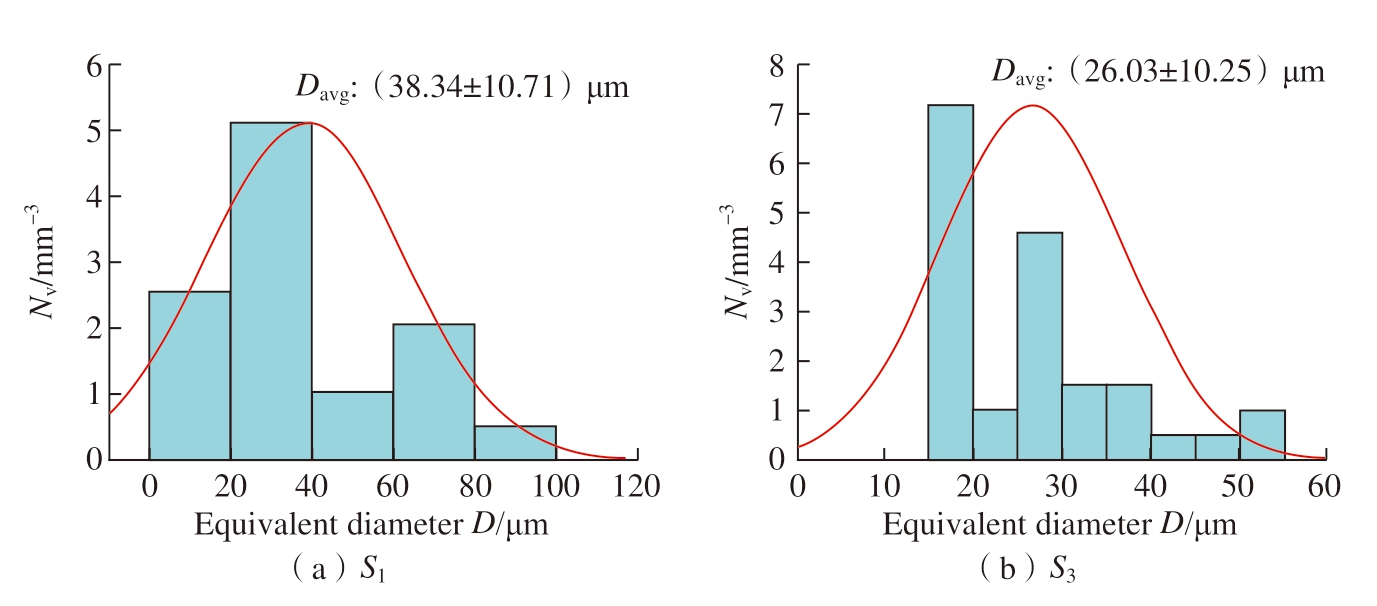
图5 CA模拟孔洞的频数分布
Fig.5 Microporosity frequency distribution simulated by CA
2.3 X-CT微孔形貌表征
根据CA模型可以得到不同冷却速率下的孔洞尺寸，为了验证该模型的准确性，采用X-CT技术三维表征对应位置的孔洞尺寸与形貌，图6是轮毂6个位置试样的三维孔洞分布图（蓝色代表孔洞，红色的放大部分代表每个位置的最大孔洞形貌）。S1位置存在形状不规则的大尺寸孔洞，而S3和S5部位存在呈球形的小尺寸孔洞，S1、S3、S5的最大当量直径Dmax分别为167.68 μm、40.86 μm和40.36 μm。另外，观察图6的三维孔洞形貌与图4的CA模拟结果，可以发现孔洞特征基本一致。进一步地，采用Avizo软件量化不同位置的孔洞特征参数，如表3所示。同样地，图7展示了基于X-CT统计S1和S3位置的孔洞当量直径D频数分布。与图5相比，S1和S3部位的孔洞当量直径D分布一致，S1部位CA模拟和试验测量的孔洞平均当量直径Davg分别为（38.34±10.71） μm和 （34.18±20.32）μm，S3部位CA模拟和试验值分别为（26.03±10.25） μm和 （21.38±5.65）μm，相对误差分别为12%和22%，充分反映了该模型预测的可靠性。
表3 X-CT量化S1～S6位置的孔洞特征参数
Table 3 X-CT quantified the microporosity characteristics of S1–S6 locations
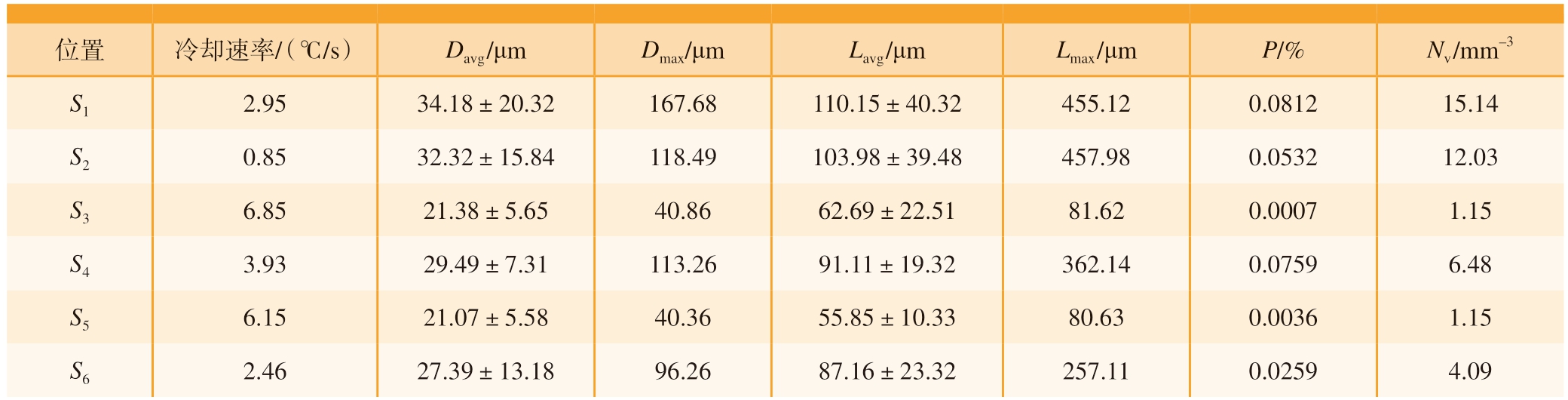
位置冷却速率/（℃/s）Davg /μmDmax/μmLavg /μmLmax /μmP/%Nv /mm–3 S12.9534.18±20.32167.68110.15±40.32455.120.081215.14 S20.8532.32±15.84118.49103.98±39.48457.980.053212.03 S36.8521.38±5.6540.8662.69±22.5181.620.00071.15 S43.9329.49±7.31113.2691.11±19.32362.140.07596.48 S56.1521.07±5.5840.3655.85±10.3380.630.00361.15 S62.4627.39±13.1896.2687.16±23.32257.110.02594.09
图6 X-CT表征三维孔洞形貌
Fig.6 X-CT characterization of 3D microporosity morphology
图7 X-CT表征的孔洞频数分布
Fig.7 Microporosity frequency distributions characterized by X-CT
2.4 孔洞参数对比验证
针对Al–Si合金，Zhang等[29]同样利用CA模型得到了平均孔洞半径和最大孔洞半径随冷却速率的增大而逐渐减小的结论，但没有评估CA模拟预测的精确性，同时没有给出相对误差值。本文将模型预测和X-CT测量的孔洞特征参数进行对比验证，如图8所示。图8（a）是孔洞平均当量直径Davg、最大当量直径Dmax的对比，可以发现S1～S6位置孔洞当量直径D的模拟值和试验值的整体趋势是一致的，说明该模型的预测效果是准确的。进一步地，统计了S1～S6孔洞平均当量直径Davg、最大当量直径Dmax的相对误差，如图8（c）所示。66%的数据点分布在30%的误差线以内，其平均相对误差分别为27%和25%，在误差允许的范围内，说明该模型能够很好地预测轮毂不同位置的孔洞尺寸。图8（b）是≥50 μm的孔洞平均长度Lavg、最大长度Lmax的比对结果，整体符合试验测量的规律。对应6个位置的孔洞平均长度Lavg、最大长度Lmax的相对误差，如图8（d）所示，60%的数据点分布在45%的误差线以内，其平均相对误差分别为42%和39%，相较于孔洞当量直径D的误差稍大，但在误差允许的范围内，能够预测不同位置的孔洞长度。
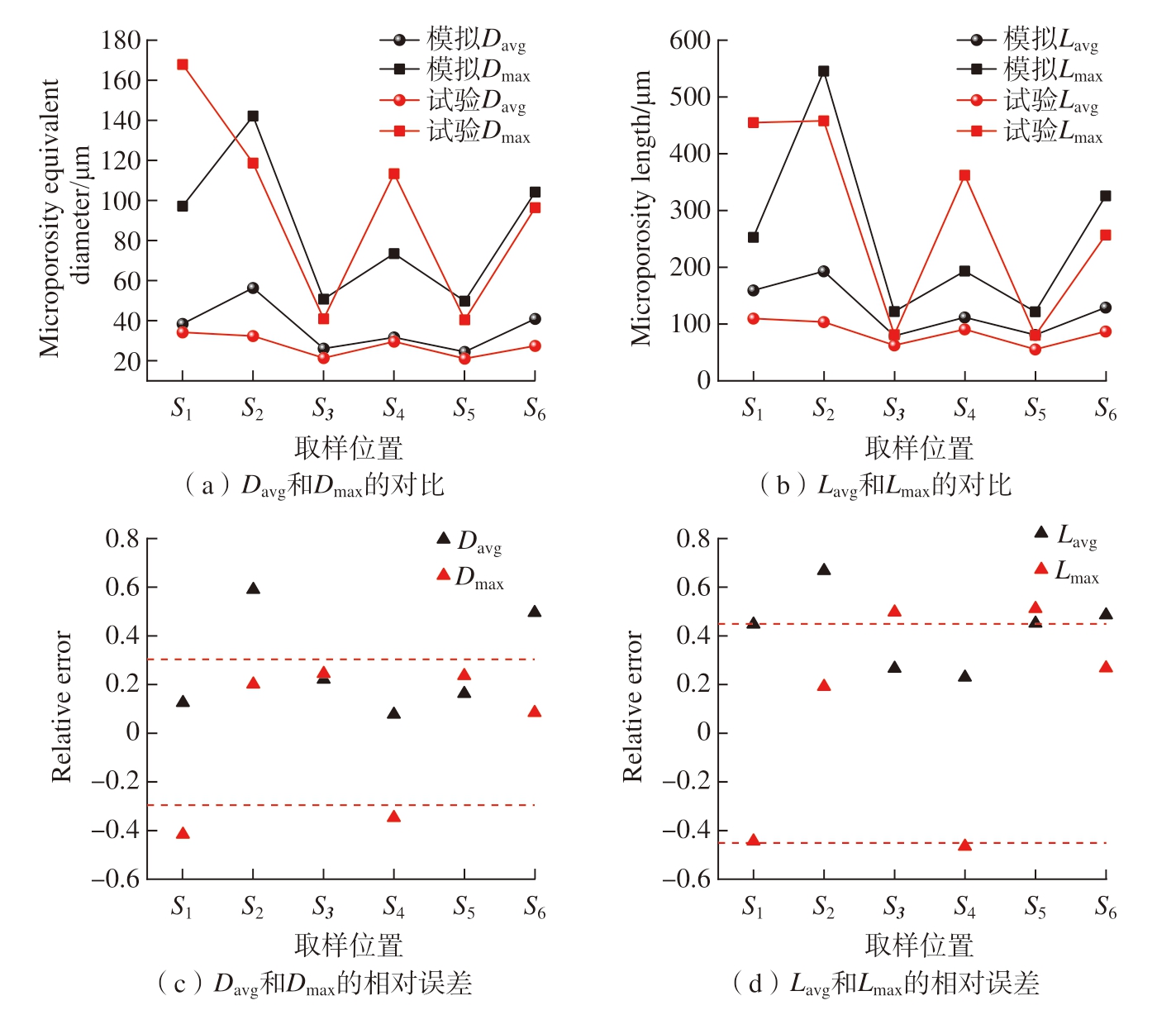
图8 CA模拟和X-CT试验的孔洞当量直径、长度对比
Fig.8 Comparison of equivalent diameter and length of microporosities by CA simulations and X-CT experiments
Gu等[30]利用CA模型预测的Al–Cu合金内部氢孔隙平均直径的平均相对误差为48.7%，与之相比，本文预测的孔洞当量直径D和孔洞长度L的精度更高，同时预测的范围更广。另外，结合表2和3的S1～S6的孔隙率，发现CA模拟的孔隙率和X-CT试验测量的孔隙率基本一致，仅S5位置的CA预测值略大于试验测量值，其余位置的平均相对误差为41%，考虑试验表征区域与模拟计算域的不同，本模型能够预测轮毂不同位置的孔隙率。相较于上述的几个孔洞参数，数量密度Nv的差异较大，特别是在S3、S5位置。综合上述孔洞参数，主要的影响因素有以下两点： （1） CA模型无法考虑低压铸造过程压力变化的问题[31]，因为在低压铸造过程中伴随初始阶段升压、中间阶段保压、凝固完成后降压过程，CA无法动态跟踪压力的变化，只能设置初始压力值，从而导致出现预测精度问题；（2）CA模型无法考虑轮毂自身形状的复杂性，特别是在内轮缘和外轮缘部位，该部位具有壁薄、区域小、铝液充形快等特点[32]，导致在相同较高冷速条件下，其孔洞数量较少，进而影响孔洞数量密度Nv的预测精度。另外，本文CA模型暂时没有考虑缩孔的影响，同样导致某些部位出现预测精度的问题。
综合以上孔洞特征参数的对比结果，孔洞当量直径D的预测效果最佳，相对误差均在25%左右；其次是孔洞长度L，孔洞平均长度Lavg和最大长度Lmax的相对误差分别是42%和39%；孔隙率P和数量密度Nv次之。
3 结论
本文开发了一种基于元胞自动机的Al–Si合金孔洞缺陷多尺度预测模型，基于X-CT技术从试验角度验证了模型的准确性，得到以下结论。
（1）基于X-CT表征发现轮辐和轮心部位存在当量直径大于100 μm的大尺寸孔洞，而内轮缘和外轮缘部位的孔洞尺寸偏小，平均当量直径分别为 （21.38±5.65） μm和（21.07±5.58） μm。
（2）该多尺度预测模型能够预测轮毂不同部位的孔洞尺寸以及三维形貌，可以作为集成计算材料工程的手段指导轮毂的合金设计及优化。
（3）该模型的预测准确率从高到低：孔洞当量直径>孔洞长度>孔隙率>孔洞数量密度；其中孔洞平均当量直径与最大当量直径的平均相对误差仅为27%和25%。
[1] CÁCERES C H, SELLING B I.Casting defects and the tensile properties of an AlSiMg alloy[J].Materials Science and Engineering: A,1996, 220(1–2): 109–116.
[2] 王兵, 王俊升.铝合金凝固过程中缺陷预测模型研究进展[J].航空制造技术, 2022,65(5): 76–86.
WANG Bing, WANG Junsheng.Research progress on defect predictions during solidification of aluminum alloys[J].Aeronautical Manufacturing Technology, 2022, 65(5): 76–86.
[3] CHEN R, XU Q Y, LIU B C.Cellular automaton simulation of three-dimensional dendrite growth in Al–7Si–Mg ternary aluminum alloys[J].Computational Materials Science, 2015,105: 90–100.
[4] 许庆彦, 杨聪, 柳百成.镍基高温合金定向凝固过程枝晶组织相场模拟研究[J].航空制造技术, 2019, 62(19): 14–20.
XU Qingyan, YANG Cong, LIU Baicheng.Phase-field simulation of dendrite growth in directionally solidified nickel-based superalloy[J].Aeronautical Manufacturing Technology, 2019,62(19): 14–20.
[5] BECKERMANN C, DIEPERS H J,STEINBACH I, et al.Modeling melt convection in phase-field simulations of solidification[J].Journal of Computational Physics, 1999, 154(2): 468–496.
[6] LEE P D, CHIRAZI A, SEE D.Modeling microporosity in aluminum–silicon alloys: A review[J].Journal of Light Metals, 2001,1(1): 15–30.
[7] LEE P D, ATWOOD R C, DASHWOOD R J, et al.Modeling of porosity formation in direct chill cast aluminum–magnesium alloys[J].Materials Science and Engineering: A, 2002, 328(1–2): 213–222.
[8] ATWOOD R C, LEE P D.Simulation of the three-dimensional morphology of solidification porosity in an aluminium–silicon alloy[J].Acta Materialia, 2003, 51(18): 5447–5466.
[9] WANG J S, LEE P D.Simulating tortuous 3D morphology of microporosity formed during solidification of Al–Si–Cu alloys[J].International Journal of Cast Metals Research,2007, 20(3): 151–158.
[10] WANG B, ZHANG M S, WANG J S.Quantifying the effects of cooling rates and alloying additions on the microporosity formation in Al alloys[J].Materials Today Communications,2021, 28: 102524.
[11] LI X X, YANG X H, XUE C P, et al.Hydrogen microporosity evolution and dendrite growth during long solidification of Al–Cu–Li alloys: Modeling and experiment[J].Journal of Materials Processing Technology, 2023, 321:118135.
[12] SUN D K, ZHU M F, WANG J, et al.Lattice Boltzmann modeling of bubble formation and dendritic growth in solidification of binary alloys[J].International Journal of Heat and Mass Transfer, 2016, 94: 474–487.
[13] HU M D, SUN D K, ZHU M F.Simulation of gas porosity formation and interaction with dendrite and eutectic structures during solidification of Al-Si alloys[J].Materials& Design, 2024, 241: 112977.
[14] GU C, RIDGEWAY C D, CINKILIC E, et al.Predicting gas and shrinkage porosity in solidification microstructure: A coupled threedimensional cellular automaton model[J].Journal of Materials Science & Technology, 2020, 49:91–105.
[15] LEE P D, CHIRAZI A, ATWOOD R C, et al.Multiscale modelling of solidification microstructures, including microsegregation and microporosity, in an Al–Si–Cu alloy[J].Materials Science and Engineering: A, 2004, 365(1–2):57–65.
[16] RAFII-TABAR H.Multi-scale computational modelling of solidification phenomena[J].Physics Reports, 2002, 365(3):245–249.
[17] HAMILTON R W, SEE D, BUTLER S, et al.Multiscale modeling for the prediction of casting defects in investment cast aluminum alloys[J].Materials Science and Engineering: A,2003, 343(1–2): 290–300.
[18] WANG J S, LI M, ALLISON J, et al.Multiscale modeling of the influence of Fe content in a Al-Si-Cu alloy on the size distribution of intermetallic phases and micropores[J].Journal of Applied Physics, 2010, 107(6): 061804.
[19] CUSATO N, NABAVIZADEH S A, ESHRAGHI M.A review of large-scale simulations of microstructural evolution during alloy solidification[J].Metals, 2023, 13(7): 1169.
[20] ZHANG Y X, XUE C P, WANG J S, et al.Quantifying the effects of hydrogen concentration and cooling rates on porosity formation in Al–Li alloys[J].Journal of Materials Research and Technology, 2023, 26: 1938–1954.
[21] LEE P D, HUNT J D.Hydrogen porosity in directionally solidified aluminium–copper alloys: A mathematical model[J].Acta Materialia, 2001, 49(8): 1383–1398.
[22] ATWOOD R C, LEE P D, SAHM P R,et al.A combined cellular automaton and diffusion model for the prediction of porosity formation during solidification[M].Damstadt: Shaker Verlag GmbH, 2000.
[23] ATWOOD R C, SRIDHAR S, LEE P D.Equations for nucleation of hydrogen gas pores during solidification of aluminium seven weight percent silicon alloy[J].Scripta Materialia, 1999,41(12): 1255–1259.
[24] QIU K, WANG R C, PENG C Q,et al.Polynomial regression and interpolation of thermodynamic data in Al–Si–Mg–Fe system[J].Calphad, 2015, 48: 175–183.
[25] LI K D, CHANG E.Mechanism of nucleation and growth of hydrogen porosity in solidifying A356 aluminum alloy: An analytical solution[J].Acta Materialia, 2004, 52(1): 219–231.
[26] WANG J S.In-situ observation and mathematical modelling of the nucleation and growth of intermetallics and micropores during the solidification of aluminium alloys[D].London:Imperial College London, 2009.
[27] MIAO Y S, XUE C P, WU X P, et al.Seeing through materials: X-ray imaging using computed tomography[J].Journal of Beijing Institute of Technology, 2023, 32(4): 494–516.
[28] CHEN R, SHI Y F, XU Q Y, et al.Effect of cooling rate on solidification parameters and microstructure of Al–7Si–0.3Mg–0.15Fe alloy[J].Transactions of Nonferrous Metals Society of China, 2014, 24(6): 1645–1652.
[29] ZHANG Q Y, WANG T T, YAO Z J,et al.Modeling of hydrogen porosity formation during solidification of dendrites and irregular eutectics in Al–Si alloys[J].Materialia, 2018, 4:211–220.
[30] GU C, WEI Y H, YU F Y, et al.Cellular automaton study of hydrogen porosity evolution coupled with dendrite growth during solidification in the molten pool of Al-Cu alloys[J].Metallurgical and Materials Transactions A, 2017,48(9): 4314–4323.
[31] ZHANG Y X, XUE C P, YANG X H,et al.Uncovering the effects of local pressure and cooling rates on porosity formation in AA2060 Al–Li alloy[J].Materials Today Communications,2023, 35: 106384.
[32] DONG G J, LI S D, MA S Z, et al.Process optimization of A356 aluminum alloy wheel hub fabricated by low-pressure die casting with simulation and experimental coupling methods[J].Journal of Materials Research and Technology, 2023, 24: 3118–3132.
