γ-TiAl合金具有高比强度、比模量,优良的抗蠕变和抗氧化性能,是当前极具发展前途的轻质耐高温结构材料[1–2]。国内外针对γ-TiAl合金及其制造技术开展了大量的研究工作,开发出多种γ-TiAl合金,包括4822、45XD、TNM、TNB等[3–4]。同时也开发出相应的铸造、锻造、增材制造、粉末冶金等技术。与之相比,采用铸造工艺制备的γ-TiAl合金部件率先取得工程化应用。2006年美国GE公司采用铸造4822合金制造了GEnX航空发动机第六、七级低压涡轮工作叶片[5],铸造4822合金展现出较好的综合力学性能,该合金长时间工作温度为650 ℃。
随着航空发动机性能的不断提升以及铸造技术的不断提高,国内外开展了航空发动机用大尺寸γ-TiAl合金铸件的研制工作,包括压气机机匣、燃烧室机匣、扩压器等部件[6–8],这类部件一般尺寸较大,应用铸造工艺时需要采用大尺寸的γ-TiAl母合金铸锭进行浇注。为了实现母合金铸锭成分的均匀性,铸锭多采用真空电磁感应悬浮熔炼方法制备,获得的母合金中元素分布均匀性较好,但该方法制备的铸件尺寸一般较小 (直径一般不超过100 mm),可用于小尺寸γ-TiAl合金铸件制备,不能满足大尺寸γ-TiAl合金铸件的研制需求。真空自耗熔炼 (Vacuum arc remelting,VAR)工艺是在真空条件下利用自耗电极与水冷结晶器之间形成电弧实现电极原材料熔化的一种工艺,钛合金铸锭一般采用该工艺制备。国内外开展了真空自耗电极电弧熔炼大尺寸γ-TiAl合金工艺研究,结果表明该方法在减少γ-TiAl母合金缺陷、控制Al元素微观偏析及Al元素挥发等方面均具有优势[9]。目前国内外开展了4822、45XD等大尺寸γ-TiAl母合金铸锭制备技术研究,但针对更高服役温度的高合金化γ-TiAl母合金铸锭制备技术研究尚未见报道。
采用数值模拟技术可以研究真空自耗熔炼工艺参数对温度场、熔池形状、热应力、流场、显微组织等的影响规律,对实际生产能够起到一定的指导作用[10]。但是这些研究工作多是针对钛合金、钢、高温合金等传统金属材料[11–13],这些材料的塑性、金属熔液流动性以及其他物理性能与γ-TiAl合金存在明显的差异[14–15],如γ-TiAl合金铸锭室温、800 ℃塑性分别为0.3%、3%,显著低于传统金属材料;γ-TiAl合金室温、1000 ℃杨氏模量分别为170 GPa、130 GPa,显著高于传统金属材料。因此,γ-TiAl合金真空自耗熔炼过程中的熔池、温度场分布等特性与传统金属显著不同。目前相关的研究较少,而且一般是针对较小尺寸的母合金铸锭 (直径不超过150 mm)[16],为此有必要针对大尺寸γ-TiAl合金的特性开展真空自耗熔炼数值模拟研究,为大尺寸γ-TiAl母合金铸锭制备奠定基础。
本文采用数值模拟方法研究了300 mm直径的Ti–46Al–6(Nb、Cr、Ta)合金铸锭第3次真空自耗重熔过程,探索了熔炼速度、换热系数对熔池形状等的影响,并开展了实际的熔炼工艺试验,以期为理解该锭型γ-TiAl合金真空自耗熔炼过程及制定熔炼工艺提供参考。
1 数学与几何模型
1.1 数学模型
充型及凝固过程数值模拟数学模型遵守动量守恒方程、质量守恒方程及描述自由表面的体积方程[17],采用S0LA–V0F方法进行求解,方程如下。
Navier–Stokes(N–S)动量守恒方程为
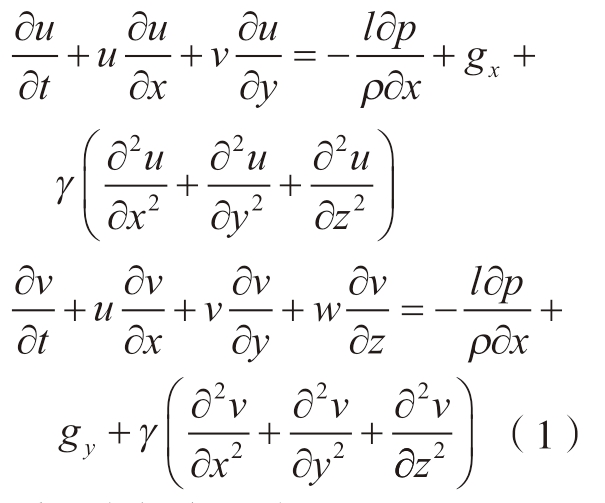
质量守恒方程为
体积方程 (VOF)为
在式 (1)~(3)中u、v、w为流速在x、y、z方向上的分量,m/s;p为流场中点的压力,Pa;γ为流体运动黏度,m2/s;ρ为金属流体的密度,kg/m3;gx、gy、gz为重力加速度在x、y、z方向上的分量,m/s2;F为体积分数,%;t为时间,s。
温度场计算采用Fourier导热偏微分方程为
式中,T为温度,℃;Q为热源项;α为热扩散率,m2/s。
1.2 假设条件
本数值模拟研究采用了如下假设。
(1)忽略电场及磁场的作用,不考虑熔池旋转的效果;
(2)合金的各项物理性能 (比热、热导率、热焓等)仅与温度有关;
(3)计算铸锭热应力时不考虑铸锭缩孔;
(4)假定合金为线弹性材料;
(5)熔炼过程中金属熔滴均匀滴落至熔池上表面。
1.3 几何模型
自耗电弧炉结晶器和自耗电极均为轴对称模型,为了减少有限元计算的网格数量,节省计算时间,求解中采用了1/2模型来计算。按实际尺寸建立了三维模型,共划分340000个网格,结晶器内径为305 mm,如图1所示[18]。
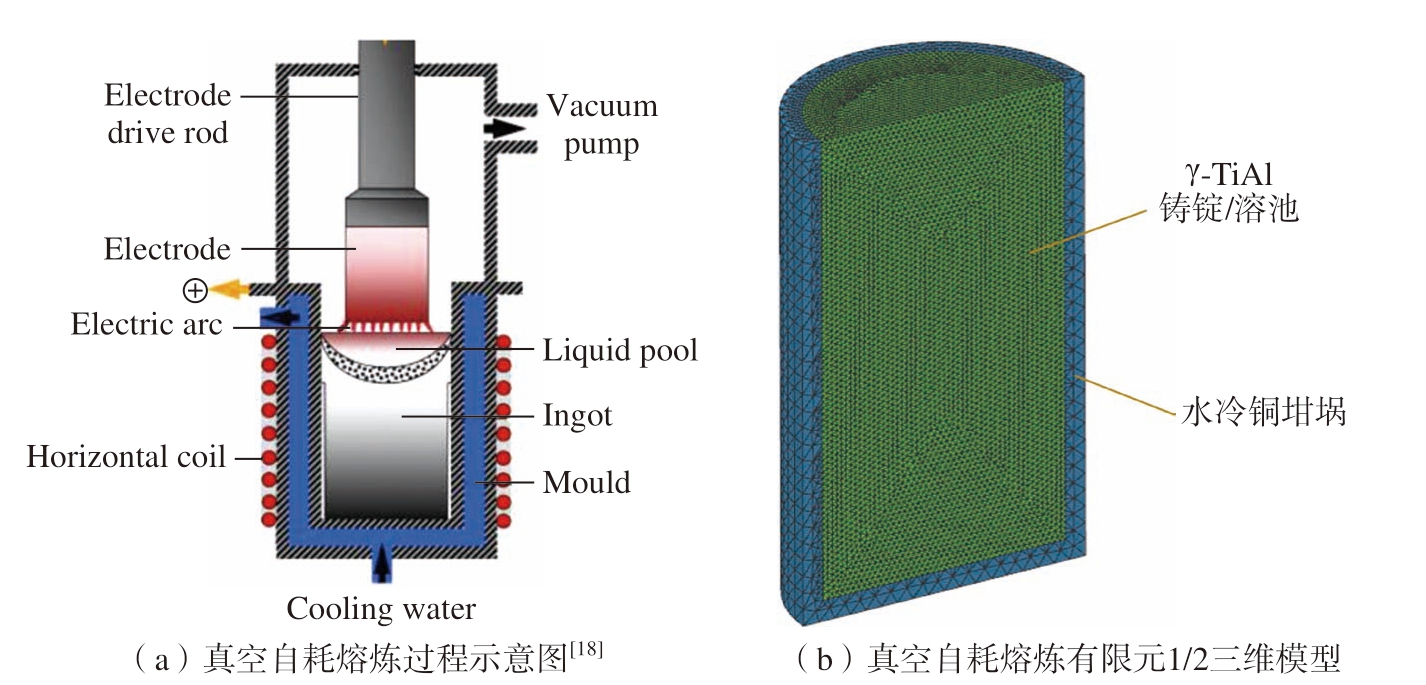
图1 真空自耗电极电弧熔炼过程示意图及有限元1/2三维模型
Fig.1 Schematic diagram of VAR process and FEM 1/2 3D model
2 试验材料
本研究试验材料采用中国航发北京航空材料研究院所研发的第三代γ-TiAl合金,即Ti–46Al–6(Nb、Cr、Ta)(体积分数,%),其物理性能、熔炼参数见图2与表1、2。
表1 Ti–46Al–6(Nb、Cr、Ta)合金的材料参数
Table 1 Material parameters of Ti–46Al–6 (Nb, Cr, Ta) alloy

密度/(g/cm3)熔点/℃比热容/(kJ/(kg·K))导热系数/(W/(m·K))潜热/(kJ/kg)4.115500.8623375

图2 γ-TiAl合金杨氏模量测试结果
Fig.2 Test results of Young’s modulus of γ-TiAl alloy
3 模拟结果与讨论
真空自耗铸锭的冶金质量与熔炼过程中金属熔池的形状、应力场密切相关。当金属熔池深度较小、熔池形状为扁平状时,枝晶沿铸锭轴向生长,该条件有利于金属中气体原子和非金属夹杂物的排除,也有助于液态金属向凝固时产生的体积收缩区域补充;当金属熔池深度较大时,铸锭结晶向径向发展,该条件不利于排气及补缩,容易产生各种缺陷[19]。另一方面,γ-TiAl合金独特的晶体结构使其塑性极为有限,在熔炼过程中容易产生热应力裂纹,该情况在大尺寸γ-TiAl合金铸锭中更为显著。大尺寸γ-TiAl合金铸锭在冷却过程中各部位的温度场分布极不均匀,这使得铸锭中存在较大的热应力,导致制备的铸件中产生裂纹[20–21]。
分析工艺参数对γ-TiAl合金铸锭中热应力的影响也是本研究关注的问题。真空自耗熔炼的工艺参数主要包括熔化电流、电压、冷却水流量等,这些参数直接影响熔炼速度、冷却效果,进而影响熔炼过程中金属熔池的形状、温度场、应力场[20]。本文针对不同工艺参数下 (表2)真空自耗熔炼过程进行了数值模拟,研究大尺寸γ-TiAl合金铸锭真空自耗熔炼过程。
表2 γ-TiAl合金真空自耗熔炼参数
Table 2 Parameters of VAR for γ-TiAl alloy

熔炼速度/(kg/min)结晶器换热系数/(W/(m2·K))3、6、9、121000、1500、2000、2500、3000
3.1 真空自耗熔炼模拟结果分析
图3给出了熔化速度6 kg/min、水冷结晶器换热系数2000 W/(m2·K)条件下不同熔炼时间的温度场分布。结果表明,在真空自耗熔炼过程中铸锭的侧面与底面均与结晶器发生热交换,这使得铸锭横向与纵向方向均存在明显的温度梯度,促使铸锭内部因不同程度的热胀冷缩而产生热应力。在实际熔炼过程中,材料在压应力作用下不易产生裂纹,而在拉应力的作用下材料更容易发生断裂,为了分析熔炼过程中铸锭的开裂倾向,本文计算了不同熔炼时间铸锭中平均法向应力的变化情况。图4给出了γ-TiAl合金熔炼过程中铸锭轴向平均法向应力场云图,在熔炼至300 s时,铸锭底部出现了明显的拉应力区域;熔炼至600 s时铸锭侧表面产生拉应力区,拉应力的最大值达到400 MPa;熔炼至900 s时铸锭表面拉应力区的体积扩大,拉应力最大值达到430 MPa;熔炼至1100 s时拉应力区体积进一步扩大,但最大拉应力值变化不多;熔炼至1400 s时,拉应力区域体积进一步增加,拉应力最大值与1100 s时相近。同时,计算了熔炼结束400 s后铸锭横截面的平均法向应力场及温度场,结果表明铸锭表面最大拉应力值降低至约180 MPa (图5)。
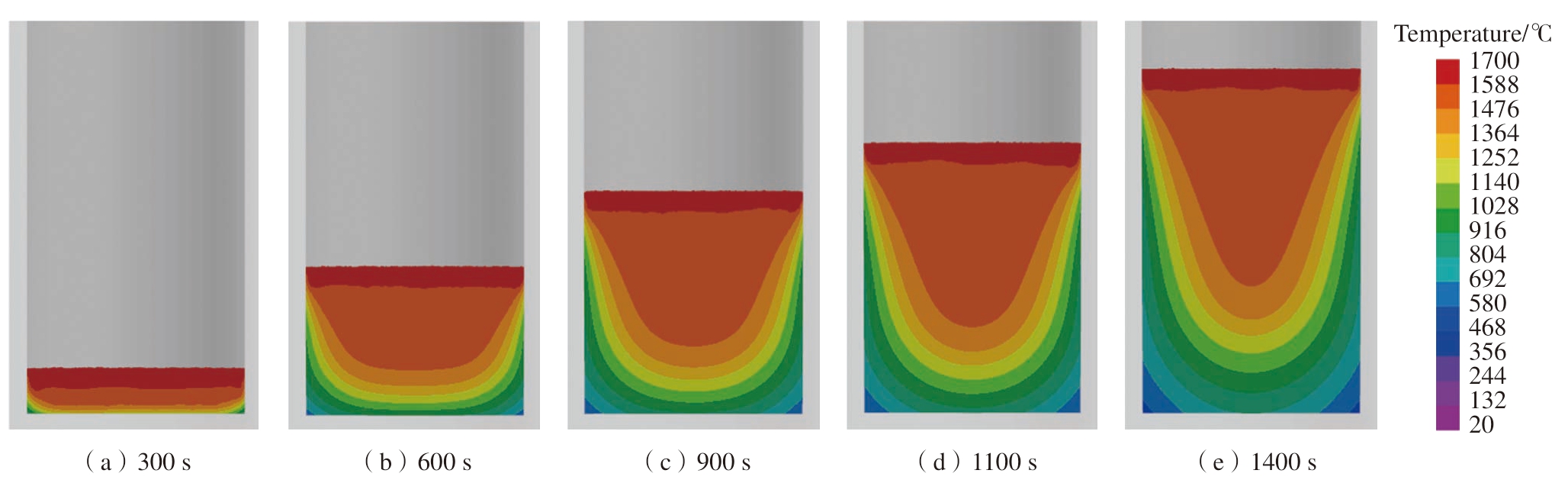
图3 γ-TiAl合金铸锭真空自耗熔炼过程中的温度场
Fig.3 Temperature field of γ-TiAl alloy ingot during VAR

图4 γ-TiAl合金铸锭真空自耗熔炼过程中铸锭的平均法向应力场
Fig.4 Averaged normal stress field of γ-TiAl alloy ingot during VAR

图5 γ-TiAl合金铸锭真空自耗熔炼结束400 s时铸锭横向平均法向应力场及温度场
Fig.5 Transverse averaged normal stress field and temperature field of γ-TiAl alloy ingot at 400 s after the end of VAR
综上分析,γ-TiAl合金在熔炼过程中铸锭表面产生拉应力,原因如下:熔炼过程中在结晶器冷却的作用下铸锭表面区域快速冷却,与铸锭内部区域相比收缩量更大,导致铸锭表面在收缩时遇阻而产生了拉应力。同样地,该原因也导致熔炼结束后铸锭表面存在拉应力。
图6给出了上述条件下的固相分布计算结果,真空自耗熔炼至300 s时,γ-TiAl合金熔液已充满结晶器底部形成熔池,在结晶器底部散热的作用下,此时熔池深度较小,呈扁平状。随着熔炼的进行,底部金属熔池冷却、凝固形成铸锭,伴随顶部高温金属液的不断输入,金属熔池顶部液面持续升高,熔池逐渐远离结晶器底部,结晶器底部的散热作用逐渐下降,形成的熔池也越来越深。随着熔炼继续进行,熔池形状也由扁平状逐渐变成V状。在熔炼过程的中后期,金属熔池形状无明显变化。
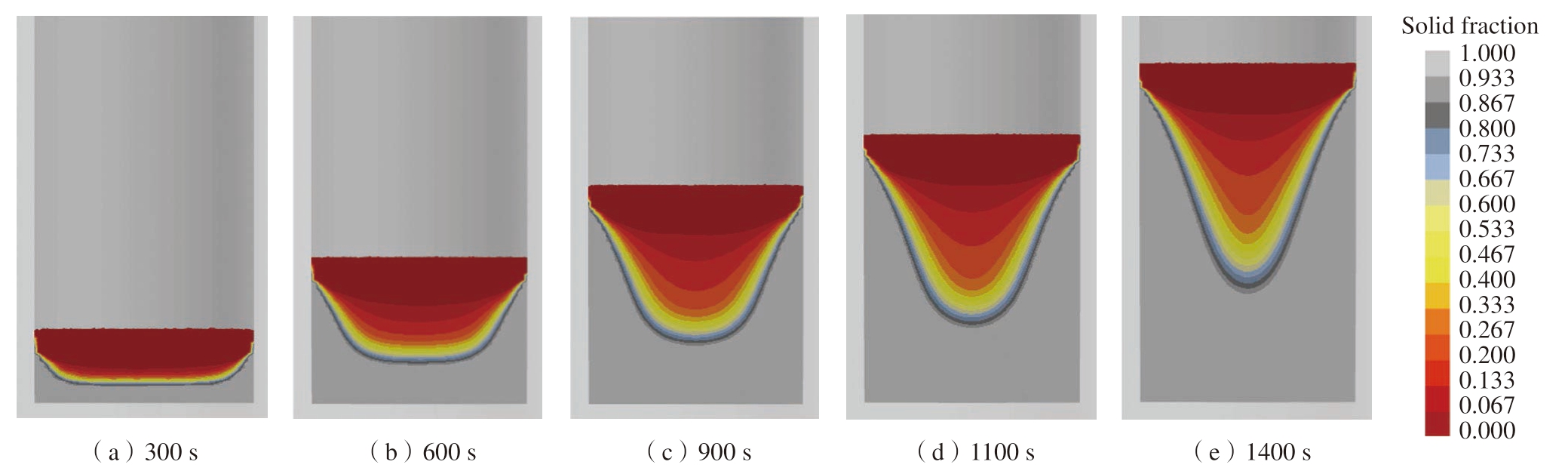
图6 γ-TiAl合金铸锭真空自耗熔炼过程中的固相率
Fig.6 Solid fraction of γ-TiAl alloy ingot during VAR
3.2 熔炼速度的影响
本文对比了熔炼速度分别为3 kg/min、6 kg/min、9 kg/min、12 kg/min真空自耗熔炼过程的温度场与固相率,如图7所示。结果表明,熔炼速度对温度场、熔池形状的影响显著,随着熔炼速度的增大熔池由浅变深,并且熔池底部逐渐变宽。金属熔池的热量输入是影响熔池深度和形状的主要原因,当熔炼速度增大时,单位时间内输入金属熔池的热量增加使得熔池深度增大。依据模拟结果绘制了不同熔炼速度条件下熔池深度随时间的变化曲线 (图8)。可以看出,当炼熔速度较小时,随着熔炼的进行熔池深度变化较小,表明此条件下熔池更易达到稳定;而当熔炼速度较大时,随着熔炼的进行熔池深度变化较大。计算了熔炼结束后500 s时铸锭中的应力场,如图9所示,铸锭中心位置为压应力区,随着熔炼速度的增大压应力区域面积增加;铸锭表面为拉应力区,随着熔炼速度的增大拉应力区域面积变化不大,但最大拉应力值有所增加,由熔炼速度为3 kg/min的120 MPa增大至熔炼速度为12 kg/min的235 MPa,增大了约1倍。熔炼速度是制定金属熔炼工艺时的重要参数[22],研究表明当熔炼速度较小时有助于获得较浅的熔池,该条件更有利于金属熔池的补缩,减小缺陷,降低产生裂纹的倾向。
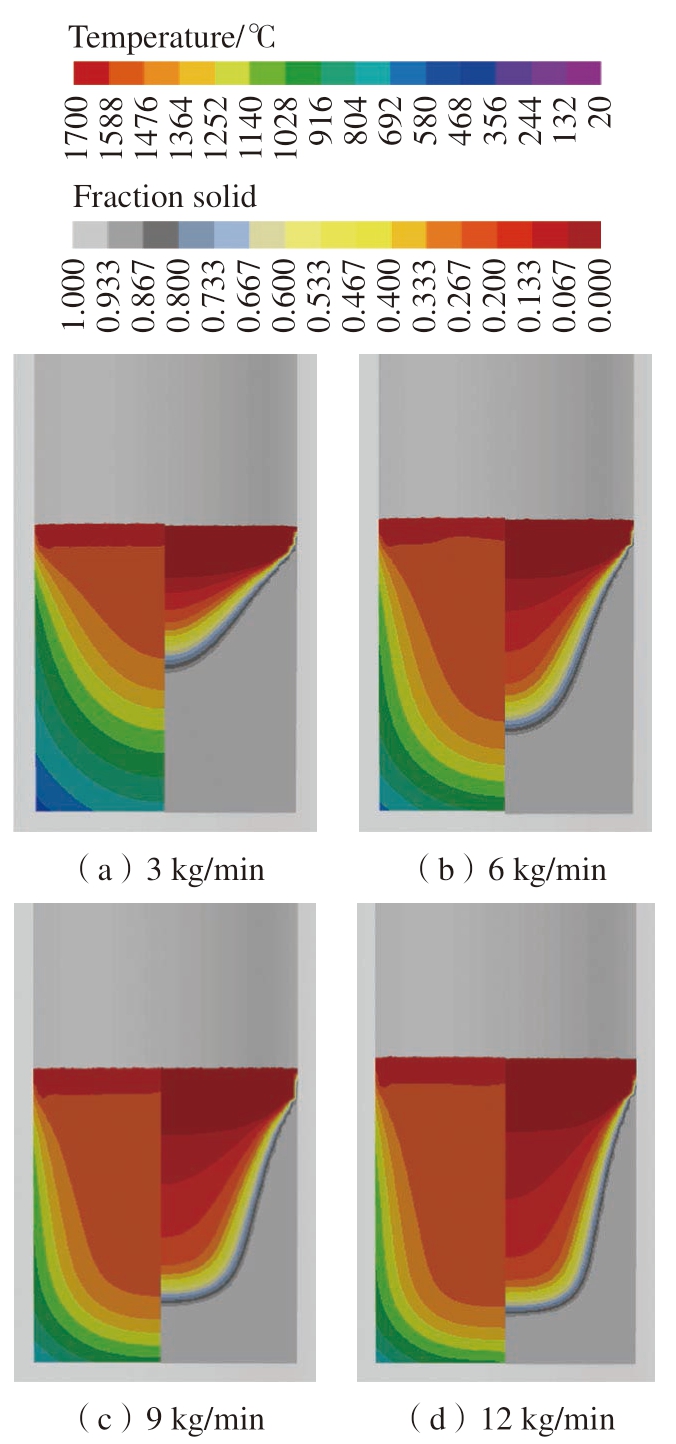
图7 γ-TiAl合金铸锭熔炼过程中的温度场与固相率云图
Fig.7 Temperature field and solid fraction cloud map of γ-TiAl alloy during VAR

图8 不同熔炼速度下熔池深度随时间的变化曲线
Fig.8 Variation curves of melting pool depth with time at different melting speeds

图9 γ-TiAl合金铸锭真空自耗熔炼结束500 s时铸锭中平均法向应力场
Fig.9 Average normal stress filed of γ-TiAl alloy ingot at 500 s after the end of VAR
3.3 换热系数的影响
真空自耗熔炼过程中,铸锭凝固后会发生体积收缩,该情况使铸锭与结晶器壁之间产生缝隙,缝隙阻隔了铸锭已凝固部分与结晶器的接触,降低了结晶器对铸锭的冷却效果。已有相关技术可以将导热性较好的氦气通入该缝隙,有效提高冷却效果,通过调节氦气的压力可以实现不同的冷却强度。如图10所示,本文对比了换热系数分别为1000 W/(m2·K)、2000 W/(m2·K)、3000 W/(m2·K)时的固相率。由结果可知,改变换热系数对熔池的形状有一定的影响,主要体现在熔池底部由宽变窄,但对熔池深度影响不大。图11给出了不同换热系数时熔炼过程中铸锭内部的应力场,可见换热系数对铸锭中的压应力、拉应力面积影响不大,对最大拉应力值的影响也不明显。
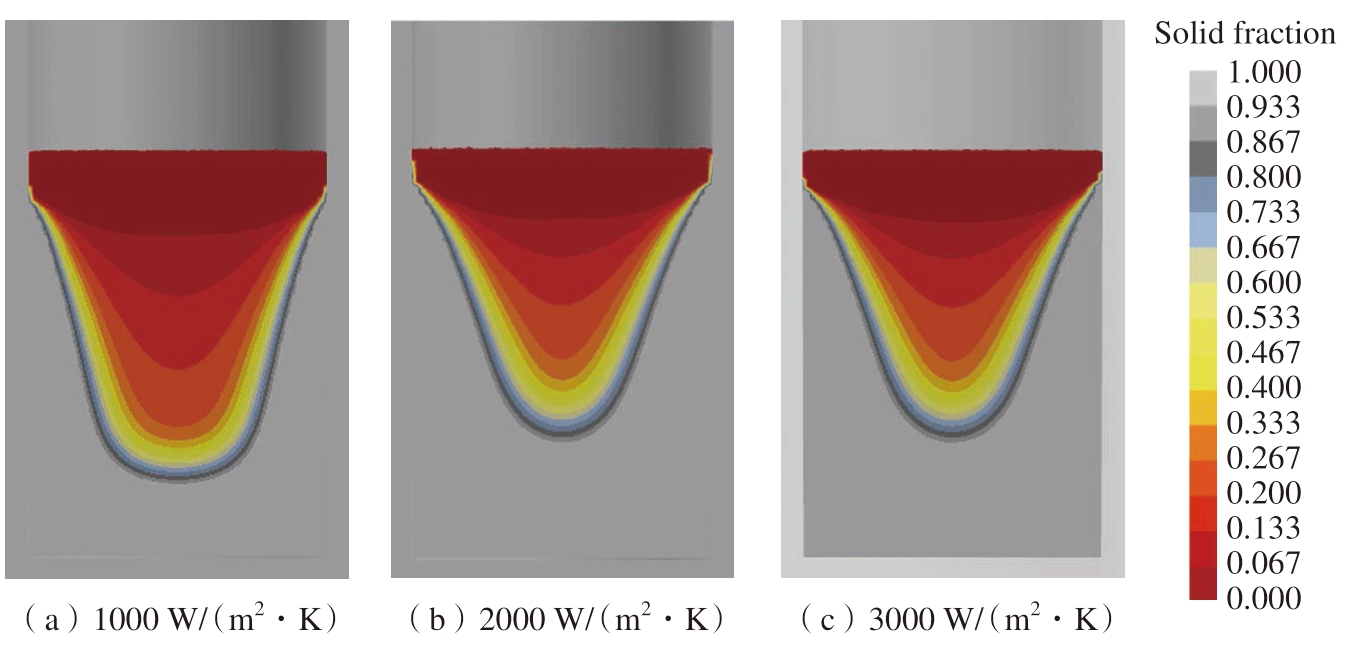
图10 不同换热系数真空自耗熔炼过程中铸锭的固相率
Fig.10 Solid fraction of ingot during VAR process with different heat transfer coefficients
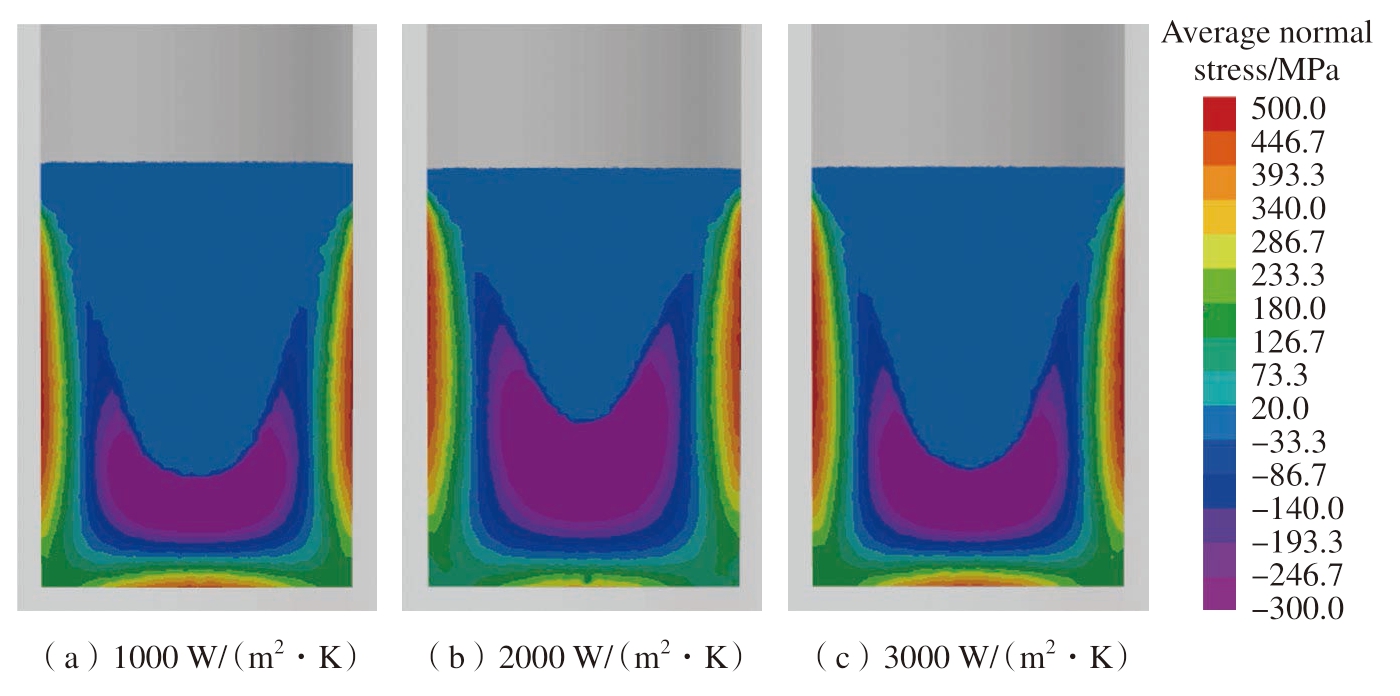
图11 不同换热系数真空自耗熔炼过程中的应力场
Fig.11 Stress field during VAR process with different heat transfer coefficients
3.4 实际熔炼结果分析
上述研究表明,熔炼速度对γ-TiAl合金真空自耗熔炼过程中熔池形状、热应力有更明显的影响。如图12所示,本文分别采用12 kg/min和6 kg/min熔炼速度制备了大规格γ-TiAl合金铸锭。采用12 kg/min熔炼速度制备的铸锭发生断裂,而采用6 kg/min熔炼速度制备的铸锭外观质量良好,未出现断裂的情况。铸锭断裂是大规格γ-TiAl合金母合金制备的主要问题,较小的熔炼速度有利于降低铸锭的热应力,但需要综合考虑生产效率与冶金质量制定适当的熔炼速度。

图12 采用不同真空自耗熔炼速度制备的300 mm直径γ-TiAl合金铸锭
Fig.12 Φ300 mm γ-TiAl alloy ingots prepared with different melting speeds
4 结论
本文采用数值模拟方法研究了300 mm直径γ-TiAl母合金铸锭的第3次真空自耗熔炼过程,分析了γ-TiAl合金不同条件下真空自耗熔炼过程中金属熔池温度梯度、熔池形状、应力场的变化规律,得到以下结论。
(1)真空自耗熔炼过程中铸锭横向与纵向均存在明显的温度梯度,铸锭心部为压应力区、铸锭表面为拉应力区。在真空自耗熔炼过程中,熔池形状逐渐由扁平状变成V状,表面拉应力区域体积逐渐增大,最大拉应力值变化不大,约为430 MPa。熔炼结束后在铸锭冷却过程中压应力与拉应力均逐渐减小,熔炼结束后400 s时最大拉应力降至180 MPa。铸锭表面产生拉应力是因为在结晶器的冷却作用下,铸锭表面区域快速冷却,与铸锭内部区域相比表面区域因冷却而产生的收缩量更大,导致铸锭表面在收缩时遇阻而产生了拉应力,熔炼结束后铸锭表面产生拉应力也是该原因。
(2)对比了不同熔炼速度对熔炼过程的影响,随着熔炼速度增大,金属熔池变深,熔池底部由尖变宽,达到稳定熔池的时间增加。熔速为3 kg/min时制备铸锭表面最大拉应力约为120 MPa,约为熔速12 kg/min制备铸锭表面最大拉应力的一半。较小的熔炼速度有利于降低铸锭表面拉应力,减小开裂的倾向,但需要综合考虑生产效率与冶金质量制定适当的熔炼速度。
(3)换热系数对熔池形状有一定影响,随着换热系数的增大熔池由U形变为V形,换热系数对熔池深度影响不大,对铸锭中的应力场影响程度较小。
[1] CLEMENS H, MAYER S.Intermetallic titanium aluminides in aerospace applications—Processing, microstructure and properties[J].Materials at High Temperatures, 2016, 33(4–5):560–570.
[2] DIMIDUK D M.Gamma titanium aluminide alloys—An assessment within the competition of aerospace structural materials[J].Materials Science and Engineering: A, 1999,263(2): 281–288.
[3] VOICE W E, HENDERSON M,SHELTON E F J, et al.Gamma titanium aluminide, TNB[J].Intermetallics, 2005, 13(9):959–964.
[4] CLEMENS H, MAYER S.Design,processing, microstructure, properties, and applications of advanced intermetallic TiAl alloys[J].Advanced Engineering Materials, 2013,15(4): 191–215.
[5] 杨锐.钛铝金属间化合物的进展与挑战[J].金属学报, 2015, 51(2): 129–147.
YANG Rui.Advances and challenges of TiAl base alloys[J].Acta Metallurgica Sinica, 2015,51(2): 129–147.
[6] LORIA E A.Gamma titanium aluminides as prospective structural materials[J].Intermetallics, 2000, 8(9–11): 1339–1345.
[7] LASALMONIE A.Intermetallics: Why is it so difficult to introduce them in gas turbine engines?[J].Intermetallics, 2006, 14(10–11):1123–1129.
[8] LAPIN J.TiAl-based alloys: Present status and future perspectives[J].Metal, 2009,19(5): 5–12.
[9] GÜTHER V, ALLEN M, KLOSE J, et al.Metallurgical processing of titanium aluminides on industrial scale[J].Intermetallics, 2018, 103:12–22.
[10] PATEL A D, MINISANDRAM R S,EVANS D G.Modeling of vacuum arc remelting of alloy 718 ingots[C]//Superalloys 2004 (Tenth International Symposium).TMS, 2004: 917–924.
[11] 赵小花, 李金山, 杨治军, 等.钛合金真空自耗电弧熔炼过程中温度场影响的数值模拟[J].特种铸造及有色合金, 2010, 30(11):1001–1004.
ZHAO Xiaohua, LI Jinshan, YANG Zhijun,et al.Numerical simulation of temperature field during vacuum arc remelting for titanium alloys[J].Special Casting and Nonferrous Alloys, 2010,30(11): 1001–1004.
[12] 王斌斌, 常辉, 李金山, 等.真空自耗电弧熔炼过程中电磁场搅拌的数值模拟[J].稀有金属材料与工程, 2009, 38(11): 1969–1973.
WANG Binbin, CHANG Hui, LI Jinshan,et al.Numerical simulation of electromagnetic stirring during vacuum arc remelting[J].Rare Metal Materials and Engineering.2009, 38(11):1969–1973.
[13] 王宝顺, 董建新, 张麦仓, 等.真空自耗电弧重熔凝固过程的计算机模拟[J].材料工程, 2009, 37(10): 81–84, 90.
WANG Baoshun, DONG Jianxin, ZHANG Maicang, et al.Computational modeling of the solidification during vacuum consumable arc remelting process[J].Journal of Materials Engineering, 2009, 37(10): 81–84, 90.
[14] 杨富仲, 张健, 张立峰, 等.镍基高温合金真空自耗数值模拟[J].钢铁研究学报,2022, 34(9): 916–924.
YANG Fuzhong, ZHANG Jian, ZHANG Lifeng, et al.Numerical simulation of vacuum arc remelting nickel-based superalloy[J].Journal of Iron and Steel Research, 2022, 34(9): 916–924.
[15] 程爱民, 马昱, 高向宙, 等.14Cr–13Co–5Mo–2Ni齿轮钢真空自耗熔炼过程的数值模拟[J].特殊钢, 2014, 35(5): 23–25.
CHENG Aimin, MA Yu, GAO Xiangzhou, et al.Numerical simulation on consumable-electrode vacuum melting process for 14Cr–13Co–5Mo–2Ni gear steel[J].Special Steel, 2014, 35(5): 23–25.
[16] 李海松, 李宏伟, 寇宏超, 等.真空自耗熔炼γ-TiAl合金铸锭凝固组织模拟[J].特种铸造及有色合金, 2012, 32(10): 901–904.
LI Haisong, LI Hongwei, KOU Hongchao,et al.Prediction of solidification microstructure in TiAl alloy ingots during vacuum arc remelting[J].Special Casting and Nonferrous Alloys, 2012,32(10): 901–904.
[17] 吴士平, 郭景杰, 贾均.TiAl基合金排气阀立式离心铸造充型及凝固过程数值模拟[J].金属学报, 2004, 40(3): 326–330.
WU Shiping, GUO Jingjie, JIA Jun.Numerical simulation of mold filling and solidification of tial base alloy exhaust valve in vertical centrifugal casting process[J].Acta Metallurgica Sinica, 2004, 40(3): 326–330.
[18] EL MIR H, JARDY A, BELLOT J P, et al.Thermal behaviour of the consumable electrode in the vacuum arc remelting process[J].Journal of Materials Processing Technology, 2010,210(3): 564–572.
[19] 丁永昌, 徐曾启.特种熔炼[M].北京: 冶金工业出版社, 1995: 207–210.
DING Yongchang, XU Zengqi.Special melting[M].Beijing: Metallurgical Industry Press, 1995: 207–210.
[20] KERMANPUR A, EVANS D G,SIDDALL R J, et al.Effect of process parameters on grain structure formation during VAR of Inconel alloy 718[J].Journal of Materials Science,2004, 39(24): 7175–7182.
[21] ZANNER F J, WILLIAMSON R L,HARRISON R P, et al.Vacuum arc remelting of alloy 718[C]//Superalloys 718 Metallurgy and Applications.TMS, 1989: 17–31.
[22] HOSAMANI L G, WOOD W E,DEVLETIAN J H.Solidification of alloy 718 during vacuum arc remelting with helium gas cooling between ingot and crucible[C]//Superalloys 718 Metallurgy and Applications (1989).TMS,1989: 49–57.
