| 航空制造技术 第67卷 第22期 110-117 2024-11-15 出版 | Aeronautical Manufacturing Techinology, Vol.67, No.22: 110-117 |
| DOI: 10.16080/j.issn1671-833x.2024.22.110 |
研究论文(RESEARCH)
基于机器视觉的直升机传动系统回转轴线标定方法
2.南京航空航天大学苏州研究院,苏州 215000
[摘要] 直升机传动系统中存在多个回转轴线,其空间位姿信息是后续装配的重要依据,传统的测量方法精度低,速度慢,难以实现数字化。针对上述问题,提出一种基于机器视觉的直升机传动系统回转轴线标定方法。首先通过视觉靶标建立绝对坐标系,其次基于Radon变换的棋盘格角点检测技术进行亚像素角点检测,然后通过Levenberg–Marquadt算法进行单目相机的绝对位姿估计,最后进行单目相机运动轨迹拟合,得到回转轴线的空间位姿信息。结果表明,此方法的标定精度优于0.35 mm,可以满足后续传动系统装配的要求。
关键词:视觉测量;回转轴线;亚像素角点;PnP问题;空间圆拟合
Calibration Method for Rotary Axis of Helicopter Transmission System Based on Machine Vision
2.Suzhou Research Institute of Nanjing University of Aeronautics and Astronautics, Suzhou 215000, China
[ABSTRACT] There are multiple rotary axes in the helicopter transmission system and their spatial pose information is an important basis for subsequent assembly. Traditional measurement methods have low accuracy and slow speed, and are difficult to realize digitalization. Aiming at the above problems, a machine vision-based rotation axis calibration method for helicopter transmission system is proposed. Firstly, the absolute coordinate system is established by the visual target, and the sub-pixel corner is detected by the checkerboard corner detection technology based on Radon transform. Then the absolute pose of the monocular camera is estimated by the Levenberg–Marquadt algorithm. Finally, the spatial pose information of the rotary axis is obtained by fitting the motion trajectory of monocular camera. Experimental results show that the calibration accuracy of this method is higher than 0.35 mm, which meets the requirements of subsequent transmission system assembly.
Keywords: Vision measurement; Rotary axis; Sub-pixel corner; PnP problem; Spatial circle fitting
引文格式:齐凯, 李泷杲, 黄翔, 等. 基于机器视觉的直升机传动系统回转轴线标定方法[J]. 航空制造技术, 2024, 67(22): 110–117.
QI Kai, LI Shuanggao, HUANG Xiang, et al. Calibration method for rotary axis of helicopter transmission system based on machine vision[J]. Aeronautical Manufacturing Technology, 2024, 67(22): 110–117.
通讯作者:李泷杲,副教授,博士,主要研究方向为飞机数字化装配与测量技术。
基金项目:中央高校基本科研业务费专项资金(NP2022421);江苏省卓越博士后计划(2022ZB217)。
近年来,随着航空工业的不断发展,新一代直升机在安全性、可靠性和先进性方面也有着更高的要求。直升机传动系统是发动机向尾翼及直升机附件提供转速和扭矩的唯一途径,其性能是影响直升机工作寿命和效率的重要指标。Muelaner等[1]的研究表明,航空航天工业中50%机械设备的损坏是由轴系同轴度误差超出正当范围导致的,因此,保证传动系统的装配精度对直升机性能具有重要意义。
现有的直升机传动系统安装调整技术规范通常要求在完成装配后,主减速器输出轴线、中减速器输入轴线、传动轴安装座孔中心连线之间的同轴度偏差不大于0.6 mm,夹角不大于10′。其中,减速器的输入、输出轴线均为回转轴线,因此需要对回转轴线空间位姿信息进行精确标定,以此作为后续装配的重要依据。
回转轴线是虚拟的直线,不能被直接测量[2],因此需要对回转运动中某一点的运动轨迹进行拟合。百分表法是目前旋转机械设备对中的常用方法[3],该方法根据百分表测头在光滑轴面形成的轨迹来确定其回转轴线的位置,属于接触式测量,当被测物体存在表面缺陷或不为圆柱体时,则无法使用此方法。在视觉测量领域,汪亭玉[4]提出了一种基于CMOS图像传感器的轴系同轴度测量方法。毕超等[5]提出了一种面向回转工作台的回转轴线标定方法,这些测量标定方法都需要电控旋转设备的参与,不适用于直升机传动系统的装配。在激光测量领域,美国(FIXTURLASER系列)、瑞典(Easy–laserD系列)、德国(OPTALIGN PLUS系列)的激光对中仪均能实现对不同轴径的同轴度进行非接触式测量[6],但这些技术都只能对多个回转轴线之间的位姿关系进行测量与标定,难以实现回转轴线与绝对坐标系下固定物理对象位姿关系的标定。
针对上述问题,本文提出一种基于机器视觉的直升机传动系统回转轴线标定方法,给出坐标系建立和图像采集的方法,采用Radon变换和基于中心线的角点检测模型,基于自适应的思想,进行亚像素棋盘格角点检测,获取多个空间特征点与其对应的图像点。利用检测结果进行坐标系转换矩阵计算,得到单目相机的绝对位姿,基于超最小二乘的思想,进行法向约束的空间圆拟合,得到单目相机的运动轨迹和回转轴线的空间位置信息。通过试验验证了该方法的标定结果具有较好的精度和稳定性,可以满足后续装配的要求,为直升机传动系统的数字化装配提供了一定的借鉴和新思路。
1
1.1
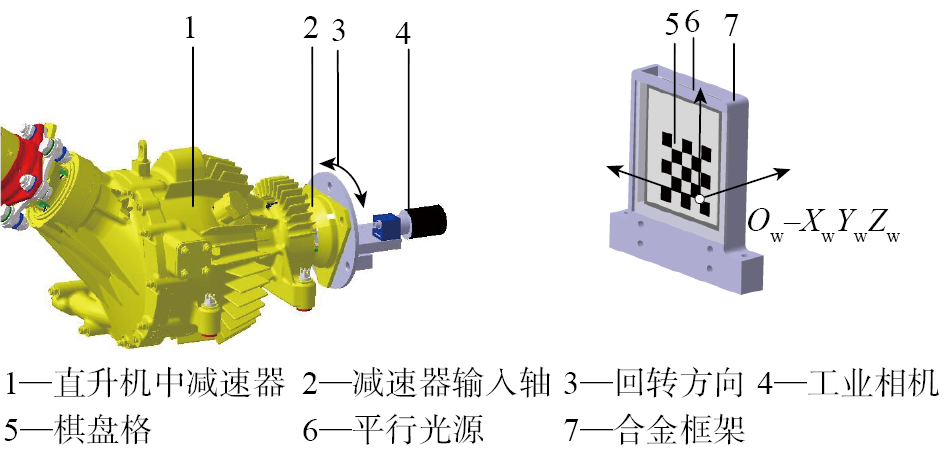
在直升机传动系统装配中,常根据主减速器输出端的回转轴线对中减速器、轴承支座的装配孔位和安装垫片进行调整。根据直升机传动系统中回转轴线的分布特点与测量需求设计视觉靶标,搭建视觉测量环境,如图1所示,工业相机与减速器端面连接,视觉靶标与装配孔连接。棋盘格是一种由黑白方块间隔组成的平面图案,相较于复杂的三维物体,平面棋盘格在相机内参标定、位姿估计等领域有着更广泛的应用。内嵌式的平行光源可以减少环境光的影响,因此设计视觉靶标主要包含棋盘格、内嵌式平行光源及合金框架,其中棋盘格除黑色方块外均为透明材质,内嵌式平行光源位于棋盘格后方。合金框架上含有与地面或其他装配基准连接的孔,因此可在视觉靶标上建立绝对坐标系Ow–XwYwZw,为后续步骤提供统一的基准。

图1
Fig.1
以相机光心为原点建立相机坐标系Oc–XcYcZc,其中相机光轴为Zc轴,当工业相机与减速器端面进行安装时,相机坐标系与回转轴线之间存在位置偏差,为避免安装偏差对标定结果的影响,在进行图像采集时需沿回转方向转动减速器输入端一周,在不同的位置采集n张图像。回转轴线标定流程如图2所示。
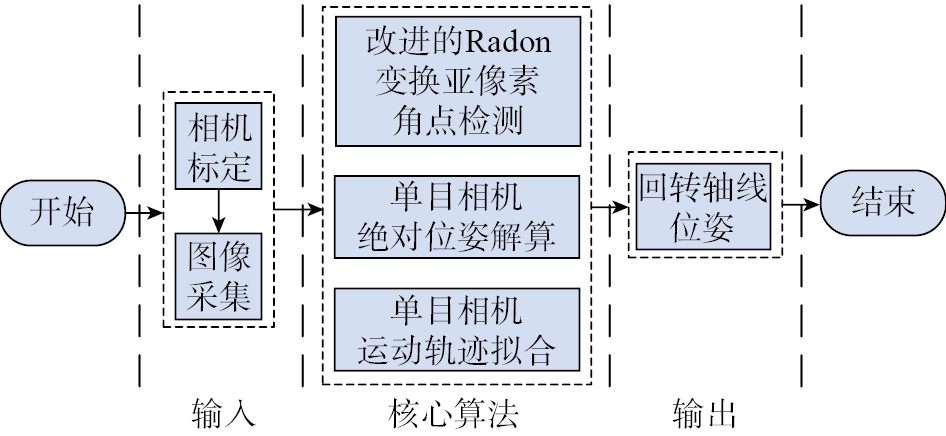
图2
Fig.2
1.2
拟合空间轴线需要对每一次图像采集时单目相机的位姿进行解算,解算过程通过多个空间特征点与其所对应的图像点来实现。本文选取视觉靶标中的角点作为空间特征点,因此角点的检测精度直接关系到标定和测量的精度。Harris算子是一种常用的角点检测工具[7],Douskos等[8]在此基础上加入亚像素细化进行角点检测,精度可达0.1像素。同样地,王民等[9]在Harris算法的基础上,引入了最小亮度变化算法、局部加权熵等方法来提取角点,但此法并不适用于灰度变化不明显的图像。Sinzinger[10]提出了一种基于模板的棋盘格角点检测算法,分为两种模型:基于中心线的检测模型(图3(a))和基于边缘线的检测模型(图3(b))。Duda等[11]利用局部Radon变换算法得到了如图3(a)所示的2条中心线及其交点,实现了角点检测;作为对照组,Duda等[11]还利用梯度检测得到了如图3(b)所示的2条边缘线及其交点,通过对比2种方法,证实了Radon变换角点检测算法具有更好的准确性和鲁棒性。Radon变换角点检测法的基本概念:以一个图像点为中心,沿所有可能存在中心线的方向计算积分,找出其中的最大值和最小值,棋盘格具有对称性,因此若该点为棋盘格角点,则两个积分值的差值将最大化。本文将通过增加自适应非极大值抑制(Soft-NMS),从而对该方法进行改进。
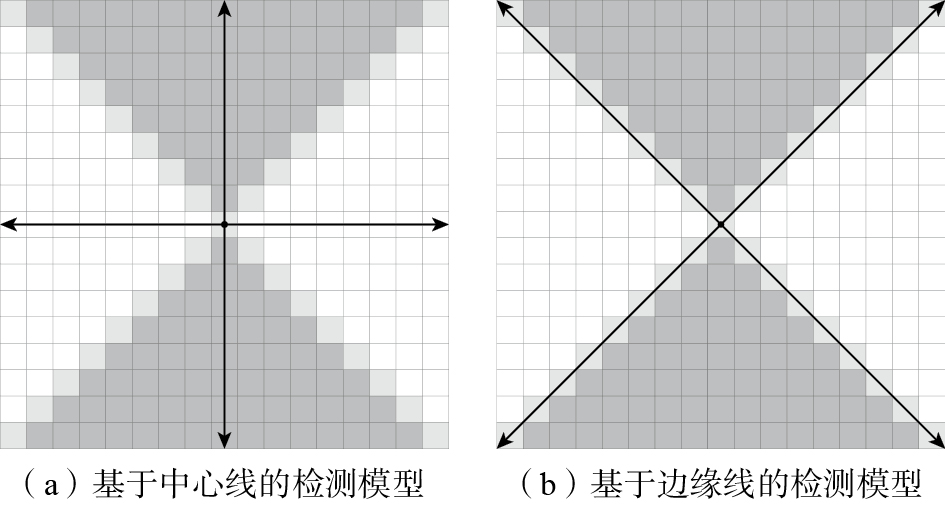
Fig.3
将某一图像点的灰度值表示为f(x,y),沿所有可能存在中心线的方向计算积分值,即以该点为原点做s=0的Radon变换R(s,α),当积分长度为2m+1时,Radon变换表示为
| (1) |
式中,G(x,y)=f(x,y)⊗Gaussian(x,y,v),采用比例因子为v的高斯卷积核对图像进行滤波处理。对于同一个图像点,所有方向上积分最大值与最小值的差值表示为
| (2) |
如图4所示,当图像点c为角点时,c处的响应函数值应为局部最大值,因此当某个图像点的响应函数fc(x,y)值为局部最大值时,该点为候选角点。需要对fc(x,y)进行非极大值抑制(NMS)筛选,在保留细节特征的条件下去除噪点和伪角点,检测出局部最大值。NMS算法是一种经典的局部最大值搜索方法,在目标检测、定位等领域中被广泛使用,其原理是对于每个选定的窗口,只保留响应度最高的特征点,丢弃其他特征点。在棋盘格角点的检测过程中,当棋盘格在图像中的占比或图像分辨率不同时,对窗口大小的选择也不同。窗口过大时会导致过滤掉本应被检测到的角点,窗口过小时会增加伪角点的产生。采用自适应非极大值抑制(Soft-NMS)算法可以解决这一问题。Soft-NMS算法的基本思想是评估候选角点的极大区域并进行排序,从而避免窗口大小选择的问题。具体的步骤为,首先设定阈值tc,从而筛选出候选角点点集S,即
| (3) |
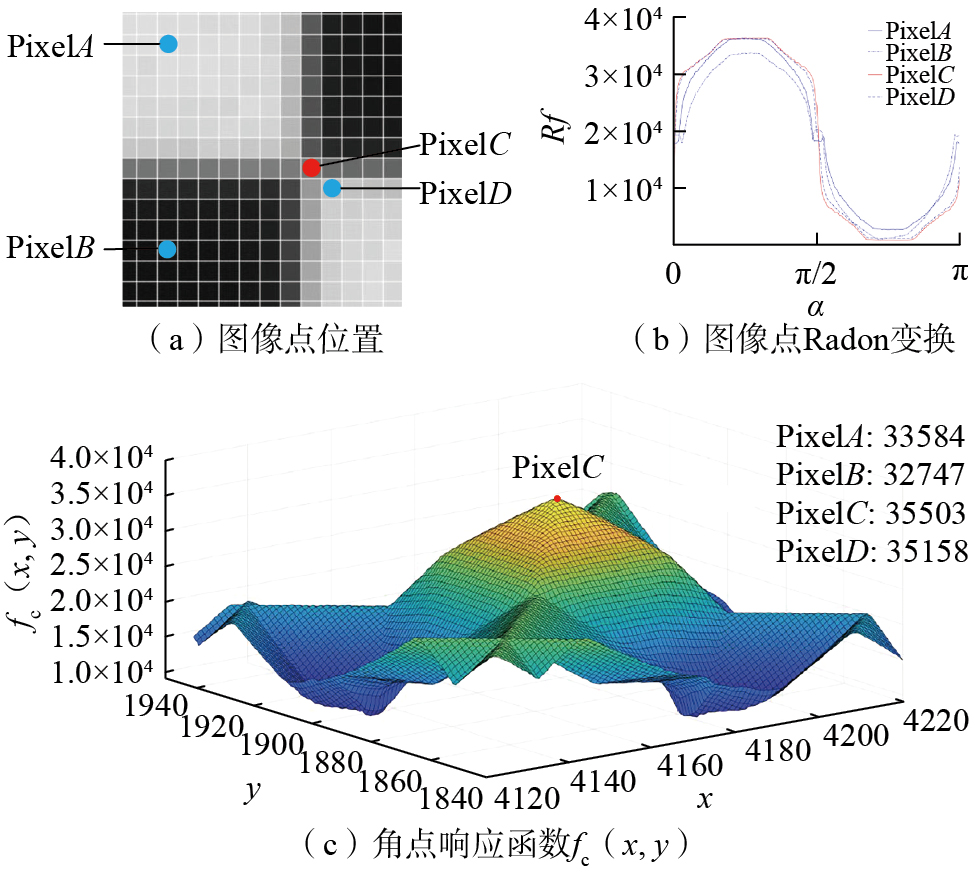
图4
Fig.4
对于每一个候选角点(xi,yi),计算其响应值fc(xi,yi)作为局部最大值的最大区域半径ri为
| (4) |
通过对比ri的大小对S中的每个点(xi,yi)进行降序排列,根据视觉靶标中棋盘格角点的个数设置数量约束Num_Chessboardcorner,选取前Num_Chessboardcorner个候选角点储存至棋盘格角点点集Chessboardcorner_Point中,完成像素级棋盘格角点的提取。
1.3
在真实世界中,棋盘格角点的坐标值不是整数,因此采用改进的Radon变换角点检测算法提取的整像素角点并不是理想的角点位置。为了提高角点的检测精度,采用梯度法实现角点位置的亚像素优化[12]。
假设理想角点的位置为c,记其邻域中任一图像点p的梯度为gp,则这个梯度的方向应与线段p–c垂直,因此有
| (5) |
考虑到真实图像中的线段宽度不会只有一个像素大小,梯度方向也不会如此理想,则理想角点c的位置应满足
| (6) |
式中,NI(c')为Chessboardcorner_Point中的像素级角点c'周围11×11的像素邻域;通过对c'求导并令求导结果为0,可得到解析解
| (7) |
将求得的亚像素角点更新至Chessboardcorner_Point中,即完成了棋盘格角点的亚像素提取,如图5所示。Lavest等[13]的研究表明,摄像机标定的重投影误差可以定性反映棋盘格角点的提取精度。为了验证亚像素角点检测方法的优越性,对于一组相同的图片,分别以该方法中像素级的检测结果和亚像素级的检测结果作为输入,采用文献[14]中的标定方法进行摄像机标定,两种输入的平均重投影误差如表1所示,结果表明,亚像素级坐标的精度优于像素级坐标的精度。

图5
Fig.5
表1
Table 1
| 组别 | 图片数量 | 平均重投影误差/pixel | 平均重投影误差/mm | ||
|---|---|---|---|---|---|
| 像素级 | 亚像素级 | 像素级 | 亚像素级 | ||
| 1 | 18 | 0.1535 | 0.0352 | 1.0754×10–2 | 2.3999×10–3 |
| 2 | 18 | 0.2110 | 0.0437 | 1.4137×10–2 | 2.9934×10–3 |
| 3 | 18 | 0.2661 | 0.0428 | 1.7829×10–2 | 2.9279×10–3 |
| 4 | 20 | 0.2514 | 0.0376 | 1.6819×10–2 | 2.565×10–3 |
| 5 | 19 | 0.2180 | 0.0407 | 1.478×10–2 | 2.8083×10–3 |
| 6 | 18 | 0.1996 | 0.0389 | 1.3573×10–2 | 2.6258×10–3 |
1.4
工业相机与减速器端面完成连接后,回转轴线与相机光轴Oc–Zc之间存在位姿偏差,如图6所示。当转动减速器端面一周并在任意角度进行图像采集时,由回转运动的特性可知,光心Oc的运动轨迹为空间圆⊙1,且⊙1、Oc–Zc与回转轴线存在以下约束:回转轴线经过⊙1的圆心,回转轴线与Oc–Zc的夹角不变,回转轴线与⊙1所在的平面垂直。因此,可通过Oc–Zc的运动轨迹拟合对回转轴线进行位姿解算,运动轨迹的拟合需要在减速器端面的旋转过程中进行采样并进行单目相机绝对位姿的估计,通过多个空间特征点及其对应的图像点来估算相机的位姿信息,即PnP(Perspective-n-Point)问题[15]。
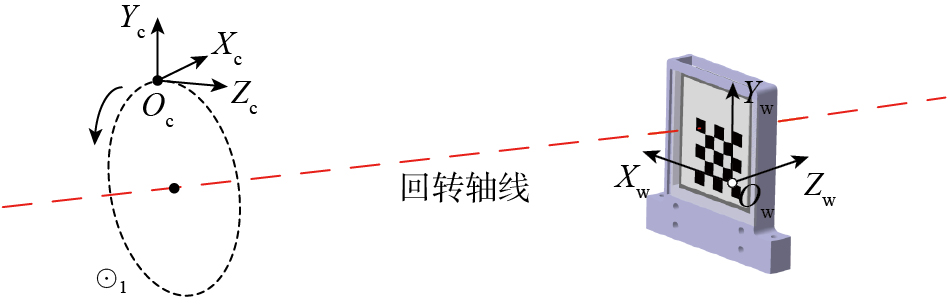
图6
Fig.6
相机成像模型中包含像素坐标系Op–uv、相机坐标系Oc–XcYcZc、绝对坐标系Ow–XwYwZw,其中qi=[ui,vi]T为像素坐标点,为相机坐标系下的三维点,为绝对坐标系下的三维点,从像素坐标系到绝对坐标系的转换关系表示为
| (8) |
式中,λ为缩放因子;A为相机内参矩阵;为绝对坐标系和相机坐标系之间的转换矩阵。在PnP问题中相机内参矩阵为已知,一组绝对坐标点及与其对应的像素坐标点为输入量,旋转矩阵R和平移向量T为待求解量。
目前应用比较广泛的PnP问题求解算法主要可分为解析算法和迭代算法,解析算法中包含直接线性变换(Direct linear transform,DLT)[16]、EPnP[17]等,迭代算法中包含正交迭代算法(LHM)[18]、Levenberg–Marquadt(LM)[19]优化算法等。为了提高回转轴线的标定精度,针对本文方法中所使用的棋盘格视觉靶标,对几种主流PnP算法进行对比,具体如下。
(1)DLT算法:将看作一个包含12个未知量的矩阵,将式(8)转化为方程组形式后共包含3个方程,消去缩放因子λ后包含2个方程,即每组2D–3D匹配点可以对应2个方程,则至少需要6组匹配点才能解出12个未知量。
(2)EPnP算法:该方法的基本概念是将绝对坐标系下的三维点转换至相机坐标系下,然后采用ICP(Iterative closest point)法计算待求矩阵,可求解4组以上匹配点的位姿问题。
(3)UPnP算法[20]:在EPnP算法的基础上估算了焦距,因此适用于未进行相机标定的情况。
(4)OPnP算法[21]:该方法采用Gröbner基进行最优化求解,具有很高的求解精度和鲁棒性,但可能会得到多个解析解。
(5)LM算法:是一种非线性优化算法,目标是为了最小化系统误差,其迭代过程为,给出一个初始R,求出此时最优化的T后,再求出最优解R,从而不断更新R和T。
上述方法得到重投影误差的均值和中值,如图7所示,在本文测量环境下,共包含110组2D–3D匹配点,LM算法具有更高的求解精度,因此单目相机绝对位姿的估计步骤如下。
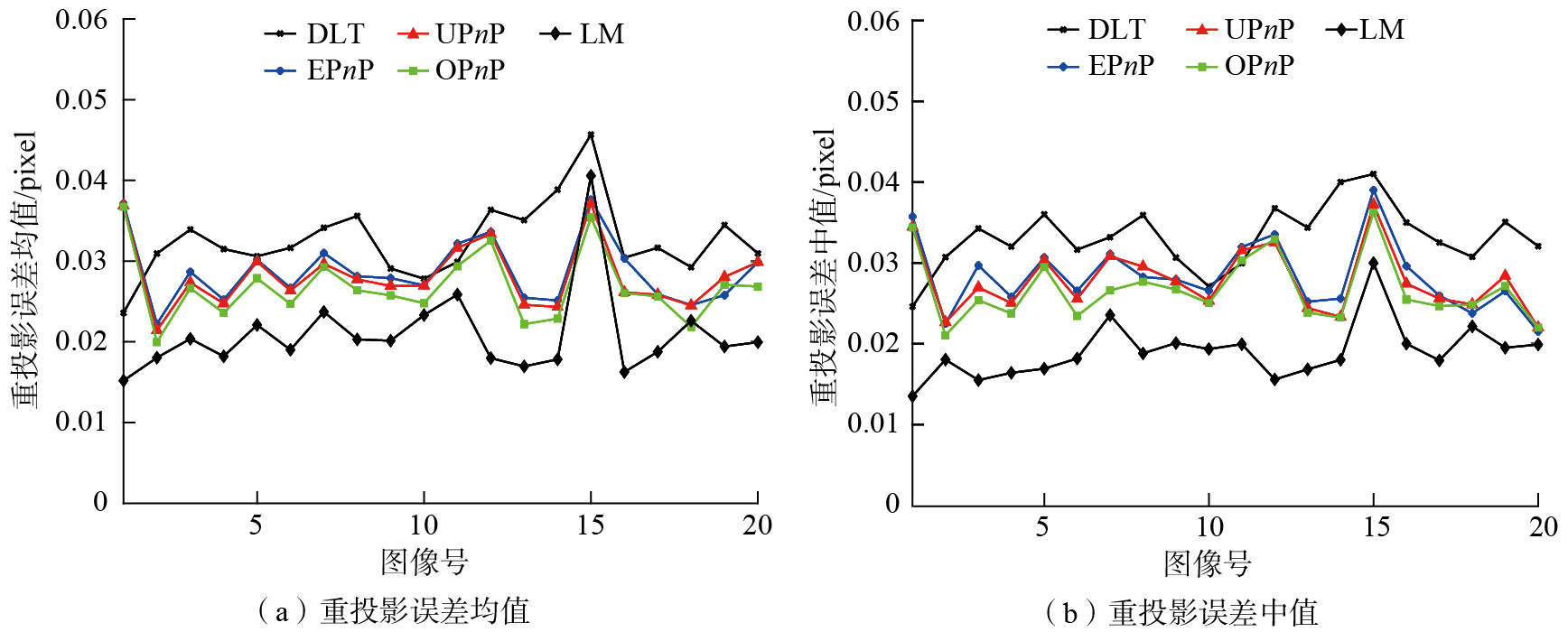
图7
Fig.7
(1)以棋盘格视觉靶标最靠近右下角的角点作为绝对坐标系原点Ow(0,0,0),每一个棋盘格都是5 mm×5 mm的正方形,则原点上方相邻点的坐标为(0,5,0),左侧相邻点的坐标为(5,0,0),以棋盘格平面作为Ow–XwYw平面,以棋盘格平面法向作为Ow–Zw轴,将110个角点的坐标储存至点集Worldcorner_Point中;
(2)通过行列数目的约束,调整Worldcorner_Point内部点的顺序,使之与Chessboardcorner_Point形成对应关系;
(3)通过LM算法解算出,可以表示视觉靶标在相机坐标系下的位姿,求逆得到,即完成了单目相机绝对位姿的估计。
1.5
转动减速器端面一周,在不同位置采集n张图像,利用单目相机的n次绝对位姿估计结果拟合单目相机的运动轨迹,进而获得回转轴线的空间位姿信息。
相较于平面圆拟合,空间圆拟合的方法更多、复杂度更高,主要分为两类:(1)将空间圆看作一个球体与过球心平面相交所形成的圆,首先利用球面上两点的中垂面经过圆心拟合出球体,然后与所有三维点拟合出的平面联立,解出空间圆的信息;(2)将所有三维点投影至拟合平面,得到这些点在平面的二维坐标,从而将问题转化为平面圆的拟合。上述两种方法都需要对三维点所在的平面进行拟合,而该平面的法向量就是回转轴线在绝对坐标系中的方向向量,因此该平面的拟合精度直接影响最终的标定精度。通过测试可知,在单目相机绝对位姿估计中,与光心Oc相比,光轴方向Oc–Zc的测量结果具有更高的稳定性,因此在减速器端面旋转过程中,确定回转轴线与Oc–Zc的夹角不变这一约束条件进行平面法向量的求解,并以法向量为约束进行平面求解和噪点过滤。对于Oc–Zc的测量结果ni=(ai,bi,ci)T(i=1,2,3,…),建立空间圆的平面方程Ax+By+Cz–D=0,平面单位法向量为n=(A,B,C)T,则
| (9) |
式中,;。其中,θ为回转轴线与Oc–Zc的夹角。代入Oc的测量结果pi=(xi,yi,zi)T(i=1,2,3,…),得到
| (10) |
设置阈值tD,去除的pi后,再次计算式(10)直至所有的pi都满足阈值要求,得到空间圆所在平面Ax+By+Cz–D=0。将噪点过滤后的pi投影至该平面,空间圆拟合问题便转换成了平面圆的拟合问题,利用超最小二乘法进行平面圆拟合[22],再将拟合结果转换至绝对坐标系,得到半径R和圆心坐标O(x,y,z)T。至此,完成了回转轴线的空间位姿求解,即回转轴线的标定过程(图8),其中轴线的单位方向向量n=(A,B,C)T,且经过回转中心O(x,y,z)T。
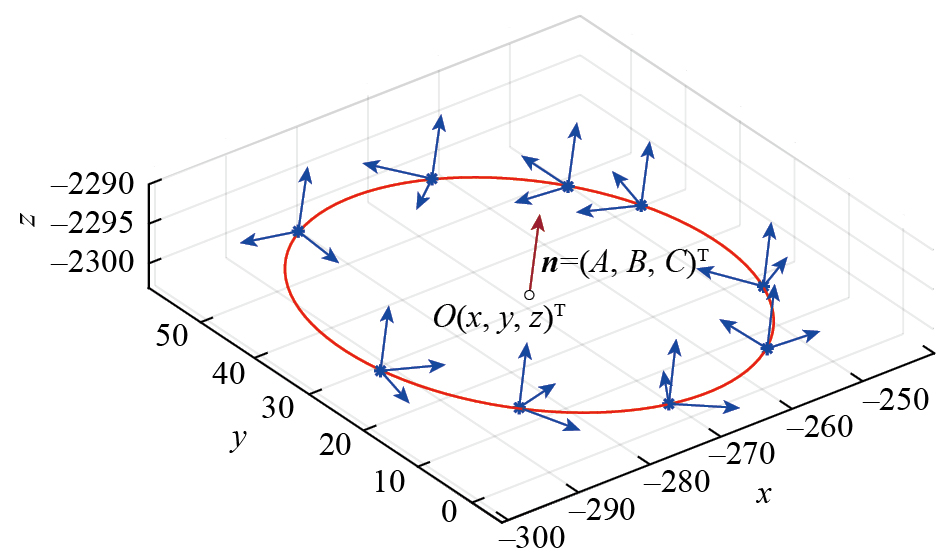
图8
Fig.8
2
为了验证基于机器视觉回转轴线标定方法的准确性和鲁棒性,在图9所示的测量环境下进行回转轴线的标定。带有内嵌式光源的棋盘格视觉靶标固连于传动系统精密驱动平台,视觉靶标的合金框架中置有4个激光靶球孔位,工业相机与直升机中减速器模拟件的输入端面固连,镜头端面正对视觉靶标,确保旋转端面一周时,在任意位置都可清晰捕捉到完整的棋盘格图像。试验平台采用MER2–2000–19U3C工业数字相机(大恒图像公司),分辨率为5496×3672,像素尺寸为2.4 μm;镜头为HN–5024–20M–C1定焦镜头(大恒图像公司),焦距为50 mm,工作距离为1400~1500 mm。

图9
Fig.9
为验证准确性,使用本方法完成一次回转轴线的标定后,移动传动系统精密驱动平台并再次进行回转轴线标定,与通过激光跟踪仪和激光靶球求解得到的第二次回转轴线空间位姿信息进行对比,得到回转中心偏差和角度偏差。为验证鲁棒性,通过多次调整传动系统精密驱动平台改变视觉靶标位姿,检验本方法的标定准确度,具体试验步骤如下。
(1)完成相机内参标定,打开平行光源,在视觉靶标上放置4个激光靶球,在视觉靶标方圆2 m内且无遮挡的环境中放置Leica激光跟踪仪;
(2)通过本方法获取方向向量n0=(A0,B0,C0)T,回转中心点O0=(x0,y0,z0)T,通过激光跟踪仪获取当前视觉靶标空间位姿信息,为了去除激光靶球孔的加工误差和棋盘格与合金框架之间的装配误差,靶球孔位与棋盘格之间的位置关系通过影像测量仪进行测量;
(3)移动传动系统精密驱动平台,通过本方法获取方向向量n1=(A1,B1,C1)T,回转中心点O1=(x1,y1,z1)T,通过激光跟踪仪获取当前视觉靶标空间位姿信息并解算出两次视觉靶标的位姿转换关系T,根据激光跟踪仪的测量结果,当前回转轴线的方向向量为Tn0=(AL,BL,CL)T,回转中心点TO0=(xL,yL,zL)T,因此本方法标定的回转中心偏差,夹角偏差;
(4)移动传动系统精密驱动平台,重复步骤(2)和(3),记录10组数据;
(5)分析试验数据。
表2
Table 2
| 组别 | 激光跟踪仪回转中心/mm | 本方法回转中心/mm | 回转中心偏差∆d/mm |
|---|---|---|---|
| 1 | (28.231264, –38.975975, –1454.41411) | (28.230994, –38.986733, –1454.22463) | 0.1897853 |
| 2 | (29.106781, –37.502500, –1454.50288) | (29.030165, –37.5997845, –1454.4536) | 0.1332770 |
| 3 | (41.483309, –58.606570, –1444.11256) | (41.430794, –58.774107, –1443.91845) | 0.2617349 |
| 4 | (52.156907, –36.111005, –1454.33231) | (52.185457, –36.101210, –1454.47434) | 0.1452018 |
| 5 | (24.320059, –63.53972, –1451.889710) | (24.376088, –63.53831, –1451.784730) | 0.1190044 |
| 6 | (22.555230, –13.457549, –1448.08754) | (22.457763, –13.352598, –1447.90276) | 0.2337909 |
| 7 | (38.297811, –25.879255, –1447.69180) | (38.326113, –26.028777, –1447.56077) | 0.2008151 |
| 8 | (23.856921, –37.525785, –1449.39907) | (24.045881, –37.673381, –1449.59937) | 0.3124269 |
| 9 | (30.162960, –53.231899, –1454.35694) | (30.342091, –53.112668, –1454.22828) | 0.2507137 |
| 10 | (51.817766, –34.305501, –1450.19098) | (51.951819, –34.327089, –1450.28223) | 0.1635934 |
表3
Table 3
| 组别 | 激光跟踪仪方向向量 | 本方法方向向量 | 夹角偏差∆θ/(°) |
|---|---|---|---|
| 1 | (0.12522332, –0.0297464, 0.9917867) | (0.12504176, –0.0296542, 0.9918113) | 0.01175 |
| 2 | (0.1252873, –0.0296033, 0.99178190) | (0.12530635, –0.02963789, 0.9917791) | 0.00226 |
| 3 | (0.1195233, 0.11829111, 0.98575929) | (0.11952678, 0.11838824, 0.9857472) | 0.00561 |
| 4 | (0.10525278, 0.11848343, 0.9873619) | (0.10509786, 0.11840763, 0.9873875) | 0.00999 |
| 5 | (0.00009806, –0.19611613, 0.9805807) | (0.0001177, –0.1961633, 0.98057124) | 0.00297 |
| 6 | (0.2873347, –0.0095778, 0.95778235) | (0.28736079, –0.0096783, 0.9577735) | 0.00597 |
| 7 | (0.1104634, –0.0110424, 0.9938188) | (0.1104574, –0.01115837, 0.9938182) | 0.00665 |
| 8 | (–0.21696704, –0.0002212, 0.9761789) | (–0.2169615, –0.0001139, 0.97618016) | 0.00616 |
| 9 | (–0.3162920, –0.0001096, 0.9486619) | (–0.316287, –0.0002477, 0.94866357) | 0.00792 |
| 10 | (–0.2249006, 0.0000780, 0.9743817) | (–0.22489677, 0.00015366, 0.9743826) | 0.00434 |
现有直升机传动系统的装配要求通常为同轴度偏差不大于0.6 mm,夹角误差不大于10′。通过本方法标定所得回转轴线空间位姿的范围为0.1190044~0.3124269 mm,平均回转中心偏差∆d为0.201034 mm;夹角偏差范围为0.00226°~0.01175°,平均夹角偏差∆θ为0.00636°。激光跟踪仪在2 m工作距离下的测量精度小于0.03 mm,因此可知,本方法的标定精度优于0.35 mm,可满足传动系统后续装配的要求。
3
针对直升机传动系统的装配需求,提出了一种基于机器视觉的直升机传动系统回转轴线标定方法。利用改进的Radon变换角点检测算法提取视觉靶标上的关键特征,提高了检测器的准确性和鲁棒性,解决了非极大值抑制时难以确定窗口大小的问题。对比了5种常见PnP问题的求解方法,根据对比结果选用Levenberg–Marquadt优化算法进行单目相机的绝对位姿估计,最后进行了法向约束的空间圆拟合,得到回转轴线的空间位姿信息,为后续装配提供依据。将此方法的标定结果与激光跟踪仪的测量结果进行对比,多次试验结果表明,此方法的标定精度优于0.35 mm,能够满足直升机传动系统后续装配的需求。
参考文献