激光喷丸强化是一种由传统喷丸强化发展而来的新型表面强化技术，相较于传统表面强化技术具有残余压应力层深、表面质量好、工艺可控性强等优点[1-2]。激光喷丸强化效果与残余应力分布密切相关，建立高效的残余应力预测模型是激光喷丸强化的关键环节。固有应变模型是一种能够实现高效预测残余应力的建模方法[3]，在激光喷丸工艺中有广阔的应用前景。然而固有应变难以直接测量，如何准确获取固有应变是限制固有应变模型应用的主要问题。
目前固有应变主要通过X射线衍射方法测量或者通过动态仿真获取。Korsunsky[4-5]和Salvati[6]等通过高分辨率的高能同步辐射X射线衍射法测量固有应变引起的弹性应变分布，并假设总应变为线性分布，通过一系列基函数拟合满足力平衡条件和变形协调方程的固有应变分布。DeWald等[7]通过测量残余应力，将残余应力分解为激光喷丸应力和平衡应力，并假设平衡应力为线性分布，通过曲线拟合去除平衡应力得到喷丸应力，进而由弹性本构计算得到三维固有应变分布。Ali Faghidian等[8]改进了Korsunsky的方法，使用一系列双调和基函数拟合固有应变，并在拟合过程中引入正则项，获得更平滑的固有应变拟合结果。通过测量方法反求固有应变的精度受所选取基函数影响，而且依赖残余应力或残余弹性应变的测量精度，测量过程也较为复杂。通过激光喷丸动态仿真直接获取固有应变是另一确定固有应变的途径。Achintha等[9]基于激光喷丸单点动态冲击仿真模型获取了稳定的固有应变分布，但其仿真使用的冲击压力模型为空间均匀分布的三角波，与实际激光喷丸冲击压力不符，且单点冲击难以反映实际激光喷丸强化的多点搭接效应，因此所得到的固有应变并不可靠。Hu等[10]根据Fabbro激光冲击压力模型标定出激光冲击压力随时间的分布，并根据光斑能量分布假设空间压力分布为高斯分布，建立多点搭接激光喷丸模型，并通过代表区域的塑性应变均值确定固有应变。基于动态仿真模型获取固有应变虽然提高了求解效率，但由于其工艺参数与仿真输入冲击压力需要进行多次复杂的标定过程，而且存在标定误差，获取的固有应变结果精度有限。近些年，上海交通大学Zhang等[11]首先提出了基于激光喷丸变形几何特征的固有应变反求方法，相较于通过残余应力、应变测量和动态仿真具有更高的计算效率，并且现有设备可以非常精确地测量变形特征，展现出广阔的应用前景。杨荣雪[12]通过动态仿真获取初步固有应变，然后通过实际喷丸变形几何特征对仿真固有应变进行修正，提高了动态仿真获得的固有应变的精度，但该方法依然依赖动态仿真提供的初始结果并且修正需要通过多步迭代，过程复杂。罗明生[13]通过建立激光喷丸变形的固有矩控制方程，得到了激光喷丸变形与固有应变的关系，为通过激光喷丸变形几何特征反求固有应变提供了理论基础。
建立通过变形几何特征进行固有应变反求方法可以大大提高反求效率和精度，对实现激光喷丸强化残余应力预测，推进激光喷丸成形技术应用具有重要意义，但目前仍然缺乏相关的深入研究。本文基于固有应变与变形的有限元方程，分析了由可测变形反求固有应变不完备的原因，提出了激光喷丸变形几何特征结合动态仿真的固有应变反求方法，并通过开展激光喷丸试验从变形和残余应力两方面对反求方法进行了验证。研究结果表明，基于激光喷丸几何特征的固有应变反求方法可以可靠地实现固有应变反求，反求结果可以用于变形和残余应力预测。
1 激光喷丸基本原理与固有应变
1.1 激光喷丸强化原理
激光喷丸强化技术是一种由传统喷丸强化发展而来的新型表面强化技术，通过激光诱导产生的冲击压力使材料发生塑性变形从而引入残余压应力来达到材料强化效果。其作用原理如图1所示，利用高能短脉冲激光辐照提前覆在零件表面的吸收层，使吸收层瞬间发生气化产生等离子体蒸汽，在约束层的作用下形成高压冲击波，冲击向材料内部传播，使零件表面产生塑性变形，在零件表面引入残余压应力以抵消工作过程中外载引起的拉应力，从而提高零件疲劳寿命，起到强化效果[14]。激光喷丸引入的塑性应变的大小和分布决定着残余压应力的大小和分布，对激光喷丸的强化效果起着决定性影响。
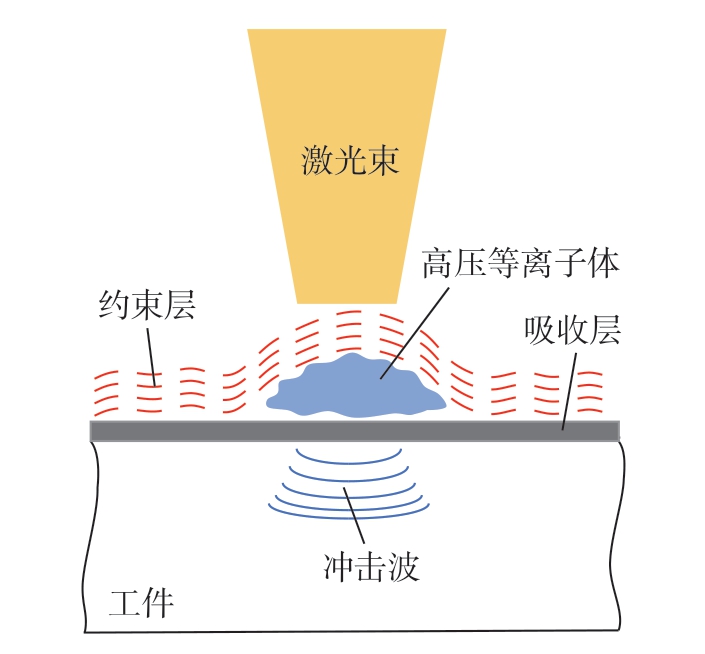
图1 激光喷丸强化原理
Fig.1 Principle of laser peening strengthening
1.2 固有应变基本概念
固有应变是20世纪70年代由日本学者引入的概念，用于分析预测焊接过程产生的变形[15]。固有应变是结构中存在的所有非弹性应变的总和，包括塑性应变εp、热应变εth、相应变εph等，如式 （1）所示，是结构存在初始变形和残余应力的根本原因。
在激光喷丸强化中，固有应变主要为塑性应变，不协调的塑性应变使材料内部发生弹性变形，塑性应变的大小和分布决定了试件的残余应力大小、分布及变形特征，如图2所示，M为固有应变产生的等效弯矩；
为x方向残余应力。由于固有应变引起残余应力和变形的过程是弹性过程，通过建立固有应变模型能够高效地实现残余应力的预测。并且激光喷丸工艺是由单个光斑按照一定路径扫描冲击，产生的固有应变具有局部性的特点，只与工艺参数相关，具有结构无关性，建立固有应变反求方法可以为固有应变模型提供数据支撑。
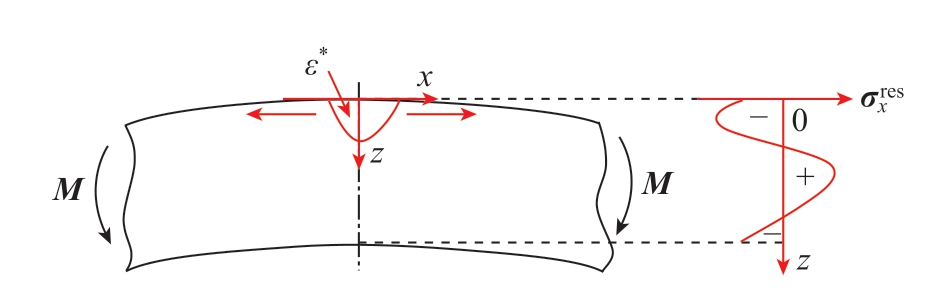
图2 激光喷丸强化固有应变
Fig.2 Eigenstrain of laser peening strengthening
2 基于几何特征的固有应变反求模型
固有应变模型是一种弹性静力学模型，相较于基于物理过程的动态仿真模型有着极高的计算效率，在复杂结构残余应力和成形工艺变形预测中得到广泛应用。在进行固有应变法建模时，一般通过等效的方式进行固有应变加载，如等效热应变、等效载荷等方式。这些建模方法都没有给出显式的固有应变与变形之间的关系，难以通过这些方法反求固有应变。因此，需要通过弹性力学基本原理和有限元理论建立固有应变与变形的关系方程，并基于此建立基于几何特征的固有应变反求方法。
2.1 固有应变数值模型
根据固有应变理论，总应变张量εij是弹性应变张量
和固有应变张量
之和，即
由弹性体虚功原理可知，在平衡体中应力、应变与外载荷之间的变分关系为
式中，σij为应力张量；
为体载荷；
为边界载荷；ui为位移；δεij是某个虚位移δui产生的虚应变；Ω为物体所占据的空间区域；Γσ为载荷所作用的边界区域。
结合弹性变形的线弹性物理方程，将总应变公式（式 （2））代入虚功原理变分方程 （式 （3））中，可以得到
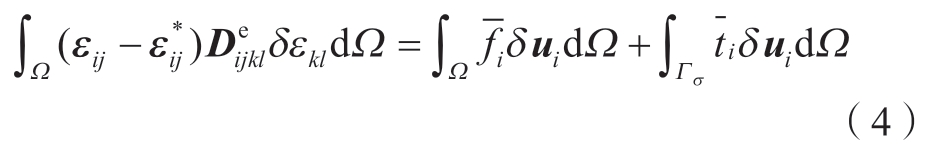
式中，
为材料弹性系数张量；δεkl为弹性体中的虚应变。
在激光喷丸条件下，试件不受外力作用，材料内部应力和应变与边界条件无关，只由固有应变决定。这时边界载荷和体载荷都为0，即
，此时，式（ 4）可以简化为
根据有限单元理论，将式 （5）采用三维线性八节点单元进行离散化，可以得到表示“固有应变-变形位移”的固有应变数值模型有限元方程式。即
式中，K为刚度矩阵；d为节点位移向量； λ为固有应变系数；ε*为固有应变。由式 （6）可以看出，节点位移与固有应变之间有限元方程为线性方程，此式为实现固有应变反求提供了理论基础。
2.2 激光喷丸几何特征与固有应变
激光喷丸在材料中引入了不协调的塑性应变，即固有应变，为保持材料内部连续，试件将通过发生弹性变形来保证内部变形协调。由式 （6）可知，试件各点的变形与固有应变具有对应关系。由于变形量可以方便地通过测量仪器进行精确测量获取，结合固有应变数值模型建立起的固有应变与变形控制方程，理论上可以通过变形实现精确的固有应变反求。并且反求和变形预测都基于控制方程，因此反求结果也能够准确实现变形预测。但是，只有试件表面变形是可测的，如图3所示，测量不完备将导致固有应变反求存在不适定问题，使得固有应变反求问题为多解，因此必须通过引入其他约束条件才能实现反求。
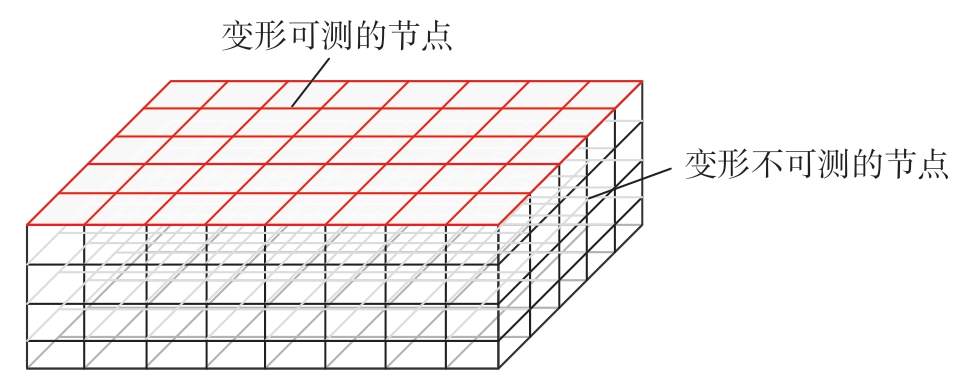
图3 可测位移与不可测位移
Fig.3 Measurable and unmeasurable displacement
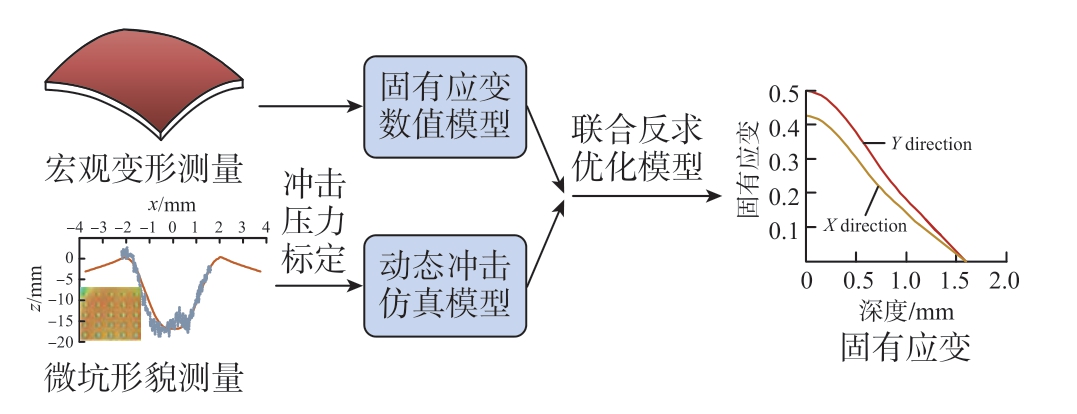
图4 固有应变联合反求过程示意图
Fig.4 Schematic diagram of the joint inversion of eigenstrain
动态冲击模型仿真获取固有应变虽然效率低且不准确，但是真实地模拟了激光喷丸物理过程，所得到的固有应变反映了激光喷丸固有应变的物理意义，这恰好是几何变形反求固有应变时无法反映的。因此，以式（6）为基础推导出表面变形与固有应变的关系，结合动态冲击模型仿真得到的固有应变作为约束条件，建立融合变形几何和初始固有应变信息反求固有应变的方法，可以解决单纯从几何变形无法反求固有应变的问题。
2.3 固有应变反求优化模型
激光喷丸固有应变反求需要考虑两个目标，即反求得到的固有应变既要使理论变形与实际变形误差最小，也要和动态仿真得到的初始固有应变分布趋势尽可能一致。因此可以综合变形和初始固有应变建立多目标优化模型。
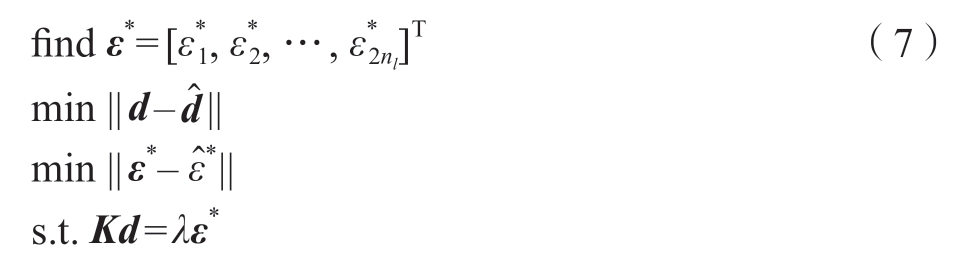
式中，ε*为固有应变列向量；nl为深度方向的单元个数；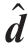
为实际变形位移；
为动态冲击模型仿真得到的初始固有应变。第1个目标函数保证反求得到的固有应变计算的理论变形与实际变形的误差最小，能够实现激光喷丸变形的预测；第2个目标函数保证反求得到的固有应变与动态冲击模型得到的初始固有应变具有相同变化趋势，能够实现残余应力分布的预测；约束条件为固有应变和变形位移有限元方程。
由于材料内部位移无法测量，导致变形位移的测量具有不完备性，即实际变形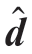
中只有表面的位移z是可以通过试验测量获取的。因此，在建立联合反求优化模型时，首先需要推导表面可测特定位移z与固有应变ε*之间的约束方程。由式（ 6）可知，d与ε*之间为线性关系，而z是d的一部分，因此z与
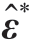也具有线性关系，即
式中，Frr为反映固有应变与表面变形的广义柔度矩阵，可由式（ 6）推导得到。
上述反求优化模型是多目标优化，为便于优化求解，可以通过加权求和转化为单目标优化。但是，两个目标函数反映着不同的意义和目标，一方面希望反求得到的固有应变能准确地实现变形预测，另一方面希望反求得到的固有应变可以反映动态冲击过程，实现可靠的残余应力预测。假设实际固有应变与动态仿真得到的初始固有应变具有比例关系，即ε*=mε*，为消除量纲影响对两个目标函数进行归一化处理，并将归一化之后两个目标给予相同权重，构建联合反求优化模型的目标函数。反求优化模型的建立过程如下。
假设全覆盖均匀激光喷丸的固有应变只沿深度方向变化，表示为
，在深度方向可离散为
即待求优化变量，测量得到表面变形
，动态冲击仿真模型得到的初始固有应变
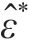，将目标归一化并加权求和构建联合反求优化模型。
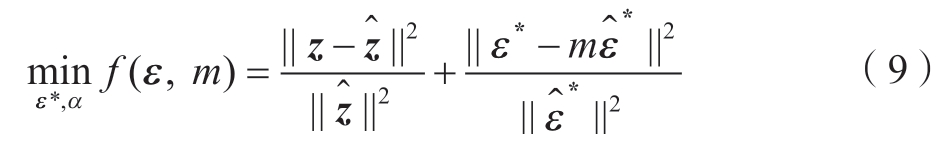
式中，m为实际固有应变与初始固有应变之间的比例系数。
3 试验方法
根据上述方法进行固有应变反求试验，首先进行平板单点冲击试验测量坑形标定激光喷丸冲击压力，通过动态仿真获取初始固有应变。然后对标准平板试样进行激光喷丸试验并测量表面变形。结合测量变形和初始固有应变，通过联合反求优化模型，优化反求固有应变。联合反求过程如图 4 所示。
3.1 激光喷丸与变形测量
为了实现激光喷丸固有应变联合反求，首先对标准平板试样进行激光喷丸试验，试验过程如图5（a）所示。平板尺寸为100 mm×100 mm×4 mm，材料为Al 2024-T351。由于激光喷丸过程中存在水约束层，试样边界会影响水流质量，并且试样边缘需要夹具装夹，无法实现全覆盖激光喷丸，因此实际激光喷丸范围为中心80 mm×80 mm的区域，喷丸区域如图5（b）所示，激光扫描方向定义为X方向，垂直于激光扫描方向为Y方向。激光喷丸试验装置为Nd∶YAG固体脉冲激光器，波长1064 nm，脉冲宽度15 ns，出光频率5 Hz。对试验试样分别采用6 J、8 J、10 J、12 J和14 J 5个不同能量进行激光喷丸，光斑直径为4 mm，光斑搭接率为20%。试验时试样表面覆盖黑胶带作为吸收层，水作为约束层，试样由安装在机器人上的固定夹具夹持，由机器人带着按照预定的喷丸路径运动。
图5 激光喷丸试验示意图
Fig.5 Schematic diagram of the experiment of laser peening
图6（a）是在不同能量下进行激光喷丸后的试样。由薄板弹性变形理论可以推出，全覆盖喷丸条件下，平板试样的表面变形为抛物面[13]，理论上测量两个点就可以完全确定抛物面参数。但是实际测量会受到表面粗糙度影响，为避免其影响，测量试样X、Y两个方向的中轴线变形，如图6（b）所示。其中，Hx、Hy分别为x方向和y方向的弧弓高。通过三维表面形貌仪，使用LK- G80激光位移测头进行变形测量，测头的重复精度为0.2 μm，测量过程中形貌仪步长设定为100 μm。为避免试样表面粗糙度对固有应变联合反求的影响，对测量得到的中心线轮廓使用二次函数进行拟合得到轮廓曲线方程，进而获得抛物面方程，然后在有限元单元节点处进行插值得到单元结点位移。经过拟合后的变形位移曲线如图7所示。可以看出，随着激光能量增大，试件变形越来越大。
图6 激光喷丸平板变形试样与测量位置
Fig.6 Laser peening deformed plate specimen and measured position
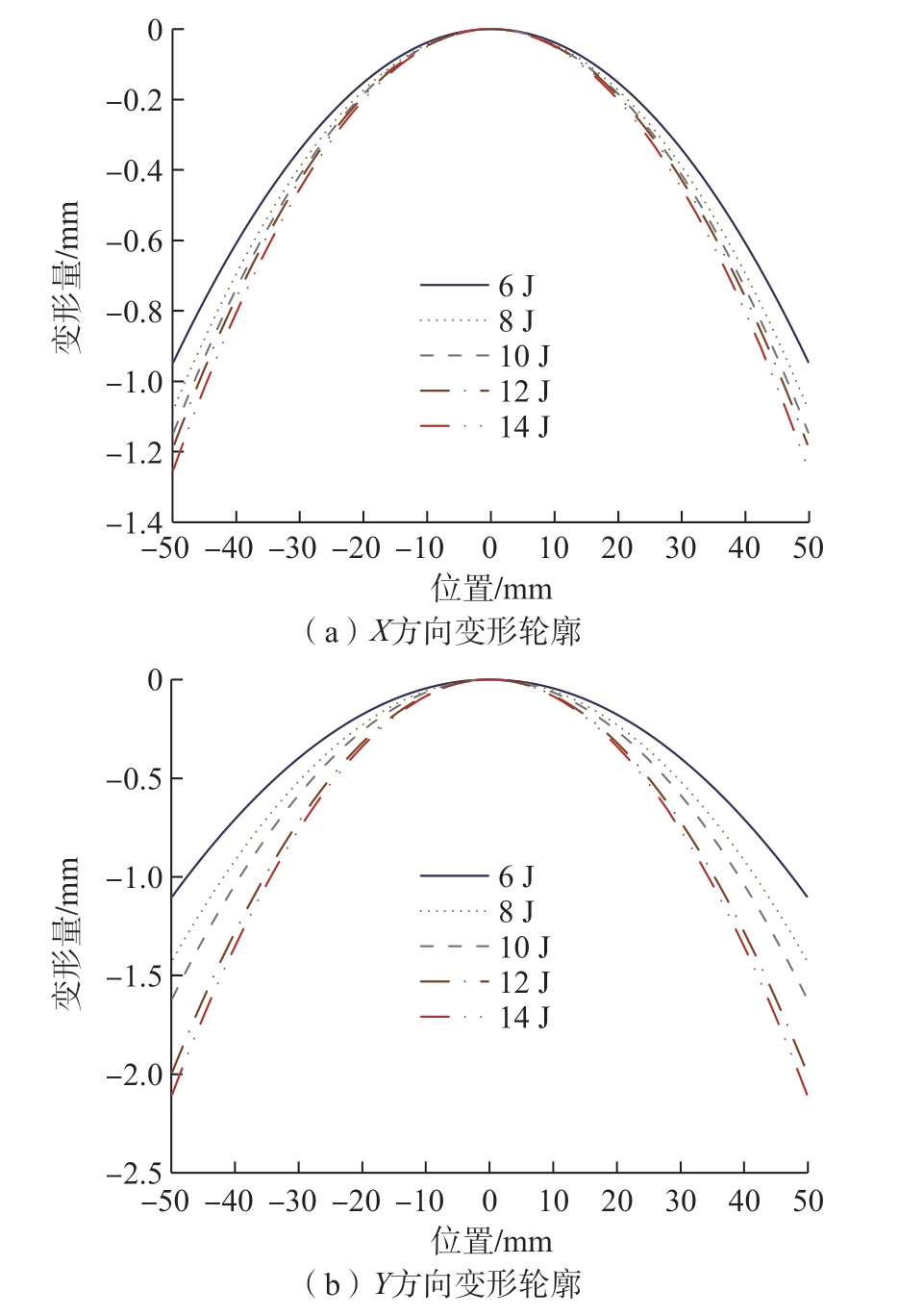
图7 中心线拟合变形轮廓
Fig.7 Profile of center lines after fitting
3.2 初始固有应变标定
在联合反求固有应变时，建立动态冲击仿真模型获取初始固有应变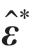
需要对激光冲击压力进行标定。动态冲击仿真以Fabbro激光冲击压力模型[16-17]描述的冲击压力作为输入，该模型将激光冲击压力的变化分为两个阶段，第1阶段为激光诱导等离子体并产生冲击压力的过程，第2阶段为在冲击压力引起的动力学响应过程。模型中待标定参数主要有两个，即冲击压力时间分布参数α和空间分布参数β[12]。
图8所示为冲击压力的参数标定和初始固有应变的获取过程，首先在平板试样上进行单点激光冲击试验得到冲击微坑并测量微坑形貌，获取不同激光能量下的坑深和半高宽（ FWHM）；设定冲击压力参数，通过Fabbro模型计算冲击压力，然后进行单点动态冲击仿真获得仿真坑深和半高宽与试验测量结果进行匹配，根据匹配误差不断迭代激光冲击压力参数，直至匹配误差满足精度要求，完成冲击压力参数标定。将标定得到的参数代入Fabbro模型计算不同能量的激光冲击压力，以对应能量的冲击压力为输入，建立多点搭接动态仿真模型，获得不同能量对应的初始固有应变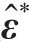
。
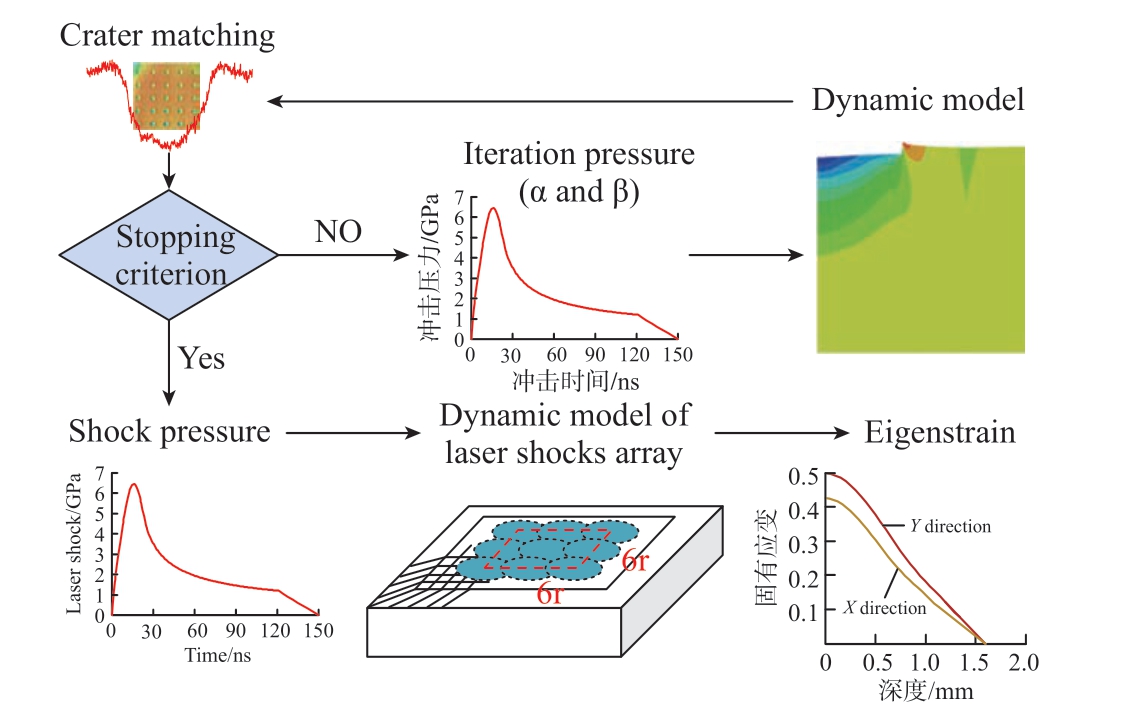
图8 激光冲击压力标定
Fig.8 Laser shock pressure determination
将根据坑深和半高宽标定得到的冲击压力参数代入Fabbro模型，得到不同激光能量下的冲击压力随时间变化曲线，如图 9 所示。
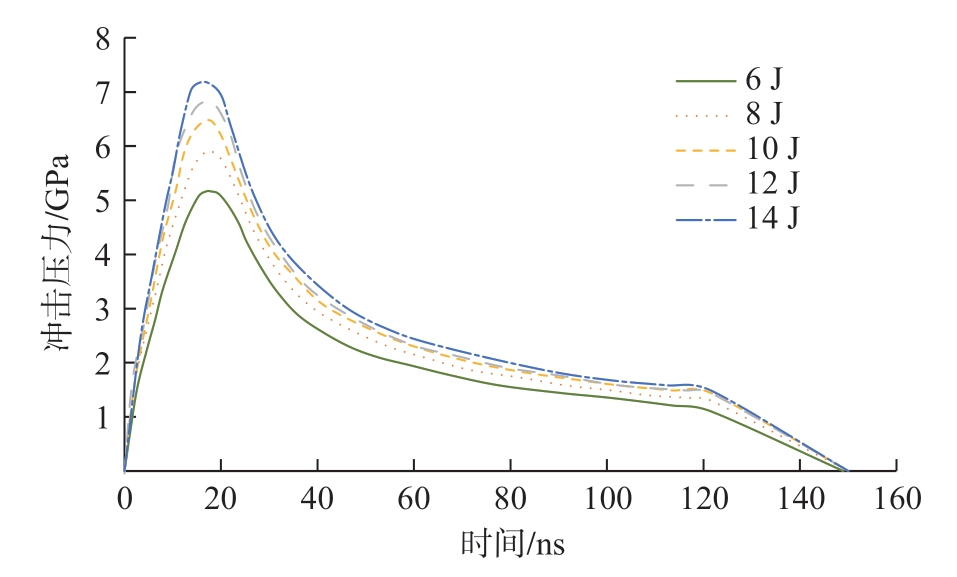
图9 不同能量下标定的激光冲击压力
Fig.9 Determined laser shock pressure under different laser energies
完成不同能量的冲击压力标定后，使用ABAQUS建立多点搭接动态仿真模型获得初始固有应变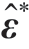
。模型的尺寸为24 mm×24 mm×6 mm，为避免应力波反射的影响，在模型四周使用无限单元（ CIN3D8），中心16 mm×16 mm区域使用六面体缩减积分单元（ C3D8R），单元尺寸0.267 mm×0.267 mm×0.2 mm，如图10所示。冲击压力区域为圆形，直径4 mm，搭接率为20%，为保证结果收敛，分析步步长设为1 ns，并设置人工阻尼加速应力波收敛速度，提高仿真效率[17-18]。冲击压力的时间和空间分布参数由Fabbro模型使用标定参数计算得到。由于激光冲击为动态过程，材料本构选择Johnson-Cook模型，其中弹性模量E为73100 MPa，初始屈服应力A为369 MPa，硬化常数B为684 MPa，硬化指数n为0.73，应变率常数C为0.0083。从仿真结果提取X和Y方向的固有应变作为初始固有应变，不同能量对应的初始固有应变如图11所示。
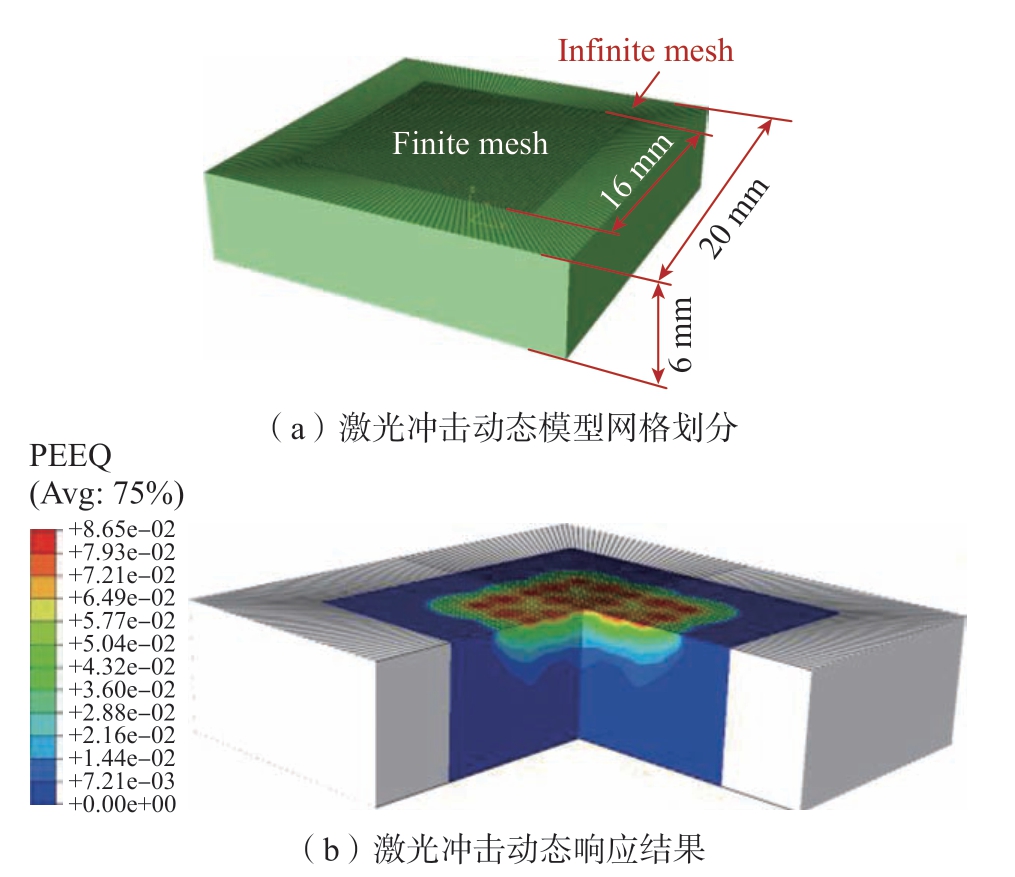
图10 激光冲击多点搭接动态仿真模型
Fig.10 Dynamic explicit simulation model of arrayed laser shocks
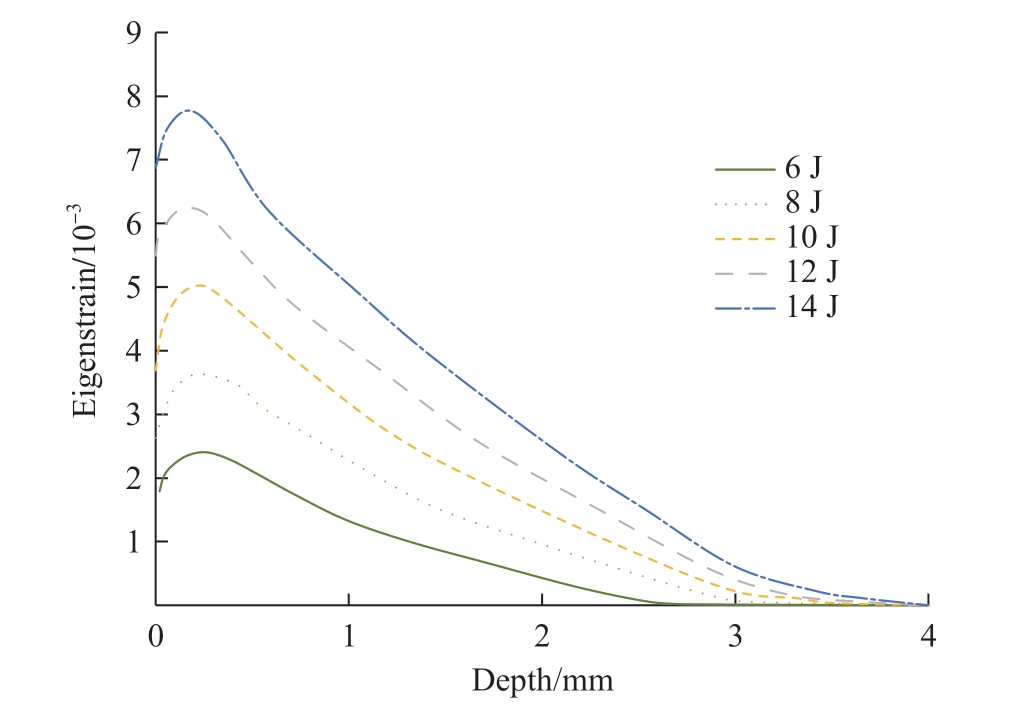
图11 初始固有应变
Fig.11 Initial eigenstrain
4 结果与讨论
4.1 固有应变反求结果
将平板激光喷丸试验变形和仿真初始固有应变代入固有应变反求优化模型，进行固有应变反求。首先对平板试样进行有限元离散化，单元尺寸为2 mm×2 mm，厚度方向单元数量为9，并约束试样表面中心节点。表面位移
为图7拟合轮廓的单元节点处位移，初始固有应变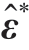
为图11动态冲击仿真得到的固有应变。调用MATLAB优化求解工具箱求解联合反求优化模型（式（ 9）），得到不同能量下的激光喷丸固有应变，如图12所示。可以看出，随激光能量增大，对应的固有应变也逐渐增大，并且固有应变在两个方向上有所差异，在相同能量下，垂直于激光扫描方向（ Y方向）的固有应变略大于激光扫描方向（ X方向）的固有应变，这体现了变形历史的影响。
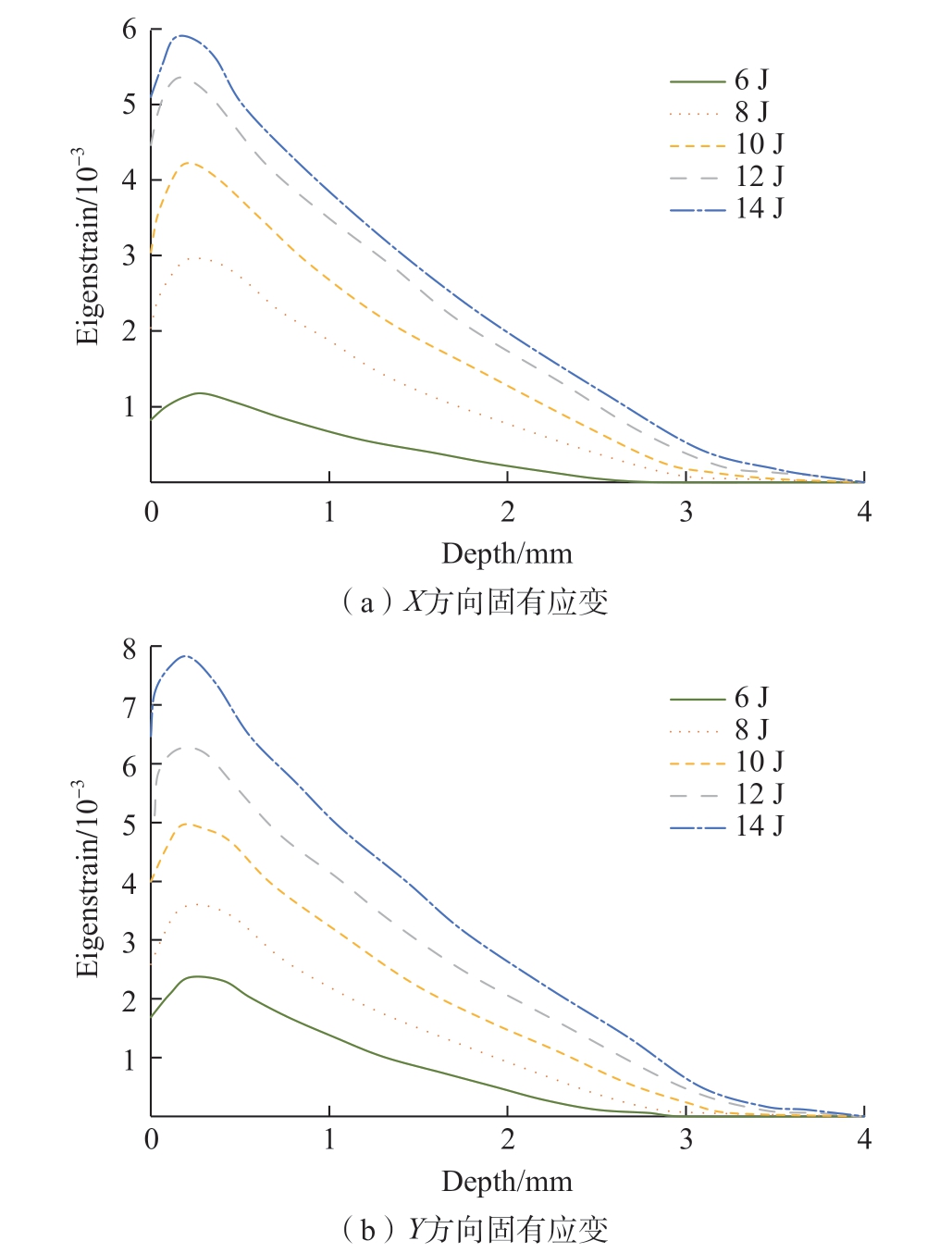
图12 不同能量固有应变反求结果
Fig.12 Results of eigenstrain inverse under different laser energies
4.2 结果验证
使用反求计算得到的固有应变建立仿真模型，计算变形并比较仿真结果与试验测量结果，验证所建立的固有应变反求方法的可靠性，测量与仿真结果如图13所示。可以看出，激光能量从6 J增大到14 J，仿真与预测变形均逐渐增大，其中垂直于激光扫描方向变形弧弓高从1.12 mm增大至2.18 mm，平行于激光扫描方向变形弧弓高从0.91 mm增大至1.24 mm，这是由于变形历史原因，即垂直于激光扫描路径方向变形对平行方向变形产生了抑制作用，并且仿真与试验变形基本完全一致。这说明反求方法从基于几何反求固有应变具有多解中优化得到了与初始值最接近的固有应变分布，即反求结果既反映了几何变形，又反映了物理意义。
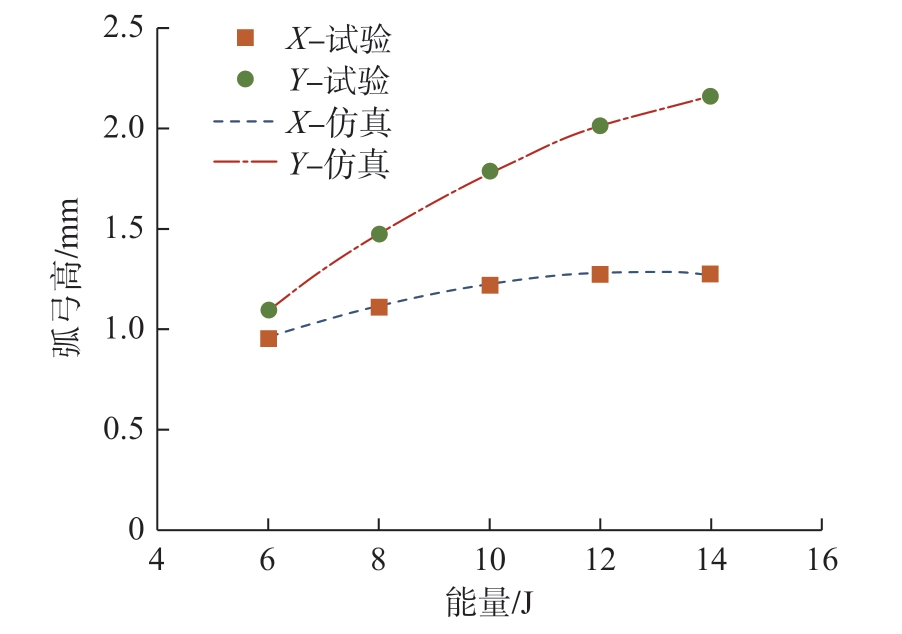
图13 测量和预测变形量
Fig.13 Measured and predicted deformation
为验证反求结果可以可靠地进行残余应力分布预测，测量喷丸后试样的残余应力沿深度的分布并与反求固有应变预测的残余应力比较。残余应力验证试样尺寸为100 mm×100 mm×6.7 mm，激光能量6 J和12 J。残余应力采用Xstress 3000X型X射线衍射仪进行测量，通过电解腐蚀法逐层去除表面的材料，获取残余应力沿深度的分布。残余应力点间距离约0.15 mm，并采用联合反求得到的6 J和12 J激光能量下的固有应变计算理论残余应力，残余应力测量与理论预测结果如图14所示。可以看出，测量结果与预测结果在变化趋势上与总体保持一致，说明基于特征参量联合反求固有应变具有可靠性。
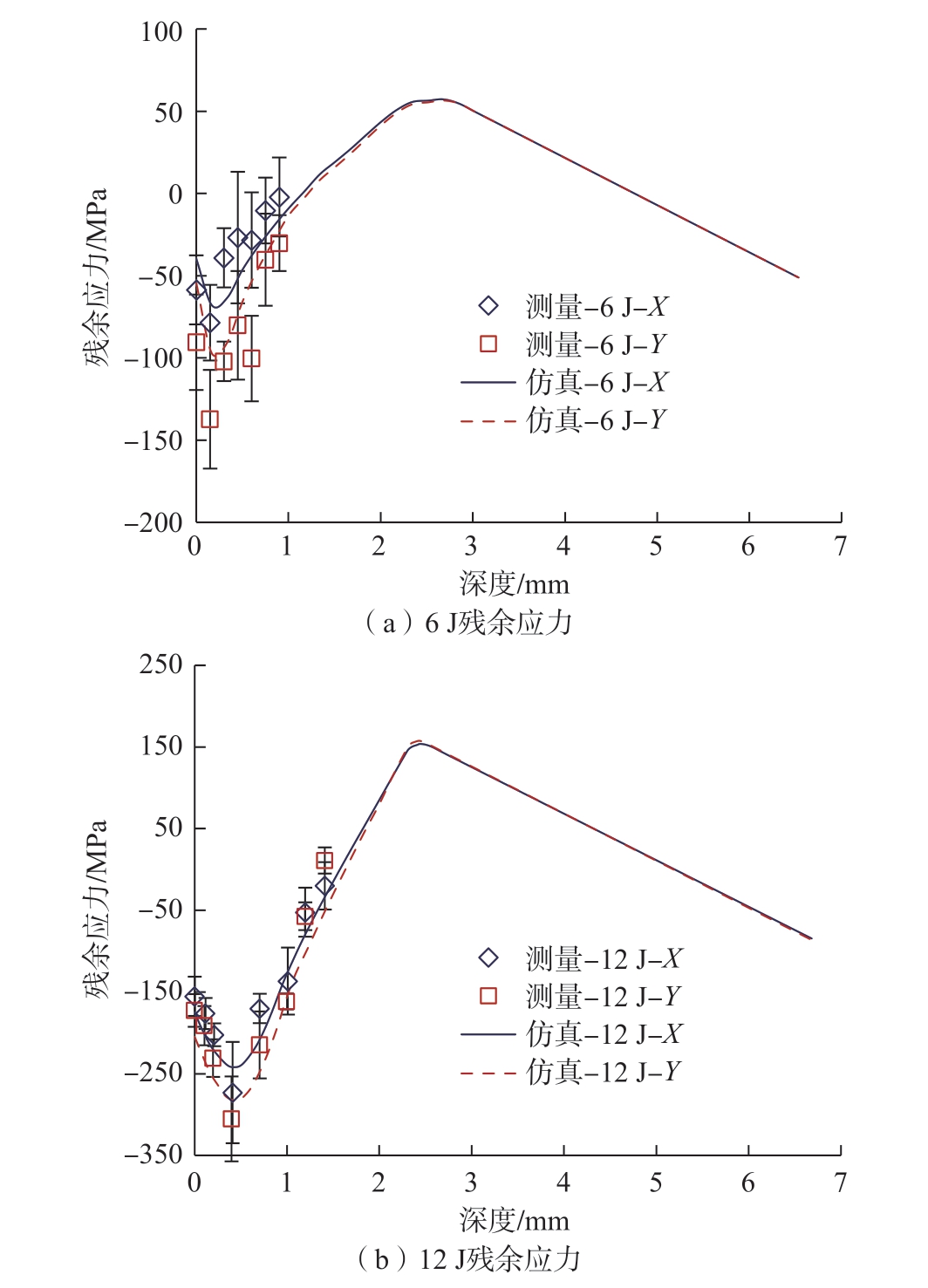
图14 测量和预测残余应力分布
Fig.14 Distribution of measured and predicted residual stress
5 结论
本文基于有限元基本理论，利用激光喷丸变形与动态冲击仿真，建立了基于几何特征的固有应变反求方法，通过试验反求了不同能量下的固有应变，并验证了反求结果的准确性。得出如下结论：
（1）基于弹性力学和有限元理论，结合激光喷丸变形和初始固有应变建立了固有应变优化反求方法，能够高效地实现激光喷丸固有应变反求，且反求结果能够准确地预测激光喷丸变形和残余应力分布；
（2）所建立的固有应变反求方法相较于通过测量残余应力和动态仿真的方法，兼顾了测量成本和结果精度，为进行大量工艺试验建立激光喷丸固有应变工艺数据库提供了有效手段。
[1] 李伟, 李应红, 何卫锋, 等. 激光冲击强化技术的发展和应用[J]. 激光与光电子学进展, 2008, 45(12): 15-19.LI Wei, LI Yinghong, HE Weifeng, et al. Development and application of laser shock processing[J]. Laser & Optoelectronics Progress, 2008, 45(12):15-19.
[2] WAN Z D, GUO W, JIA Q, et al. Effects of laser shock peening on microstructure and mechanical properties of TIG welded alloy 600 joints[J].Materials Science and Engineering: A, 2021, 808: 140914.
[3] SHOKRIEH M M, JALILI S M, KAMANGAR M A. An eigenstrain approach on the estimation of non-uniform residual stress distribution using incremental hole-drilling and slitting techniques[J].International Journal of Mechanical Sciences, 2018, 148: 383-392.
[4] KORSUNSKY A M. Eigenstrain analysis of residual strains and stresses[J]. The Journal of Strain Analysis for Engineering Design, 2009,44(1): 29-43.
[5] KORSUNSKY A M, REGINO G M, NOWELL D. Variational eigenstrain analysis of residual stresses in a welded plate[J]. International Journal of Solids and Structures, 2007, 44(13): 4574-4591.
[6] SALVATI E, LUNT A J G, YING S, et al. Eigenstrain reconstruction of residual strains in an additively manufactured and shot peened nickel superalloy compressor blade[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 320: 335-351.
[7] DEWALD A T, HILL M R. Eigenstrain-based model for prediction of laser peening residual stresses in arbitrary three-dimensional bodies Part 1: Model description[J]. The Journal of Strain Analysis for Engineering Design, 2009, 44(1): 1-11.
[8] ALI FAGHIDIAN S. A smoothed inverse eigenstrain method for reconstruction of the regularized residual fields[J]. International Journal of Solids and Structures, 2014, 51(25-26): 4427-4434.
[9] ACHINTHA M, NOWELL D. Eigenstrain modelling of residual stresses generated by laser shock peening[J]. Journal of Materials Processing Technology, 2011, 211(6): 1091-1101.
[10] HU Y X, GRANDHI R V. Efficient numerical prediction of residual stress and deformation for large-scale laser shock processing using the eigenstrain methodology[J]. Surface and Coatings Technology,2012, 206(15): 3374-3385.
[11] ZHANG Z, HU Y, YAO Z. Shape prediction for laser peen forming of fiber metal laminates by experimentally determined eigenstrain[J].Journal of Manufacturing Science and Engineering, 2017, 139(4): 041004.
[12] 杨荣雪. 激光喷丸成形固有应变反求方法及带筋壁板成形形状预测[D]. 上海: 上海交通大学, 2017.YANG Rongxue. Inverse method of laser peening forming inherent strain and prediction of ribbed panel forming shape[D]. Shanghai: Shanghai Jiao Tong University, 2017.
[13] 罗明生. 激光喷丸成形固有应变建模理论及工艺规划方法[D]. 上海: 上海交通大学, 2019.LUO Mingsheng. Modeling theory and process planning method of laser peening forming inherent strain[D]. Shanghai: Shanghai Jiao Tong University, 2019.
[14] 杨启, 付雪松, 周文龙. 激光喷丸表面强化技术的研究综述[J]. 航空制造技术, 2020, 63(12): 14-22.YANG Qi, FU Xuesong, ZHOU Wenlong. Research status and application progress of laser shot peening surface strengthening technology[J]. Aeronautical Manufacturing Technology, 2020, 63(12): 14-22.
[15] UEDA Y, KIM Y C, YUAN M G. A predicting method of welding residual stress using source of residual stress[J]. Quarterly Journal of the Japan Welding Society, 1988, 6(1): 59-64.
[16] FABBRO R, FOURNIER J, BALLARD P, et al. Physical study of laser-produced plasma in confined geometry[J]. Journal of Applied Physics, 1990, 68(2): 775-784.
[17] ZHANG W W, YAO Y L, NOYAN I C. Microscale laser shock peening of thin films, part 1: Experiment, modeling and simulation[J]. Journal of Manufacturing Science and Engineering, 2004, 126(1): 10-17.
[18] HU Y X, HAN Y F, YAO Z Q, et al. Three-dimensional numerical simulation and experimental study of sheet metal bending by laser peen forming[J]. Journal of Manufacturing Science and Engineering, 2010,132(6): 061001.