碳纤维增强复合材料 (Carbon fiber reinforced polymer,CFRP)因密度低、比强度高、抗腐蚀性强与设计自由度灵活等优良性能,常作为结构与功能零件应用于航空、船舶及汽车制造领域[1-2]。但CFRP加工表面极易产生凹坑和毛刺缺陷[3-4]。螺旋铣孔是一种针对构件装配需求的关键技术,偏心加工特征使得其在加工精度、生产效率与适用性等方面表现出优势[5]。然而,CFRP螺旋铣孔加工质量与切削参数、刀具结构与纤维方向等因素相关,如刀具或加工参数选择不当会造成孔质量下降与孔径偏差[6]。
研究学者对CFRP螺旋铣孔工艺、刀具结构及纤维方向等因素展开研究。张顺等[7]通过CFRP普通螺旋铣孔与超声振动辅助螺旋铣孔 (UVHM)的单因素试验,发现UVHM的切削力大幅降低,且孔壁质量更优。周兰等[8]结合螺旋铣孔专用刀具几何特征,通过对未变形切屑的分析,实现了对螺旋铣孔加工切屑和几何形貌的预测。万敏等[9]考虑纤维方向对切削力系数的影响,成功建立了切削力预测模型。上述研究大多基于螺旋铣孔试验,但试验无法直观呈现出CFRP加工过程中应力和应变场的分布情况,同时,在宏观尺度下不能动态观测纤维和基体的失效过程,从而难以深入探究不同纤维方向下CFRP螺旋铣孔的成屑机制。
当前,有限元仿真技术不仅可以动态反映出切削区内材料的去除过程,还能够模拟加工过程中难以测量的应力、应变与温度场等的分布情况[10],成为探究CFRP加工机制的有效途径。秦旭达等[11]采用在层间设置零厚度内聚单元的方法,建立宏观CFRP有限元模型,用于模拟螺旋铣孔中CFRP的层间损伤。但宏观有限元模型无法体现纤维和基体的失效机制。因此,Yan等[12]利用有限元方法将钻削划分为一组连续微小正交切削单元,探究了不同纤维方向下CFRP的切削力、加工表面形貌差异与能量耗散机制。Zhang等[13]建立了钻削微刃切削模型来揭示毛刺的成形机制和孔出口处开裂的新型断裂准则。此外,Zhou等[14]根据斜角切削理论建立了球头铣刀螺旋铣孔微刃切削模型,基于不同阶段的位置参数提出一个全周期切削力模型。考虑螺旋铣孔刀具侧刃铣削属于断续的斜角切削,故将斜角切削理论与微刃切削模型相结合,可用于探究CFRP螺旋铣孔的成屑机制。
综上,本文构建不同纤维方向下的基体相、纤维相及界面相CFRP螺旋铣孔微刃斜角切削模型来探究其加工过程中的成屑机制,阐明纤维方向和加工参数对切削力的影响,并获得不同加工参数下的试验切削力。与切削力仿真值进行对比,验证仿真模型对试验切削力的预测效果,为相关研究提供参考。
1 螺旋铣孔运动学原理
螺旋铣孔过程中,刀具围绕自身轴线进行自转,同时沿螺旋轨迹 (铣刀绕孔轴线公转+轴向进给)进给,如图1所示,可通过调整偏心距来实现“同刀多孔”,提高了加工效率。图1中,Rt为刀具半径;Rh为待加工孔半径;v为斜角切削速度;i为刀具倾斜角。
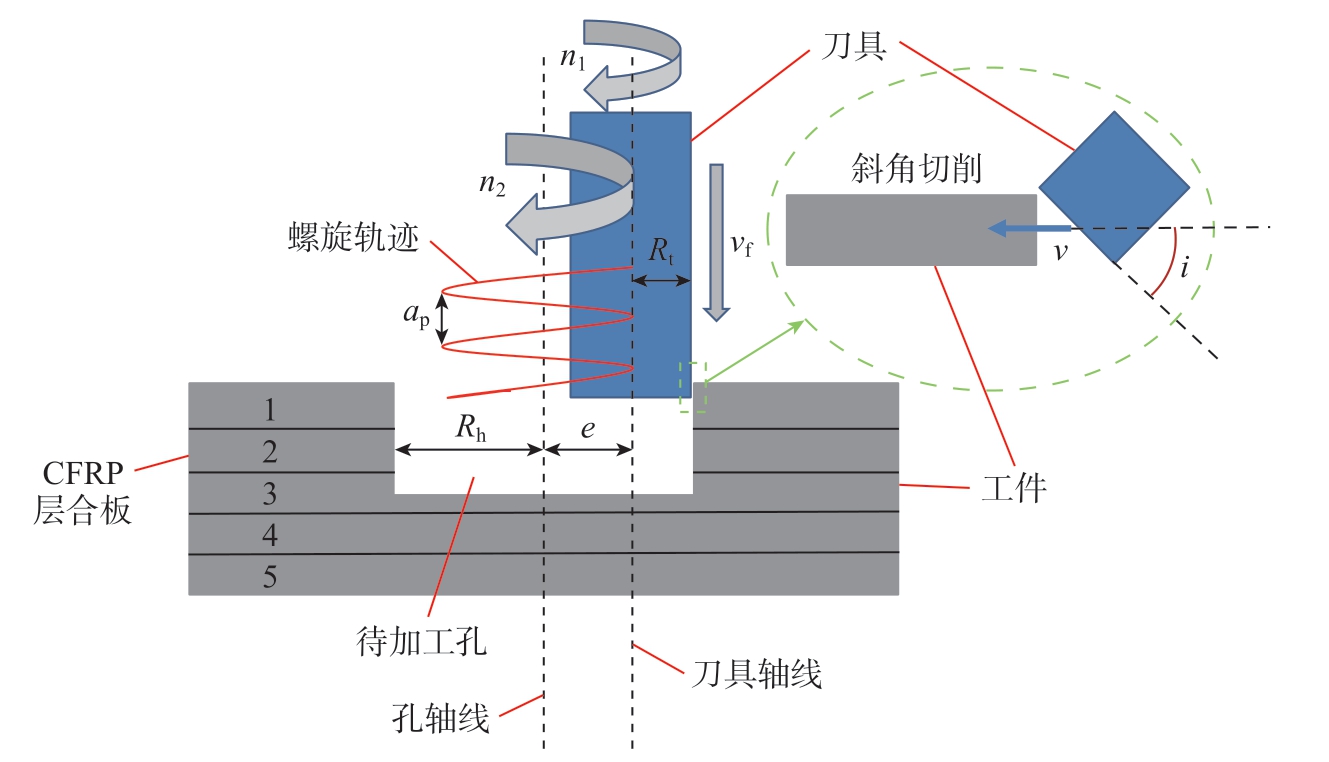
图1 螺旋铣孔运动学原理
Fig.1 Kinematic principle of helical milling
切削加工理论中,切削速度、切削深度与进给量为主要要素。图1中n1和n2分别为刀具自转和公转速度,相应的角速度ω可表达为
螺距 (轴向切削深度)ap计算公式为
式中,vf为刀具的轴向进给速度。
刀具的切向每齿进给量ft与轴向进给量fa计算公式为

式中,e为偏心距;N为齿数。
由于螺旋铣孔中刀具某点的速度由自转、公转及轴向进给的合速度构成,根据矢量叠加法,合速度方向与切削刃不成直角,结合斜角切削理论[15],螺旋铣孔铣刀侧刃切削属于斜角切削,且倾斜角与铣刀螺旋角一致,如图2所示,其中h1为切削深度。刀具切削刃上某点的切削速度为
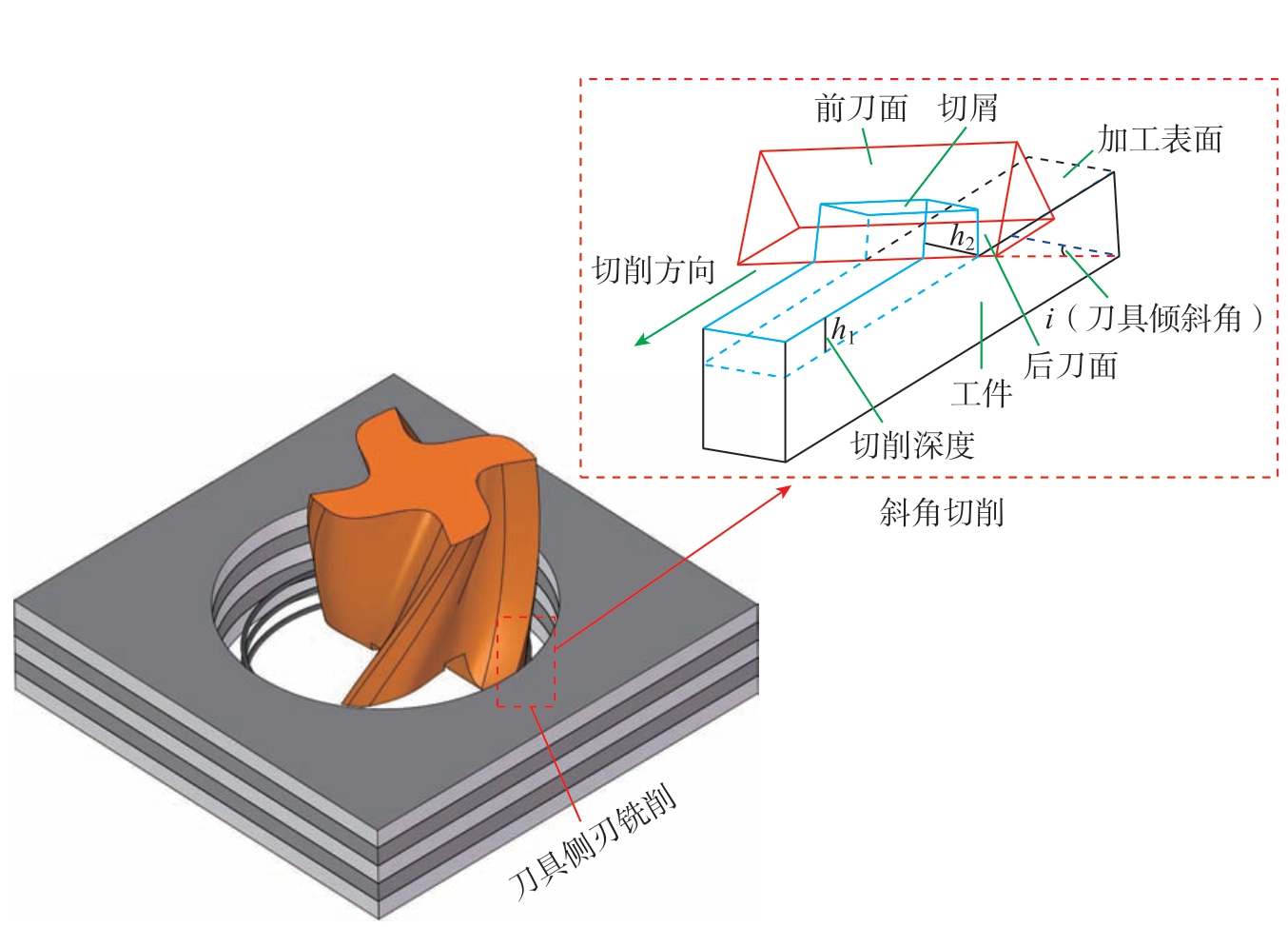
图2 螺旋铣孔铣刀侧刃铣削原理
Fig.2 Kinematic principle of cutter side edge milling in helical milling
式中,Rr为铣刀刃端某点到铣刀中心的距离。由于螺旋铣孔时刀具的主轴转速远大于公转转速,所以切削刃上各点的速度可简化为
2 材料本构
2.1 纤维本构
纤维具有弹性和正交各向异性(沿纤维横截面方向的横向同性)的特性。纤维失效准则存在多种,如Hashin准则、Tsai-Wu准则及最大应力准则等[16]。本文采用最大应力准则,因为此准则成功代表了实际观测下的纤维断裂行为。当最大主应力达到纤维拉伸强度极限或最小主应力达到纤维压缩强度极限时,纤维发生失效。纤维损伤机制为

式中,Xt和Xc为纵向抗拉强度和抗压强度;Yt和Yc为横向抗拉强度和抗压强度;σii为纤维应力张量分量。纤维拉压应力、剪切应力与应变的关系曲线如图3(a)和 (b)所示。
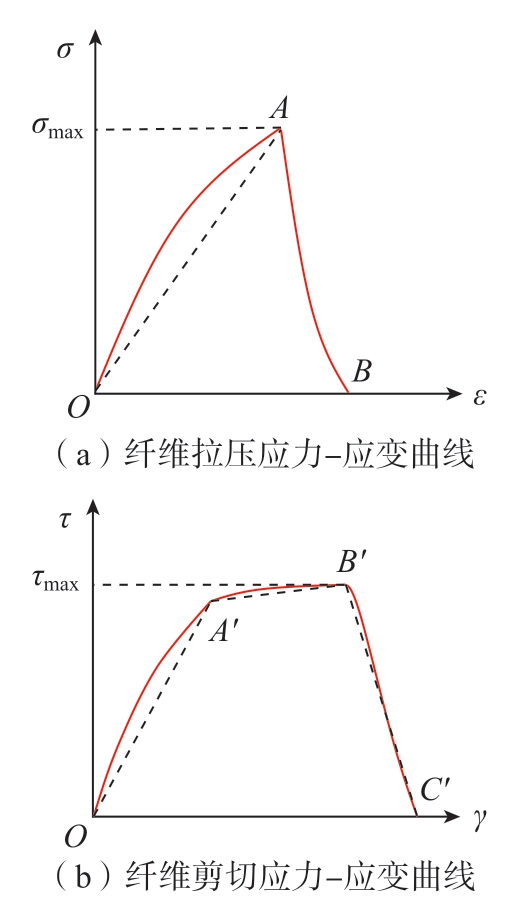
图3 纤维应力-应变曲线
Fig.3 Stress-strain curve of fiber
2.2 环氧树脂基体本构
树脂基体具有各向同性和弹塑性的特性,其拉伸或压缩条件下的应力-应变曲线如图4所示[17],点O至点A为线性弹性阶段,遵循Von Mises准则,σe为基体的弹性极限。在塑性阶段 (始于点A),应力达到基体的屈服应力 (σy),若应力在B点 (极限应力σmax)达到基体抗拉极限或抗压极限时,基体发生损伤。点B至点C是以杨氏模量 (Emd)降低为特征的降解阶段。新模量的计算公式为
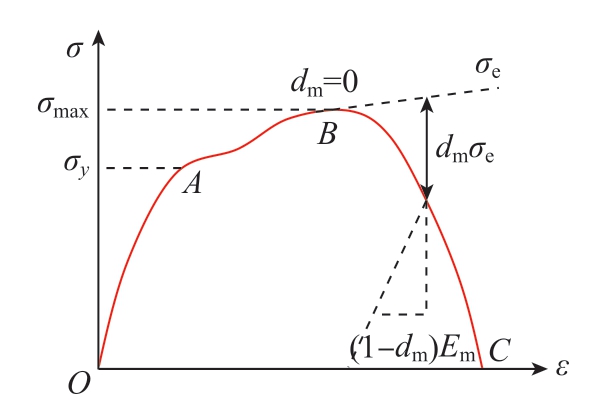
图4 环氧树脂基体应力-应变曲线[17]
Fig.4 Stress-strain curve of epoxy resin matrix[17]
式中,dm为损伤变量;Em为基体的杨氏模量。
2.3 纤维-基体界面本构
通常使用3种方法来定义纤维-基体界面性质:基于牵引分离定律的小厚度内聚单元法、零厚度内聚单元法与基于表面的内聚行为法[18]。本文采用基于表面的内聚行为法,此方法的优势体现在避免内聚单元网格的过度畸变与额外的计算成本,使用非耦合模式来简化弹性行为。弹性矩阵表示为
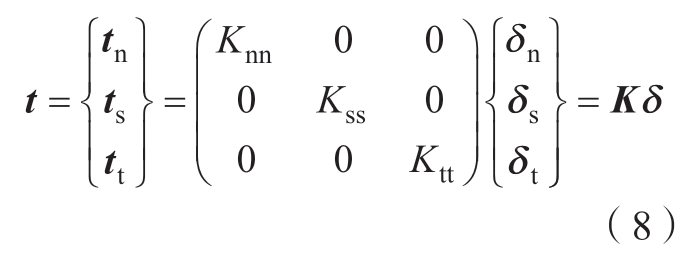
式中,牵引应力矢量t由分量tn、ts和tt组成,分别表示界面处的法向应力和剪切应力;Knn为界面法向刚度;Kss与Ktt为界面切向刚度;相应的牵引分离用δn、δs和δt表示。当最大接触应力比达到1时,损伤开始,表示为
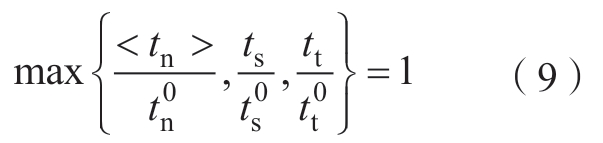
式中,![]() 分别是法向和切向的屈服强度。当损伤开始时,使用线性损伤模型来模拟内聚作用的损伤演化,表示为
分别是法向和切向的屈服强度。当损伤开始时,使用线性损伤模型来模拟内聚作用的损伤演化,表示为
式中,![]() 指加载期间有效分离位移的最大值;
指加载期间有效分离位移的最大值;![]() 指相对于损伤开始时的有效分离位移;
指相对于损伤开始时的有效分离位移;![]() 指完全失效时的有效分离位移。界面的牵引分离响应曲线如图5所示。
指完全失效时的有效分离位移。界面的牵引分离响应曲线如图5所示。
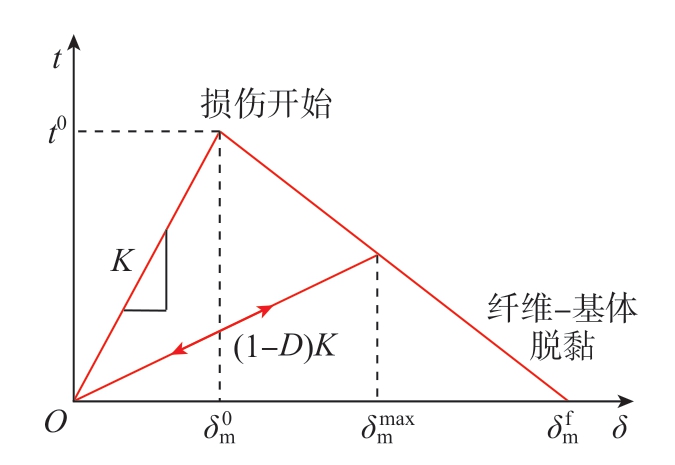
图5 界面牵引分离响应曲线
Fig.5 Traction separation response curves of interface
3 CFRP斜角切削有限元建模
3.1 几何模型与网格划分
利用ABAQUS软件进行CFRP几何体的建模,纤维切削几何模型如图6(a)所示。α与γ分别为刀具前与后角; 1方向为纤维铺设方向,2与3方向所构成平面为纤维横截面所在平面。纤维方向角 (θ)定义为刀具切削方向顺时针旋转至与纤维铺设方向重合时所经过的角度 (图6(a)中θ为90°)[19]。不同θ使得CFRP材料存在不同的失效方式,从而导致切屑形态、切削力及其变化规律、切削后表面质量等均有所差异。因此在切削加工中,不同的纤维方向会与切削方向形成不同的切削关系,可总结为:
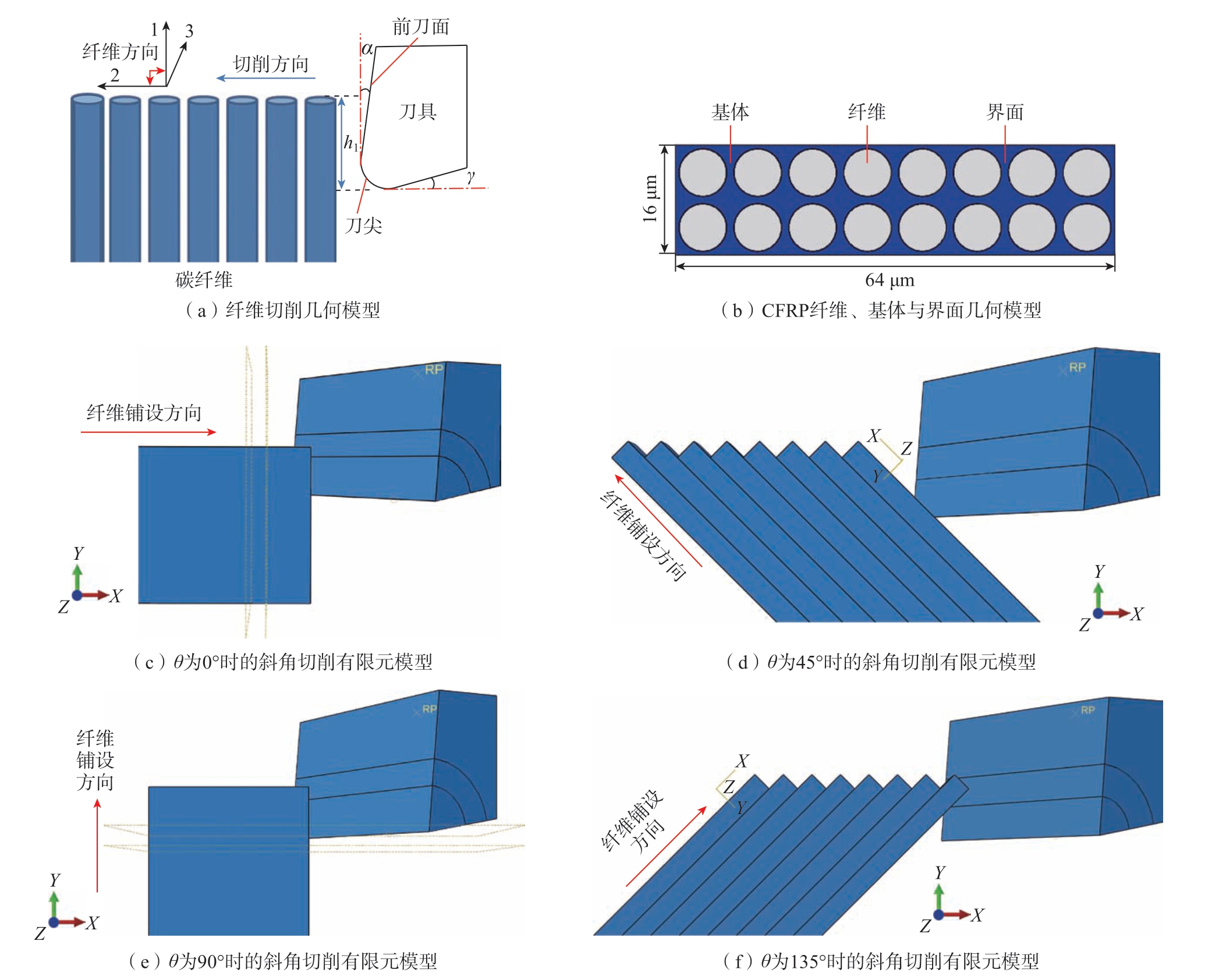
图6 CFRP几何模型与有限元模型
Fig.6 CFRP geometry model and finite element model
(1)θ = 0°(180°),纤维方向与切削方向一致,定义为平行切削;
(2)0° < θ < 90°,纤维方向与切削方向形成锐角,定义为顺纤维切削,以45°为代表;
(3)θ = 90°,纤维方向与切削方向垂直,定义为垂直切削;
(4)90° < θ < 180°,纤 维 方 向 与切削方向形成钝角,定义为逆纤维切削,以135°为代表。
故选取典型纤维方向角θ = 0°、45°、90°与135°建立CFRP三维微观模型,尺寸为64 μm×16 μm×100 μm,纤维直径为7 μm,体积分数为60%,代表性体积单元 (RVE)边长为8 μm,纤维、基体与界面三相几何模型如图6(b)所示。不同θ下的斜角切削有限元模型如图6(c) ~(f)所示。模型网格划分如图7所示,其中基体部分平均网格尺寸为1 μm,纤维部分平均网格尺寸为0.75 μm,如图7(a)所示。刀具为锋利刃型,刃口半径为2 μm,α为5°,γ为10°,网格划分由远离刀尖端 (平均网格尺寸为3 μm)细化过渡至刀尖处(平均网格尺寸为0.3 μm),如图7(b)所示。网格划分方式均采用进阶算法,通过扫略方式生成适合线性动态计算的缩减积分沙漏控制八结点线性六面体单元C3D8R。
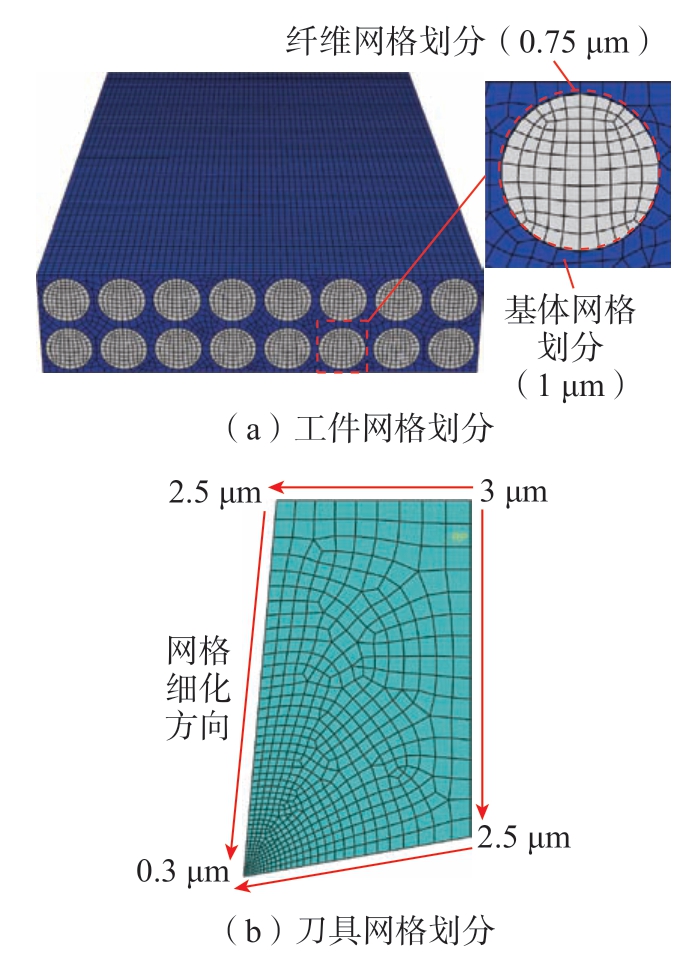
图7 模型网格划分
Fig.7 Model of meshing
3.2 有限元关键设置
刀具与工件的相互作用服从库仑摩擦定律,摩擦系数设定为0.3[20],接触应力表示为
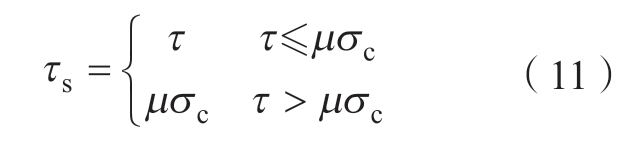
式中,σc为加工区域的名义应力;τs为加工区域的摩擦应力;τ为材料的剪切应力;μ为摩擦系数。
有限元仿真流程如图8所示,其中,刀具被设定为刚体。模型边界条件:通过在刀具上定义参考点以控制刀具的进给,如图9(a)所示,对CFRP工件底部和左端 (远离刀具端)在所有方向上均施加约束 (X、Y、Z三方向上的平动与转动自由度被完全固定,即UX=UY=UZ=UR1=UR2=UR3=0),如图9(b)所示。CFRP材料的力学性能如表1所示,其中纤维相的力学性能利用VUMAT子程序定义,vp为泊松比。
表1 CFRP材料各相的力学性能[12]
Table 1 Mechanical property of CFRP material phases[12]
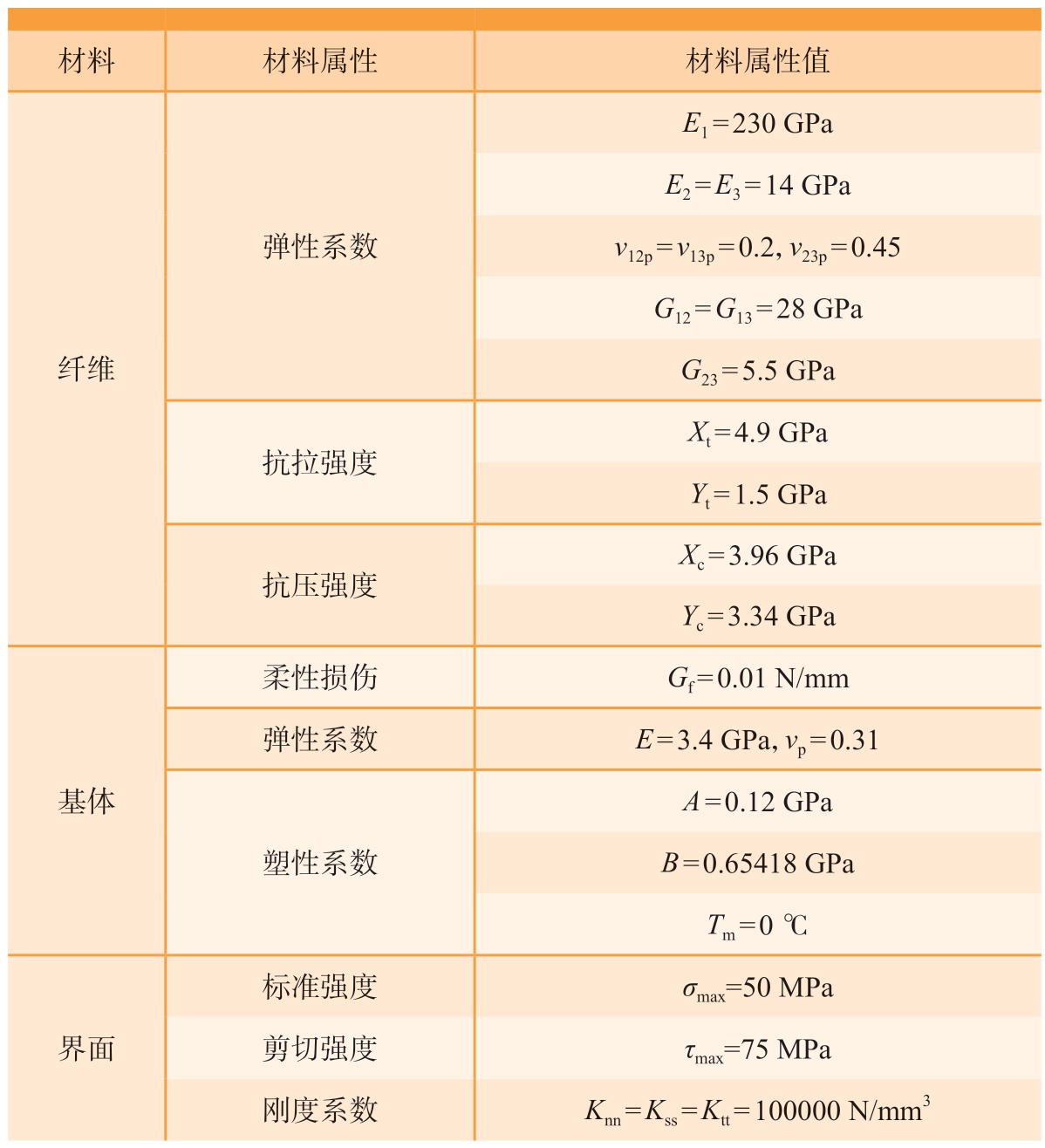
材料 材料属性 材料属性值弹性系数纤维E1 = 230 GPa E2 = E3 = 14 GPa v12p = v13p = 0.2,v23p = 0.45 G12 = G13 = 28 GPa G23 = 5.5 GPa抗拉强度Xt = 4.9 GPa Yt = 1.5 GPa抗压强度Xc = 3.96 GPa Yc = 3.34 GPa柔性损伤 Gf = 0.01 N/mm弹性系数 E = 3.4 GPa,vp = 0.31基体塑性系数A = 0.12 GPa B = 0.65418 GPa Tm = 0 ℃界面标准强度 σmax=50 MPa剪切强度 τmax=75 MPa刚度系数 Knn = Kss = Ktt = 100000 N/mm3
图8 有限元仿真流程
Fig.8 Process of finite element simulation
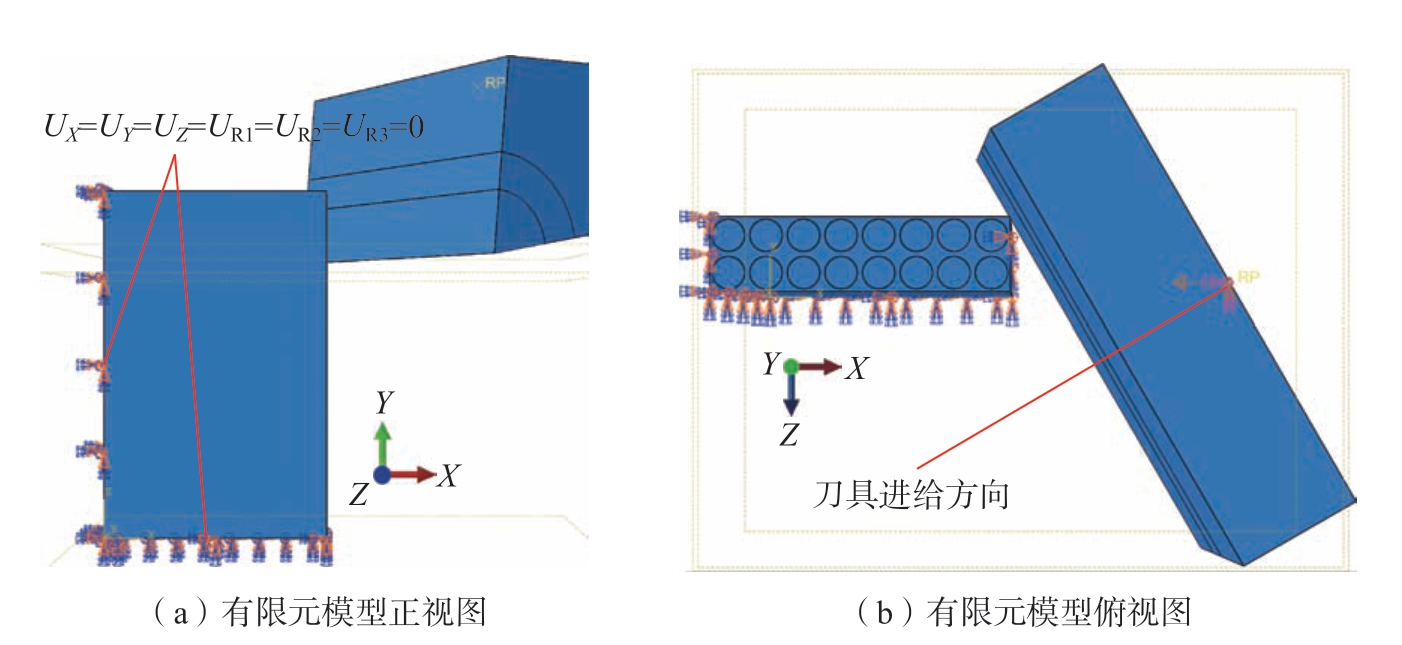
图9 模型边界条件设置
Fig.9 Boundary condition setting of the model
3.3 网格无关性验证
通过改变CFRP工件指定区域的单元尺寸,其余因素保持不变,总结CFRP工件网格单元数量从67075个到1073200个过程中切削力的变化规律,如图10所示。可得,随工件网格单元数量的增加,切削力先降低后趋于稳定,故综合考虑计算时间与精度,将工件网格单元数量划分为268300个。对于刀具模型,采用相同方法进行验证,由于刀具被设定为刚体,故不考虑刀具的网格畸变,因此不再过多描述。
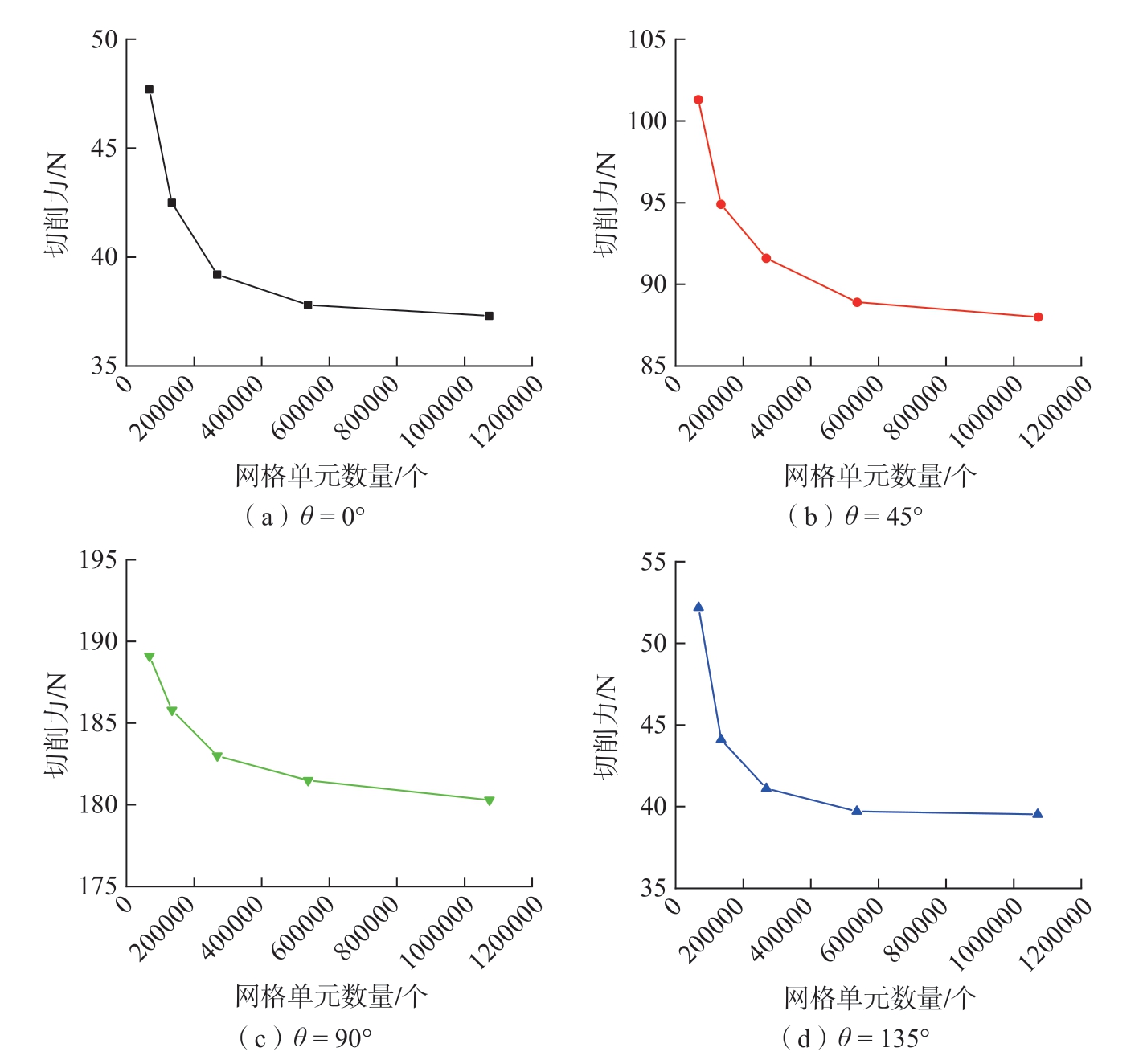
图10 网格单元数量对切削力的影响
Fig.10 Effect of mesh number on cutting force
4 材料失效机制与残余应力
4.1 不同纤维方向的CFRP失效机制
选取典型纤维方向角θ(0°、45°、90°与135°),根据式 (5),得到微刃切削速度v = 190 m/min(对应铣刀主轴转速nz = 6000 r/min)、切削深度h = 20 μm(对应ft = 0.02 mm/z)及刀具倾斜角i = 30°(对应铣刀螺旋角β = 30°),分析该参数下CFRP的材料失效机制。
当θ为0°时,工件应变和纤维失效仿真结果如图11所示。图11(a)中,工件首先受刀尖和前刀面的挤压作用,基体在局部表面发生开裂,产生剥离裂纹,且纤维发生弯曲变形。等效塑性应变 (PEEQ)最大值主要分布在基体开裂与固定端形变区域。图11(b)中,稳定加工阶段,基体严重开裂,纤维沿平面外方向出现明显断裂,但界面未出现大规模失效,纤维-基体仅局部脱黏,纤维轻微拔出,最终形成块状切屑,并沿前刀面向平面外方向剥离,在加工区域易排出。加工表面类似于金属切削时的剪切面,未形成明显亚表面缺陷。等效塑性应变最大值不仅分布于基体开裂与固定端形变区域,并扩大至已加工表面。图11(c)中,纤维发生弯曲失效,且呈现集体式断裂,不同纤维间的断裂位置较为接近 (由于纤维被定义为弹性结构,因此不含等效塑性应变,故采用Mises应力代表纤维的失效过程)。
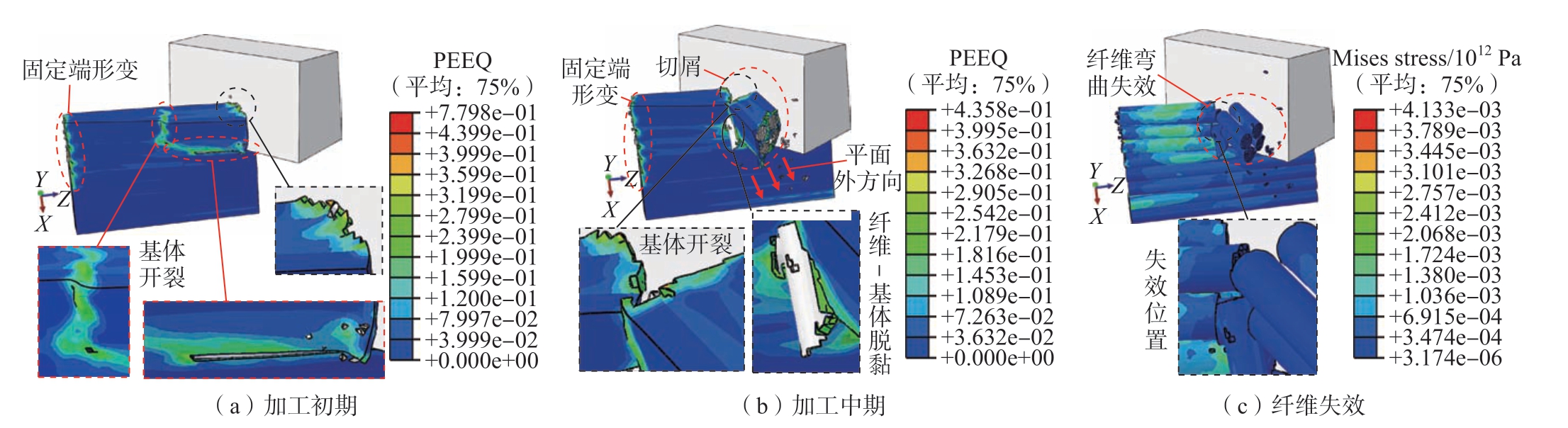
图11 θ为0°的CFRP应变及纤维失效仿真结果
Fig.11 Simulation results of CFRP strain and fiber failure at θ of 0°
当θ为45°时,工件应变和纤维失效仿真结果如图12所示。图12(a)中,工件首先受刀尖的挤压作用,基体发生微小开裂,且少量纤维发生剪切失效。等效塑性应变最大值主要分布在工件-刀尖接触区域。图12(b)中,稳定加工阶段,前刀面推挤使得基体沿切削方向与纤维方向均产生开裂,纤维沿刀具切削方向依次发生剪切失效,局部出现纤维-基体脱黏与纤维拔出现象,形成条状切屑。纤维失效位置大致处于同一剪切线上,因此加工表面质量较好。等效塑性应变最大值主要分布于基体开裂与已加工表面区域。图12(c)中,纤维受力超过自身剪切屈服强度极限,且未达到自身弯曲屈服强度极限,故最终发生剪切失效。
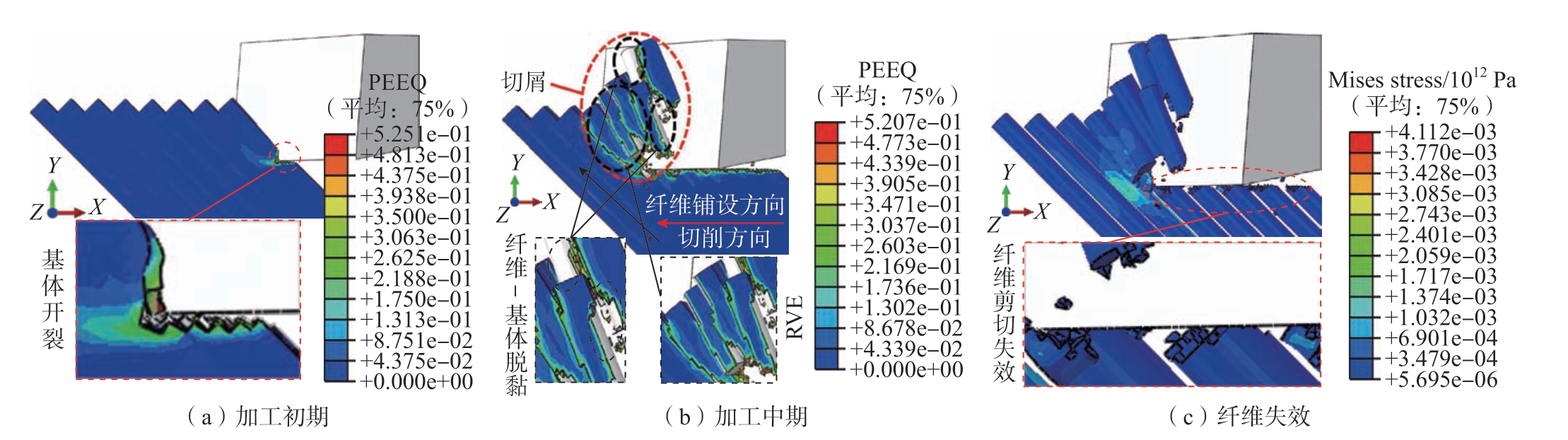
图12 θ为45°的CFRP应变及纤维失效仿真结果
Fig.12 Simulation results of CFRP strain and fiber failure at θ of 45°
当θ为90°时,工件应变和纤维失效仿真结果如图13所示。图13(a)中,工件首先受刀尖的挤压作用,基体沿刀具进给与纤维方向均产生微裂纹,少部分纤维发生剪切失效,且伴随着不同程度的弯曲变形。等效塑性应变最大值主要分布在基体开裂与未加工区域,并在未加工区域沿刀具进给方向延伸,并轴向传递至纤维深处,此现象是纤维即将突破基体的包裹,对基体产生破坏前的挤压应力导致的。图13(b)中,稳定加工阶段,基体发生大量不规则开裂,界面严重失效,纤维-基体脱黏与纤维拔出现象明显,故形成短棒状切屑,少部分加工切屑堆积于前刀面,其余加工切屑则沿前刀面向外剥离,纤维断口处呈现不规则形貌,形成大量亚表面缺陷,加工表面质量较差。等效塑性应变最大值不仅分布于基体开裂与未加工区域,并扩大至已加工表面。图13(c)中,纤维剪切与弯曲失效并存,由于同一纤维在剪切失效的过程中弯曲变形同样发生,且纤维间的相互挤压作用同时会使未与刀具接触的部分纤维受到弯曲应力,故随刀具进给,纤维所受应力在相近时段内均达到自身剪切、弯曲屈服强度极限,进而发生失效,并体现在多个纤维亚表面上。
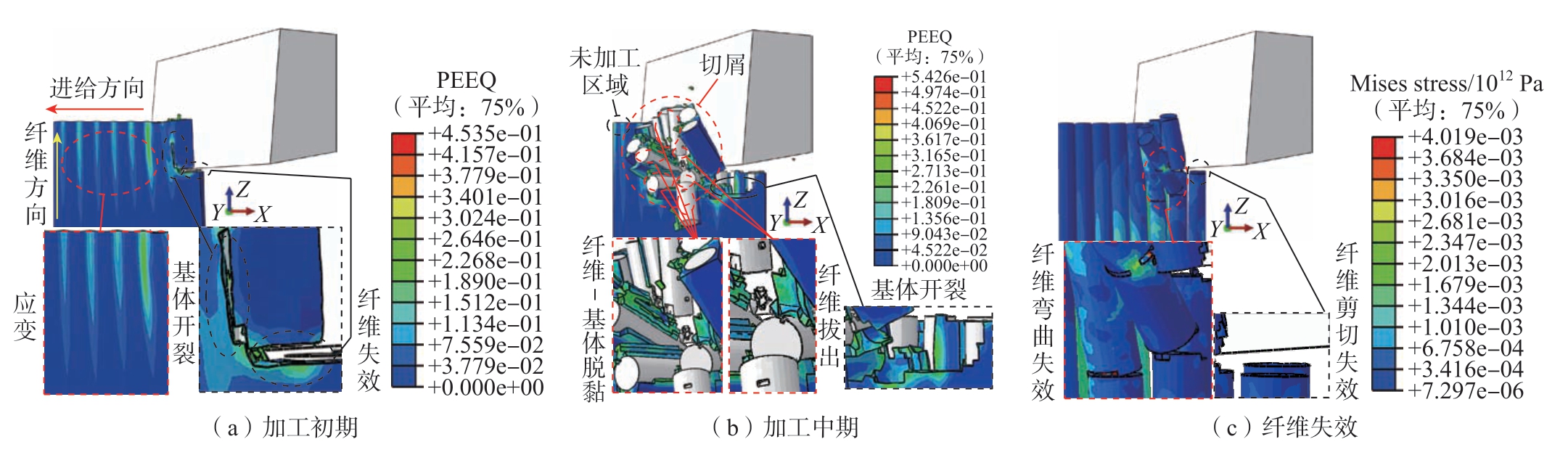
图13 θ为90°的CFRP应变及纤维失效仿真结果
Fig.13 Simulation results of CFRP strain and fiber failure at θ of 90°
当θ为135°时,工件应变和纤维失效仿真结果如图14所示。图14(a)中,工件首先受前刀面的挤压作用,基体发生局部开裂,纤维发生弯曲微变形。等效塑性应变最大值主要分布于基体形变与开裂区域。图14(b)中,稳定加工阶段,基体开裂严重,纤维失效位于不同纤维表面,同时出现纤维-基体局部脱黏现象,形成条状切屑,相似于θ为45°的切屑形貌。纤维断口呈锯齿状。等效塑性应变最大值主要分布于基体开裂与已加工表面区域,并呈轴向扩展。图14(c)中,纤维发生弯曲失效,由于刀具前刀面率先接触工件,此时,纤维受前刀面与纤维间的相互挤压作用,进而发生弯曲变形,挤压应力达到自身弯曲屈服强度极限后失效,且多处弯曲失效后,刀具刃端开始接触工件,故不参与纤维失效过程。
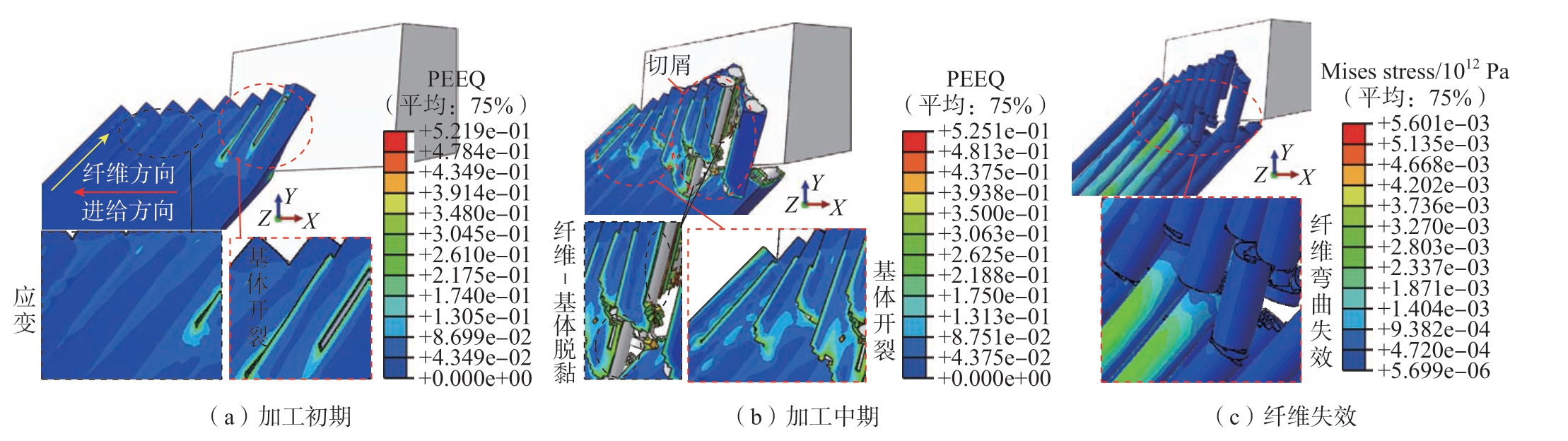
图14 θ为135°的CFRP应变及纤维失效仿真结果
Fig.14 Simulation results of CFRP strain and fiber failure at θ of 135°
4.2 刀具倾斜角对切屑尺寸的影响
CFRP螺旋铣孔微刃斜角切削中,刀具倾斜角 (i)能够反映铣刀结构。对此,基于有限元后处理的测量模块,总结仿真过程中i = 0°与i = 30°时不同θ下的斜角切削切屑平均尺寸,结果如图15所示。可得,i = 30°的切屑均不同程度长于i = 0°的切屑,因为i = 30°时刀具对材料的挤压程度小于i = 0°时的情况,且挤压力能够沿平面外方向得到分解,这使得切屑在前刀面的堆积程度降低,并以更大的体积呈现。
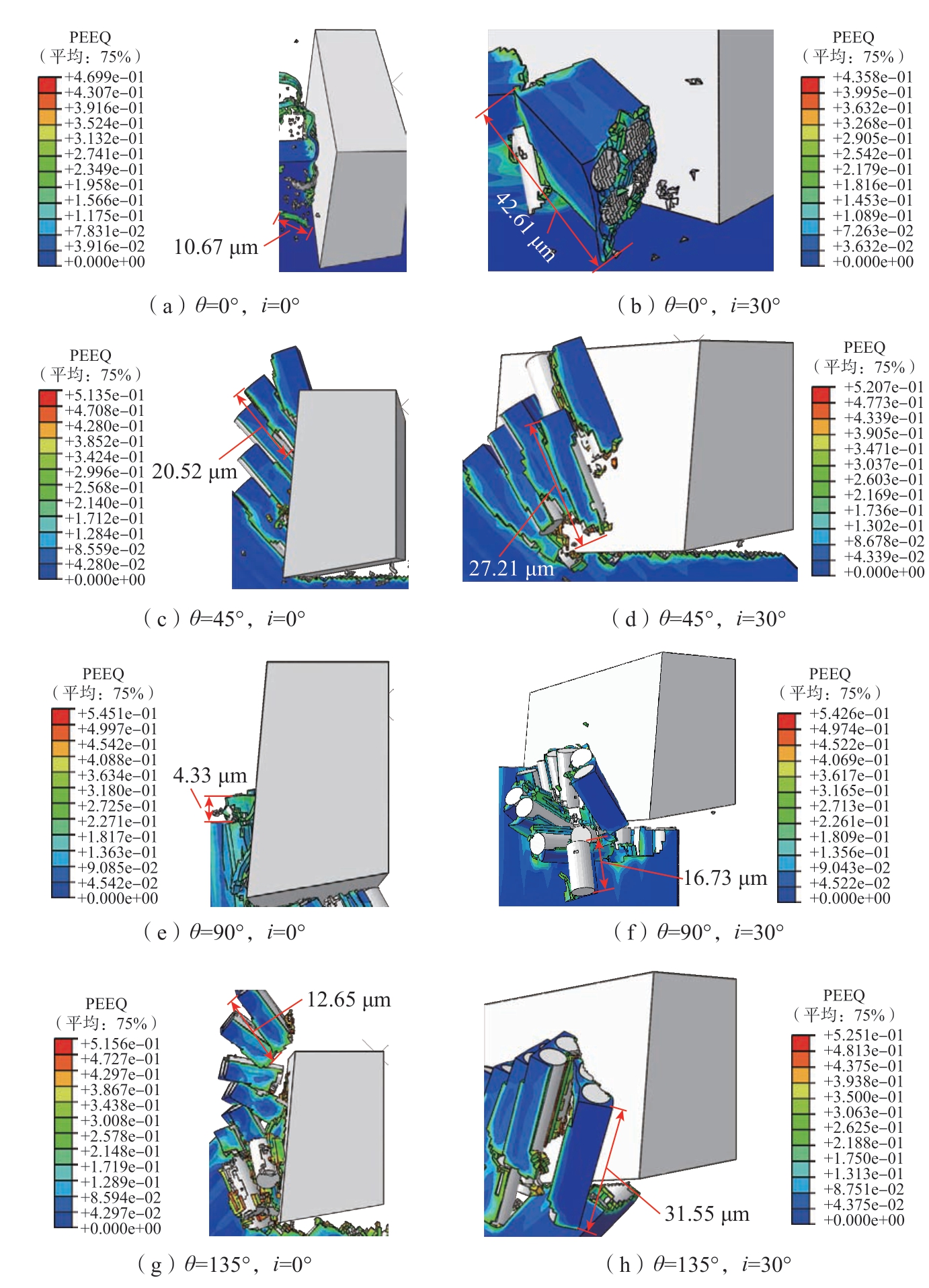
图15 i = 0°与30°时斜角切削切屑尺寸
Fig.15 Chip size for oblique cutting at i = 0° and 30°
此外,i对切屑尺寸的影响如图16所示。其中,θ为0°时,随i的增大,曲线斜率变化较大,因为此时的纤维屈曲向弯曲失效转变;θ为45°时,随i的增大,曲线变化较为平缓,因为此时纤维发生剪切失效,断口位置较为规则;θ为90°时,切屑尺寸随i的增大呈较稳定的增长趋势,因为此时纤维剪切与弯曲失效并存,i的增大会改变纤维的弯曲断裂位置,但对纤维剪切失效影响较小;θ为135°时,切屑尺寸与i无相关性,因为此时纤维发生弯曲失效,i的增大会改变纤维的断口数量,但并不呈正相关,当i增大到一定程度时,切屑尺寸对i变化的敏感程度降低。
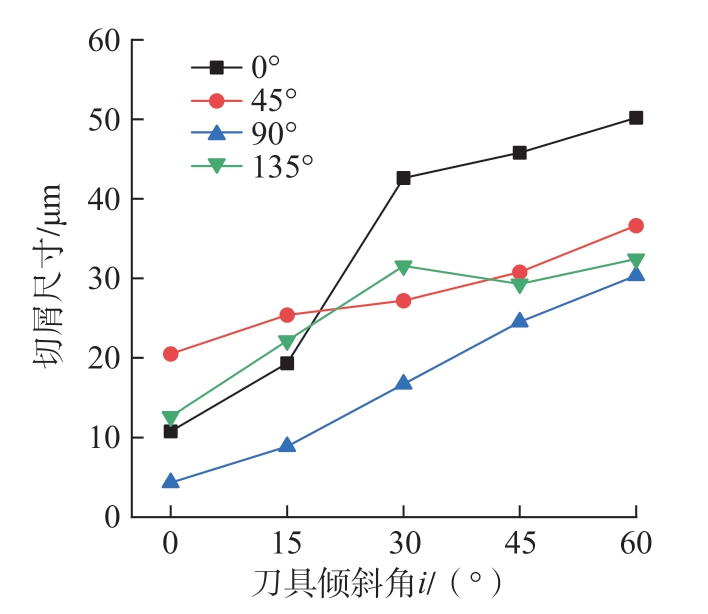
图16 刀具倾斜角对切屑尺寸的影响
Fig.16 Influence of tool oblique angle on chip size
4.3 残余应力仿真结果分析
以已加工区域残余应力最大值作为研究对象,提取距已加工表面每2.5 μm进行递进的残余应力最大值分布数据 (包括X方向残余应力值和Y方向残余应力最大值),如图17所示。距已加工表面深度增加时,X、Y方向残余应力的变化规律呈先减后增,趋于平稳,并最终趋于0,整体变化趋势呈“√”状分布。此现象主要源于热力耦合作用下,加工表面拉应力层、亚表面压应力层分别主要受切削热、机械载荷影响,故距加工表面较浅区域均呈现残余拉应力。随层深的递进,热效应主导的残余拉应力会急剧减退,由于拉、压残余应力达到平衡,受机械效应影响的残余压应力增大明显,最终在12.5 μm左右达到极值。随着层深的进一步递进,机械效应不断衰减,残余压应力最终趋于0。此外,X方向残余应力大于Y方向,因为斜角切削过程中,切向 (X方向)的塑性效应比轴向 (Y方向)更为显著;且经刀具后刀面加工后,纤维会产生明显的回弹效应,使得切向比轴向产生更大的残余应力。
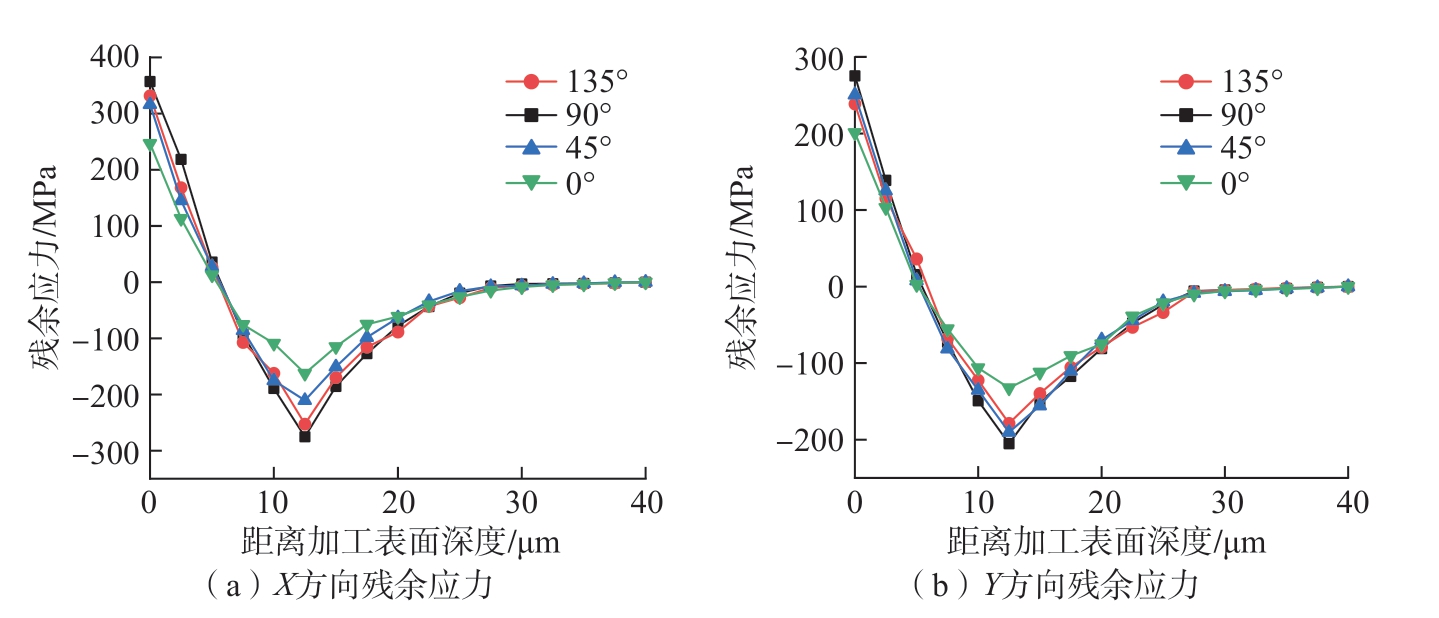
图17 距加工表面不同深度下的残余应力变化规律
Fig.17 Change law of residual stress at different depths from the machined surface
当切削深度为20 μm时,不同切削速度 (130~320 m/min)下的残余应力最大值仿真结果如图18(a)所示。可知,随着切削速度的增大,工件残余应力最大值在整体变化趋势上与切削速度呈正相关。这是因为切削速度增大使得单位时间内刀具与工件摩擦程度加剧,从而产生更高的切削热量且其无法及时传导,堆积在切屑底层,最终导致切削热主导的残余应力增大。
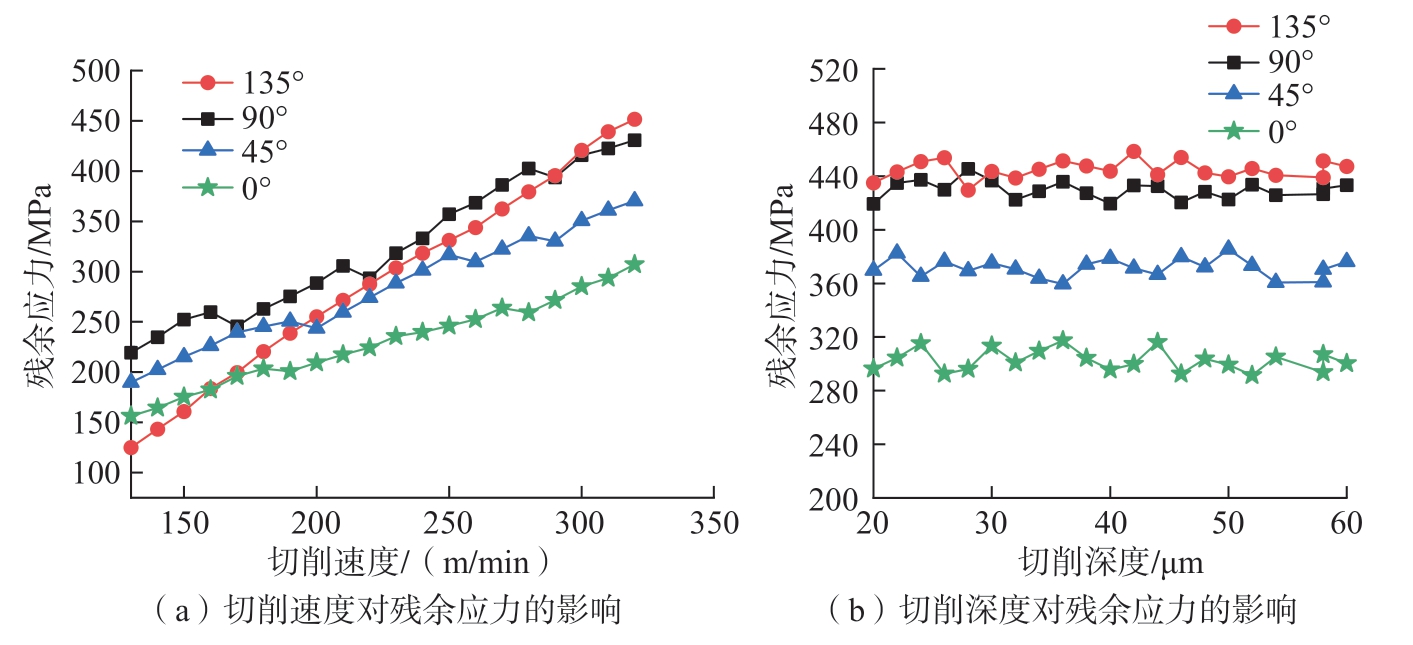
图18 加工参数对残余应力的影响规律
Fig.18 Influence law of machining parameters on residual stress
当切削速度为320 m/min时,不同切削深度 (20~60 μm)下的残余应力最大值仿真结果如图18(b)所示。可知,随着切削深度的增大,残余应力最大值曲线变化无显著规律,即残余应力与切削深度无明显相关性。这是因为切削深度增大后,加工区产生的热量虽增高,但同时增大了刀具前刀面的工作面积,故刀具的传热面积也同比例增加,改善了散热条件,使得切削温度变化不明显。因此,残余应力未受切削深度显著影响。
5 切削力仿真与试验分析
基于KUKA机器人 (搭配3个伺服电机实现刀具的自转、公转及轴向进给运动)、螺旋铣执行器、测力仪Kistler9257B(切削力采集频率约为40 kHz)与数据记录仪Kistler5073等设备开展试验,如图19所示。
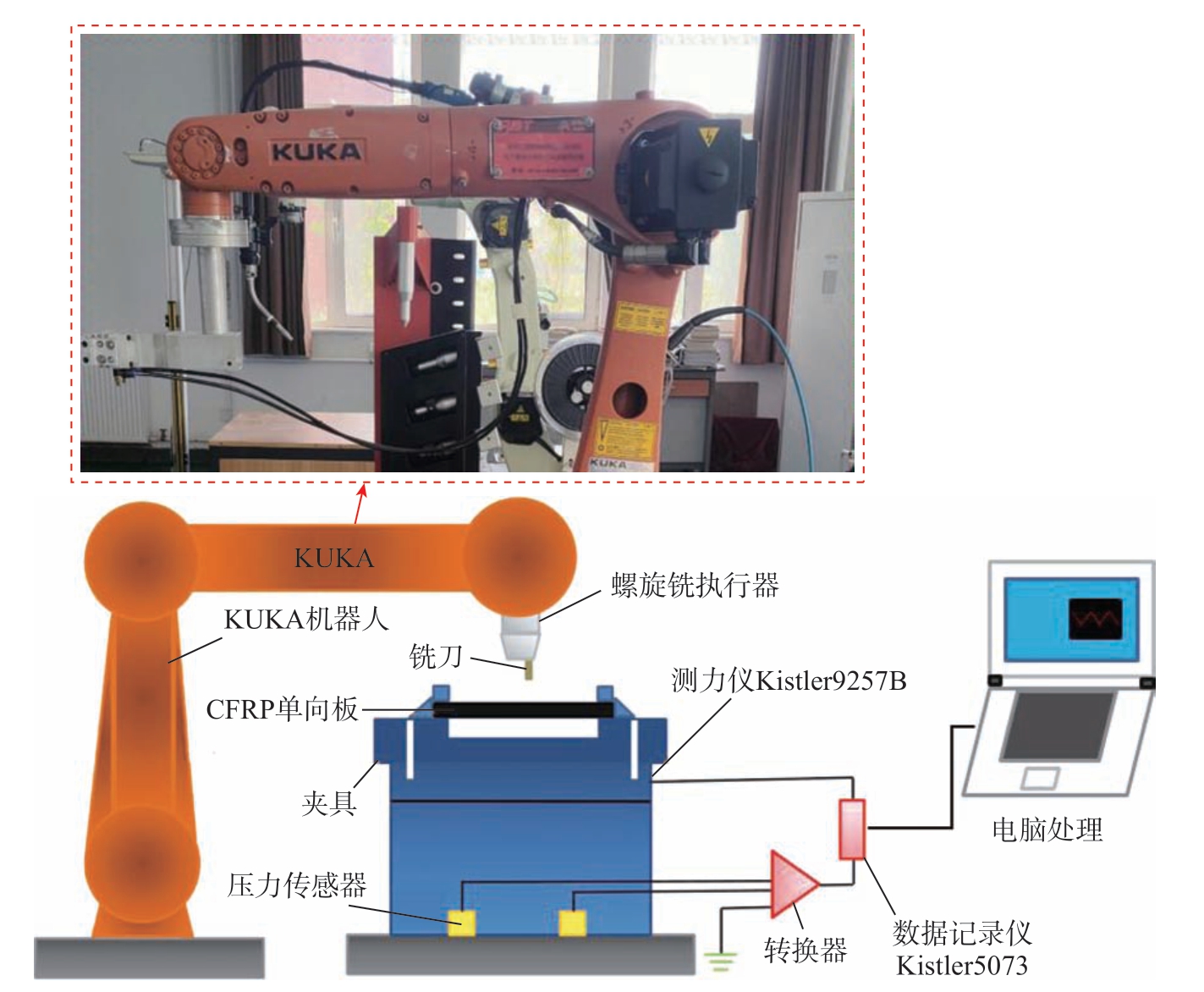
图19 螺旋铣孔试验平台
Fig.19 Test platform of helical milling
试验刀具选用硬质合金四齿立铣刀,刀径d为10 mm,螺旋角β为30°,CFRP工件采用单向铺设方式,尺 寸为128 mm×128 mm×4 mm,待加工孔径为16 mm。第1组试验中螺旋铣孔刀具主轴转速设定为4000 r/min、6000 r/min、8000 r/min、10000 r/min与12000 r/min,切向每齿进给量设定为0.02 mm/z。由于铣刀的刀刃线速度方向与纤维方向夹角从0°到360°改变,为保证试验对比的有效性,选取此组参数加工不同θ的CFRP螺旋铣孔,在同一加工周期内(铣刀某齿由接触工件到切出工件,如图20所示)的径向力 (FX、FY)和Fr表示为
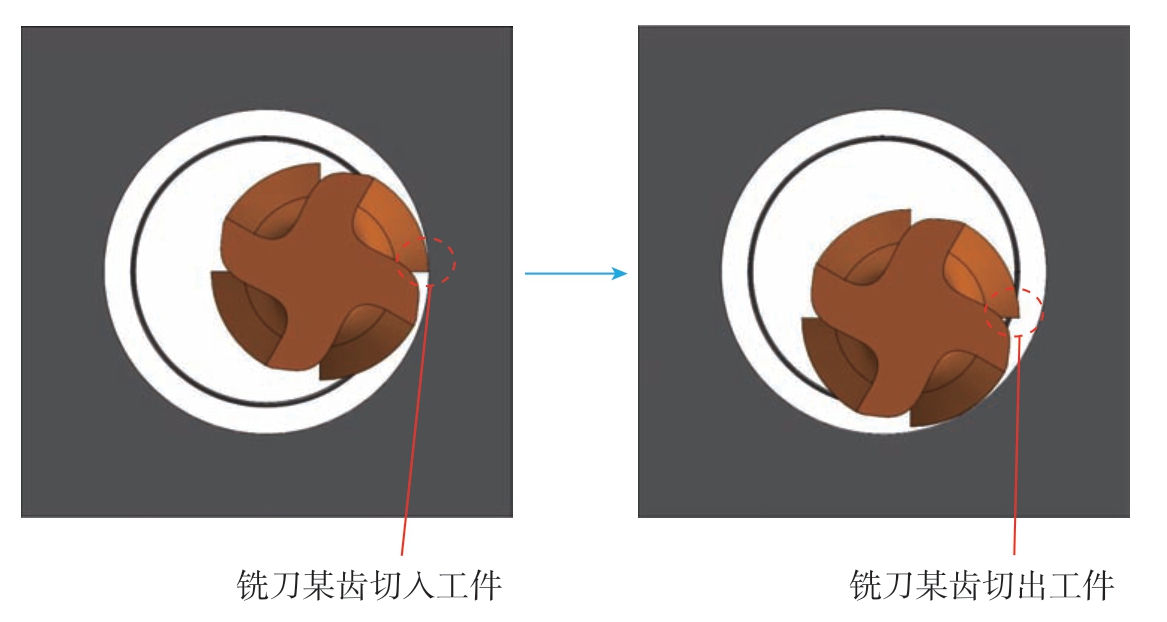
图20 螺旋铣孔某刀齿随加工位置变化
Fig.20 Variation of a tool tooth with machining position in helical milling
为保证切削力预测的有效性,将有限元模型 (RVE)通过阵列增大至原始模型的1×103倍,将模型调整至与试验相对应的尺寸。同时,为使仿真中切削速度与试验中刀具主轴转速相对应,根据式 (5),计算出切削速 度 为130 m/min、190 m/min、250 m/min、310 m/min与370 m/min。切削深度设定为20 μm。仿真中不同θ下,切削速度为130 m/min且切削深度为20 μm时稳定切削阶段的径向切削力均值与试验切削力 (试验过程中最初每齿进给时间内的稳定切削力均值)信号对比如图21所示,切削力仿真值整体略小于试验值,且力信号振幅较试验值更小。
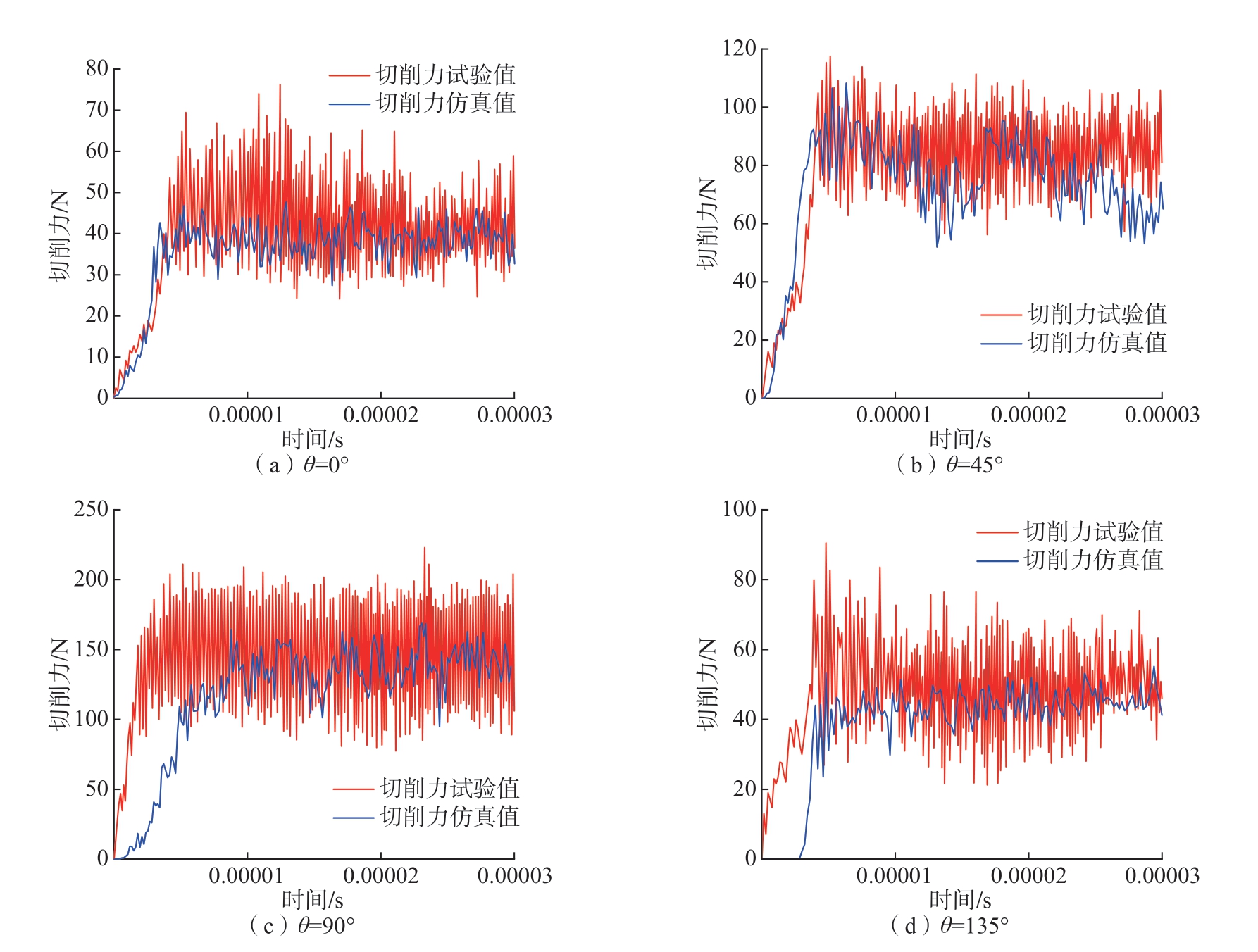
图21 不同θ的切削力信号仿真与试验对比
Fig.21 Simulation and experimental comparison of cutting force signal at different θ
切削速度为130 m/min且切削深度为20 μm时的切削力仿真与试验值随θ的变化规律如图22所示。首先,当θ为0°时,切削力呈最小值;当0° < θ≤90°时,切削力呈增大趋势,直至增大到90°,切削力达到峰值,此时,90°为纤维剪切失效与弯曲失效共存的临界纤维方向;超过90°时,纤维剪切失效占比降低,弯曲失效占比增加,即当90° < θ < 135°时,切削力呈下降趋势;最后,θ增大至180°时,切削力、纤维断裂行为同0°时保持一致,随θ的不断增大 (大于180°),切削力与纤维断裂行为呈周期性循环。综上,切削力受θ显著影响,即CFRP显著的各向异性。
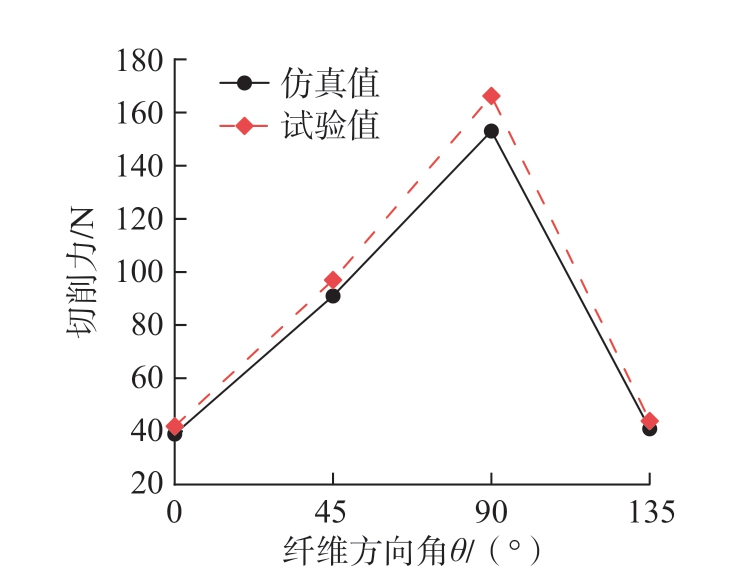
图22 切削力随θ的变化规律
Fig.22 Variation law of cutting force with θ
上述规律源于θ为45°和90°时的切削力主要由CFRP受挤压造成的纤维剪切破坏引起,而θ为0°和135°时则由基体剥离与纤维弯曲失效为主,相较于剪切破坏,刀具挤压程度更低,因此θ为0°和135°时的切削力明显小于45°和90°时的情况,并在90°时呈现最大值。这是因为此时切削方向垂直于纤维方向,挤压力仅存在于切向,而45°时的挤压力需要得到法向分解,故小于θ为90°时的挤压力。切削力在0°时呈现最小值,因为切削力主要由基体剥离与纤维弯曲失效引起,且不同纤维间的断裂位置较为接近,此外界面完整度高,无额外的力导致其发生脱黏失效。
切削力随切削速度的变化如图23所示。切削力均与切削速度呈正相关,切削速度增大使刀具与工件接触区域的摩擦力增大,同时,挤压作用更加剧烈,从而使纤维从变形到失效、回弹的过程更加急剧,最终导致切削力增大。θ为90°时切削力呈现最大值,且随切削速度增大的切削力增值最大,此时仿真与试验最大值分别为207.42 N与226.70 N,两者之间最大误差为10.81%。
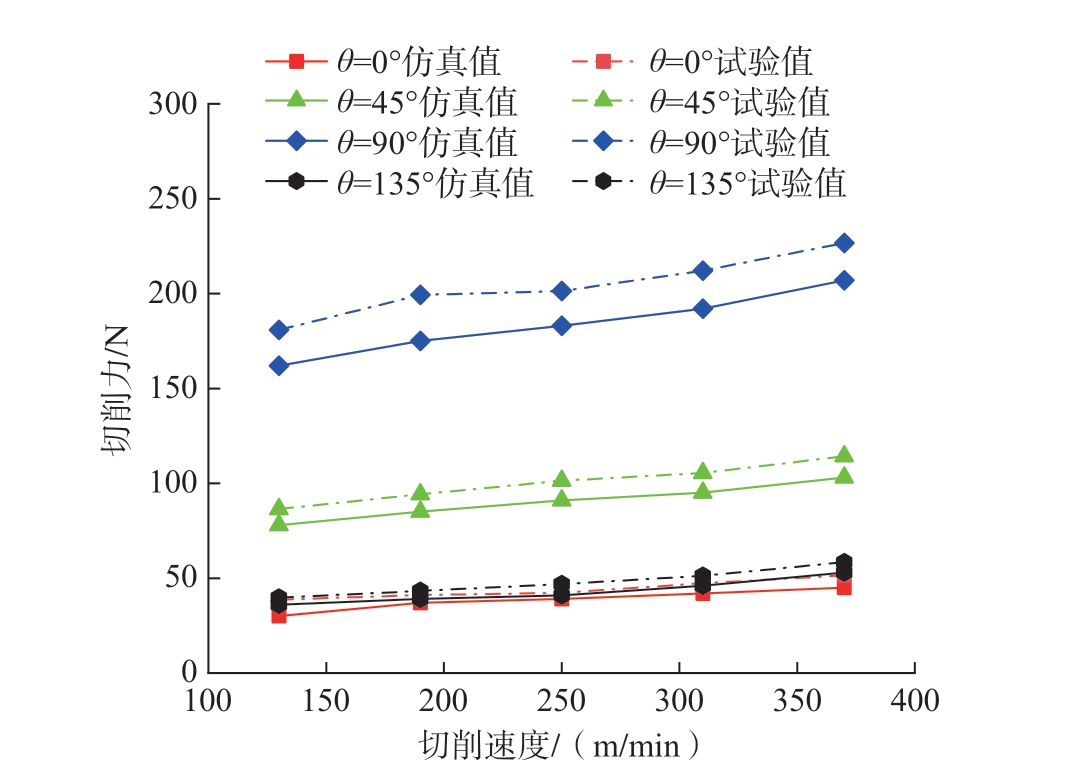
图23 不同切削速度下切削力仿真与试验值对比
Fig.23 Comparison of simulated and experimental values of cutting force at different cutting speeds
第2组试验中螺旋铣孔切向每齿进给量 (对应刀具公转速度与微刃切削深度,切向每齿进给量越大,即公转速度越高,微刃切深越厚)设定为0.02 mm/z、0.03 mm/z、0.04 mm/z、0.05 mm/z与0.06 mm/z,刀具主轴转速设定为8000 r/min。将仿真模型中切削深度设定为20 μm、30 μm、40 μm、50 μm与60 μm,切削速度设定为250 m/min,得到切削力随切削深度的变化,如图24所示,切削力均与切削深度呈正相关,由于切削深度的增加,刀具与工件的接触面积增大,同时与刀尖接触位置的纤维层更深,进而使得材料去除更加困难,最终导致切削力增大。θ为90°时切削力呈现最大值,且随切削深度增加的切削力增值最大,此时仿真与试验最大值分别为216.31 N与230.56 N,两者之间最大误差为8.52%。
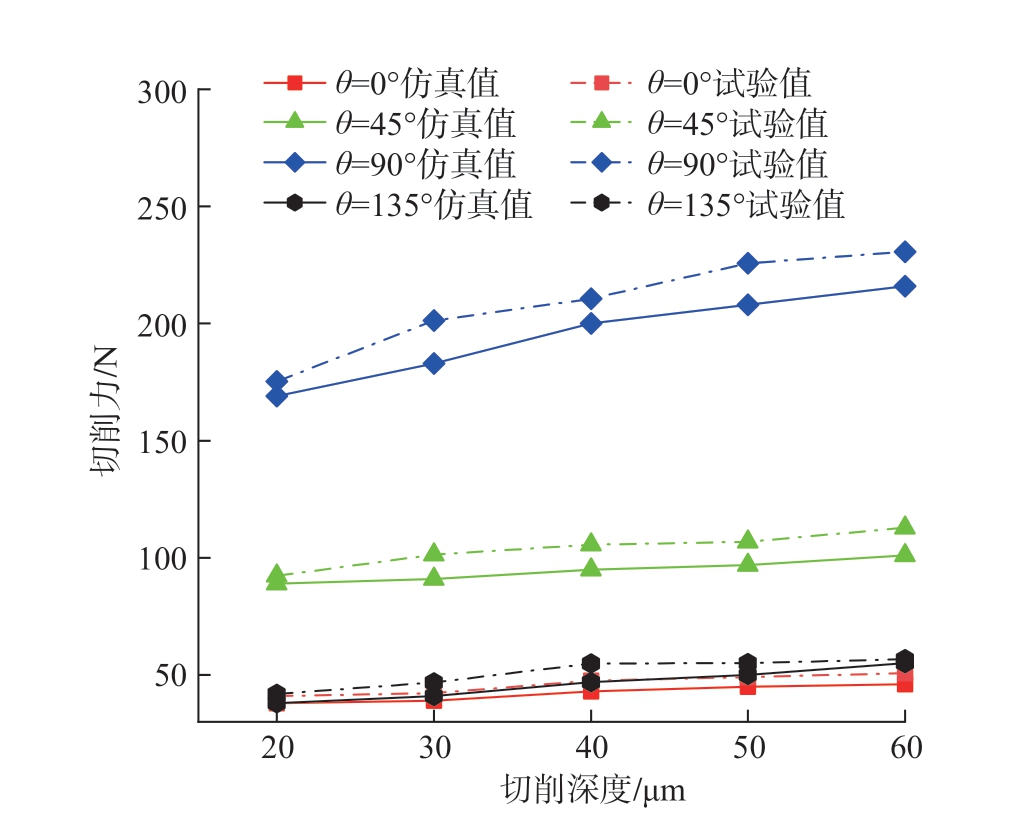
图24 不同切削深度下切削力仿真与试验值对比
Fig.24 Comparison of simulated and experimental values of cutting force at different cutting depths
仿真分析结果与试验结果的误差源于:螺旋铣孔中微刃可视为铣刀侧刃上的某点,故不能完全代表铣刀侧刃整体结构;仿真中刀具被设定为刚体,忽略了其变形的影响;工件材料一旦到达自身损伤极限便会进行单元完全删除,故不再受力。但实际加工中,通常会使用冷却剂来控制加工温度,防止树脂基体软化[21]。部分失效的工件材料将继续保留于加工表面[22],加工后的纤维会发生明显的弯曲回弹,对铣刀侧刃后刀面产生反作用力;加工中的能量吸收由纤维与基体间的界面脱黏决定,而仿真中界面由基于表面的内聚行为法构建,无法完全还原实际加工中的界面失效。同时,在切削加工过程中,刀具与工件之间的摩擦会产生较高温度,进而导致材料软化,显著影响切削行为,最终导致仿真结果略小于试验结果。
6 结论
(1)当纤维方向角θ为0°时,纤维失效机制为弯曲失效,切屑形貌呈块状;当θ为45°与135°时,纤维失效机制分别为剪切失效与弯曲失效,切屑形貌均呈条状;当θ为90°时,纤维弯曲与纤维剪切失效均存在,切屑形貌呈短棒状。
(2)当θ为0°、45°、90°时,切屑尺寸均与刀具倾斜角 (i)呈正相关,其中θ为0°的曲线斜率变化较为急剧,θ为45°的曲线斜率较平缓,θ为90°的曲线呈稳定增长趋势,θ为135°时的切屑尺寸与i无相关性。任一θ下,加工残余应力最大值均与切削速度呈正相关,与切削深度无明显相关性。
(3)切削力受θ影响显著,当0° < θ < 90°时,切削力呈增大趋势,90° < θ < 135°时,切削力呈降低趋势,在θ为90°时呈现最大值,0°时呈现最小值。不同θ下,切削力均与切削速度呈正相关,仿真与试验切削力最大值分别为207.42 N与226.70 N,两者之间最大误差为10.81%;不同θ下,切削力均与切削深度呈正相关,仿真与试验切削力最大值分别为216.31 N与230.56 N,两者之间最大误差为8.52%。本研究实现了对试验中同工况切削力的有效预测。
[1] 徐锦泱. 碳纤维增强树脂基复合材料钻削缺陷研究进展[J]. 航空制造技术, 2022,65(22): 24-33.XU Jinyang. Research advances in drillinginduced defects of carbon fiber reinforced polymers[J]. Aeronatical Manufacturing Technology, 2022, 65(22): 24-33.
[2] 金启豪, 陈娟, 彭立明, 等. 碳纤维增强树脂基复合材料与铝/镁合金连接研究进展[J]. 材料工程, 2022, 50(1): 15-24.JIN Qihao, CHEN Juan, PENG Liming, et al. Research progress in joining of carbon fiberreinforced polymer composites and aluminum/magnesium alloys[J]. Journal of Materials Engineering, 2022, 50(1): 15-24.
[3] GENG D X, LIU Y H, SHAO Z Y,et al. Delamination formation, evaluation and suppression during drilling of composite laminates:A review[J]. Composite Structures, 2019, 216:168-186.
[4] DURANTE M, BOCCARUSSO L,DE FAZIO D, et al. Circular cutting strategy for drilling of carbon fiber-reinforced plastics (CFRPs)[J]. Materials and Manufacturing Processes, 2019,34(5): 554-566.
[5] 杨国林, 董志刚, 康仁科, 等. 螺旋铣孔技术研究进展[J]. 航空学报, 2020, 41(7): 623311.YANG Guolin, DONG Zhigang, KANG Renke, et al. Research progress of helical milling technology[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(7): 623311.
[6] 董志刚, 高宇, 康仁科, 等. 钛合金螺旋铣孔孔径偏差研究[J]. 航空学报, 2021,42(3): 423841.DONG Zhigang, GAO Yu, KANG Renke,et al. Hole diameter deviation in helical milling of titanium alloy[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 423841.
[7] 张顺, 焦锋, 王雪, 等. CFRP单向板超声振动辅助螺旋铣孔孔壁的质量试验[J].机械设计与研究, 2021, 37(5): 117-122.ZHANG Shun, JIAO Feng, WANG Xue,et al. Study on surface quality of hole wall in ultrasonic vibration-assisted helical milling of unidirectional CFRP[J]. Machine Design &Research, 2021, 37(5): 117-122.
[8] 周兰, 安国升, 李光奇, 等. 基于等效刃型矢量法的钛合金螺旋铣孔切削力机械模型研究[J]. 航空制造技术, 2023, 66(14): 52-58.ZHOU Lan, AN Guosheng, LI Guangqi,et al. Research on mechanistic model of cutting force in helical milling of titanium alloy based on equivalent cutting edge vector method[J].Aeronautical Manufacturing Technology, 2023,66(14): 52-58.
[9] 万敏, 杜宇轩, 张卫红, 等. 单向CFRP螺旋铣削力建模[J]. 航空学报, 2021, 42(10):524134.WAN Min, DU Yuxuan, ZHANG Weihong,et al. Cutting force modeling in helical milling process of unidirectional CFRP[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(10):524134.
[10] 盛方怡, 杨国林, 孟凡通, 等. 沉头孔螺旋铣削加工有限元仿真分析[J]. 航空学报, 2024, 45(1): 428690.SHENG Fangyi, YANG Guolin, MENG Fantong, et al. Finite element simulation analysis in helical milling of countersunk hole[J]. Acta Aeronautica et Astronautica Sinica, 2024, 45(1):428690.
[11] 秦旭达, 唐心凯, 葛恩德, 等. CFRP三维铣削仿真模型的建立及层间损伤分析[J].宇航材料工艺, 2020, 50(1): 22-29.QIN Xuda, TANG Xinkai, GE Ende, et al.Establishment of 3D milling simulation model for CFRP and analysis of interlaminar damage[J].Aerospace Materials & Technology, 2020, 50(1):22-29.
[12] YAN X Y, ZHANG K F, CHENG H,et al. Force coefficient prediction for drilling of UD-CFRP based on FEM simulation of orthogonal cutting[J]. The International Journal of Advanced Manufacturing Technology, 2019, 104(9): 3695-3716.
[13] ZHANG B Y, WANG F J, WANG Q, et al. Novel fiber fracture criteria for revealing forming mechanisms of burrs and cracking at holeexit in drilling carbon fiber reinforced plastic[J].Journal of Materials Processing Technology, 2021,289: 116934.
[14] ZHOU Z T, WANG H Y. Full lifecycle cutting force prediction in ball helical milling based on oblique cutting analysis[J]. The International Journal of Advanced Manufacturing Technology, 2023, 124(5): 1623-1638.
[15] 王海艳, 周秩同, 武晔, 等. 基于斜角切削理论的钛合金螺旋铣孔切削力建模[J].中国机械工程, 2023, 34(2): 142-147.WANG Haiyan, ZHOU Zhitong, WU Ye, et al. Modeling of cutting force in helical milling of titanium alloys based on oblique cutting theory[J].China Mechanical Engineering, 2023, 34(2):142-147.
[16] 唐心凯. CFRP低损伤铣削刀具及其切削工艺优化研究[D]. 天津: 天津大学, 2019.TANG Xinkai. Research on CFRP low damage milling tool and its cutting process optimization[D]. Tianjin: Tianjin University, 2019.
[17] HOBBIEBRUNKEN T, FIEDLER B, HOJO M, et al. Microscopic yielding of CF/epoxy composites and the effect on the formation of thermal residual stresses[J]. Composites Science and Technology, 2005, 65(10): 1626-1635.
[18] XU X F, JIN X L. 3-D finite element modeling of sequential oblique cutting of unidirectional carbon fiber reinforced polymer[J].Composite Structures, 2021, 256: 113127.
[19] 秦旭达, 朱圣富, 李士鹏, 等. 不同纤维方向角时碳纤维增强树脂基复合材料切削力建模[J]. 宇航材料工艺, 2020, 50(6): 31-40.QIN Xuda, ZHU Shengfu, LI Shipeng, et al. Modeling of cutting force for carbon fiber reinforced plastic with different fiber orientation angle[J]. Aerospace Materials & Technology,2020, 50(6): 31-40.
[20] 刘枭鹏, 李鹏南, 李树健, 等. 基于零厚度内聚力单元单向碳纤维增强树脂基复合材料微观切削机理研究[J]. 宇航材料工艺,2019, 49(5): 22-26.LIU Xiaopeng, LI Pengnan, LI Shujian, et al.Microscopic cutting mechanism of unidirectional carbon fiber reinforced plastics based on zero thickness cohesive element[J]. Aerospace Materials& Technology, 2019, 49(5): 22-26.
[21] WANG B, WANG Y F, ZHAO H, et al. Mechanisms and evaluation of the influence of cutting temperature on the damage of CFRP by helical milling[J]. The International Journal of Advanced Manufacturing Technology, 2021,113(7): 1887-1897.
[22] 李树健, 周永超, 陈蓉, 等. 考虑孔隙缺陷的CFRP微观切削仿真与实验研究[J].复合材料学报, 2023, 40(1): 625-636.LI Shujian, ZHOU Yongchao, CHEN Rong,et al. Simulation and experimental study of CFRP micro cutting considering voids defects[J]. Acta Materiae Compositae Sinica, 2023, 40(1): 625-636.
