薄壁结构以其轻质高强、比吸能高等优点，被广泛应用于航空航天、船舶、汽车等领域^[1–2]。随着人们对结构安全性的日益关注，如何提高结构的耐撞性、设计新型吸能结构，已经成为当前研究的热点问题。多孔材料被压缩时具有较长的应力平台，这正是优异吸能结构所急需的性能。蜂窝结构作为最有效的传统吸能结构，其耐撞性问题得到了广泛关注，并在汽车等装备的设计和制造中得到了广泛应用。当前大部分研究的蜂窝结构是六边形或其演化结构^[3]。Yang等^[4]将三角形管与正弦波纹板相结合构建了一种新型的波纹蜂窝，这是一种高效的吸能结构，与传统蜂窝结构相比，其比吸能（Specific energy absorption，SEA）提高了73.8%，载荷效率提高了近3倍。Oruganti等^[5]利用有限元法研究了六边形和圆形蜂窝的蠕变变形，证明紧密排列的圆形蜂窝比同等密度的六边形蜂窝具有更优的共面性能，其弹性模量是六边形结构的7.5倍。近年来，研究人员越发重视通过创新设计来提高结构的性能^[6–8]。Yang等^[9]将花瓣状细观结构融入到传统圆形蜂窝结构中，结果表明，该结构的SEA较传统圆形结构提升了近2倍。Zhang等^[10]为提高蜂窝结构的耐撞性能，将层次微结构引入到传统蜂窝结构中，提出了一种新型四圆弧蜂窝结构；引入层次微结构后，与正圆形蜂窝结构相比，四圆弧蜂窝结构的平台应力与能量吸收效率得到了大幅度提升，分别提高了45.8%与56.3%。由以上研究可知，圆弧蜂窝结构具有良好的设计性与优异的吸能性能，其平均碰撞力和SEA都较传统结构有了大幅度提高。

“仿生学”概念早在20世纪50年代便被提出，是一门通过借鉴生物系统的结构、功能和机制用以设计新技术、新材料和新系统的学科。其核心思想与创新结构设计的目的不谋而合，为了提高蜂窝结构的耐撞性，研究人员开始将仿生理念融入到新型蜂窝结构的设计中。Huang等^[11]受到竹子层级微结构的启发，提出了一类仿生多胞圆管结构，该结构相较传统圆管结构SEA提高了67.69%。郭婷等^[12]根据甲壳虫外壳芯柱的微结构设计了仿甲壳虫芯柱吸能结构，通过LS-DYNA软件对结构进行准静态分析后优化了原有模型；结果表明，优化后模型相较普通圆管具有更优的吸能性能和更稳定的压缩载荷。雀尾螳螂虾具有锤状的螯肢，可以承受高速冲击并有效吸收冲击能量，Huang等^[13]以螯肢为灵感设计了一种具有3层圆柱体的新型仿生蜂窝，分析了胞元数量在轴向与斜向的载荷对其耐撞性的影响。邓敏杰等^[14]基于马尾草茎秆的结构特征设计出一种新型仿生薄壁结构，并与双圆管结构的耐撞性能进行对比，结果发现，其SEA与压缩力效率相较传统结构分别提高了34.74%与37.50%。Lakes等^[15]结合仿生理念对层级结构进行了定义，提出将层级结构引入轻质多孔蜂窝结构中，形成的层级蜂窝结构可有效提高多孔材料强度与吸能性能。Fang等^[16]结合层级概念，利用小胞元代替传统六边形蜂窝的边长，经过分析研究后发现，层级结构可有效提高蜂窝结构的吸能性能。Ha等^[17]观察巨型睡莲和龙血树的分型树状结构，提出了一种仿生分形多胞圆管结构，并研究了不同分形阶数对此结构耐撞性能的影响，结果表明，SEA会随着分形阶数的增加而增大，其中2阶仿生分形圆管的SEA较传统圆管提升了35.43%。李响等^[18]考虑到层级因子的影响，基于传统蜂窝结构提出了一种形内自相似层级类蜂窝结构，研究发现，在等密度的前提下，增加层级数可同时提高结构SEA和载荷效率。马芳武等^[19]提出了一种仿生自相似分层蜂窝结构，并对结构在正向和斜向碰撞工况下的耐撞性能展开研究；通过仿真和试验发现，这种仿生自相似分层蜂窝结构在多碰撞工况下均具有稳定的变形模式，相比于传统蜂窝结构，表现出更好的综合耐撞性能。Gao等^[20]将管状结构与仿生理念和层级因子相结合，提出了仿生层级多胞六边形管状结构，并分析不同层级与壁厚对其压溃行为的影响，发现仿生管结构可明显降低峰值碰撞力，且与六边形管状结构相比，其SEA最大可提高146%。

自然界经过亿万年的演化，形成了众多高效的结构，通过仿生学，研究人员可从自然界中获得结构创新设计的灵感，其核心思想对推动结构功能一体化具有深远的影响。本文基于仿生学概念，以益母草的根茎及四方竹为仿生原型，结合蛛网结构的层级概念提出一种仿生类弧形层级蜂窝结构，利用简化超折叠理论建立理论模型，对结构进行研究，并分析层级数量与尺寸参数对结构耐撞性的影响，为提高蜂窝材料的耐撞性能提供新的参考方向与理论依据。

1　仿生类弧形层级蜂窝有限元分析

1.1　仿生结构设计

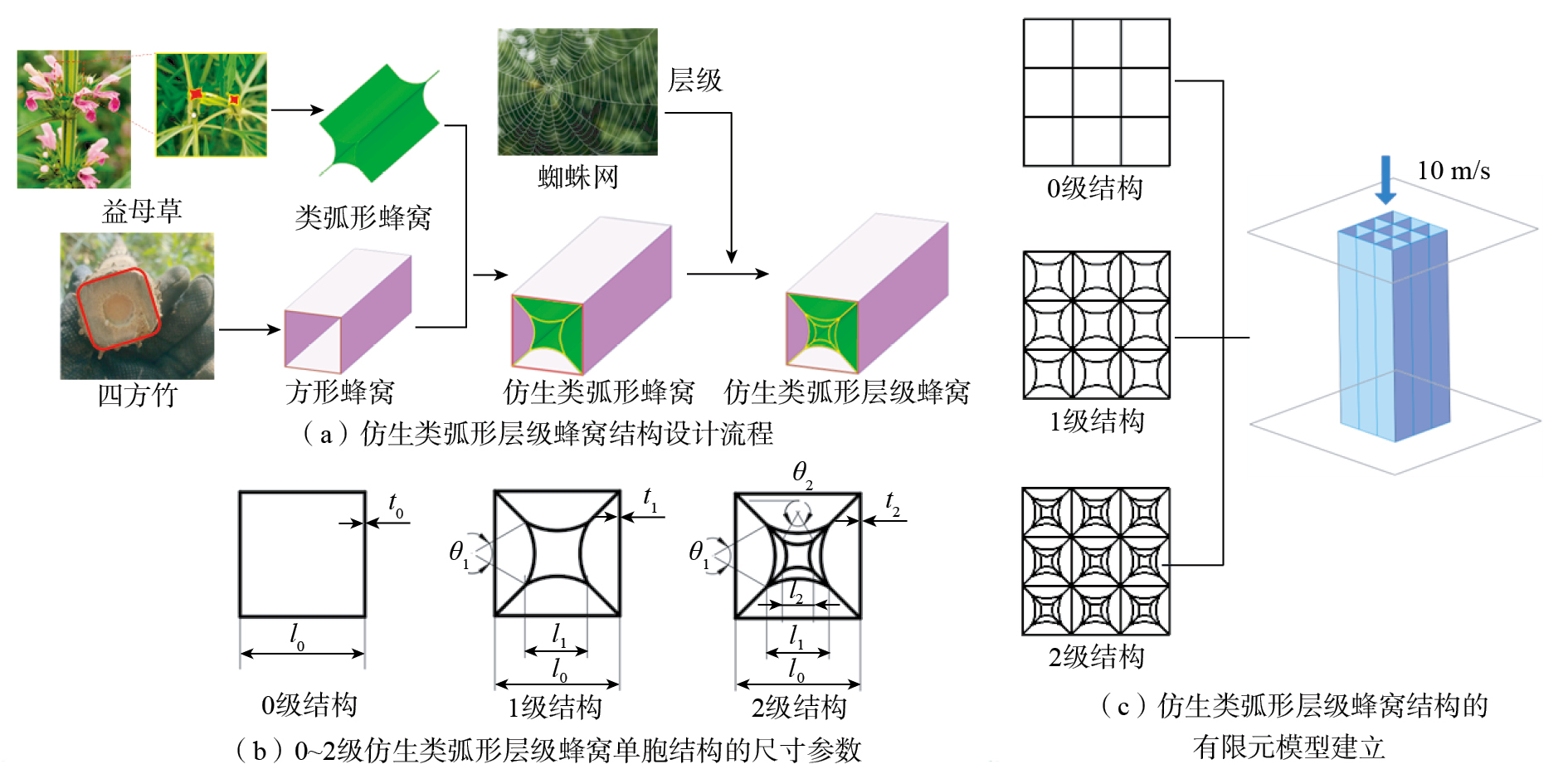
在长期的自然选择下，植物的根茎结构已具有承受各种外力并保持稳定的能力。大部分植物的茎为圆柱形，但唇形科植物（如薄荷、益母草、夏枯草等）的茎为四棱形。该结构特征赋予这类植物茎更高的刚性，有效防止茎在风或其他外力作用下过度弯曲或折断，对唇形科植物在各种环境条件下的生长和生存提供有力的保护。本文引入蛛网层级构型设计理念，以益母草的根茎与四方竹为仿生原型，设计一种仿生类弧形层级蜂窝结构，流程如图1（a）所示。

图1　仿生类弧形蜂窝结构的结构设计

Fig.1　Design of the bionic arc-like hierarchical honeycomb structure

1.2　有限元模型建立

将方形蜂窝结构与弧形蜂窝结构相结合，引入层级因子，仿生类弧形层级蜂窝单胞结构0~2级结构的尺寸参数如图1（b）所示。3种仿生类弧形层级蜂窝单胞结构最外围的方形长度为l₀，0级结构胞元壁厚为t₀；1级结构弧形弦长为l₁，弧形圆心角为θ₁，结构胞元壁厚为t₁；2级结构弧形弦长为l₂，弧形圆心角为θ₂，胞元壁厚为t₂；所有层级结构面外方向的高度为h。本文中取l₀=18 mm，t₀=0.3 mm，高度h=120 mm，弧形圆心角θ₁=θ₂=60°，层级结构系数为0.5。由图1（b）中0级结构到2级结构的规律，可定义层级结构系数γ为

式中，l_n+1为第n+1级结构的弧形弦长，mm；l_n为第n级结构的弧形弦长，mm；l₀为方形蜂窝结构的壁长，mm。

使用ABAQUS软件探究仿生类弧形层级蜂窝结构的耐撞性。如图1（c）所示，将蜂窝结构置于两块板之间，因为两板在冲击过程中不参与变形，故将两板都定义为刚性板，底部刚性板全固定并与蜂窝结构绑定，顶部刚性板质量为600 kg，以10 m/s的初速度沿轴向冲击蜂窝结构，总位移设定为总变形量的80%，即为96 mm。通常，接触包括结构本身的自接触及结构与面板的接触，因此摩擦系数设定为0.2^[21]。考虑到计算速度与模拟结果的准确性，在网格收敛性分析后，将夹芯结构网格尺寸设置为2 mm，上下刚性板网格尺寸设置为4 mm。对蜂窝夹芯采用各向同性材料模型进行建模，分别采用实体单元（C3D8R）和壳单元（S4R）对平板和蜂窝结构进行网格划分。蜂窝基体采用理想弹塑性材料铝合金Al6061T6，其力学参数为密度ρ=2700 kg/m³，杨氏模量E=68.9 GPa，屈服应力σ_y=276 MPa，极限应力σ_u=310 MPa，泊松比υ=0.33^[22]。

1.3　有限元模型验证

选择0级结构，采用与文献[23]中同样的结构参数和有限元设置，其他参数设置与上文有限元模型相同，将本文的仿真结果与文献[23]中的试验结果进行对比，结果如图2所示。仿真变形与文献试验变形在整体轮廓上吻合较好，研究结果基本一致，验证了本文中有限元模型的可靠性。

图2　仿真与文献试验结果对比^[23]

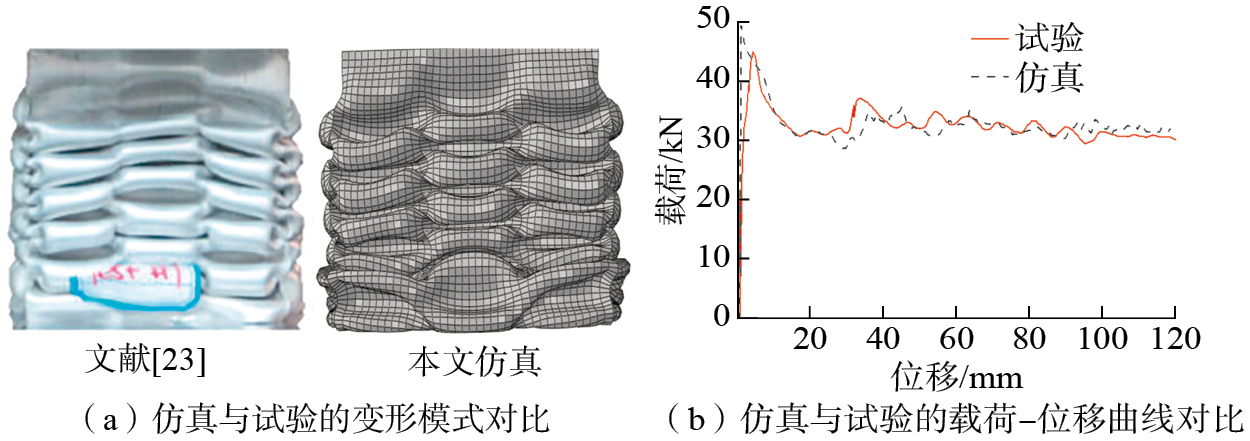
Fig.2　Results comparison of simulation and experiments in literature^[23]

1.4　仿生类弧形层级蜂窝理论模型的建立

为研究本文结构的耐撞性能，采用以下耐撞性评价指标^[24]，分别为峰值碰撞力（Peak collision force，PCF）、平均碰撞力（Mean collision force，MCF）和SEA。

式中，F(δ)为结构在压缩位移为δ时的碰撞力，kN；d为结构完全屈曲的位移，即密实位移，mm；EA为碰撞过程中结构变形所吸收的总能量；SEA为在碰撞过程中单位质量蜂窝结构所吸收的能量，kJ/g；m为蜂窝结构的质量，g。

过高的PCF不利于结构的稳定变形，影响吸能效果，尤其是在汽车碰撞中，较高的PCF会导致乘客受伤或死亡^[25]，因此PCF越小，车辆的耐撞性能越好。MCF可以间接反映结构的吸能性能，其值越大，结构的吸能效果越好。

理论分析可以大幅节约分析时间和计算成本，为蜂窝结构后期的结构优化提供重要的指导作用。本文采用简化超折叠单元理论来分析仿生类弧形层级蜂窝结构的耐撞性^[26]，如图3所示。图3（a）中阴影部分为3个变形区域，中间的三角区受拉，上、下2个三角区受压。同时该折叠单元还包括3条固定绞线，假设在折叠过程中胞壁厚度和折叠波长2H保持不变，则1个折叠单元的MCF可以通过计算1个折叠波长的能量守恒得到；对于完全压溃的折叠单元，根据能量守恒，加载过程外力所做的功将转化为塑性弯曲变形能和薄膜变形能，即

式中，MCF为压缩过程中的平均碰撞力，kN；E_b为弯曲变形能，kJ；E_m为薄膜变形能，kJ；η为有效破碎距离系数，是有效破碎距离和折叠波长2H的比值，受结构厚度与边长的影响，且结构实际压溃变形距离无法到达2H，Wierzbicki等^[27]的研究发现，η的范围通常为0.7~0.75，本文中η取值为0.73。

图3　基本折叠单元与0~2级仿生类弧形层级蜂窝结构基本单元示意图

Fig.3　Schematic diagram of basic folding unit and basic units of 0–2 layers of bionic arc-like hierarchical honeycomb structure

当面板发生弯曲时会产生3条塑性绞线，弯曲变形能可通过3条塑性绞线的转动被耗散，可表示为

式中，$M_0={\sigma }_0{t}_0^2\text{/4}$，为全塑性弯矩，N·m；${\sigma }_0=({\sigma }_{\text{y}}+{\sigma }_{\text{u}})\text{/}2$，为材料的流动应力，其中σ_y和σ_u分别为材料的屈服应力和极限应力，MPa；α_i为每个绞线的转角；L_i为每个单元板的长度。

当折叠单元完全压平时，3条塑性绞线旋转角度分别为π/2、π、π/2。弯曲变形能可表示为

式中，L_c为面板总长度。

为计算仿生类弧形层级蜂窝结构面外冲击载荷下的薄膜变形能，将其划分为8种基本单元：角单元2P型、T型单元、十字形单元crisscross、角单元3P–Ⅰ型、5面板单元5P型、8面板单元8P型、角单元3P–Ⅱ型、角单元4P型，如图3（b）所示。

本文中角单元2P型和十字形单元crisscross的薄膜变形能可通过下式计算^[28]。

3面板角单元的薄膜变形能为^[29]

T型单元和角单元3P–Ⅰ型都可视为3面板单元，对应的夹角分别为90°和45°，故T型单元和角单元3P–Ⅰ型的薄膜变形能可按下式计算。

n-panel单元的薄膜变形能为

5面板单元与8面板单元属于n-panel单元，薄膜变形能可按下式计算。

熊俊^[30]推导出了角单元3P–Ⅱ型与角单元4P型的薄膜变形能计算公式如下。

对于本文中的结构，角单元3P–Ⅱ型与角单元4P型的夹角分别为60°和30°，故薄膜变形能为

对于胞元为a×a排列的0级仿生类弧形蜂窝结构，其总薄膜变形能为

其中，$N_1=4$，$N_2=4\times (a-1)$，N₃=（a–1）²。

则0级仿生类弧形蜂窝结构的总薄膜变形能可表示为

0级仿生类弧形蜂窝结构截面总线段长度L_c0可表示为

则0级仿生类弧形蜂窝结构的总弯曲变形能为

将式（14）和（16）代入式（2）可得

假设单元在折叠破碎过程中为理想变形，即

即可推导出H为

将式（19）代入式（17）得到

若仿生类弧形层级蜂窝结构轴向高度为d，压缩完全时，结构的总吸能可表示为

则0级结构的SEA可表示为

由此推导，可求得n级仿生类弧形蜂窝的总薄膜变形能为

n级仿生类弧形蜂窝结构截面的总线段长度L_cn可表示为

则n级仿生类弧形蜂窝结构的总弯曲变形能为

故n级仿生类弧形蜂窝结构的MCF为

若n级仿生类弧形蜂窝结构的轴向高度为d，压缩完全时，结构总吸能可表示为

则SEA可表示为

将0级仿生类弧形蜂窝结构的参数代入上式即可求得MCF₀=11.90 kN，MCF的仿真值为11.14 kN，将计算结果与仿真结果作对比，如图4所示。可以看出，理论值与仿真值误差为6.8%，证明此理论分析的可靠性，可作为后续研究的理论参考。

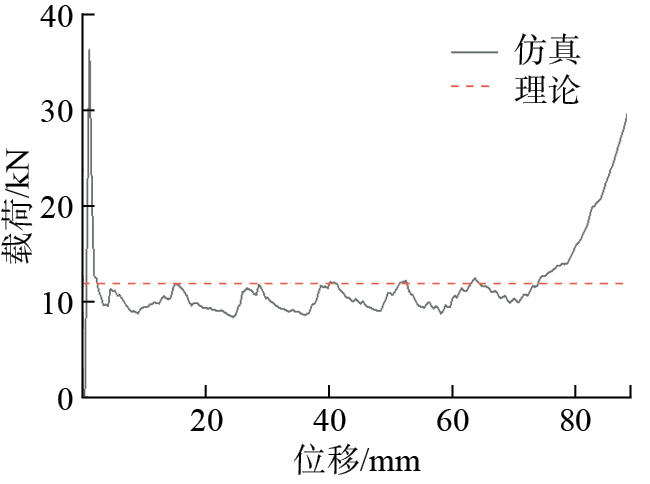
图4　0级仿生类弧形层级蜂窝结构理论与仿真结果对比

Fig.4　Comparison of theoretical and simulation result of 0-layer bionic arc-like hierarchical honeycomb structure

2　结果与讨论

2.1　层级因子影响

在受到冲击载荷时，蜂窝结构的变形模式会直接对结构整体的吸能特性造成影响。改变壁厚使t₀=0.3 mm，t₁=0.12 mm，t₃=0.10 mm，在等质量的前提下研究0级、1级和2级仿生类弧形蜂窝结构受到轴向载荷时的变形模式。图5为3种层级蜂窝结构在不同变形量下的变形图。可知，3种层级蜂窝在10 m/s冲击速度下的变形模式基本一致，均是从冲击端向固定端开始发生逐层变形，最后直到芯层被完全压溃。增加层级数会使结构产生更多的褶皱，从而吸收更多的能量。3种仿生类弧形层级蜂窝结构具有稳定的压缩过程，满足工程领域对吸能构件的基本需求。

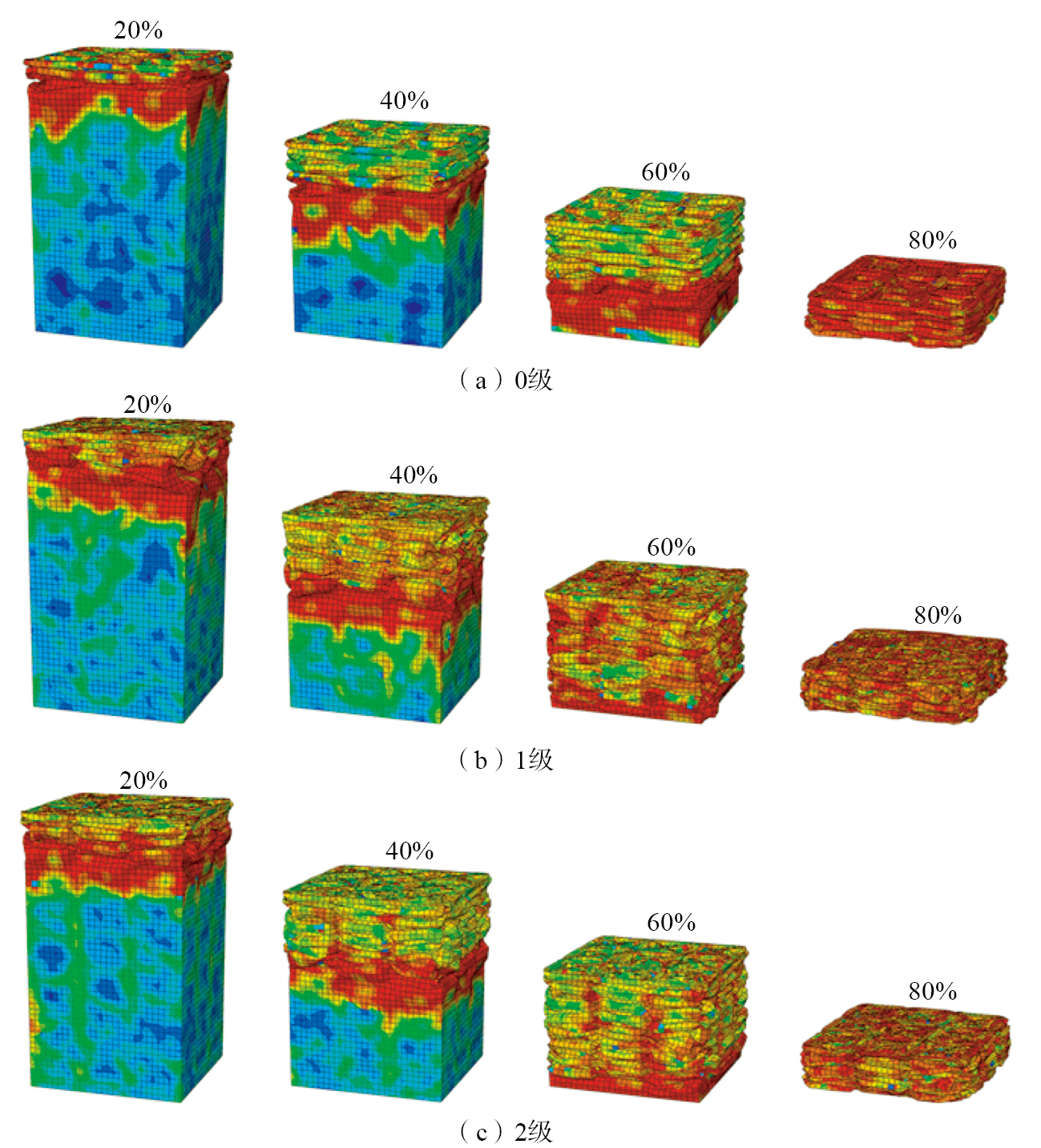
图5　仿生类弧形层级蜂窝在轴向载荷下的变形模式

Fig.5　Deformation pattern of the bionic arc-like hierarchical honeycomb structure under axial loading

图6为仿生类弧形层级蜂窝结构经有限元分析后所得到的载荷-位移曲线和SEA-时间曲线。由图6（a）可知，3种仿生类弧形层级蜂窝结构动力学性能的变化规律基本一致，在承受冲击的初始阶段，蜂窝结构表现出较大的刚度，此时曲线从0开始急剧升高直至峰值；在冲击的中期阶段，蜂窝结构出现规律的塑性变形，从而呈现出稳定的吸能阶段。进入平台阶段，载荷会出现小幅度的波动现象，这是由于蜂窝结构出现局部失稳所致；在冲击后期，蜂窝结构出现大变形直至完全压溃后进入密实化阶段。从图6（a）还可知，PCF随着蜂窝层级的升高而降低，1级结构与2级结构的PCF分别较0级结构降低了16.14%和16.11%；但1级结构与2级结构的MCF相比0级结构提升明显，分别提高了25.46%和29.98%，且有更加平缓的平台段，表明1级和2级结构吸能更为稳定。从图6（b）可以看出，3种蜂窝结构的SEA随着层级的增加而增大。其中2级结构的吸能效果最优，2级结构与1级结构的SEA较0级结构的SEA分别提高了23.11%与19.99%（t=9.6 ms）。综上所述，层级因子对于仿生类弧形层级蜂窝结构的耐撞性能具有显著影响，在不改变结构质量的情况下，增加层级可以有效降低PCF并大幅度提高吸能性能，表明本文所提出的仿生类弧形层级蜂窝结构可作为良好的吸能构件。

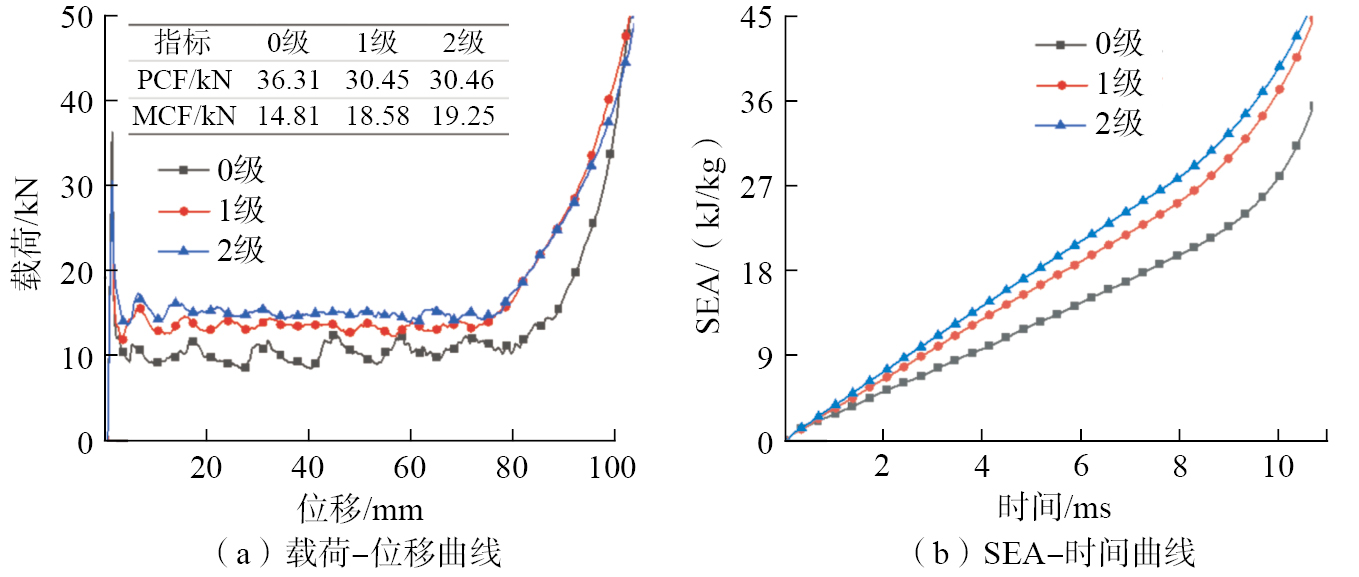
图6　0~2级仿生类弧形层级蜂窝结构的耐撞性能

Fig.6　Crashworthiness of 0–2 layers bionic arc-like hierarchical honeycomb structure

2.2　尺寸参数分析

通过有限元方法进一步研究尺寸参数对仿生类弧形层级蜂窝结构耐撞性能的影响，仿生类弧形层级蜂窝结构的壁长与壁厚对PCF、MCF及SEA的影响如图7所示。从图7（a）可以看出，在面外冲击载荷下，壁长与壁厚的增大可提高结构的整体刚度，因而不同层级仿生类弧形蜂窝结构的PCF均逐渐增大。在同等尺寸参数下，1级结构、2级结构与0级结构相比，PCF有所下降，但在壁长小且壁厚大的区域，上述层级影响的效果微弱，这是因为较大的厚径比会造成蜂窝结构整体失稳，从而导致PCF增大，但总体而言，层级结构可以有效降低PCF。从图7（b）可以看出，各层级仿生类弧形蜂窝结构的MCF随着壁长和壁厚的增加而增大，且壁厚的影响更加显著。造成这一现象的原因是，相较于壁长，壁厚对蜂窝结构等效密度的增加更为显著，而更高的等效密度必然会使结构吸收更多的能量，因而MCF的提升更加明显；且同种尺寸参数下，随着蜂窝层级的增加，MCF出现大幅度提升。从图7（c）可以看出，不同层级仿生类弧形蜂窝结构的SEA随着蜂窝壁厚的增大而增大，随着蜂窝壁长的增大而减小。产生这一现象的原因是，壁长与壁厚的增加均会引起MCF增大，且壁厚的影响更为明显，更大的MCF会导致更多的能量吸收，因此壁厚的小幅度提高即可显著提高MCF，进而提高SEA，而壁长的增大对MCF的增幅较小，但会大幅提升蜂窝结构的质量，此时能量吸收的增幅已无法平衡蜂窝结构质量剧增的效果，从而导致SEA降低；在同等尺寸参数下，蜂窝结构的SEA随着层级的增加而增大。综上所述，仿生类弧形层级蜂窝结构的胞元壁厚和壁长均会对结构的面外耐撞性产生影响，但壁厚的影响更显著，同时，增加层级可有效降低结构的PCF，并提高MCF和SEA。

图7　尺寸参数对仿生类弧形层级蜂窝结构面外耐撞性的影响

Fig.7　Influence of dimensional parameters on the out-of-plane crashworthiness of the bionic arc-like hierarchical honeycomb structure

3　结论

（1）在等质量的前提下，随着仿生类弧形层级蜂窝结构层级的增加，PCF有下降趋势，且1级结构与2级结构的MCF相比0级提升明显，分别提高了25.46%和29.98%。

（2）在面外冲击载荷的作用下，壁长与壁厚的增加会提高整体结构的刚度，从而提高PCF。但在同等尺寸参数条件下，随着层级数量的增加，PCF显著下降。

（3）壁厚和壁长对蜂窝结构的MCF具有显著影响，其中壁厚对蜂窝结构的MCF提升效果更加明显。这是由于相较壁长，壁厚的增加会使蜂窝结构的等效密度大幅度提升，等效密度的增加是引起仿生类弧形层级蜂窝结构吸能效果提升的直接原因，从而提高蜂窝结构整体的MCF。

（4）不同仿生类弧形层级蜂窝结构的SEA随着壁厚的增加而增大，随着壁长的增加而下降，这是因为壁厚的小幅度提高可显著提升MCF，进而提高SEA，壁长的增大会导致蜂窝结构的质量大幅提升，当能量吸收的增幅无法平衡蜂窝结构质量剧增的效果时，便会导致SEA降低。