金属多孔结构具有轻质^[1]、比表面积大^[2]、比强度高^[3]、热/声学性能良好^[4–5]及可设计性高^[6]等特点，被广泛应用于航空航天等领域关键零部件中^[7]，如机翼、热交换器等。在服役过程中，金属多孔结构往往承受较复杂的载荷，不仅要满足轻量化的要求，还须具有优异的隔热性能^[8]。与规则多孔结构相比，梯度多孔结构能结合不同孔隙率、孔隙尺寸、孔隙分布等特征，获得更优异的性能（如高强度^[9]、高能量吸收^[10]和电磁吸收特性^[11]）以适应不同的工况条件。传统加工方法（如发泡等）在梯度多孔结构成形时存在难以实现复杂结构、形状，尺寸可变性受限，以及生产效率较低等问题^[12]。激光选区熔化（Selective laser melting，SLM）增材制造技术成形的复杂零件具有高精度、高密度、高表面质量等优点^[13]，因此特别适合制造高几何自由度^[14]、特殊晶胞类型和可控尺寸的梯度多孔结构^[15]。

基于Voronoi分割法的梯度多孔结构可以通过调整种子的位置、数量或其他参数，使结构根据不同情况自适应地调整自身的荷载和边界条件，从而实现性能优化^[16]。基于Voronoi的梯度多孔结构研究主要集中在力学性能方面。Ajdari等^[17]构建了分层密度梯度Voronoi模型并进行了力学性能仿真研究，与均匀Voronoi多孔结构相比，梯度Voronoi多孔结构的屈服强度提高了62%，梯度结构的整体有效弹性模量和屈服强度均有所提升。林伟等^[18]设计了“向内”梯度结构和“向外”梯度结构，发现基于Voronoi方法设计的梯度点阵结构具有高强度、抗冲击和吸能减振等良好的力学性能。Wang等^[19]提出了一种自上而下的概率球设计方法构建Voronoi多孔支架，并通过SLM制备多孔试样，该试样表观弹性模量范围为0.14~2.37 GPa，抗压强度范围为1.94~116.61 MPa。Guo等^[20]聚焦孔隙率控制准则，研究了不同冲击速度和方向下，不同孔隙度梯度的Voronoi梯度多孔结构的冲击性能响应。Zhao等^[21]通过SLM制造了7种密度分级的Voronoi蜂窝夹层结构，通过在蜂窝芯层的跨度中分配更高的相对密度单元，同时逐渐降低密度，实现了材料良好的抗弯阻力、比能量吸收和更高的承载能力。Liu等^[22]结合拓扑优化方法和Voronoi多孔结构设计技术，引入了一种新的梯度密度非均匀多孔结构设计方法，拓扑优化后的梯度Voronoi多孔结构表现出更高的强度和稳定性。

目前基于Voronoi的梯度多孔结构设计的梯度变化方式单一，对不同变化方式的梯度Voronoi多孔结构的力学性能报道仍较少。因此，本文提出了一种基于Voronoi分割法的梯度多孔结构设计方法，设计了沿径向方向上初始间距与最终间距尺寸不同的梯度变化多孔结构。通过有限元仿真（FEM）分析和压缩试验，探究不同梯度Voronoi多孔结构的力学性能和能量吸收特性，揭示Voronoi多孔结构在不同梯度条件下的变形机制与其力学性能之间的密切联系，为提升航空航天关键零部件轻量化、结构强度和抗冲击能力等提供理论基础和参考价值。

1　试验及方法

1.1　Voronoi多孔结构设计

Voronoi图可以进行如下定义^[23]。对于m维欧几里得空间上的一组数量为k（k≥2）的种子，即

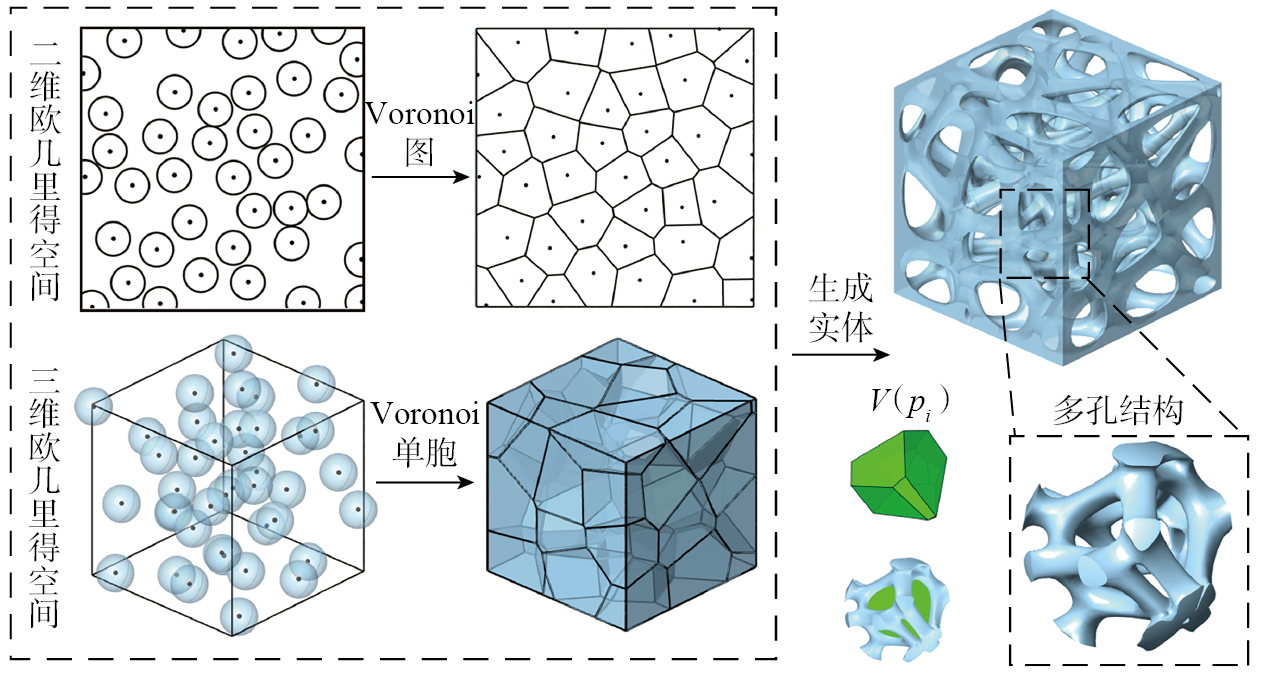
式中，m表示维度；R表示空间；p_k表示空间内的第i个种子（i=1,…,k）；P表示空间内所有种子的集合。如图1所示，以这些种子为圆心的圆进行半径等速率扩张后产生的边界图形称为Voronoi图，二维平面内，Voronoi图的边界由相邻种子的垂直平分线组成；而在三维空间内，Voronoi图的边界由相邻种子连线的中垂面组成。因此，Voronoi图可以由下式进行定义。

式中，d(p,p_i)表示位置p与种子p_i之间的欧几里得距离；V(p_i)表示与种子p_i相对应的Voronoi多边形。本文使用Grasshopper软件进行Voronoi不规则多孔结构的可控设计，基于三维空间上Voronoi–Tessellation分割算法，将Voronoi多边形根据体中心和面中心进行缩放（体缩放系数S_v，面缩放系数S_f），并根据缩放后的几何边线生成的网格进一步获得Voronoi多孔结构。由于结构的孔隙部分体积基本由缩小后的Voronoi单元体积构成，因此Voronoi多孔结构的孔隙率近似等于体缩放系数S_v，并能够通过Grasshopper的体积测算组件反馈调节获得孔隙率精确的模型。Voronoi多孔结构基于Voronoi图设计而成，Voronoi图则受种子的数量和分布控制。因此，通过对种子的参数控制可进一步实现Voronoi多孔结构的孔隙尺寸梯度设计。

图1　基于Voronoi的多孔结构设计原理

Fig.1　Design principle diagram of porous structure based on Voronoi

图2展示了可控Voronoi不规则多孔结构的设计流程。首先在三维空间上建立长方体几何边界，在几何边界内部生成s层规则的种子点阵，第i层与第i+1层点阵间的间距设置为A_i，第i层种子与种子的间距设为B_i（图2（a））。使用概率球法对点阵进一步进行变换，使用式（3）对点的x、y、z坐标进行随机抖动。

式中，R为概率球半径，控制孔隙点阵抖动的范围；rand为随机数，取值范围为0~1。如图2（b）所示，对z轴方向上的参数A_i进行梯度设置，同时设置第i层的间距参数B_i，获得沿着z轴分布的梯度点阵，并进一步形成不同孔径分布的梯度Voronoi多孔结构。

图2　梯度Voronoi多孔结构设计原理图

Fig.2　Schematic diagram of gradient Voronoi porous structure design principle

本文将梯度方向调整为径向方向，设计了由中心轴沿着径向方向孔径梯度变化的Voronoi多孔结构，如图3（a）所示，此时第i层点阵分布在不同直径的第i层圆柱曲面上，梯度尺寸A_i为圆柱曲面的间距，并且种子的x、y坐标转化为相对于圆柱曲面的u、v坐标，z轴对应径向方向。如图3（b）所示，本文分别设计了孔隙率为70%（即材料体积分数30%），径向方向上初始间距A₁与最终间距A_n尺寸变化为2倍、3倍、4倍的圆柱多孔结构模型（以下分别命名为G–2、G–3、G–4），其中，初始间距A₁=0.5 mm，圆柱模型高10 mm，直径12 mm。

图3　径向梯度Voronoi多孔结构设计示意图

Fig.3　Schematic diagram of radial gradient Voronoi porous structure design

1.2　建立FEM仿真模型

使用ABAQUS软件对梯度Voronoi多孔结构进行准静态压缩仿真以分析结构内部的受力状态。如图4所示。FEM仿真模型由压缩板、固定板及梯度Voronoi多孔结构组成，梯度Voronoi多孔结构放置于固定板上，并由压缩板进行加载。FeCoCrMn体系高熵合金具有高强度、优异延展性、抗辐射损伤稳定性和耐腐蚀性^[24]，是航空领域复杂零部件的潜在材料。通过Li等^[25]对该合金材料的前期研究，得到用于梯度Voronoi多孔结构的材料属性参数为密度7.7584 g/cm³、弹性模量160.78 GPa、泊松比0.33、延伸率17.1%。考虑到金属的硬化效应，使用Johnson–Cook（J–C）本构模型，基于前期获得的合金拉伸曲线^[25]，设置J–C参数：A=468.3 MPa、B=1397.6 MPa、n=0.665、C=0.0417，由于准静态压缩试验变形过程不涉及剧烈温度变化，取m=0。将压缩板、固定板分别与参考点1和参考点2绑定并设置为刚性平板，平板与梯度Voronoi多孔结构间的法向接触设置为硬接触，切向接触设置为摩擦接触。固定板完全固定，压缩板沿轴向加载8 mm。使用Hypermesh软件进行网格划分，为了保证仿真模型的精确性，采用修正的二次四面体网格（C3D10M），网格尺寸设置为0.1 mm。

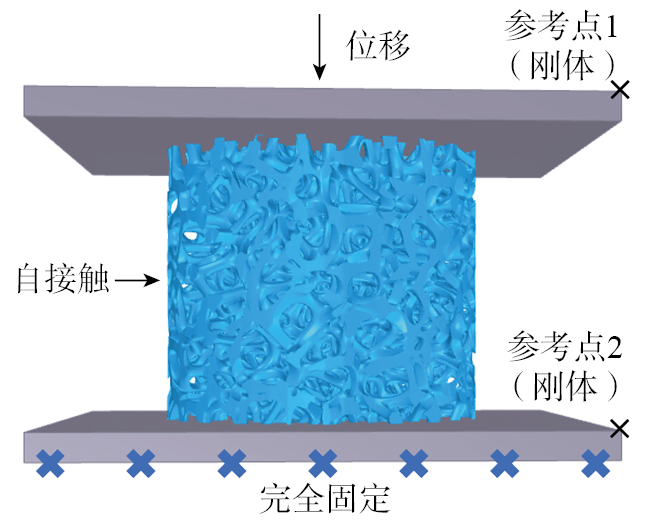
图4　FEM仿真模型

Fig.4　FEM simulation model

1.3　试样制备

采用Fe50Mn30Co10Cr10合金粉末（佛山市钺丰材料科技有限公司）进行结构成形，其化学组成如表1所示。粉末颗粒呈球形，粒径尺寸在5~75 μm区间，粉末的平均粒径尺寸约30 μm。使用Laseradd Dimetal–100（广州雷佳增材科技有限公司）制备梯度Voronoi多孔结构，经过前期工艺优化^[25]，采用的SLM成形工艺参数为激光功率180 W、扫描速度500 mm/s、扫描间距70 μm、层厚30 μm、扫描角度67°。成形过程处于氩气保护状态，以防止成形过程中发生氧化反应。成形后的梯度Voronoi多孔结构在酒精中进行30 min的超声波振动清洗以去除表面黏结的粉末，SLM成形原理和成形后的梯度Voronoi多孔结构如图5所示。

表1　Fe50Mn30Co10Cr10高熵合金化学组成（质量分数）

Table 1　Chemical composition of Fe50Mn30Co10Cr10 high-entropy alloy (mass fraction)

%

图5　SLM成形的梯度Voronoi多孔结构

Fig.5　Structure of gradient Voronoi porous structures by SLM

1.4　压缩测试

使用CMT5105电子万能试验机（三思永恒科技（浙江）有限公司）对梯度Voronoi试样进行单轴压缩试验。将样品水平放置于压缩平台上，设置加载速度为0.5 mm/min，压缩应变0.8，即压缩终止位移设置为8 mm。缓慢下移压缩机，待预载荷达到5 N时开始输出力–位移曲线，将输出的力–位移曲线进行数据转化后得到压缩应力–应变曲线，即

式中，σ为应力，MPa；F(x)为压缩载荷，N；S为试样的表面积，mm²；ε为应变；d为压缩位移，mm；h为试样高度，mm。每种跨度尺寸的梯度Voronoi多孔结构使用3个试样进行重复的机械测试以获得压缩特性曲线。梯度Voronoi多孔结构的能量吸收曲线依据应力–应变曲线计算得到，即

式中，ε¹为致密化应变，即应力–应变曲线的斜率接近压缩弹性模量时的压缩应变。此外，本文对梯度Voronoi多孔结构的能量吸收效率η进行了评估，即

2　结果及讨论

2.1　应力–应变曲线分析

对不同尺寸跨度（G–2、G–3和G–4）的梯度Voronoi多孔结构进行压缩试验和FEM仿真，得到各试样的力学响应特性，如图6所示。可知，所有试样在压缩过程中首先经历弹性阶段，并经过一段应力平台期，然后逐渐致密化。在应变前期（应变<40%），仿真曲线略高于压缩试验曲线，这是由于3种梯度Voronoi多孔结构中都存在尺寸细小（杆径约150 μm）的支杆，SLM成形存在的一些微孔和未熔缺陷使得试样的完整性降低，从而影响力学性能^[26]。较大的尺寸跨度可以改善这种现象，从图6可以看出，随着尺寸梯度增加，仿真与试验曲线的吻合度提升。这是由于试样中的部分支杆尺寸变大，结构整体受成形缺陷的影响变小。在应变后期（应变>40%），可以观察到仿真曲线略低于压缩试验曲线，为了保证仿真的收敛性，设置移除FEM仿真计算中变形失效的网格单元，这使得高应变下的仿真曲线数值要略低于试验曲线^[27]。相较于G–2，G–3和G–4梯度Voronoi多孔结构的应力平台存在波动，这种波动在应变接近20%时发生，这是由结构内部大尺寸支杆的交错变形断裂引起的，即在压缩过程中，较粗的支杆会承担更多的载荷，因此较粗的支杆发生断裂时，较细的支杆所受到的载荷会骤然增加，并发生连锁断裂，形成锯齿状的应力–应变响应特性。比较3种梯度尺寸下的应力–应变试验曲线可以发现，相较于G–2梯度Voronoi多孔结构，G–3和G–4梯度Voronoi多孔结构都具备更高的流动应力平台，而在接近致密化的区域，G–2梯度Voronoi多孔结构的流动应力明显提升，并超过G–3和G–4梯度Voronoi多孔结构，其中G–4梯度Voronoi多孔结构表现出最低的流动应力，这种变化是由梯度多孔结构在不同压缩阶段内部受力形式的变化引起的。

图6　不同跨度尺寸的梯度Voronoi多孔结构压缩试验和仿真应力–应变曲线图

Fig.6　Compression test and simulation stress–strain curves of gradient Voronoi porous structures with different spans

2.2　压缩强度

图7展示了G–2、G–3和G–4梯度Voronoi多孔结构的压缩屈服强度和弹性模量。如图7（a）所示，试验与仿真的屈服强度误差随着跨度尺寸的增加而减小，试验数据表明G–4梯度Voronoi多孔结构的屈服强度最高，达到22.93 MPa，G–3梯度Voronoi多孔结构的屈服强度为21.82 MPa，均高于G–2梯度Voronoi多孔结构（17.81 MPa）。梯度Voronoi多孔结构孔隙尺寸跨度的增加会提升结构的屈服强度，这可能归因于跨度尺寸更大的多孔结构内部存在更粗的支杆^[28]。如图7（b）所示，梯度Voronoi多孔结构的试验弹性模量范围在0.886~1.045 GPa间，其中G–2和G–4梯度Voronoi多孔结构的弹性模量较低，较低的弹性模量能够对能量吸收起到一定的缓冲作用。此外，仿真的弹性模量明显远高于试验数据，这可能是由于瞬态动力学模拟中的应力波传递较慢，模型的弹性变形不均匀导致的。

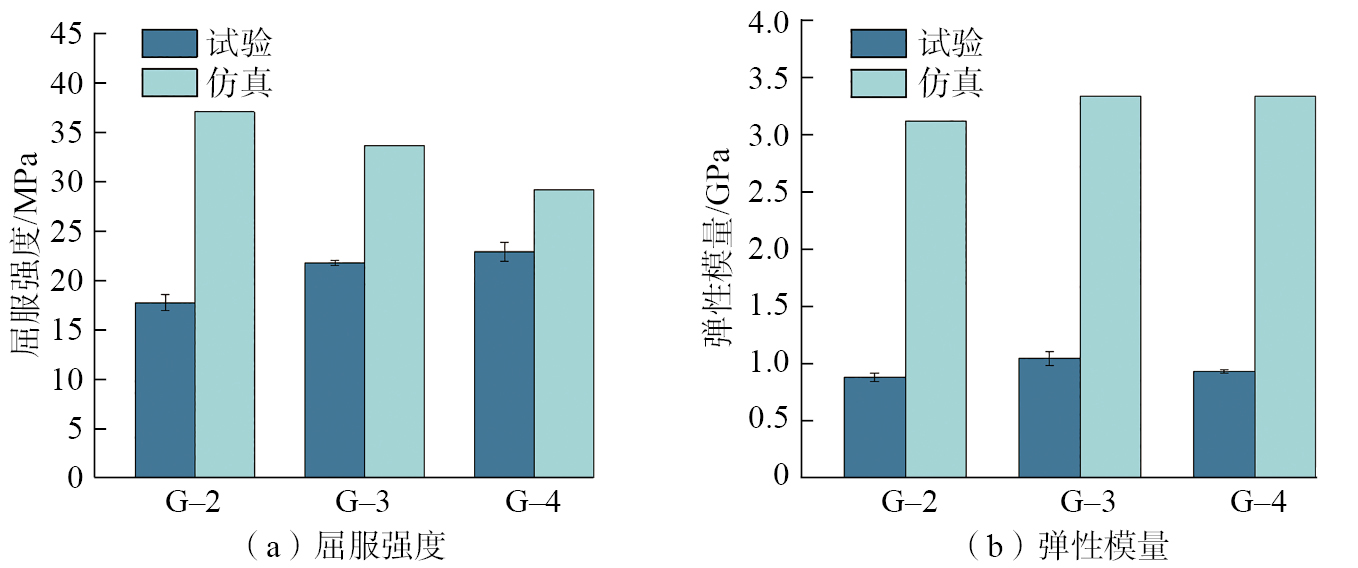
图7　不同跨度尺寸梯度Voronoi多孔结构的力学性能

Fig.7　Mechanical properties of gradient Voronoi porous structures with different spans

为了进一步了解梯度Voronoi多孔结构的内部受力状态，分析了5%应变下3种梯度Voronoi多孔结构的Mises应力分布云图。如图8所示，由于梯度Voronoi多孔结构孔隙具有随机分布的特性，加载过程中结构内部的应力传递不均匀，3种梯度多孔结构都存在空间上不规则分布的集中应力，相较于有序分布的晶格结构，梯度Voronoi多孔结构出现的不均匀应力分布现象致使压缩过程中内部的支杆结构随应变的增加发生批次断裂，这种断裂形式有助于应力平台的形成，并提升结构的能量吸收效率。此外，从图8可以看到，应力集中主要出现在支杆上而不是支杆的连接节点处，因此梯度Voronoi多孔结构内部的弯曲断裂失效更倾向于发生在支杆上。

图8　5%应变下不同跨度尺寸梯度Voronoi多孔结构内部的Mises应力分布云图

Fig.8　Mises stress distribution cloud map inside the gradient Voronoi porous structures with different spans at 5% strain

2.3　变形分析

多孔结构的应力–应变曲线特性取决于压缩过程中结构内部的变形行为，因此对不同应变下（10%、30%和50%）梯度Voronoi多孔结构的等效塑性应变进行分析，结果如图9所示（红色虚线间的区域为主要变形区域）。可以看出，10%应变下，梯度Voronoi多孔结构的大部分支杆处于小变形状态，塑性变形主要发生在结构的中心区域。由于中心区域过于密集的孔隙分布和连接约束，支杆与支杆在变形过程中更容易发生挤压变形，而梯度Voronoi多孔结构边界部位的支杆结构由于孔隙形态的不完整性而拥有更大的变形自由度，这是边界区域塑性变形较小的主要原因。在变形过程中，由于大部分支杆结构还未达到受力极限，因此梯度Voronoi多孔结构的流动应力会随着应变的增加而增大。随着应变的增加，接近轴心的细小薄弱支杆发生断裂失效，此时大尺寸支杆结构还未达到损伤极限，并承担主要载荷，这种变形行为使得流动应力近乎保持不变并形成应力平台。应变达到30%时，变形损伤由支杆尺寸小的中间区域扩散至支杆尺寸大的边界区域。随着孔隙空间被压缩，断裂损伤的支杆开始相互接触，并填充结构中的孔隙部分，整个梯度Voronoi多孔结构逐渐致密化。当应变达到50%时，3种结构的内部几乎被损伤的支杆和碎屑完全填充并接近致密，而边界区域由于较大孔隙的存在仍具备能量吸收潜力，这一现象在G–4梯度Voronoi多孔结构中尤为明显。对比3种结构的变形云图可以发现，随着跨度尺寸的增加，梯度Voronoi多孔结构内部的孔隙变大，弱化了致密化过程中支杆的接触填充作用，因此更大尺寸跨度的梯度Voronoi多孔结构在应变后期具有更低的流动应力。

图9　不同跨度尺寸梯度Voronoi多孔结构在不同应变下的等效塑性应变云图

Fig.9　Equivalent plastic strain cloud maps of gradient Voronoi porous structures with different spans at different strains

2.4　能量吸收

梯度Voronoi多孔结构的能量吸收能力如图10（a）所示，G–3梯度Voronoi多孔结构表现出最强的能量吸收能力，这是由于该结构在应变过程中保持着较高的流动应力；G–2梯度Voronoi多孔结构在应变前期的能量吸收能力较弱，但在后期增强并超过G–4梯度Voronoi多孔结构，这是由应变后期流动应力的提升引起的，应变后期流动应力的提升则是由内部结构之间的填充接触引起的，而G–4梯度Voronoi多孔结构边界过大的孔隙结构弱化了这种效应。此外，对梯度Voronoi多孔结构的能量吸收效率进行了评估，如图10（b）所示。可知，3种梯度Voronoi多孔结构的能量吸收效率均随着应变的增加而提升，其中，G–4梯度Voronoi多孔结构的能量吸收效率最高，G–3梯度Voronoi多孔结构次之，G–2梯度Voronoi多孔结构的能量吸收效率最低，表明梯度Voronoi多孔结构跨度尺寸的增加明显提升了结构的能量吸收效率。

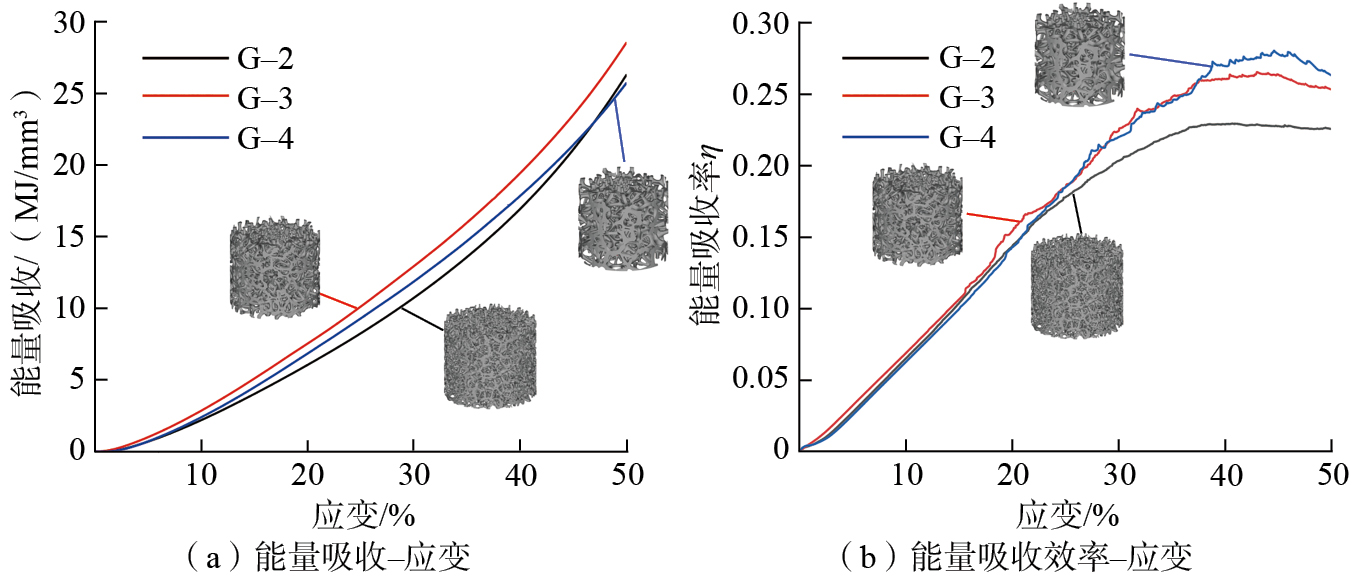
图10　不同跨度尺寸的梯度Voronoi多孔结构能量吸收和能量吸收效率与应变关系曲线

Fig.10　Relationship curves between energy absorption/energy-absorption efficiency and strain of gradient Voronoi porous structures with different spans

因此，Voronoi多孔结构的梯度设计能够调节结构的能量吸收能力和能量吸收效率，通过适当的跨度尺寸调节，能够使Voronoi多孔结构在具备高能量吸收的同时还保持较高的能量吸收效率，如G–3梯度Voronoi多孔结构在保持最高能量吸收能力的同时，其能量吸收效率接近G–4梯度Voronoi多孔结构，这为研究人员使用同等材料获得更高性能的设计提供了参考。

3　结论

（1）Voronoi多孔结构的梯度设计会影响结构的力学性能，3种不同跨度尺寸的梯度Voronoi多孔结构的屈服强度顺序为G–4（22.93 MPa）>G–3（21.82 MPa）>G–2（17.81 MPa），表明梯度Voronoi多孔结构的屈服强度随着跨度尺寸的增加而提升，这是由于更大跨度尺寸的梯度Voronoi多孔结构内部存在更粗的支杆结构，改善了结构的力学强度。

（2）G–3表现出最强的能量吸收能力，这表明适中的跨度尺寸梯度设计可以使梯度Voronoi多孔结构在应变平台阶段和致密化阶段都具备较高的流动应力，从而表现出更强的能量吸收能力。此外，梯度Voronoi多孔结构的能量吸收效率会随着跨度尺寸的增加而提升，区域间的不均匀致密化行为能够提升结构的能量吸收效率。

（3）有限元分析表明，梯度Voronoi多孔结构的内部变形机制相似，变形损伤主要先发生在靠近中心区域的薄弱支杆处，随着应变的增加而扩展到边界的粗支杆。此外，更小跨度尺寸的Voronoi多孔结构会形成更多的局部致密化区域，更小的孔隙和更高的孔隙密度使得内部支杆结构的变形更剧烈，这加剧了结构内部的致密化行为。