近年来航空、汽车等领域对复杂曲面类型的零件加工制造需求愈发旺盛[1]，带动了机械制造技术的革新。复杂曲面的加工方式主要有专用数控机床加工、人工磨抛、机器人磨抛。虽然专用数控机床加工技术成熟，但在加工复杂曲面时存在加工痕迹明显和表面硬化的问题，采用人工磨抛加工时，加工效率和表面一致性难以保证[2]。砂带磨抛加工技术可以大大提高表面一致性，获得更可靠的加工质量，因此被越来越多地应用到复杂曲面制造中[3]。将工业机器人与砂带磨抛加工相结合，不仅可以减轻工人劳力，还大大提高了加工效率。现阶段的机器人砂带磨抛技术还存在诸多问题有待完善，本研究就机器人砂带磨抛的加工精度进行研究，主要探究砂带磨抛工艺参数对复杂曲面表面材料去除深度的影响。
砂带作为一种柔性磨抛加工工具，其特性决定了在使用砂带进行加工时不能固定获得材料去除深度，需要建立机器人砂带磨抛加工的材料去除深度预测模型，即建立材料去除深度与各工艺参数及工件接触表面曲率半径的数学表达式。目前，对于不同磨抛加工系统中材料去除深度模型的研究已有了一定的成果 。早在1972年Preston[4]就提出假设，将速度和压强除外的一切因素（如工件表面粗糙度、工件材料、砂带材料等）的作用全部归为一个比例常数K，可建立材料去除率与压强、瞬时速度的线性关系。Preston 方程作为一个经验性假设，在磨抛去除领域被广泛利用。韩国科学技术院Yang 等[5]就根据Preston 假设提出了材料去除率模型，并通过试验确定了系数K 的值，应用该模型指导加工。张军峰等[6]基于Preston 方程建立百叶轮柔性磨抛材料去除深度预测模型，确定材料去除深度的主要影响因素，并通过模拟仿真和试验验证了模型准确性。朱天宝等[7]基于Preston 方程和Herts 理论，提出了一种复杂曲面磨抛的材料去除模型，分析了材料去除量的影响因素及规律。Wang 等[8]通过分析磨料颗粒和工件表面相互作用，计算参与切削的所有磨粒的去除体积，建立了一种线性工件表面材料去除深度预测模型，并设计试验验证该模型。Zhang 等[9]分析工具与工件表面的几何和机械特性及抛光条件，引入抛光磨损指数，提出基于赫兹分布的材料去除率计算方法。上述方法中均对砂带磨抛加工系统中材料去除深度的预测进行了研究，但对于机器人砂带磨抛系统中材料去除深度预测缺少精确的理论依据，仍需要进一步试验探究。
为了实现对机器人砂带磨抛加工过程中材料去除深度的预测，本文以不同曲率半径的试验件作为研究对象，通过研究砂带磨抛加工不同曲率半径的试验件分析各工艺参数对工件表面材料去除深度的影响规律，并基于多元非线性回归方程建立材料去除深度预测模型。建立的材料去除深度预测模型对机器人砂带磨抛加工系统的磨抛质量尤为重要，通过机器人砂带磨抛加工试验来确定各影响因素与材料去除深度之间的关系，再结合多元非线性回归方程，计算得到机器人砂带磨抛加工材料去除深度预测模型。
1 试验设备与方法
试验材料选用被广泛应用于航空发动机中的镍基高温合金[10]，其化学成分见表1[11]。试验选用金字塔Trizact – 407EA 砂带 （3M 公司），砂带粒度型号包括A20、A60、A110。本研究采用三维扫描仪GOM ATOS Q（8MZEISS 公司）对加工前后的试验件进行扫描，再通过扫描模型对比检测材料的磨抛去除深度，三维扫描仪详细技术参数如表2 所示。通过多次扫描获得的试验件点云数据规模可达千万量级，结合GOM Inspect 软件的点云数据处理能力，在计算截面间距时精确到0.001 mm。
表1 试验材料的化学成分（质量分数）[11]
Table 1 Chemical composition of the test material (mass fraction)[11] %
C Cr Ni + Co Al Ti Fe Nb + Ta Co Mn Si≤0.08 14 ～ 17 ≥70.0 0.40 ～ 1.00 2.25 ～ 2.75 5.00 ～ 9.00 0.70 ～ 1.20 ≤1.00 ≤0.35 ≤0.35
表2 GOM 扫描仪技术参数
Table 2 Technical parameters of GOM scanner
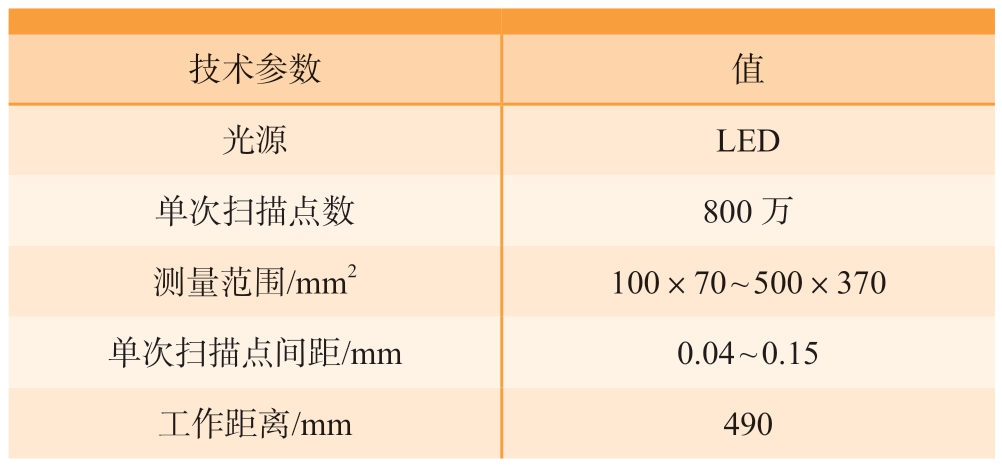
技术参数 值光源 LED单次扫描点数 800 万测量范围/mm2 100×70 ～ 500×370单次扫描点间距/mm 0.04 ～ 0.15工作距离/mm 490
本试验设计搭建了机器人复杂曲面砂带磨抛加工试验平台，如图1 所示。该平台主要由KUKA 机器人、六维力传感器、工控机、三维扫描仪、气动砂带机及试验件组成。平台内可分为力控、打磨、检测3 部分。图2 为系统磨抛力控制流程图，利用安装在砂带机和机器人法兰盘之间的六维力传感器对磨抛过程的接触力进行实时采集，结合团队提出的基于位置的阻抗控制策略[12]，通过对接触力和机器人位姿的修正，实现对磨抛过程中砂带与工件表面接触力的控制。打磨过程为工具型，即打磨工具—气动砂带机固定安装在KUKA 机器人末端，通过工具接近被加工零件，并在其表面按照所规划的路径走刀，结合力控系统实现零件表面的磨抛加工过程。
图1 机器人复杂曲面砂带磨抛加工系统
Fig.1 Robot abrasive belt grinding and polishing system for complex curved surfaces
图2 机器人砂带磨抛接触力控制策略
Fig.2 Control strategy for contact force of robot abrasive belt grinding and polishing
图3 为材料去除深度检测流程图，先利用扫描仪分别建立磨抛前后的三维模型，然后将其输入GOM Inspect 软件进行预对齐及局部最佳拟合对齐，由对齐效果可见，在未磨抛区域的各法向间距测量均为0 附近，接着在磨抛区域创建多个截面进行检测，可输出基于截面曲线的法向间距。为了消除切入切出时接触状态转换带来的影响，数据处理时忽略切入切出段的间距再计算平均数，即可得到材料去除深度。
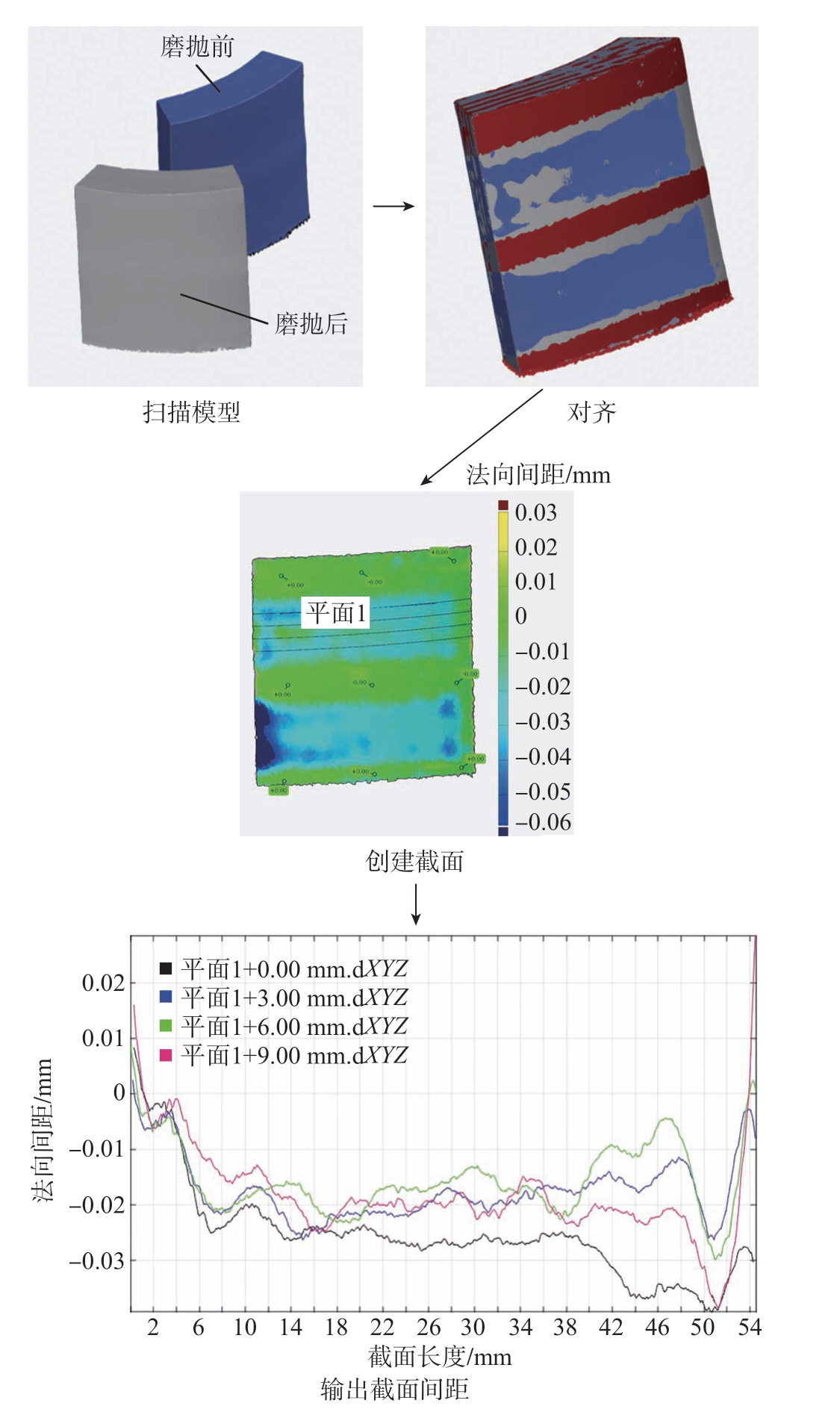
图3 材料去除深度检测流程图
Fig.3 Flow chart of material removal depth detection
2 多工艺参数试验
2.1 磨抛接触区域
对磨抛接触区域砂带与工件的接触力进行分析，如图4 所示。磨抛加工时，需要先标定工具坐标系，设置工具TCP（Tool central point），再对工件表面进行轨迹规划，轨迹点均匀分布在轨迹点上，工具TCP 将会依据轨迹点进行移动。本试验利用气动砂带机打磨杆侧面贴附的橡胶片作为基底与工件接触，由于橡胶片具有良好的弹性，对磨抛加工过程中存在的振动具有一定的抗干扰作用，易于实现高效稳定的磨抛加工，且可以获得较好的表面一致性。在工件与橡胶片接触时，仅对工具TCP 磨抛力分析，磨抛力可以分为垂直于砂带表面的接触力Fn、沿砂带机进给方向的磨抛切削力Fa、沿轨迹切线方向的滑动摩擦力Ft，橡胶片在接触力Fn 作用下发生弹性形变，而工件在砂带磨粒的磨抛作用下发生塑性形变，实现工件表面的材料去除。
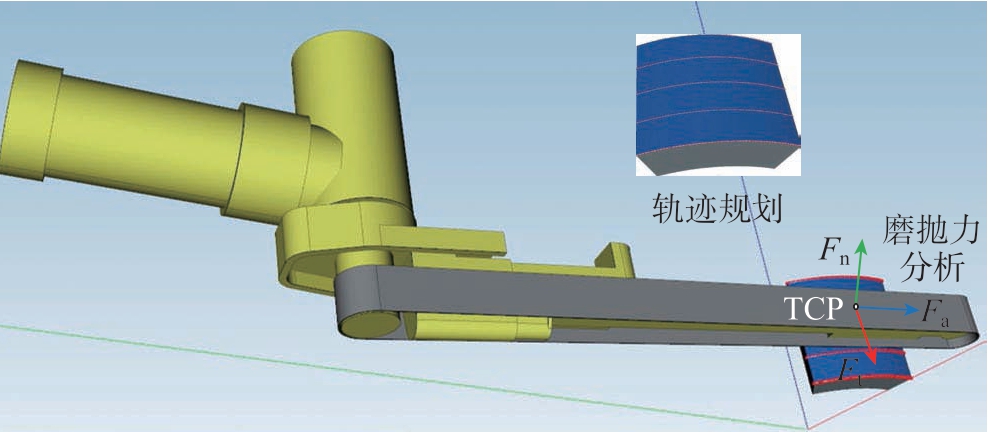
图4 磨抛接触力示意图
Fig.4 Schematic diagram of grinding and polishing contact forces
对砂带机接触不同曲率半径的试验件时砂带与试验件表面的接触情况进行分析，砂带机与试验件接触示意图如图5 所示。
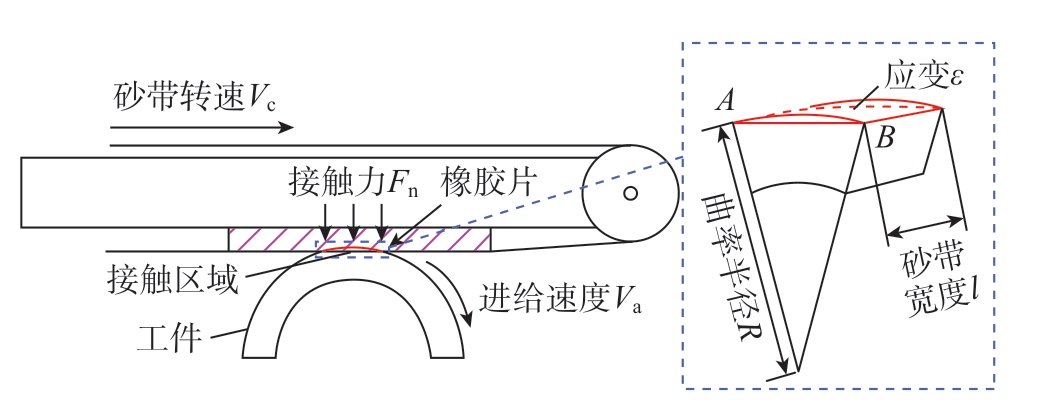
图5 砂带机与试验件接触示意图
Fig.5 Schematic diagram of the contact between the sanding machine and the test piece
在砂带磨抛过程中，曲率半径和接触力的改变主要影响砂带与工件有效的接触长度。将弧长
所需的长度定义为砂带与工件有效的接触长度L。
从运动学角度可得
式中，t 为单个磨粒单转有效接触时间；Va、Vc 为砂带进给速度和砂带转速。
从力学角度计算可得
式中，Fn 为法向接触力；P 为平均压强；l 为砂带宽度。
由式 （3）杨氏模量E 计算公式，根据几何关系可计算橡胶片发生的应变，可得式 （4）。
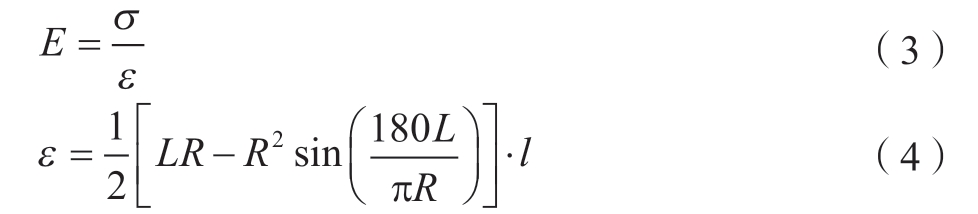
式中，σ 为应力；ε 为应变。
磨抛过程中，由上位机的力控程序对接触力Fn 进行控制并保持基本恒定，即由橡胶片产生的应力σ 保持不变，同时砂带宽度l 也一定，在此基础上综合考虑式（3）和 （4）可以发现，工件曲率半径R 的不同会直接影响到有效接触长度L，再结合式 （1）和 （2）不难看出，曲率半径的变化也会影响砂带机对工件表面的平均压强，从而影响磨粒对表面材料磨削去除作用。综合以上分析，工件曲率半径对磨抛加工存在着一定的影响，需要对其进行进一步的试验研究。
2.2 试验方案设计
在本试验搭建的机器人砂带磨抛加工试验平台中，存在诸多因素影响材料去除深度，其中主要有磨粒特性（磨粒材料及大小）、工件材料及几何特性、磨抛接触力以及砂带机转速和进给速度等。机器人的刚度、重复定位精度及设备固有振动频率等为试验平台的不可控因素，砂带机的供给气压不变，确定转速为9500 r/min，所以暂不考虑砂带机转速对材料去除深度的影响。在保持其他因素不变的前提下，以进给速度、接触力和工件曲率半径为磨抛工艺参数，以材料去除深度作为试验结果进行试验，图6 为试验设备及磨抛后试验件。
图6 试验设备及磨抛后试验件
Fig.6 Experimental equipment and test pieces after grinding and polishing
表3 为同一进给速度Va = 3 mm/s、砂带粒度A60 时，不同曲率半径、接触力得到的材料去除深度试验数据集。表4 为同一接触力Fn = 8 N、工件曲率半径R = 51.6 mm 时，进给速度–材料去除深度试验数据集。
表3 不同曲率半径、接触力得到材料去除深度
Table 3 Material removal depth obtained by diffe ent curvature radii and contact forces μm
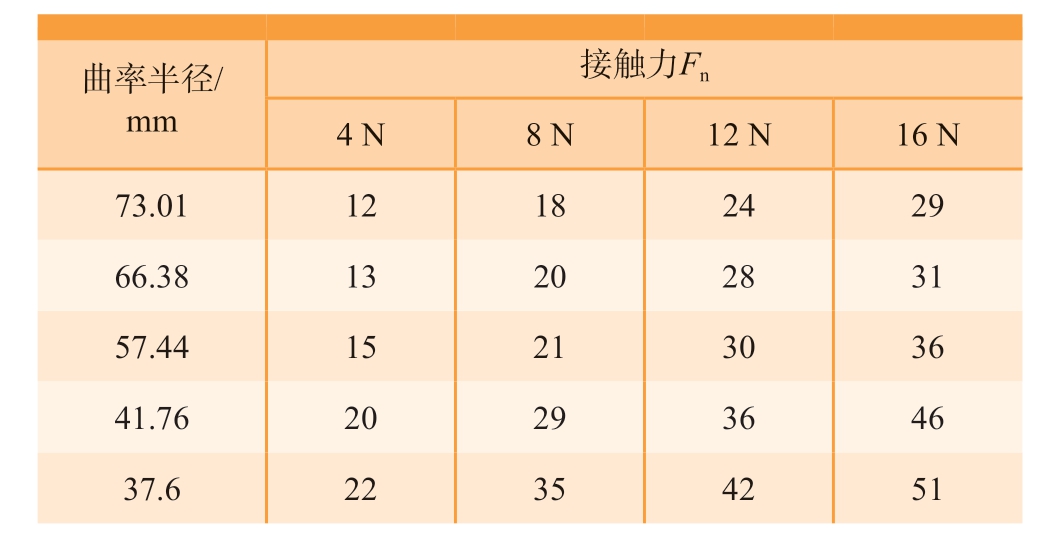
曲率半径/mm接触力Fn 4 N 8 N 12 N 16 N 73.01 12 18 24 29 66.38 13 20 28 31 57.44 15 21 30 36 41.76 20 29 36 46 37.6 22 35 42 51
表4 不同进给速度得到材料去除深度
Table 4 Obtaining material removal depth at diffe ent feed rates
进给速度va/（mm/s） 材料去除深度/μm 均值/μm 误差棒/μm 1.0 60 62 59 60.3 1.814754 1.5 45 45 47 45.7 1.289703 2.5 31 29 32 30.7 1.457166 3.5 23 22 26 23.7 1.625833 5.0 18 17 19 18 1.053565
2.3 试验数据分析
通过表3 和4 试验数据获得材料去除深度曲线，如图7 和8 所示。
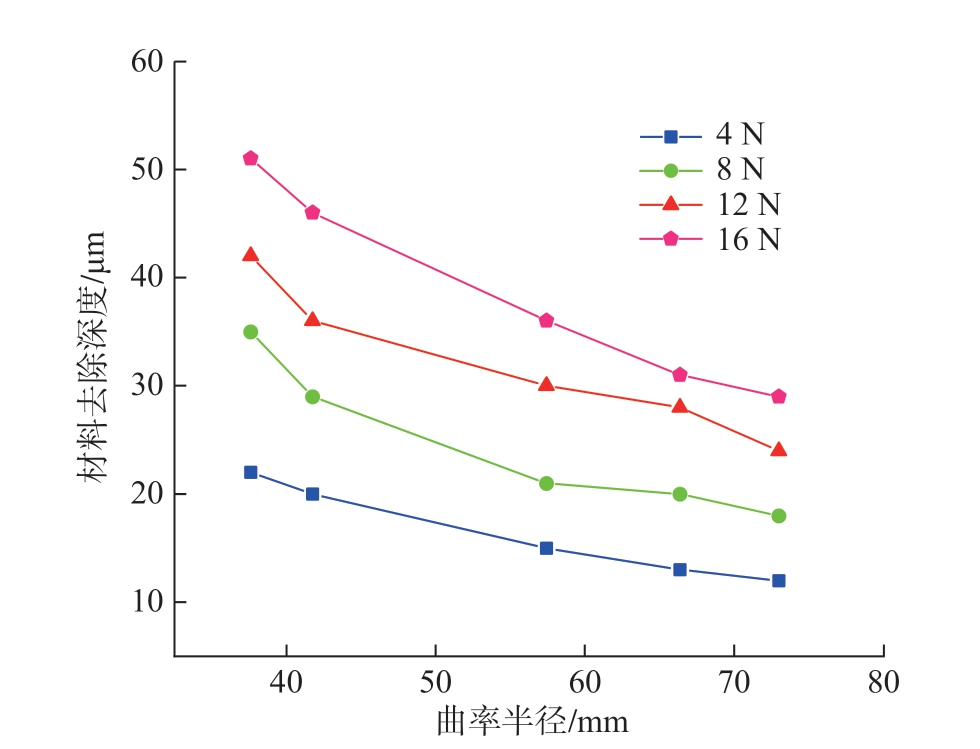
图7 接触力和曲率半径对材料去除深度的影响
Fig.7 Effect of contact fo ce and curvature radius on material removal depth
图7 为接触力和曲率半径对材料去除深度的影响。在同一进给速度Va = 3 mm/s，砂带粒度为A60 的条件下，进行不同接触力和曲率半径参数的试验，得到图7中4 条不同接触力曲线依次由小到大从下往上分布，说明材料去除深度与磨抛接触力呈正相关，即材料去除深度随着磨抛接触力的增大而增大。每条曲线都表示在同一接触力下，去除深度与工件曲率半径的关系，可以看到曲线一致呈下降趋势，则说明了去除深度在一定范围内会随着工件曲率半径的变大而减小。
在磨抛过程中，进给速度也会对材料去除深度产生一定影响，图8 所示为在相同的接触力Fn = 8 N 和工件曲率半径R = 51.6 mm 下，不同进给速度对材料去除深度的影响。试验结果显示，砂带机的进给速度与材料去除深度呈负相关，即进给速度越大，材料去除深度随之减小，且在进给速度逐渐增大的过程中，材料去除深度趋于平缓。
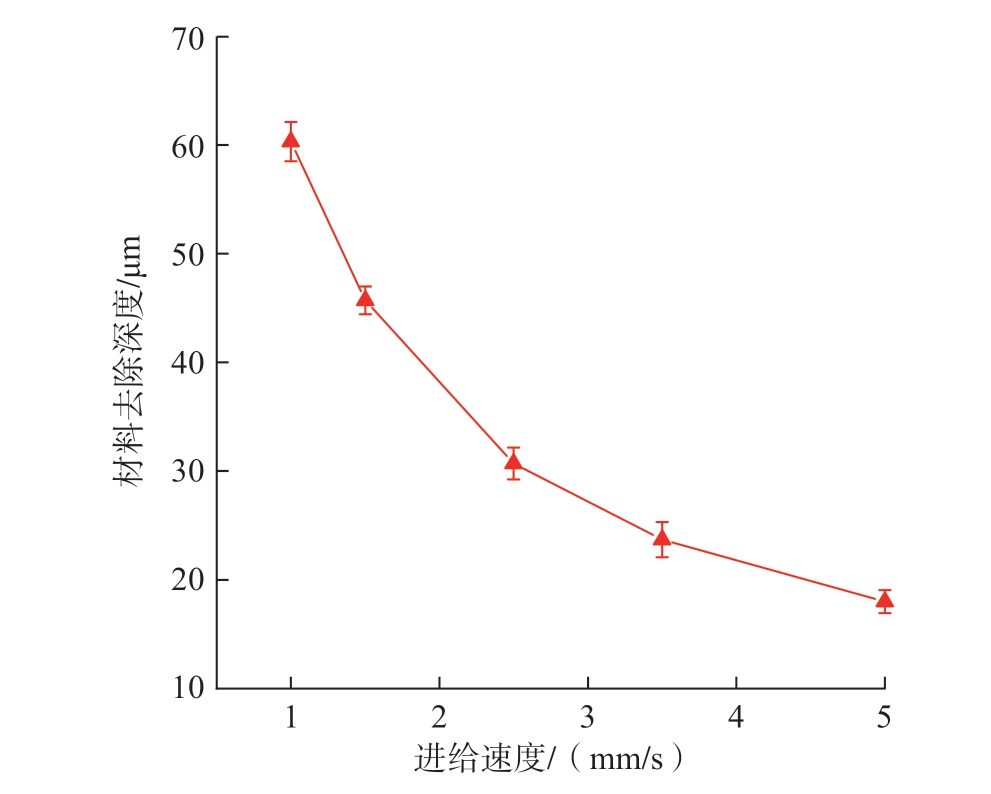
图8 进给速度对材料去除深度的影响
Fig.8 Effect of feed speed on material emoval depth
另外，利用扫描电镜观察磨抛后的砂带状况，可以发现在不同接触力下砂带的磨损情况，如图9 所示。不难发现，随着接触力的增大，砂带的金字塔磨粒磨损情况愈发严重，甚至发生了挤压破碎的现象，因此在设计建立材料去除深度预测模型所需的试验方案中，将只考虑可以有效磨抛产生材料去除的接触力Fn = 4 N、8 N、12 N，避免接触力Fn = 16 N 造成砂带失效。
图9 不同接触力的砂带磨损情况
Fig.9 Abrasion of abrasive belt with diffe ent contact forces
在实际加工中需要依据工件的加工余量进行工艺参数设计，根据上文所述多工艺参数试验数据所得，磨抛加工余量一般在0.05 ～ 0.13 mm。并结合以上磨抛去除规律，在建立材料去除深度预测模型时，设定各影响因素区间与水平数，如表5 所示，其中砂带粒度设为类别预测变量，进给速度、接触力、曲率半径设为连续预测变量，试验方案利用SPSS 软件建立混合正交表，并在机器人砂带磨抛试验平台进行磨抛加工试验。表6 为根据混合正交表进行试验得到的混合正交试验数据集。
表5 影响因素区间与水平数
Table 5 Influencing factor interval and level number
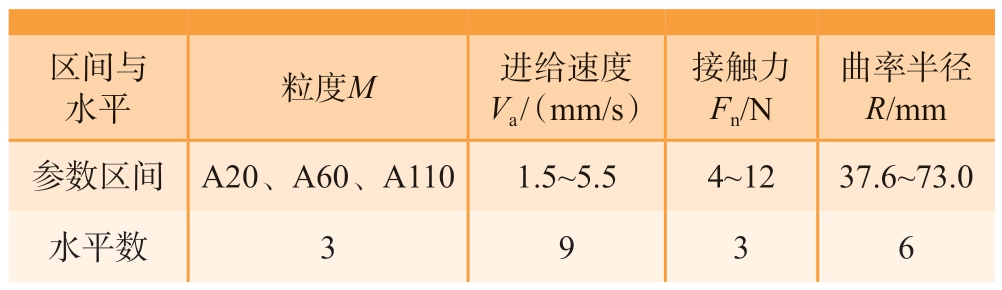
区间与水平 粒度M 进给速度Va /（mm/s）接触力Fn/N曲率半径R/mm参数区间 A20、A60、A110 1.5～5.5 4～12 37.6～73.0水平数 3 9 3 6
表6 混合正交试验数据集
Table 6 Mixed orthogonal experimental data set
试验序号 粒度M 进给速度Va /（mm/s）接触力Fn/N曲率半径R/mm材料去除深度H/μm 1 A20 1.5 12 66.38 23 2 A20 2.5 4 66.38 11 3 A110 3.5 12 51.61 22 4 A60 2.5 4 41.76 24 5 A20 5.5 12 57.44 11 6 A20 4.0 4 66.38 8⋮⋮⋮⋮⋮⋮77 A20 4.5 12 66.38 9 78 A20 2.0 12 73.01 14 79 A60 1.5 12 66.38 44 80 A110 2.5 8 73.01 18 81 A60 2.0 8 66.38 25
3 基于多元非线性回归方程的材料去除深度预测模型
在机器人砂带磨抛试验平台中，影响材料去除深度的工艺参数主要有砂带粒度、进给速度和Z 向接触力。砂带粒度反映了黏附在砂带基材上的磨粒大小，其大小主要影响切削刃的大小。因为在实际生产加工中，砂带粒度是砂带固有的物理特性，具有确切的规格大小，不能作为回归预测模型中的连续变量，因此需要将不同粒度的砂带进行一般分类，即将不同粒度规格的砂带作为类别变量。本研究主要使用A20、A60、A110 3种粒度，可得到对应3 种砂带粒度下的多元非线性回归模型，满足日后在机器人砂带磨抛加工中对材料去除深度的预测及工艺参数的选择，有效提升机器人砂带磨抛加工精度。
根据Cabaravdic 等[13]所提出材料去除深度与工艺参数呈指数关系，确定设砂带粒度为类别预测变量，进给速度、接触力、曲率半径为连续预测变量，材料去除深度为响应，分别建立3 种不同砂带粒度的材料去除深度预测模型，即
式中，H 为材料去除深度；K 为材料去除深度影响系数；β1、β2、β3 为回归参数。
对式 （5）两边取对数，转化成多元线性方程。
设y = lnH，β0 = lnK，x1 = lnVc，x2 = lnF，x3 = lnR
可得
式中，β0，…，β3 为回归参数；x1，…，x3 为回归变量。
设 （xi1，xi2，xi3，yi）T （其中i = 1，2，3，…，81）是 （xi1，xi2，xi3，yi）的81 组观测值，则Y =（y1，y2，…，y81）T，β =（β0，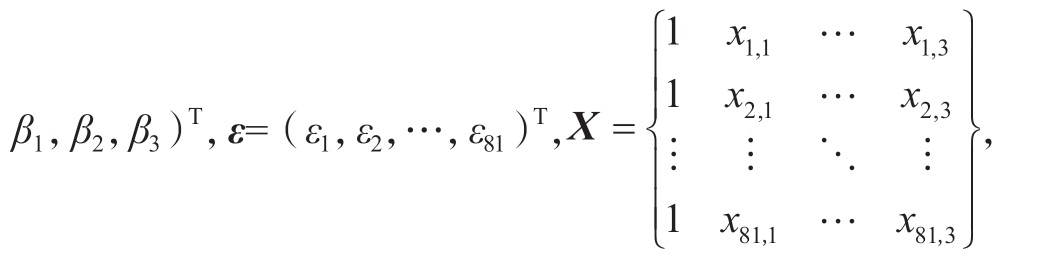
则该矩阵表达式为
利用最小二乘法寻求β 估计值 ，根据式 （8）得
将81 组试验数据分为3 种粒度分别进行取对数处理。再将X 和Y 代入式 （9）中，可以求得
因此，机器人砂带磨抛多元非线性材料去除深度预测模型可以表示为
至此，得到了一个有关于砂带粒度、进给速度、接触力、曲率半径的机器人砂带磨抛曲面材料去除深度预测模型。将预测值与实际测量值进行对比分析，可得图10 所示的去除深度预测值与实际测量值对比。可以看到，利用材料去除深度预测模型得到的预测值和实际测量的去除深度之间的误差在合理范围内。
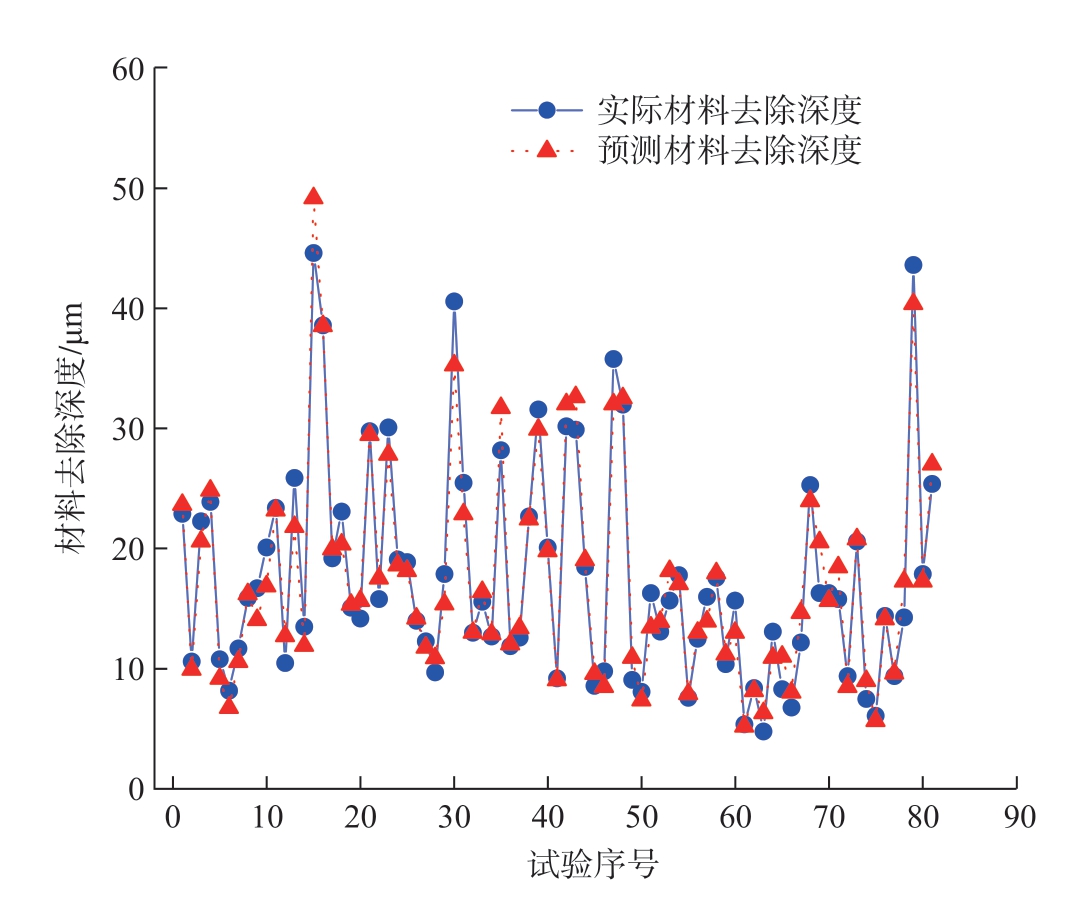
图10 去除深度预测值与实际测量值对比
Fig.10 Comparison between predicted removal depth and actual measured value
对试验数据的误差值和准确率进行分析，如图11所示，误差均值为1.45 μm，误差区间为–5.34 ～ 4.57 μm，计算可得所建立的材料去除深度预测模型的准确率为91.04%，为机器人砂带磨抛材料去除深度控制和预测提供可靠的理论依据。
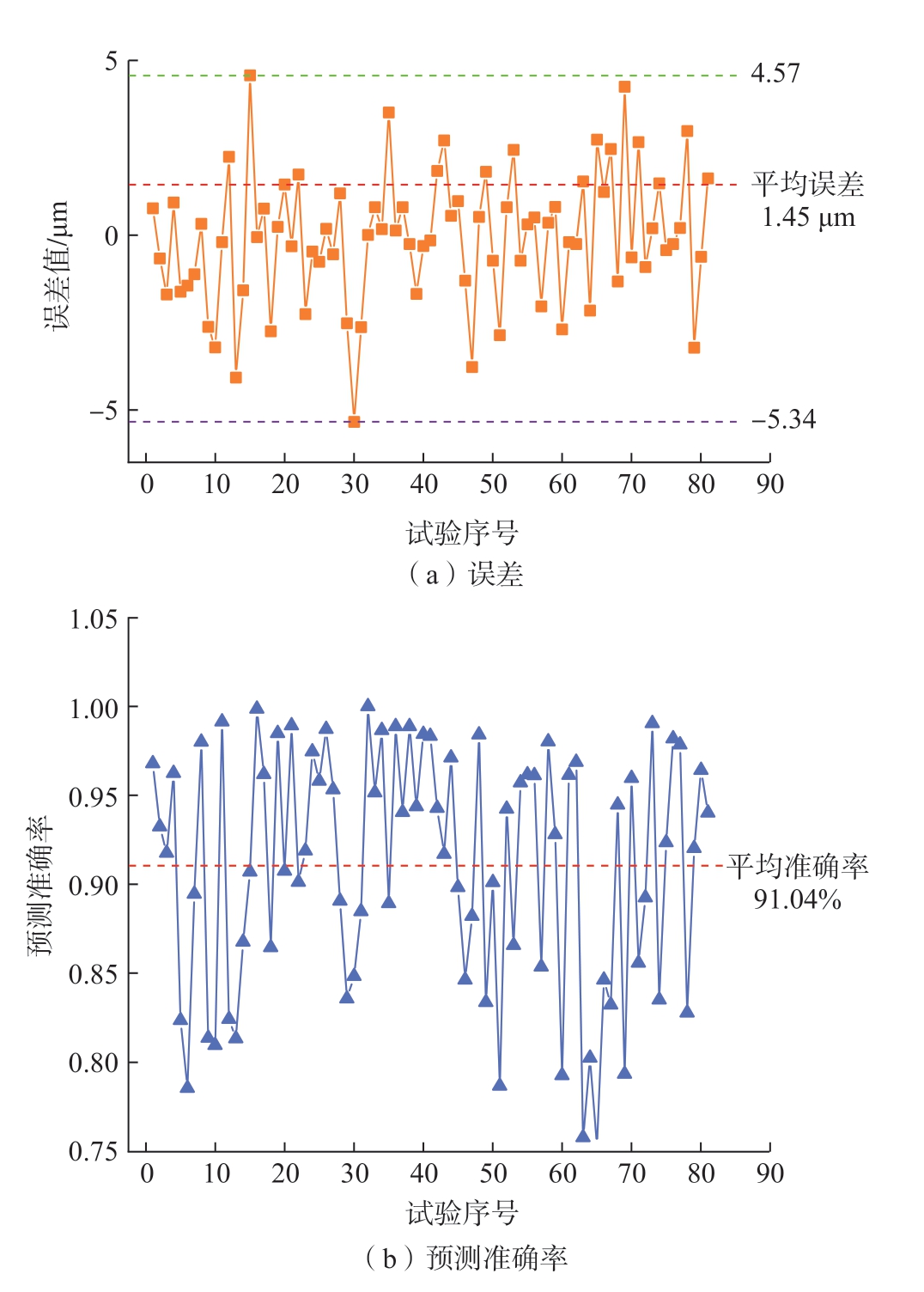
图11 试验数据的误差和预测准确率分析
Fig.11 Error and prediction accuracy analysis of experimental data
4 材料去除深度预测模型回归分析
对于利用混合正交试验数据集建立的机器人砂带磨抛多元非线性材料去除深度预测模型是否能够准确预测材料去除深度与各影响因素之间的关系，不仅仅需要考虑模型的准确率，还需要进行模型的回归分析。本文回归分析采用F 检验法确定预测数据和测量数据是否存在显著性差异，以检验整个方程，即所有影响因素（解释变量）对材料去除深度 （被解释变量）的影响，但F 检验未说明各个影响因素对材料去除深度的影响，所以还需要进行t 检验判断模型是否存在系统误差，即检验单个影响因素对材料去除深度的影响，过程如下。
（1）F 检验。
样本标准偏差S 的平方公式为
式中，n 为样本数；H′为预测值；
为样本均值。
计算F 统计量，即
式中，MSA 为组间方差；MSE 为组内方差。
计 算 得F = 271.13，查F 表 知F0.05（4，∞） = 2.37，F = 271.13 > F0.05（4，∞），所以式 （11）的机器人砂带磨抛多元非线性材料去除深度预测模型没有显著差异，即说明各影响因素材料 （解释变量）适合用于估计去除深度 （被解释变量）。
（2）t 检验。
t 统计量计算公式为
该统计量t 在零假设u = u0 为真的条件下服从自由度为n 的t 分布。
t 检验中，t 值的正负说明该解释变量对被解释变量的影响规律，t 值的绝对值大小反映各解释变量对被解释变量的影响程度。对各工艺参数具体分析可知，进给速度的t 检验为t = – 25.85，意味着进给速度会对去除深度产生显著的负向影响关系；接触力的t 检验为t = 14.19，意味着接触力会对去除深度产生显著的正向影响关系；曲率半径的t 检验为t = –14.09，意味着曲率半径会对去除深度产生显著的负向影响关系。再比较各工艺参数t 值绝对值大小，说明进给速度对材料去除深度的影响最大，接触力和曲率半径对材料去除深度的影响近似一样。
综上所述的F 检验和t 检验结果均符合多工艺参数试验的结论，表明模型不存在自相关性，可用于机器人磨抛加工的工件表面材料去除深度预测。
5 结论
（1）以不同曲率半径的高温合金试验件为研究对象，设计并进行多工艺参数试验，探究机器人砂带磨抛加工的工件表面去除深度的重要影响因素。试验数据表明，进给速度、接触力、工件曲率半径对去除深度影响显著。
（2）根据多工艺参数试验结果分析，结合实际加工情况，优化了工艺参数的设定，从而更加合理地设计混合正交试验，有利于提高材料去除深度预测模型实用性和准确性。
（3）本研究提出了一种包含曲率半径的机器人砂带磨抛加工材料去除深度的预测和控制模型，模型平均预测准确率为91.04%，平均预测误差为1.45 μm，误差区间为–5.34 ～ 4.57 μm，并对模型进行回归分析，结果表明，该预测模型能够很好地预测工件表面材料去除深度。
[1] 于富明. 基于工件曲率的变压力砂带磨削技术研究[D]. 沈阳: 东北大学, 2017.YU Fuming. Research on variable pressure abrasive belt grinding technology based on workpiece curvature[D]. Shenyang: Northeast University, 2017.
[2] 黄云, 肖贵坚, 邹莱. 整体叶盘抛光技术的研究现状及发展趋势[J]. 航空学报, 2016, 37(7): 2045–2064.HUANG Yun, XIAO Guijian, ZOU Lai. Current situation and development trend of polishing technology for blisk[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2045–2064.
[3] 黄云, 侯明明, 刘阳, 等. 航空发动机钛合金叶片机器人浮动砂带磨削技术及其试验研究[J]. 航空制造技术, 2020, 63(5): 14–19.HUANG Yun, HOU Mingming, LIU Yang, et al. Robotic floating belt grinding technology and experimental study on aero-engine titanium alloy blade[J]. Aeronautical Manufacturing Technology, 2020, 63(5): 14–19.
[4] PRESTON F W. The theory and design of plate glass polishing machines[J]. Journal of the Society of Glass Technology, 1927, 11: 214–256.
[5] YANG M Y, LEE H C. Local material removal mechanism considering curvature effect in the polishing process of the small aspherical lens die[J]. Journal of Materials Processing Technology, 2001, 116(2–3):298–304.
[6] 张军锋, 史耀耀, 蔺小军, 等. 基于修正Preston方程的百页轮抛光材料去除深度建模[J]. 中国机械工程, 2022, 33(22): 2711–2716.ZHANG Junfeng, SHI Yaoyao, LIN Xiaojun, et al. Modeling of material removal depth in ABFW polishing based on modified Preston equation[J]. China Mechanical Engineering, 2022, 33(22): 2711–2716.
[7] 朱天宝, 金晓怡, 陈志鹏, 等. 复杂曲面柔性抛光材料去除模型研究[J]. 组合机床与自动化加工技术, 2020(9): 76–79, 83.ZHU Tianbao, JIN Xiaoyi, CHEN Zhipeng, et al. Research on material removal model for flexible surface polishing of complex surfaces[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(9): 76–79, 83.
[8] WANG G L, WANG Y Q, XU Z X. Modeling and analysis of the material removal depth for stone polishing[J]. Journal of Materials Processing Technology, 2009, 209(5): 2453–2463.
[9] ZHANG L, TAM H Y, YUAN C M, et al. An investigation of material removal in polishing with fixed abrasives[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2002, 216(1): 103–112.
[10] 丁文锋, 苗情, 李本凯, 等. 面向航空发动机的镍基合金磨削技术研究进展[J]. 机械工程学报, 2019, 55(1): 189–215.DING Wenfeng, MIAO Qing, LI Benkai, et al. Review on grinding technology of nickel-based superalloys used for aero-engine[J]. Journal of Mechanical Engineering, 2019, 55(1): 189–215.
[11] 刘猛, 李爱民, 张欢欢, 等. 冶炼工艺对GH4145 合金显微组织和力学性能的影响[J]. 中国冶金, 2020, 30(10): 17–21.LIU Meng, LI Aimin, ZHANG Huanhuan, et al. Effect of melting technologies on microstructure and mechanical properties of GH4145 superalloy[J]. China Metallurgy, 2020, 30(10): 17–21.
[12] 李论, 王正佳, 赵吉宾, 等. 整体叶盘研磨抛光机器人接触力阻抗控制方法研究[J]. 航空制造技术, 2022, 65(9): 60–68.LI Lun, WANG Zhengjia, ZHAO Jibin, et al. Research on contact force impedance control method of blisk grinding and polishing robot[J].Aeronautical Manufacturing Technology, 2022, 65(9): 60–68.
[13] CABARAVDIC M, KUHLENKTTER B. Optimizing belt grinding processes: Modeling of the belt grinding process with elastic contact trolley or roller[J]. MO Metalloberflache Beschichten von Metall und Kunststoff, 2005, 59(4): 44–47.