碳纤维增强基复合材料 （CFRP，简称复材）因具有高比强度、高比刚度、耐疲劳、耐腐蚀等优点现已被大量应用于航空工业中[1–5]。由于复材成型精度较差，需要后续通过铣边来达到尺寸精度、装配和表面质量要求[6]。对于大型复材构件的铣边，其尺寸使得传统机床难以胜任，因此通常使用机器人进行铣边加工[7–9]。但机器人本身的弱刚性导致其加工时容易发生颤振，铣边质量下降并影响机器人寿命和精度[10–18]。在多工位铣边大型复材构件时，工件位置固定，机器人站位决定了机器人加工时的位姿，进而决定了机器人铣边时的刚度。因此，在大型复材构件机器人铣边中，站位优化对提升机器人刚度、加工质量、加工效率有重要意义。
对于大型构件，通常采用多工位加工和多机器人加工，这两种方式都须对机器人进行合理的任务分配和站位优化，因此许多学者对机器人任务分配做了大量研究。Zhou 等[19]研究了单机器人路径规划、多机器人任务分配、多工位分配3 个子问题的求解，并基于此提出了利用遗传算法的嵌套迭代优化方法。于乾坤等[20]基于约束和关节可用度指标，建立了关于站位的单点和连续喷涂任务代价函数，并结合内点罚函数法构建了最优站位的求解方法。任书楠等[21]定义了基座可行位置空间，并提出了一种通过基座可行位置空间的交集确定机械臂的停站位置的站位规划方法。陶波等[22]对移动机器人加工动力学进行了理论建模和实验分析，得到了移动机器人加工的动力学特性，并设计了一种用于恒力匀速磨抛加工的Takagi – Sugeno（T – S）模糊控制器。
为综合考虑机器人弱刚性和大型复材构件机器人站位对铣边加工的影响，本文将结合其他学者对机器人刚度的研究成果，建立一种与机器人站位相关的刚度指标函数，再以刚度指标和空间可达性为依据进行机器人铣边任务分配，并以此为基础利用站位优化算法对机器人的站位进行优化计算。最后搭建机器人铣边平台，开展相关试验以验证站位优化对铣边质量的影响。
1 机器人运动学和刚度模型
1.1 机器人运动学模型
为计算机器人末端刚度，使用标准Denavit-Hartenberg（D-H）参数法建立机器人运动学模型，构建机器人运动学逆解的求解方法。KUKAKR500 机器人为六自由度关节型机器人，加工范围为1200～2830 mm，运动关节为回转型，对此机器人进行标准D-H 参数建模[23]。按照标准D-H 参数法建立机器人各连杆坐标系，如图1 所示，并确定机器人各连杆参数，如表1 所示。
表1 标准D-H 模型参数
Table 1 Parameters of standard D-H model
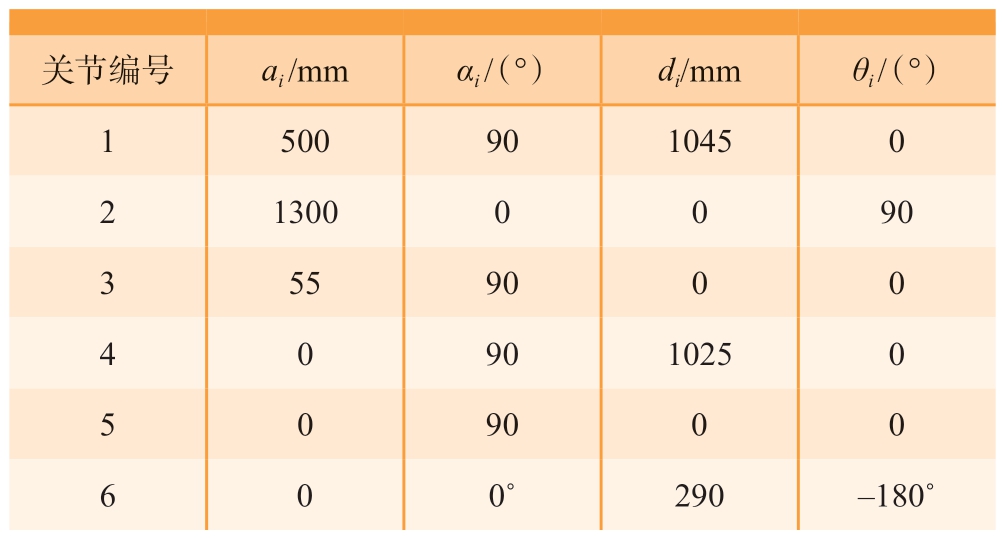
关节编号 ai /mm αi /（°） di/mm θi /（°）1 500 90 1045 0 2 1300 0 0 90 3 55 90 0 0 4 0 90 1025 0 5 0 90 0 0 6 0 0˚ 290 –180˚
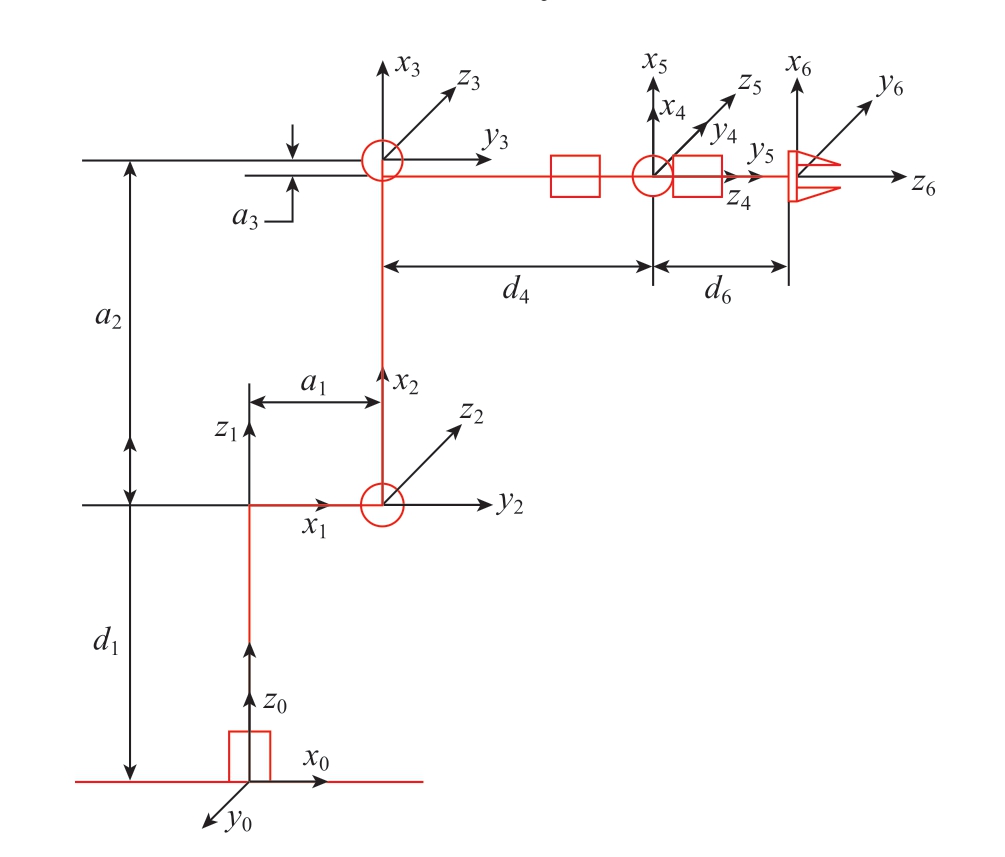
图1 机器人D-H 模型
Fig.1 Robot D-H model
在标准D-H 参数机器人模型中的关节坐标变换矩阵[23–24]为
式中，Rot 为坐标旋转矩阵；Trans 为坐标平移矩阵；z 和x 为旋转轴；θ 为关节转角；a 为连杆长度；α 为连杆扭转角；d 为连杆偏距。
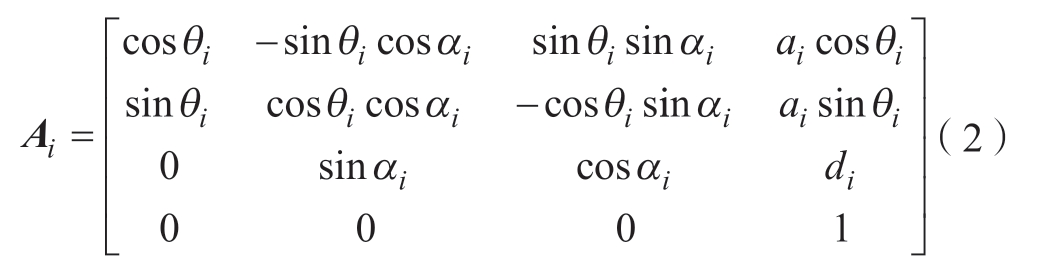
对每个关节坐标系进行连续变换可以得到从基坐标到末端坐标的坐标变换公式，即
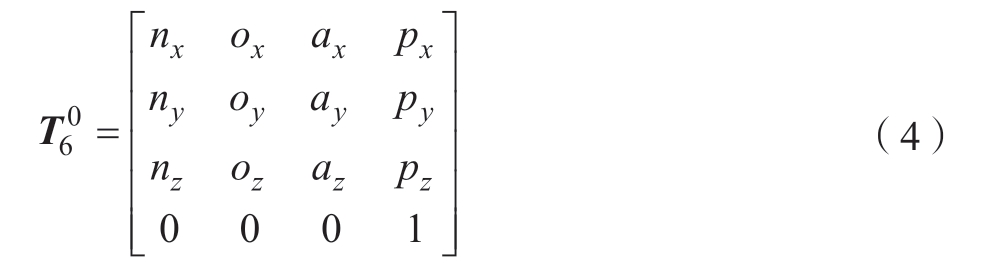
式中，
即为机器人的运动学正解。
由于工位优化为离线优化，无响应时间的要求，且需要考虑机器人的路径规划和任务分配以及路径中每个点位的刚度情况，同时为保证机器人关节角不发生剧烈变化，需要对每个关节角的变化幅度加以约束。根据以上考虑，选择使用数值解求运动学逆解。
设Ptarget 为机器人末端的目标位姿，θtarget 为目标位姿下的机器人关节角且满足
设θ0 为初始估计值，θ 逐渐逼近θtarget，则对f（θ）在θ0 处进行泰勒展开，可得
式中，θ0 处的雅可比矩阵
。令Δθ = θ – θ0，保留至第一阶，并假设J（θ0）可逆，可得
由Newton-Raphson 法可得
令
将θ1 重新代入并重复上述过程，产生一系列θ 值{θ0，θ1，θ2， …}，并最终收敛于θtarget 处，在实际使用中，迭代过程会在满足设定的阈值ε，即| g（θk）– g（θ k+1）| / | g（θ k）|≤ε 之后停止，将此时的结果作为最终解[25]。
1.2 机器人刚度模型
对于串联机器人，其刚度模型为
式中，K 为机器人笛卡儿刚度矩阵；Kθ为机器人关节刚度矩阵；Jθ为机器人雅可比矩阵。
由于机器人末端所受力矩和实际的扭转变形较小，因此此处只考虑位移变形d 和末端受力f 之间的关系。
假设末端受到大小为一个单位的力作用时，则有
式 （12）描述的是三维空间中的一个椭球面，其随机器人位姿变化而变化，称为刚度椭球。其物理意义是该椭球面上沿给定方向的轴长反映该方向上的刚度大小，如图2 所示。
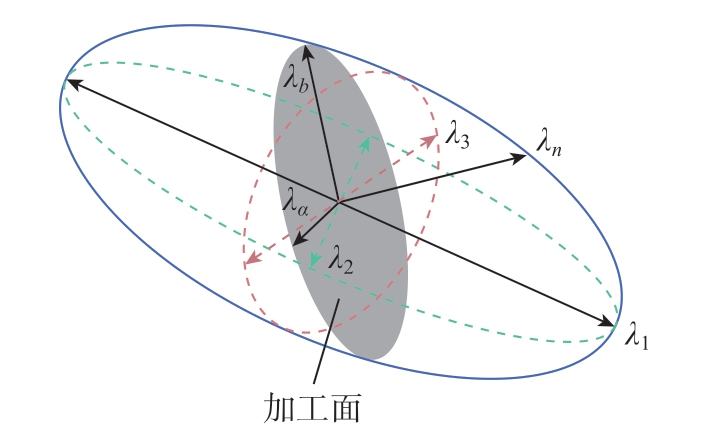
图2 刚度椭球
Fig.2 Stiffness ellipsoi
由于机器人铣削加工时表面质量受多个方向刚度的综合影响，需要选用能够综合反映机器人刚度性能的指标，由于刚度椭球的体积V 与刚度椭球3 个轴长的乘积相关，能够表征机器人的综合刚度性能。
因此将刚度性能指标ka 确定为
1.3 刚度函数
由于工件的几何形状和摆放位置已经确定，机器人原点和工件加工点的相对位置只和机器人在第7 轴上的位置相关，因此机器人末端位姿P、机器人原点在第7轴上的距离L、机器人关节角θ 之间的映射关系为
刚度矩阵与机器人雅可比矩阵相关，可表示为
Jθ为关于关节角θ的函数，若工件上的目标点固定，则刚度指标ka 可表示为
第7 轴上的每个机器人站位，即机器人原点至第7轴原点的距离可定义一个集合{X1，X2，X3，…，Xn}，在Xn 站位下，机器人刚度指标可表示为
对于每个Xn，寻找在其站位下整个工件轮廓中的刚度指标最小的值作为该站位的刚度评价值。
2 机器人铣边站位优化
2.1 机器人加工任务分配
对于机器人站位构成的集合P{X1，X2，X3，…，Xn}中的每个元素Xn，需要对应的分配加工任务，设Wi 为工件上的某一点，若Wi 与Xn 的距离L 与机器人加工范围R满足
则Wi 被视为该位置下的可加工点。
所有待加工点Wi{X，Y，Z}构成一个集合W{W1，W2，W3，…，Wn}，W 也可视为一个3×m 的矩阵W，计算该矩阵中所有点到Xn 站位下机器人原点On 的距离，得到一个距离矩阵Dn。
之后判断每个点位是否位于该站位下的可加工范围内。
之后对
进行逻辑运算，由于判断时只须考虑元素的正负，因此对其作简化，将
中所有负值视为0，所有非负值视为1。矩阵
中的0 表示对应的点位无法被加工，1 表示可以被加工。对于Pi 中所有站位Xn，分别计算对应的
，并对所有
进行或运算获得逻辑矩阵Ω。Ω 中若存在0 值，则W{W1，W2，W3，…，Wm}中存在当前Pi 中所有站位Xn 下都无法加工的点，即该站位组合Pi 无法满足可达性要求；当Ω 中不存在0 值时，则Pi 满足可达性要求，将Pi 作为可选站位组合，并将每个站位Xn 下的可达点位保存为Wn。
存在某些点Wi同时处于多个站位的可达范围内时，先将其搁置，待其他点位处理完毕后，需要对其进行如下判断以确定该点位所属的加工站位：
（1）选择一个距离已分配点位最近的未分配点位；
（2）寻找距离该未分配点位最近的已分配点位；
（3）将该未分配点位分配至找到的已分配点位所属的站位；
（4）重复步骤 （1）～（3），直至所有点位分配完毕或超出可达范围分配失败。
2.2 优化算法
工位优化的目标是获得使整体刚度最大化的机器人站位。首先，对于Pi 中的每个站位Xn，按照机器人可达性分配在该站位下的所有工件加工点位Wm，并将其储存到机器人可加工点位中Winm = Wm，在每个站位都分配完成后检查是否已分配所有工件加工点位，若结果为否，则对下一个Pi 进行相同操作，若当前Pi 都无法满足要求，则令n = n + 1 并重新生成Pi，重复上述计算直至满足要求；之后，对Winm 中的每个点位求逆解，获得机器人关节角，并计算机器人末端刚度指标，将所有点位Winm 中的最低刚度作为此站位Xn 下的刚度，再将所有站位{X1，X2，X3，…，Xn}中的最低刚度作为Pi 的刚度；最后，以Pi 的刚度最大为指标进行优化，获得使刚度最大的Pi，作为最终优化结果。站位优化流程如图3 所示。优化过程的伪代码如图4 所示。
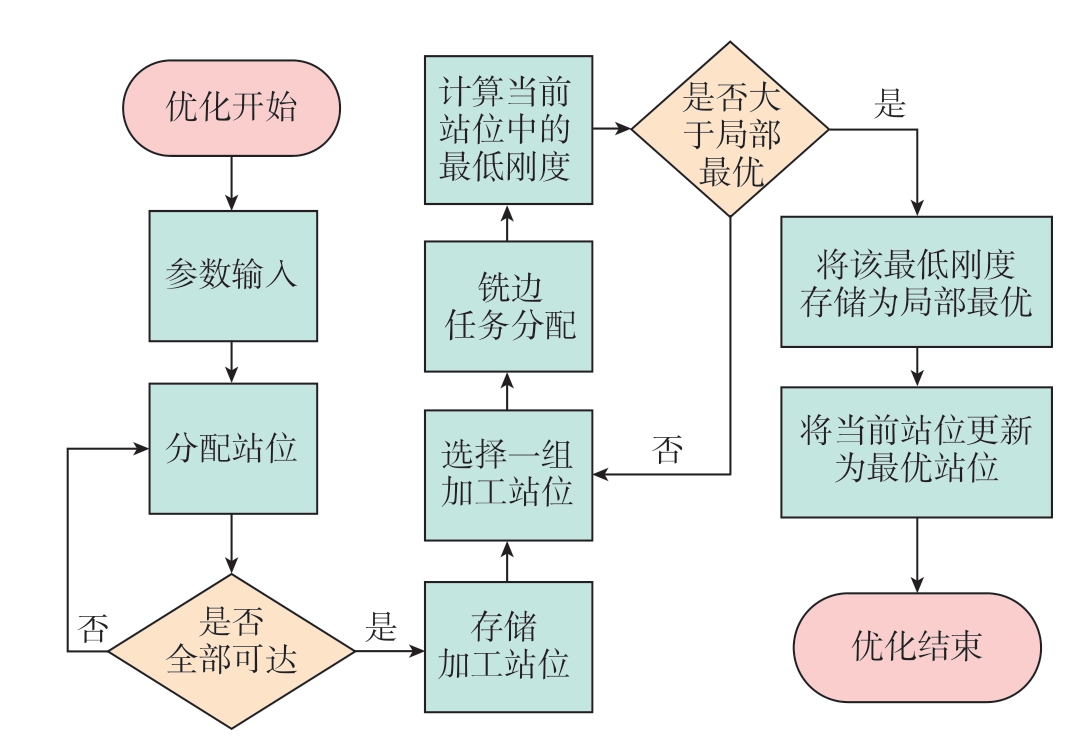
图3 站位优化流程
Fig.3 Station optimization process
图4 站位优化算法
Fig.4 Station optimization algorithm
2.3 站位优化结果
为验证所提优化算法的有效性，对大型工件的轮廓简化模型进行站位优化。首先对工件站位分配进行预处理，将工件轮廓抽象为加工点位的集合，如图5 所示，并根据机器人工作空间对其进行站位的可达性判断，筛选出可行的工位组合。机器人的原始站位如图6 所示。
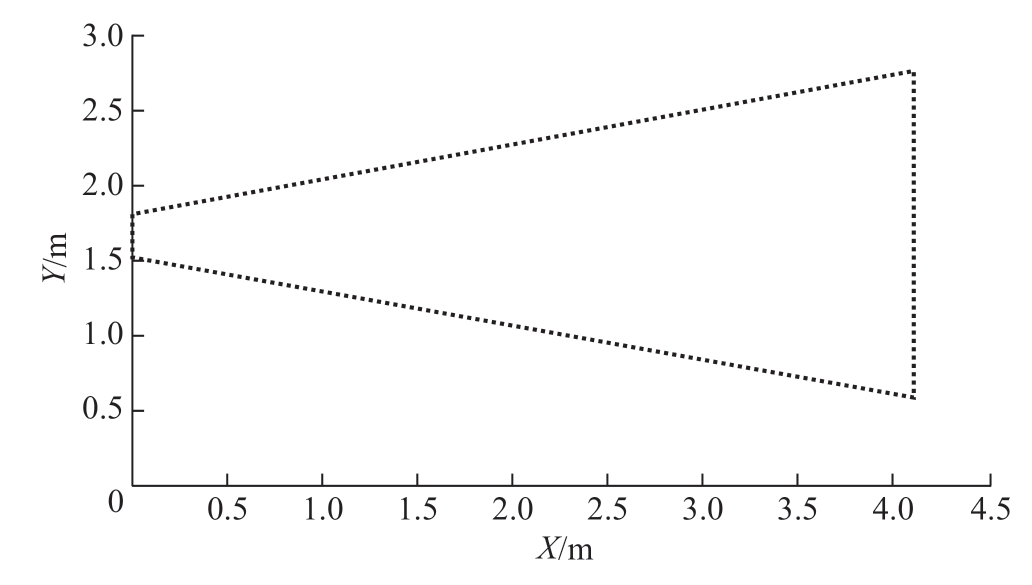
图5 工件轮廓点位
Fig.5 Workpiece contour point position
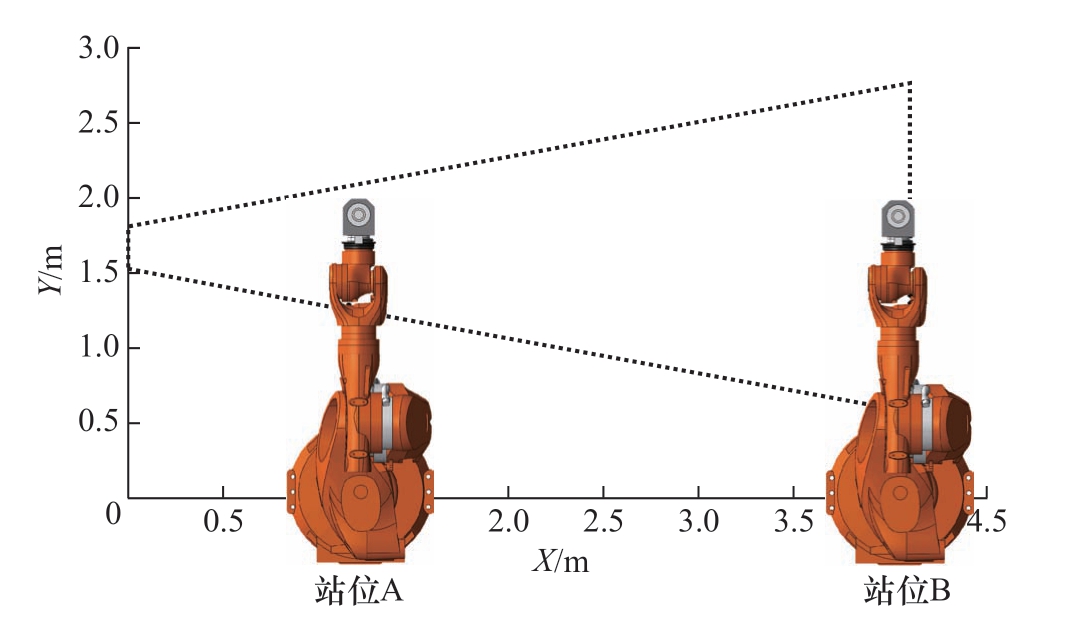
图6 机器人原始站位分配
Fig.6 Robot original station assignment
在第7 轴上间隔0.1 m 取一个站位，组成原始的站位空间。在站位空间中，Z 轴上的一个点表示一组机器人站位组合，而工件作为一个二维流形在Z 轴方向上叠加。对每个站位上的加工点位进行可达性检验，由此获得初始站位空间和工件加工点位分布，如图7 所示。
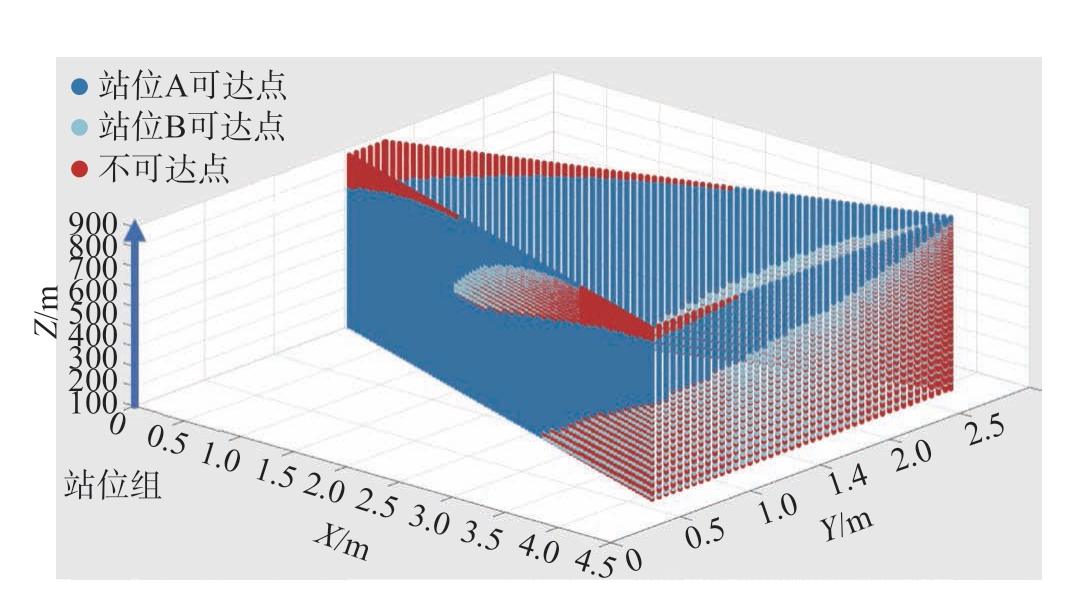
图7 原始站位空间
Fig.7 Original station space
根据机器人工作空间范围和工件尺寸，筛选出初始站位组合空间中满足机器人空间可达性要求的站位组合，将其作为可达站位空间，如图8 所示。
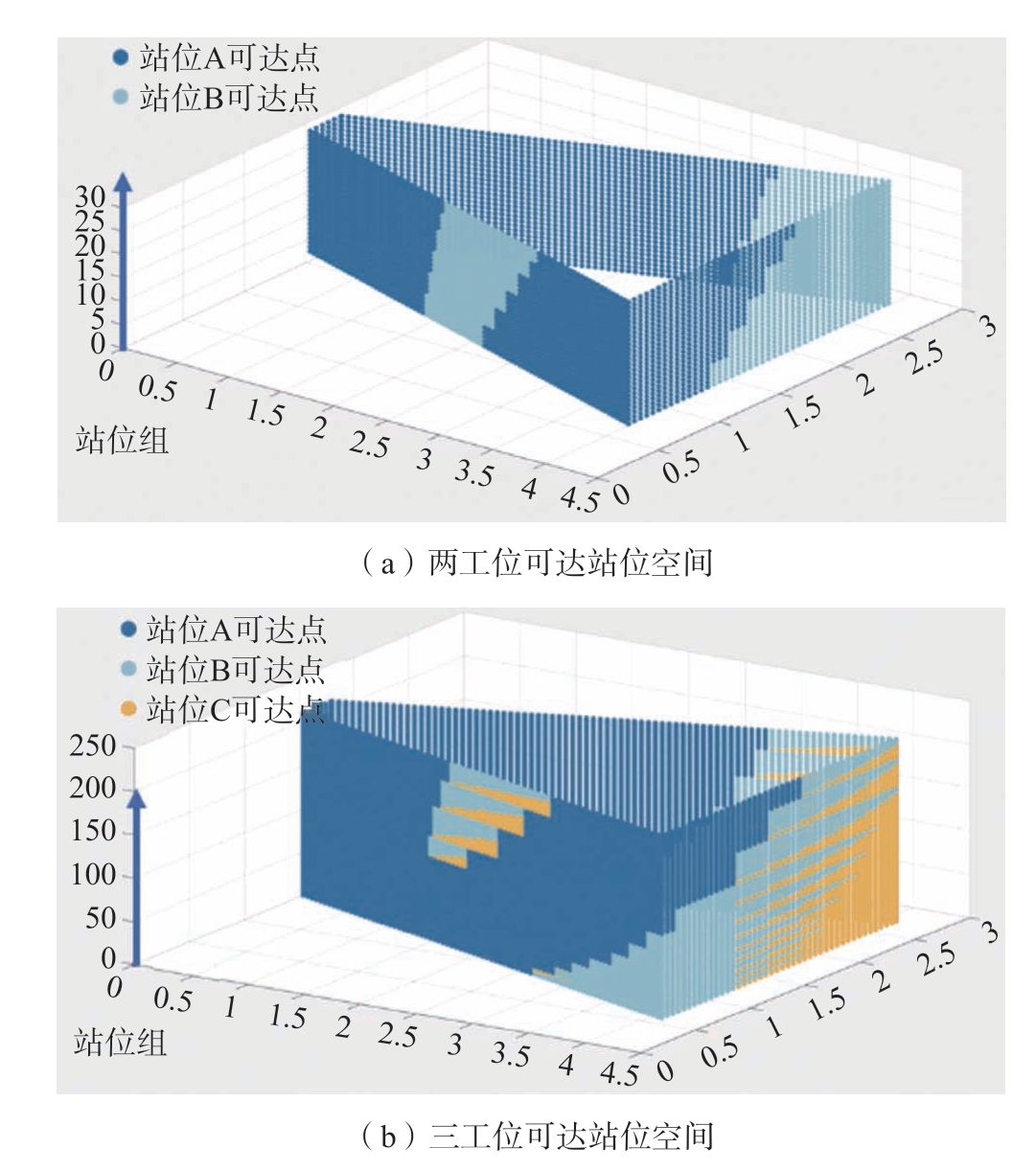
图8 可达站位空间
Fig.8 Reachable station space
由可达性筛选出的可行站位组合，并根据由刚度函数计算所得刚度指标进行优化，获得使整体刚度最优的站位组合，如图9 所示，站位优化结果为 （2.1，3.9），即两个工位中，一个工位位于第7 轴上距原点2.1 m 处，另一个位于3.9 m 处。
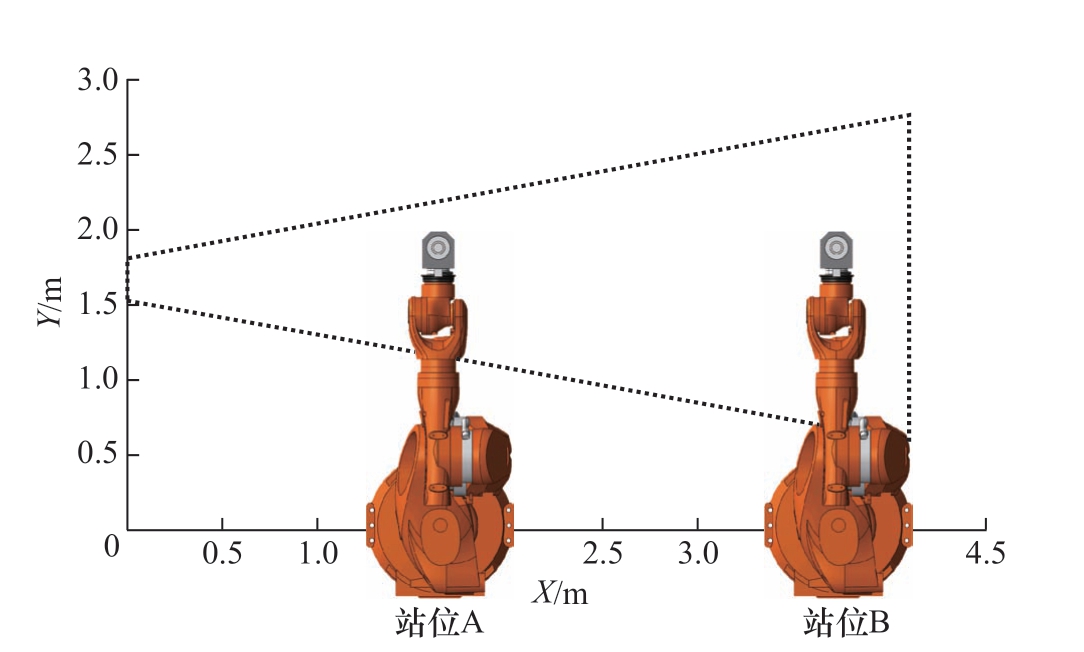
图9 刚度优化站位
Fig.9 Stiffness optimization statio
进行不同站位的加工任务分配，结果如图10 所示。
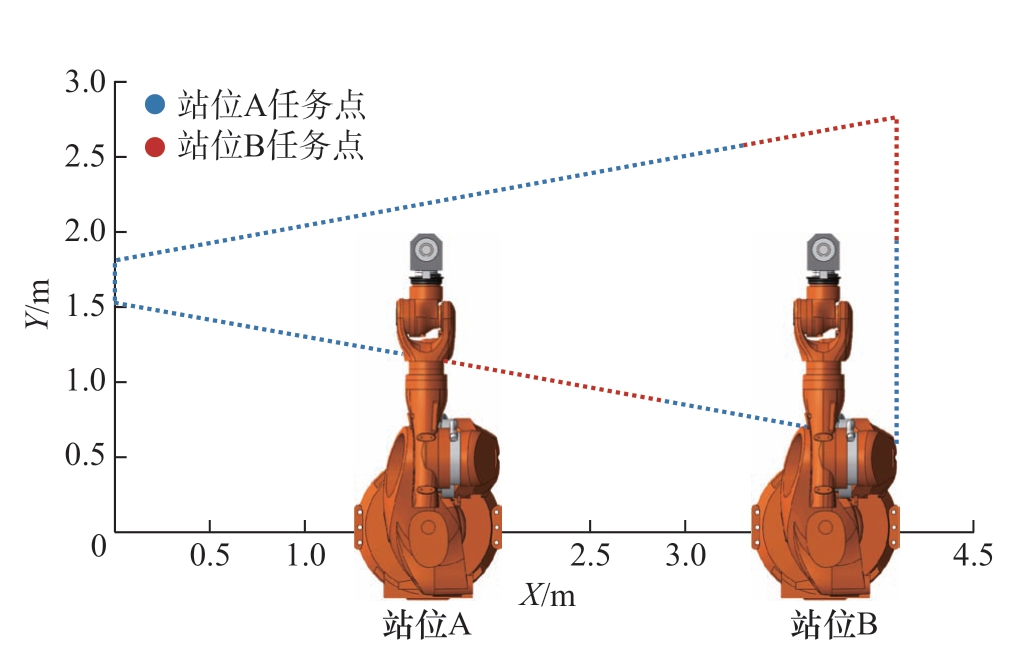
图10 多站位任务分配
Fig.10 Multi-station task allocation
3 站位优化效果试验
选择3 个固定的工件位置，并分别计算优化前和优化后的站位中加工这3 个位置时的位姿和刚度情况，以验证站位优化对机器人加工刚度的改善效果。站位优化后，机器人原点位置改变而工件位置不变，因此机器人铣边时的位姿发生改变，如图11 所示。铣边站位优化前后的位姿和刚度如表2 所示，与优化前的刚度相比，优化后3 个位置的刚度分别提升27.4%、33.0%、26.4%。
表2 机器人的位姿和刚度
Table 2 Robot posture and stiffnes
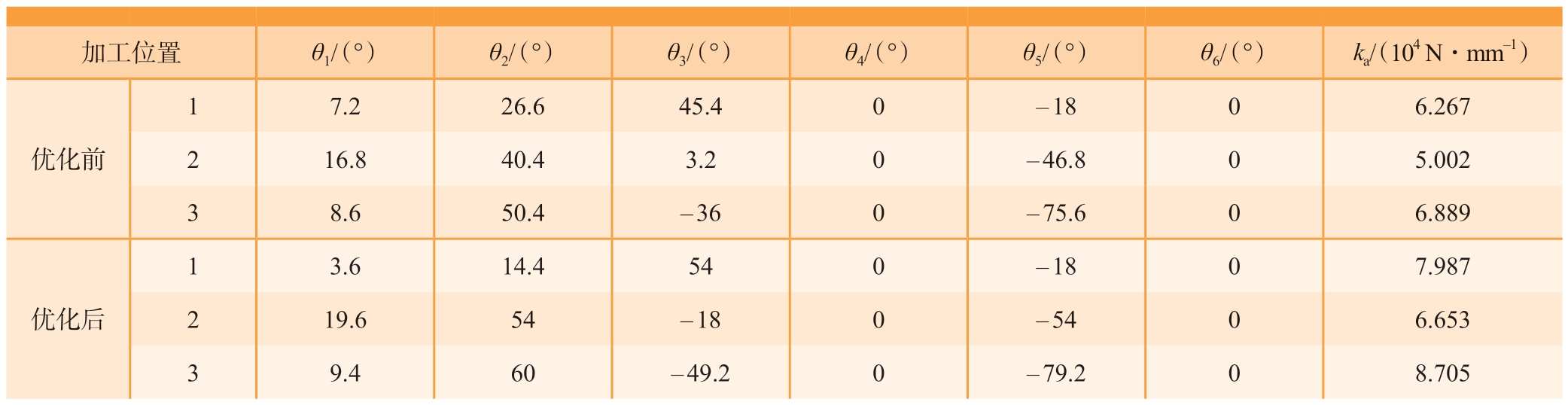
加工位置 θ1/（°） θ2/（°） θ3/（°） θ4/（°） θ5/（°） θ6/（°） ka/（104 N·mm–1）优化前1 7.2 26.6 45.4 0 – 18 0 6.267 2 16.8 40.4 3.2 0 – 46.8 0 5.002 3 8.6 50.4 – 36 0 – 75.6 0 6.889优化后1 3.6 14.4 54 0 – 18 0 7.987 2 19.6 54 – 18 0 – 54 0 6.653 3 9.4 60 – 49.2 0 – 79.2 0 8.705
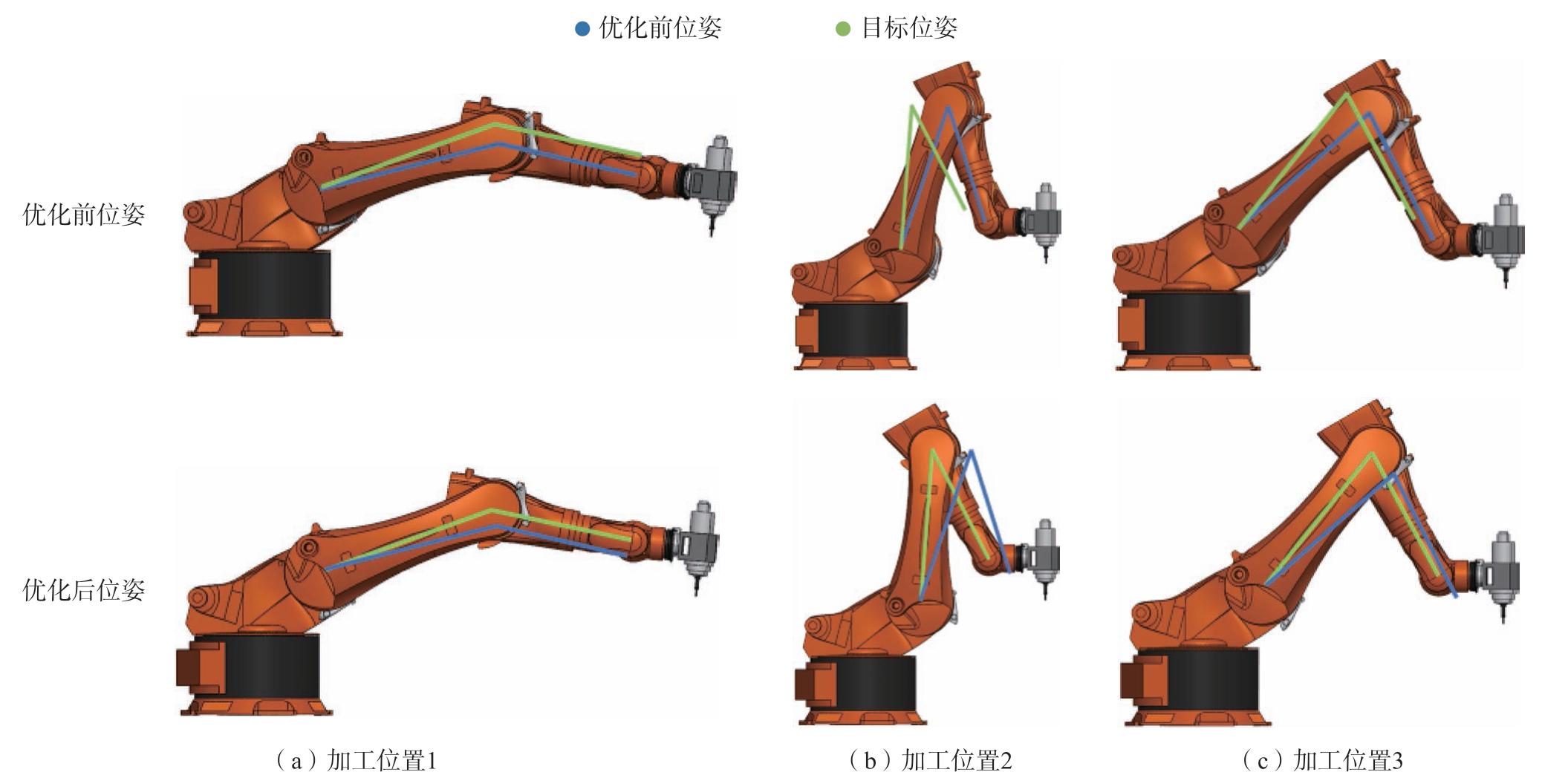
图11 优化前后位姿
Fig.11 Posture before and after optimization
为验证实际工况下的优化效果，设计了铣边加工验证试验。加工机器人为KUKA– KR500–R2830 机器人，超声加工系统由超声刀柄和超声电源组成。试验中，通过调节超声电源的输出电流来实现超声振幅的调节，铣边刀具为美福D8–PCD 两刃立铣刀，工件夹持方式为螺纹装夹，通过M6 螺丝将CFRP 工件固定于工装台上。机器人内置的末端测力仪为9105– NET– Omega160 型六轴力/扭矩传感器 （ATI 公司），用于测量铣边加工时的铣削力状态。在机器人末端搭载的电主轴上安装PCB–356–A15 型三轴加速度传感器，用以测量加工时的机器人状态。本试验所用试件为CFRP 薄板件，采用双向交织铺层，铺层角为90°，工件尺寸为300 mm×400 mm×4 mm。试验加工现场如图12 所示。
图12 铣边加工试验设备
Fig.12 Milling edge processing experimental equipment
对优化前后的机器人加工情况进行试验对比。选取一组普通站位与最优站位进行对比，如图13 和图14所示，在其他加工条件一致的情况下对两种站位下铣边的铣削力和铣边质量进行对比。
图13 站位优化前机器人铣边加工位姿
Fig.13 Robot edge-milling processing position before station optimization
图14 站位优化后机器人铣边加工位姿
Fig.14 Robot edge-milling processing position after station optimization
机器人铣边加工试验中的位姿信息如表3 所示。
表3 铣边加工试验中的机器人位姿
Table 3 Robot posture in milling edge processing test （°）
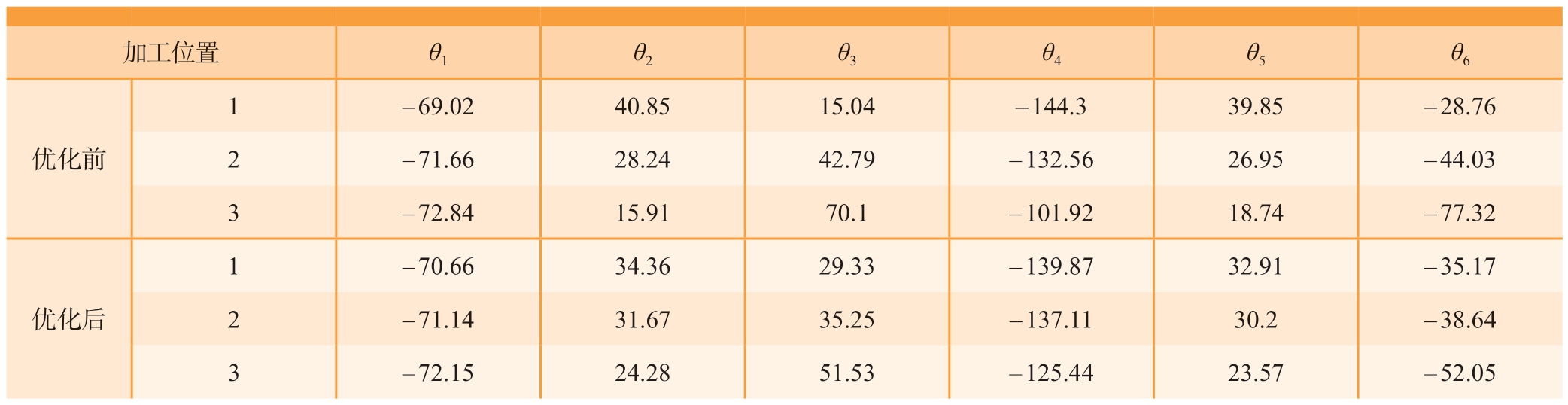
加工位置 θ1 θ2 θ3 θ4 θ5 θ6优化前1– 69.02 40.85 15.04 – 144.3 39.85 – 28.76 2– 71.66 28.24 42.79 – 132.56 26.95 – 44.03 3– 72.84 15.91 70.1 – 101.92 18.74 – 77.32优化后1– 70.66 34.36 29.33 – 139.87 32.91 – 35.17 2– 71.14 31.67 35.25 – 137.11 30.2 – 38.64 3– 72.15 24.28 51.53 – 125.44 23.57 – 52.05
图15 和图16 分别为站位优化前后的铣削力。通过对比可以发现，站位优化前后铣削力由700 N 降至500 N 以下，下降约28.6%，证明站位优化能够减小铣边加工时的铣削力。
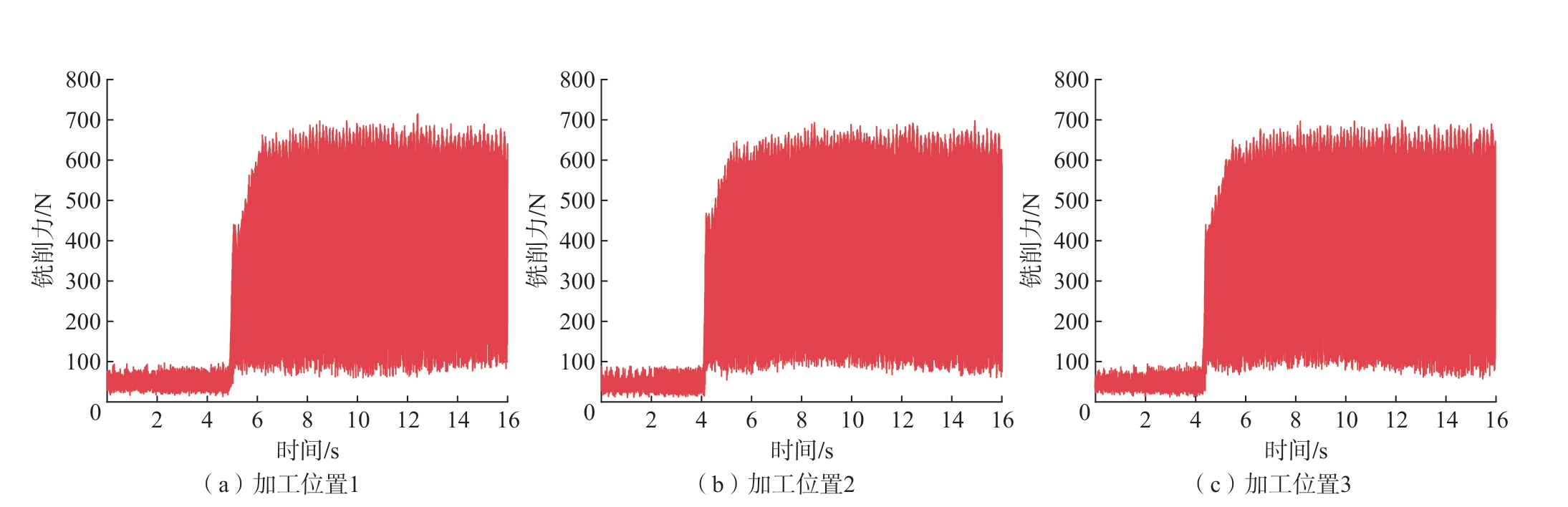
图15 站位优化前铣削力
Fig.15 Milling force before station optimization
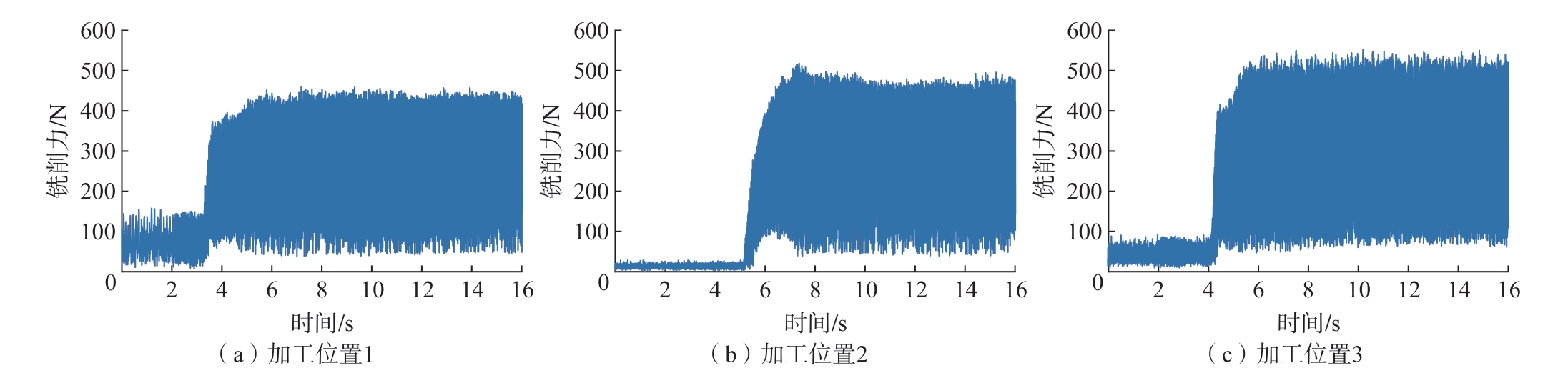
图16 站位优化后铣削力
Fig.16 Milling force after station optimization
利用激光显微镜对6 个位姿下机器人CFRP 铣边加工获得的样件进行表面粗糙度的观测，如图17 所示，获得的结果如图18 和图19 所示。试验结果表明，加工站位优化可使加工质量提升33%以上，证明所提基于刚度的站位优化能够使机器人加工效果明显提升。
图17 样件观测设备
Fig.17 Sample observation equipment
图18 站位优化前铣边质量
Fig.18 Edge-milling quality before position optimization
图19 站位优化后铣边质量
Fig.19 Edge-milling quality after position optimization
4 结论
提出了一种基于刚度的机器人铣边站位优化方法，该方法可用于机器人铣边加工大型CFRP 构件。提供了一种基于空间可达性的站位规划方法和一种基于刚度的站位优化方法和任务分配方法，并通过试验验证了方法的有效性，得出结论如下。
（1） 基于机器人静刚度模型建立了一种与机器人站位相关的刚度函数，并基于此函数和空间可达性进行了机器人铣边任务分配。
（2） 通过站位优化改变了机器人铣边时的位姿，使机器铣边时的刚度提升20%以上，并通过铣边任务分配算法保证了铣边任务的连续性。
（3） 刚度的改善使铣边加工时的铣削力降低了28%以上。刚度的提高和铣削力的降低改善了最终的铣边质量，试验证明，相比优化前，基于刚度的机器人铣边站位优化能够使铣边质量提升33%以上。
[1] 廖文和, 郑侃, 孙连军, 等. 大型复杂构件机器人加工稳定性研究进展[J]. 航空学报, 2022, 43(1): 156–175.LIAO Wenhe, ZHENG Kan, SUN Lianjun, et al. Review on chatter stability in robotic machining for large complex components[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(1): 156–175.
[2] 董松, 郑侃, 孟丹, 等. 大型复杂构件机器人制孔技术研究进展[J]. 航空学报, 2022, 43(5): 23–40.DONG Song, ZHENG Kan, MENG Dan, et al. Robotic drilling of large complex components: A review[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(5): 23–40.
[3] 王乾杰. 面向大型航空构件装配的异形垫片机器人加工系统设计与实现[D]. 武汉: 华中科技大学, 2020.WANG Qianjie. Design and implementation of robot machining system for special-shaped gasket for assembly of large aviation components[D].Wuhan: Huazhong University of Science and Technology, 2020.
[4] 郝大贤, 王伟, 王琦珑, 等. 复合材料加工领域机器人的应用与发展趋势[J]. 机械工程学报, 2019, 55(3): 1–17.HAO Daxian, WANG Wei, WANG Qilong, et al. Applications and development trend of robotics in composite material process[J]. Journal of Mechanical Engineering, 2019, 55(3): 1–17.
[5] 顾钒. 基于工业机器人的陶瓷基复合材料旋转超声制孔关键技术研究[D]. 杭州: 浙江大学, 2020.GU Fan. Research on key technology of rotary ultrasonic drilling of ceramic matrix composites based on industrial robot[D]. Hangzhou:Zhejiang University, 2020.
[6] 于建华, 丁志纯, 雷力明. 复合材料磨削切边关键技术及装置研究[J]. 制造技术与机床, 2017(10): 70–74.YU Jianhua, DING Zhichun, LEI Liming. Study on key technology and device of CFRP boundary machining[J]. Manufacturing Technology& Machine Tool, 2017(10): 70–74.
[7] 王毅. 大型构件机器人铣孔加工控制系统开发及加工误差分析[D]. 哈尔滨: 哈尔滨工业大学, 2021.WANG Yi. Development of control system for large-scale component robot hole milling and analysis of machining error[D].Harbin:Harbin Institute of Technology, 2021.
[8] 王立凡. 大型薄壁构件镜像加工装备运动控制技术研究[D].大连: 大连理工大学, 2019.WANG Lifan. Study on motion control of mirror milling equipment for large thin-walled parts[D]. Dalian: Dalian University of Technology,2019.
[9] 郭毅伟. 机器人加工装备研发及在压铸件铣边中的应用[D].厦门: 厦门大学, 2018.GUO Yiwei. Development of robot processing equipment and its application in milling of die castings[D]. Xiamen: Xiamen University,2018.
[10] WANG G F, DONG H Y, GUO Y J, et al. Chatter mechanism and stability analysis of robotic boring[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(1): 411–421.
[11] 倪鹤鹏. 机器人铣削加工轨迹规划与颤振稳定性研究[D].济南: 山东大学, 2019.NI Hepeng. Research on trajectory planning and flutter stability of robot milling[D]. Jinan: Shandong University, 2019.
[12] SUN L J, ZHENG K, LIAO W H, et al. Investigation on chatter stability of robotic rotary ultrasonic milling[J]. Robotics and Computer-Integrated Manufacturing, 2020, 63: 101911.
[13] 董辉跃, 吴杨宝, 郭英杰, 等. 机器人精镗飞机交点孔的颤振分析与识别[J]. 浙江大学学报(工学版), 2018, 52(8): 1517–1525.DONG Huiyue, WU Yangbao, GUO Yingjie, et al. Chatter analysis and identification in robotic fine boring of aircraft intersection holes[J].Journal of Zhejiang University (Engineering Science), 2018, 52(8):1517–1525.
[14] 王战玺, 张晓宇, 李飞飞, 等. 机器人加工系统及其切削颤振问题研究进展[J]. 振动与冲击, 2017, 36(14): 147–155, 188.WANG Zhanxi, ZHANG Xiaoyu, LI Feifei, et al. Review on the research developments of robot machining systems and cutting chatter behaviors[J]. Journal of Vibration and Shock, 2017, 36(14): 147–155,188.
[15] 伍健. 工业机器人不同姿态下的刚度与铣削颤振研究[D].长春: 吉林大学, 2020.WU Jian. Research on stiffness and milling chatter of industrial robots in different postures[D]. Changchun: Jilin University, 2020.
[16] NGUYEN V, JOHNSON J, MELKOTE S. Active vibration suppression in robotic milling using optimal control[J]. International Journal of Machine Tools and Manufacture, 2020, 152: 103541.
[17] PAN Z X, ZHANG H, ZHU Z Q, et al. Chatter analysis of robotic machining process[J]. Journal of Materials Processing Technology, 2006, 173(3): 301–309.
[18] GIENKE O, PAN Z X, YUAN L, et al. Mode coupling chatter prediction and avoidance in robotic machining process[J]. The International Journal of Advanced Manufacturing Technology, 2019,104(5): 2103–2116.
[19] ZHOU B, ZHOU R, GAN Y H, et al. Multi-robot multistation cooperative spot welding task allocation based on stepwise optimization: An industrial case study[J]. Robotics and Computer-Integrated Manufacturing, 2022, 73: 102197.
[20] 于乾坤, 王国磊, 任田雨, 等. 一种移动喷涂机器人的高效站位优化方法[J]. 机器人, 2017, 39(2): 249–256.YU Qiankun, WANG Guolei, REN Tianyu, et al. An efficient base position optimization method for mobile painting robot[J]. Robot, 2017,39(2): 249–256.
[21] 任书楠, 杨向东, 王国磊, 等. 大部件喷涂中的移动机械臂站位规划[J]. 吉林大学学报(工学版), 2016, 46(6): 1995–2002.REN Shunan, YANG Xiangdong, WANG Guolei, et al. Base position planning of mobile manipulator for large parts painting[J].Journal of Jilin University (Engineering and Technology Edition), 2016,46(6): 1995–2002.
[22] 陶波, 赵兴炜, 丁汉. 大型复杂构件机器人移动加工技术研究[J]. 中国科学(技术科学), 2018, 48(12): 1302–1312.TAO Bo, ZHAO Xingwei, DING Han. Study on robotic mobile machining techniques for large complex components[J]. Scientia Sinica(Technologica), 2018, 48(12): 1302–1312.
[23] 马克 W. 斯庞, 赛斯·哈钦森, M. 维德雅萨加. 机器人建模和控制[M]. 贾振中, 译. 北京: 机械工业出版社, 2016: 40–47.SPONG M W, HUTCHINSON S, VODYASAGAR M. Robot modeling and control[M]. JIA Zhenzhong, Trans. Beijing: China Machine Press, 2016: 40–47.
[24] 约翰 J.克雷格. 机器人学导论[M]. 贠超, 译. 4 版. 北京: 机械工业出版社, 2006: 53.CRAIG J J. Introduction to robotics: Mechanics and control[M].YUAN Chao, Trans. 4th ed. Beijing: China Machine Press, 2006: 53.
[25] 凯文 M.林奇, 朴钟宇. 现代机器人学: 机构、规划与控制[M]. 于靖军, 贾振中, 译. 北京: 机械工业出版社, 2019: 138–140.LYNCH K M, PARK F C. Modern robotics: Mechanics, planning and control[M]. YU Jingjun, JIA Zhenzhong, Trans. Beijing: China Machine Press, 2019: 138–140.