有限元方法是预测材料失效行为的有效手段。为了获得较为精准的结果,需要对材料的损伤模型中的参数进行准确测定[1]。目前常用的损伤模型有GTN损伤模型、Johnson– Cook(J– C)损伤模型、Cockroft– Latham(C– L)损伤模型等[2]。其中J– C 损伤模型由于其成熟的参数测量方法被广泛应用于描述金属材料的损伤行为,如伍星星等[3]采用考虑应力三轴度损伤的J– C 失效模型,成功预测了尖头弹侵彻金属板形成的花瓣型破口形状;Ullah 等[4]基于J– C 本构模型和J– C 破坏准则,探究了铣削零件内的残余应力分布,以及零件服务性能的疲劳寿命。J– C 损伤模型主要考虑应力三轴度、应变率与温度对材料损伤的影响,其参数也有多种标定方法。如吴少洋等[5]通过圆棒缺口试样的准静态拉伸试验和有限元模拟确定了损伤与应力三轴度之间的关系,接着又通过不同应变率下的拉伸试验与霍普金森拉杆 (SHTB)冲击试验确定了损伤与应变率之间的关系;Bao 等[6]设计了压缩、拉剪、纯拉伸试样等研究材料损伤与应力三轴度的关系;门建兵等[7]通过相关试验获得了EFP 材料J– C 损伤模型参数并进行了参数验证;Hu 等[8]通过试验获得45CrNiMoVA 材料的J– C 损伤模型参数并通过SHTB 对比试验验证了参数的有效性。
综上所述,虽然已有一些关于J– C 损伤模型参数测定的工作,但针对的均是均质材料。而合金钢材料在服役前大多要进行渗碳热处理,这会在材料表面形成一定厚度的表面变质层[9–10],即材料表面因碳浓度不同而造成沿深度方向力学性能的不同,同时其动态失效参数也会不同。为此,本研究针对工程中广泛应用的18CrNiMo7–6 合金钢,就其渗碳热处理后变质层的J– C 损伤模型参数的测定开展研究工作,对于评估18CrNiMo7–6 合金钢构件在渗碳热处理后的动态断裂行为具有重要的理论研究和工程应用价值。
1 渗碳热处理后表面变质层J– C 损伤参数的获取
渗碳热处理过后的18CrNiMo7–6 材料,表面会产生变质层,相较于热处理前的均质材料,材料沿层深力学性能会有所变化。由于变质层的特殊性,不能采用传统的圆棒试样,而需要采用薄板拉伸试样来获得在不同应力三轴度和应变率下的失效应变值。
1.1 J– C 损伤模型
J– C 损伤模型[11]的定义为
式中,Δεeq 是等效塑性应变增量;εf 是失效应变,在积分周期内,累计的损伤参数D 达到1 时,材料即失效。其中εf 与应力三轴度、应变率和温度有关,具体形式为

式中,D1、D2、D3、D4、D5 是常量,与材料有关;σ*是应力三轴度;![]() 是试验中的实际应变率;
是试验中的实际应变率;![]() 是参考应变率;T*是无量纲温度。从式(2)中可以看出,D1、D2、D3 用于描述应力三轴度与失效应变的关系;D4 用于描述应变率与失效应变的关系;D5 用于描述温度与失效应变的关系。
是参考应变率;T*是无量纲温度。从式(2)中可以看出,D1、D2、D3 用于描述应力三轴度与失效应变的关系;D4 用于描述应变率与失效应变的关系;D5 用于描述温度与失效应变的关系。
在动态失效类问题的有限元分析中,若材料未发生明显的温升现象,通常可将参数D5 忽略。因而限于试验条件,本文仅对D1、D2、D3、D4 4 个参数进行测量,未对D5 进行测量。
1.2 试验材料与方案
本研究中所选用的材料为渗碳热处理后的18CrNiMo7–6,其合金钢元素成分如表1 所示。渗碳热处理工艺为:首先在900 ℃的条件下进行渗碳,在碳势0.3%的环境下保持40 min;然后在碳势1.15%的环境下保持3 h;最后在碳势0.85%的环境下保持2 h,炉冷至820 ℃,继续空冷至650 ℃回火3 h,再加热至830 ℃进行淬火,之后在180 ℃进行15 h 的低温回火,工艺曲线见图1。在渗碳热处理后,对试样进行沿层深方向硬度的测量,使用 HVW–1000Z 微机全自动显微硬度计测量。采用500 g 载荷加载,保荷10 s,保证每两个压痕之间的间距为3 个对角线长度以上,每个试样同一深度下进行5 次硬度测量,去掉最大值与最小值,取剩余3 次的平均值作为测量结果,如图2 所示。可以看出,其硬度值在2 mm左右逐渐平稳,因此设定变质层厚度为0~2 mm。
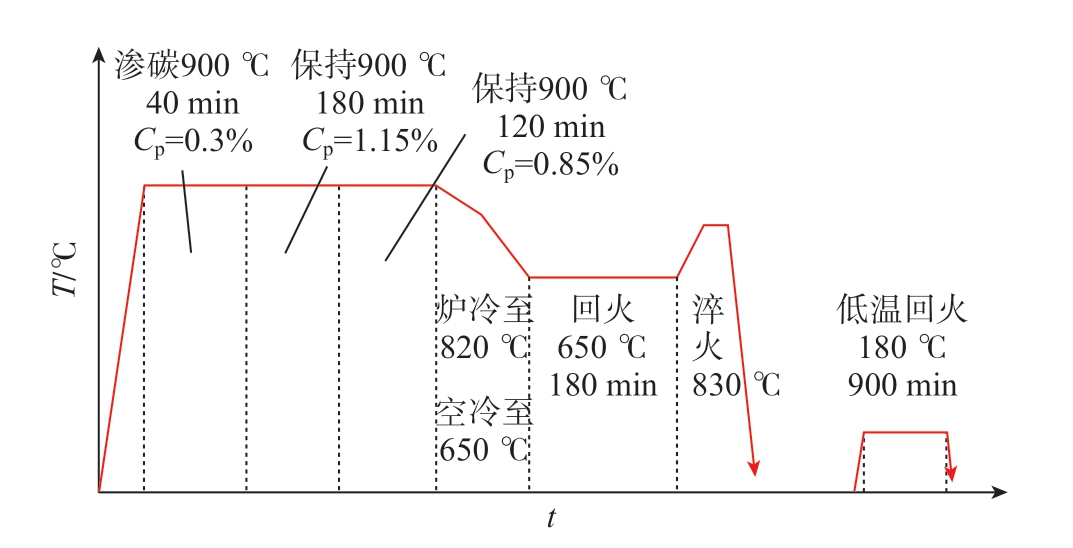
图1 渗碳热处理工艺曲线
Fig.1 Carburization heat treatment process curve
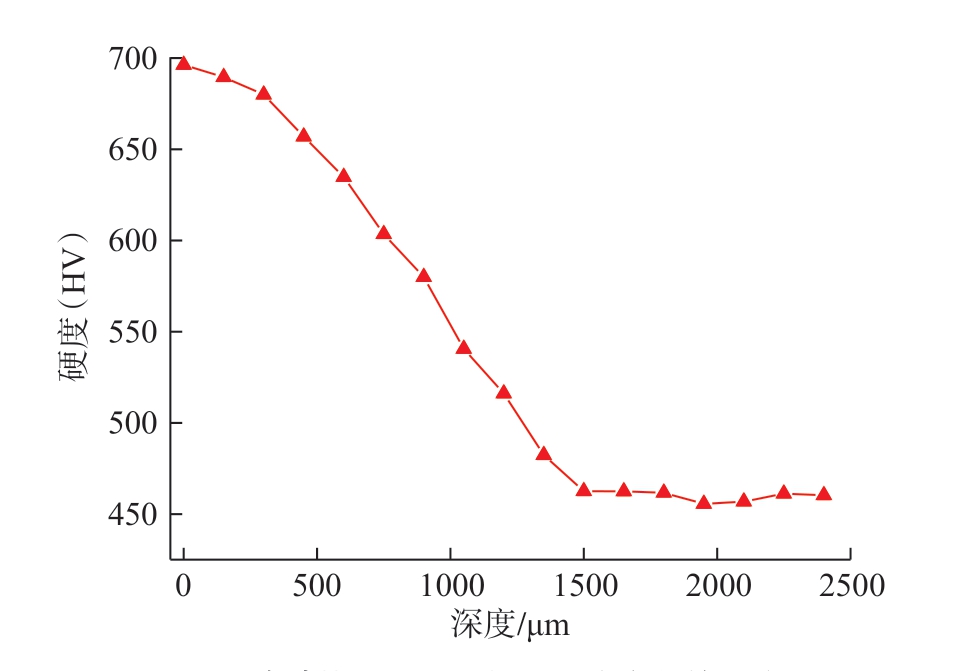
图2 渗碳热处理后材料沿深度方向的硬度
Fig.2 Hardness of the material along depth after heat treatment
表1 18CrNiMo7–6 合金钢的化学成分( 质量分数)
Table 1 Chemical composition of 18CrNiMo7–6 steel(mass fraction) %

C Si Mn S P Cr Ni Mo Fe 0.21 0.34 0.72 0.004 0.01 1.58 1.4 0.26 余量
为了获得不同层深处的失效参数,首先对试样进行分层,每0.4 mm 为一层,共划分5 层。在测取D1、D2、D3 时,为了得到不同的应力三轴度试样,采用图3 所示的试样进行拉伸试验,不同断裂角度的缺口试样在拉伸过程中会有不同的应力三轴度,对于平面应力状态的试样,其初始应力三轴度计算方法如式 (3)所示[12]。计算得出30°、45°、60°、90°断裂缺口试样的初始应力三轴度分别为0.105、0.167、0.236、0.33。
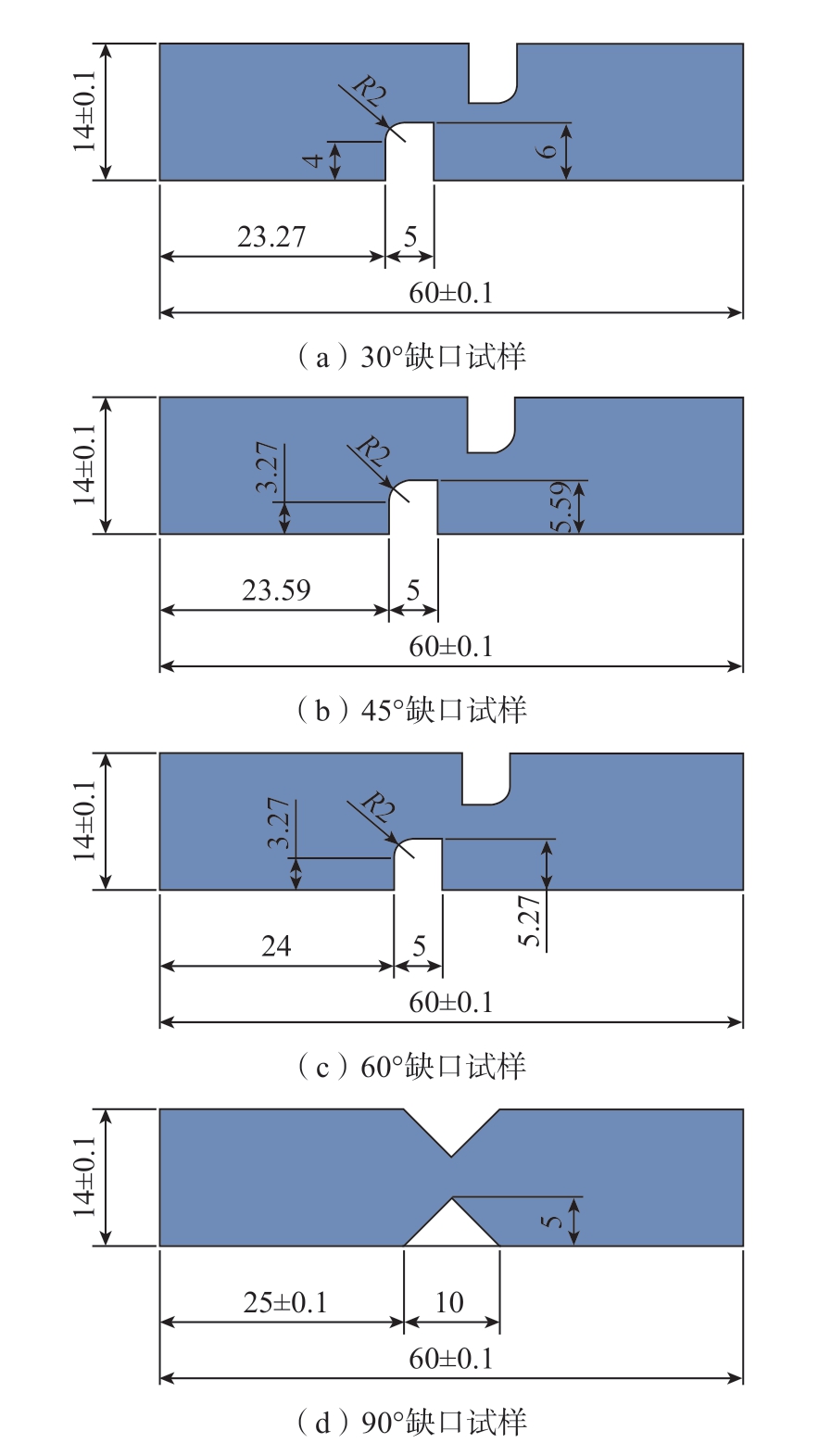
图3 不同应力三轴度的试样(mm)
Fig.3 Samples with diffe ent stress triaxiality (mm)
用线切割的方法在渗碳热处理后的块状钢材表面切取薄板试样,对试样表面进行打磨,经三维形貌仪测量,每一片试样表面粗测度均低于0.3 μm。接着采用岛津拉伸试验机对不同层深处的不同应力三轴度的试样进行单轴拉伸,在试样的表面制作散斑以得到拉伸过程中的应变值,同时在试样表面标定20 mm 的距离以得到拉伸过程中准确的载荷–位移曲线。拉伸过程为准静态拉伸,拉伸速率为0.2 mm/min。采用非接触式三维全场应变测量系统 (DIC),根据散斑的位移获得不同应力三轴度下的试样局部的准确失效应变值。
在拟合D4 时,对于低应变率拉伸,采用MTS 万能试验机进行拉伸;对于高应变率拉伸,本研究采用宽脉冲动态拉伸系统和FASTCAM 超高速摄影设备进行动态拉伸试验,按照GB/T 30069. 2—2016《金属材料高应变速率拉伸试验 第2 部分:液压伺服型与其他类型试验系统》的相关规定设计试样尺寸,如图4 所示。为了保证试验的一致性,不同应变率下的拉伸均采用同样尺寸的试样。宽脉冲动态拉伸系统示意图如图5 所示。通过调整撞击杆的初始撞击速度来改变试样的应变率,失效应变由超高速摄影机配合DIC 分析软件获得,拍摄帧率为60000 帧/s。

图4 高速拉伸薄板试样(mm)
Fig.4 Sheet specimen for high-speed tensile (mm)
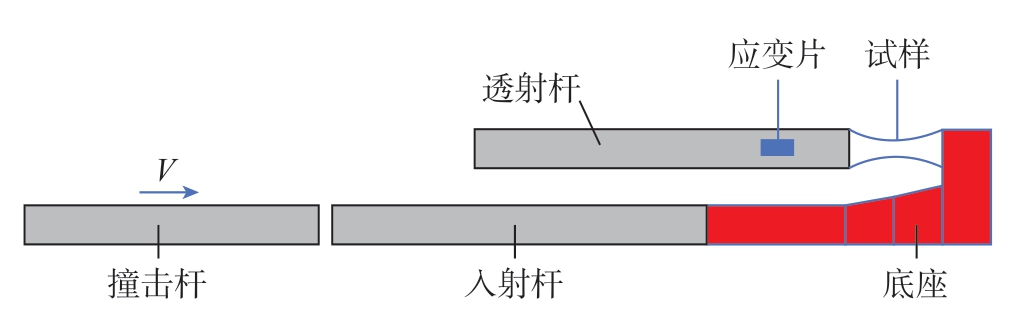
图5 宽脉冲动态拉伸系统示意图
Fig.5 Schematic diagram of wide pulse dynamic stretching system
2 试验结果与讨论
2.1 失效应变与应力三轴度的关系
每个工况均拉伸3 次以保证结果的可靠性。由于试样过多,本文以0.4 ~ 0.8 mm 深度处90°试样为例,演示参数提取及拟合过程。在试样拉伸的过程中,由于试样的塑性变形,应力三轴度是不断变化的,为此,本文用相同的工况对试验过程进行了有限元仿真分析。为保证仿真的准确性,提取仿真中的载荷位移曲线,与DIC软件分析得到拉伸过程中的准确载荷位移曲线进行比较,通过不断调整仿真中的应力–应变值,最终让仿真与试验的载荷–位移曲线重合,提取结果如图6 所示。

图6 仿真与试验载荷–位移曲线对比
Fig.6 Comparison of load–displacement curve between simulation and experiment
接着提取仿真中的应力三轴度,由于在缺口处试样的形状突变会产生应力集中 (图7),本文提取试样中心单元的应力三轴度随应变ε 的变化值,如图8 所示。同时本文选取应力三轴度的平均值作为等效应力三轴度,这样既考虑到了试样变形对应力三轴度的影响,也考虑到了应变累积效应对应力三轴度的影响,计算公式如式(4)所示[13–14],最终得到等效应力三轴度为0.56。
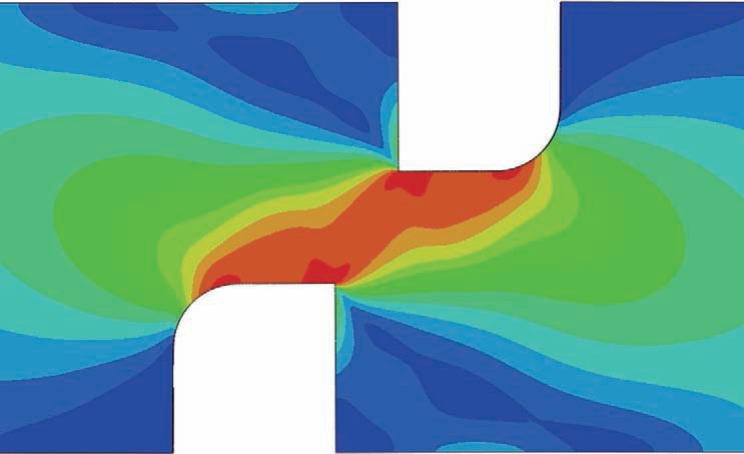
图7 试样典型应力分布云图
Fig.7 Typical stress distribution nephogram of the sample
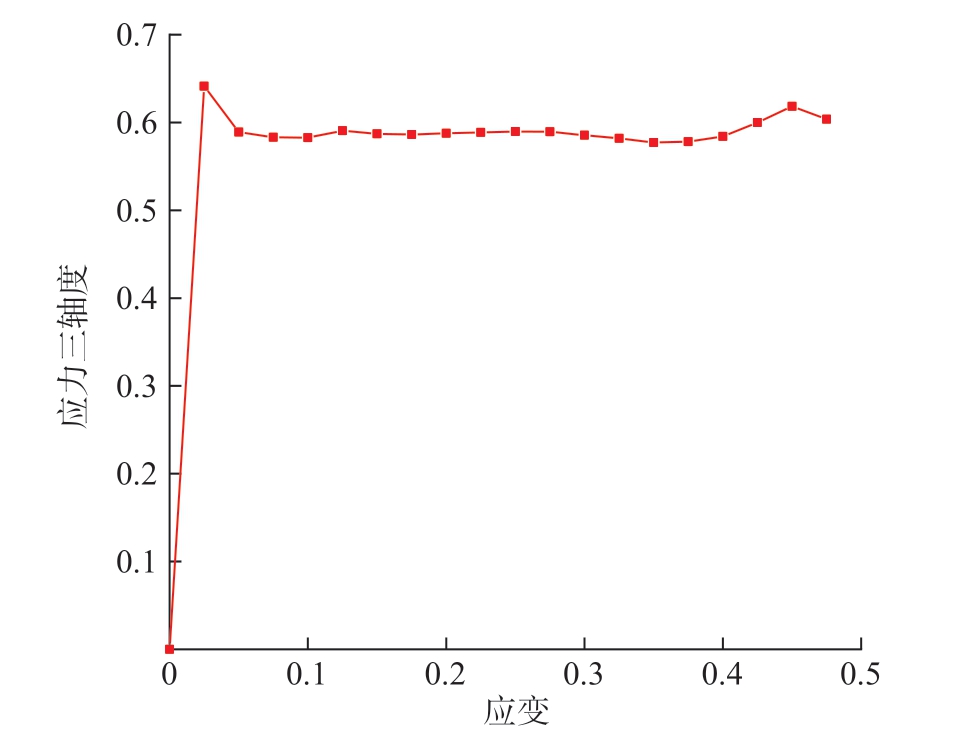
图8 应力三轴度随应变变化
Fig.8 Stress triaxiality versus strain
最后提取试验中试样失效应变,采用DIC 软件分析试样每个时刻的应变值,选取断裂时刻的最大应变值作为失效应变,如图9 所示。由此即可得到0.4 ~ 0.8 mm层深处的材料在应力三轴度为0.56 时对应的失效应变为0.89。得到失效应变与应力三轴度之间的对应值后,根据式 (2)拟合曲线,此时D4、D5 参量所在项均视为1,即对应力三轴度与失效应变的关系没有影响,最终拟合曲线如图10 所示,变质层不同层深处与应力三轴有关的失效参数如表2 所示。

图9 准静态拉伸下由DIC 分析得到的失效应变
Fig.9 Failure strain obtained from DIC analysis under static stretching
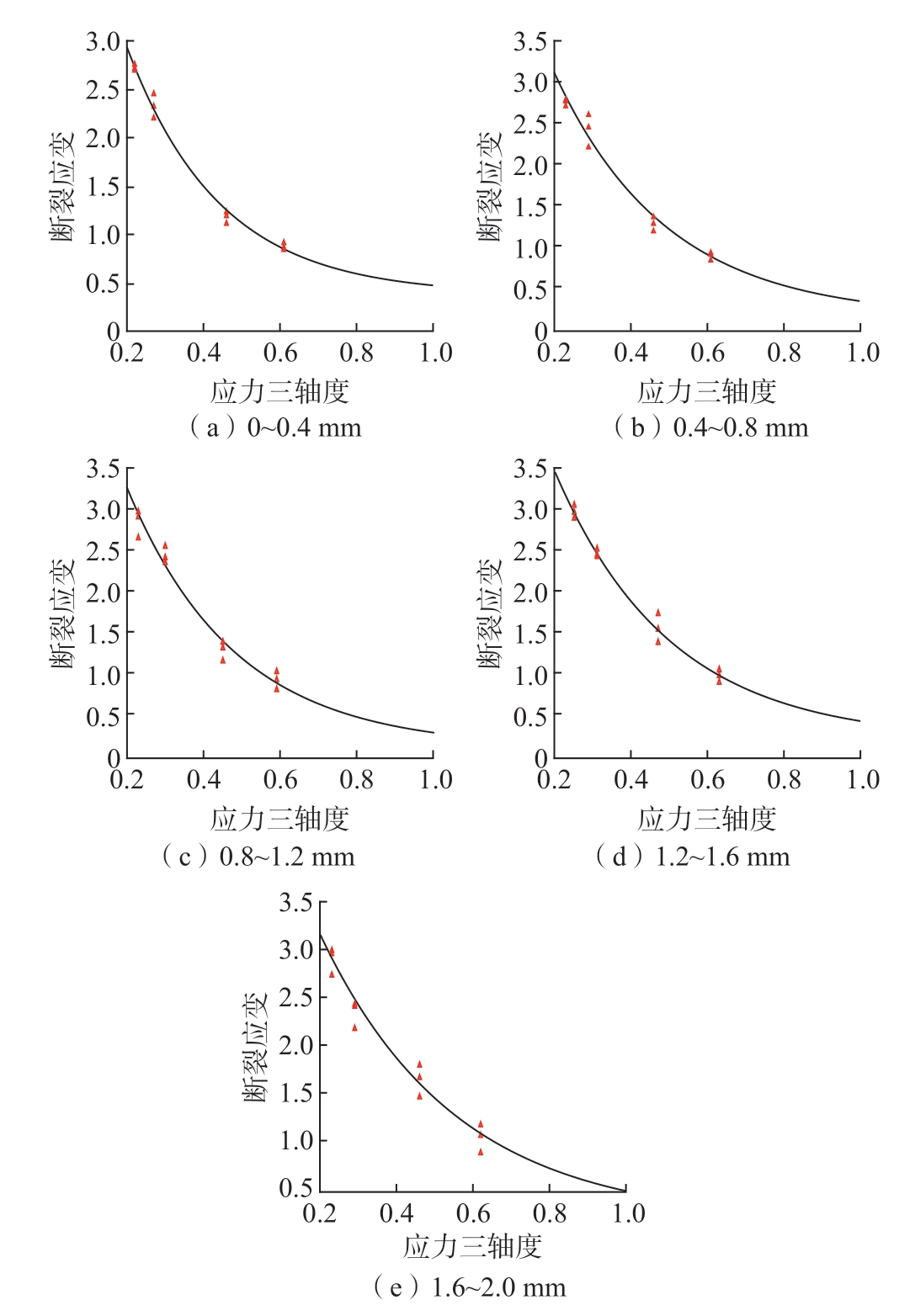
图10 不同层深处失效应变与应力三轴度之间的关系
Fig.10 Relationship between failure strain and stress triaxiality at diffe ent depths of layers
表2 不同层深处与应力三轴有关的失效参数
Table 2 Failure parameters related to stress triaxial at diffe ent depths
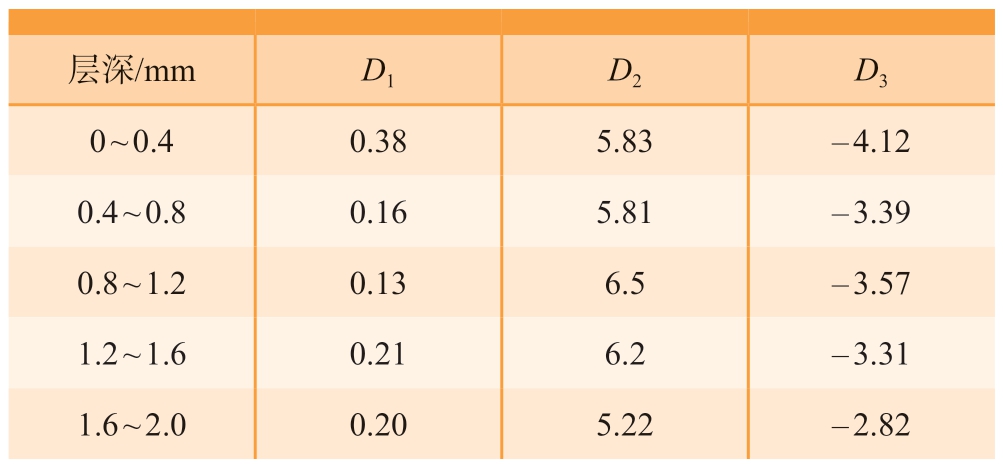
层深/mm D1 D2 D3 0 ~ 0.4 0.38 5.83 – 4.12 0.4 ~ 0.8 0.16 5.81 – 3.39 0.8 ~ 1.2 0.13 6.5 – 3.57 1.2 ~ 1.6 0.21 6.2 – 3.31 1.6 ~ 2.0 0.20 5.22 – 2.82
从图10 和表2 可以看出,同一层材料的失效应变随应力三轴度的增大而减小;而沿层深方向,在同一应力三轴度水平下,失效应变随层深增大而增大。这表明对于渗碳热处理后的材料,其表层材料的韧性比较差,在应变值相对较小时即发生断裂。
2.2 不同层深处失效应变与应变率的关系
同样以0.4 ~ 0.8mm 深度处试样为例,演示提取结果。在MTS 试验机上进行应变率为0.1 的拉伸试验,根据试样的形状,控制拉伸速度为2 mm/s;在宽脉冲动态拉伸系统中,改变气泵的气压以改变撞击杆的撞击速度,通过DIC 软件可以得到不同试样的应变率大小,同时观察示波器显示的试样应变信号值以保证拉伸过程的平稳性。由于只能控制气泵的气压,无法精确控制应变率的具体值,其值只能由DIC 软件分析获得,如图11 所示。经DIC 处理得到每个应变率下对应的失效应变,在应变率分别为0.1 s–1、154 s–1、221 s–1、475 s–1、800 s–1 时,试样的失效应变分别为0.51、0.20、0.18、0.16、0.12。

图11 由DIC 分析得到的失效应变
Fig.11 Failure strain obtained from DIC analysis
得到每一层的应变率与失效应变的关系后,根据式(2)拟合曲线,此时D1、D2、D3、D5 量的所在项均视为1,即对应变率与失效应变的关系没有影响。最后拟合失效应变与应变率曲线如图12 所示,拟合得到不同层深处与应变率有关的失效参数,如表3 所示。
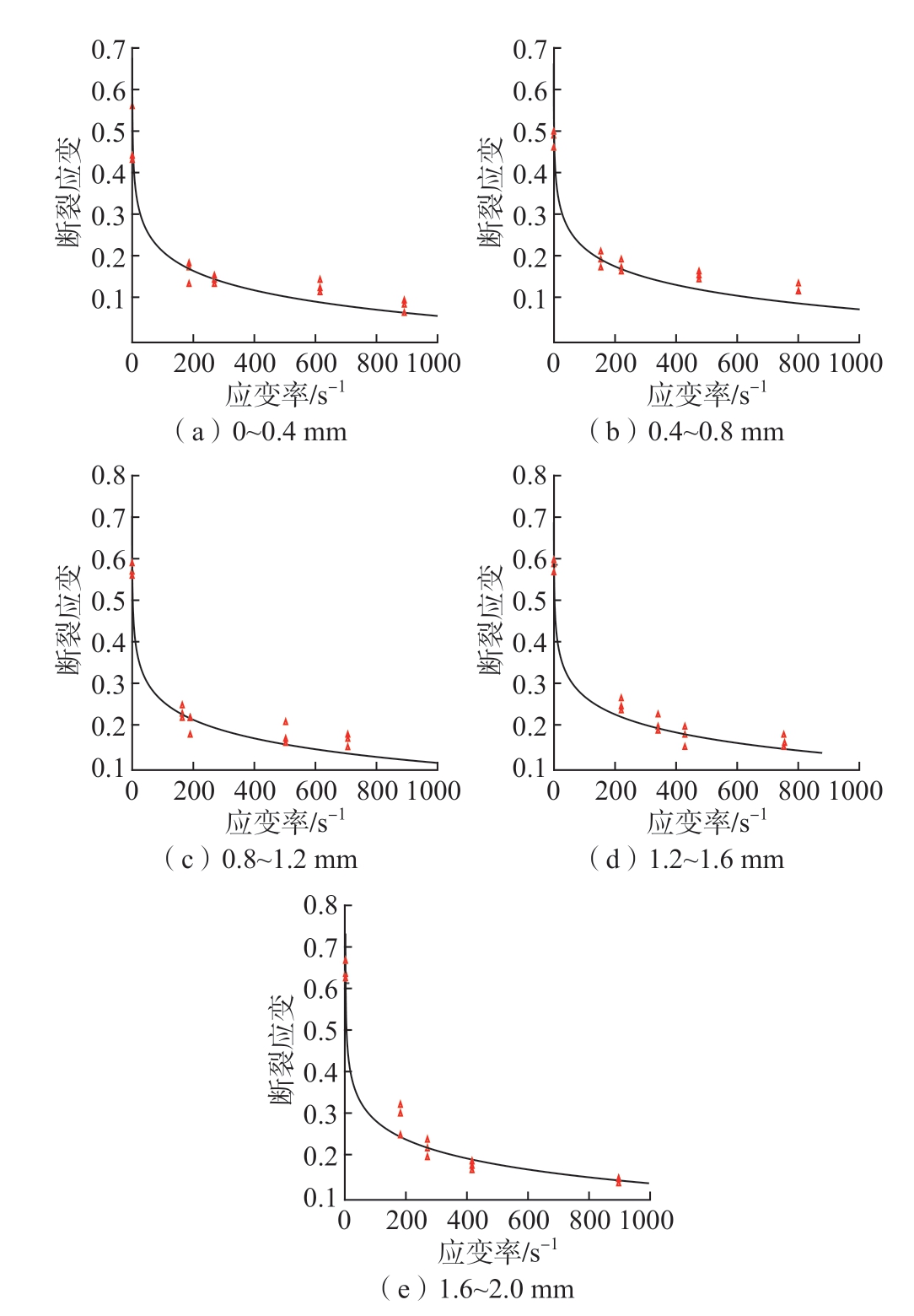
图12 不同层深处失效应变与应变率之间的关系
Fig.12 Relationship between failure strain and strain rate at diffe ent depths of layers
表3 不同层深处与应变率有关的失效参数
Table 3 Failure parameters related to strain rate at diffe ent depths

层深/mm 0 ~ 0.4 0.4 ~ 0.8 0.8 ~ 1.2 1.2 ~ 1.6 1.6 ~ 2.0 D4 – 0.068 – 0.066 – 0.065 – 0.064 – 0.062
从图12 和表3 中可以看出,对于渗碳热处理后的材料,整体材料失效应变受应变率影响较大,呈现出明显的应变率弱化趋势,随着应变率的增加,其失效应变不断减小,且在同一应变率水平下,失效应变随层深增大而增大。
2.3 参数准确性的验证
在验证参数D1、D2、D3 时,将失效参数输入拉伸模型中,在0.4 ~ 0.8 mm 层深处90°试样拉伸仿真中,其断裂时刻最大应变如图13 所示,为0.837,与试验DIC 所得失效应变0.89 误差为6.0%。同时提取其拉伸–位移曲线,如图14 所示,试验中断裂位移为0.473 mm,仿真中断裂位移为0.50 mm,误差为5.7%。
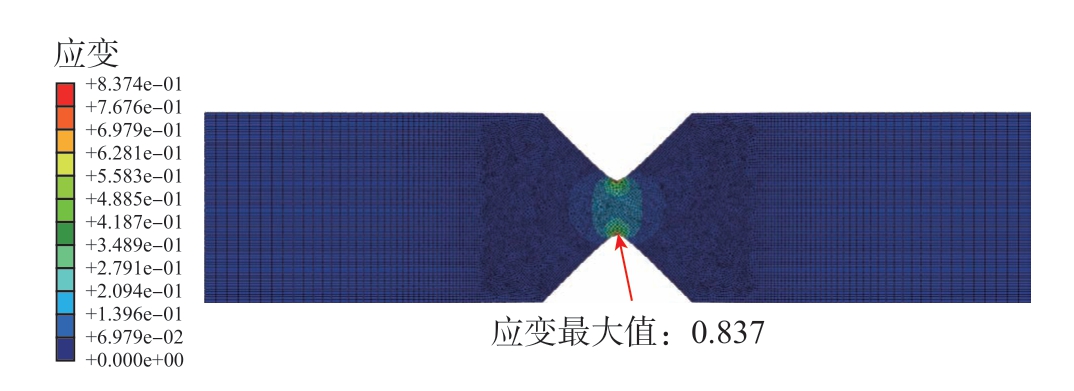
图13 90°试样仿真所得失效应变
Fig.13 Failure strain obtained from 90° specimen by simulation
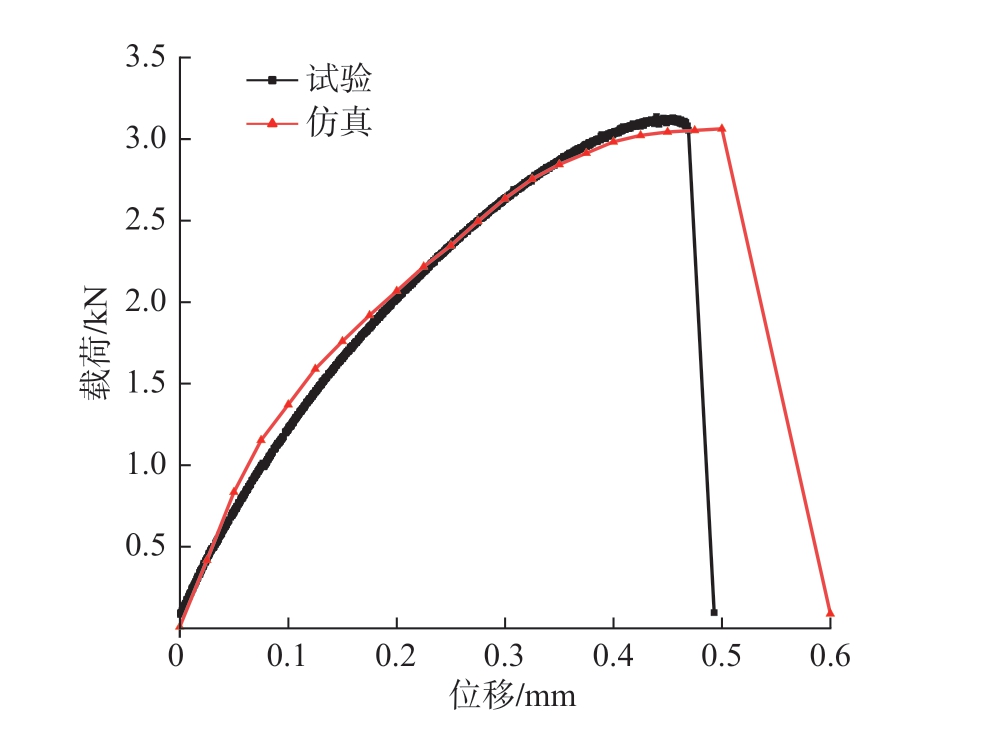
图14 带损伤参数的仿真与试验载荷–位移曲线对比
Fig.14 Comparison of load–displacement curves between simulation and experiment with damage parameters
在验证参数D4 时,将失效参数输入不同应变率的拉伸模型中,在0.4 ~ 0.8 mm 层深处薄片拉伸试样模型右夹持端施加全约束,左端施加位移载荷,通过改变位移载荷的大小,即可控制试样的拉伸速率。图15 是在不同拉伸速率下试样断裂时刻的应变云图,可以看出,在应变率分别为0.2 s–1、213 s–1 时,失效应变分别为0.527、0.214,与在应变率为0.1 s–1、221 s–1 时,失效应变分别为0.51、0.18 相比,误差分别为3%、18.9%。
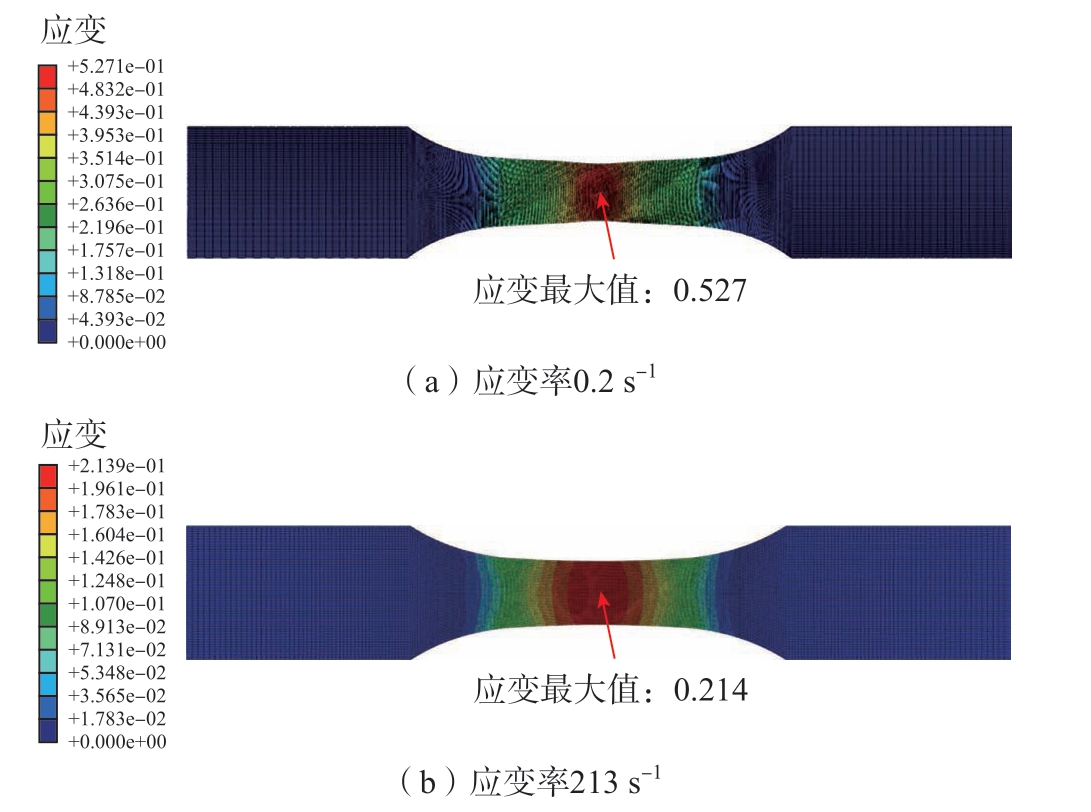
图15 仿真中不同应变率下试样断裂应变
Fig.15 Fracture strain of specimen under diffe ent strain rates in simulation
3 结论
针对渗碳热处理后材料的J– C 损伤参数,本文基于18CrNiMo7–6 合金钢,采用万能试验机和宽脉冲动态拉伸系统辅以DIC 设备对变质层分层后各层深处的J– C损伤参数进行测定,得到了如下结论。
(1)对于渗碳热处理后的18CrNiMo7–6 材料,同一层材料的失效应变随应力三轴度的增大而减小;且沿层深方向,在同一应力三轴度水平下,失效应变随层深增大而增大。这表明渗碳热处理后材料的表层材料的韧性比较差,在应变值相对较小时即发生断裂,层深越深,材料的韧性越好,越不容易发生断裂。
(2)对于渗碳热处理后的18CrNiMo7–6 材料,整体材料失效应变受应变率影响较大,呈现出明显的应变率弱化趋势,随着应变率的增加,其失效应变不断减小,且在同一应变率水平下,失效应变随层深增大而增大。
(3)为渗碳热处理后的18CrNiMo7–6 材料提供了准确的分层J– C 失效参数,对其动态断裂行为提供了数据支撑。同时验证了分层测定渗碳热处理后靶材各层J – C 失效参数的可行性,对各种渗碳热处理后材料的失效行为仿真预测有着重要的意义。
[1] 陈刚, 陈忠富, 徐伟芳, 等. 45钢的J– C损伤失效参量研究[J].爆炸与冲击, 2007, 27(2): 131–135.CHEN Gang, CHEN Zhongfu, XU Weifang, et al. Investigation on the J– C ductile fracture parameters of 45 steel[J]. Explosion and Shock Waves,2007, 27(2): 131–135.
[2] 赵江波, 谢延敏, 刘程, 等. 基于损伤耦合粘塑性模型的AZ31B镁合金温变形行为研究[J/OL]. 热加工工艺, [2024–06–07]. https://d.wan fangdata.com.cn/periodical/rjggy202407026.ZHAO Jiangbo, XIE Yanmin, LIU Cheng, et al. Study on warm deformation behavior of AZ31B magnesium alloy based on damage coupled viscoplastic model[J/OL]. Hot Working Technology, [2024–06–07]. https://d.wanfangdata.com.cn/periodical/rjggy202407026.
[3] 伍星星, 刘建湖, 张伦平, 等. 尖头弹侵彻金属板花瓣型破口成形过程仿真分析[J]. 中国舰船研究, 2018, 13(3): 110–117.WU Xingxing, LIU Jianhu, ZHANG Lunping, et al. Numerical simulation analysis of petaling formation process of plate penetrated by sharp-nosed missile[J]. Chinese Journal of Ship Research, 2018, 13(3): 110–117.
[4] ULLAH I, ZHANG S, WAQAR S. Numerical and experimental investigation on thermo-mechanically induced residual stress in highspeed milling of Ti–6Al–4V alloy[J]. Journal of Manufacturing Processes,2022, 76: 575–587.
[5] 吴少洋, 张建伟, 卢凤强, 等. 18CrNiMo7–6合金钢J– C损伤模型失效参数研究[J]. 郑州大学学报(工学版), 2023, 44(1): 70–76.WU Shaoyang, ZHANG Jianwei, LU Fengqiang, et al. Investigation on failure parameters of J– C damage model of 18CrNiMo7–6 alloy steel[J].Journal of Zhengzhou University (Engineering Science), 2023, 44(1): 70–76.
[6] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81–98.
[7] 门建兵, 卢易浩, 蒋建伟, 等. 杆式EFP 用钽钨合金JC 失效模型参数[J]. 高压物理学报, 2020, 34(6): 136–143.MEN Jianbing, LU Yihao, JIANG Jianwei, et al. Johnson-Cook failure model parameters of tantalum-tungsten alloy for rod-shaped EFP[J]. Chinese Journal of High Pressure Physics, 2020, 34(6): 136–143.
[8] HU X, XIE L J, GAO F N, et al. On the development of material constitutive model for 45CrNiMoVA ultra-high-strength steel[J]. Metals,2019, 9(3): 374.
[9] 赵振业. 高强度合金应用与抗疲劳制造[J]. 功能材料信息,2009, 6(2): 15–16.ZHAO Zhenye. Application of high-strength alloys and anti-fatigue manufacturing technology[J]. Functional Material Information, 2009, 6(2):15–16.
[10] XU G T, LUO J, LU F Q, et al. Characterization of fracture toughness for surface-modified layer of 18CrNiMo7–6 alloy steel after carburizing heat treatment by indentation method[J]. Engineering Fracture Mechanics, 2022, 269: 108508.
[11] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J].Engineering Fracture Mechanics, 1985, 21(1): 31–48.
[12] 陈继恩. 基于应力三轴度的材料失效研究[D]. 武汉: 华中科技大学, 2012.CHEN Jien. Research of material failure basic on stress triaxiality[D].Wuhan: Huazhong University of Science and Technology, 2012.
[13] BØRVIK T, HOPPERSTAD O S, BERSTAD T. On the influence of stress triaxiality and strain rate on the behaviour of a structural steel. Part II.Numerical study[J]. European Journal of Mechanics–A, 2003, 22(1): 15–32.
[14] TENG X, WIERZBICKI T. Evaluation of six fracture models in high velocity perforation[J]. Engineering Fracture Mechanics, 2006, 73(12):1653–1678.