紧固件作为一种重要的通用基础件，在工业中具有举足轻重的作用，特别是在航空航天领域，无论是飞机的连接装配还是飞行器部段之间的连接，都需要使用大量的紧固件[1–2]。然而，由于极端使用环境及条件的影响，航空航天领域使用的紧固件在多种复杂载荷的作用下，经常面临发生失效的风险，严重威胁飞行器的安全[3]。为了改善螺栓等紧固件的性能，需要在紧固件表层引入残余压应力，实现紧固件表层性能的强化[4]。表面滚压工艺是实现螺栓表面强化、提高其疲劳寿命的重要技术途径。Wu 等[5]对近净成形叶片进行了超声滚压工艺研究，结果表明，经过滚压后叶片表面形成了一定深度的残余应力层，表明滚压加工可以通过引入残余压应力改善构件力学性能。对于螺栓而言，其头杆连接处在轴向拉压载荷作用下容易发生破坏。刘福超等[6]以构件滚压后的残余应力为主要研究对象，根据有限元仿真结果分别分析了滚压力、滚针半径、摩擦系数、滚压道次和滚压速度对残余应力分布的影响，揭示了滚压工艺参数和残余应力变化情况的对应关系。Zhang 等[7]以仿真和试验相结合的方法研究了杯型构件滚压时摩擦系数和滚子半径等参数对滚压效果的影响，确定了满足加工要求的滚压工艺参数。虽然针对表面滚压工艺的研究取得了一定的成果，但是目前针对高精度钛合金螺栓根部圆角的滚压技术，还存在残余应力分布状态不明晰，加工实践中工艺条件仍采用试错法，缺乏有效的工艺参数理论指导等问题。
本研究针对高精度螺栓实际生产中面临的上述问题，以TC4 钛合金高精度沉头螺栓为研究对象，开展根部圆角滚压强化的残余应力分布及参数优化研究，建立了滚压强化工艺有限元模型，分析了螺栓根部圆角滚压强化工艺对残余应力分布的影响规律，并基于仿真结果和改进优化算法完成了滚压工艺参数的优化，为提高螺栓的圆角滚压强化工艺效果奠定理论基础。
1 螺栓根部圆角滚压强化的模型
本研究中的高精度沉头螺栓材料为Ti–6Al–4V 钛合金 （TC4），其头杆连接处有半径为0.6 mm 的过渡圆角。图1 所示为螺栓根部圆角滚压强化工艺的示意图。在进行螺栓根部圆角滚压强化时，需要在滚压的螺栓根部圆角位置附近安装3 个滚轮，滚轮转动并向螺栓的中心进给，对螺栓根部施加一定的滚压力。经过一定时间的滚压操作，滚轮退回到原始位置，即完成一次对螺栓根部圆角的滚压加工。
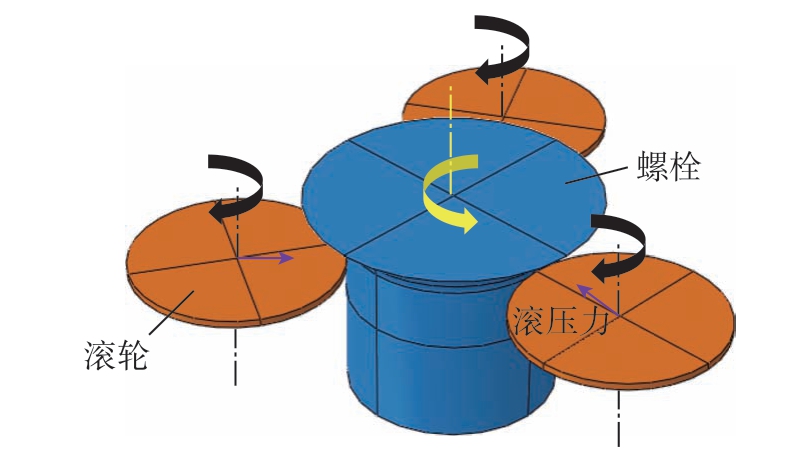
图1 螺栓根部圆角滚压强化工艺的示意图
Fig.1 Schematic diagram of rolling strengthening process at root fillet of bol
为了分析滚压工艺参数对高精度螺栓根部圆角残余应力的影响，建立了螺栓根部圆角滚压强化的有限元仿真模型。模型中滚轮发生转动和进给运动，而滚压螺栓只发生转动，并产生塑性变形。为了保证有限元仿真的收敛性，考虑到滚压强化所使用的滚轮相较于被加工螺栓有更高的强度及刚度，分析时将滚轮视作刚体。
根据螺栓实体零件的尺寸及形状建立其三维模型。因为研究主要关注螺栓根部圆角处的残余应力，故只截取圆角附近约5 mm 范围的区域进行建模，如图2 所示。滚压强化过程有限元仿真采用ABAQUS 软件显式动力学分析方法，按照滚压加工时滚轮进给、滚压以及卸载3 个分析步进行仿真。由于螺栓根部圆角及滚轮间需要设置相互作用属性，定义滚轮与螺栓根部圆角受滚压区域为面面接触，相互作用滑移为有限滑移。对螺栓及滚轮设置相应的运动边界条件，限制螺栓只能绕其中心轴旋转，而滚轮既可以在水平面上沿直线向螺栓中心进给，又能绕其自身的中心轴旋转，由此达到滚压加工的效果。滚压力施加在滚轮中心，方向指向螺栓中心。仿真中对螺栓圆角附近的网格进行细化，且全部采用结构网格进行分析。螺栓的基体及滚轮网格单元类型使用C3D8R 单元；对于具有表面涂层的螺栓，其根部圆角区域定义蒙皮并使用M3D4R 单元。
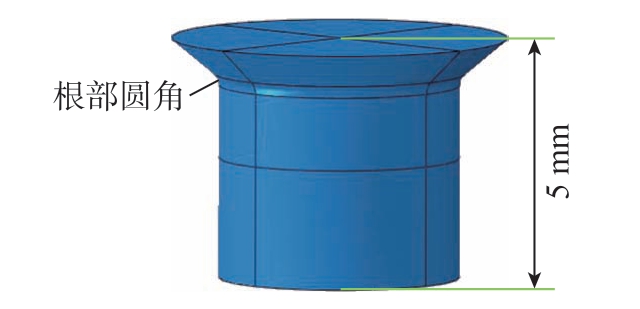
图2 螺栓根部圆角的模型
Fig.2 Model of root fillet of bol
根据对疲劳断裂螺栓头杆连接处的断口形貌长期的观察分析可知，其疲劳源一般位于根部圆角表面或表面附近的位置，且裂纹会随着交变载荷的施加不断向螺栓中心延伸。因此需要重点研究滚压强化后螺栓根部圆角表面至中心一定距离内的残余应力分布情况。为了表征某一种滚压工艺条件下螺栓根部圆角处残余应力的分布情况，制定了螺栓根部圆角强化仿真的残余应力提取路径，如图3 所示。首先在螺栓模型的一个截面上，取螺栓径向3 个等分角度的路径作为该截面上的应力提取路径，如图3（a）所示。而对每个螺栓模型在根部圆角的上、中、下轴向3 个位置的截面各取一条路径（Path–1，Path–2 和Path–3）计算其残余应力，如图3（b）所示。为了获得可靠而准确的仿真结果，分析每个螺栓模型中9 条路径的残余应力，并计算其平均值，实现对残余应力的综合评价。
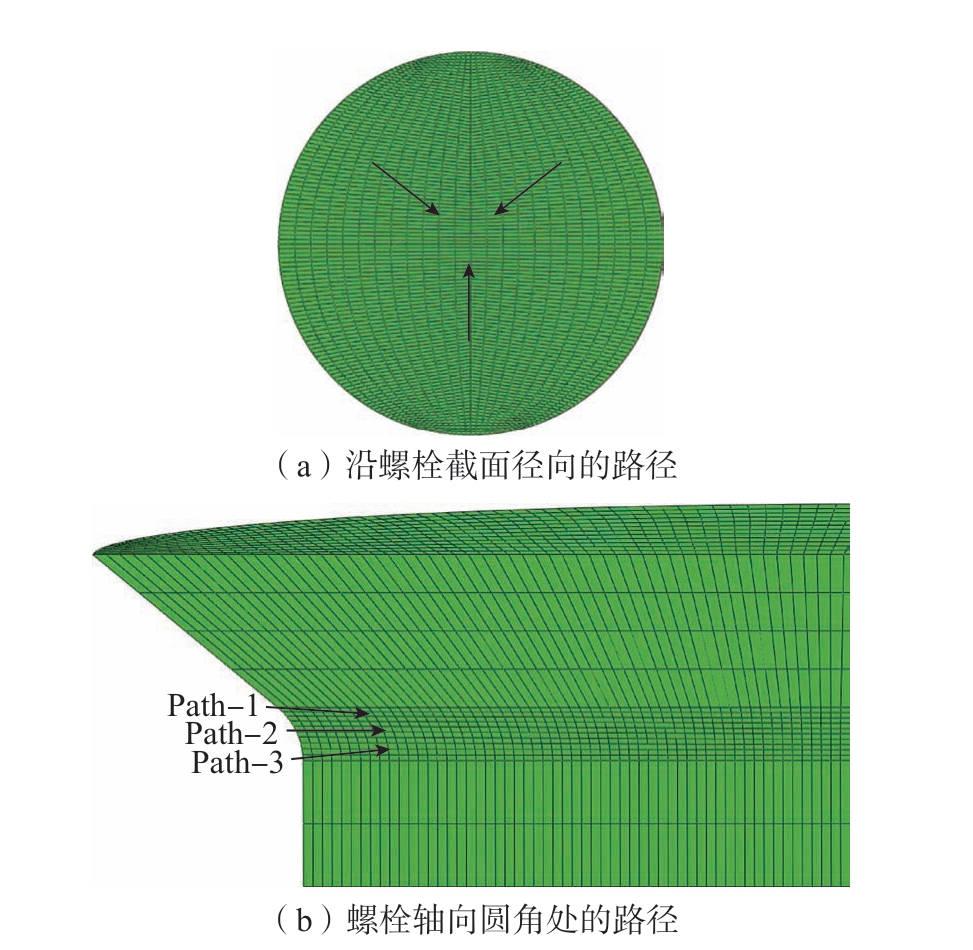
图3 螺栓根部圆角强化仿真的残余应力提取路径
Fig.3 Extraction paths of residual stress in root fillet st engthening simulation of bolt
工程上常用基于试验数据的Johnson– Cook 模型作为描述金属材料特性的本构模型，其形式简单，引入了材料的应变强化、应变率强化及热软化参数，如式 （1）所示。
式中，σeq 为等效应力；A 为屈服强度系数；B 为应变强化系数；C 为应变速率强化系数；m 为软化指数；n 为硬化指数；ε 为等效塑性应变；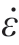
为等效塑性应变率；
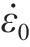为参考应变率；T *=（T′ – Ta）/（Tmelt – Ta），T′为温度，Ta 为环境温度，Tmelt 为熔点温度。
本文研究的高精度螺栓材料为TC4 钛合金，组织类型是密排六方结构和体心立方结构的混合体。采用Johnson– Cook 模型可以分析TC4 钛合金在不同应变率下的力学行为[8]。因此，在螺栓根部圆角滚压的有限元仿真中采用该模型描述螺栓材料的塑性行为。TC4 钛合金材料参数及Johnson– Cook 本构模型的参数分别如表1 和表2 所示[9–10]。
表1 TC4 的材料参数[9]
Table 1 Material parameters of TC4[9]
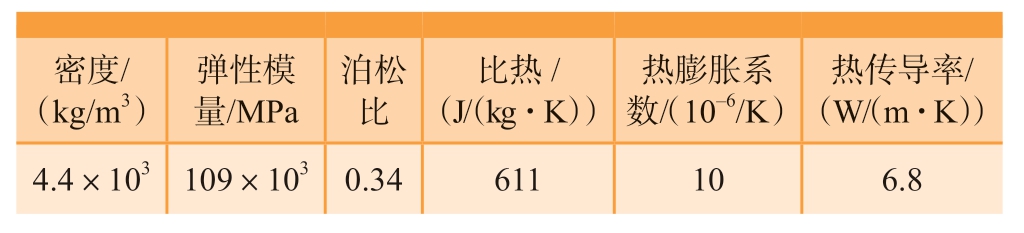
密度/（kg/m3）弹性模量/MPa泊松比比热/（J/（kg·K））热膨胀系数/（10–6/K）热传导率/（W/（m·K））4.4×103 109×103 0.34 611 10 6.8
表2 Johnson– Cook 模型参数[10]
Table 2 Johnson– Cook model parameters[10]
A/MPa B/MPa C m n 874 583 0.003 0.95 0.316
2 螺栓根部圆角滚压强化仿真
2.1 仿真条件设置
结合螺栓根部圆角滚压强化工艺的实际情况，对滚压速度、滚压时间、摩擦系数、涂层厚度和滚压力进行分析，研究其对滚压强化后的圆角残余应力分布的影响。其中，摩擦系数的变化反映了不同的螺栓表面滚压润滑情况。对5 个加工工艺参数设置约束范围，其中滚压速度v（r/min）∈[400，500]，滚压时间t（s）∈[1.5，2.5]，摩擦系数f∈[0.1，0.5]，涂层厚度T（μm）∈[0，20]，滚压力F（N）∈[588，784]。每个参数分别设置5 个水平，得到表3 所示的因素水平表。滚压仿真设计出表4 所示的L25（56）正交参数表，按照工艺参数组合进行25 组仿真。
表3 滚压工艺参数因素水平
Table 3 Factor levels of rolling process parameters
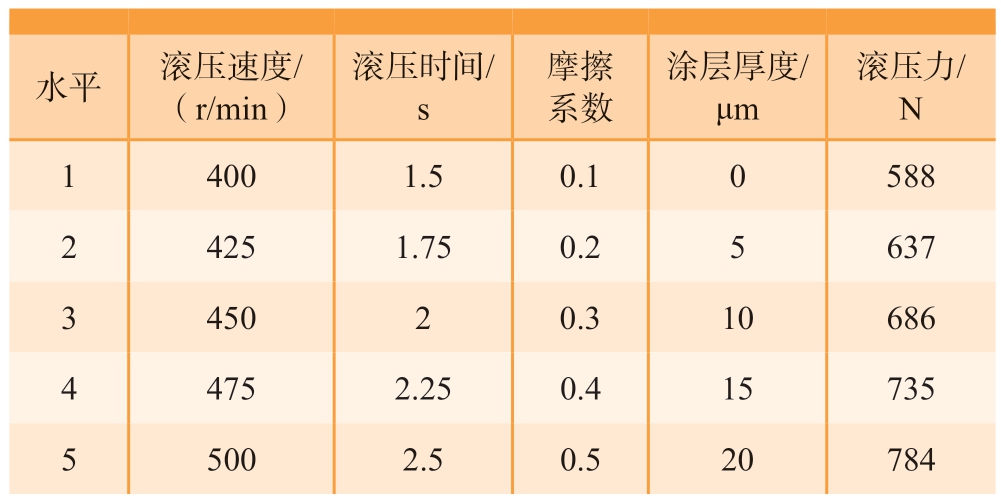
水平 滚压速度/（r/min）滚压时间/s摩擦系数涂层厚度/μm滚压力/N 1 400 1.5 0.1 0 588 2 425 1.75 0.2 5 637 3 450 2 0.3 10 686 4 475 2.25 0.4 15 735 5 500 2.5 0.5 20 784
表4 圆角滚压强化仿真正交参数
Table 4 Orthogonal parameters for fillet olling strengthening simulation
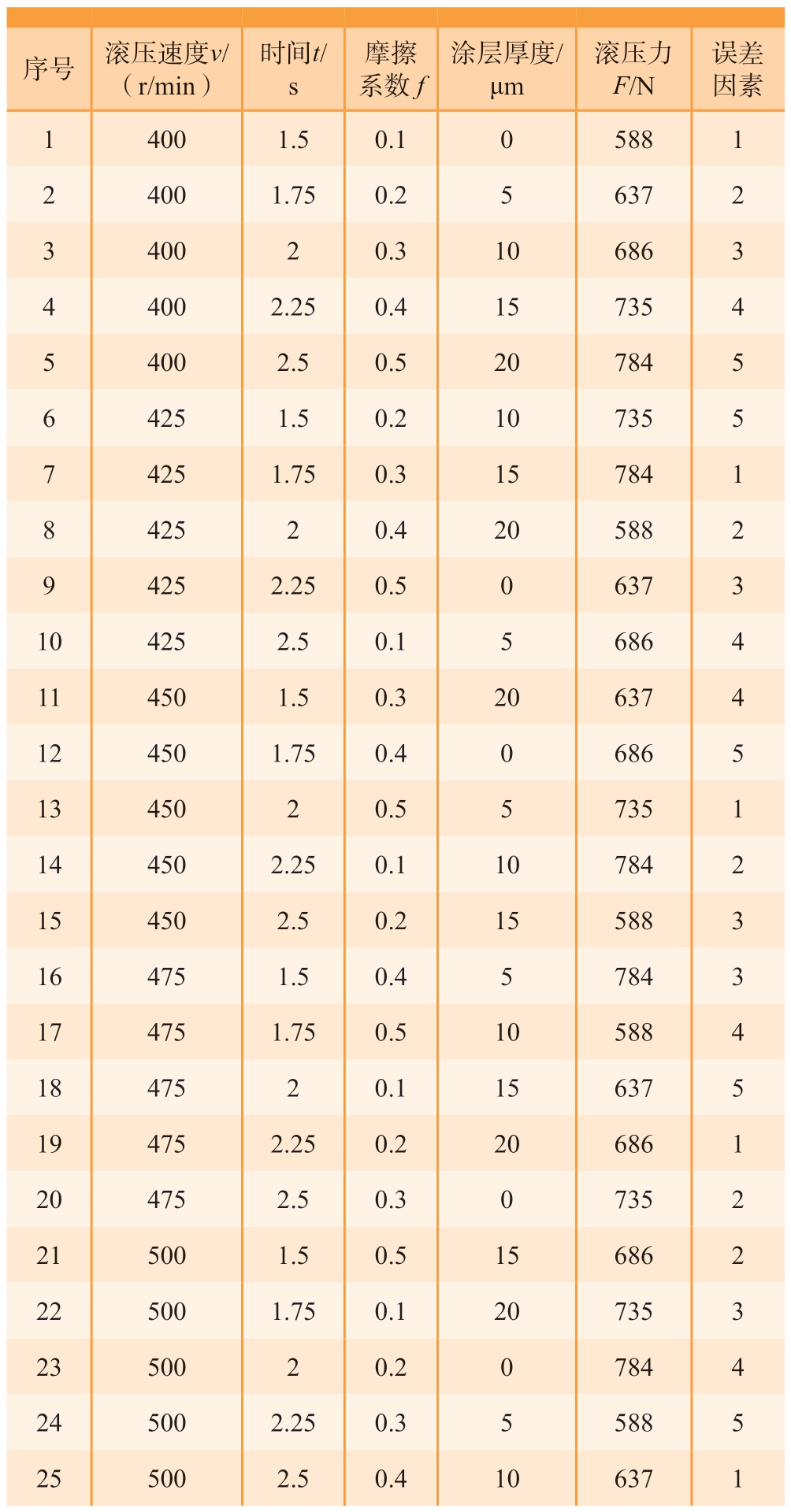
序号 滚压速度v/（r/min）时间t/s摩擦系数f涂层厚度/μm滚压力F/N误差因素1 400 1.5 0.1 0 588 1 2 400 1.75 0.2 5 637 2 3 400 2 0.3 10 686 3 4 400 2.25 0.4 15 735 4 5 400 2.5 0.5 20 784 5 6 425 1.5 0.2 10 735 5 7 425 1.75 0.3 15 784 1 8 425 2 0.4 20 588 2 9 425 2.25 0.5 0 637 3 10 425 2.5 0.1 5 686 4 11 450 1.5 0.3 20 637 4 12 450 1.75 0.4 0 686 5 13 450 2 0.5 5 735 1 14 450 2.25 0.1 10 784 2 15 450 2.5 0.2 15 588 3 16 475 1.5 0.4 5 784 3 17 475 1.75 0.5 10 588 4 18 475 2 0.1 15 637 5 19 475 2.25 0.2 20 686 1 20 475 2.5 0.3 0 735 2 21 500 1.5 0.5 15 686 2 22 500 1.75 0.1 20 735 3 23 500 2 0.2 0 784 4 24 500 2.25 0.3 5 588 5 25 500 2.5 0.4 10 637 1
在研究圆角残余应力分布规律时，为了更好地反映一定深度范围内圆角残余应力的平均分布情况，需要对残余应力积分中值进行研究，其计算过程如式（2）所示。
式中，Sa 为残余应力积分中值；Sd 为沿螺栓半径方向上各处的残余应力值；l 为所研究的残余应力分布区间长度，本文中取1/3 螺栓半径长度。正交仿真分析的对象即为上述残余应力积分中值。
2.2 基于正交分析方法的圆角滚压强化仿真
2.2.1 圆角残余应力的分布规律
以残余应力积分中值Sa 为研究对象，得到使其取最小值的滚压加工参数组合，并获得滚压圆角表面的残余应力云图和残余应力沿螺栓半径随距离变化的曲线。图4 所示为典型的螺栓根部圆角表面及内部残余应力分布情况，其中横坐标为对应点到螺栓表面距离与半径长度之比。在计算平均残余应力时，圆角上、中、下的平均残余应力由螺栓的3 个径向角度等分路径对应计算得出，最终的平均残余应力为9 个路径的平均值。结合其余各组仿真结果，螺栓根部圆角残余应力分布曲线变化趋势大致呈现以下规律：在圆角表面的残余应力数值最小，即产生最大残余压应力。随着到圆角表面距离的增加，残余应力数值逐渐增大，在某点处出现转折，残余应力在该点先减小后增大，最终残余应力的大小基本保持不变，在较小的取值范围内波动。此外，在圆角中部到表面一定距离内往往可以取得更小的残余应力；圆角上部在距离表面一段距离后出现了残余拉应力区域；而圆角下部残余应力的变化情况较为剧烈，无明显单调性。
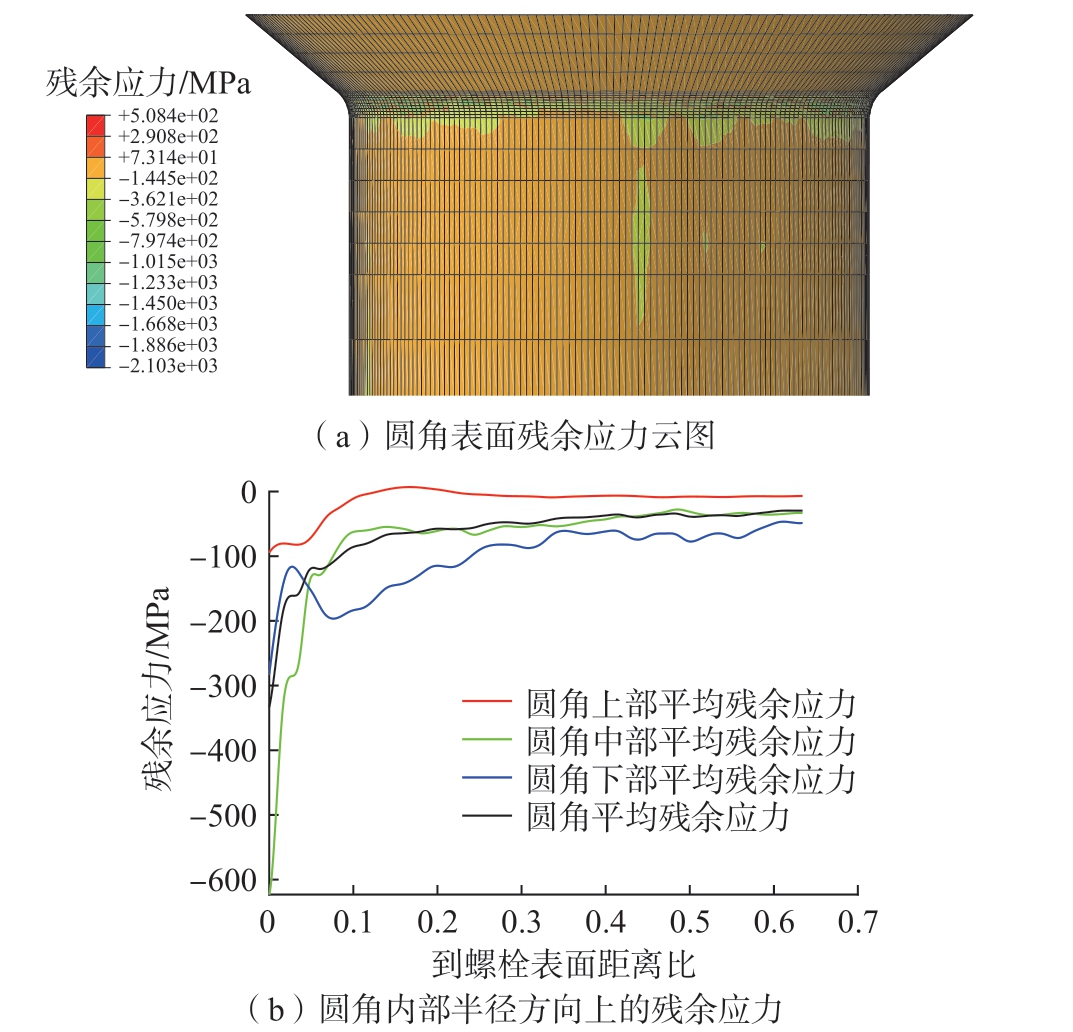
图4 典型螺栓根部圆角表面及内部残余应力分布情况
Fig.4 Distribution of residual stress on root fillet surface and inside of a typical bolt
螺栓根部圆角被滚压的过程中，其表面附近的材料经历了弹性压缩变形、塑性变形和弹性恢复3 个阶段。材料在弹性压缩阶段后会随着滚轮载荷的施加逐渐达到屈服，进而发生塑性变形。螺栓材料的塑性变形将成为其滚压加工后残余压应力的主要诱因。随着滚压过程的进行，滚压载荷将不再对已加工区域发生作用，区域内距离圆角表面较近的材料弹性变形恢复，同时挤压过程中局部材料也会产生拉伸效应，引起内部拉伸变形，因此会出现残余拉应力区域。此外，螺栓根部圆角平均残余应力随着到圆角表面距离的变化规律与TC4钛合金拉伸试验的结果具有一定的相似性[11–12]。出现这种相似性的原因在于，螺栓根部圆角滚压过程从微观时间尺度上看实际上是对材料施加载荷和卸去载荷的过程，并且表面材料的应变在滚压中向螺栓内部传递。螺栓钛合金材料沿径向不同的材料形变，反映了滚压作用下不同载荷作用时刻的材料形变特征。在材料应变率一定的情况下，加载时间与材料应变以及残余应力存在着显著的对应关系。
螺栓根部圆角的上、中、下3 部分 （Path–1，Path–2和Path–3）残余应力分布规律存在差异，是由于滚轮对圆角的接触作用区域主要集中在圆角中部，该区域在较大载荷的直接作用下产生了较大的残余压应力；而因为圆角上部直径较中部略大，且受滚轮直接滚压的作用较小，滚压后其内部的压应力不足以完全抵消圆角上部产生的拉应力，因此出现了残余拉应力区域；而圆角下部则因为直径较小，在实际滚压加工过程中并没有全程受到滚轮的直接作用，故只呈现圆角中部残余应力部分区间的分布特征。
2.2.2 圆角滚压强化仿真结果的正交分析
经过对25 组数据的仿真分析，采用正交方法优选滚压加工参数组合为：滚压速度475 r/min、滚压时间2 s、摩擦系数0.1、涂层厚度15 μm、滚压力637 N。为探究各工艺参数对残余应力积分中值影响程度，对正交仿真结果进行极差分析。圆角滚压残余应力积分中值正交仿真结果的极差分析如表5 所示，其中ki 为同一参数水平下的平均结果，R 为各参数的极差。
表5 残余应力积分中值极差分析
Table 5 Range analysis of integral median of residual stress MPa
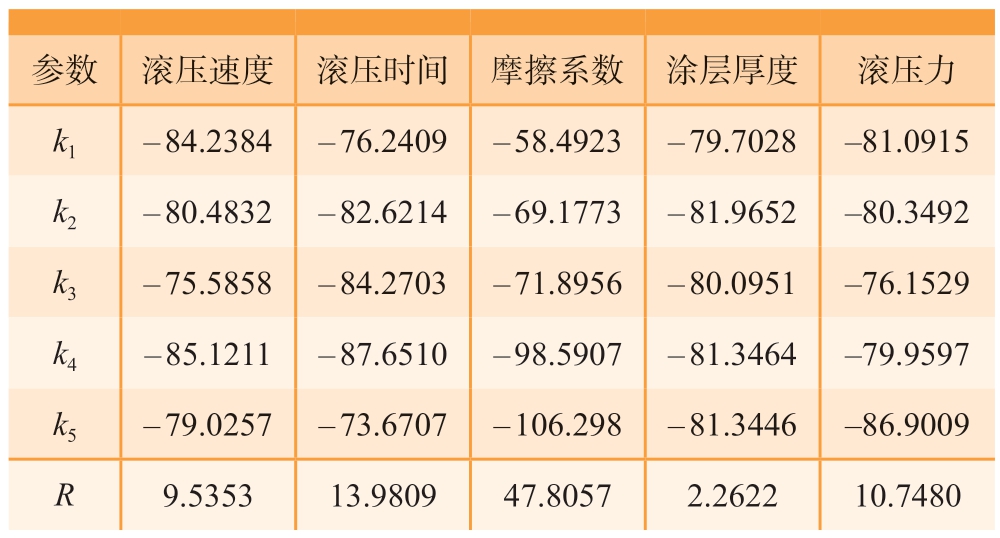
参数 滚压速度 滚压时间 摩擦系数 涂层厚度 滚压力k1 – 84.2384 – 76.2409 – 58.4923 – 79.7028 –81.0915 k2 – 80.4832 – 82.6214 – 69.1773 – 81.9652 –80.3492 k3 – 75.5858 – 84.2703 – 71.8956 – 80.0951 –76.1529 k4 – 85.1211 – 87.6510 – 98.5907 – 81.3464 –79.9597 k5 – 79.0257 – 73.6707 – 106.298 – 81.3446 –86.9009 R 9.5353 13.9809 47.8057 2.2622 10.7480
经分析可知，对于残余应力积分中值，影响程度最大的因素是摩擦系数，影响程度最小的为涂层厚度，其影响程度远小于误差因素，其余工艺参数影响程度由大到小排列顺序为滚压时间、滚压力及滚压速度。值得注意的是，涂层厚度对沿螺栓半径方向某一段距离内平均残余应力的大小几乎没有影响，因此考虑平均残余应力分布情况时可以忽略螺栓表面涂层厚度这一因素。
3 圆角滚压强化工艺的参数优化
3.1 工艺参数优化的数学模型
对螺栓根部圆角的滚压工艺参数进行优化，需要建立以工艺参数为变量的残余应力数学模型。一般情况下多元二次函数可以较准确地描述变量之间的关系，基于这一前提使用回归分析方法建立该数学模型。然而，考虑到仿真结果数据不满足等方差假定，因此采用加权回归分析的方法进行分析。权重取估计值平方的倒数，迭代两次，在Minitab 数据分析软件中可以得到残余应力的回归公式，即
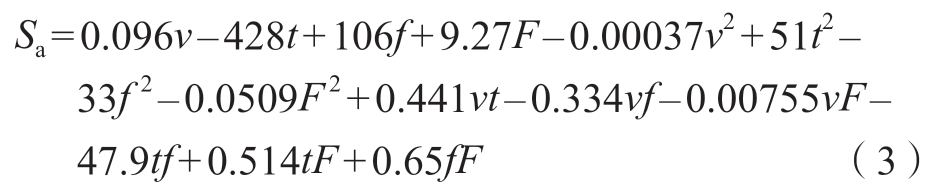
在极差分析中发现涂层厚度对残余应力平均大小的影响可以忽略， 因此在建立数学模型时对于涂层厚度项不予考虑。
根据数学模型的特点，本文采用约束优化问题的复合形法进行求解。针对一般的凸规划问题，复合形法易获得全局最优解。然而，分析前述构建的残余应力–工艺参数模型，发现残余应力目标函数为非凸函数，优化求解过程中可能会陷入局部最优解。因此需要对传统的复合形法进行改进，使优化结果为全局最优点。改进复合形法的实现原理可以表述为：在边界条件约束的范围内取一定数量的初始点，针对不同初始点分别应用复合形法进行优化，最终在所有优化结果当中选择最优点作为全局最优解。改进复合形法的优化算法使用MATLAB 软件编写，其流程框图如图5 所示。
图5 改进复合形法的流程图
Fig.5 Flowchart of improved complex method
3.2 工艺参数优化的计算结果及仿真验证
采用改进复合形法以残余应力积分中值取最小，即残余压应力最大为目标进行参数优化，获得了优化的滚压工艺参数及残余应力积分中值Sa。优化后的滚压工艺参数组合为滚压速度400 r/min、滚压时间2.5 s、摩擦系数0.5、滚压力588 N。采用改进复合形法优化获得的螺栓表面残余压应力为– 124.615 MPa。
利用上述优化后的螺栓根部圆角滚压强化工艺参数进行有限元仿真验证。有限元仿真验证获得的表面残余应力云图及残余应力沿螺栓半径随距离比变化的曲线如图6 所示，其中圆角上、中、下的平均残余应力由螺栓的3 个径向角度等分路径对应计算得出，最终的平均残余应力为9 个路径的平均值。在滚压圆角附近存在显著的残余压应力作用区，而且通过比较前述正交仿真的残余应力云图可知，残余压应力作用区相对均匀，如图6 （a）所示。从图6（b）优化后圆角内部半径方向上的残余应力变化曲线可知，拉应力区域有所减少，平均残余压应力增加。
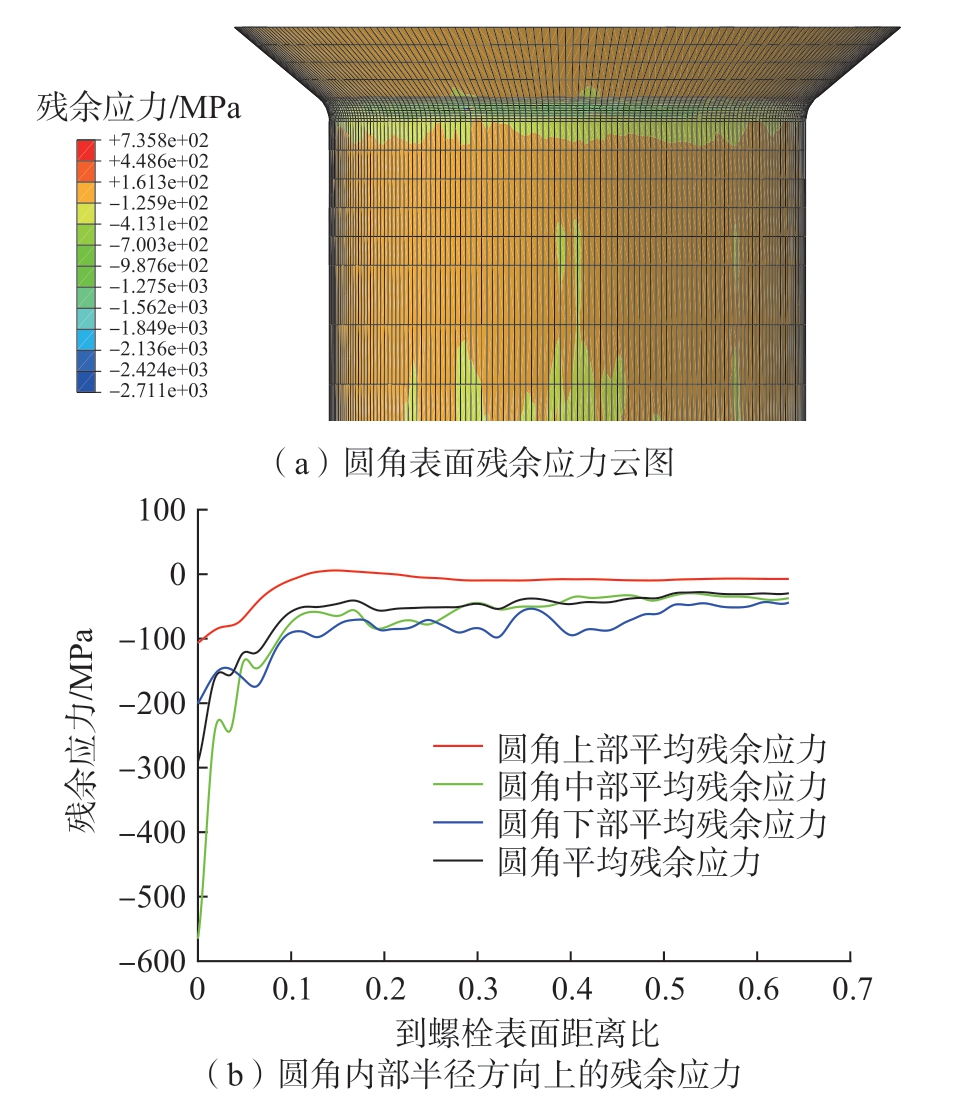
图6 优化后表面及内部残余应力的分布情况
Fig.6 Distribution of surface and internal residual stress after optimization
使用优化后的滚压强化工艺参数，仿真所得到的平均残余应力值为–127.315 MPa。对于以残余应力积分中值为目标的优化结果，优化值与有限元仿真值仅存在2.12%的误差，且残余应力值小于所有经过仿真参数组合的结果，优化的效果较为显著。因此，使用残余应力积分中值作为圆角滚压强化工艺参数优化的目标是可行的，能够有效表征螺栓根部圆角滚压强化的残余应力状态。优化所获得的工艺参数和最大残余压应力将为螺栓根部圆角的滚压工艺提供理论依据。
3.3 工艺参数优化结果的试验验证
采用上述优化后的滚压工艺参数，在自动圆角滚压机床FR–FX2–AC（英国阿斯顿技术有限公司）上对高精度钛合金沉头螺栓进行滚压试验。螺栓采用A6×22–T，材料为钛合金Ti–6Al–4V。图7 为滚压后螺栓外观及根部圆角局部光学显微镜图像。结果表明，螺栓根部圆角滚压后表面光滑平整，无明显的裂纹或其他缺陷，整体滚压质量较高，间接验证了滚压工艺参数优化的有效性。
图7 滚压后螺栓的外观和根部圆角图像
Fig.7 Appearance and root fillet image of bolt afte rolling
4 结论
本文对TC4 钛合金高精度沉头螺栓根部圆角滚压强化工艺进行数值仿真和参数优化研究，获得圆角残余应力的分布规律，构建了工艺参数优化的数学模型，获得了优化后的工艺参数，并采用有限元仿真和试验进行了验证。主要结论如下。
（1）螺栓根部圆角滚压强化后，残余应力分布表现为规律性特征。残余应力积分中值可以有效地描述滚压后螺栓根部圆角内的残余应力。通过对螺栓根部圆角滚压强化后残余应力积分中值的影响分析，得到了关键滚压参数对残余应力积分中值由大到小排列顺序，即摩擦系数、滚压时间、滚压力、滚压速度及涂层厚度。
（2）以螺栓根部圆角残余应力积分中值数值最小，即残余压应力最大为目标，使用改进复合形法完成了参数优化，并采用仿真和试验验证了优化参数的有效性。所获得的优化参数为滚压速度400 r/min、滚压时间2.5 s、摩擦系数0.5、滚压力588 N。
[1] 李蒙, 凤伟中, 关蕾, 等. 航空航天紧固件用钛合金材料综述[J]. 有色金属材料与工程, 2018, 39(4): 49–53.LI Meng, FENG Weizhong, GUAN Lei, et al. Summary of titanium alloy for fastener in aerospace[J]. Nonferrous Metal Materials and Engineering, 2018, 39(4): 49–53.
[2] 朱行欣, 胡晓培. 国内航空航天用高温合金紧固件发展现状[J]. 金属制品, 2023, 49(3): 1–3.ZHU Hangxin, HU Xiaopei. Development status of superalloy fasteners for domestic aerospace[J]. Metal Products, 2023, 49(3): 1–3.
[3] 孙淑玲, 王琦. 航空航天螺纹紧固件失效模式及预防[J]. 航空标准化与质量, 2022(1): 39–43.SUN Shuling, WANG Qi. Aerospace threaded fastener failure modes and prevention[J]. Aeronautic Standardization & Quality, 2022(1): 39–43.
[4] 王燕礼, 朱有利, 杨嘉勤. 滚压强化技术及在航空领域研究应用进展[J]. 航空制造技术, 2018, 61(5): 75–83.WANG Yanli, ZHU Youli, YANG Jiaqin. Rolling reinforcement technology and its research application progress in aviation field[J].Aeronautical Manufacturing Technology, 2018, 61(5): 75–83.
[5] WU D B, LV H R, WANG H, et al. Surface micro-morphology and residual stress formation mechanisms of near-net-shaped blade produced by low-plasticity ultrasonic rolling strengthening process[J].Materials & Design, 2022, 215: 110513.
[6] 刘福超, 雷丽萍, 曾攀. 滚压有限元模型数值模拟[J]. 塑性工程学报, 2012, 19(2): 17–21.LIU Fuchao, LEI Liping, ZENG Pan. Surface rolling FE model for numerical simulation[J]. Journal of Plasticity Engineering, 2012, 19(2): 17–21.
[7] ZHANG B H, NING S P, WEI Z, et al. Simulation and experimental study on roll-forming limit of cup[J]. Materials, 2022, 15(4): 1279.
[8] 惠旭龙, 牟让科, 白春玉, 等. TC4钛合金动态力学性能及本构模型研究[J]. 振动与冲击, 2016, 35(22): 161–168.HUI Xulong, MU Rangke, BAI Chunyu, et al. Dynamic mechanical property and constitutive model for TC4 titanium alloy[J]. Journal of Vibration and Shock, 2016, 35(22): 161–168.
[9] XU X, OUTEIRO J, ZHANG J, et al. Machining simulation of TI6AL4V using coupled Eulerian-Lagrangian approach and a constitutive model considering the state of stress[J]. Simulation Modelling Practice and Theory, 2021, 110: 102312.
[10] ZOU L, WANG T T, WANG C, et al. Modelling and analysis of the effect of nonlinear time-varying contact deformation on flexible precision grinding process[J]. The International Journal of Advanced Manufacturing Technology, 2021, 115(1): 77–89.
[11] 杨洋, 吴凡, 陈玮. 电子束熔丝成形TC17钛合金显微组织与拉伸性能研究[J]. 航空制造技术, 2020, 63(13): 24–29.YANG Yang, WU Fan, CHEN Wei. Investigation of microstructure and tensile properties of TC17 alloy fabricated by electron beam wire deposition[J]. Aeronautical Manufacturing Technology, 2020, 63(13): 24–29.
[12] 喻秋, 李顺才, 邵明辉, 等. 典型航空用合金准静态拉压力学性能研究[J]. 塑性工程学报, 2019, 26(6): 157–167.YU Qiu, LI Shuncai, SHAO Minghui, et al. Study on quasi-static tensile and compressive mechanical properties of typical aerospace alloys[J]. Journal of Plasticity Engineering, 2019, 26(6): 157–167.