闭式整体叶盘叶间流道弯扭狭窄且多以难切削材料制成,采用传统数控铣削加工时存在刀具可达性较差、材料难切削及刀具损耗严重等技术难点;数控电火花加工虽然解决了刀具可达性差和工件材料难切削的问题,但其加工效率低且加工过程中存在电极损耗。电解加工利用电化学阳极溶解原理进行材料去除,具有加工效率高、工具阴极无损耗和不受工件材料机械性能限制等特点,因此在复杂型腔加工中具有技术优势,可使整体叶盘的生产效率和经济性得到较大提升[1]。但电解加工间隙分布规律复杂,特别是对于具有复杂型腔的整体构件,其成形规律有待进一步深入研究。
胡宝文等[2]基于MATLAB 软件求解加工间隙内多物理场耦合方程,以研究成形规律并应用于叶片电解加工;万能等[3]针对传统有限元法在边界计算精度不足的问题,提出等几何法以提高电解加工过程仿真精度;Zhang 等[4]基于电场仿真得出叶片尾缘复杂曲面成形规律并优化了阴极厚度;赵明飞等[5]通过有限元法模拟了球形阴极对工件阳极成形过程的影响,并通过工艺试验对仿真模型的正确性进行了验证;孙伦业等[6]建立了加工间隙数学模型,以分析阴极侧壁绝缘、电解液特性及工艺参数对成形过程的影响,提高了GH4169材料整体叶盘的加工精度;Klocke 等[7–8]则建立了钝化电解液中阳极形貌的预测模型,并对某发动机部件电解加工成形过程进行了跨学科建模。
现有研究主要解决弯扭型面的成形过程建模问题,对复杂深型腔直流和脉冲振动耦合电解加工的动态建模研究较少。针对某型闭式叶盘电解加工时余量分布不均的问题,从叶间流道和阴极几何形状出发,基于型面离散化方法制定流道电解加工成形规律的总体研究方案,并通过工艺试验验证该总体方案的可行性。
1 总体研究方案
闭式整体叶盘叶间流道几何结构复杂,加工过程中材料去除量分布不均,降低了余量分布均匀性,其结构如图1 所示。

图1 闭式整体叶盘叶间流道
Fig.1 Channels of integral shrouded blisk
该流道的拷贝成形加工可采用型面为自由曲面的成形阴极实现,其中叶盆阴极完成无预孔毛坯的开槽与叶盆曲面的拷形加工,叶背阴极则利用加工出的预孔通液,完成叶背曲面的拷形加工。加工过程中,阴极上某点法向速度影响该点到工件阳极表面的法向距离,导致阳极腐蚀速度发生变化,最终影响加工后的工件形状。而法向速度则由阴极进给速度和该点法向与进给方向夹角决定,对于复杂曲面阴极,各点的上述夹角通常不同,各点对应的阳极成形规律因此存在差异,需研究特定点对应夹角处的成形规律。故首先对阴极型面作离散化处理,将其视作由无数条截面线构成,并将截面线离散化为点集;其次建立特定点的成形过程模型,采用规则形状阴极模拟流道的电解加工过程,验证上述模型的正确性;最后将成形规律应用至曲线上所有点,并根据流道加工后的余量实测结果验证各点余量的计算是否可行。
2 特定夹角处成形过程
以叶盆阴极为例,截面线离散化如图2 所示。

图2 阴极截面线离散化
Fig.2 Discretization of cathode section line
则在某点处,阴极表面法向与进给方向夹角为固定值,记为γ。为研究该点对应的阳极表面成形规律,对各点法向与进给方向夹角均为γ 的规则形状阴极加工过程进行分析,其加工间隙如图3 所示。
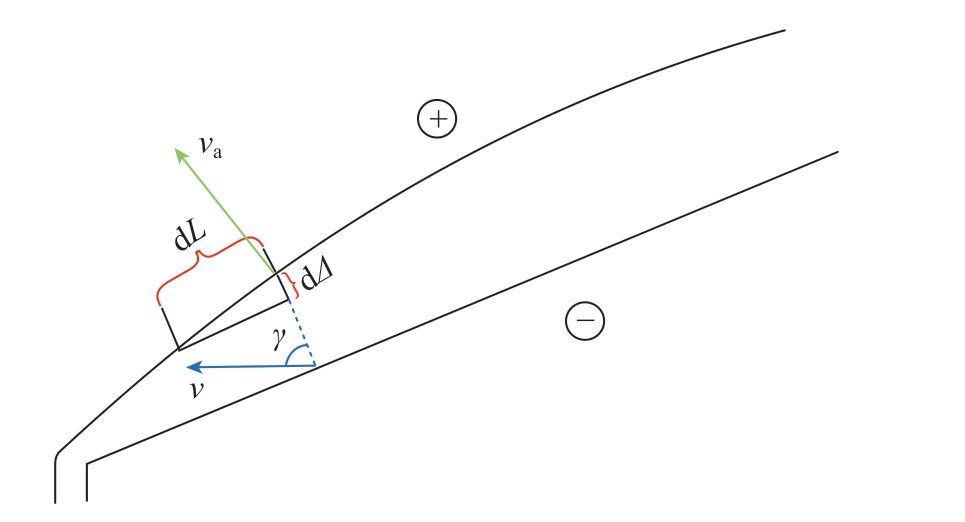
图3 规则形状阴极加工间隙示意图
Fig.3 Sketch map of machining gap of cathode with regular shape
图3 中,v 为阴极进给速度;va 为阳极表面腐蚀速度;Δ 为加工间隙;L 为电解液流程长度。由于流道材料去除量较大且结构弯扭,采用直流电解加工快速去除余量,在阴极进给一段距离后采用脉冲振动耦合电解加工改善流场稳定性。由图3 可得,直流电解加工间隙满足式 (1)微分方程。
式中,η 为电流效率;ω 为工件材料体积电化当量;i 为阳极表面电流密度;t 为加工时间。dΔ/dL 是各点腐蚀速度不均所产生的间隙变化率,在间隙入口处,其仅与γ 角和待加工区几何形状有关,因此可求出其准确值。但在流程长度L 处,该变化率与已加工出的阳极形貌有关,无法求得其准确值,因此用L 差值为0.01 mm 的两点连线斜率近似代替,并引入修正系数k。从而可基于修正的有限差分法建立阴极上各点加工间隙Δn 的方程组,即
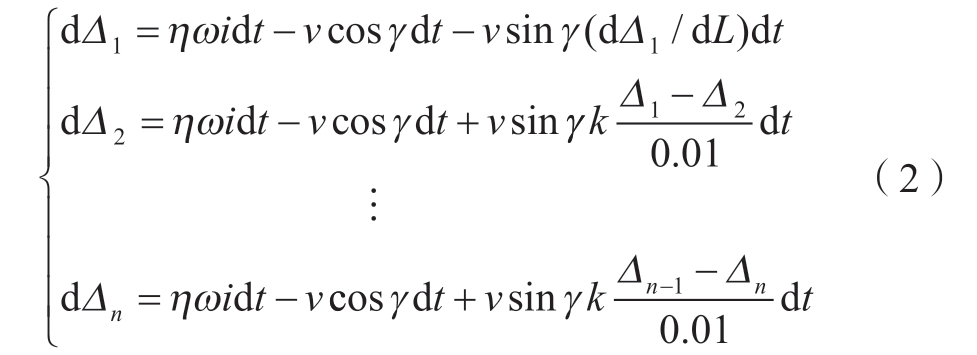
式中,ηω – i 曲线受电解液、工件材料、温度等因素影响,多通过试验测定或基于溶解机理假设进行拟合。工件材料为2Cr13,基于已有研究中的假设及试验结果,将ηω – i 曲线拟合为式 (3)形式[9–13]。
式中,λ、kp、r 是无量纲系数,通过试验数据拟合得到[13]。
采用脉冲振动耦合电解加工时,阴极振动相位和脉冲电源导通角耦合原理如图4 所示,其中,a、b 分别为在1 个振动周期内阴极在靠近、远离工件时的电源导通时长;T 为振动周期。
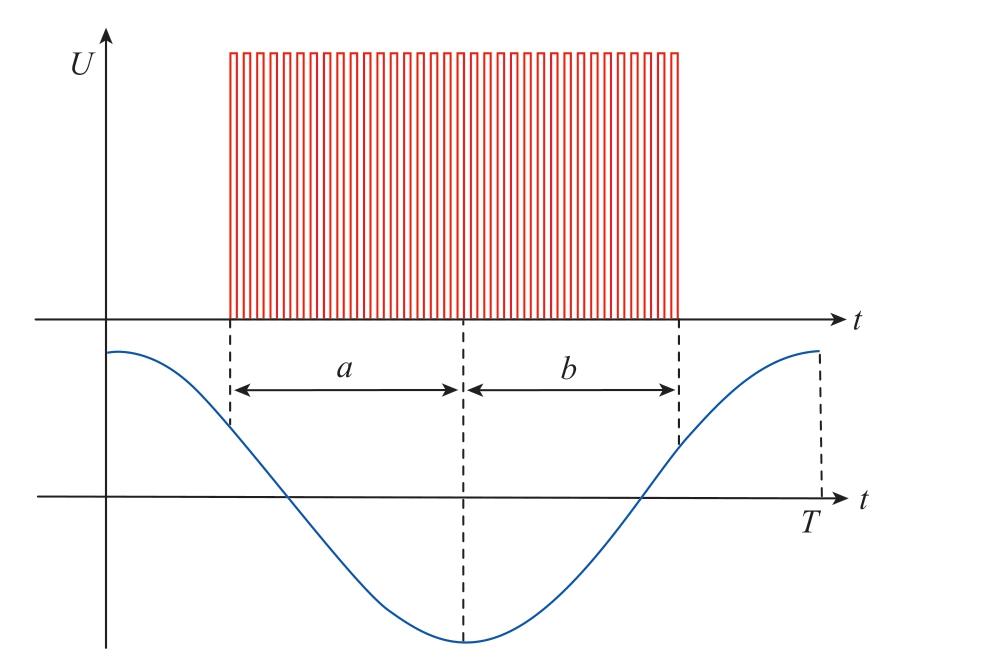
图4 脉冲振动耦合
Fig.4 Pulse-vibration coupling
考虑到引入脉冲函数后计算刚性较差,为提高计算精度,对脉冲电压U 作等效处理,即
式中,![]() 为等效直流电压;f(T1,D)是幅值为1 的脉冲方波函数;T1 为脉冲电源周期;D 为脉冲电源占空比。
为等效直流电压;f(T1,D)是幅值为1 的脉冲方波函数;T1 为脉冲电源周期;D 为脉冲电源占空比。
脉冲振动耦合电解加工间隙可用微分方程描述为
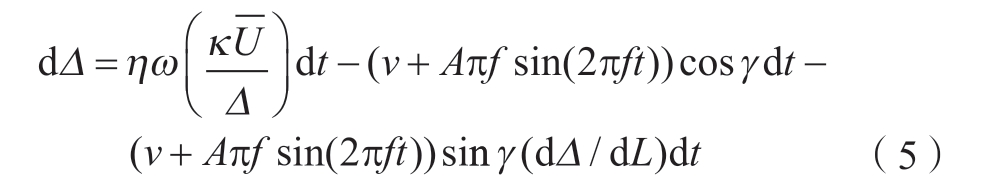
式中,κ 为电解液电导率;A 为阴极振幅;f 为振动频率。求解各点加工间隙时,将式 (5)写成式 (2)形式,求解区间则变为[T/2 – a,3T/2 – a]。其中,在区间[T/2 + b,3T/2 – a]上令腐蚀速度为0 以模拟导通角,并将求解结果作为下一振动周期的初始加工间隙。
由于修正的有限差分法中含有阴极上距离为0.01 mm 的两点法向间隙差值,计算时需以各点初始法向间隙作为初值条件,因此各点初始加工间隙按图5 求取,程序以一定时间步长迭代计算出加工结束时刻的间隙值。
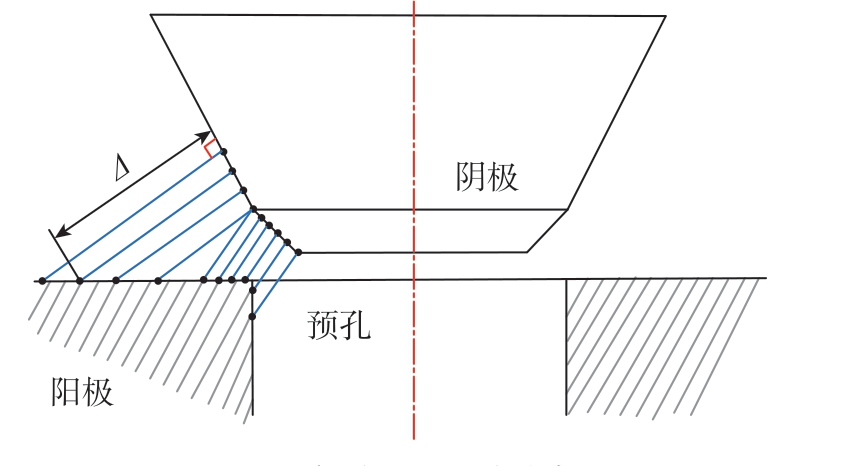
图5 初始加工间隙分布
Fig.5 Distribution of initial machining gap
3 基于DAE 的加工间隙计算
代数微分方程 (DAE)是一种可同时描述多个变量的数学模型,其中部分变量满足代数方程,其余则满足微分方程。直流电解加工阶段,电化学反应持续进行,加工间隙内不断产生氢气泡和焦耳热,使电解液电导率发生变化,应引入计算。
考虑平衡状态,令某点处电解液平均流速u、气泡率β、加工间隙Δ、电解液压力P、温度Te、电导率κ 及部分变量的乘积或导数分别为y1 ~ y9,则相互耦合的物理场满足的代数微分方程为
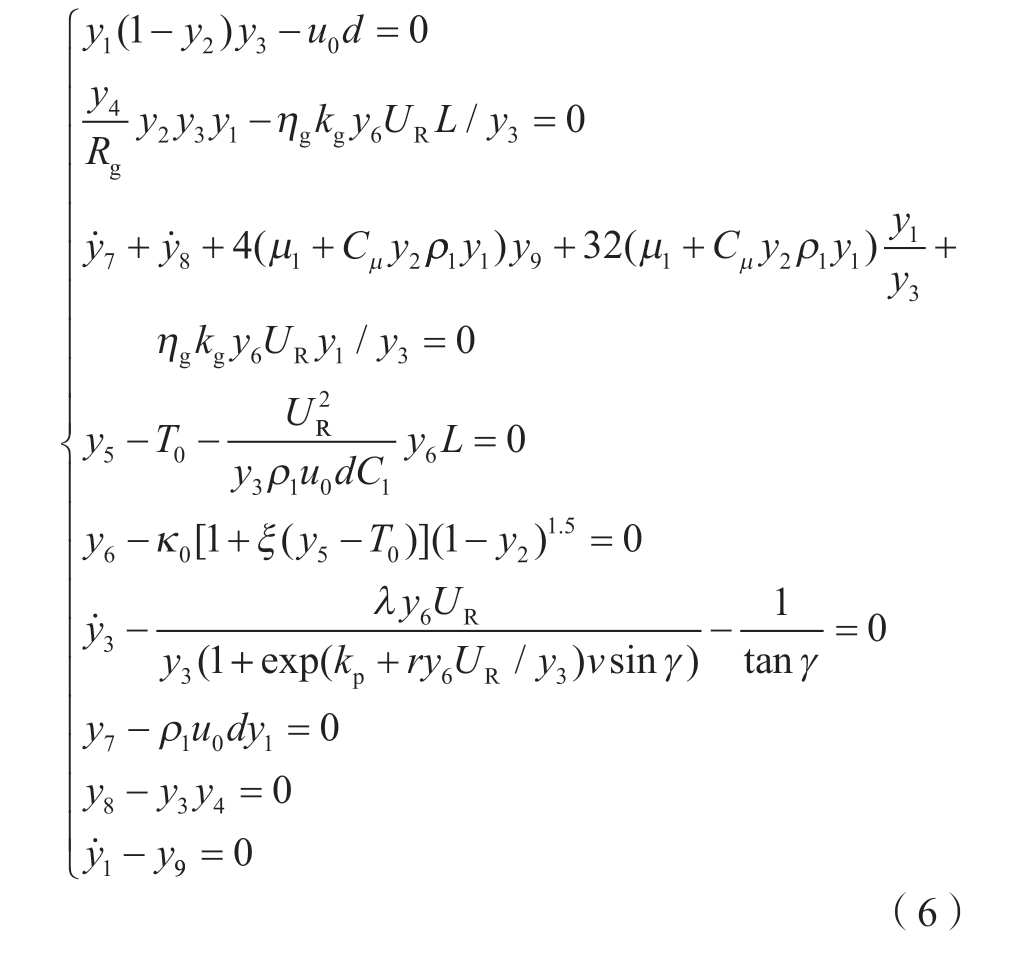
式中,κ0 为电解液初始电导率;ξ 为电导率温度系数,可取0.002;T0 为电解液初始温度;UR 为阴阳极间欧姆压降;ρl为液相密度;Cl为液相比热容; ηg为析氢电流效率;kg 为氢气质量电化当量;Rg 为摩尔气体常数; u0 为间隙入口处流速;d 为间隙入口宽度;µl 为液相动力黏度;Cµ为雷诺应力系数,可取0.6。
计算时,首先设置各物理量初始值和求解的流程长度区间,其中,y3 初始值设为区间起始点对应的加工间隙,则程序以一定流程长度为步长迭代计算出不同流程处加工间隙。
脉冲振动耦合电解加工阶段,由于单个振动周期内腐蚀时间极短,脉冲电源关断后阴极在上抬的过程中使间隙内电解液得到及时更新,维持电导率相对恒定,因此可视电导率为常数,故式 (6)所示DAE 方法已不再适用于脉冲振动耦合电解加工。
4 型腔电解加工数值分析
由于阴极型面为自由曲面,因此式 (5)中增量dL用弧长增量ldγ 代替,l 为阳极上某点曲率半径。从而可得变化率dΔ/dL = dl/ldγ, 改写成有限差分形式则为(Δi–1–Δi)/[(Δi + ρi)γi],其中,ρi 为阴极上某点处曲率半径;γi 为相邻两点γ 角差值。同时拟合图2 所示曲线使其参数化,则可建立阴极上不同点处的脉冲振动耦合电解加工间隙微分方程组,即
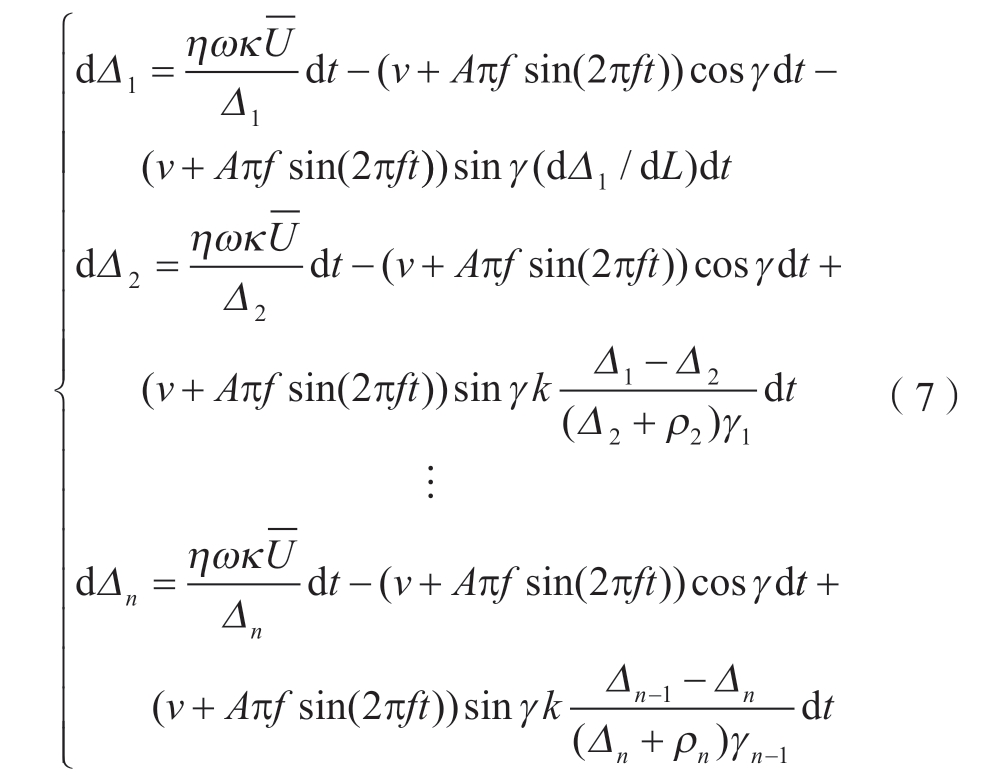
图2 所示曲线参数化拟合结果如图6 所示,据曲线拟合方程即可计算各点对应γ 角。
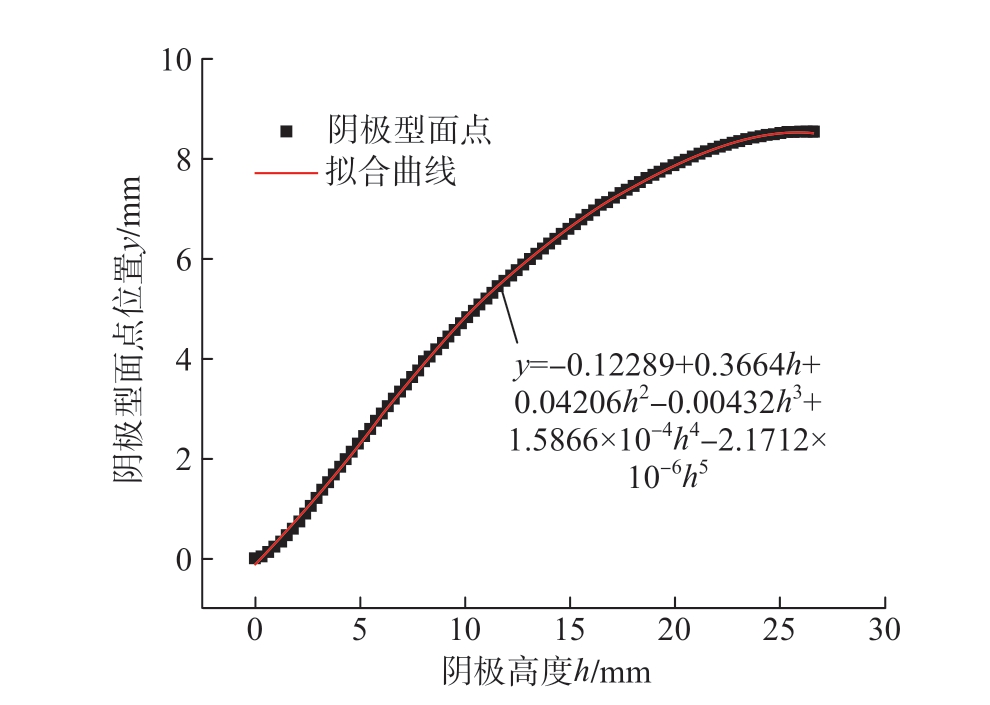
图6 阴极截面线拟合结果
Fig.6 Fitting result of cathode curve
对式 (7)中加工电压和进给速度作替换则将其转化为直流电解加工间隙微分方程组。而在运用DAE 方法时,由于离散化后相邻两点距离极短,因此将相邻两点间曲线近似视为直线,并将前一段流程中各物理量迭代计算结果作为下一段流程初始条件进行赋值,如图7所示。其中,γj 为某点γ 角;y(1+9(j – 1),z) ~ y(9 + 9(j – 1),z)为迭代过程中的物理场变量。

图7 DAE 迭代计算示意图
Fig.7 Sketch map of DAE interation
5 工艺试验及成形规律
5.1 试验准备
为验证曲面上不同点处γ 角对成形过程的影响,取γ 角为90°、80°、60°和45°的典型值进行试验。所用阴极和精密电解加工机床实物分别如图8 和9 所示,电解液主要成分为NaNO3,电导率为8.07 S/m,温度为294.5 K,入口压力和出口背压分别为1 MPa 和0.4 MPa。

图8 阴极实物图
Fig.8 Real products of cathodes

图9 精密电解加工机床
Fig.9 Precise electrochemical machine tool
5.2 试验方法
根据总体研究方案,先对γ 角为90°的柱状阴极采用正流式通液,将试验件加工出预孔,其余角度的阴极利用预孔实现侧流式通液,以模拟流道电解加工过程,如图10 所示。

图10 通液方式
Fig.10 Electrolyte flow mode
5.3 试验结果
针对直流电解加工,运用式 (2)所示修正的有限差分法和式 (6)所示DAE 方法计算加工间隙,并与实测结果对比,优选更准确的计算模型。针对脉冲振动耦合电解加工,验证式 (7)所示修正的有限差分法可行性。为建立复杂型腔在不同加工模式下电解加工间隙分布规律的数学模型提供依据。
(1)直流电解加工试验及分析。
直流电解加工参数如表1 所示,计算及试验实测结果对比如图11 所示,其中k 值为变化步长为0.5 时计算与实测结果最接近的修正系数。由图11(a)和(b)可知,当γ 角为45°和60°时,对于不同的γ 角和工艺参数,计算结果与实测结果接近时k 值变化较大,说明式 (2)所示修正的有限差分法对直流电解加工的适应性较差,而DAE 方法适应性更好,加工间隙的计算值与实测值的变化趋势及大小更为接近。且由图11(c)中1–1 和1 – 2 数据对比可知,当γ 角达到80°时,在相同的加工电压下,阴极对工件侧壁的二次腐蚀随进给速度降低而加剧,加工间隙沿流程逐渐增大,修正的有限差分法已不能反映其变化规律,但DAE 方法仍具有较好的适应性。综上,DAE 方法可更准确地计算直流电解加工时的加工间隙。
表1 直流电解加工参数
Table 1 Parameters of direct current ECM

序号 加工电压U/V 进给速度v/(mm/min) γ角/(°)1 – 1 30 0.40 80 1 – 2 30 0.30 80 1 – 3 20 0.30 80 1 – 4 30 0.50 60 1 – 5 24 0.65 60 1 – 6 20 0.80 60 1 – 7 20 0.90 45 1 – 8 24 0.65 45 1 – 9 20 0.80 45
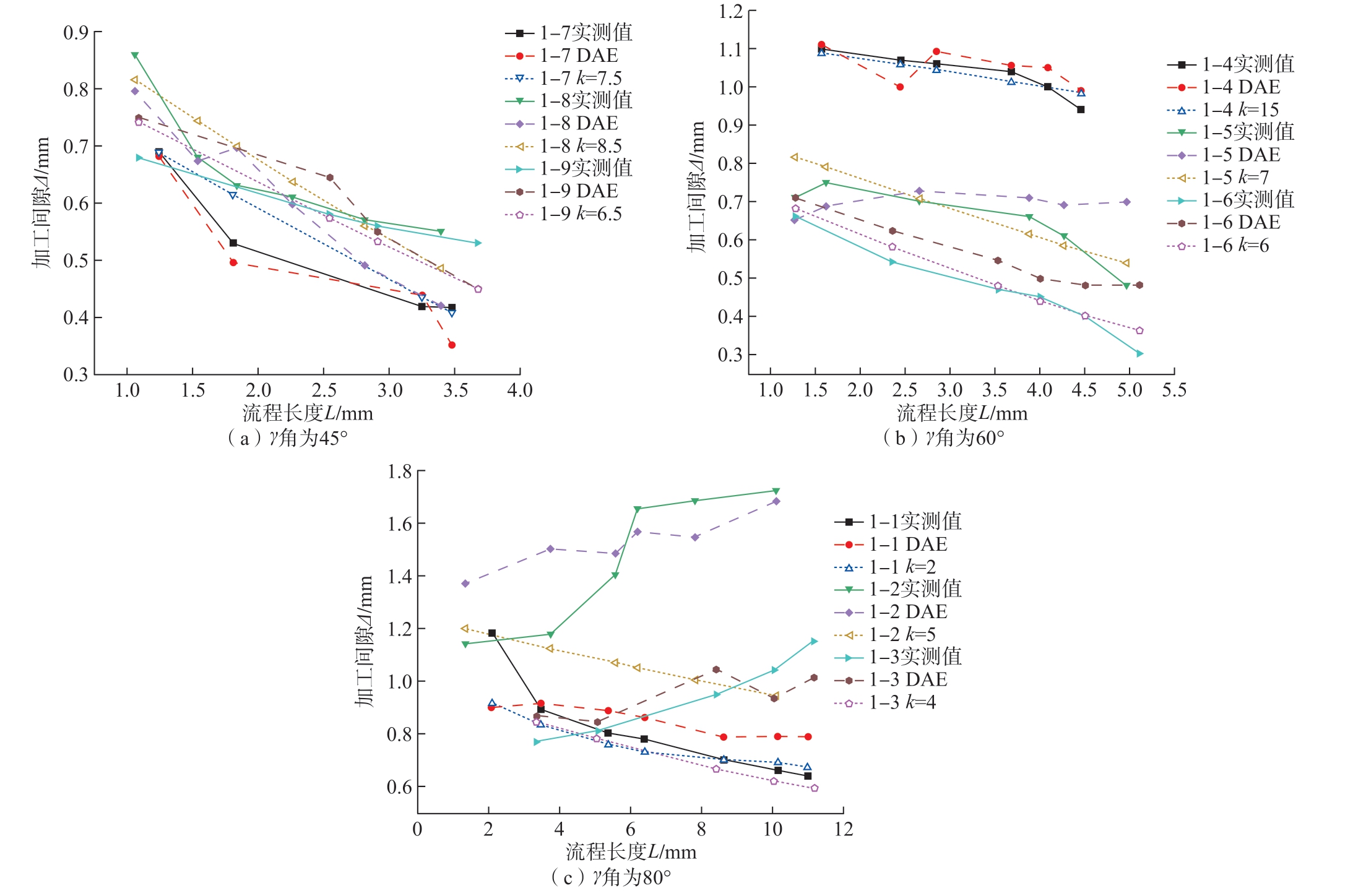
图11 直流电解加工结果对比
Fig.11 Comparison of direct current ECM results
(2)脉冲振动耦合电解加工试验及分析。
脉冲振动耦合电解加工参数如表2 所示,计算及试验实测结果对比如图12 所示。当γ 角为80°时,由于电导率相对恒定,即使以较低进给速度加工,阴极对工件的二次腐蚀作用也相对较小,加工间隙沿流程逐渐减小,因此脉冲振动耦合电解加工可使不同γ 角阴极的加工间隙分布趋于一致,由图12(a)和(b)可知,当γ 角为45°和60°时,k 值对不同工艺参数的适应性较好,但对于不同的γ 角,计算结果与实测结果接近时k 值变化较大,故式(7)所示修正的有限差分法应用于复杂型腔时,对γ 角较小的点,其微分方程的k 值拟按该点处γ角线性插值。由图12(c) 中2–1 和2–4 数据对比可知,当γ 角达到80°时,k 值对占空比的适应性较差,故应用于复杂型腔时,对γ 角≥80°的点,其微分方程的k 值拟按占空比参数线性插值,以更准确地计算不同工况条件下脉冲振动耦合电解加工时的加工间隙。
表2 脉冲振动耦合电解加工参数
Table 2 Parameters of pulse-vibration coupling ECM

序号 加工电压U/V 占空比D 导通角度θ/(°) 振动频率f / Hz 进给速度v/(mm/min) γ角/(°)2 – 1 30 0.6 240 30 0.40 80 2 – 2 30 0.6 240 30 0.35 80 2 – 3 32 0.6 240 30 0.40 80 2 – 4 30 0.8 200 30 0.40 80 2 – 5 20 0.6 240 30 0.70 60 2 – 6 20 0.6 240 30 0.80 60 2 – 7 18.5 0.6 240 30 0.80 60 2 – 8 18.5 0.8 200 30 0.80 60 2 – 9 24 0.6 240 30 0.80 45 2 – 10 20 0.6 240 30 0.80 45 2 – 11 20 0.8 200 30 0.80 45

图12 脉冲振动耦合电解加工结果对比
Fig.12 Comparison of pulse-vibration coupling ECM results
(3)闭式整体叶盘电解加工试验及分析。
开展闭式整体叶盘电解加工试验,闭式整体叶盘电解试验件如图13 所示,并采用三坐标测量机测量叶片对应截面的余量值,将其与计算结果进行对比。依据规则阴极试验结论,将DAE 方法和修正的有限差分法分别用于复杂型腔的直流和脉冲振动耦合电解加工间隙预测,修正系数 k 按γ 角插值,在γ 角达到 80°时修正系数则按占空比插值,修正系数k 线性插值图如图14 所示。电解加工后的叶片对应截面线余量分布的实测值和计算值对比如图15 所示,可知,理论余量值与实测值变化规律基本一致,最大误差控制在0.15 mm,满足闭式整体叶盘电解加工工序要求,所建立的电解加工间隙计算模型可较准确地反映实际加工间隙分布。

图13 电解加工后的闭式整体叶盘试验件
Fig.13 Closed integral disc test piece after ECM

图14 修正系数插值图
Fig.14 Sketch map of correct factors interpolation
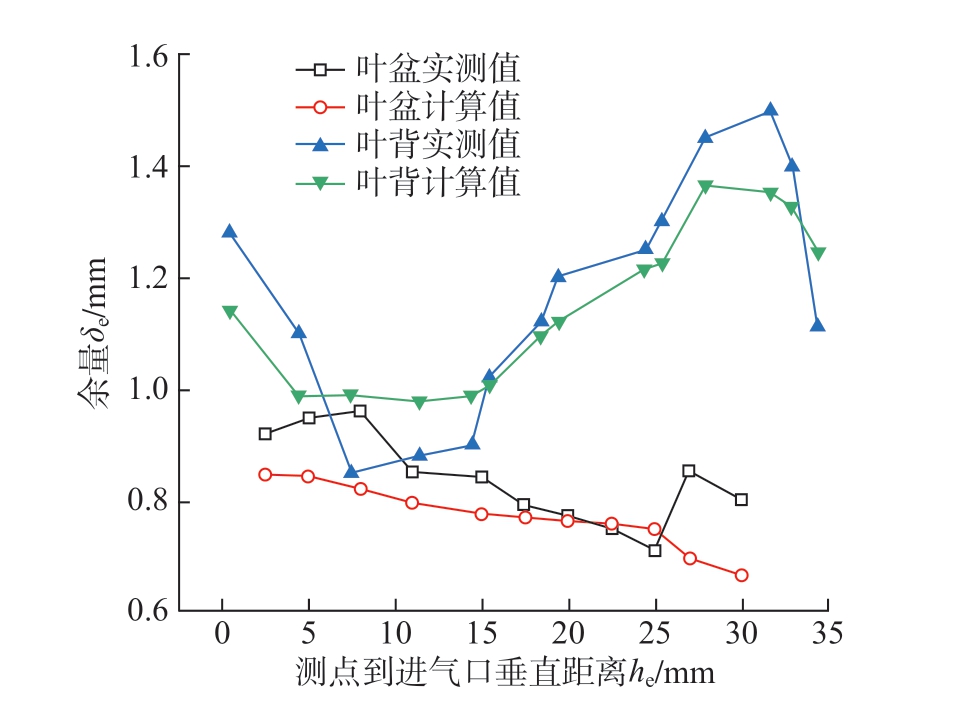
图15 叶片对应截面线余量分布
Fig.15 Distribution of blade corresponding cross-sectional line margin
6 结论
以型腔电解加工为研究对象,通过修正的有限差分法和DAE 方法建立加工间隙微分方程模型,并进行加工间隙分布工艺试验验证。得到结论如下:
(1)建立规则形状阴极加工间隙微分方程并开展验证试验,分析特定γ 角对应的电解加工分布规律,并通过离散化复杂形状阴极,最终得到阴极各离散点处对应加工间隙的计算模型;
(2)微分方程可行性验证试验结果表明,DAE 方法和修正的有限差分法分别适用于闭式整体叶盘流道的直流和脉冲振动耦合电解加工;
(3)对电解加工后闭式整体叶盘叶盆、叶背的余量检测结果显示,除进排气边等未加工的区域外,叶片对应截面线处的余量分布规律与计算值基本一致,最大误差控制在0.15 mm,验证了流道曲面电解加工间隙计算过程的正确性。
[1] 张明岐, 张志金, 黄明涛. 航空发动机压气机整体叶盘电解加工技术[J]. 航空制造技术, 2016, 59(21): 86–92.ZHANG Mingqi, ZHANG Zhijin, HUANG Mingtao.Electrochemical machining technology of aeroengine compressor blisk[J].Aeronautical Manufacturing Technology, 2016, 59(21): 86–92.
[2] 胡宝文, 穆瑞元, 黄亮, 等. 航空叶片电加工多物理场耦合仿真及试验研究[J]. 制造技术与机床, 2021(9): 43–48.HU Baowen, MU Ruiyuan, HUANG Liang, et al. Multi-field coupling simulation and experimental research on aero blade electrolytic machining process[J]. Manufacturing Technology & Machine Tool,2021(9): 43–48.
[3] 万能, 段永吉, 张森堂, 等. 基于等几何法的叶片电解加工过程仿真方法研究[J]. 航空制造技术, 2016, 59(22): 40–47.WAN Neng, DUAN Yongji, ZHANG Sentang, et al. Research on blade electrochemical machining process simulation based on isogeometric method[J]. Aeronautical Manufacturing Technology, 2016,59(22): 40–47.
[4] ZHANG J C, ZHU D, XU Z Y, et al. Improvement of trailing edge accuracy in blisk electrochemical machining by optimizing the electric field with an extended cathode[J]. Journal of Materials Processing Technology, 2016, 231: 301–311.
[5] 赵明飞, 傅秀清, 干为民, 等. 球形阴极电解成形过程仿真试验研究[C]//第16 届全国特种加工学术会议论文集(上). 哈尔滨: 哈尔滨工业大学出版社, 2015: 491–495.ZHAO Mingfei, FU Xiuqing, GAN Weimin, et al. Research on forming process of spherical cathode ECM by simulation and experiments[C]//Proceedings of the 16th National Conference on Non-Traditional Machining (Part I). Harbin: Harbin Institute of Technology Press, 2015: 491–495.
[6] 孙伦业, 徐正扬, 朱荻. 镍基高温合金整体叶盘叶栅通道电解加工的成形精度控制[J]. 机械科学与技术, 2013, 32(8): 1230–1234, 1238.SUN Lunye, XU Zhengyang, ZHU Di. The accuracy control of Nibased superalloy blisk channels by electrochemical machining[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(8): 1230–1234,1238.
[7] KLOCKE F, HARST S, ZEIS M, et al. Modeling and simulation of the microstructure evolution of 42CrMo4 steel during electrochemical machining[J]. Procedia CIRP, 2018, 68: 505–510.
[8] KLOCKE F, ZEIS M, KLINK A. Interdisciplinary modelling of the electrochemical machining process for engine blades[J]. CIRP Annals, 2015, 64(1): 217–220.
[9] LOHRENGEL M M, KLÜPPEL I, ROSENKRANZ C, et al. Microscopic investigations of electrochemical machining of Fe in NaNO3[J]. Electrochimica Acta, 2003, 48(20–22): 3203–3211.
[10] MAYANK G, CHU F C, MASANORI K. Analysis of reactions determining current efficiency in electrochemical machining[J].Procedia CIRP, 2018, 68: 511–516.
[11] 葛媛媛, 徐家文, 赵建社, 等. 镍基高温合金GH4169 电解加工ηω – i 曲线测定[J]. 宇航材料工艺, 2006, 36(4): 38–41.GE Yuanyuan, XU Jiawen, ZHAO Jianshe, et al. Research on characteristic of ηω – i in ECM high temperature nickel alloy(GH4169)[J].Aerospace Materials & Technology, 2006, 36(4): 38–41.
[12] 王蕾. 发动机叶片高精度电解加工阴极设计系统及实验研究[D]. 南京: 南京航空航天大学, 2006.WANG Lei. The study on precisely cathode design system of turbine blades and experiments in electrochemical machining (ECM)[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2006.
[13] 柳傲. 恒间隙法测定电解加工电流效率曲线研究[D]. 南京:南京航空航天大学, 2017.LIU Ao. Investigation on the current efficiency curve measured with constant interelectrode gap in electrochemical machining[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2017.