飞机蒙皮具有尺寸大、难加工的特点，在这种薄壁类零件上铣出减重槽成为加工中的难点。化学铣削能有效加工复杂曲面零件和难加工材料，是薄壁类零件加工的主要方法。化铣首先要在零件表面涂覆一层可去除的保护性胶膜，然后通过刻型划线的方式确定需要化铣的区域并去除待加工区域的保护性胶膜，将零件浸入化铣池中，从而对没有胶膜的区域进行化学腐蚀加工[1]。
飞机蒙皮要求其表面光滑、无划伤，因此化铣过程中刻型工艺至关重要。传统的化铣刻型工艺采用人工刻线方式，需要借助加工样板、定位销等工具，该方式生产效率低下、劳动强度大、成本高，并且加工精度受样板精度和操作人员熟练度的影响，容易出现化铣区根部缺陷[2]。近年来五轴激光刻型机逐步发展，通过数控刻型技术能够实现在保护性胶膜上刻型出需要铣切的形状，大大提升了刻线的精度和效率。
刻型线精度检测是激光刻型工艺的关键，传统的样板比对方法需要技术人员通过肉眼判断，当测量大型曲面零件时会存在检测效率低、结果可靠性差的问题，已经无法满足激光刻型高效率、高精度的检测需求。在机测量技术是当前加工测量领域自动化、高效化的发展趋势，为实现高效、高精度的刻型线精度检测技术提供了研究方向[3–4]。在机精度检测包括接触式和非接触式测量方法。接触式测量方法通过探针与被测零件表面逐点接触能够实现微米级的测量精度，因此被广泛应用于复杂曲面轮廓在机测量。Huang 等[5]采用接触式测量探头对火箭贮箱箱底零件进行在机测量，提高了箱底零件的加工轮廓精度。Rahman 等[6]采用接触式测量探头实现了对球面磨削零件的在机轮廓测量。陈岳坪等[7]采用接触式测量探头对零件进行在机测量并实现了曲面重构和加工误差补偿，但接触式在机测量效率低，难以适用于大尺寸飞机蒙皮的轮廓精度测量。非接触式测量效率高，在大尺寸飞机蒙皮检测方面有明显优势。非接触测量主要包括激光测量、视觉检测等方案。张旭苹等[8]通过立体视觉测量系统实现大尺度三维几何尺寸的测量。全燕鸣等[9]将双目相机安装到机床主轴上，实现工件尺寸的三维在机测量。童康康等[10]通过双目相机的视觉检测方式对激光刻型精度进行检测，但该方法难以获取刻型槽的槽深信息，在复杂工作环境下视觉检测的精度和稳定性仍存在问题。激光测量能够对大范围曲面零件进行高精高效测量[11–12]，例如，Liu 等[13]将激光传感器集成到铣槽加工机床中，实现了薄壁件外轮廓的高效测量；Song 等[14]基于激光扫描仪来测量飞机蒙皮表面轮廓，并对比了不同算法对曲面法向测量精度的影响；Zeng 等[15]基于线激光对箱底零件焊缝宽度进行测量，实现了0.3 mm 焊缝的精准检测；石循磊等[16]基于线激光扫描飞机表面轮廓，实现锪窝孔参数的快速提取；章绍坤[17]建立了2D 线激光曲面在机测量系统，大幅提高曲面轮廓特征精度。
化铣激光刻型在机检测与传统的在机检测都是利用机床本身的运动实现工件表面轮廓的在位测量。两者区别在于化铣激光刻型线的槽宽在0.5 mm 左右且截面呈V 形，一般的在机测量 （如红宝石接触探头）难以测量这种狭小区域，并且飞机蒙皮长度可以达到几 m，接触式测量方法效率低下，不适合大范围轮廓检测；非接触测量 （例如视觉在机检测）难以准确测量刻型槽的槽深信息，测量精度有待提高。而线激光能够实现快速扫描测量，测量分辨率和精度高，适用于大型飞机蒙皮刻型槽的轮廓的扫描。
综上所述，现有方法主要针对曲面轮廓进行精度检测，但是在激光刻型线的在机精度检测方面，尚未发现已发表的线激光技术的相关应用，因此亟须基于2D 线激光开发出高效率、高精度的化铣激光刻型在机精度检测技术，替换传统的人工检测方法，提高化铣激光刻型工艺的准确性和效率，保证化铣刻型的产品质量。
针对化铣激光刻型在机精度检测的需求，本文研究了基于2D 线激光的化铣激光刻型工艺在机精度检测技术，并通过激光刻型在机精度检测试验验证了所提出方法的有效性。
1 激光刻型在机精度检测系统运动学变换
化铣激光刻型在机精度检测系统的运动部件为五轴激光刻型机和线激光器。五轴激光刻型机实现了对曲面工件的激光刻型加工，线激光器偏置安装于激光刻型机末端，根据预定的轨迹沿刻型线进行扫描。为获得刻型线的点云数据，需要建立线激光传感器与五轴激光刻型机的运动学模型，确定激光测量坐标系与工件坐标系之间的变换关系。
1.1 五轴激光刻型机运动学模型
为得到激光测量坐标系 （Laser-sensor coordinate system，SCS）与 工 件 坐 标 系 （Workpiece coordinate system，WCS）之间的变换关系，建立图1 所示的测量系统运动学模型，可得测量系统的坐标变换链[18]，即
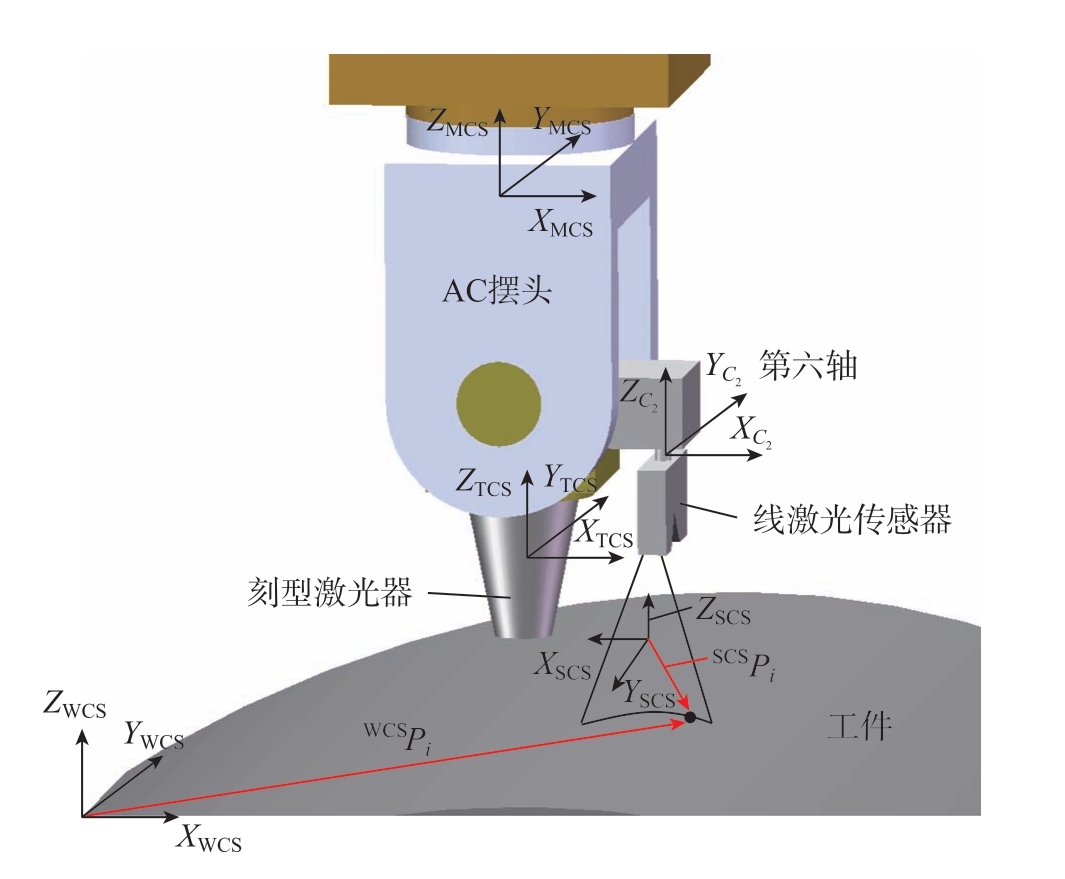
图1 线激光在机精度检测系统运动学模型
Fig.1 Kinematic model of on-machine accuracy measurement system based on 2D laser profile
式中，WCSPi 和SCSPi 分别为线激光采样点i 在WCS 和SCS 下的齐次坐标向量；
和
分别为工具坐标系（Tool coordinate system，TCS）到WCS 和SCS 到TCS的齐次变换矩阵。
可以根据五轴机床正运动学获得，以本研究使用的龙门式AC 双摆头激光刻型机为例，WCS 到TCS的坐标变换矩阵为
式中，
为WCS 到机床坐标系 （Machine coordinate system，MCS）的齐次变换矩阵；
为C 轴坐标系到MCS 的齐次变换矩阵，3 个平动轴的变换矩阵也集成于齐次变换矩阵
中；
为A 轴坐标系到C 轴坐标系的齐次变换矩阵；
为TCS 到A 轴坐标系的齐次变换矩阵。
实际测量过程中，数控系统会将运动学变换集成，因此式 （2）可简化为
式中，WCSPt 表征3 个平动轴对结果的影响，通常基于刀具末端中心在 WCS 的坐标，设定刀长为 0，通过3 个平动轴位置坐标获取WCSPt；WCSRt 是由A 轴和C 轴的位置得到的旋转矩阵；a 和c 分别表示A 轴和C 轴相对于初始位置转过的角度。
1.2 线激光传感器运动学模型
如图2 所示，线激光传感器单次采样会采集XZ 平面内的N 个测点，X 轴方向的分辨率为δ，第i 个测量点Z 轴方向的数据为di，因此SCSPi 的表达式为
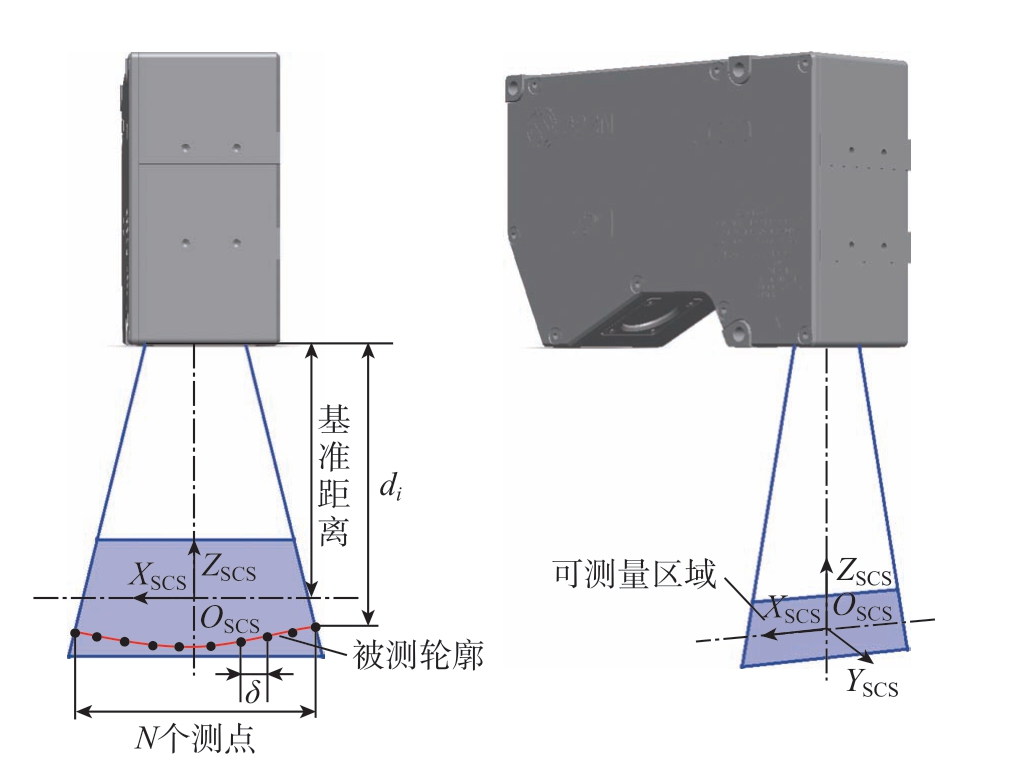
图2 激光测量坐标系示意图
Fig.2 Schematic diagram of laser-sensor coordinate system
对于未能接收到反射激光的测点，激光器将返回异常值作为提示，因此对无效数据需要进行剔除以免干扰正常的测点数据。
激光刻型槽的截面形状都是向外开放的凸多边形，当线激光沿垂直于刻型槽截面方向测量不会出现遮挡。如果工件曲率过大，可能存在测量头部分与工件干涉的情况，导致不能满足线激光垂直于刻型槽截面方向测量。本研究中的应用对象 （飞机蒙皮）大都为小曲率曲面，因此在实际应用中并未出现刻型槽由于角度无法检测完全的问题。
由于测量过程中线激光和刻型槽需要保持垂直以精确测量刻型槽截面轮廓，因此需要在机床末端增加平行于线激光轴向的第6 轴，将线激光器固连在第6 轴上，
可以通过线激光器的位姿标定获得，即
式中，
为第6 轴β2 坐标系到TCS 的齐次变换矩阵，LTCS, C2, x、LTCS, C2, y、LTCS, C2, z 为C2 轴坐标系原点在TCS 坐标系中的位置坐标。
表示SCS 和第6 轴坐标系之间的位姿关系，在线激光安装完成后，该矩阵可视为一常数矩阵，通过3个欧拉角参数和3 个位移参数表示，即
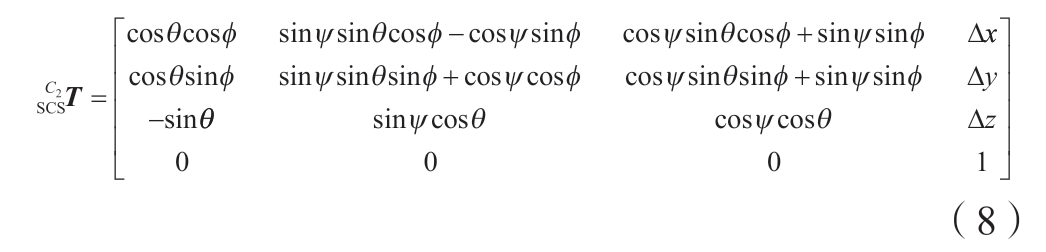
式中，章动角θ、旋进角Ψ 和自转角φ 为3 个欧拉角参数，Δx、Δy、Δz 为 SCS 原点在第6 轴坐标系中的三维坐标表示，此6 个常数参数即为待标定量，可通过线激光器位姿标定求解。
在实际线激光器位姿标定过程中，通常将机床旋转轴置于零位，于是式 （1）可简化为
式中，WCSPi = [xi yi zi 1]T 由三坐标测量机基于工件坐标系测量标定块得到，其标定方法可使用文献[17]所述的激光传感器安装位姿标定实现，SCSPi 可由线激光数据得到，因此构建出测量方程为
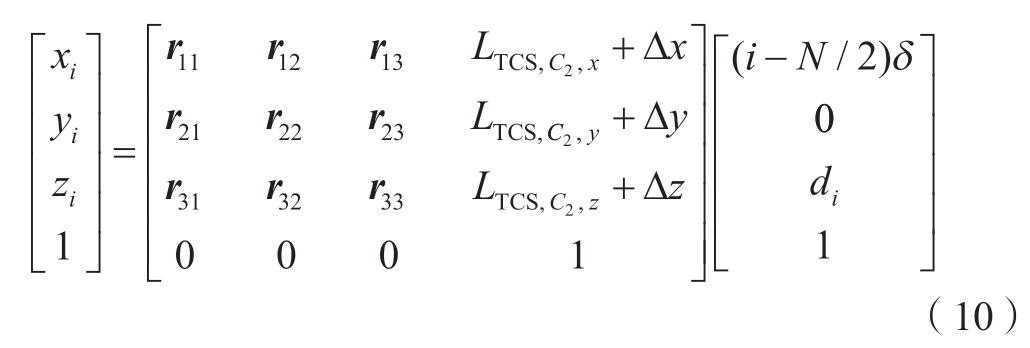
式中，rjk 为旋转矩阵分量，测量多个测点数据能够构造超定方程组，通过最小二乘拟合可以得到变换矩阵
。
综上，通过构建激光测量坐标系与工件坐标系之间的变换关系，在实际测量过程中基于线激光传感器测得的任意点i 在SCS 中的位置SCSPi，结合式 （1）即可解算出该点在工件坐标系中的位置，从而获得刻型线扫描的实际三维点云，为刻型线精度检测与评价奠定基础。
2 刻型线精度检测与评价方法
为了提高刻型线扫描的效率，通过后处理软件修改激光刻型加工的ATP 文件生成扫描轨迹，扫描得到连续多帧数据，每一帧记录一个时刻的线激光数据以及对应的刀轴坐标。对每一帧的线激光数据进行处理，提取出单帧刻型槽截面轮廓特征，通过各单帧特征提取结果对刻型线轮廓进行重构，并计算激光刻型轮廓加工精度。
2.1 刻型槽截面轮廓特征提取算法
首先对每一帧数据进行预处理，剔除原始测量数据中的异常值。由于刻型槽宽度远小于相邻刻线之间的距离，为避免单帧截面扫描数据中存在多个相邻刻型槽影响，可截取中间t 个数据作为特征提取的区域。t 可根据刻型槽实际宽度设置，将截取后的数据集记为{（xi，zi）|1≤i≤t}。
截取的单帧刻型槽截面轮廓数据如图3 所示，包含表面段和凹槽段两部分，槽宽和槽深的定义见标注。采用连续函数模板匹配的方式提取刻型槽的特征，基于双曲正切函数构造刻型槽截面模板函数为
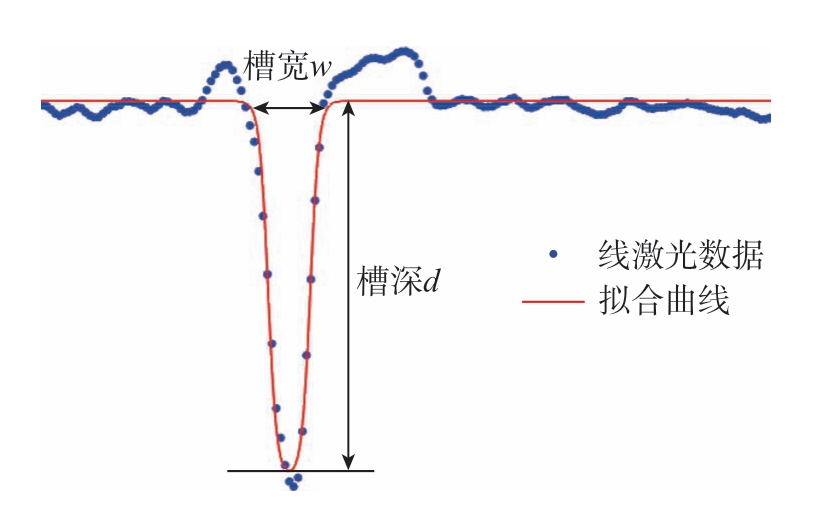
图3 刻型槽截面轮廓特征
Fig.3 Section profile characteristics of g ooves
式中，x0 表示刻型槽的中心位置；z0 表示表面段的纵坐标；d 和w 分别表示刻型槽的深度和宽度；α 表示相似系数。
根据实际刻型槽截面恰当选取近似α 值，绘制不同α 值的拟合结果，如图4 所示。可以看出，针对实际刻型槽形状，当α 值为20 时拟合效果最好，后续计算中α值均取为20。使用实际数据到拟合函数的距离作为拟合精度的评价指标，计算结果表明该方法的拟合精度为（0.0081±0.0072） mm。以槽深为例，拟合误差为2.59%，因此该拟合方法能够准确提取刻型槽的特征。
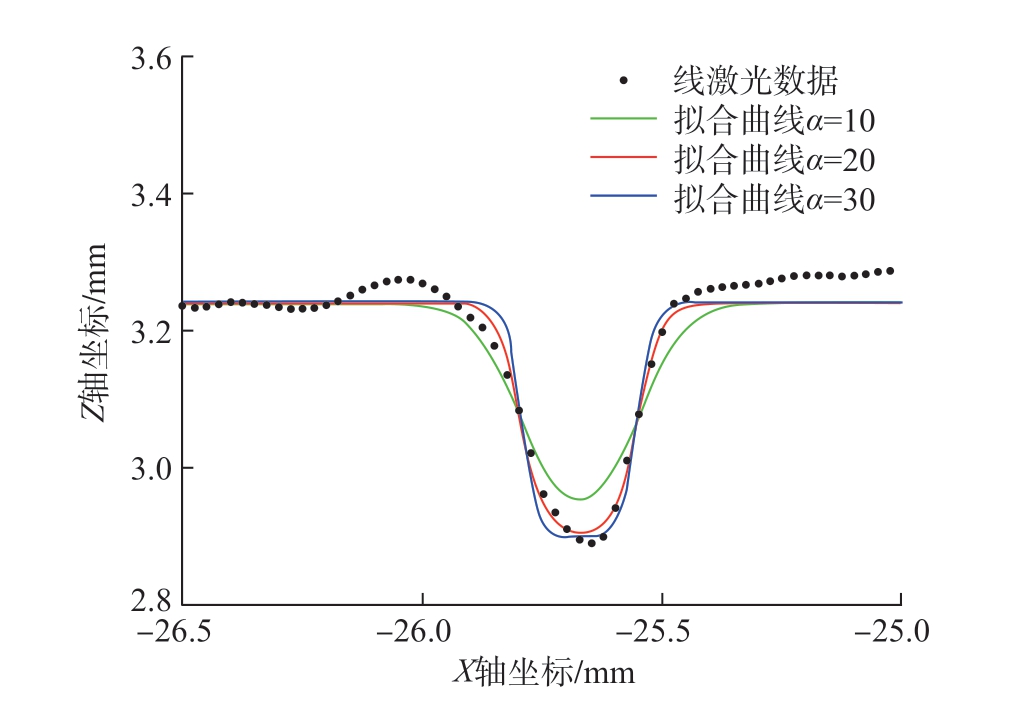
图4 不同α 值对拟合结果的影响
Fig.4 Influence of diffe ent α on the fitting esults
使用双曲正切模板函数的前提是数据表面段水平，而测量得到的截面轮廓数据可能整体具有一定倾角，因此需要首先对数据进行水平修正。
通过拟合表面段直线能够得到实际数据与水平数据之间的变换关系，对整个数据集进行直线拟合，搜索数据集中距离直线最远的点记为槽底点 （xd，zd）。对于i∈[1，t]，满足条件为
式中，k1 和b1 为拟合的直线的斜率和截距。
确定槽底点后，截去凹槽段特征，将槽底点左右l/δ个点去除，l 表示槽宽的预设值，可以通过预先测量获得。对去除凹槽特征后的数据集重新进行直线拟合得到表面段直线方程，斜率和截距分别为k2 和b2。
将原数据集旋转到水平，旋转变换表示为
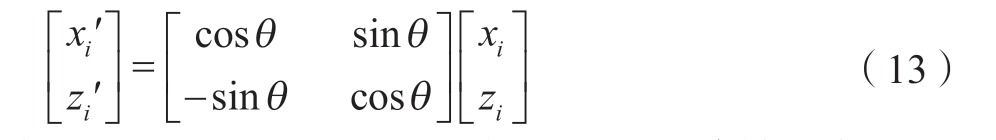
式中，θ = arctank2； （xi′，zi′）表示（xi，zi）旋转到水平后的点。
采用式 （11）中的连续函数作为模板对旋转后的数据集{（xi′，zi′）| 1≤i≤t}进行拟合，设未知参数X=[x0′，z0′，d，w]，可构建如下最优化问题。
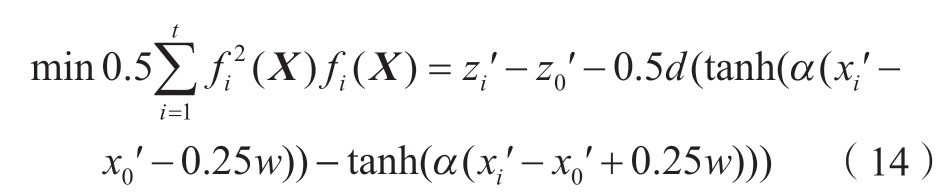
式 （14）为典型的非线性最小二乘问题，可采用Levenberg-Marquardt 算法[19]对该优化问题进行求解，具体求解步骤如下。
（1）计算雅可比矩阵。
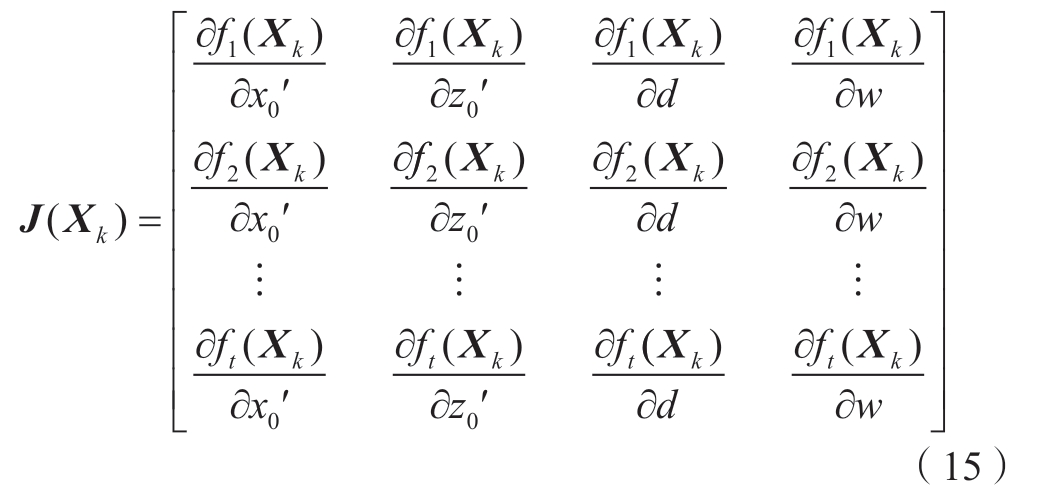
（2）列出增量方程。
式中，H（Xk）=J（Xk）J（Xk）T 表示海塞矩阵；g（Xk）= – J（Xk）f（Xk）；D 为系数矩阵，一般取为单位阵。
（3） 更新阻尼因子µ，其更新策略如下。
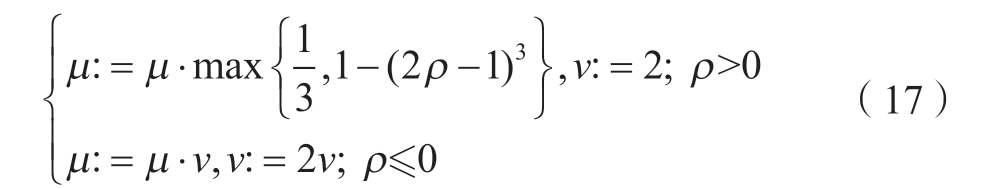
式中，ρ 为比例因子，计算方式为
（4）计算下一步迭代的参数值。
（5）判断新的参数值是否满足迭代终止条件
，ε 为迭代终止误差判定阈值，取值为10–5。如果满足则结束迭代，不满足则回到步骤 （1）进行下一次迭代。
从算法求解结果X 中提取中心点 （x0′，z0′），并根据式 （13）的逆变换旋转回原数据位置 （x0，z0）。
综上，通过单帧刻型槽截面轮廓特征提取算法可以得到刻型槽的特征，包括刻型槽的中心位置（x0，z0）、刻型槽的深度d 和宽度w。对所有扫描数据进行逐帧处理可得到加工面上所有刻型槽截面的轮廓特征，为激光刻型线质量检验提供标准。
2.2 刻型线轮廓重构与误差计算
提取完所有刻型槽截面轮廓特征后得到刻型线实际中心点集，由于工件一次刻型加工中一般存在多个独立的刻型区域轮廓，为准确分析刻型线轮廓误差，需要将扫描得到的刻型线中心点云分割对应至相应轮廓区域。
由于线激光扫描频率可达到2500 Hz，相邻扫描点之间的间距远小于轮廓与轮廓之间点云的间距，通过欧式聚类的方法能够对这种特点的点云进行快速分类，相比于k-means 聚类，欧式聚类不需要知道分类的数量，减小了人工识别刻型线轮廓数量的工作，并且充分利用点云组内距离远小于组间距离的特点，通过欧式距离计算能够实现快速分类，计算效率高。
基于欧式聚类的点云分割[20]流程 （图5），首先给定初始点P，通过kd-tree 数据结构快速搜索距离P 点最近的k 个点，将欧式距离小于设定阈值的点聚类于集合{Gi}，如果{Gi}中元素继续增加，则选取未在集合中的点作为新的初始点，如果{Gi}中元素不再增加则输出该集合，若还有剩余点则新建{Gi+1}集合，继续聚类操作，反之则结束聚类过程。k 的值以及阈值根据刻型线轮廓的实际情况确定，一般可将k 设置为5，阈值设置为5 mm。
图5 基于欧式聚类的点云分割流程图
Fig.5 Flow chart of point cloud segmentation based on Euclidean clustering
刻型线实际中心点云在经过点云分割后需要与理论轮廓点云进行匹配，以建立理论轮廓和实际轮廓之间的对应关系。其中理论轮廓点云可通过CAD 软件对工件数模提取线轮廓后进行离散化得到，并同样使用欧式聚类算法进行分割。由于具有对应关系的理论和实际轮廓的形心之间的距离一般小于非对应关系轮廓间形心的距离，因此可以通过搜索最近形心点进行轮廓匹配。
所有理论轮廓形心的集合为{Ti|1≤i≤s}（s 为刻型线轮廓数量），所有实际轮廓形心的集合为{Ri|1≤i≤s}，则与实际轮廓形心Ri 对应的理论轮廓形心下标j 满足
通过计算各形心的匹配关系将理论轮廓和实际轮廓一一对应，接着对匹配过的轮廓进行误差计算。轮廓误差可能产生的形式可分为整体误差和局部误差。如图6 所示，整体误差有偏移和伸缩两种类型，偏移主要来自于刻型机与工件之间的基准误差，以及刻型机本身的静态误差等，伸缩主要来自于工件装夹后产生的弹性变形。局部误差是实际刻线在理论轮廓附近的误差，主要来自于机床动态误差等。
图6 轮廓误差的主要形式
Fig.6 Main forms of contour error
首先计算理论轮廓和实际轮廓之间的整体偏移误差，理论轮廓点集为{Pi|1≤i≤a}，实际轮廓点集为{Qi|1≤i≤b}，计算出理论轮廓形心和实际轮廓形心之间的偏移矢量E，即
根据偏移矢量E 对实际轮廓点集{Qi}进行补偿得到{Qi′}，使得补偿后形心与理论轮廓形心重合，补偿后的轮廓误差主要包含伸缩和局部误差两种类型，对补偿后的点集进行最近点匹配。
对于理论轮廓点集中的每一个点，如果直接匹配与其最近的实际轮廓点，可能会在拐角处出现点对不匹配现象，因此需要通过最近点匹配算法确定每一个理论点对应的实际点。图7 为各种不同情况下最近点匹配算法的示意过程，具体步骤如下。
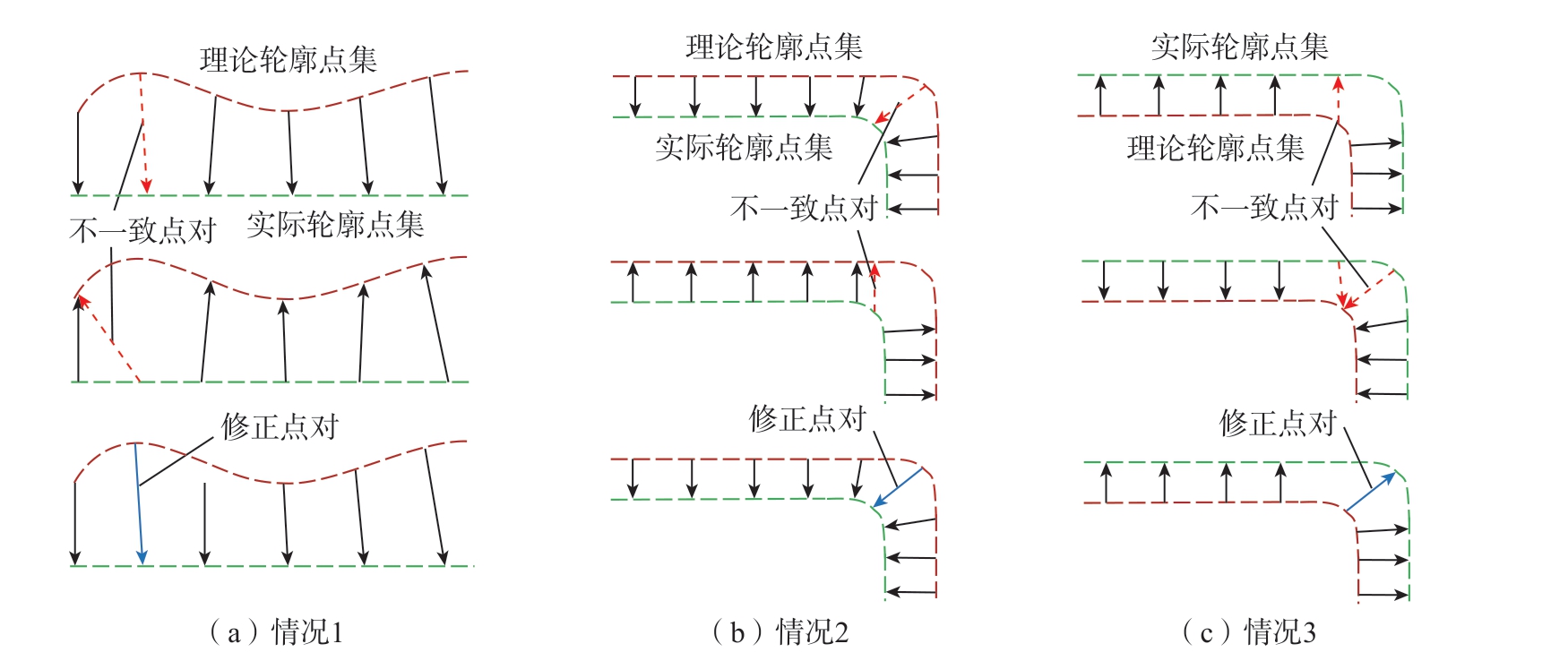
图7 最近点匹配算法示意图
Fig.7 Schematic diagram of the nearest point matching algorithm
（1）理论点集向补偿后的实际点集查询最近点并配对，设点Pi 的最近点为Qj′，则配对集合MP={（Pi，Qj′）|1≤i≤a}；
（2）补偿后的实际点集向理论点集查询最近点并配对，设点Qk′的最近点为Pl，则配对集合MQ={（Qk′，Pl）|1≤k≤b}；
（3）对配对集合MP 中所有点对进行校正，对任意点Pi 在集合MQ 查找包含该点的点对，分3 种情况讨论。
情况1：集合MQ 中没有包含Pi 的点对，如图7（a）中红色箭头所示的情况，认为MP 中的点对 （Pi，Qj′）匹配正确不需要修改。
情况2：集合MQ 中有一个包含Pi 的点对，即集合MP 中有一个满足l = i 的点对 （Qk′，Pi），如图7（b）中红色箭头所示的情况，此时修正后Pi的匹配点满足式（22）。
情况3：集合MQ 中有多个包含Pi 的点对，即集合MP 中有多个满足l = i 的点对，如图7（c）中红色箭头所示情况。点对表示为{（Qc′，Pi）|c∈[1，b]}，找出其中距离Pi最远的匹配点，此时情况3可转化为情况2求解。
每个点的误差值来源于整体误差和局部误差的共同影响，因此定义某一轮廓上的匹配点加工误差为
式中，δ1 和δ2 为整体误差影响因子和局部误差影响因子，这里δ1 和δ2 均取值为1。
通过基于模板匹配的单帧刻型槽截面轮廓特征提取算法和基于最近点匹配的轮廓误差计算方法得到刻型线的槽宽、槽深和加工轮廓误差，为激光刻型精度、质量的检测提供依据。
3 试验验证
为了验证上述方法的有效性，在刻型机加工完成的样件上进行线激光在机精度检测试验。试验平台如图8所示，试验样件为长200 mm、宽200 mm 的6061 铝合金板，表面覆盖有胶膜，样件表面共有11 道刻线，按x 轴方向由小到大依次编号为1～11。试验所用线激光器为深视SR7140 线激光器，该线激光器的X 轴轮廓点数为3200，X 轴分辨率为25 μm，Z 轴测量精度为±0.024 mm。
图8 激光刻型在机精度检测试验平台
Fig.8 Laser engraving on-machine accuracy test platform
由于采用刻型机带动线激光器扫描的在机检测方式，机床本体的几何误差会引入到后续计算出的点云位置中。其中机床的定位误差反映在刻型线的轮廓误差中，是本文需要检测的；而重复定位误差会对在机检测的结果造成影响，因此在加工与测量前需要预先测量几何误差并补偿。本研究使用的刻型机补偿后重复定位精度不超过0.05 mm，远低于化铣刻型线加工精度0.5 mm，并且在检测时采用多次扫描取平均值的方式进一步减小重复定位误差。
试验流程如图9 所示，将线激光器偏置安装于激光刻型机末端，通过后处理将激光刻型的ATP 文件转化为线激光器扫描轨迹。首先对实际零件进行线激光扫描，得到线激光点云数据，通过单帧截面参数拟合得到刻型线的槽宽、槽深及点位信息；再对刻型线点位进行坐标变换获得实际轮廓的中心点云；将由零件数模刻型线离散出的理论轮廓点云和实际轮廓点云进行点云分割、轮廓匹配以及轮廓精度计算得到最终的轮廓误差值。
图9 激光刻型在机精度检测试验流程
Fig.9 Experiment flow of laser engraving on-machine accuracy testing
对样件上所有刻型线进行扫描，采用2.1 节提出的刻型槽截面轮廓特征提取算法对数据进行处理，得到每一帧的刻型槽截面信息，其中部分帧处理结果如图10所示。可以看出，刻型槽两端由于激光烧结形成小凸台，通过刻型槽截面轮廓特征提取算法可以准确识别出槽宽、槽深及刻型槽的位置信息，并不会受到刻型槽两端凸起的影响。
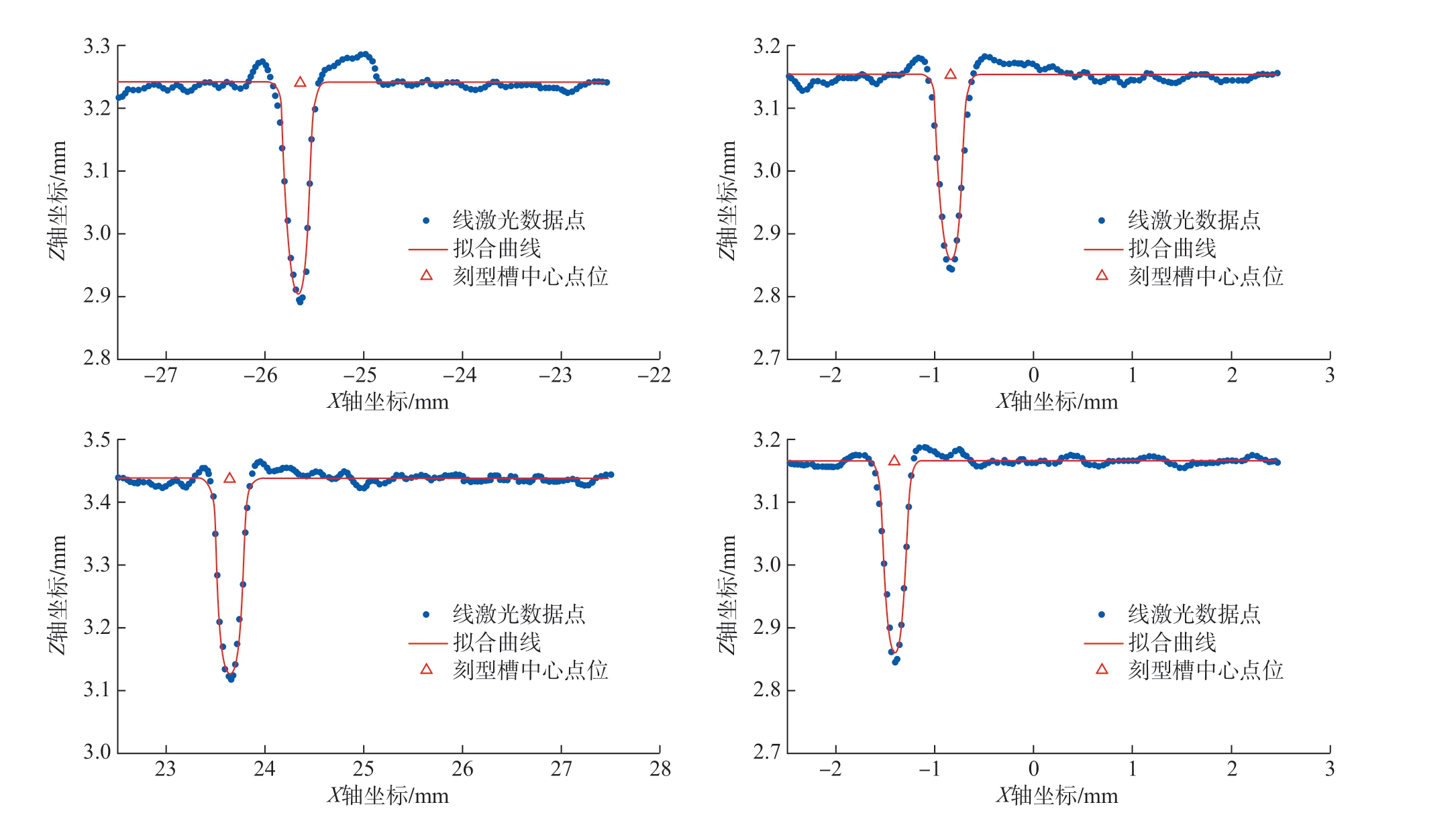
图10 刻型槽截面轮廓特征随机提取结果
Fig.10 Randomly extracting results of profile featu e of notch section
试验测得全部扫描数据的槽宽统计值为 （0.4806±0.0163） mm，槽深统计值为 （0.3124±0.0148） mm。表1 列出了前6 组计算结果，可以看出，不同轮廓的槽宽和槽深在均值附近小范围波动，刻型线的槽宽和槽深的一致性好，没有出现刻型线过宽和槽深过浅的情况。因此可以认为刻型机的激光刻型效果良好，刻型线均匀性高。
表1 不同刻型线轮廓槽宽与槽深结果对比
Table 1 Comparison of groove width and depth results for diffe ent engraving lines
轮廓编号 槽宽/mm 槽深/mm 1 0.4952±0.0155 0.3264±0.0162 2 0.4723±0.0141 0.3219±0.0138 3 0.4770±0.0138 0.3169±0.0124 4 0.4733±0.0137 0.3163±0.0113 5 0.5015±0.0157 0.3063±0.0122 6 0.4723±0.0142 0.3061±0.0121 7 0.4756±0.0161 0.3069±0.0135 8 0.5003±0.0121 0.3059±0.0133 9 0.4668±0.0119 0.3077±0.0143 10 0.4695±0.0161 0.3065±0.0143 11 0.4828±0.0190 0.3155±0.0137
得到刻型槽单帧轮廓匹配结果之后，通过第1 节的坐标变换理论得到每一帧刻型线点位在工件坐标系下的实际坐标，并根据2.2 节的算法对所有点进行点云分割和轮廓匹配，最终计算出理论刻型轮廓与实际刻型轮廓之间的误差。表2 列出了前6 组计算结果，不同刻型线轮廓加工误差的统计值为 （0.1486±0.0576） mm，最大轮廓误差为0.3105 mm，结果满足激光刻型线轮廓加工精度要求。
表2 不同刻型线轮廓误差对比
Table 2 Comparison of contour errors of diffe ent engraving lines
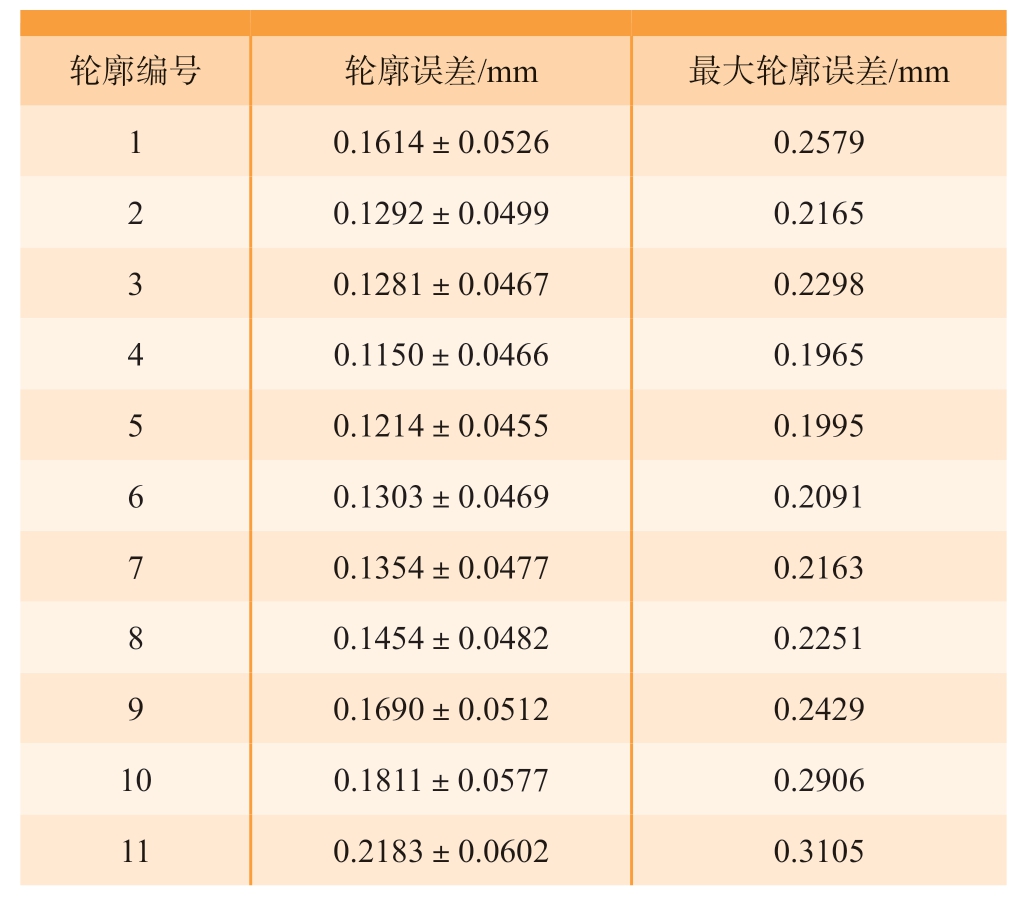
轮廓编号 轮廓误差/mm 最大轮廓误差/mm 1 0.1614±0.0526 0.2579 2 0.1292±0.0499 0.2165 3 0.1281±0.0467 0.2298 4 0.1150±0.0466 0.1965 5 0.1214±0.0455 0.1995 6 0.1303±0.0469 0.2091 7 0.1354±0.0477 0.2163 8 0.1454±0.0482 0.2251 9 0.1690±0.0512 0.2429 10 0.1811±0.0577 0.2906 11 0.2183±0.0602 0.3105
绘制刻型线轮廓误差分布如图11 所示，可以看出，各刻型线的轮廓误差分布相似。Y 方向轮廓误差呈现两端和中部较低的现象，误差大的点位主要分布在Y = 20 mm 和Y = 60 mm 附近。X 方向的轮廓误差呈现两端大中间小的现象，最大的点位于编号为11 的轮廓线上。
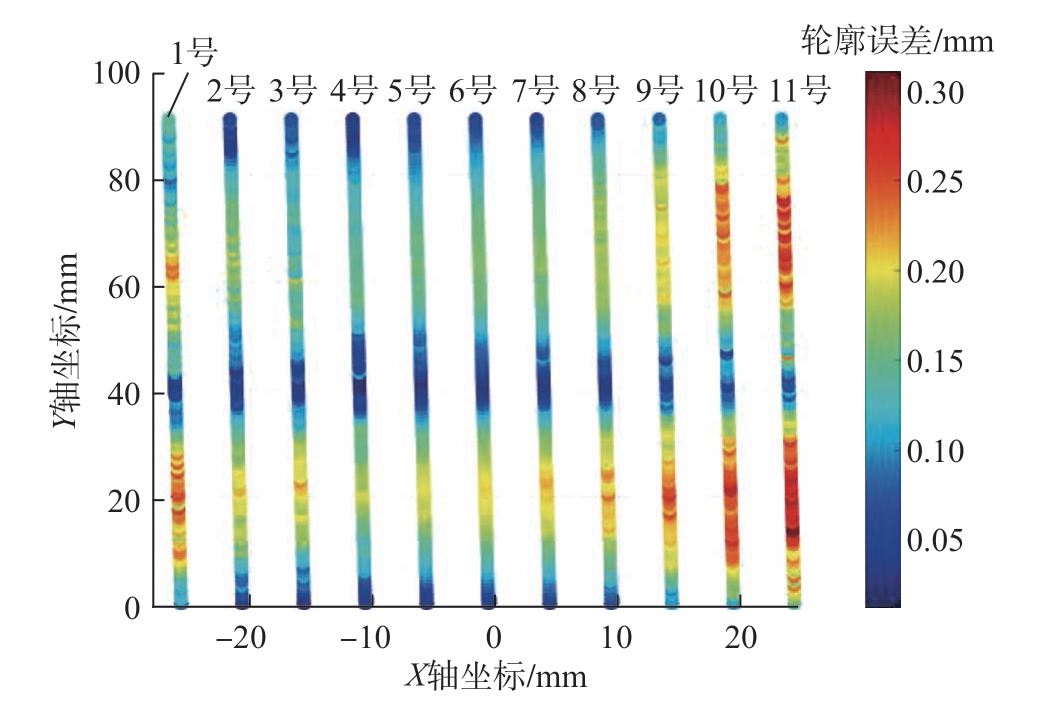
图11 刻型线轮廓误差分布
Fig.11 Distribution of engraving line contour error
计算出的轮廓误差主要包括偏移误差、弯曲变形误差和局部误差。偏移误差的统计值为 （0.0255±0.0148）mm，占总误差的17.16%，表征为刻型线形心的偏移，其主要来自于刻型机与工件之间的基准误差及刻型机本身的静态误差等。弯曲变形误差主要来自于工件装夹后产生的弹性变形，绘制编号为1 的轮廓附近理论数模表面与实际表面Z 方向的偏差如图12 所示。可以看出，实际样件在Z 方向发生弯曲变形，并且弯曲变形产生的误差和理论点位与实际点位的偏差变化趋势基本一致，由此可知，误差主要来自于实际样板Z 方向的弯曲变形，弯曲变形误差的统计值为 （0.1108±0.0458） mm，占总误差的74.56%。图12 中理论点位与实际点位的偏差围绕弯曲变形产生误差波动，这种波动误差表现为局部误差，主要来自于刻型机在运动过程中产生的动态误差等，局部误差的统计值为 （0.0123±0.0062） mm，占总误差的8.28%。
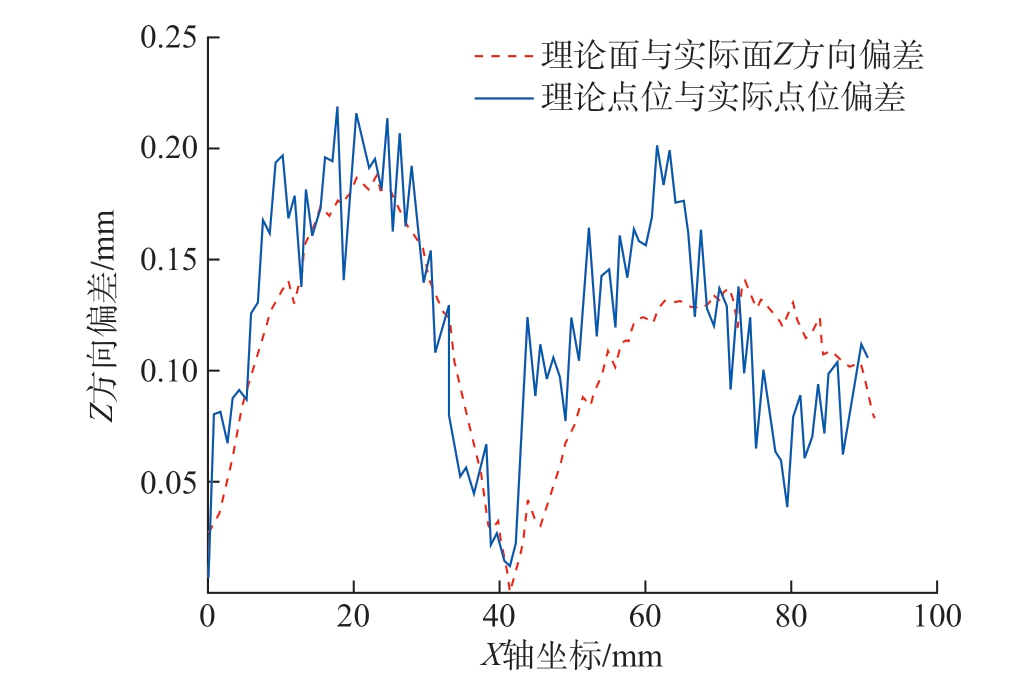
图12 工件变形误差与刻型线加工误差的对比
Fig.12 Comparison of workpiece deformation error and engraving line machining error
综上，刻型线的误差主要来源于装夹后的实际工件与理论数模之间的弯曲弹性变形，为保证刻型线轮廓精度，在实际加工中，首先需要选择合适的柔性工装和夹持点，减小装夹后的弯曲变形，还可以通过曲面自适应匹配方法获取理论曲面和实际曲面之间的映射关系[17]，减小弯曲弹性变形的影响。其次，刻型机的静态误差和动态误差也会对刻型线的轮廓误差造成影响，因此在加工前需要对机床的静态误差和动态误差进行测量和校准。
综合以上试验结果，本文提出的刻型线轮廓精度在机检测技术能够准确识别出刻型线的槽宽、槽深及位置信息，并通过轮廓匹配计算出所有匹配点的误差，为加工误差溯源、加工工艺改进和提高刻型线的轮廓精度提供了重要分析依据。
4 结论
（1）为了对激光刻型加工工艺中的刻型线轮廓精度与质量进行高效高精度的测量，本文开发了基于2D线激光的化铣激光刻型工艺在机精度检测系统，通过建立五轴激光刻型机与线激光传感器的运动学模型，构建激光测量坐标系与工件坐标系之间的变换关系，据此获得刻型线扫描点云。
（2）提出了刻型槽截面轮廓特征提取算法与轮廓误差计算方法，可准确识别刻型线的槽宽、槽深以及轮廓误差。通过刻型工件扫描试验验证了所提出方法的可行性，有效地检测出刻型线的槽面质量均匀性、轮廓精度以及主要误差来源，为进一步改进加工工艺，提高刻型加工的精度和质量提供了重要参考数据。
[1] 甘忠, 王亮, 谭海兵, 等. 大型立体化铣样板设计与制造方法探索[J]. 航空制造技术, 2013, 56(17): 78–80, 88.GAN Zhong, WANG Liang, TAN Haibing, et al. Exploration of design and manufacturing method to stereoscopic chemical-milling template with jumbo size[J]. Aeronautical Manufacturing Technology, 2013, 56(17): 78–80, 88.
[2] 殷世坤, 郭岩, 解二伟, 等. 化铣生产中激光刻型技术的应用优势探讨[J]. 电镀与精饰, 2021, 43(3): 32–36.YIN Shikun, GUO Yan, XIE Erwei, et al. Discussion on the application advantages of laser engraving technology in open milling production[J].Plating and Finishing, 2021, 43(3): 32–36.
[3] 李文龙, 王刚, 田亚明, 等. 在机测量技术与工程应用研究进展[J]. 航空制造技术, 2022, 65(5): 14–35.LI Wenlong, WANG Gang, TIAN Yaming, et al. Research progress of on-machine measurement technology and its engineering applications[J].Aeronautical Manufacturing Technology, 2022, 65(5): 14–35.
[4] 冯晓冰, 杜正春, 葛广言, 等. 基于在机测量的薄壁件加工综合误差建模与补偿[J]. 航空制造技术, 2022, 65(6): 14–20.FENG Xiaobing, DU Zhengchun, GE Guangyan, et al. Comprehensive error modeling and compensation in manufacturing of thin-walled parts based on on-machine measurement[J]. Aeronautical Manufacturing Technology,2022, 65(6): 14–20.
[5] HUANG N D, YIN C H, LIANG L, et al. Error compensation for machining of large thin-walled part with sculptured surface based on on-machine measurement[J]. The International Journal of Advanced Manufacturing Technology, 2018, 96(9): 4345–4352.
[6] SAZEDUR RAHMAN M, SALEH T, LIM H S, et al.Development of an on-machine profile measurement system in ELID grinding for machining aspheric surface with software compensation[J].International Journal of Machine Tools and Manufacture, 2008, 48(7–8):887–895.
[7] 陈岳坪, 高健, 邓海祥, 等. 复杂曲面零件在线检测与误差补偿方法[J]. 机械工程学报, 2012, 48(23): 143–151.CHEN Yueping, GAO Jian, DENG Haixiang, et al. On-line inspection and machining error compensation for complex surfaces[J]. Journal of Mechanical Engineering, 2012, 48(23): 143–151.
[8] 张旭苹, 汪家其, 张益昕, 等. 大尺度三维几何尺寸立体视觉测量系统实现[J]. 光学学报, 2012, 32(3): 148–155.ZHANG Xuping, WANG Jiaqi, ZHANG Yixin, et al. Large-scale threedimensional stereo vision geometric measurement system[J]. Acta Optica Sinica, 2012, 32(3): 148–155.
[9] 全燕鸣, 黎淑梅, 麦青群. 基于双目视觉的工件尺寸在机三维测量[J]. 光学 精密工程, 2013, 21(4): 1054–1061.QUAN Yanming, LI Shumei, MAI Qingqun. On-machine 3D measurement of workpiece dimensions based on binocular vision[J]. Optics and Precision Engineering, 2013, 21(4): 1054–1061.
[10] 童康康, 张丽艳, 叶南. 航空零件化铣胶膜激光刻线的视觉检测技术研究[J]. 机械制造与自动化, 2019, 48(4): 201–205.TONG Kangkang, ZHANG Liyan, YE Nan. Visual inspection of laser etching curves on chemical milling adhesive film of aircraft parts[J]. Machine Building & Automation, 2019, 48(4): 201–205.
[11] LI Y D, GU P H. Free-form surface inspection techniques state of the art review[J]. Computer-Aided Design, 2004, 36(13): 1395–1417.
[12] SHARIFZADEH S, BIRO I, LOHSE N, et al. Abnormality detection strategies for surface inspection using robot mounted laser scanners[J]. Mechatronics, 2018, 51: 59–74.
[13] LIU H B, WANG Y Q, HUANG X P, et al. Isoplanar-based adaptive sampling for model-unknown sculptured surface coordinate metrology using non-contact probe[J]. The International Journal of Advanced Manufacturing Technology, 2013, 64(9): 1695–1707.
[14] SONG T, XI F, GUO S, et al. A comparison study of algorithms for surface normal determination based on point cloud data[J]. Precision Engineering, 2015, 39: 47–55.
[15] ZENG C, HU Y H, SHI J, et al. On-machine measurement and compensation of assembling gap for 5-axis friction stir welding based on 2D laser profilometer[C]//2019 IEEE 5th International Conference on Mechatronics System and Robots (ICMSR). Piscataway: IEEE, 2019: 70–75.
[16] 石循磊, 杜坤鹏, 张继文, 等. 基于线激光扫描的飞机表面锪窝孔参数提取方法[J]. 机械工程学报, 2020, 56(8): 148–154.SHI Xunlei, DU Kunpeng, ZHANG Jiwen, et al. Method for extracting hole parameters of aircraft surface based on linear laser scanning[J]. Journal of Mechanical Engineering, 2020, 56(8): 148–154.
[17] 章绍坤．航空航天薄壁件五轴加工的轮廓与壁厚误差补偿方法[D]. 上海：上海交通大学, 2020.ZHANG Shaokun. Compensation method for profile and wall thickness errors in five-axis machining of aerospace thin-walled parts[D]. Shanghai:Shanghai Jiao Tong University, 2020.
[18] 毕庆贞, 丁汉, 王宇晗. 复杂曲面零件五轴数控加工理论与技术[M]. 武汉: 武汉理工大学出版社, 2016: 15–34.BI Qingzhen, DING Han, WANG Yuhan. Theory and technique for five-axis NC machining of complex surface part[M]. Wuhan: Wuhan University of Technology Press, 2016: 15–34.
[19] LAMPTON M. Damping-undamping strategies for the Levenberg-Marquardt nonlinear least-squares method[J]. Computers in Physics, 1997, 11(1): 110–115.
[20] 孙红岩, 孙晓鹏, 李华. 基于K-means 聚类方法的三维点云模型分割[J]. 计算机工程与应用, 2006, 42(10): 42–45.SUN Hongyan, SUN Xiaopeng, LI Hua. 3D point cloud model segmentation based on K-means cluster analysis[J]. Computer Engineering and Applications, 2006, 42(10): 42–45.