近年来，随着现代工业技术的发展，机器人广泛应用于航空航天、汽车制造、电子装配、精密医疗操作等领域。为了获得稳态精度和快速动态响应，需要高精度的机器人轨迹跟踪能力[1]。
使用时间的增加、机械臂各关节之间的不确定因素及人为的一些操作等会导致机器人系统出现各种各样的性能损失，发生相关的故障[2]，从而影响机器人轨迹跟踪的精度。因此，为了有效解决在系统运行中出现的故障，需要一种良好的容错控制方法，保证机器人系统在出现故障时能够正常运作，从而降低生产工作中的成本损失和系统维修的额外成本，减小生产过程中安全事故发生的概率[3]。容错控制 （Fault-tolerant control，FTC）方法主要分为两大类，分别为被动容错控制 （Passive faulttolerant control，PFTC）和主动容错控制 （Active fault-tolerant control，AFTC）[4]。其中，被动容错控制的主要思想是使用鲁棒控制技术来处理机器人系统中存在的故障问题。但是被动容错控制的能力是有限的，通常无法准确获得机器人系统中存在的故障信息。与之相比，主动容错控制的主要解决机制是从故障观测器中获得对故障的估计，再进一步对获得的故障估计信息进行补偿处理以消除故障[5–6]。Zhao 等[7]提出了一种基于强化学习的非线性系统分散容错控制，其通过构建与各辅助子系统执行器故障估计相关的改进成本函数，将原来的控制问题转换为一系列分散的最优控制策略。Zhang 等[8]提出了一种基于动态学习的机械臂主动容错控制方案，借助动态学习理论构建动态分类器，以快速准确地获得故障信息，并选择与当前故障系统对应的正确控制器来补偿故障。但此类基于数据驱动的方法在应用过程中因依赖数据，当数据不充分时无法有效工作。Piltan 等[9]提出了一种运用Takagi-Sugeno（T-S）模糊高阶技术的自适应滑模观测器，在线检测识别机器人系统的故障信息，从而对系统故障进行补偿。Piltan 等[10]针对存在执行器故障的非线性机器人系统，提出了一种基于机器学习的神经自适应、高阶、可变结构的观测器来估计故障，从而实现容错控制。但此类方法在规则训练中需要较大的计算量，过程较为繁琐，在实际应用中会受到一定的局限。
在实际的工业操作中，除了系统内部出现故障会影响机器人的轨迹跟踪，一些加工任务与环境接触也会对机器人的轨迹跟踪产生影响，因此还需要对机器人末端进行柔顺控制。常用的柔顺控制方法有刚度控制、阻抗控制和导纳控制，或者这几种控制之间的混合控制[11]。项文凭等[12]提出一种基于力传感器的下肢康复训练机器人柔顺控制方案，该方案通过力传感器将检测到的力作用于阻抗控制力外环，当人–机交互力大于设定阈值时机器人进行柔顺运动。许家忠等[13]提出了一种基于位置控制的阻抗控制方案，该方案通过接触力反馈信号给出控制机器人末端参考位置的方法来进行机器人末端的柔顺控制。陈卓强等[14]将导纳控制应用于康复机器人，以优化其在人–机交互过程中的柔顺度。段锐等[15]通过可操作度和笛卡儿位置判断机器人是否在奇异位置或工作空间附近，根据三角函数规划和阻尼质量比修改导纳参数中的阻尼值与质量值，进而使机器人在奇异位置和工作空间极限位置实现平稳安全的操作。Yao等[16]提出了一种工业机器人在物理人–机交互中的无传感器自适应导纳控制，该方案用导纳控制将检测到的力转换为机器人的参考位置和速度，用径向基函数 （RBF）网络在线更新阻尼参数，以减少接触力变化和降低接触力，使物理人–机交互更自然更容易。在上述文献所提出的柔顺控制方法中，使用固定参数的导纳控制和阻抗控制无法更有效地适应时变环境；使用变参数的导纳控制方法同样在实际应用中过程较为繁琐，数据计算量较大，且当数据不充分时，无法更加有效地工作。
因此，本文提出一种位置控制为自抗扰的变导纳自适应主动容错控制方法，其能够在抑制外部干扰的同时消除内部关节故障对机器人运动所带来的影响；且提出具有使用方法简单、鲁棒性强、能适应环境特征变化等优点的模糊控制在线调整导纳参数的方案，提高机器人末端的柔顺性，确保机器人系统在与外界环境接触时能够正常运行。
1 工业机器人数学模型
1.1 运动学模型
机器人运动学建模即建立机器人各关节变量与末端位姿的关系。正向运动学为通过给定机器人的各关节变量来计算机器人的末端位姿。通过Denavit-Hartenberg（D-H）法，得到表示6 自由度机器人相邻连杆坐标系位姿变换关系的齐次变换矩阵，即
式中，ai、αi、di 为第i 根连杆长度、连杆扭角、连杆偏距；θi 为第i 个关节转角，i = 1，2，…，6。
通过将各关节的变量代入各自齐次变换矩阵中，得到
共6 个矩阵，6 自由度机器人末端相对于基坐标系的位姿可由这6 个齐次变换矩阵依次相乘来表示，
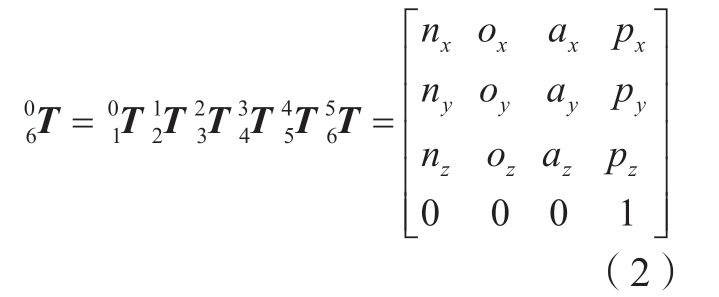
式中，[n，o，a]为机器人末端姿态的欧拉角矩阵；p 表示末端位置。
通过齐次变换矩阵，由机器人关节变量可得出笛卡儿空间中的机器人末端位姿信息，从而完成正向运动学建模。取机器人末端位置笛卡儿坐标的三维向量x = [ px py pz]T，故机器人正向运动学方程为
式中，q 为机器人关节位置。逆向运动学建模则为逆向推导正向运动方程中的数学关系。由此，则完成机器人运动学建模。
1.2 动力学建模
根据文献[17]，由拉格朗日法得到简化后的关节空间中具有6 个自由度的动力学模型，
式中，
表示机械臂的各关节角速度、角加速度向量；M（q）∈R6×6为惯性项；
为向心力和科氏力项；
为摩擦力项；G（q）∈R6×1 为重力项；τd 为建模误差引起的不确定项；w∈R6×1为外部干扰；τ∈R6×1 表示扭矩或力。
因为实际摩擦相关参数难以得到，润滑得当可以适当忽略摩擦因素，故不考虑F（
），且由于建模误差较小，对后续计算影响不大，故可在后续计算中忽略此项。因此，简化后的动力学模型为
在机器人系统工作的过程中，由于外界环境的复杂性和不确定因素的存在，机器人系统的执行器容易发生故障。当存在执行器故障时，机器人系统的控制力矩可以表示为
式中，u∈R6×1为控制转矩；uf∈R6×1代表执行器偏差故障。则机器人动力学模型式 （5）可改写为
进一步，式 （7）可改写为
式中，故障引起的系统损失项H =M –1（q） uf。在实际应用中，系统因故障造成的损失项的值虽然是未知的，但通常是有界的，因此可以假设||H||≤K。其中K 为故障引起系统损失的界，是一个未知常数。
2 变导纳自适应主动容错控制设计
为了消除工作过程中执行器外部出现的干扰、内部出现的故障、机器人末端与外界环境交互影响，使机器人在非结构环境中更加高效自主精准地执行任务，提出以自抗扰为位置控制的变导纳自适应主动容错控制方法。其控制结构如图1 所示，其中自抗扰控制器在实现位置控制的同时消除执行器外部干扰，而在其基础上所提出的自适应主动容错控制器消除执行器内部故障，变导纳控制器提高机器人末端的柔顺性能。
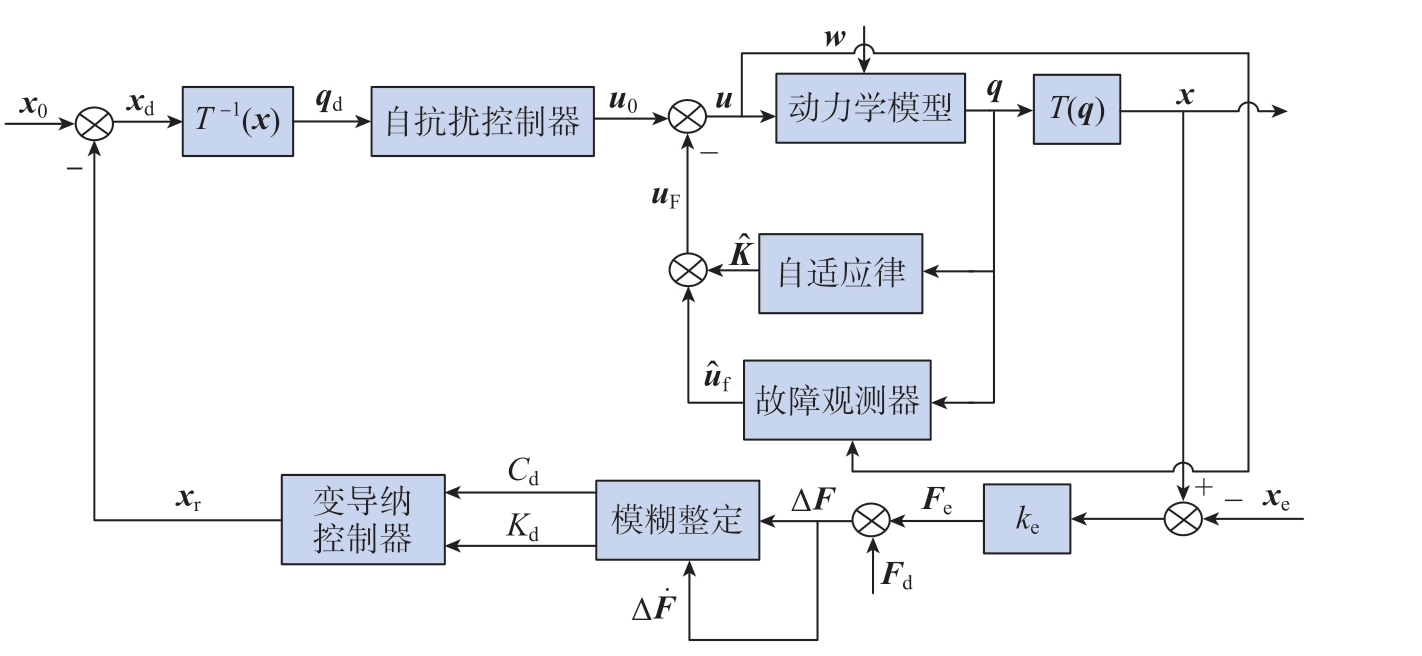
图1 变导纳自适应主动容错控制结构
Fig.1 Structure of variable admittance adaptive active fault-tolerant control
2.1 自抗扰控制器
自抗扰控制是在PID 控制算法基础上进行改进的新型控制方法，主要由跟踪微分器、非线性状态反馈控制律、扩张状态观测器3 部分组成。
跟踪微分器主要针对被控对象的输入特点对其提取所需要的信号，设计为
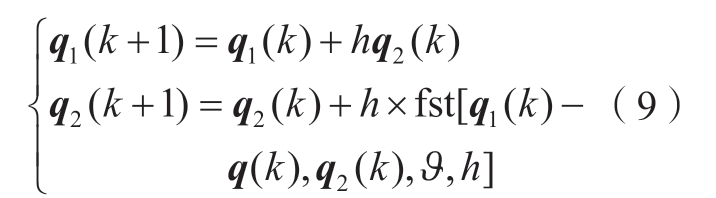
式中，h 为采样周期； 为跟踪增益；q1 和q2 分别为位移参考值qd 和速度参考值qd的跟踪值；q（k）为第k 时刻的输入信号；函数fst（·）为根据离散型微分跟踪器推导出的快速跟踪信号控制综合函数。
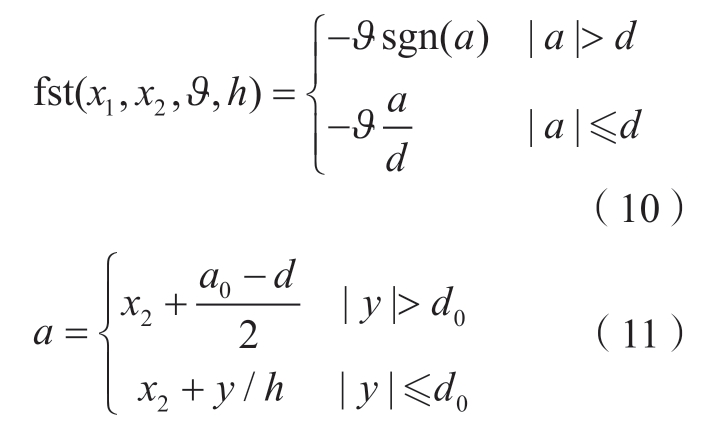
式中，
。
扩张状态观测器主要是对系统中的重要变量进行跟踪，对系统扰动进行补偿的，表达式[18]设计为
式中，β1、β2、β3 均为观测器增益；z1、z2和z3 分别为位移输出值q、速度输出值
和扰动w 的跟踪值；α 用于控制饱和函数的斜率，避免控制信号骤变过快而引起系统振荡和不稳定，通常为一个小于1 的正数。fal（·）为避免出现高频振荡现象的饱和函数，表示为
非线性状态反馈控制律是一种非线性的组合方式，设计为
式中，u0 为非线性状态反馈控制律；u 为在接收到扩张状态观测器观测扰动之后的状态补偿控制律；kp 和kd为非线性状态反馈控制增益；z3/b 为系统所受干扰的补偿项。
2.2 自适应主动容错控制器
为了获得精确的故障信息，需要通过专用的故障观测器实现对故障的估计。为了便于观测器的设计，首先设计一个辅助变量δ[19]。
对v 求导，
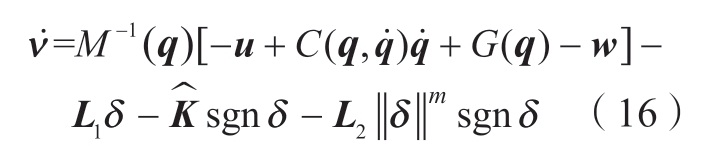
式中，L1 和L2 为观测器的正定增益矩阵；m∈（0，1）。为获得执行器中的故障信息，首先估计故障所引起的系统损失项的大小，即
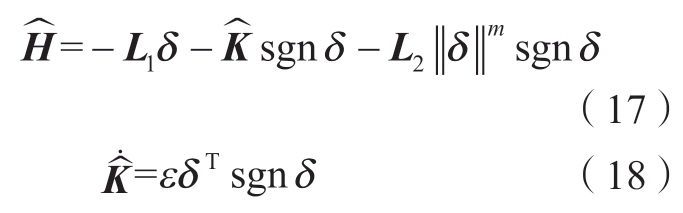
式中，
为故障引起系统损失项H 的估计值；
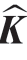为损失项的界K 的估计值；ε 为正常数；H 的估计误差ΔH = H –
；K 的估计误差ΔK = K –
。因此，设计自适应故障观测器，即
式中，
为故障uf 的估计值；uf 的估计误差为
。
结合位置控制中的非线性状态反馈控制律式 （14），设计自适应主动容错控制律，即
式中，机器人系统故障的补偿项uF =
。
引理1[20]：对于任意实数ζ1>0，ζ2>0，0<l<1，系统有限时间稳定的李雅 普 诺 夫 条 件 是
，且有时间Tr 满足
，其 中V（t0） 为V的初始值。
定理1：对于执行器存在故障的机器人系统 （式 （7）），采用自适应故障观测器 （式 （15）～ （19）），故障的估计误差能够在有限时间ts 内收敛到0。
证明：构造李雅普诺夫函数，
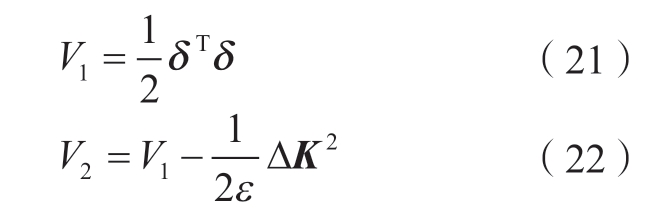
对式 （21）求导，并将式 （8）、（15）及 （16）代入，可得
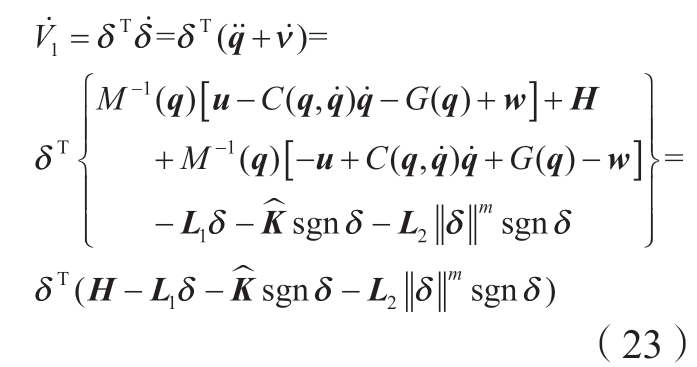
对式 （22）求导，并将式 （18）代入，则有
由于K – H≥0，因此式 （24）可写为
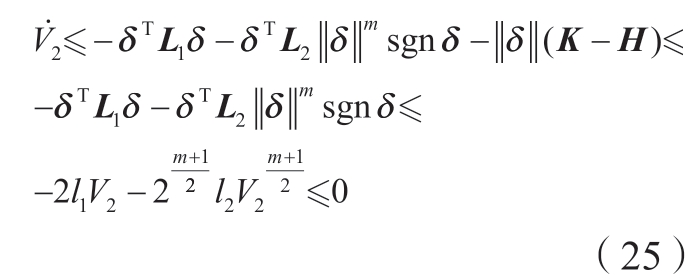
式中，l1 和l2 为故障观测器增益矩阵L1 和L2 中的最小元素。
根据式 （25），对于任意实数l1 > 0，l2 > 0，0 < m < 1，机器人系统在有限时间稳定的李雅普诺夫条件是
，同时根据引理1 可知，自适应故障观测器误差稳定的有限时间。
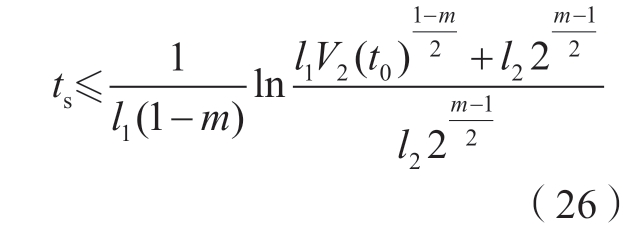
式中，V2（t0）为李雅普诺夫函数V2（·）在时间t = 0 时的值。又根据式 （25），可以得出对于所有的t≥ts，辅助变量δ = 0 且
。根据式 （8）和式 （15）～（17），又有
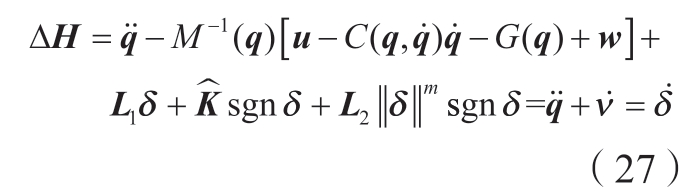
因此，由式 （25）和 （27）可得，对于系统，故障引起损失项的估计误差能够在有限时间ts 内趋于0，即
，又因为ΔH = M –1（q）Δuf，且M（q）为常数项，所以
则定理1 得证。
2.3 变导纳控制器
导纳控制将机器人与外界环境接触过程等效为一个弹性模型，与阻抗控制不同的是，它不需要对机器人的动力学方程进行建模，而是通过建立机器人位置与末端接触力的关系，然后通过调节导纳参数来实现对机器人与环境接触力的控制[21–22]。机器人与外界环境接触的交互过程可以等效为一个“质量–弹簧–阻尼”模型，如图2 所示。其中，ke 为环境刚度；xe 为环境参考位置；x 为机器人末端实际位置；Fd 为机器人末端与环境期望接触力。将环境当作弹性体，机器人与环境实际接触力Fe则为
图2 机器人与环境交互等效模型
Fig.2 Equivalent model of robot-environment interaction
适用于机器人系统的过程：当机械臂末端在受到一个与外界环境接触力Fd – Fe 后，将其转化为虚拟位移xr；然后由此位置偏移量调整给定位置x0，得到一个期望位置xd；其经逆向运动学方程转换为关节转角期望值qd，之后将此期望关节转角输入位置控制器得到控制力矩，将其作用于动力学模型 （式 （7））得到输出关节转角；最后经正向运动学方程 （式（3））得到机器人随所受外力调整的输出位置x，从而实现机械臂末端的柔顺控制。其动力学方程表示为
式中，Md、Cd 和Kd 分别表示期望惯性、阻尼和刚度的参数
分别表示机械臂末端偏移量的加速度、速度、位移。对式 （28）进行拉氏变换，可得
Fd 与Fe 之间的差值为力误差ΔF，其中，机器人的导纳特性可通过调节惯性、阻尼、刚度参数来变换。但为了使机器人在实际环境工作时能够随着外界环境的变化实时进行导纳参数的调节，从而改善机器人末端柔顺控制性能，采用模糊控制对阻尼Cd 和刚度Kd 进行调节，将惯性系数Md 作为不变系数，以改变机器人阻尼刚度系数，得到更加清晰有效的结果。
图3 为模糊控制输入量力误差ΔF 与力误差导数ΔF隶属度函数分布，其论域区间为[–3，3]与[–6，6]。图4 为模糊控制输出量期望阻尼Cd与期望刚度Kd 隶属度函数分布，其论域区间为[0，1]与[0，10]。定义模糊变量的模糊集均为{负大 （NB），负中 （NM），负小 （NS），零 （Z），正小（PS），正中 （PM），正大 （PB）}。其主要控制原理：通过所制定的49 条模糊控制规则，实时调整ΔF 与ΔF隶属度，以得到实时的参数Cd 和Kd。
图3 模糊控制输入量隶属度函数分布
Fig.3 Distribution of membership function of fuzzy control input
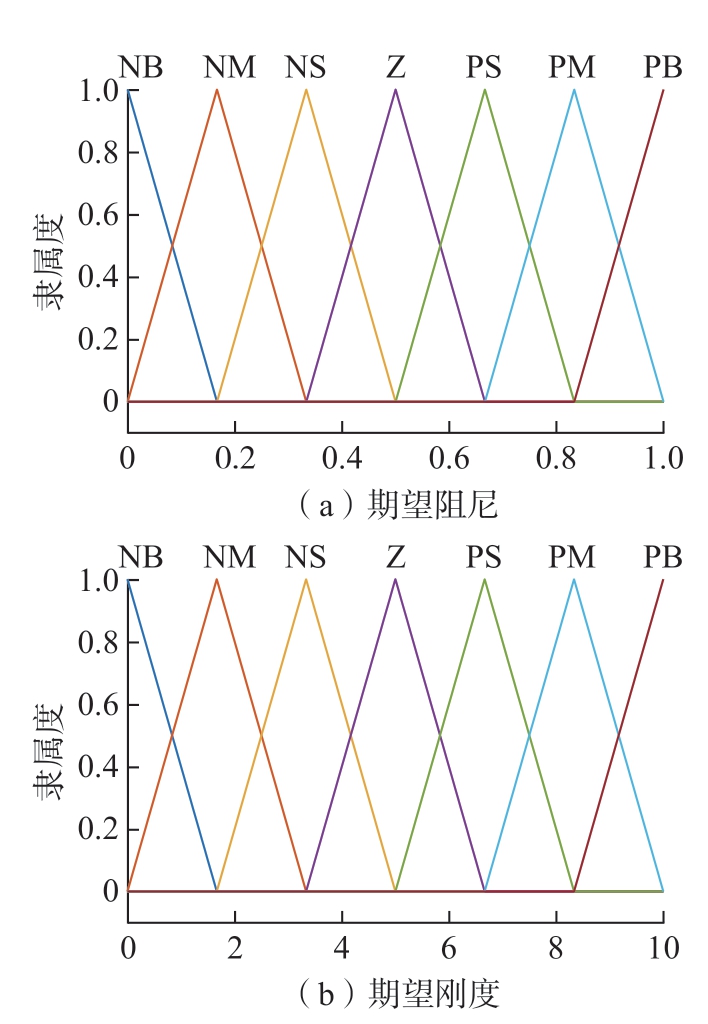
图4 模糊控制输出量隶属度函数分布
Fig.4 Distribution of membership function of fuzzy control output
3 仿真与试验验证
为了验证所提控制方法的有效性，在满足机器人运动学建模过程中齐次变换矩阵式 （1）的转换条件下，通过Matlab 机器人工具箱模拟图5所示的现场实体机器人，建立的6 自由度机器人模型如图6 所示。机器人系统相应的控制参数设置如表1所示。
表1 机器人系统控制参数
Table 1 Control parameters in robot system
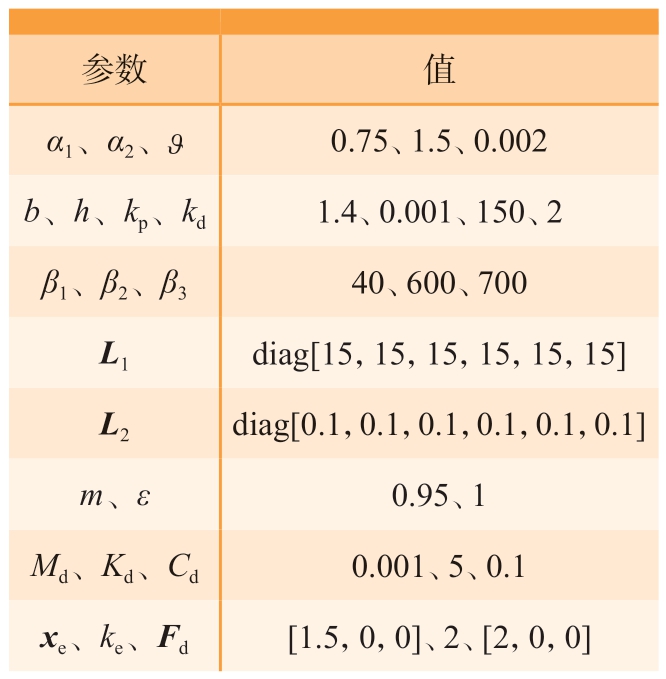
参数 值α1、α2、 0.75、1.5、0.002 b、h、kp、kd 1.4、0.001、150、2 β1、β2、β3 40、600、700 L1 diag[15，15，15，15，15，15]L2 diag[0.1，0.1，0.1，0.1，0.1，0.1]m、ε 0.95、1 Md、Kd、Cd 0.001、5、0.1 xe、ke、Fd [1.5，0，0]、2、[2，0，0]
图5 现场实体机器人
Fig.5 On-site physical robot
图6 IRB – 4600 型模拟机器人
Fig.6 IRB – 4600 simulation robot
设机器人系统所受外部干扰为
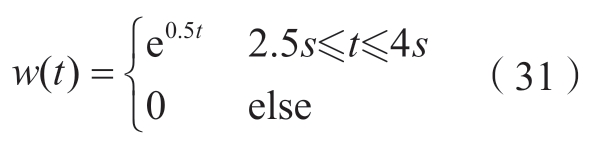
图7 为对机器人系统外部干扰的估计。红色实线为实际扰动，蓝色虚线为自抗扰控制器中的扩张状态观测器 （式 （12））对式 （31）所示外部干扰的估计。可以看出，仅在扰动突变处出现少许估计误差，且稳态误差小于0.013，误差百分比小于0.26%，证明了扩张状态观测器的有效性。
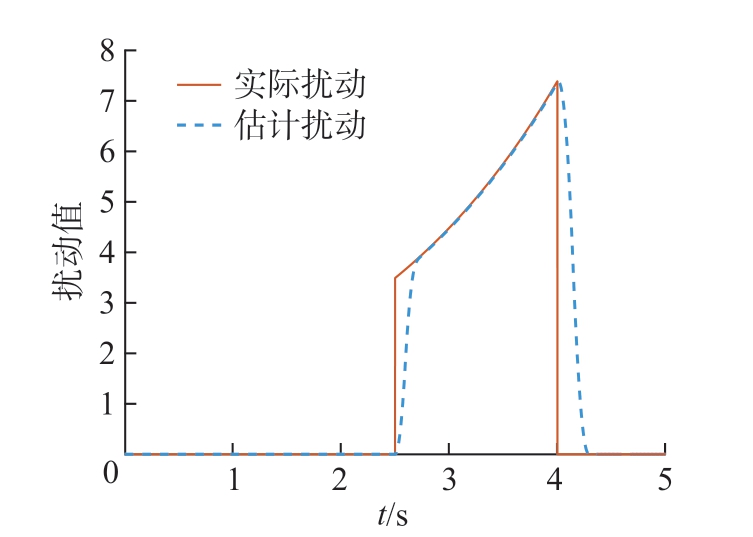
图7 机器人系统外部干扰估计
Fig.7 Estimation of external interference in robot systems
设机器人系统内部关节1、关节3 分别发生故障情形，即
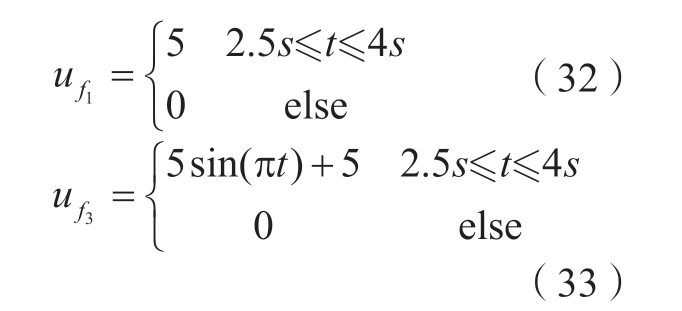
图8 为当机器人系统关节1、关节3 发生式 （32）和 （33）所示的故障时，自适应故障观测器对故障的估计响应曲线。可以看出，在加入故障以后，观测器能够较为准确地观测出故障，仅在故障突变处，如第2.5 s、第4 s 处存在少量观测误差，且关节1 最大误差百分比约为0.22%，关节3 最大误差百分比约为1.46%，证明在实际工作中如果执行器出现故障，自适应故障观测器能够较好地实现对故障的检测，从而使控制器能够对执行器出现的故障进行较为理想的补偿。因此在图9 中可以发现，机器人的实际位置轨迹能够很好地跟踪期望的位置轨迹，仅在2.5 s 执行器出现故障时出现少量跟踪误差，关节1 最大误差百分比约为0.88%，关节3 最大误差百分比约为0.51%。且从图10 可以看到在实现容错控制的过程中，关节1、关节3 控制输入力矩虽出现持续的抖振，但整体趋于稳定。因此，所提容错控制方法能够有效地消除在实际工作中执行器出现故障所带来的影响。
图8 关节1 和关节3 故障估计
Fig.8 Fault estimation of joint 1 and joint 3
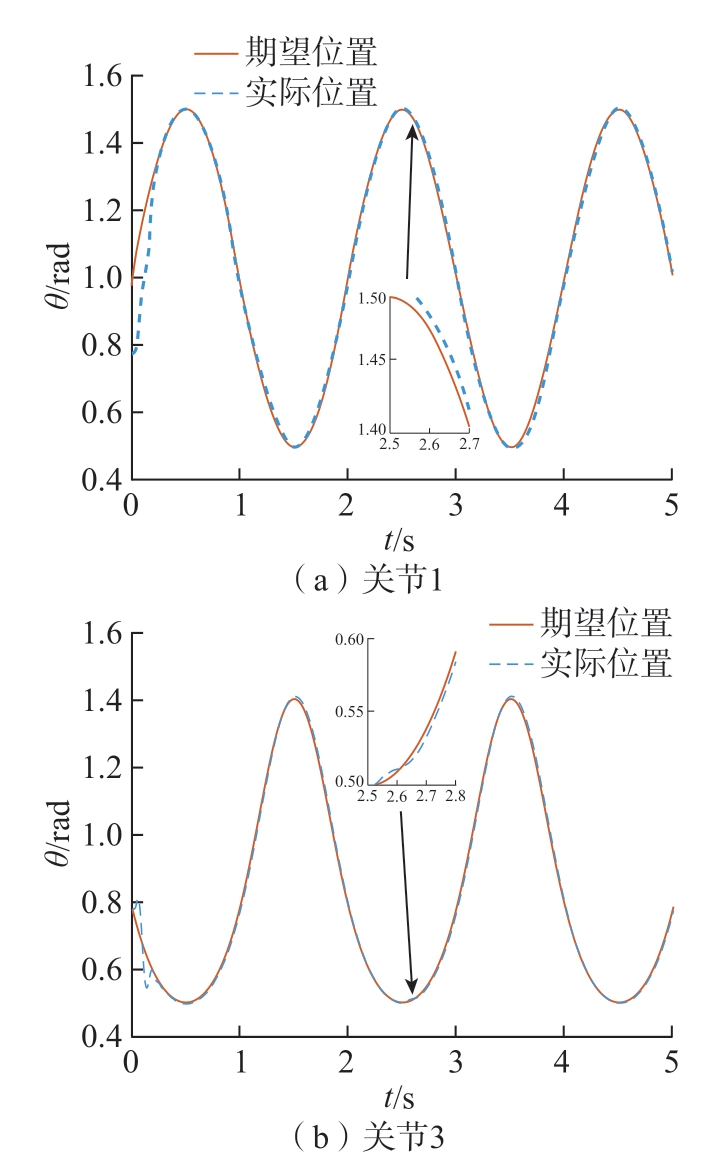
图9 关节1 和关节3 位置跟踪
Fig.9 Position tracking of joint 1 and joint 3
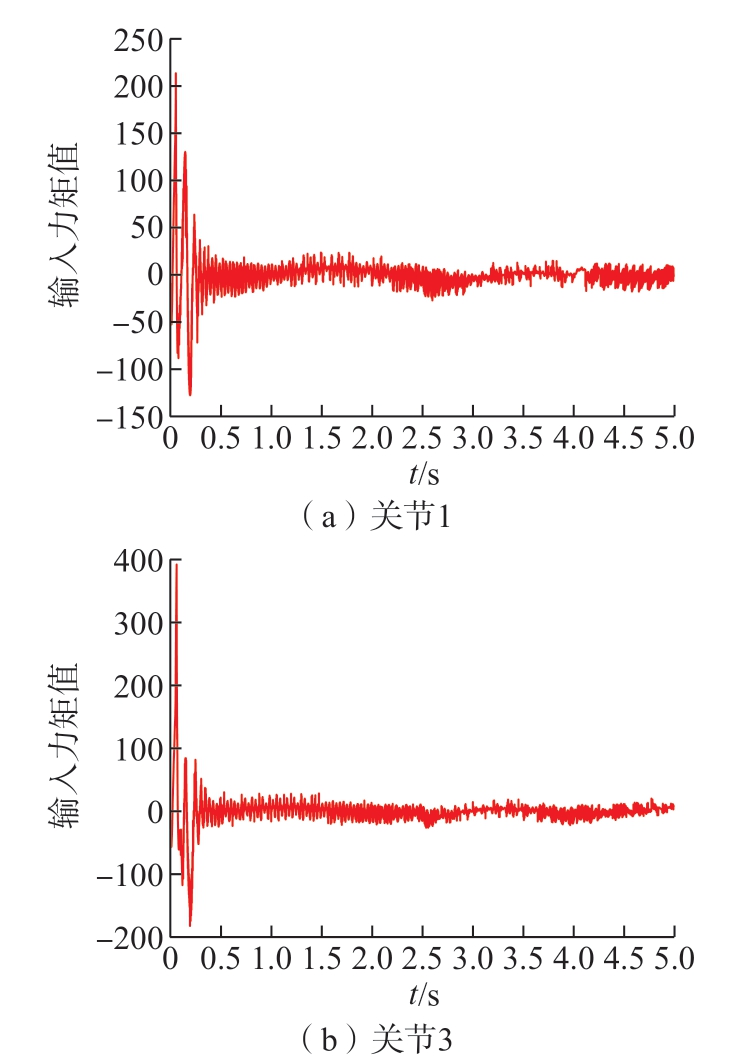
图10 关节1 和关节3 控制输入力矩
Fig.10 Control input torque of joint 1 and joint 3
假设机器人末端x、y、z 3 个方向的期望轨迹： 0.3sin（πt）+0.6、0.6、0.3cos（πt）+0.6。图11 为在容错控制作用下执行器出现故障与受外部干扰时机器人末端3 个方向的轨迹跟踪。可以看出，在出现上述状况后，机器人末端仍然能够较好地跟踪期望轨迹，仅在2.5 s 之后，即出现故障与干扰后有少量跟踪误差，x、y、z 3个方向的最大跟踪误差百分比约为0.71%、0.9%、1.56%。
图11 机器人末端轨迹跟踪
Fig.11 Robot end trajectory tracking
通过式 （28）与已知条件可模拟机器人末端与环境接触力约为3 N。当机器人末端x 方向受此接触力1 ～ 2 s时，在导纳控制作用下沿x 方向的运动轨迹如图12 所示，可以观察到当机器人系统出现执行器内部故障及机器人末端x 方向受力时，在容错控制与导纳控制作用下，机器人末端x方向也能较好地跟踪在外力作用下的期望轨迹，但在2 s 左右和2.5 s 后会出现些许跟踪偏差。其中 2 s 左右出现的跟踪偏差的最大百分比约为2.73%，可由所提变导纳控制方法解决； 2.5 s 后出现的跟踪偏差为执行器出现故障与受外部干扰时的正常情况，控制器可以及时地补偿消除故障与干扰带来的影响。图13 为所提变导纳控制作用下机器人末端x 方向受到外力时的运动轨迹，不难看出，2 s 左右机器人末端x 方向的运动轨迹更加地贴合受到外力时的期望轨迹，此时位置跟踪最大误差百分比下降为1.13%，亦如图14 与15 在操作空间中机器人末端运动轨迹所示，从图14 点 （0.5334，0.5995，0.8955）～（0.8368，0.5999，0.7889）与 图15 点 （0.5645，0.6048，0.902）～（0.8381，0.6003，0.7866）可以看到，在变导纳控制作用下机器人末端实际运动轨迹与期望轨迹更加贴合。因此与导纳控制作用下的运动轨迹相比，其主要优势就在于能够根据外界环境进行导纳参数的实时调整，如图16 所示，在无外力接触的情况下，调整阻尼值为0.5，刚度值为5，而当在1 ～ 2 s 持续受到外力时，调整阻尼值为0.1667，刚度值为8.333。
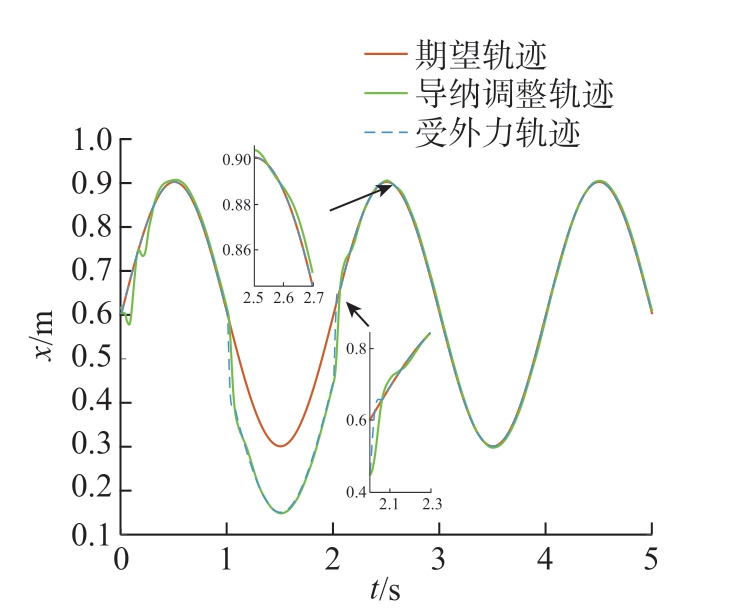
图12 导纳控制作用下x 方向受外力时机器人运动轨迹
Fig.12 Robot motion trajectory under external force in the x-direction under admittance control
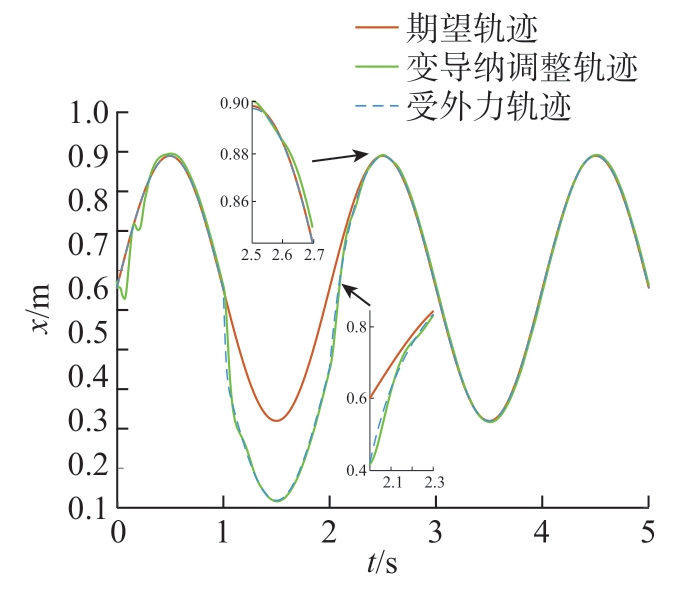
图13 变导纳作用下x 方向受外力时机器人运动轨迹
Fig.13 Robot motion trajectory under external force in the x-direction under variable admittance
图14 操作空间中导纳控制调整下的机器人末端运动轨迹
Fig.14 Robot end motion trajectory under admittance control adjustment in operating space
图15 操作空间中变导纳控制调整下的机器人末端运动轨迹
Fig.15 Robot end motion trajectory under variable admittance control adjustment in operating space
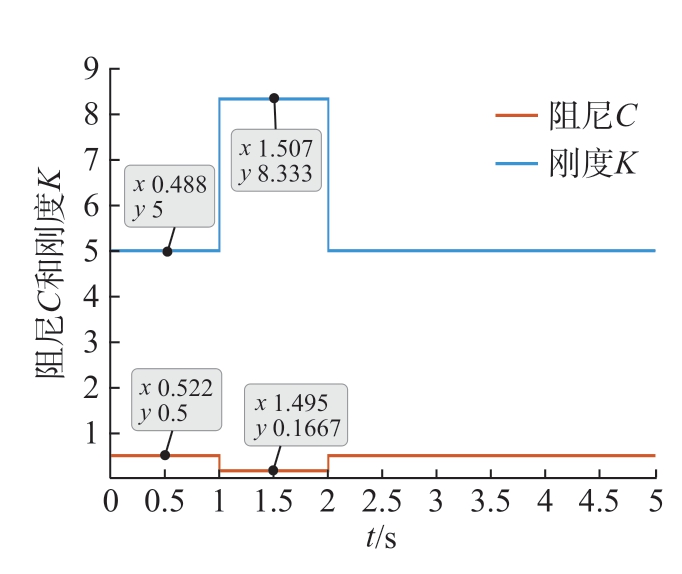
图16 变导纳阻尼和刚度值变化
Fig.16 Variations in admittance damping and stiffness values
因此，通过上述仿真试验，验证了所提方法不仅能够抑制外部扰动及有效解决机器人内部出现的故障问题，而且大大提高了机器人末端柔顺控制性能。
4 结论
在自抗扰位置控制的基础上将变导纳控制和主动容错控制策略相结合，提出了一种新型的工业机器人控制方法，得到的主要结论如下。
（1）所提方法不仅实现了在复杂环境下对机器人的高精度控制，还能够有效地避免机器人在运动中发生碰撞或其他意外情况，保证了机器人的稳定性和安全性。
（2）通过仿真试验，所提方法具有较高的可靠性和实用性，解决了一系列工业机器人在实际作业中可能遇到的问题，为工业机器人的智能化和自主化控制提供了新思路和方法。
未来，将继续深入研究工业机器人的控制方法，进一步提高其控制精度和容错能力，以满足工业生产中对机器人控制的更高要求，同时将研究应用到实际生产中，促进工业机器人的发展和应用。
[1] ZHU D C, DU B L, ZHU P C, et al.Adaptive backstepping sliding mode control of trajectory tracking for robotic manipulators[J].Complexity, 2020, 2020: 3156787.
[2] 赵扬, 刘霞. 机器人系统的加权快速终端滑模主动容错控制[J]. 信息与控制, 2023,52(3): 360–368.ZHAO Yang, LIU Xia. Weighted fast terminal sliding mode active fault-tolerant control for robotic system[J]. Information and Control,2023, 52(3): 360–368.
[3] SUN W W, WANG Y Z, YANG R M.L2 disturbance attenuation for a class of timedelay Hamiltonian systems[J]. Journal of Systems Science and Complexity, 2011, 24(4): 672–682.
[4] CEN Z H, NOURA H, AL YOUNES Y.Systematic fault tolerant control based on adaptive Thau observer estimation for quadrotor UAVs[J].International Journal of Applied Mathematics and Computer Science, 2015, 25(1): 159–174.
[5] JIN X Z, ZHAO Y X, WANG H, et al.Adaptive fault-tolerant control of mobile robots with actuator faults and unknown parameters[J].IET Control Theory & Applications, 2019, 13(11):1665–1672.
[6] HE X, WANG Z D, QIN L G, et al.Active fault-tolerant control for an Internet-based networked three-tank system[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6):2150–2157.
[7] ZHAO Y W, WANG H Q, XU N, et al.Reinforcement learning-based decentralized fault tolerant control for constrained interconnected nonlinear systems[J]. Chaos, Solitons & Fractals,2023, 167: 113034.
[8] ZHANG F K, WU W M, SONG R, et al. Dynamic learning-based fault tolerant control for robotic manipulators with actuator faults[J].Journal of the Franklin Institute, 2023, 360(2):862–886.
[9] PILTAN F, PROSVIRIN A E, KIM J M. Robot manipulator active fault-tolerant control using a machine learning-based automated robust hybrid observer[J]. Journal of Intelligent & Fuzzy Systems, 2020, 39(5): 6443–6463.
[10] PILTAN F, PROSVIRIN A E,SOHAIB M, et al. An SVM-based neural adaptive variable structure observer for fault diagnosis and fault-tolerant control of a robot manipulator[J].Applied Sciences, 2020, 10(4): 1344–1370.
[11] ZENG G W, HEMAMI A. An overview of robot force control[J]. Robotica, 1997,15(5): 473–482.
[12] 项文凭, 潘海鸿. 基于力传感器的下肢康复机器人柔顺控制[J]. 组合机床与自动化加工技术, 2023(10): 124–127.XIANG Wenping, PAN Haihong. Flexibility control of lower limb rehabilitation robot based on force sensors[J]. Modular Machine Tools and Automated Processing Technology, 2023(10):124–127.
[13] 许家忠, 郑学海, 周洵. 复合材料打磨机器人的主动柔顺控制[J]. 电机与控制学报, 2019, 23(12): 151–158.XU Jiazhong, ZHENG Xuehai, ZHOU Xun.Active and compliant control of the composite polishing robot[J]. Electric Machines and Control,2019, 23(12): 151–158.
[14] 陈卓强, 李林. 导纳控制在康复机器人中的应用[J]. 医疗装备, 2022, 35(18): 23–27.CHEN Zhuoqiang, LI Lin. Application of admittance control in rehabilitation robot[J].Medical Equipment, 2022, 35(18): 23–27.
[15] 段锐, 王冲冲, 王习昌, 等. 基于导纳控制框架的机器人奇异规避方法[J]. 机械设计与研究, 2022, 38(5): 6–10, 16.DUAN Rui, WANG Chongchong, WANG Xichang, et al. Singularity avoidance method of robot based on admittance control[J]. Machine Design & Research, 2022, 38(5): 6–10, 16.
[16] YAO B T, ZHOU Z D, WANG L H,et al. Sensorless and adaptive admittance control of industrial robot in physical human–robot interaction[J]. Robotics and Computer-Integrated Manufacturing, 2018, 51: 158–168.
[17] 胡盛斌, 陆敏恂. 空间三关节机器人自适应双模糊滑模控制[J]. 同济大学学报(自然科学版), 2012, 40(4): 622–628.HU Shengbin, LU Minxun. Adaptive double fuzzy sliding mode control for three-links spatial robot[J]. Journal of Tongji University (Natural Science), 2012, 40(4): 622–628.
[18] 俞经睿, 朱毅成, 冉晨阳, 等.基于自抗扰控制的机器人定位策略[J]. 控制理论与应用, 2023, 40(4): 772–779.YU Jingrui, ZHU Yicheng, RAN Chenyang,et al. Robot positioning strategy based on active disturbance rejection control[J]. Control Theory and Application, 2023, 40(4): 772–779.
[19] YANG P, MA X, WANG J, et al.Disturbance observer-based terminal sliding mode control of a 5-DOF upper-limb exoskeleton robot[J]. IEEE Access, 2019, 7: 62833–62839.
[20] REN H J, DENG G, HOU B, et al. Finite-time command filtered backstepping algorithm-based pitch angle tracking control for wind turbine hydraulic pitch systems[J]. IEEE Access, 2019, 7: 135514–135524.
[21] HOGAN N, BUERGER S. Impedance and interaction control[M]//Kurfess T R. Robotics and automation handbook. Boca Raton: CRC Press, 2004.
[22] AL-SHUKA H F N, LEONHARDT S, ZHU W H, et al. Active impedance control of bioinspired motion robotic manipulators: An overview[J]. Applied Bionics and Biomechanics,2018, 2018: 8203054.
