在航空工业中,铆接孔的加工质量对飞机安全性和使用寿命有至关重要的影响[1-2]。在国内的生产中,普遍仍通过工具进行人工检测,导致铆接高度的检测效率很难满足航空工业的需求。因此,本文采用机器视觉的方法对铆接高度差进行亚像素级的检测。
亚像素边缘检测是通过分解图像边缘附近的像素来精确定位、细化边缘的方法。从20世纪70年代起,不少专家提出了一些有效的亚像素边缘定位的方法,如形心法、灰度重心法、拟合法等[3]。目前,应用最为广泛的是Hough变换[4],也是曲线检测领域中最有成效的方法[5]。Hough变换的核心思想是点-线的对偶性,即把图像空间中的复杂边缘特征信息转化为参数空间中的聚类检测问题[6]。在参数空间不超过二维的情况下,使用Hough变换可达到理想的效果[7]。随着参数空间的增大,Hough变换的计算时间也会急剧上升,并占用大量存储空间[8]。为了避免巨大的计算量和内存消耗,研究者提出了随机Hough变换[9],该算法采用多到一的映射,但由于随机采样造成的无效累积,使算法效率降低。
综上,本文以3D激光轮廓传感器作为图像采集模块,设计出铆接高度差检测系统的整体机械结构,提出了一种优化的Hough变换铆接高度差亚像素检测方法,实现了对铆接表面高度差 (铆钉头相对于铆接表面的高度)高精度、高效率的检测。
1 检测系统结构设计
本文设计的检测系统结合3D激光轮廓传感器Demo文件,以及客户端软件3DMVS的SDK文件开发包,进行二次开发并集成Halcon图像深度学习识别算法,利用算法库对采集到的图像进行坐标系统一与数据拼合重构,最终得到铆接孔的形貌。将3D激光轮廓传感器和光栅尺测头装配在同步传送装置上,驱动传送装置带动光栅尺触发脉冲,使3D激光轮廓传感器在Y方向做直线运动,将采集的数据通过千兆网卡传输到工控机上,在客户端软件上设置参数后便可实时输出高精度三维点云数据和铆接高度差检测结果。测量系统结构如图1所示。

图1 测量系统结构框图
Fig.1 Structure block diagram of measurement system
2 铆接孔图像处理
2.1 铆接孔图像处理流程
根据采集铆接孔图像的特点,制定相应的图像处理流程,如图2所示。首先,通过3D激光轮廓传感器获取铆接孔图像,采用灰度变换法对所采集的原始图像进行增强处理,利用局部阈值分割法进行图像分割,然后通过Canny算法进行边缘粗提取,再利用优化的Hough变换进行亚像素级的边缘精细提取,提取出铆接孔和铆钉钉头的圆环区域,最后结合RANSAC算法进行圆拟合,利用开发算子get_current_region_z( )分别提取内外圆环区域的高度平均值,再通过函数height_Z( )将所得的高度平均值作差即可得到铆接表面的高度差。

图2 图像处理流程图
Fig.2 Flow chart of image processing
2.2 图像增强
图像在获取的过程中,由于噪声、光线等因素的影响,可能会导致图像的某些重要特征丢失,需要图像增强来改善图像质量,丰富所需信息量。空间域处理法是图像增强最基本的方法之一,分为点运算和邻域运算。空间域是组成图像像素的集合,这种方法直接作用于图像中的像素灰度值,基本以灰度映射为基础进行运算处理[10]。
若利用点运算处理一幅输入图像,所输出的灰度值会相对局限。根据运算前预设的规则,输入图像中的每个像素灰度会依次转换成输出图像所对应像素的灰度值,且不会改变像素的空间位置。综合对比增强效果后,选用空间域点运算中的灰度变换进行图像增强。
2.2.1 灰度变换
在数字图像处理中,灰度变换是一种十分直接的图像处理方法,可遵循一定的变换关系逐点对输入图像中各个像素灰度值进行处理。灰度变换原理:增大图像动态范围,使输入图像的弱对比度得到扩展,以达到更加清晰的显示效果。定义g(x,y) 为输入图像;f(x,y)为输出图像;(x,y)为点的邻域,其表达式为
式中,G为关于g(x,y)的一种运算。若对于单个像素,即 (x,y)代表1×1的单位邻域,其输出结果只取决于g(x,y)的像素灰度值。
2.2.2 线性变换
线性变换为灰度变换常用的方法之一,假设输入图像的灰度范围为[m,n],线性变换后输出图像的灰度范围为[p,q],令系数![]() ,则输入图像g(x,y)每点的灰度值与输出图像f(x,y)相应点灰度值的对应关系可表达为
,则输入图像g(x,y)每点的灰度值与输出图像f(x,y)相应点灰度值的对应关系可表达为
2.2.3 增强处理
图像增强流程:首先对原始图像进行灰度化,然后采用invert_image算子进行图像取反,增强图像中嵌入的灰度细节,最后利用emphasize算子增强铆接孔图像的边缘细节。铆钉原始图像如图3(a)所示,铆钉钉头与铆接板颜色不均衡且边缘分界不明显;灰度化图像如图3(b)所示,比原始图像颜色均衡;图3(c)为使用线性灰度变换后的取反图像,凸显边缘;图3(d)为图像增强处理后的效果图,与原始图像对比不难看出,边缘轮廓处的像素值变化更加清晰明显。

图3 图像增强效果图
Fig.3 Sketch of image enhancement
2.3 局部阈值分割
相对于原始图像,经过预处理后的图像更便于后续的图像分割,但仍为二维数字图像。图像分割可以将得到的数字图像在像素级别上分割为互不交叠的区域,使图像在同一区域内呈现相似性,不同区域间呈现明显的差异性[11]。图像分割的主要目的是将感兴趣的特征从复杂背景中分离出来,以便进行目标识别和场景分析[12]。
阈值分割法是一种非常重要的分割技术[13],基于区域实现图像分割,根据选定的灰度阈值将图像分割成不同的区域,原理简单且易于实现[14]。阈值分割法可分为全局阈值分割和局部阈值分割。全局阈值分割法是相对于整幅图像的像素而言,且对光照条件要求较高,如果图像光线较暗或光照不均匀,可能导致分割失败[15];而局部阈值分割法则是通过局部像素灰度的不同,计算每个像素的阈值,适用于灰度分布呈现不规则状态的图像。相对于全局分割算法,采用分块思想的局部分割方法可实现更为理想的分割效果。
局部阈值分割法,其原理为在像素的邻域内,以单个或多个指定像素的特性来计算图像中所有点的阈值。由于铆接孔原始图像前景灰度与背景灰度区分不明显,因此,采用Halcon中的局部阈值分割算子dyn_threshold进行局部灰度对比,并找到邻域中合适的阈值对铆接孔图像进行分割。该算子首先设定一个合适的阈值,利用平滑滤波器对原始图像进行适当平滑,然后对比均值处理后的图像与原始图像的局部像素差异,将差异大于设定值的像素点提取出来,分割效果如图4所示。

图4 局部阈值分割效果图
Fig.4 Sketch of local threshold segmentation
2.4 基于优化Hough变换的亚像素级边缘提取
传统图像处理算法提取的边缘精度都为像素级[16]。基于一阶图像边缘检测方法 (如Sobel算子、Prewitt算子、Kirsch算子等)利用图像灰度一阶导数的极大值和极小值提取边缘;基于二阶图像边缘检测方法 (如Laplace算子、Canny算子等)通过穿越零点的方法搜索图像边缘[17]。随着机器视觉检测的快速发展,像素级精度的边缘检测已经无法满足图像处理的需求,更高精度的检测方法,即亚像素级别的边缘检测算法也应运而生[18]。理想情况下边缘提取方法会提取出完整的边缘信息,但实际中由于光照、噪声等环境因素的影响,获取的边缘信息往往是间断或离散的状态。
2.4.1 Canny算法边缘提取粗定位
图像边缘是指图像周围有阶跃变化或屋顶变化的像素点,主要存在于目标与背景、区域与区域之间,是图像最基本的特征。目前,通用的轮廓边缘检测方法主要以Canny算法为基础进行改进,基于最优化的Canny算法基本思想:在图像中找出局部幅值最大梯度的像素点,使用两个阈值分别检测强边缘与弱边缘,并利用亮度、颜色和纹理来检测图像边缘位置[19]。Canny算法能有效抑制噪声,具有信噪比大、精度高等优点,优于其他微分算子[20]。
优化的Canny算法边缘检测的基本步骤如下[21]。
(1)利用一阶导数按行和列对原始图像进行卷积降噪,并采用二维高斯滤波器消除噪声,从而得到平滑图像。设v(x,y)为图像数据,σ为标准差,使用的高斯函数R(x,y)可表达为
(2)采用一阶偏导的有限差分计算平滑后图像的梯度幅值和梯度方向,通过2×2邻域一阶差分卷积模板计算出
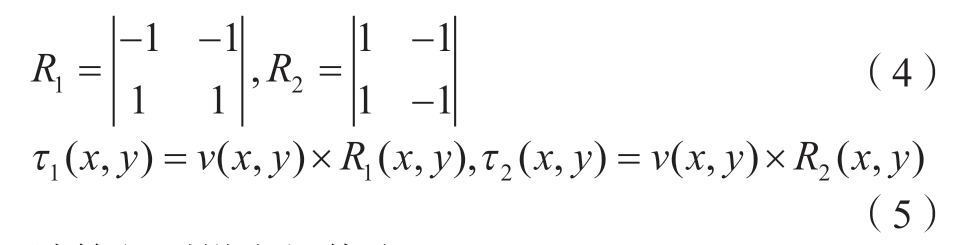
计算得到梯度幅值为
梯度方向角度为
梯度方向角度一般取0、45°、90°、135°。
(3)对梯度幅值进行非极大值抑制处理,即将非局部最大值点置0,以保留局部梯度最大点,排除非边缘像素,获取细化边缘。
(4)利用双阈值算法检测并连接边缘。双阈值算法原理:设置两个滞后阈值,高阈值W1和低阈值W2,得出对应的边缘图像K1(i,j)和K2(i,j),由于K1(i,j)图像有间断点,若想将其边缘修补成完整的轮廓,需在K2(i,j)的邻域点位置不断搜索并连接到K1(i,j)轮廓上的边缘,直到K1(i,j)轮廓连接完整。
Canny算法边缘检测后的效果图如图5所示。

图5 Canny算法边缘检测
Fig.5 Edge detection in Canny algorithm
2.4.2 优化的Hough变换亚像素级的边缘提取
经典Hough变换在参数复杂的图像轮廓中存在计算时间长、噪声干扰严重、无法精确检测图形边界等缺点。为改善以上不足,本节提出了一种在Canny算法边缘检测的基础上,加入优化的Hough变换对已识别的边缘图像再进行亚像素级的精确提取,减少图像复杂背景的干扰,改善提取边缘算法的效率和精度。
经典Hough变换提供了一种搜寻图形轮廓的方法,将图像空间转换到参数空间,本质上是对二维参数空间中具有关联性的像元进行聚类,搜索参数空间累积对应点,以便将这些像元统一用某一解析形式表达出来[22],尤其在搜索直线时表现出极其准确的精度,即使图形轮廓有间断或存在干扰,依然能够准确地识别检测目标。影响Hough变换运算时间的因素主要有参数空间的离散化程度、维数、模型复杂程度、峰值检测等[23]。但类似椭圆这种图形轮廓,由于其参数复杂,往往会导致计算量增多,实时性也有所降低。
经典Hough变换的核心思想是采用一种投票机制,通过筛选最高的投票分数来判断最高分圆弧的存在,对于参数复杂的图形轮廓处理时间过长。优化的Hough变换本质是一种模板匹配方法,通过几何分析有效地避免了为每个非零像素都投票的过程。这种算法利用可更新模板,缩短了处理时间并且减少了所需的存储空间,在搜索圆、椭圆等复杂图形轮廓时都具有较高的鲁棒性。
优化后Hough变换的核心步骤如下。
(1)首先设定邻域块大小 (一个圆形的领域,一般选取3、5、7…),取像素点权重为一个高斯窗口,根据每个像素点到邻域中心点的距离计算权值,阈值取相邻区域的加权平均值。由于相邻领域都很小,能够把大于这个像素的领域删除,累加便得到阈值参数 α,即对每个像素点进行动态采样,对采样位置上的相邻像素点进行阈值判定并逐一筛选邻域,直到确定出初始阈值大小。
(2)初始化特征参数的累加器数组,随机抽取一个最小点集{H},根据此点集计算新搜索到的圆和已保存在累加器数组中圆的相似度,若相似度超过设定阈值,则用这两个圆的平均值替换掉累加器数组中的圆。
(3)计算结束后,对特征参数的累加器数组值αi进行相应的更新。
(4)当累加器数组值αi大于设定阈值α时,判断此特征参数是否含有足够多的图像特征点,若满足,则输出此特征参数并将其从图像和累加器数组中删除,以便算法更快地搜索其他圆。
(5)重复步骤2~4,直至算法循环次数达到设定阈值或所有圆都被识别出时,算法停止。
设 (a,b)为圆心坐标,r为圆的半径,定义二维空间中圆的方程为
若要完全确定一个圆,在圆上随机选取3个点(c1,d1)、(c2,d2)、(c3,d3),将这 3个点代入式(8)中得到

求解方程组可得到圆心坐标 (a,b)和半径r。
设定初始误差值 ε,取第i点(ci,di),代入式(8)中求出半径ri,然后再代入式(10)。
求出误差εi并判断εi与ε关系,εi < ε时,将此圆确定为候选圆,累加器数组加1,当累加器数组的值αi达到设定阈值α时,便确定为真圆;εi≥ε时的点为无效点。
经过优化的Hough变换提取的铆接孔边缘如图6所示。

图6 优化的Hough变换亚像素边缘提取
Fig.6 Sub-pixel edge extraction in optimized Hough transform
2.5 像素级与亚像素级3D点云图像对比
将Canny算法提取的像素级灰度图和优化的Hough变换提取的亚像素级灰度图转换为3D点云数据,并分别绘制相应的纹理图和轮廓线,如图7所示。灰度图像转为3D点云图像,实际上就是平面灰度值的立体呈现,即提取灰度图中每个像素的行列坐标作为3D点云的X、Y坐标,像素的灰度值 (0 ~ 255之间的整数)作为三维点的Z坐标。简单说就是将一张灰度图像拆成了X、Y和Z 3个数组,然后将这3个数组转为点云数据。

图7 像素与亚像素级3D点云图像
Fig.7 3D point cloud images at level of pixel and sub-pixel
对比图7(a)和(c)不难看出,亚像素级的纹理图像素突变点明显有所减少,像素分明,而且图像轮廓趋于平滑,而像素级边界则呈现锯齿形。
轮廓线与地图上的等高线原理基本相同,等高线越密集,表示地表坡度越陡,轮廓线越密集,表示像素分布越离散;等高线越稀疏,表示地表坡度越缓,轮廓线越稀疏,表示像素分布越均衡。如图7(b)和(d)所示,亚像素级的轮廓线分布更为离散,表示像素分布更加均衡。
2.6 基于RANSAC算法的圆拟合
RANSAC算法是一种鲁棒性强,适用于大比例外点的参数估计算法,可以在一组包含内点和外点的数据集中,通过迭代的方式计算数据的最佳模型,计算步骤如下[24]。
步骤1:在数据集中随机选取最小数据集{L},计算出模型的参数。
步骤2:用获取的模型计算所有点,定义误差小于设定阈值以内的点为内点,否则为外点。
步骤3:重复步骤1和2,当迭代次数达到预设值后,选取保存内点数最多的模型参数作为最佳模型。
RANSAC算法最少迭代次数N满足
式中,QL为置信度,表示所选最小数据集{L}中,至少有一个是内点的概率;γ为所选数据是外点的概率。
置信度QL与迭代次数N的关系式为
RANSAC算法拟合过程排除了局外点的干扰,并估计出高精度的模型参数,拟合结果如图8所示。

图8 RANSAC拟合圆
Fig.8 Circle fitting in RANSA
3 检测试验与数据分析
3.1 检测设置
开始检测前,分别设置铆接钉头高度差(阶差)的基准值为0,极限偏差值为- 100 μm,即表示阶差在- 100~0 μm 范围内的铆接孔均为合格孔,用绿色圆环显示,否则为不合格孔,用红色圆环显示。偏差设置如图9所示。

图9 极限偏差设置
Fig.9 Limit deviation setting
3.2 检测结果
利用专用塞尺人工检测铆接高度差,这种塞尺由一组具有不同厚度级的薄钢片组成,在斜边上标有刻度,进行测量时,用干净的布把塞尺测量表面擦拭干净,将塞尺插入被测钉头边缘上,一边来回拉动塞尺,一边调整。如果拉动时的阻力过大或过小,则说明该高度差小于或大于塞尺上所标出的数值,这时可改变薄钢片数量,直到感觉稍有阻力时拧紧锁紧螺母,说明该间隙值接近塞尺上所标出的数值,此时塞尺所标出的数值即为被测高度差。
人工进行多次测量取其均值,并将其作为参考,检验机器视觉检测结果的准确性。为了使检测结果真实准确,选取铆接板上的5行6列共30个铆接位置进行重复检测,记录每个位置的铆接高度差,并对测量出的数据进行了统计分析,检测结果如图10所示。

图10 检测结果(μm)
Fig.10 Test results (μm)
3.3 数据分析
将3次机器视觉检测的铆接高度差数据进行对比,如图11所示。可以看出,3条曲线整体变化趋势基本相同,说明对于相同位置的3次检测结果极为接近。经过分析计算,3条曲线上对应的相同点波动相差都不超过10 μm,即铆接高度差的重复测量精度可达到±10 μm。
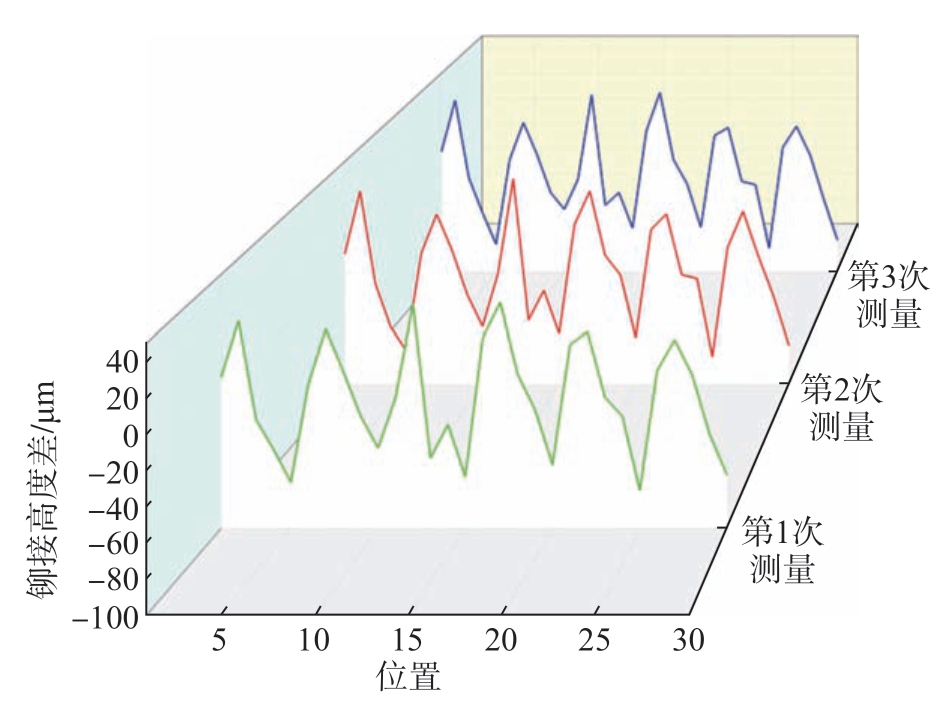
图11 3次机器视觉铆接高度差检测对比
Fig.11 Comparison of three times of riveting height diffeence detection by machine vision
将3次机器视觉检测的铆接高度差分别与人工测量均值数据作差,求出3组铆接高度差的偏差值数据,并绘制三维锥型图,如图12所示。可以看出,每点偏差值均在10 μm以内,说明机器视觉测量系统检测结果的高精度性。
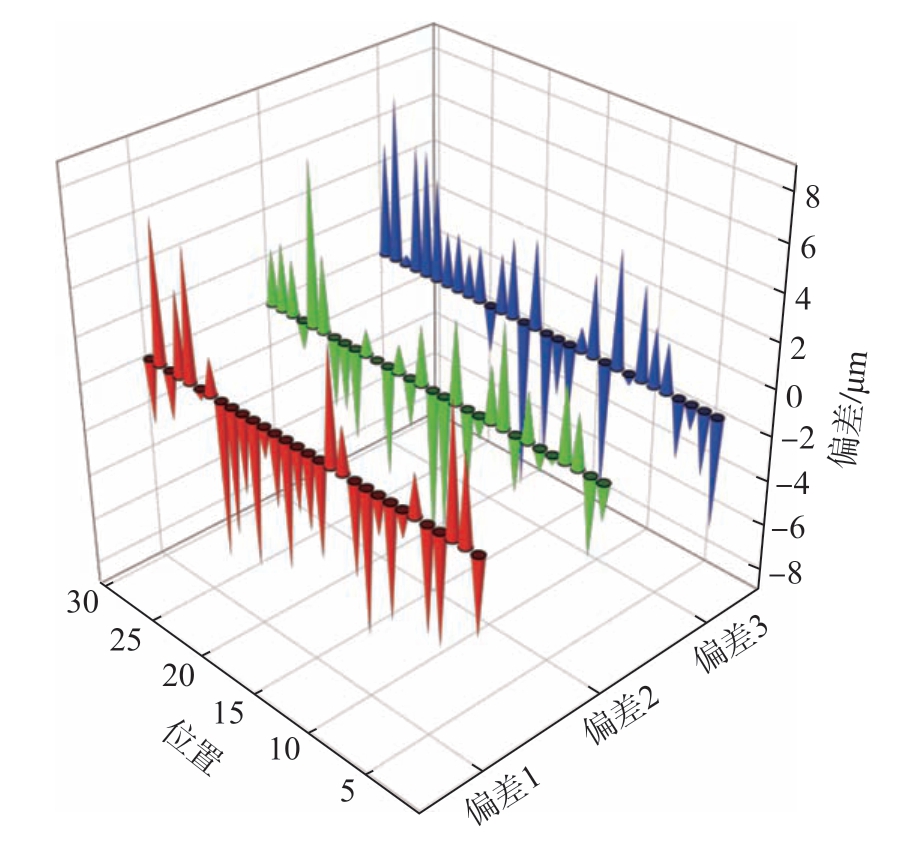
图12 人工、机器视觉测量偏差
Fig.12 Deviation of manual and machine vision measurement
4 结论
(1)针对飞机铆接高度差的检测问题,本研究提出了一种基于优化的Hough变换的亚像素级边缘检测方法。该方法检测出的圆孔边缘轮廓信息相对完整,实现了亚像素级的边缘检测。
(2)设计了铆接高度差检测系统,在对30个位置的铆接孔进行重复检测,并与人工检测结果对比之后,证明该系统检测结果的偏差值不超过10 μm,重复测量精度可达到±10 μm。
(3)该检测系统可以同时测量多个位置的铆接孔高度差,实现了对铆接高度差的高精度、高效率测量。
[1] EGUTI C C A, TRABASSO L G. Design of a robotic orbital driller for assembling aircraft structures[J]. Mechatronics, 2014, 24(5):533-545.
[2] ZHAN Q, WANG X. Hand-eye calibration and positioning for a robot drilling system[J]. The International Journal of Advanced Manufacturing Technology, 2012, 61(5-8): 691-701.
[3] ROHDE O K, JR HEALY D M, BERENSTEIN C A, et al. Measuring image similarity to sub-pixel accuracy[C]//3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro.Piscataway: IEEE, 2006: 638-641.
[4] DAUGMAN J G. High confidence visual recognition of persons by a test of statistical independence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11): 1148-1161.
[5] HOUGH P V. Method and means for recognizing complex patterns: US1771560A[P]. 1962-05-13.
[6] HOUGH P V. Machine analysis of bubble chamber pictures[C]//Proceedings of Int Conf High-Energy Accelerators and Instrumentation. Geneva, 1959: 554-556.
[7] 刁燕, 吴晨柯, 罗华, 等. 基于改进的概率Hough变换的直线检测优化算法[J]. 光学学报, 2018, 38(8): 170-178.DIAO Yan, WU Chenke, LUO Hua, et al. Line detection optimization algorithm based on improved probabilistic Hough transform[J]. Acta Optica Sinica, 2018, 38(8): 170-178.
[8] LYU P, WEI G H, CUI W. Short-range multitarget motion parameter estimation method based on Hough transform[J]. Chinese Journal of Electronics, 2019, 28(2): 344-348.
[9] 贾小军, 魏远旺, 廖伟志, 等. 基于多阈值和改进的Hough变换检测电表接线圆孔尺寸[J]. 光电子·激光, 2018, 29(10): 1074-1081.JIA Xiaojun, WEI Yuanwang, LIAO Weizhi, et al. Detection of circular hole size of electric meter connection based on multi-threshold and improved Hough transform[J]. Journal of Optoelectronics·Laser, 2018, 29(10): 1074-1081.
[10] 郭永坤, 朱彦陈, 刘莉萍, 等. 空频域图像增强方法研究综述[J]. 计算机工程与应用, 2022, 58(11): 23-32.GUO Yongkun, ZHU Yanchen, LIU Liping, et al. Research review of space-frequency domain image enhancement methods[J]. Computer Engineering and Applications, 2022, 58(11): 23-32.
[11] 梁新宇, 林洗坤, 权冀川, 等. 基于深度学习的图像实例分割技术研究进展[J]. 电子学报, 2020, 48(12): 2476-2486.LIANG Xinyu, LIN Xikun, QUAN Jichuan, et al. Research on the progress of image instance segmentation based on deep learning[J]. Acta Electronica Sinica, 2020, 48(12): 2476-2486.
[12] YILMAZ A, JAVED O, SHAH M. Object tracking: A survey[J]. ACM Computing Surveys, 2006, 38(4): 13-19.
[13] SEZGIN M, SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146-165.
[14] 赵小川. MATLAB图像处理-能力提高与应用案例[M]. 北京: 北京航空航天大学出版社, 2014.ZHAO Xiaochuan. MATLAB image processing-ability improvement and application case[M]. Beijing: Beihang University of Press, 2014.
[15] LI G, ZHAO Y, ZHANG L, et al. Entropy-based global and local weight adaptive image segmentation models[J]. Tsinghua Science and Technology, 2019, 25(1): 149-160.
[16] HUANG J W, ZHANG L Q, JIANG Z Y, et al. Heterogeneous parallel computing accelerated iterative subpixel digital image correlation[J].Science China Technological Sciences, 2018, 61(1): 74-85.
[17] TANG W, ZHU L C, WANG Q M. Recognition of FAST reflector nodes based on Canny operator[J]. Research in Astronomy and Astrophysics, 2020, 20(8): 126.
[18] TRUJILLO-PINO A, KRISSIAN K, ALEMÁN-FLORES M, et al. Accurate subpixel edge location based on partial area effect[J].Image and Vision Computing, 2013, 31(1): 72-90.
[19] MARTIN D R, FOWLKES C C, MALIK J. Learning to detect natural image boundaries using local brightness, color, and texture cues[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2004, 26(5): 530-549.
[20] 宋志刚, 王龙山, 陈向伟. 利用数字图像处理技术检测锥螺纹[J]. 吉林大学学报(工学版), 2004, 34(2): 248-251.SONG Zhigang, WANG Longshan, CHEN Xiangwei. Detection of conical thread with digital image processing technology[J]. Journal of Jilin University (Engineering and Technology Edition), 2004, 34(2):248-251.
[21] 段红燕, 邵豪, 张淑珍, 等. 一种基于Canny算子的图像边缘检测改进算法[J]. 上海交通大学学报, 2016, 50(12): 1861-1865.DUAN Hongyan, SHAO Hao, ZHANG Shuzhen, et al. An improved algorithm for image edge detection based on Canny operator[J]. Journal of Shanghai Jiao Tong University, 2016, 50(12): 1861-1865.
[22] 束志林, 戚飞虎. 一种新的随机Hough快速圆检测算法[J].计算机工程, 2003, 29(6): 87-88, 110.SHU Zhilin, QI Feihu. A novel algorithm for fast circle detection using randomized Hough transform[J]. Computer Engineering, 2003,29(6): 87-88, 110.
[23] LI F, XIONG J J, LAN X H, et al. Hypersonic vehicle trajectory prediction algorithm based on Hough transform[J]. Chinese Journal of Electronics, 2021, 30(5): 918-930.
[24] 徐岩, 安卫凤. 基于改进随机抽样一致算法的视觉SLAM[J].天津大学学报(自然科学与工程技术版), 2020, 53(10): 1069-1076.XU Yan, AN Weifeng. Visual SLAM based on the improved RANSAC algorithm[J]. Journal of Tianjin University (Science and Technology), 2020,53(10): 1069-1076.