飞机装配具有过程复杂、工作量大、周期长等特点[1],作为飞机制造的最后环节,其生产效率直接影响整架飞机的生产制造能力[2]。目前,飞机装配普遍以装配站位为基础管理单元。在各站位内以飞机架次为标签来跟踪与控制在装产品的生产状态[3]。对于稳定运行的装配站位,其生产布局、工艺结构与资源配置都相对固定,不同架次之间的主要差异体现在规定的交付时间和关键物料配置方案两方面,其中物料配置方案指架次开铆所需关键零部件送达站位的时间集合。由于飞机装配作业过程繁杂并存在大量随机扰动,工期超前或滞后现象频发,造成下游站位对于本站位特定架次的规定交付时间呈现较为严重的波动性。与此同时,由于部分飞机零部件具有外形庞大、不易存储的特点,装配现场尽量避免关键物料在站边滞留,从而减少相应的仓储成本。因此,现场管理者需要频繁地依据不断变化的交付要求对在装架次关键物料配置方案进行优化;再依据优化结果对上游站位或外部供应商提出明确的物料交付要求。综上所述,飞机装配站位亟须一种基于当前架次生产条件,快速又准确的关键物料配置方案优化手段。此外,如今新一代信息技术在装配现场的广泛应用[4]及先进智能算法的持续发展,为开发智能化的装配管理与优化方法提供了更加理想的研究环境。
要实现飞机装配站位物料配置优化,首先需要解决在装架次生产状态评估问题。可靠的评估结果是引导优化算法对物料配置方案迭代寻优的基础。由于飞机装配作业涉及的工艺、资源和物流等要素繁多,各要素之间的相互作用复杂,解析各类输入要素与在装架次进度、仓储成本等性能指标之间的量化关联非常困难,研究人员一直难以构造相对准确且可解释性强的因果分析模型。相较而言,离散事件仿真既能有效刻画各类随机特性,又能全面覆盖制造系统内关键生产要素,被认为是目前复杂系统性能分析的一种可靠手段[5],广泛应用于飞机装配生产线[6]。但是,离散事件建模过程专业性要求高,模型参数定义和赋值过程复杂,造成模型参数更新与运行需要占用大量资源并相当耗时[7],因此该类建模分析方法虽然在装配现场被广泛用于准确评估装配状态,但是在效率上无法应用于有大量候选物料配置方案的优化场景。
为了提高复杂制造系统中仿真评估的效率,一些学者提出基于仿真数据来构建仿真代理模型,从而简化表达特定输入参数与系统性能指标之间量化关系。其中,人工神经网络凭借其优良的泛化和非线性映射等能力被广泛用于生产参数配置代理建模,并表现出可靠的评估准确性[8]。然而与其他生产参数配置方案不同,飞机装配站位内各关键物料的配置时间按照架次开铆顺序有着明确的先后顺序关联,而一般的全连接反向传播神经网络 (BP neural network,BPNN)由于其结构的限制,往往只能单独处理离散输入,即任意两个输入前后毫无关联,难以学习输入参数之间的序列信息[9]。因此,本文采用在时序分析领域广泛使用,具备序列输入分析能力的循环神经网络 (Recurrent neural network,RNN)来构建装配站位物料配置方案的仿真评估代理模型。为了进一步提高模型的评估效果,基于门控循环单元(Gated recurrent unit,GRU)改进RNN的仿真代理模型(GRU仿真代理模型)。在构建仿真代理模型的基础上,将其作为目标函数评估模型,与遗传算法相结合实现物料配置方案的全局迭代优化。最后,采用离散事件仿真平台验证算法输出的最优方案。
1 优化方法框架
考虑到离散事件仿真分析的可靠性与局限性,构建了包含了离散事件仿真、面向架次状态评估的仿真代理模型、物料配置方案全局优化算法的集成优化框架,如图1所示。首先,从现场积累的大量仿真历史数据中采集并整理出用于仿真代理模型训练和测试的学习样本。然后,考虑装配现场对于关键物料配置优化的关注重点,选取在装架次预计完工时间和关键物料平均滞留时间作为评估输出指标,由此基于仿真样本数据构建两个仿真代理模型来分别评估上述两个性能指标。采用启发式优化算法来实现物料配置方案的全局寻优,在优化过程中将构建的两个仿真代理模型作为所有备选方案的目标函数评估模型,同时保证了对所有方案评估的准确性与效率。最后,为了充分保证输出方案的可靠性,将优化算法输出的最优方案再代入到离散事件仿真平台进行验证,将验证通过的优化方案反馈至装配现场,为管理者提供建议与参考。
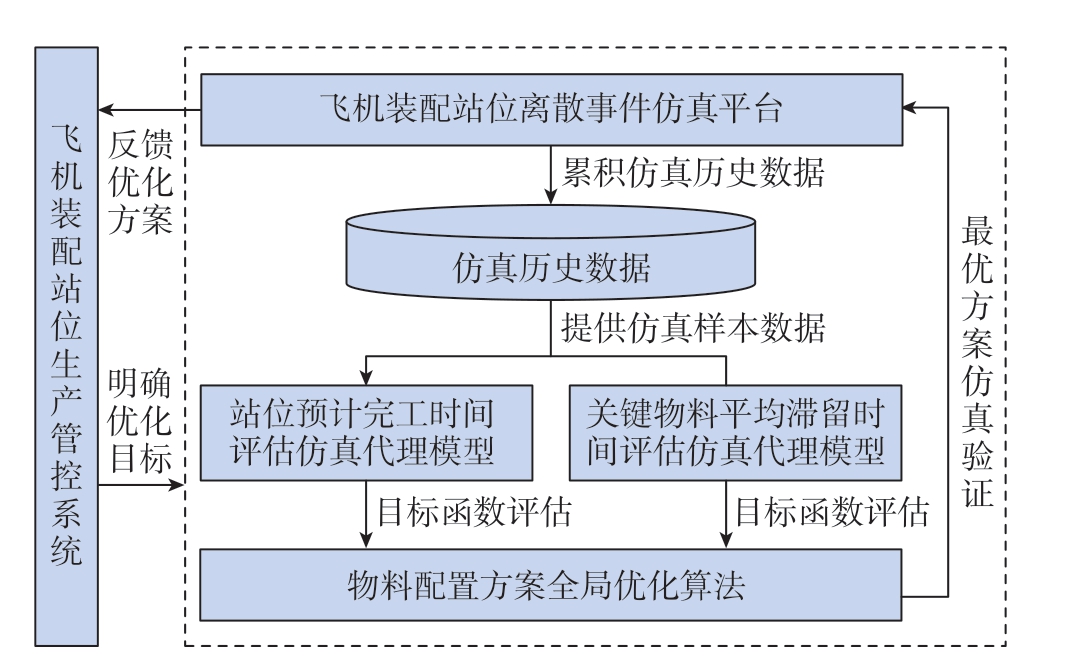
图1 飞机装配站位关键物料配置方案优化框架
Fig.1 Optimization framework of key material configuration fo aircraft assembly station
2 基于GRU改进循环神经网络的仿真代理建模
本文所要构建的关键物料配置方案仿真评估代理模型以关键物料配置方案为输入,其中关键物料可以根据现场对于物料短缺历史情况的调查,以及现场人员的经验来选取。基于站位内作业网络顺序结构,将各关键物料按照架次开铆顺序依次排列,形成一维数组的形式,即
式中,MR表示一个装配站位的关键物料配置方案;![]() 表示编号为id_t(使用id_t来映射所选的各项关键物料在管控系统中编号)的物料计划配置到该站位的时间与架次开工时间的差值,其中,t表示该关键物料在当前配置方案中的排序;T表示该配置方案中所选取的关键物料总数。
表示编号为id_t(使用id_t来映射所选的各项关键物料在管控系统中编号)的物料计划配置到该站位的时间与架次开工时间的差值,其中,t表示该关键物料在当前配置方案中的排序;T表示该配置方案中所选取的关键物料总数。
根据上文分析,选取了在装架次预计完工时间Et和关键物料平均滞留时间Rt两个性能指标作为仿真代理模型的输出。构建两个仿真代理模型分别输出这两个指标,使两个模型的网络结构和权重参数能够分别契合两个指标与物料配置方案的非线性关系,从而提高各自的准确性。而面向复杂的预测问题,通常需要建立多层网络模型。根据以上分析,基于RNN的仿真代理模型如图2所示,其中st表示对应第t个输入单元的网络中间层的输出。
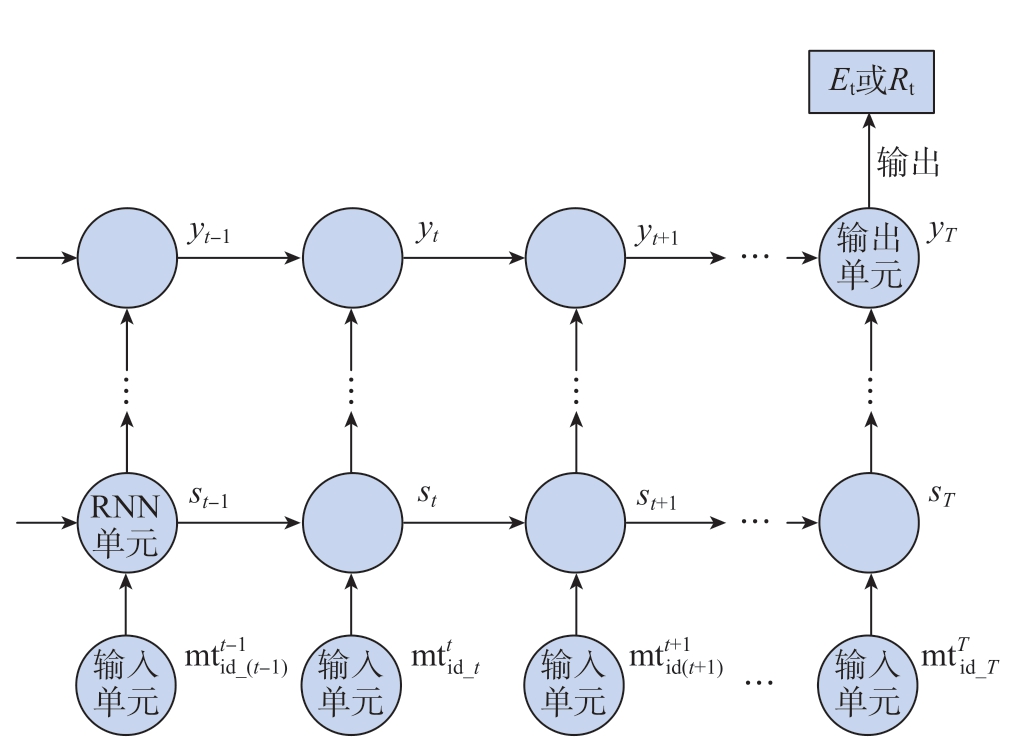
图2 基于RNN的物料配置方案仿真评估代理模型结构
Fig.2 Proxy model structure for simulation evaluation of material configuration based on RN
而朴素RNN网络存在对前序信息利用能力不足,极易发生梯度消失与梯度爆炸等问题。在本文应用问题中,如果使用朴素RNN网络将导致在物料配置方案评估过程中出现越早到站的关键物料分配越小的权重系数,这明显是与实际生产情况不符的。为此,引入GRU来替换图2中仿真代理模型的RNN单元。GRU已在时序分析领域被证明可对序列中的长期依赖关系建模,将其应用于物料配置方案评估建模,可以充分地对完整的配置方案与生产状态指标间关联关系进行建模。GRU和长短期记忆神经网络[10] (Long short-term memory,LSTM)都是基于朴素RNN的变形,均能够克服朴素RNN梯度消失问题,而GRU具备更简单的结构,更高效。GRU的核心由重置门和更新门组成[11],GRU内部单元结构如图3所示,其中,σ为Sigmoid激活函数。
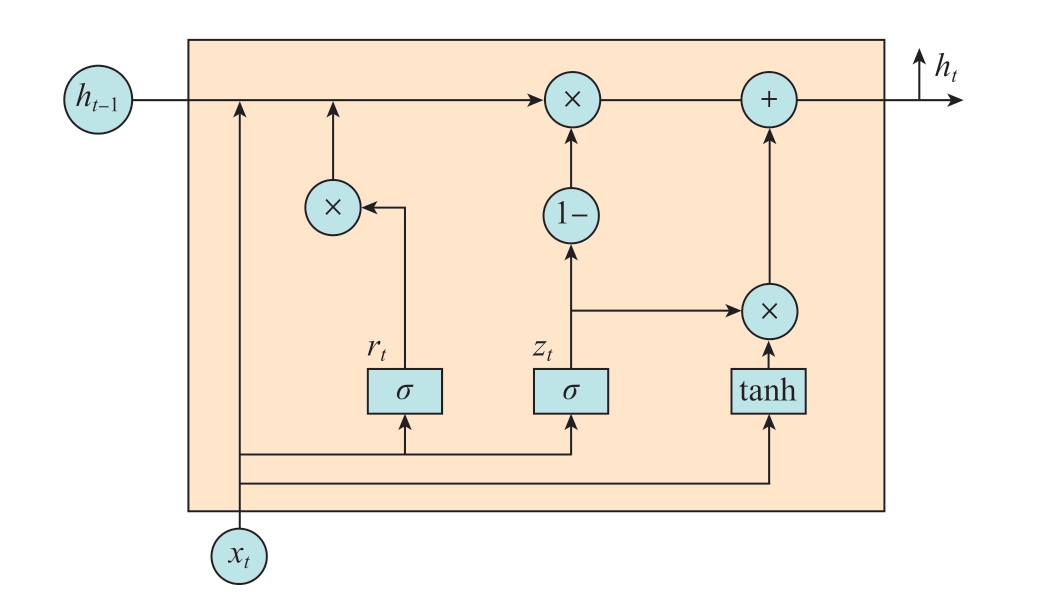
图3 GRU内部单元结构
Fig.3 Internal unit structure of GRU
简单来说,GRU通过前序的状态变量ht-1和当前的输入变量xt来自主学习并控制此单元内两个门控的权重 (rt和zt)。因此,在实际生产状态指标评估的过程中,GRU网络单元可以按适当的权重捕捉所有前序物料的配置信息。
3 基于遗传算法的物料配置方案优化
3.1 优化问题建模
一般来说,任何工程优化问题都需要先构建其数学模型,明确优化目标和相关约束,从而为启发式优化算法明确优化空间和搜索方向。结合实际飞机装配站位的生产特点和需求,定义关键物料配置方案优化问题的目标函数和约束条件。
(1)目标函数。
构建仿真代理模型来评估在装架次的预计完工时间Et和关键物料的平均滞留时间Rt。因此,在本文方法应用过程中不需要通过复杂的解算公式来计算这两个指标,只需要关注指标的工程含义和优化方向即可,本文方法降低了对实践者专业知识的要求。目标函数通过加权Et和Rt两个指标组成,根据上述指标建立目标函数如下。
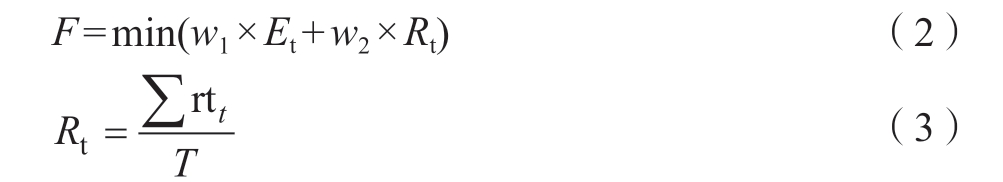
式中,F为物料的平均停留及完工时间之和;w1和w2表示权重系数,其大小可根据现场优化侧重点进行调整;rtt表示物料编号为id_t的关键物料的平均滞留时间。
(2)约束条件。
约束1:w1 + w2 = 1
约束2:![]()
约束1限制两个权重系数总和。约束2限制了每一种关键物料送达站位时间的波动范围,ubt和lbt分别表示上、下界。与此同时,其他生产要素 (如作业、资源、设备)之间相关约束都在仿真代理环境中得到了验证,不需要在优化过程中再次重复检验。
3.2 遗传算法流程
遗传算法作为最具代表性的进化算法,具有求解速度快、随机性强、过程简单和鲁棒性好等优点,一直作为广大学者解决启发式优化问题的基准算法。因此,本文采用标准遗传算法作为物料配置方案全局优化引擎,通过实数编码使得算法种群中每个个体代表一个唯一的物料配置方案,而本文的创新点在于使用仿真评估代理模型作为目标函数评估模型,集成到遗传算法来评估所有种群个体的两个性能指标 (Et、Rt)。本文所采用遗传算法的主要流程如图4所示。

图4 遗传算法主要流程
Fig.4 Main process of GA
4 实例验证
本文以某型飞机的翼身对接站位为实例对象,从基于GRU的仿真代理评估和最终输出的优化结果两方面验证所提出方法的准确性和适用性。通过在装配现场对物料历史短缺情况的详细调查,并结合现场管理者的生产经验,选取了内襟翼、整流罩等18种配置时间波动较为频繁的关键物料组成了完整的物料配置方案,作为本实例的优化对象。
4.1 基于GRU的仿真代理评估验证
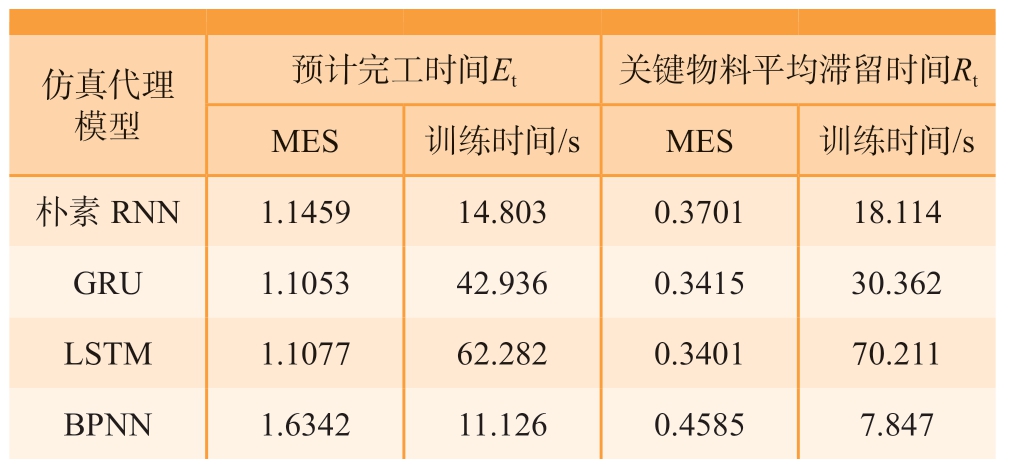
为了充分验证基于GRU的仿真代理模型对物料配置方案评估效果,在采用相同的仿真数据训练集和网络参数的情况下,对比朴素RNN、GRU、LSTM及BPNN 4种代理模型的评估准确性和学习效率。具体来说,采用均方误差 (Mean square error,MSE)指标来评价各模型的评估准确性,该指标越小说明模型评估的准确性越好;采用训练时间来对比各模型的学习效率,训练时间越短说明模型学习效率越高。试验结果如表1所示,并得出以下结论。
表1 仿真代理模型评估效果对比
Table 1 Comparison of the simulation agent models
预计完工时间Et 关键物料平均滞留时间Rt MES 训练时间/s MES 训练时间/s朴素RNN 1.1459 14.803 0.3701 18.114 GRU 1.1053 42.936 0.3415 30.362 LSTM 1.1077 62.282 0.3401 70.211 BPNN 1.6342 11.126 0.4585 7.847仿真代理模型
(1)朴素RNN、GRU及LSTM代理模型由于具备输入顺序分析能力,这3个模型对于物料配置方案评估的准确性明显优于不具备顺序分析能力的BPNN模型。
(2)GRU模型虽然没有结构更为简单的朴素RNN和BPNN模型的学习效率高,但是与评估准确性相当的LSTM模型相比,GRU模型明显具备更高的学习效率。
(3)在两个指标的评估上,GRU模型的评估准确性与LSTM模型非常接近,无论采用哪个模型与遗传算法相集成,都对后续优化方向的影响不大。因此,综合考虑模型的学习效率,应采用GRU模型来构建物料配置方案评估的仿真代理模型,并且学习效率的优势会随着所研究问题规模的增大而更加明显。
(4)具体来看,构建的GRU仿真代理模型对于架次预计完工时间的评估值与仿真标签值的均方误差达到1.1053,对于物料平均滞留时间的均方误差达到0.3415。
综上所述,基于GRU的仿真代理模型在关键物料配置方案评估方面有着可靠的准确性以及良好的训练效率。进一步从仿真测试集中随机选取25组样本,以折线图的形式直观展示并比较了GRU和BPNN模型在相同仿真样本集下的评估结果,以预计完工时间 (Et指标)为例,评估结果如图5所示。可以看出,两个模型的评估结果都能够近似拟合仿真标签值。但还要从所有样本的变化趋势上看哪个模型评估结果与仿真标签值在变化趋势上更加契合。为此,分别计算GRU和BPNN模型评估结果与仿真标签值的皮尔逊相关系数(越接近1说明两组数据相关性越强,反之,越接近0说明相关性越弱)。试验显示,GRU模型评估结果与仿真标签值的相关系数为0.985,BPNN模型评估结果的相关系统为0.878。以上分析说明,使用GRU模型的评估结果在单点数值和整体趋势两方面都较好地拟合仿真了标签值,用来评判物料配置方案优劣性时,GRU模型比BPNN模型更加可靠。
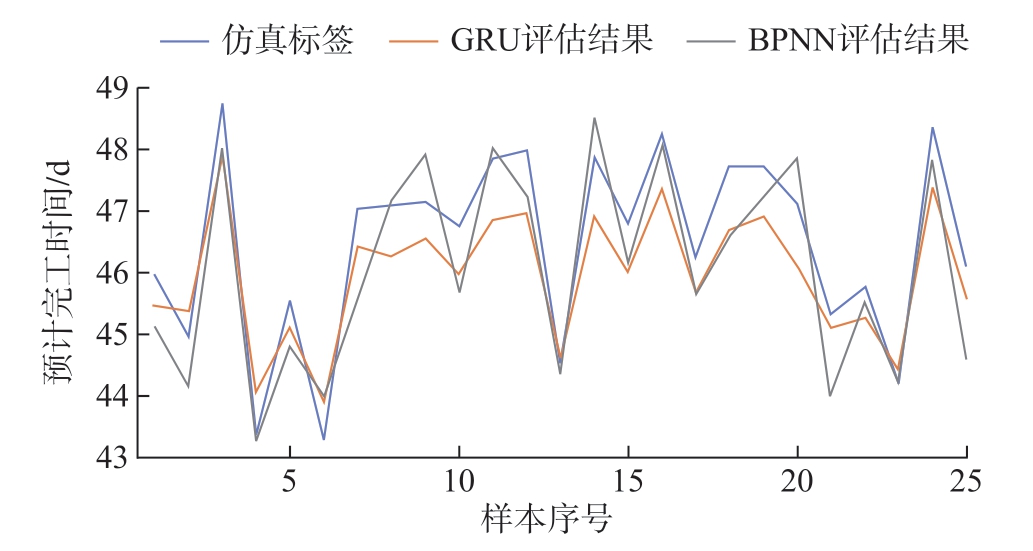
图5 预计完工时间评估比较
Fig.5 Comparison of the estimated completion time evaluation
4.2 优化结果仿真验证
以该装配站位的某架次历史数据为依据,设计两种实际应用场景分别验证本方法优化结果的可靠性。
场景1:该架次还未开工,所有关键物料均未配置到站位,因此所有物料的配置时间都需要优化;
场景2:该架次已开工,所建立的关键物料配置方案中前14项物料都已配置到站位,而后4项物料的配置时间需要依据此刻的生产要求以及前序配置情况进行优化,将前14项物料的配置时间按照历史真实数据来替换。
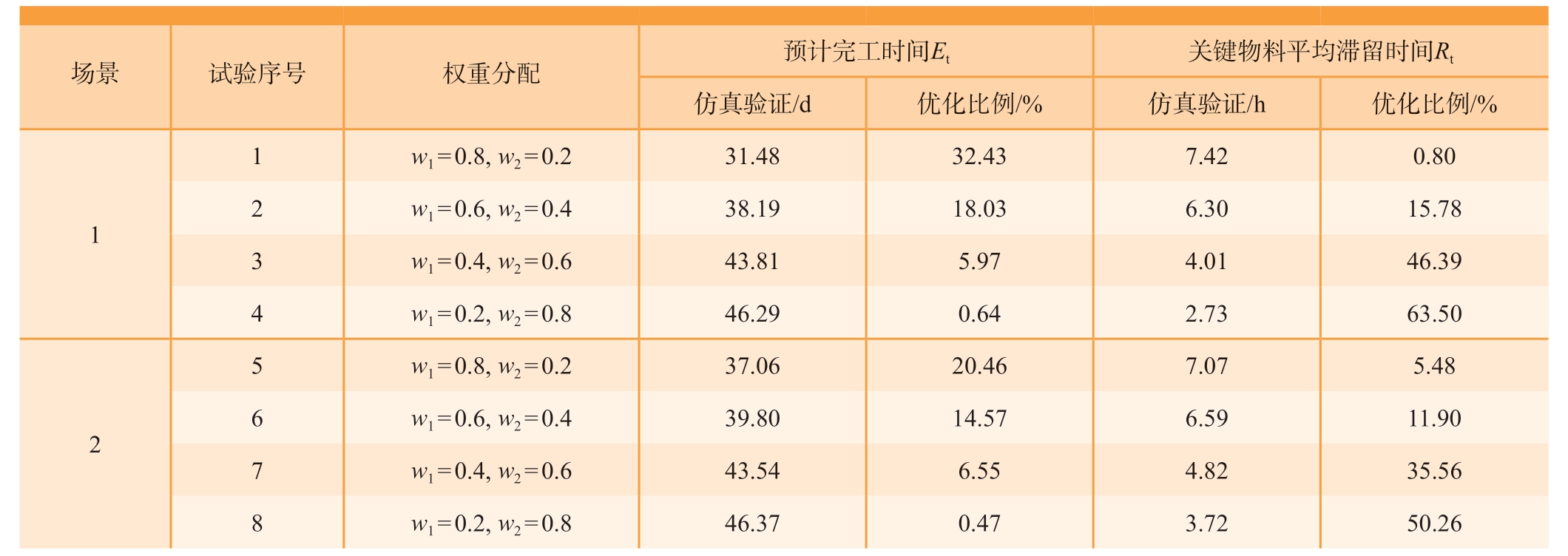
在两种场景中分别设置多组不同优化目标权重的组合,将各组输出的优化方案输入到离散事件仿真平台来验证Et和Rt两个性能指标的仿真评估值,结果如表2所示,同时将完整历史数据代入仿真计算,得到未优化情况下Et和Rt指标值 (Et = 46.59 d,Rt = 7.48 d),从而观察各组试验中对两个指标的优化比例 (优化比例=|优化前值-优化后值| /优化前值)。
表2 优化结果仿真验证
Table 2 Simulation verification of optimization esults
场景 试验序号 权重分配 预计完工时间Et 关键物料平均滞留时间Rt仿真验证/d 优化比例/% 仿真验证/h 优化比例/%w1 = 0.8, w2 = 0.2 31.48 32.43 7.42 0.80 2 w1 = 0.6, w2 = 0.4 38.19 18.03 6.30 15.78 3 w1 = 0.4, w2 = 0.6 43.81 5.97 4.01 46.39 4 w1 = 0.2, w2 = 0.8 46.29 0.64 2.73 63.50 1 1 w1 = 0.8, w2 = 0.2 37.06 20.46 7.07 5.48 6 w1 = 0.6, w2 = 0.4 39.80 14.57 6.59 11.90 7 w1 = 0.4, w2 = 0.6 43.54 6.55 4.82 35.56 8 w1 = 0.2, w2 = 0.8 46.37 0.47 3.72 50.26 5 2
从验证结果可以看出,面向两种不同的实际应用场景,研究人员均能够使用本文方法,通过对权重的分配,实现对预计完工时间Et和关键物料平均滞留时间Rt两个指标的优化。从场景2的4组优化结果中可以看出,当在装架次已完成大部分装配工作时,通过优化最后几项关键物料的配置时间仍然可以一定程度上实现对以上两个指标的优化。
5 结论
(1)提出了一种将仿真代理模型作为目标函数评估模型与遗传算法相结合,实现物料配置方案全局优化的方法,为现场提供了一种能够权衡准确性和效率的新思路。
(2)通过仿真样本构建验证了基于GRU改进循环神经网络面向物料配置方案评估的准确性和学习效率,对于架次预计完工时间的评估值与仿真标签值的均方误差为1.1053,对于物料平均滞留时间的均方误差为0.3415。
(3)以实际架次的历史数据为依据,通过离散事件仿真平台验证了优化方法能够有效实现对架次预计完工时间和物料平均滞留时间两项指标的优化。
[1] 马腾, 贾晓亮, 孙冰洋. 飞机装配生产线资源追踪及可视化研究[J]. 航空制造技术, 2020, 63(6): 64-72.MA Teng, JIA Xiaoliang, SUN Bingyang. Aircraft assembly shopfloor resources tracing and visualization[J]. Aeronautical Manufacturing Technology, 2020, 63(6): 64-72.
[2] 龙安林, 何凤涛, 蒋超, 等. 飞机大部件装配能力测算方法研究[J]. 航空制造技术, 2021, 64(3): 83-86, 102.LONG Anlin, HE Fengtao, JIANG Chao, et al. Research on evaluating method of assembly capacity of large aircraft component[J]. Aeronautical Manufacturing Technology, 2021, 64(3): 83-86, 102.
[3] 王伟, 王旭东, 孟飙. 飞机生产中的批架次管理技术[J]. 沈阳航空航天大学学报, 2015, 32(6): 87-92.WANG Wei, WANG Xudong, MENG Biao. Shipset management technology in aircraft production[J]. Journal of Shenyang Aerospace University, 2015, 32(6): 87-92.
[4] 郑守国, 张勇德, 谢文添, 等. 基于数字孪生的飞机总装生产线建模[J]. 浙江大学学报(工学版), 2021, 55(5): 843-854.ZHENG Shouguo, ZHANG Yongde, XIE Wentian, et al. Aircraft final assembly line modeling based on digital twin[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(5): 843-854.
[5] DOS SANTOS C H, MONTEVECHI J A B, DE QUEIROZ J A, et al. Decision support in productive processes through DES and ABS in the digital twin era: A systematic literature review[J]. International Journal of Production Research, 2022, 60(8): 2662-2681.
[6] 屈琦, 贾晓亮, 郑植元, 等. 飞机部件装配生产线仿真研究[J]. 航空制造技术, 2017, 60(4): 54-59.QU Qi, JIA Xiaoliang, ZHENG Zhiyuan, et al. Simulation of aircraft components assembly line[J]. Aeronautical Manufacturing Technology,2017, 60(4): 54-59.
[7] JIA Y, TIAN H, CHEN C, et al. Predicting the availability of production lines by combining simulation and surrogate model[J]. Advances in Production Engineering & Management, 2017, 12(3): 285-295.
[8] AZADEH A, NEGAHBAN A, MOGHADDAM M. A hybrid computer simulation-artificial neural network algorithm for optimisation of dispatching rule selection in stochastic job shop scheduling problems[J].International Journal of Production Research, 2012, 50(2): 551-566.
[9] 陈聪, 候磊, 李乐乐, 等. 基于GRU改进RNN神经网络的飞机燃油流量预测[J]. 科学技术与工程, 2021, 21(27): 11663-11673.CHEN Cong, HOU Lei, LI Lele, et al. Prediction of aircraft fuel flow based on recurrent neural network[J]. Science Technology and Engineering,2021, 21(27): 11663-11673.
[10] ZHANG Y Z, XIONG R, HE H W, et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018,67(7): 5695-5705.
[11] 孙翊文, 王宇璐, 傅昆, 等. 交互门控循环单元及其在到达时间估计中的应用[J]. 中国科学(信息科学), 2021, 51(5): 822-833.SUN Yiwen, WANG Yulu, FU Kun, et al. Interactive gated recurrent unit and its application for estimated time of arrival[J]. Scientia Sinica(Informationis), 2021, 51(5): 822-833.