随着航空航天器结构轻量化需求的增加，复合材料得到大量应用。复合材料与传统机体结构材料（如铝合金、钛合金等金属材料）混合得到的异种叠层复合材料的应用成为必然趋势，因而其结构的装配连接也成为航空航天装配工艺研究中具有工程价值的一大热点。铆接是航空航天器结构装配连接的主要方式之一，因而异质叠层复合材料结构铆接工艺的研究对新材料的应用具有现实意义。作为主流装配连接方式，铆接的工艺过程为强非线性变形过程，因此铆接变形可以通过分析铆接结构、工艺、材料等参数进行研究。异种叠层材料由于材料自身属性的差异进一步增加了装配连接工艺过程的研究难度，例如在同等制孔质量条件下，叠层异质材料属性的差异引起铆接后形成的干涉量等铆接质量参数存在变化，此种变化在同种材料的铆接工艺中不会出现。确定异种叠层材料装配连接的工艺参数时须考虑两种材料的不同要求，确定最佳工艺参数组合时的难度更高，因此需要进行参数灵敏度分析，确定这些情况下的重要工艺参数，从而有针对性地进行分析研究，为异种叠层材料铆接工艺的研究提供相关的方法参考和研究依据。
灵敏度分析（Sensitivity analysis，SA）主要研究的是系统输入参数的不确定性与输出响应不确定性的关系[1]。研究人员出于不同目的提出了各种SA 技术[2]。其中，Sobol[3]、Homma[4]等开发的基于方差的技术在过去被实践者广泛研究。基于方差的SA 旨在通过观察输入的整个分布范围，将模型输出方差分配到不同的模型输入集，但在基于方差的系数计算中，输出样本的生成是计算量最大的一步，也是其适用性的主要限制因素，而Borgonovo[5]开发的基于矩独立技术的重点是寻找那些会导致模型概率密度函数发生平均偏移的输入，其计算成本较小，相较于基于方差的SA 来说，更加易于实现。
铆接工艺参数的选择对铆接质量具有非常重要的影响，该操作具有一定的复杂性和不确定性[6]。黄涛等[7]采用曲线拟合方法，建立了镦头尺寸和干涉量之间的数学模型，揭示了干涉量和镦头尺寸参数之间的相互关系，并通过试验验证了模型的准确性和可靠性。李超等[8]为了提高铆接质量、减小干涉量分布的不均匀性，提出了一种基于BP 神经网络的优化方法，该方法显著提高了干涉量的均匀程度并有效降低了板件的变形程度。Wang 等[9]利用Kriging算法和粒子群算法对铆接力、镦粗时间、镦粗停留时间等铆接工艺参数进行了优化，从而减小了整体装配的变形，提高了最终产品的尺寸精度。Yin[10]和Fang[11]等使用全局灵敏度分析法量化了各铆接工艺参数对铆接质量不确定性的影响，并得到了输入变量的全局灵敏度排序结果。
上述研究表明，在异质叠层复合材料的铆接工艺参数灵敏度分析中，大多研究只关注铆接过程中铆钉、铆模、母材参数等单因素对干涉量的影响。现以异质叠层复合材料的铆接过程为研究对象，选取干涉量作为输出响应值，以异质叠层复合材料的材料属性和几何参数作为输入变量，采用基于随机森林方法的代理模型建立铆接过程的工艺参数–铆接干涉量的函数关系，使用基于矩独立的PAWN 方法建立异质叠层复合材料铆接工艺参数的灵敏度分析模型。
1 异质叠层复合材料仿真建模
1.1 几何建模
本文采用平锥头铆钉对CFRP/Al 异质叠层复合材料板进行铆接，铆接部件主要有CFRP 板、Al 板、铆钉、铆模、顶铁，铆接过程使用有限元软件进行建模和分析。上板（Al）的尺寸为30 mm×30 mm×2 mm，下板（CFRP）的尺寸为30 mm×30 mm×3 mm，CFRP 板和Al 板上的孔径为4.1 mm；铆钉的钉杆直径为4 mm，铆钉钉杆长度根据《航空制造手册》[12]中的相关公式选取（式（1）），计算后选取钉杆长度为10 mm 的铆钉。
式中，L 为铆钉钉杆的长度，mm；∑δ为铆接件即上板和下板的总厚度，mm；d 为平锥头铆钉的直径，mm。
图1 为有限元仿真装配的示意图，其中，下板CFRP（T700）属于各向异性材料，将厚度为3 mm 的CFRP 母材在厚度方向上切为30 层，每层厚度均为0.1 mm，每层的排布方向为[0/90°]，每层的纤维铺设角通过建立局部坐标系来确定；上板和铆钉的材料分别采用航空航天领域常见的铝合金2024–T3[13] 和2A10–T4[14]，二者的材料属性如表1所示。
表1 铝合金的材料属性
Table 1 Material properties of aluminum alloys
熔点Tmelt/℃2024–T3 2.796 72.4 0.33 369 684 0.73 1.7 0.0083 25 502 2A10–T4 2.770 73.8 0.33 256.81 623.7 0.2002 1.539 0.0133 25 —材料 密度/（g·cm–3）杨氏模量/GPa 泊松比υ 初始屈服强度A/MPa硬化系数B/MPa应变硬化系数n热软化系数m应变率系数C室温Troom/℃
图1 有限元仿真装配示意图
Fig.1 Schematic diagram of simulation assembly by finite element method
1.2 本构模型及材料属性
由于铆接属于高应变率的成型过程，所以采用工程上常用的Johnson–Cook 本构关系，可将应变速率、塑性应变对材料的影响均考虑在内，Johnson–Cook 本构关系如式（2）所示。
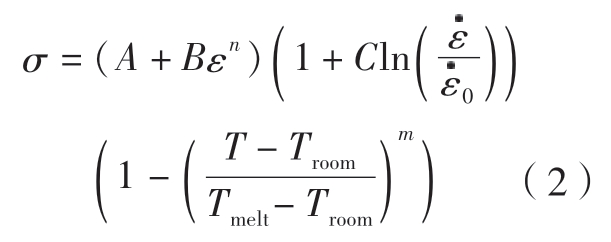
式中，A 为材料的初始屈服强度；B为硬化系数；C 为应变率系数；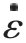 
为等效塑性应变率； 
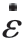0 为参考应变率；T 为材料的实时温度；Troom 为室温；Tmelt 为材料的熔点；n 为应变硬化系数；m 为热软化系数。
利用基于横贯各向异性的无损伤刚度矩阵和应变得到CFRP 的本构模型，该模型的本构关系如式（3）和（4）所示。
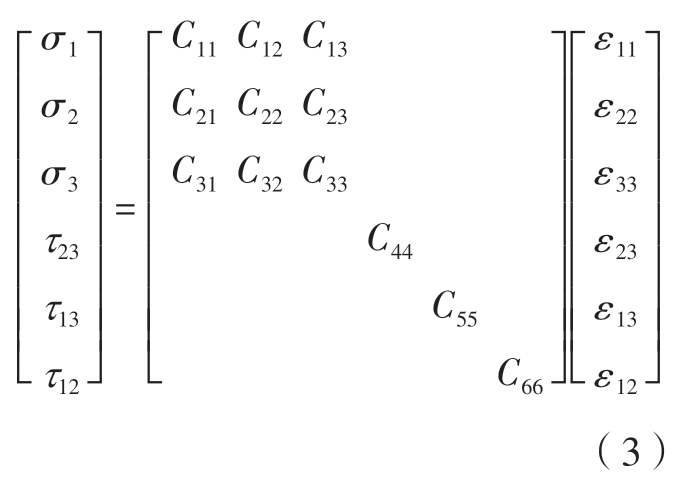
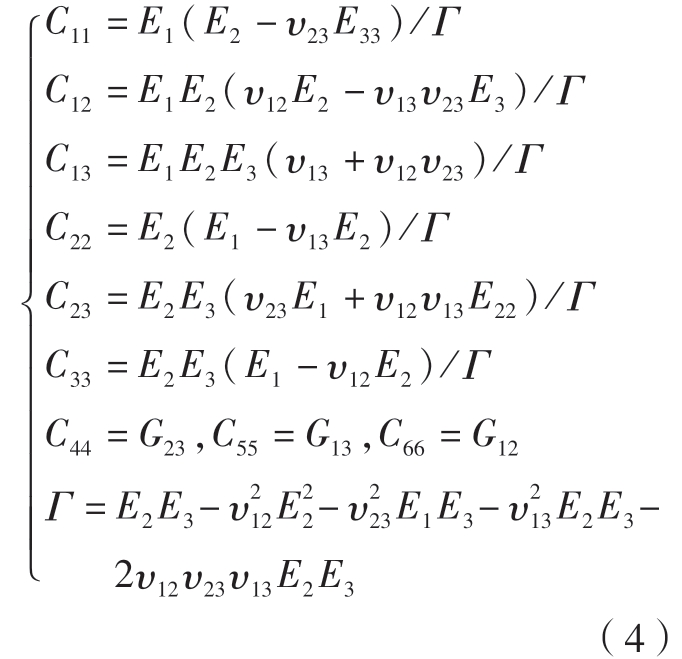
式中，1、2、3 分别代表X、Y、Z 3 个方向；12、13、23 分别代表XY、XZ、YZ 3 个 平 面；E1、E2、E3 为 弹 性 模 量；G12、G13、G23 为剪切模量；υ12、υ13、υ23为泊松比；Γ 为工程常数。
由于铆接过程中，CFRP 会发生损伤，将CFRP 的三维Hashin 失效判断准则[15]编入VUMAT 子程序，然后将子程序接入有限元软件的外接端口，CFRP 的详细材料属性和损伤参数见表2 和3。
表2 CFRP 材料属性
Table 2 Material properties of CFRP
E1/GPa E2/GPa E3/GPa G12/GPa G13/GPa G23/GPa υ12 υ13 υ23 112 8.2 8.2 4.5 4.5 3 0.3 0.3 0.4
表3 CFRP 损伤参数
Table 3 Damage parameters of CFRP
注：XT、YT 和ZT 分别为X、Y、Z 3 个方向上的拉伸强度；XC、YC 和ZC 分别为X、Y、Z 3 个方向上的压缩强度；S12、S13 和S23 为剪切强度。
ρ/（kg·m–3） XT /MPa XC /MPa YT=ZT /MPa YC=ZC /MPa S12=S13/MPa S23/MPa 1600 1900 1000 84 250 60 110
本文所用的各向异性材料在铆接过程中考虑了非线性剪切过程中应力与应变之间的关系，纤维的拉断失效和压断失效、面内基体的拉裂损伤和压溃损伤、面外基体的拉裂损伤和压溃损伤以及纤维–基体剪出等破坏形式的三维Hashin 失效的判断准则如式（5）～（11）所示。
纤维拉断（FT）失效，ε1>0：
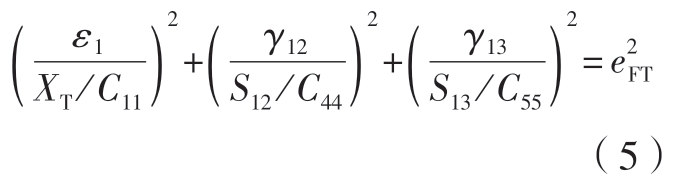
纤维压断（FC）失效，ε1<0：
面内基体拉裂（IMT）损伤，ε2>0：
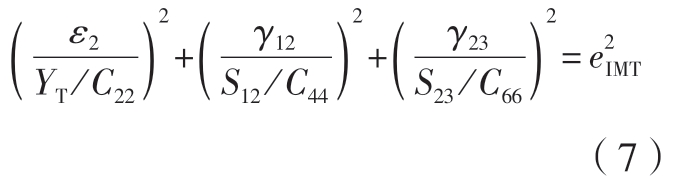
面内基体压溃（IMC）损伤，ε2<0：
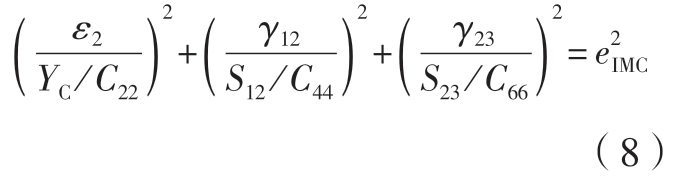
面外基体拉裂（OMT）损伤，ε3>0：
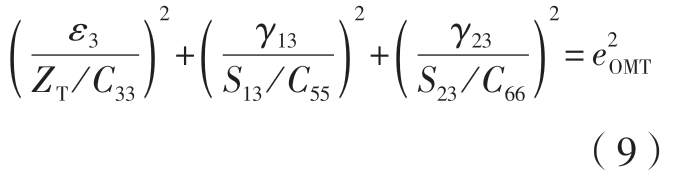
面外基体压溃（OMC）损伤，ε3<0：
纤维–基体剪出（FMS），ε1<0：
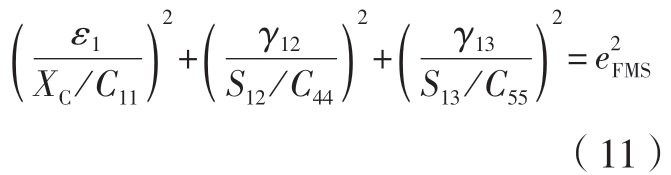
式中，εi（i=1，2，3）为正应变；γij（i，j=1，2，3；i≠j）为 剪 切 应 变；Cij（i，j=1，2，3，4，5，6；i=j）为刚度矩阵中的元素；XT 和XC 为沿层合板纵向的拉伸强度和压缩强度；YT 和YC 为沿层合板横向的拉伸强度和压缩强度；ZT和ZC 为沿层合板厚度方向的拉伸强度和压缩强度；S12、S13 和S23 分别为层合板相应方向的剪切强度；e 为失效因子，即当e ≥1 时，开始产生损伤。
1.3 网格单元划分及边界条件
铆接过程中，大变形区域通常集中在被铆钉和顶铁覆盖的薄壁板处，因此对大变形区域即铆接孔周围3倍于铆钉直径的区域网格进行了加密，加密区域的网格设定为0.3 mm，外围区域设定为1 mm。由于铆接过程中铆钉的塑性应变较大，所以对铆钉的网格划分要求高于母材，本文中将铆钉的网格大小设定为0.2 mm，铆模和顶铁的网格大小设定为1.2 mm，铆钉和铆模的网格划分结果如图2 所示。
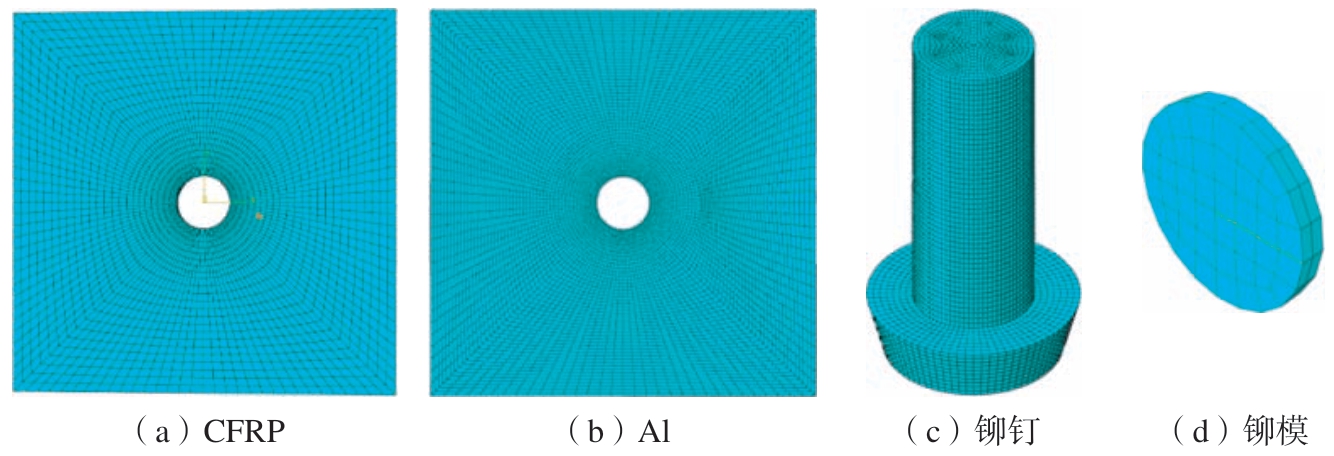
图2 模型网格划分
Fig.2 Model meshing
整个铆接过程分为载荷的施加和释放两个阶段，两个阶段中均对2块母材施加了一些约束，如图3 所示。为铆模设置1 个参考点，通过给该参考点施加位移载荷来实现铆模在Z 方向上的移动，然后通过与钉杆上表面的摩擦接触来完成铆接，此处位移设置为3.2 mm，并对顶铁和母材的X 方向进行全约束。
图3 边界条件及载荷设置
Fig.3 Boundary conditions and load settings
2 模型仿真结果分析与验证
2.1 结果分析
铆接产生的翘曲变形对装配不利，会影响连接强度，尤其是在多钉连接的情况下，还会影响铆钉的安装和定位，而且这种影响会随着安装铆钉的增加而被放大，致使母材发生变形、应力集中等不利状况。图4 展示了母材铆接后未约束边缘端的翘曲变形情况，出现这种情况的原因是铆钉钉杆在受力之后首先呈鼓形，使得两板贴合处先受到径向的挤压作用，此时Al 板的上表面和CFRP 板的下表面还未被挤压；由于Al 和CFRP的材料属性差异，使得母材边缘发生翘曲变形，随后铆钉与Al 板的上表面接触挤压；镦头成型时，Al 板上表面孔周围受到轴向的挤压力，这使得边缘处的翘曲变形更加严重，此时加大铆接位移，母材的翘曲变形将会更加明显，且孔心到边缘的翘曲程度呈增大趋势。
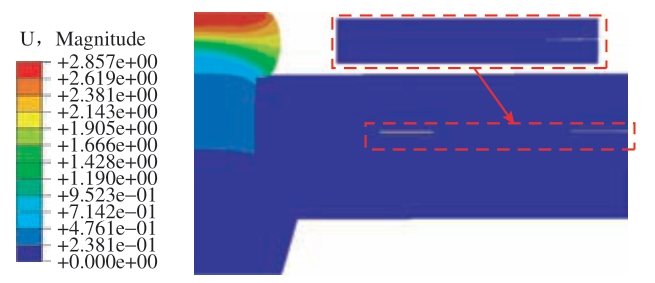
图4 母材未约束边缘端的翘曲变形
Fig.4 Warping and deformation of unconstrained edge of base material
本文后续研究中着重关注铆接孔内的干涉量水平，提取计算结果.odb 文件中的最后一帧中与约束方向垂直的另一个水平方向上6 个节点的孔径变形值，根据式（12）计算铆接干涉量，取6 个节点干涉量的平均值作为整个模型的铆接干涉量。图5 为在孔壁内部取值的6 个位置（I1～ I6）。
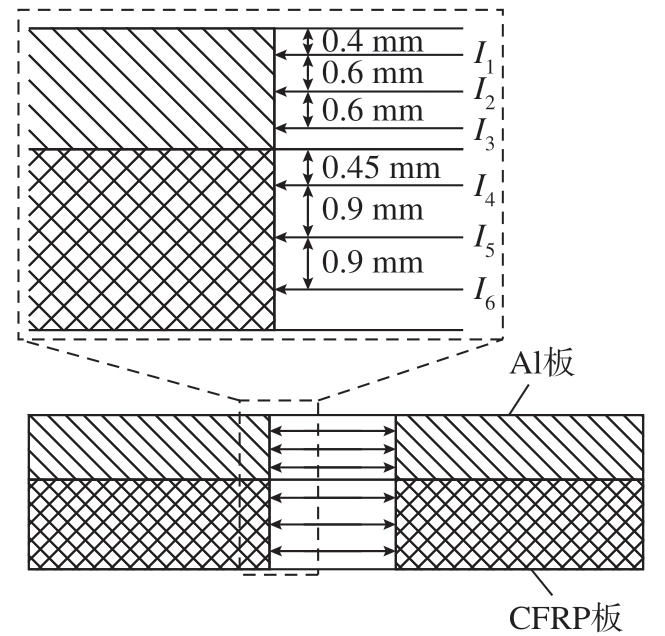
图5 取值位置
Fig.5 Position of value markers
式中，D 为铆接变形后的孔径，mm；D0 为原始孔径，mm。
由于Al 和CFPR 材料性能的差异，导致铆钉与CFPR 之间的干涉量整体明显小于铆钉与Al 的干涉量，并且铆钉与CFRP 之间各点的干涉量都小于2%，6 个取值点铆接干涉量的变化情况如图6 所示。在铆接成型的开始，由于铆钉未与母材接触，故干涉量为0，随着铆钉被陆续压入铆接孔并持续施压，干涉量持续增大。由于镦头镦粗成型过程的特点，母材靠近镦头端区域的干涉虽然晚于其余部位出现，但其增速却最大，最终铆接完成后的干涉量也最大，因此，该处更容易出现应力集中现象。值得注意的是，I2 点的干涉量很小，这是因为铆钉钉杆在和母材表面发生挤压后，使得该点处的材料受到了镦头侧方材料的挤压，所以该处孔径变化比I1 点和I3 点处小。载荷卸载后，干涉量会发生一定回弹，然后保持稳定；铆接完成时，相较于其他取值点，I3 点的回弹最明显，这是因为Al 板的3 个取值点中，该点距离CFRP 板最近，该处产生的变形有一部分暂时被CFRP所承受，当卸去载荷时，该变形又从CFRP 板回还至I3 点处。
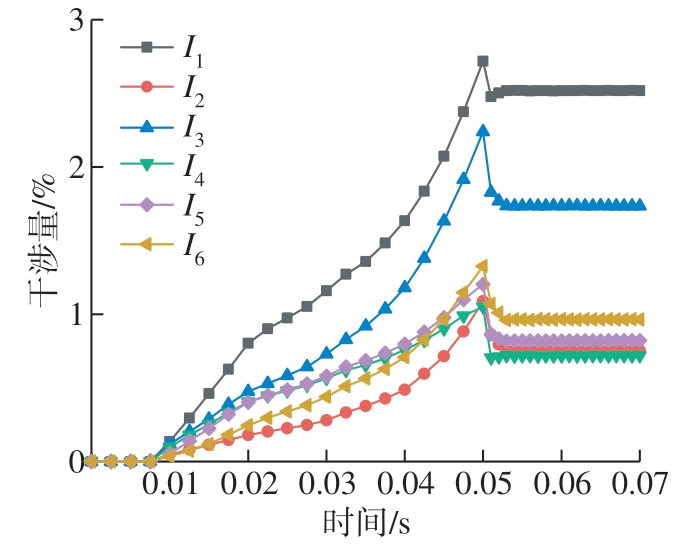
图6 铆接干涉量变化
Fig.6 Variation of riveting interference amount
2.2 试验验证
通过铆接试验，将工程中常用的质量评价指标（铆接干涉量）作为试验和有限元模型计算结果的对比指标，为减小试验中的诸多不确定性误差，将进行5 次铆接试验，结果取5 次试验结果中各指标的平均值。5次试验均在长140 mm、宽30 mm 的试件上进行，为避免间距效应，即避免5 次铆接试验中铆钉将铆接孔的材料挤向下一个铆接孔的方向，从而影响下一个孔的铆接试验，故将孔间距取为20 mm。试验中所用铆接试件如图7 所示。
图7 铆接试件
Fig.7 Riveting workpiece
为最大程度地确保铆接质量，减少铆接过程中对铆接质量不利的不确定性因素，进行铆接试验前需要对铆接孔进行质量检测，以尽可能降低铆接孔中的不利因素对最终铆接质量的影响，检测CFRP 板上孔周围的损伤情况和两板上铆接孔的直径误差。
（1）CFRP 板损伤检测。
由于CFRP 属于各向异性材料，在钻孔过程中可能会产生各种损伤，这些损伤会影响最终的铆接质量，所以在钻孔结束、铆接开始之前有必要进行损伤检测。所用仪器为图8（a）所示的OTD–5100 数字式超声波探伤仪（北京欧亚图科技有限公司），要求试件铆接孔周围10 mm 范围以内无损伤。检测后对数据进行提取分析，得到5 个孔的检测结果，如图8（b）所示；可以看出，孔周围的损伤情况很少，基本是由于钻头钻出时所带出的微小毛刺等造成的，检测结果符合铆接要求。
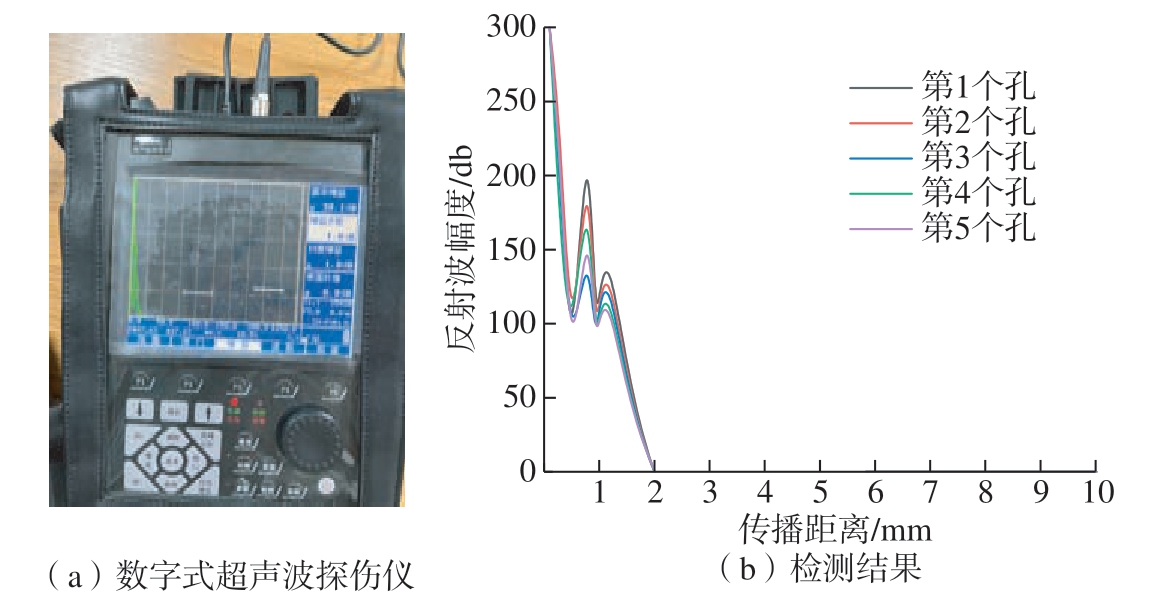
图8 检测仪器及结果
Fig.8 Testing instrument and results
（2）铆接孔直径测量。
采用游标卡尺测量铆接孔直径，每个孔测量5 次，取平均值作为最终结果，如表4 所示。将最终结果与《航空制造手册》中对铆接孔直径的偏差要求（表5[12]）进行比对可知，铆接孔的直径在误差范围内，符合铆接要求。
表4 铆接孔直径
Table 4 Riveting hole diameter mm
第1 个孔 第2 个孔 第3 个孔 第4 个孔 第5 个孔4.11 4.13 4.15 4.19 4.16
表5 铆接孔直径偏差要求[12]
Table 5 Requirements for riveting hole diameter deviation[12] mm
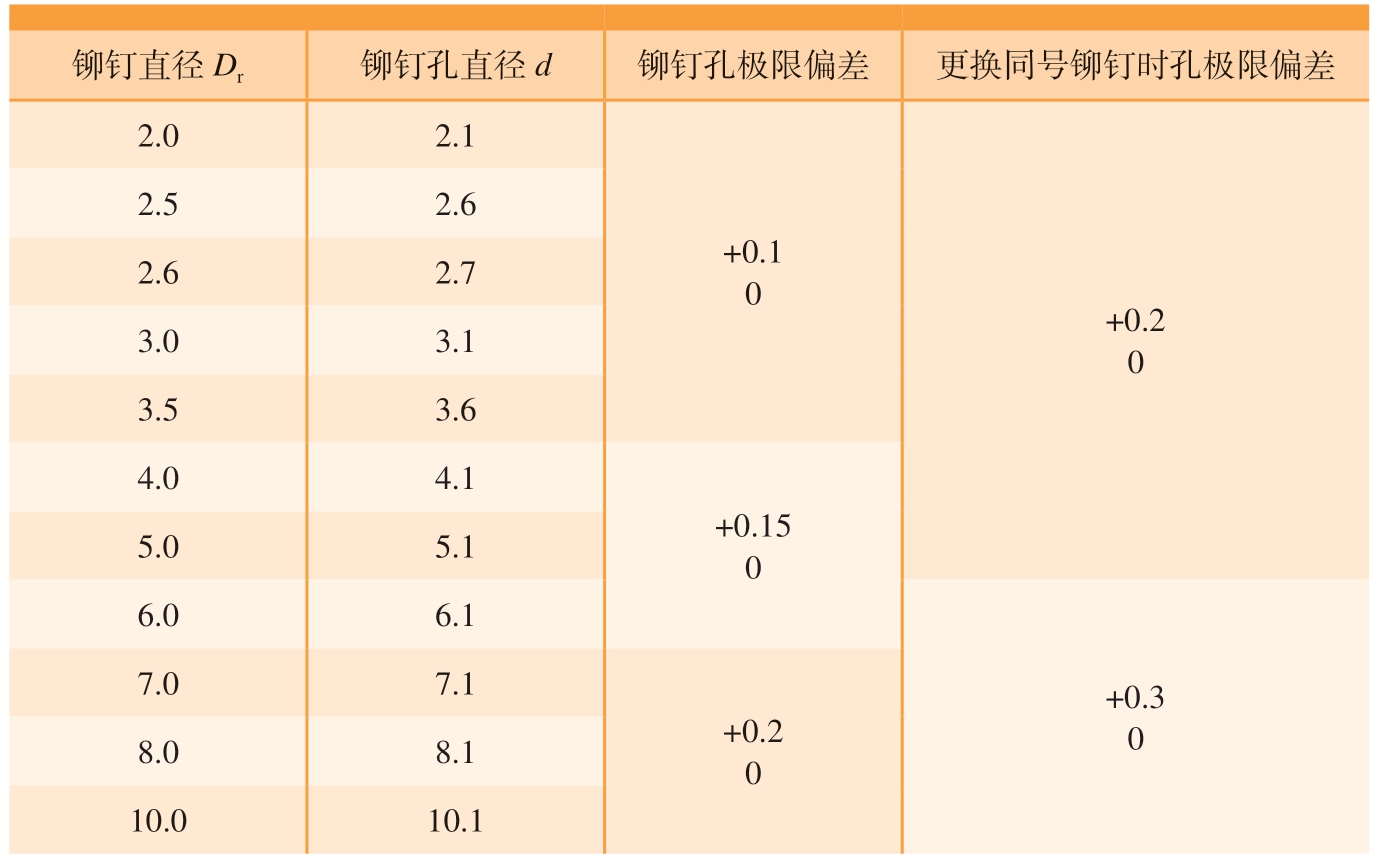
铆钉直径Dr 铆钉孔直径d 铆钉孔极限偏差 更换同号铆钉时孔极限偏差2.0 2.1 2.5 2.6 2.6 2.7 3.0 3.1 3.5 3.6 4.0 4.1+0.1 0+0.2 0 5.0 5.1 6.0 6.1+0.15 0 7.0 7.1 8.0 8.1 10.0 10.1+0.3 0+0.2 0
采用万能试验机（DR–502A，东莞市东日仪器有限公司）进行铆接试验，上冲头向下移动，移动速度设为1 mm/min，设置冲头移动的距离以实现铆接位移的加载，铆接试验如图9 所示。
图9 铆接试验示意图
Fig.9 Schematic diagram of riveting experiment
铆接过程中，由于母材材料属性存在差异，铆钉钉杆镦粗过程中，钉杆上下部分的镦粗速率存在差异；此外，铆接过程中由于母材上的孔周围的材料被铆钉镦头挤压，会受到来自镦头两个方向的挤压力作用，使母材发生变形。
铆接后的试件如图10 所示。将铆接好的试件沿铆钉中心面切开，采用图11 所示的高清电子显微镜（AO–V128S，深圳市奥斯微光学仪器有限公司）测量平台测量试件的铆接干涉量。仿真数据与试验数据结果对比如表6 所示。其中，平均干涉量为图4 中6 个位置干涉量的平均值。
表6 铆接干涉量数据对比
Table 6 Comparison of riveting interference amount
数据来源平均干涉量/%镦头高度/mm镦头直径/mm仿真 1.733 2.338 5.667试验 2.035 2.256 5.882误差 0.302 0.082 0.215
图10 铆接后试件示意图
Fig.10 Schematic diagram of riveted workpiece
图11 高清电子显微镜测量平台
Fig.11 High-definition electron microscope measurement platform
从表6 可以看出，试验结果与仿真结果平均干涉量的误差为0.302%，铆接质量评价指标的仿真与试验结果的误差小于5%，在可接受的误差范围内，所以上述仿真模型可以用于后续研究且可作为所需数据的可靠来源。
3 基于随机森林算法的CFRP/Al 铆接干涉量预测代理模型
CFRP/Al 异质叠层材料铆接过程由于材料属性间的差异，进一步增加了铆接工艺参数选定的难度。由于铆接工艺为强非线性问题，难以通过大量试验获取最优的工艺参数组合，因此借助经试验验证的有限元仿真模型并结合算法来实现铆接干涉量的预测。
在选择设计变量时，假设材料密度固定，且两种母材的长度、宽度和回弹时间不影响薄壁板的最大变形y，可以不考虑这些参数的影响，因此在参数建模过程中，共有13 个参数被评估为设计变量。
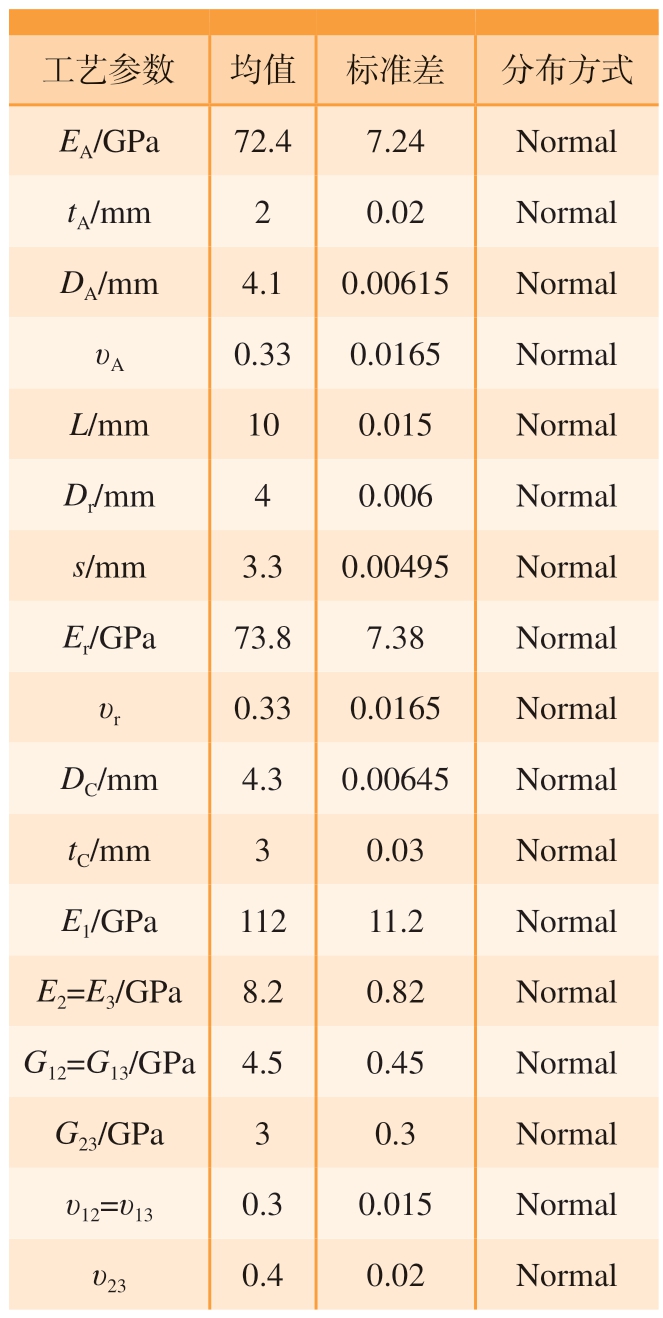
对于Al 板，研究的参数包括母材厚度tA、孔径DA、弹性模量EA、泊松比υA；对于铆钉，研究的参数包括钉杆长度L、钉杆直径Dr、铆接位移载荷s、弹性模量Er、泊松比υr；对于CFRP，研究的参数包括孔径DC、母材厚度tC，3 个方向上的弹性模量E1、E2、E3，剪切模量G12、G13、G23 和泊松比υ12、υ13、υ23；根据文献[16]所确定的17 个变量的均值、标准差和分布方式如表7 所示。
表7 铆接工艺参数的取值
Table 7 Values for riveting process parameters
工艺参数 均值 标准差 分布方式EA/GPa 72.4 7.24 Normal tA/mm 2 0.02 Normal DA/mm 4.1 0.00615 Normal υA 0.33 0.0165 Normal L/mm 10 0.015 Normal Dr/mm 4 0.006 Normal s/mm 3.3 0.00495 Normal Er/GPa 73.8 7.38 Normal υr 0.33 0.0165 Normal DC/mm 4.3 0.00645 Normal tC/mm 3 0.03 Normal E1/GPa 112 11.2 Normal E2=E3/GPa 8.2 0.82 Normal G12=G13/GPa 4.5 0.45 Normal G23/GPa 3 0.3 Normal υ12=υ13 0.3 0.015 Normal υ23 0.4 0.02 Normal
在选择样本数量时，参考前人研究结果可知，Saltelli 等[17]的研究中指出样本可以取为500～1000 组，Zhang 等[18] 通 过500 组 样 本 数 据进行系统输入与响应值间的关系拟合，发现模拟结果符合预期。本文将全局灵敏度分析运用在代理模型上，常见的抽取样本的方法有拉丁超立方抽样（Latin hypercube sampling，LHS）与蒙特卡洛抽样法（Monte Carlo sampling）。LHS 多被用于从多维度分布的样本中抽取样本，首先将一个n 维向量的每一个维度分成概率相同且分布均匀的m 个区间，然后从组成的n×m 矩阵中随机抽取一个样本；蒙特卡洛抽样法是通过计算机生成随机数函数，再通过函数生成伪随机数样本，在生成的数据点中加入一定的不确定性后再输入供予模型。
Bootstrap 是一类非参数蒙特卡洛抽样法，其实质是对观测信息进行再抽样，进而对总体的分布特性进行统计推断，Bootstrap 通过重抽样可以避免交叉验证（Cross-validation）造成的样本减少问题；其次，Bootstrap也可以用于创造数据的随机性，因为该方法充分利用了给定的观测信息，不需要模型进行其他的假设和增加新的观测，并且具有稳健性和效率高的特点，在机器学习领域应用很广泛。故此处选择Bootstrap 抽样法从样本区间里随机抽样，本文通过Bootstrap 抽取500 组试验样本，随机选取400 组样本作为训练集来建立铆接工艺参数与铆接干涉量的关系模型，其余100 组样本为测试集，用于测试该关系模型。
随机森林算法是一种基于回归树模型的集成学习算法，主要用于处理回归预测问题，通过对样本数据的随机抽样，组成多个不同的回归树，再把回归树运算结果组合起来，以获得随机森林的预测结果。因此，随机森林算法通常比回归树模型具有更好的拟合效果，在回归预测问题方面具有较好的效果。决策树是构成随机森林的基础，一个随机森林通常包含多个决策树，决策树主要用于数据集成和分类，即集成器。基于决策树的集成器符合Bagging 集成策略，其特点为构建多个独立运行的评估器，再利用评估器开展数据训练，按照投票法、平均法、多数结果法得到结果。随机森林算法的结构如图12 所示。
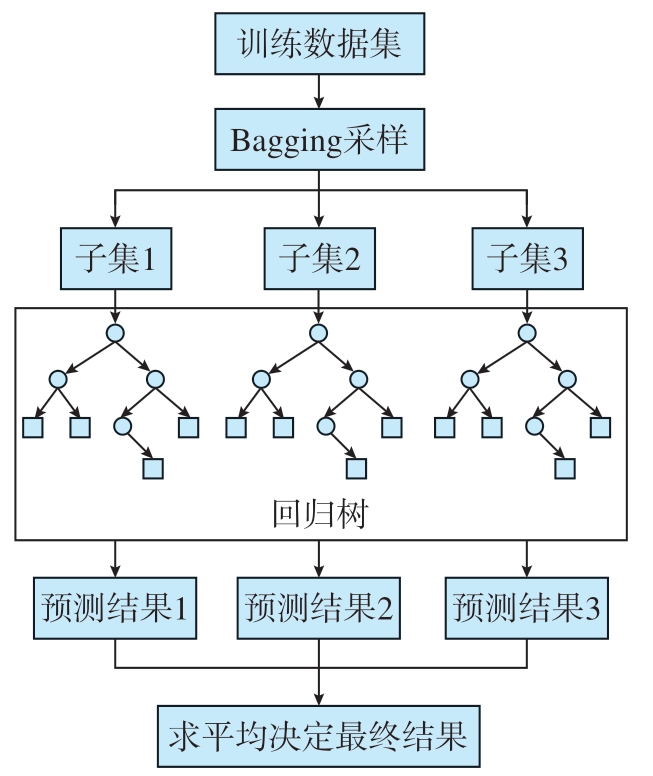
图12 随机森林算法结构
Fig.12 Random forest algorithm structure
回归树的构建过程如下：首先选取前文17 个铆接工艺参数作为输入变量，铆接干涉量作为输出；然后将所有训练数据放在根节点，在这些数据中选择最优特征，把根节点二分为2 个内部节点，再接着划分特征；最后，把训练集划分为有限个子集。子集的划分过程为：对于所有输入的特征向量，选择第j 个向量x（j）作为划分特征，选择s 作为划分点，定义两个区域如下
式中，R1（j，s）表示该特征向量划分点的左子树；R2（j，s）表示右子树。
最优的划分变量j 与划分点s可通过下式计算。
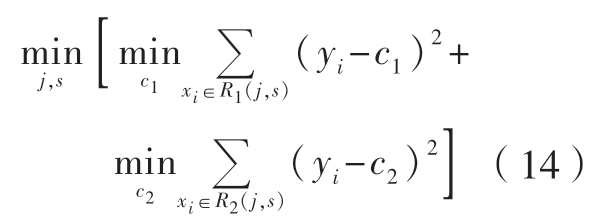
式中，yi 表示预测模型的输出值；c1表示左子树的输出变量；c2 表示右子树的输出变量。
依次将特征向量集合划分至2个子集中。重复上述划分过程，当预测值与真实值的均方误差达到期望值或回归树深度达到设定值时，停止划分。
随机森林的构造过程如下。
（1）从工艺参数的样本集中有放回地随机抽取400 组数据作为每棵子树的训练集，每组的数据量相同，作为回归树的输入数据。
（2）将抽取的400 组训练集数据组成400 棵回归树，每棵回归树都依据上述方法进行划分，得到对应的回归预测数据，共得到400 组结果p1，p2，…，p400。
（3）采用平均的方法将400 棵回归树的预测结果进行综合平均，得到最终的预测结果p，即
。
训练结束后训练集和测试集中实际值和预测值的对比如图13 和14 所示。训练集和测试集的均方误差E 分别为0.0256 和0.0325，决定系数R2 分别为0.9456 和0.8527，表明所构建的随机森林关系模型的泛化能力良好，利用它来预测CFRP/Al铆接结构的铆接干涉量合理可靠。
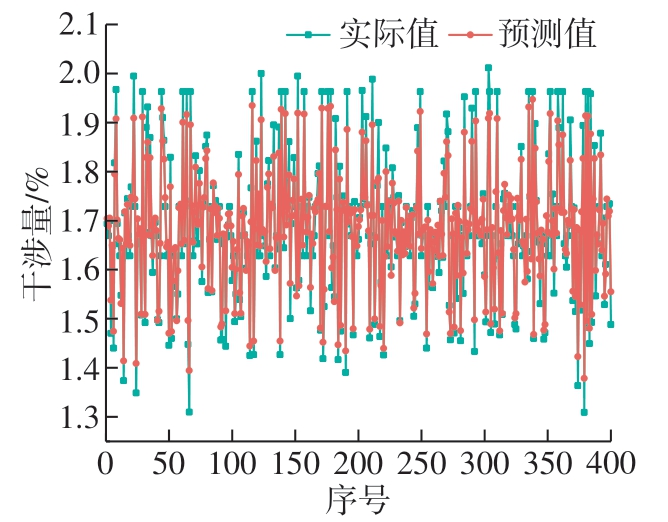
图13 训练集实际值和预测值对比
Fig.13 Comparison of actual and predicted value of the training set
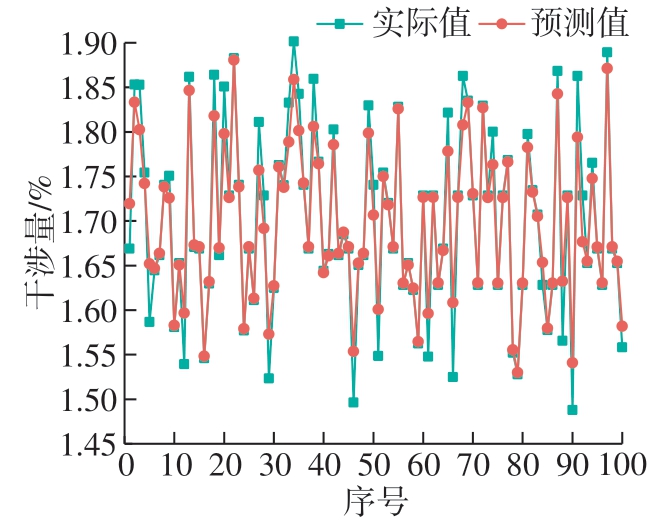
图14 测试集实际值和预测值对比
Fig.14 Comparison of actual and predicted value of the testing set
4 基于矩独立PAWN 法的铆接参数全局灵敏度分析
假设不确定性模型为Y=g（X），Y 为响应模型的相应输出，本文将铆接干涉量作为输出变量，X=（X1，X2，…，Xk）T 为一系列具有随机不确定性的输入变量，即前文所述的铆接工艺参数，k 为输入变量的维数，本文输入变量为17 个即k=17。当输入变量服从一定的概率分布时，其不确定性将通过模型传递给响应输出Y，使得响应量亦为服从一定分布规律的随机变量。记响应输出Y 的无条件概率密度函数和无条件累计分布函数分别为fY（y）、FY（y），fY |Xi（y）、FY | Xi（y）分别是Xi 取某实现值时响应量的条件概率密度和条件累积分布密度，如图15 所示。
图15 响应量的无条件和条件分布函数
Fig.15 Unconditional and cumulative distribution function of response amount
Borgonovo[5]基于输入变量对响应量概率密度函数的影响提出了一种矩独立重要性测度，该测度通过考虑响应量的无条件概率密度fY（y）与其条件概率密度fY |Xi（y）所包围的面积s（Xi）来衡量输入变量Xi 对响应量在整个分布范围内的影响，即
当考虑Xi 在整个分布区域中的变化时，s（Xi）的均值记为
通过式（15）和（16），Borgonovo将矩独立重要性测度定义为
δi 值越大，说明Xi 的分布参数对响应量Y 的不确定性影响程度越高，即在铆接过程中应更关注这些参数。
在得到代理模型之后，用基于矩独立的PAWN 法计算铆接工艺参数的灵敏度，本文所选择的比例因子n=40，输入变量个数M =17。矩独立PAWN 法计算简单，通过使用来自同一输入/输出样本数据集中不同大小的Bootstrap 重样本进行计算，即可快速估计其对Nc 和Nu（不同输入空间所对应的评估次数）所选值的鲁棒性。通过对整个输入可行性空间进行采样获得的无条件累积分布函数模型可知，评估次数Nu=500，使用仅对非固定输入进行采样获得的条件累积分布函数模型，则评估次数Nc=150，矩独立PAWN 法分析结果如图16 所示。灵敏度分析中铆接工艺参数对铆接干涉量影响程度常由全局灵敏度系数来评定，由图16 可知，铆接工艺参数对铆接干涉量的全局灵敏度系数中，异质叠层复合材料的弹性模量和厚度对干涉量的影响较大，其余几个变量的灵敏度系数较小，表明这些参数对响应值干涉量的影响程度较小；因此，在异质叠层复合材料铆接过程中，应该重点关注两块母材的弹性模量和厚度，以提高铆接的质量。
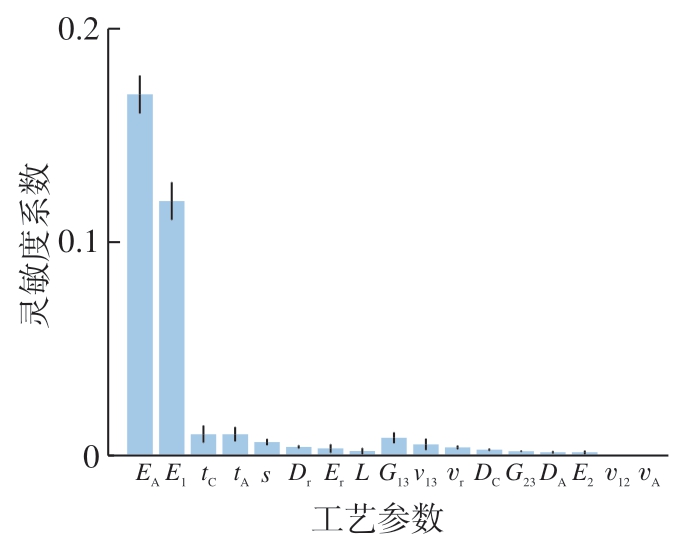
图16 矩独立PAWN 法分析结果
Fig.16 Analysis results of momentindependent PAWN method
矩独立PAWN 法也被用来聚焦于子范围y≥0.5 和y＜0.5（图17）。计算的灵敏度系数表明，在y≥0.5的子范围内，灵敏度系数几乎保持不变（与采用全范围模型输出时相比），这表明所有输入参数的影响程度相同。在y<0.5 的子范围内，除EA、E1、tA 和tC 外，所有输入参数的影响都减小了；此处的例外是异质叠层复合材料的厚度，对y<0.5 的子范围更有影响，但考虑模型输出的全范围时，EA、E1 的影响仍然相同。
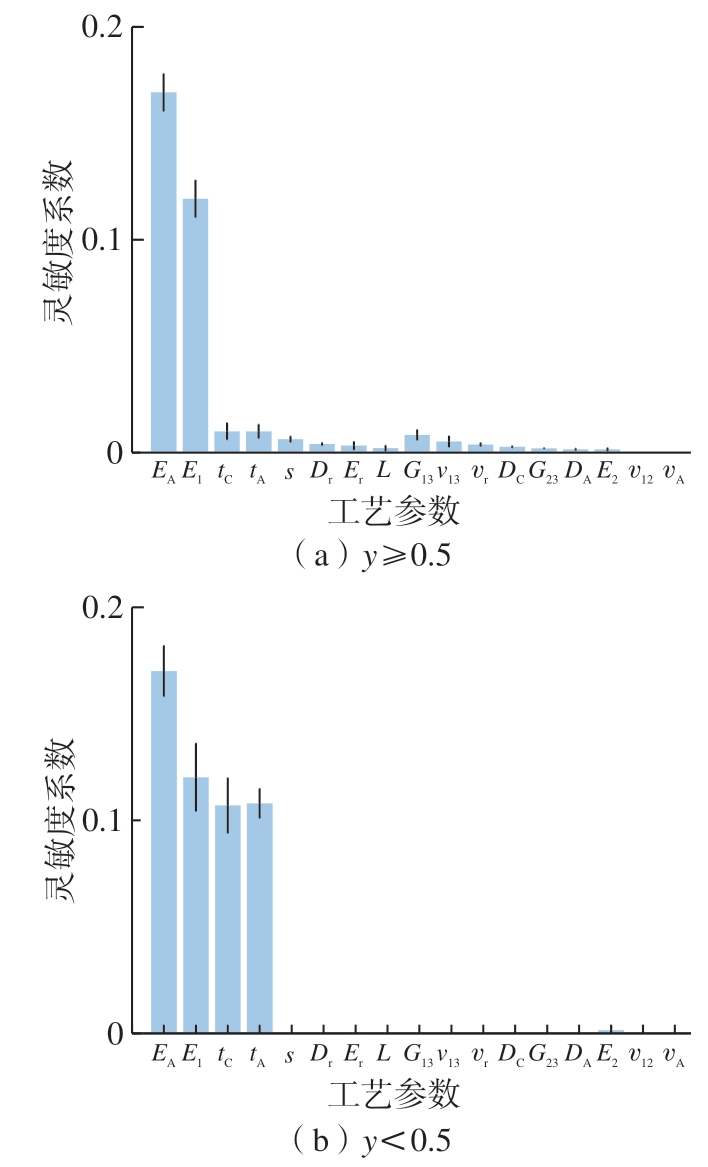
图17 子范围灵敏度结果
Fig.17 Sensitivity analysis results of the subranges
5 结论
（1）本文运用随机森林方法建立了铆接工艺参数与铆接干涉量之间的高精度代理模型，提出了基于矩独立PAWN 法的全局灵敏度分析方法，并给出了基于该方法的灵敏度系数。
（2）通过计算分析得到了17 项铆接工艺参数的近似概率分布，在确定取值点后，使用PAWN 法对铆接工艺参数进行全局灵敏度分析，得到了影响干涉量的重要铆接工艺参数。
（3）在铆接工艺参数对铆接干涉量的全局灵敏度系数中，异质叠层复合材料的弹性模量和厚度的灵敏度系数较大，分别为0.16921 和0.11837，其次是系数为0.012 的位移载荷和0.011 的铆钉直径。其余工艺参数的值较小，一些对铆接干涉量影响不显著的参数的灵敏度系数基本接近0，表明这些参数对铆接质量的影响微小。
[1] SALTELLI A.Sensitivity analysis for importance assessment[J].Risk Analysis, 2002,22(3): 579–590.
[2] CUKIER R I, FORTUIN C M,SHULER K E, et al.Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients.I Theory[J].The Journal of Chemical Physics, 1973, 59(8): 3873–3878.
[3] SOBOL I M.Sensitivity analysis for non-linear mathematical models[J].Mathematical Modeling & Computational Experiment, 1993, 1: 407–414.
[4] H O M M A T, S A LT E L L I A.Importance measures in global sensitivity analysis of nonlinear models[J].Reliability Engineering & System Safety, 1996, 52(1):1–17.
[5] BORGONOVO E.A new uncertainty importance measure[J].Reliability Engineering& System Safety, 2007, 92(6): 771–784.
[6] FÉLIX G, ANCHEYTA J, TREJO F.Sensitivity analysis of kinetic parameters for heavy oil hydrocracking[J].Fuel, 2019, 241:836–844.
[7] 黄涛, 侯红玲, 吴浪, 等.干涉配合铆接镦头尺寸与干涉量关系[J].塑性工程学报, 2023, 30(12): 113–120.
HUANG Tao, HOU Hongling, WU Lang, et al.Relationship between header size and interference amount in interference fit riveting[J].Journal of Plasticity Engineering,2023, 30(12): 113–120.
[8] 李超, 王仲奇, 常正平, 等.基于BP 神经网络和多目标粒子群算法的自动钻铆工艺参数优化方法[J].航空制造技术, 2021,64(23/24): 94–102.
LI Chao, WANG Zhongqi, CHANG Zhengping, et al.Automatic drilling and riveting process parameter optimization method based on BP neural network and multi-objective particle swarm optimization algorithm[J].Aeronautical Manufacturing Technology, 2021, 64(23/24):94–102.
[9] WANG Z Q, CHANG Z P, LUO Q, et al.Optimization of riveting parameters using Kriging and particle swarm optimization to improve deformation homogeneity in aircraft assembly[J].Advances in Mechanical Engineering, 2017, 9(8): 168781401771900.
[10] YIN J Q, GU J Y, CHEN Y D, et al.Global sensitivity analysis of riveting parameters based on a random sampling-high dimensional model representation[J].The International Journal of Advanced Manufacturing Technology,2021, 113(1): 465–472.
[11] FANG Y D, HUANG L, ZHAN Z F, et al.A framework for calibration of selfpiercing riveting process simulation model[J].Journal of Manufacturing Processes, 2022, 76:223–235.
[12] 《航空制造工程手册》总编委会.航空制造工程手册.飞机装配[M].北京：航空工业出版社，2010.
General Editorial Board of Aerospace Manufacturing Engineering Handbook.Aerospace manufacturing engineering handbook.Aircraft assembly[M].Beijing:Aviation Industry Press, 2010.
[13] CHANG Z P, WANG Z Q, JIANG B, et al.Modeling and predicting of aeronautical thin-walled sheet metal parts riveting deformation[J].Assembly Automation, 2016,36(3): 295–307.
[14] WANG J, ZHANG Y L, CHENG L X, et al.Effect of riveting parameters on the forming quality of riveted lap joints with reduced countersunk head half-crown rivet[J].The International Journal of Advanced Manufacturing Technology, 2022, 121(11):8083–8098.
[15] CHEN N J, THONNERIEUX M,DUCLOUX R, et al.Parametric study of riveted joints[J].International Journal of Material Forming, 2014, 7(1): 65–79.
[16] CUI J J, QI L, JIANG H, et al.Numerical and experimental investigations in electromagnetic riveting with different rivet dies[J].International Journal of Material Forming, 2018, 11(6): 839–853.
[17] SALTELLI A, RATTO M, ANDRES T, et al.Global sensitivity analysis.The primer[M].Hoboken: Wiley, 2007.
[18] ZHANG D, YANG Y, WU J F, et al.Global sensitivity analysis on a numerical model of seawater intrusion and its implications for coastal aquifer management: A case study in Dagu River Basin, Jiaozhou Bay, China[J].Hydrogeology Journal, 2020, 28(7): 2543–2557.
