随着新型材料的出现和制造技术的不断发展,碳纤维复合材料(CFRP)因具有轻量化、抗疲劳及比强度高等性能,在航空航天领域的使用占比逐渐升高,应用于机身蒙皮、机翼壁板等主承力结构的制造[1–2]。但由于CFRP 材料内部纤维树脂膨胀系数不同,加工固化后会因精度不高造成尺寸偏差,组装时与铝合金构件连接位置不可避免地产生装配间隙[3]。对于装配间隙,航空工业有着严格的规范要求。当间隙小于一定值时,无需填隙处理可直接使用螺栓紧固进行强制装配;但间隙超过一定值后,需要进行加垫填隙处理,避免出现较大的装配变形和应力集中情况[4–5]。CFRP 壁板多螺栓装配过程中,不同紧固顺序对装配间隙传递的影响不同,孔周区域的变形量复杂,连接过程应力集中点位动态变化,增加了壁板装配质量情况的不确定性。研究填隙补偿处理后不同紧固顺序对CFRP 壁板装配质量的影响对后续飞机的服役性能尤为重要。
目前,关于加垫补偿处理对飞机装配质量的影响已有相关研究。其中,Cheng 等[6]建立了非均匀间隙下螺栓连接装配模型,通过试验及仿真计算对比,分析了不同材料和参数的垫片对飞机壁板装配质量的影响。Yue 等[7]研究了预紧力和垫片类型对复合材料与铝合金单搭接接头结构性能的影响,发现预紧力不足和过大时,接头处刚度和峰值荷载均较低。同时,采用液体垫片时,适当增加预紧力可以提高接头处力学性能。Chang 等[8]探究了存在装配间隙的复合材料翼盒在不同螺栓拧紧顺序和安装力矩时表面装配应力的分布情况,结果显示在无垫片的情况下,仅靠施加预紧力不能完全消除间隙,仍存在局部应力集中的情况。Liu等[9]利用激光扫描技术测量了存在孔位误差时复合材料在多螺栓接头不同紧固顺序下的变形,结果显示孔位误差引起接头处产生竖向变形,强制安装上下孔会引起挤压不均匀而导致的变形不对称,同时不同紧固顺序导致复合接头处的变形分布不同。
上述研究侧重于垫片种类、预紧力等因素对螺栓连接力学性能的影响。加垫后壁板贴合面处还存在少部分装配间隙,多螺栓连接时贴合面处产生“气泡效应”的问题[10],使得紧固后部分区域装配间隙变得更大,影响最终的装配质量。对此,本文以飞机局部壁板结构为研究对象,基于ABAQUS 平台进行有限元分析,并进行试验验证,研究了9 种常见的螺栓紧固顺序对壁板整体变形及应力集中情况的影响,为现场实际装配工作提供参考。
1 研究模型及紧固顺序
飞机壁板结构尺寸较大,形状较为复杂,且装配间隙出现的位置呈随机分布。为能更好模拟填隙补偿对装配质量的影响,同时综合考虑数值计算精度、效率和可实现性,采用“局部–整体”的研究思路,选择生产现场替换的某型机机翼局部壁板结构作为研究模型,如图1 所示。截取的局部壁板结构尺寸为1000 mm×500 mm×3.2 mm,包含长桁一体成型的壁板和3 条翼肋。填隙补偿采用正方形固体垫片,边长为14 mm,厚度为施加螺栓孔周最小间隙值,每个螺栓对应不同厚度垫片,共计51 个。翼肋与壁板由φ6 mm 的螺栓连接,3 条翼肋的连接孔总计51 个,孔径为6.2 mm,相邻孔距为24 mm。
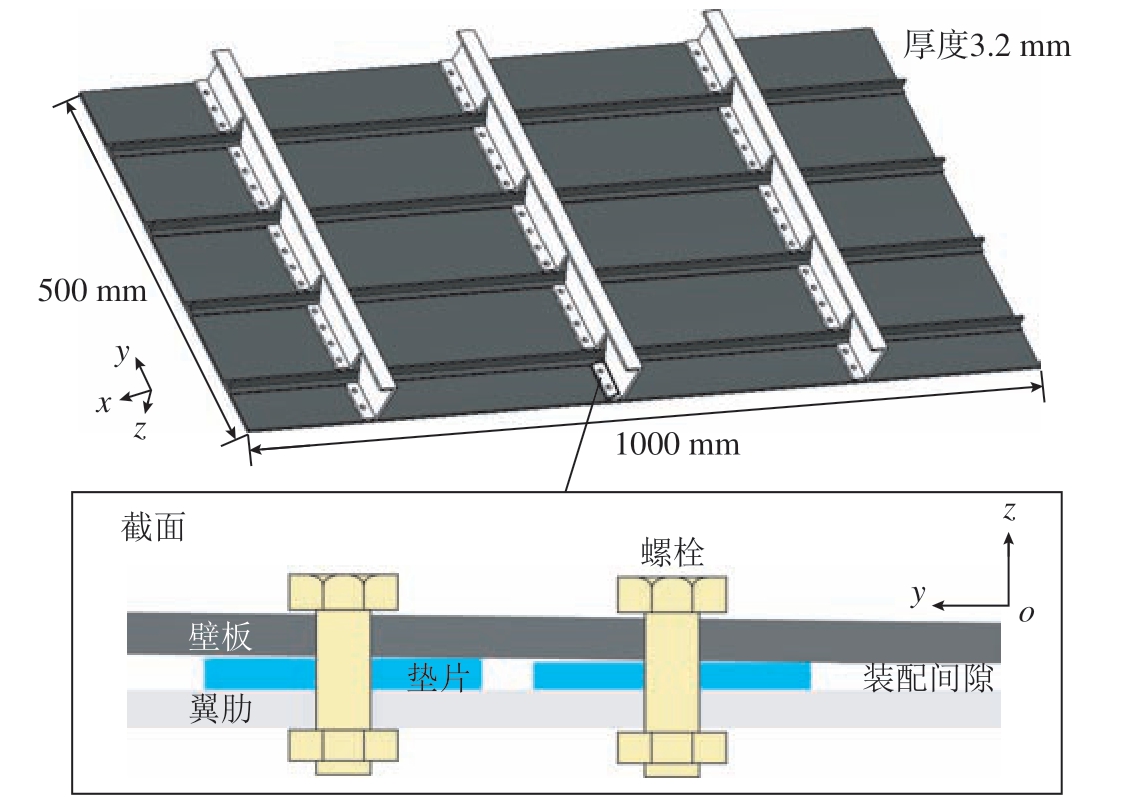
图1 局部壁板研究模型
Fig.1 Local panel research model
作为研究模型,截取出来的机翼壁板装配间隙大小及位置分布未知,本文采用激光位移三维扫描方法进行测量评估。根据测量结果,3 条翼肋连接处的间隙值如图2 所示。

图2 翼肋连接处间隙值
Fig.2 Gap value of wing rib junction
针对局部壁板加垫补偿后不同紧固顺序装配连接计算需求,对研究模型相关构件进行编号处理,如图3所示。3 条翼肋从右到左依次编号为1、2、3 号,螺栓孔以从上到下、从右到左的次序编号为1#、2#、3#、…、51#。紧固顺序以两个维度进行规划,单条翼肋方向顺序:正向顺序,即螺栓由1#孔顺次连接至17#孔;中间向外,即由中间孔位9#开始,以8#、10#顺序依次上下交替向外拧紧直至1#、17#孔连接完成;两侧向内,即由两侧孔位1#、17#开始依次上下交替向内拧紧直至9#孔连接完成。同理,翼肋顺序设置3 组不同连接次序进行连接。综上,共设计9 种紧固顺序进行装配连接,具体分组如表1所示。
表1 紧固顺序分组
Table 1 Fastening sequence grouping
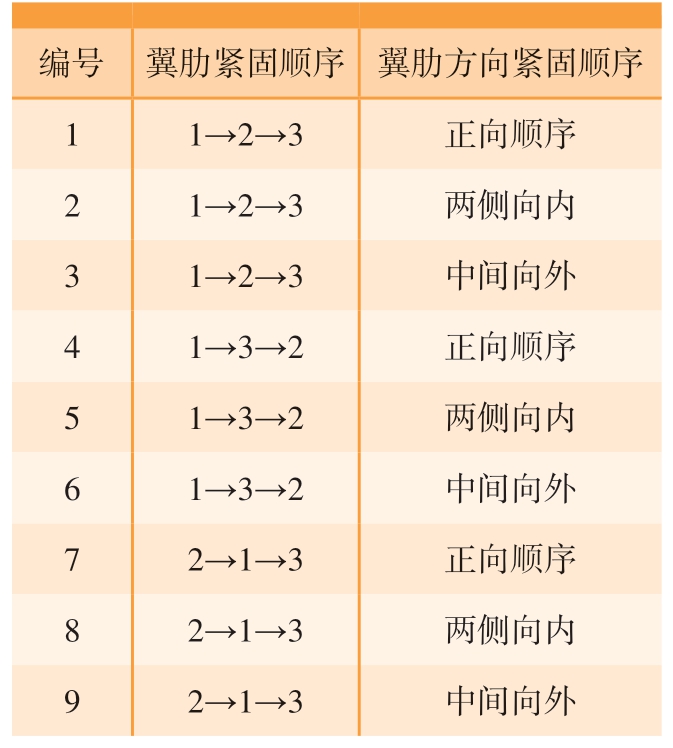
编号 翼肋紧固顺序 翼肋方向紧固顺序1 1→2→3 正向顺序2 1→2→3 两侧向内3 1→2→3 中间向外4 1→3→2 正向顺序5 1→3→2 两侧向内6 1→3→2 中间向外7 2→1→3 正向顺序8 2→1→3 两侧向内9 2→1→3 中间向外

图3 部件编号示意图
Fig.3 Diagram of part numbering
2 壁板结构装配连接有限元计算
2.1 仿真模型建立
依据上述研究模型几何特征,基于ABAQUS 2020 建立有限元模型,进行填隙补偿处理后装配过程的有限元计算,分析壁板装配质量。为简化仿真模型,提高运算效率,将螺杆、螺母和垫圈组合为整体。模型中构件间接触形式较为简单,为获得较好的应力分布情况,采用C3D8R 线性缩减积分单元进行网格划分。应力集中主要发生在螺杆与壁板结构接触区域,以螺栓孔中心为圆心切割半径为5 mm 的圆,在圆周位置增加种子排布的密度进行网格细化处理。所有构件网格规划好后进行网格质量准确性检查,整体模型中总单元数为127710,网格划分情况如图4所示。
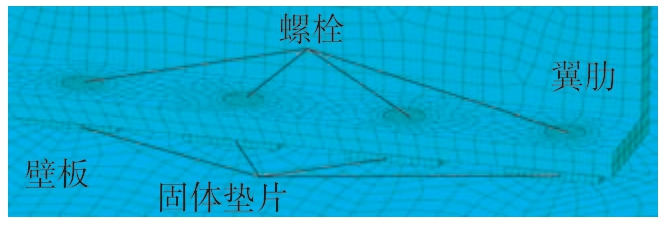
图4 有限元模型网格划分
Fig.4 Finite element model meshing
2.2 材料参数设置
仿真模型建立完成后设置各个部件的材料参数。螺栓部件为钛合金Ti–6Al–4V 材料,其弹性模量为110 GPa,泊松比为0.29,弹性极限为950 MPa[11];翼肋和固体垫片材料均为铝合金7050–T7 材料,其弹性模量为110 GPa,泊松比为0.34[12]。复合材料壁板为CCF300 碳纤维层合板,单层厚度为0.4 mm,铺层顺序为[45/0/–45/90]2s,总厚度为3.2 mm,材料力学参数如表2 所示[13]。
表2 碳纤维单层板力学参数[13]
Table 2 Mechanical parameters of carbon fiber monolayer plate[13]

力学参数 数值纵向模量E1 /GPa 125横向模量E2=E3 /GPa 8.7剪切模量G12 = G13 /GPa 3.36剪切模量G23 /GPa 3.15泊松比ν12 = ν13 0.31泊松比ν23 0.45纵向抗拉强度Xt /MPa 2500纵向抗压强度Xc /MPa 1631横向抗拉强度Yt /MPa 50横向抗压强度Yc /MPa 230抗剪强度S12= S13 /MPa 100抗剪强度S23 /MPa 120
2.3 接触属性及载荷施加
强制装配时,壁板与翼肋装配过程中存在3 组接触面,分别为螺杆与壁板、螺杆与翼肋、壁板与翼肋。加垫后内部接触关系更为复杂,增加了垫片与壁板、垫片与翼肋这两组接触面。上述5 种接触随着贴合面滑移和载荷变化不断发生改变,相对滑动位移较小,因此采用小滑移接触公式,将接触定义为法向硬接触和切向基于罚函数(Penalty)的摩擦接触。设置壁板、翼肋与垫片间的摩擦系数为0.2,其余摩擦系数均设为0.1[14]。仿真计算重点关注壁板局部结构装配质量,为简化计算,对3 条翼肋施加刚体约束,并限制其Ux、Uy 和Uz 3 个平移自由度。同时为模拟螺栓紧固过程,分别在螺栓上下两端与壁板、翼肋接触表面(从属表面与从属点集合)施加ABAQUS 软件中的Coupling 耦合约束。
螺栓预紧载荷通过ABAQUS 软件中的Bolt load 功能进行施加,数值采用航空标准化规定的最大值8000 N[15]。为计算不同紧固顺序对装配质量的影响,每个螺栓紧固单独设置1 个分析步,共计51 个分析步。每个分析步上按照不同紧固顺序的螺栓编号依次施加载荷,其他紧固顺序计算可通过更改分析步中施加载荷的对应螺栓编号次序来实现,模型整体边界条件及载荷施加如图5 所示。
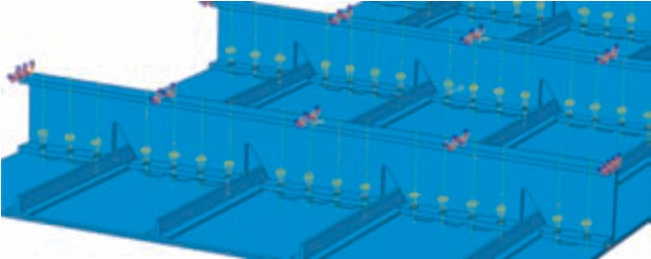
图5 边界条件及载荷施加
Fig.5 Boundary conditions and load application
2.4 失效判定及刚度退化准则
本文选取一种基于3D Hashin 失效准则和刚度退化的渐进损伤模型进行分析[16]。该失效准则可以判定纤维拉伸失效、纤维压缩失效、基体拉伸失效和基体压缩失效4 种模式,对应以下计算公式。
(1)纤维拉伸失效(σ11 ≥0)。
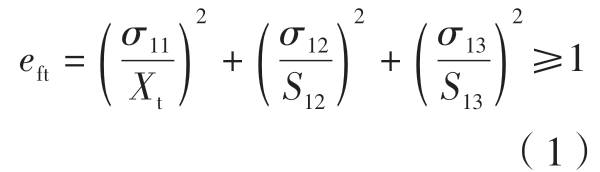
(2)纤维压缩失效(σ11<0)。
(3)基体拉伸失效(σ22+σ33 ≥0)。
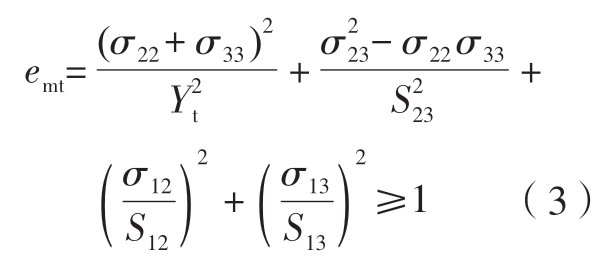
(4)基体压缩失效(σ22+σ33<0)。
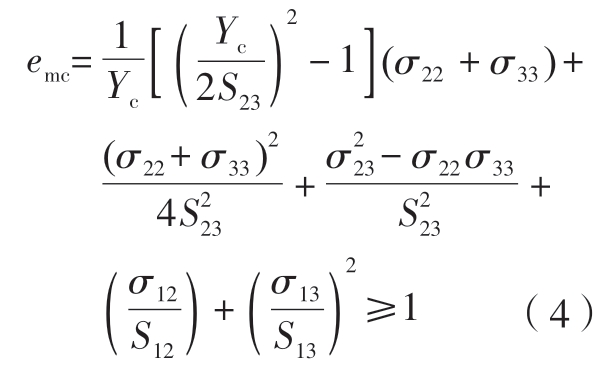
式中,σ11 为纤维方向应力;σ22 为基体方向应力;σ33 为法向应力;σ12、σ13、σ23 为切应力分量。ek(k =ft,fc,mt,mc)≥1 时表示壁板发生对应类型失效,此时采用刚度折减的方式进行性能退化处理[17],刚度矩阵通过内部相应元素与损伤变量dk 有关的系数相乘来计算刚度降低值,失效后刚度矩阵C d 为

式中,dk 为各种失效模式的损伤变量;![]() 为失效前刚度矩阵元素;
为失效前刚度矩阵元素;![]() 为失效后的刚度矩阵元素;εi 为正应变;LC 为特征长度;Gk 为各失效模式的断裂能。损伤变量dk 以指数形式更新,取值范围为0~1 递增,dk=1时代表单元完全失效。
为失效后的刚度矩阵元素;εi 为正应变;LC 为特征长度;Gk 为各失效模式的断裂能。损伤变量dk 以指数形式更新,取值范围为0~1 递增,dk=1时代表单元完全失效。
3 壁板结构装配连接试验
为验证壁板连接过程装配质量计算结果,进行了对应的装配连接试验。选择生产现场替换的局部壁板作为试验对象并搭建与仿真分析一致的测量平台,尺寸为1000 mm×500 mm×3.2 mm,材料为CCF300 碳纤维层合板,铺层顺序为[45/0/–45/90]2s。翼肋选用铝合金7050–T7 材料,连接过程近似为刚性件连接,其几何构型按数模加工,贴合面处加工为平面,然后安装在支撑型架上。与现场实际装配一致,设置3 条翼肋与局部壁板结构连接。螺栓为Ti–6Al–4V 材料,直径为6 mm。贴合面处制备3排螺栓孔,孔径为6.2 mm,相邻孔距为24 mm,共51 个。完成连接孔制备后,在壁板表面均匀喷涂白色哑光漆,风干后在白漆表面喷涂黑色散斑。装配连接过程采用CSI 公司的VIC–3D 数字图像相关(DIC)系统测量,根据现场装配工艺要求,在不影响间隙值的情况下使用穿心夹将壁板与翼肋进行预连接,然后进行对应填隙补偿。进行工业相机、三脚架、LED 光源和计算机等监测设备的连接,调整LED 光源角度和工业相机光圈进行对焦,保证DIC 图像分析软件左右两侧显示界面内散斑稳定、清晰、无过度曝光,整体试验平台如图6 所示。最后手持标定板在飞机壁板前进行空间位置标定,定义三维测量坐标系。

图6 壁板装配试验测量平台
Fig.6 Panel assembly experimental measurement platform
试验平台搭建好后启动DIC 测量系统,在试验工装后使用测扭矩扳手按照装配现场要求的扭矩数值进行安装并逐个手动拧紧螺栓,保证每个螺栓紧固时扭矩值一致。DIC系统监测时两台工业相机每3 s 自动采集1 张图像,直至最后1 个螺栓紧固后停止试验。每种拧紧顺序为1 组试验,共9 组。为了保证试验数据的高精度,每组试验重复3 次,试验后使用DIC 图像分析软件进行数据处理,得到各组不同顺序螺栓紧固后整个局部壁板结构的表面位移场。
4 结果与讨论
4.1 壁板偏移变形分析及模型验证
大尺寸飞机壁板多螺栓装配过程中,填隙补偿后贴合面仍存在残余装配间隙,x、y 两个方向会出现一定的空间偏移变形,影响最终装配质量。本文选择1→2→3 中间向外顺序,对x、y 两个方向偏移情况进行分析。为使偏移变形云图更直观清晰,在ABAQUS 软件中将变形效果放大,处理后的三维偏移变形云图如图7 所示。

图7 壁板x、y 两个方向偏移变形云图
Fig.7 Cloud maps of panel offset deformations in the x and y directions
由图7 可知,壁板边缘翼肋两端位置由于翘曲变形向内偏移明显,较其他位置向内偏移严重。壁板x、y 两个方向偏移变形数值量级小,变形云图呈现效果不明显,无法对偏移变形进行直观清晰的对比分析。因此,选择对绘制的不同紧固顺序的壁板偏移变形曲线进行分析,设定x 轴为壁板边缘位置坐标,y 轴为壁板边缘位置偏移量数值。以壁板左上角为零点,顺时针顺序(左上→右上→右下→左下→左上)进行绘制。同时选取试验所得局部壁板四边端点及中间点偏移量进行对比分析,以验证仿真计算的准确性。所得9 种紧固顺序壁板x、y 两个方向偏移量曲线如图8 所示,壁板端点及中间点偏移量数值如表3 所示。
表3 试验数据和仿真结果偏移量对比分析
Table 3 Contrastive analysis of offset between test data and simulation result mm
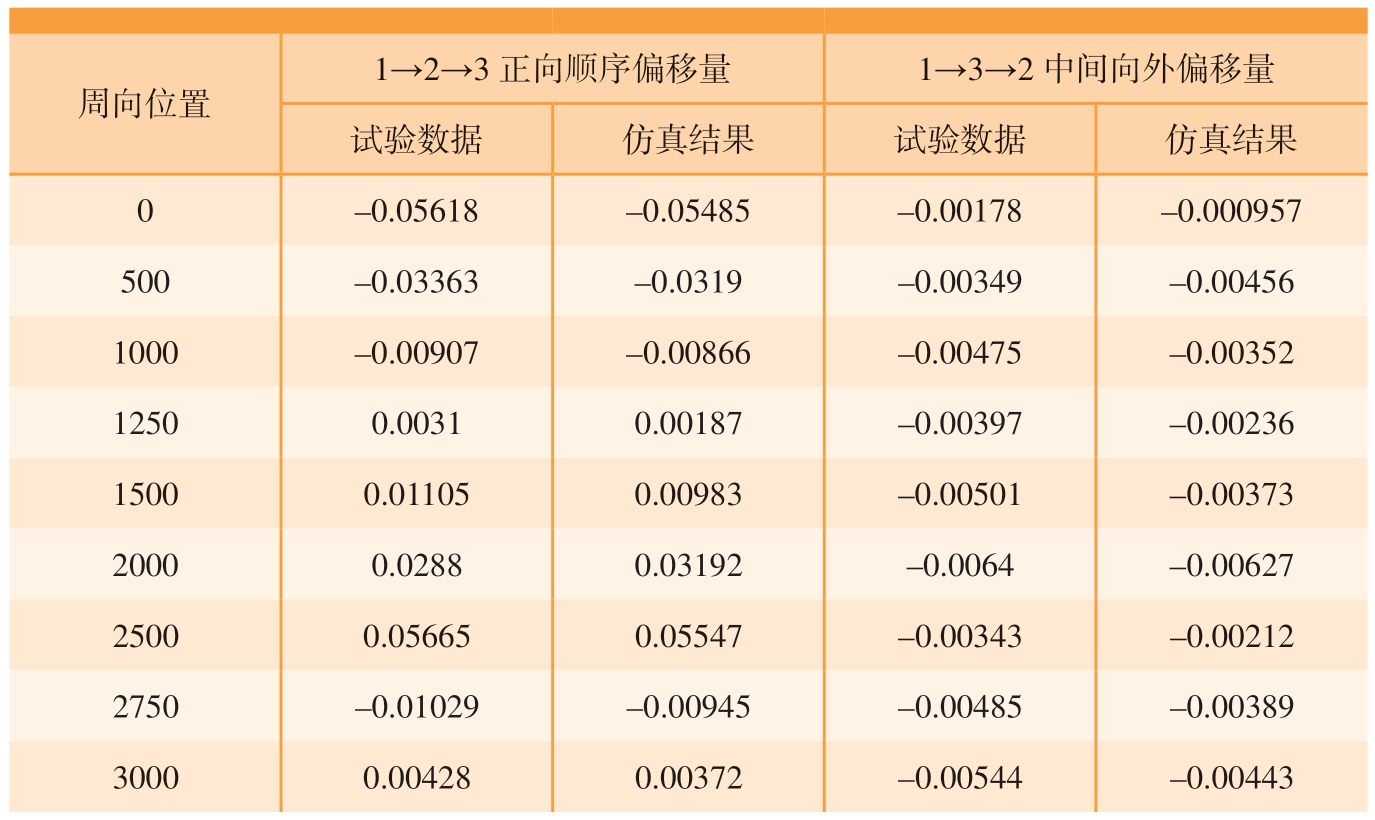
周向位置1→2→3 正向顺序偏移量 1→3→2 中间向外偏移量试验数据 仿真结果 试验数据 仿真结果0–0.05618 –0.05485 –0.00178 –0.000957 500 –0.03363 –0.0319 –0.00349 –0.00456 1000 –0.00907 –0.00866 –0.00475 –0.00352 1250 0.0031 0.00187 –0.00397 –0.00236 1500 0.01105 0.00983 –0.00501 –0.00373 2000 0.0288 0.03192 –0.0064 –0.00627 2500 0.05665 0.05547 –0.00343 –0.00212 2750 –0.01029 –0.00945 –0.00485 –0.00389 3000 0.00428 0.00372 –0.00544 –0.00443
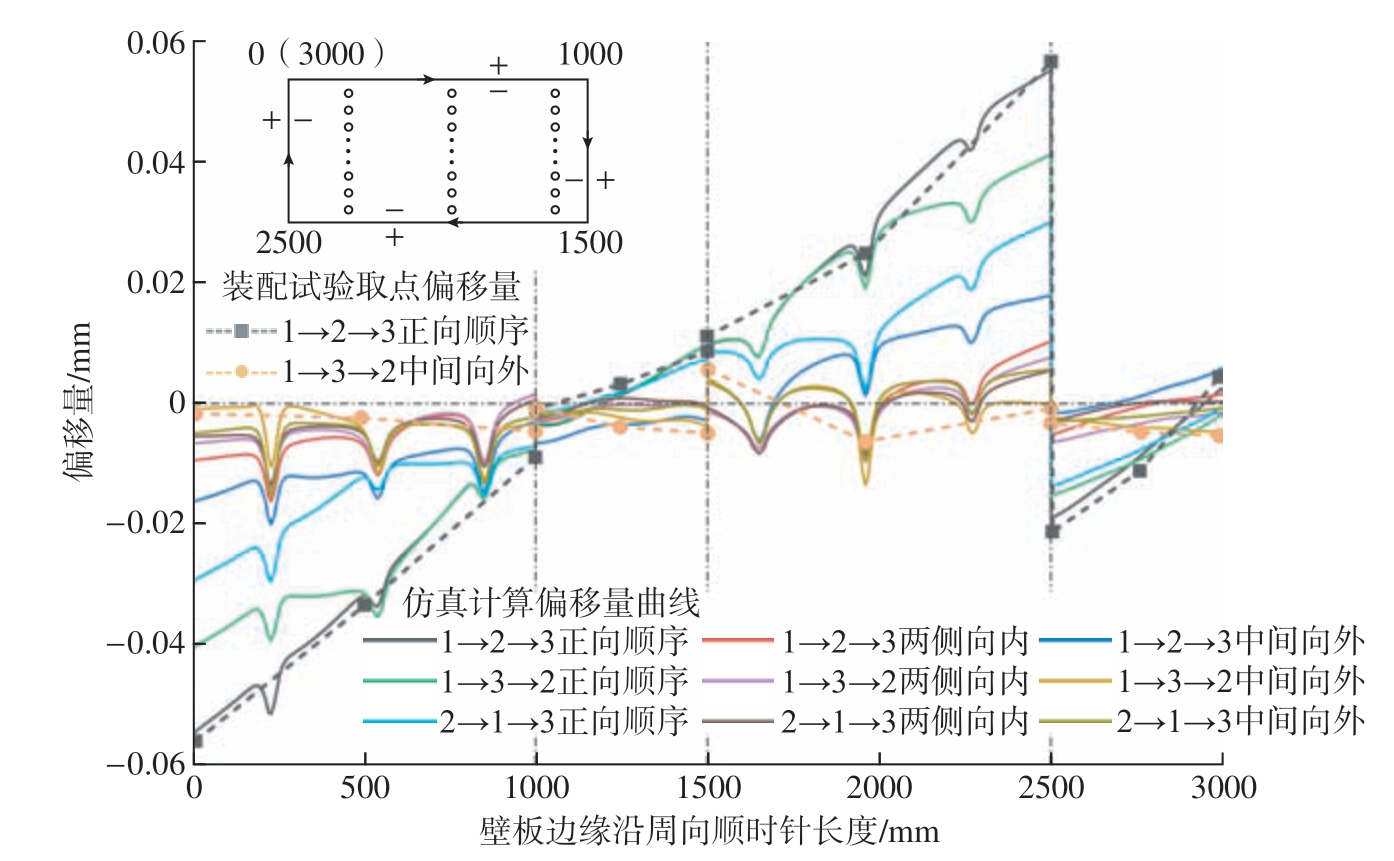
图8 局部壁板边缘偏移量曲线
Fig.8 Local panel edge offset curve
由图8 和表3 可知,1→2→3 正向顺序和1→3→2 中间向外两种紧固顺序仿真偏移量曲线与试验选取点偏移量吻合程度较好,在变形量超过0.01 mm 情况下,两种研究方式所得偏移量数值相对误差均小于10%,此时仿真计算对于局部壁板连接过程分析是有效的。9 种紧固顺序壁板各边偏移趋势保持一致,而偏移数值表现出明显差异。具体表现:在壁板顶端区域每种紧固顺序偏移量均为负值,除3 条翼肋所在边缘位置出现波动外,其余位置偏移量数值呈递减趋势;壁板右侧边缘区域3 种正向顺序偏移量在中间位置处由负值变为正值,其余路径整个范围均为负值,且数值在0.01 mm 内;壁板底部区域偏移量整体趋势递增,3 条翼肋边缘位置曲线存在波动,其中正向顺序偏移量均为正值,其余顺序波动处达到负值;壁板左侧边缘位置9 种紧固顺序偏移量呈递减趋势,整体数值在0.02 mm 以内。壁板顶端与底部区域范围内3 条翼肋所在位置边缘处偏移曲线出现波动,说明翼肋处由于螺栓紧固壁板导致内部凹陷变形大,翼肋两端区域翘曲明显,两端较其他位置向内偏移严重。壁板上下边缘偏移量曲线除翼肋两端位置外相互对称,偏移量数值相同,说明壁板在xoy 面内主要表现为以右上端点为圆心向左下方的旋转变形,左下端点偏移量最大可达0.05547 mm。
经对比分析可知,以正向顺序紧固螺栓装配连接壁板时的偏移变形较大,其中以1→2→3 翼肋顺序连接最大;其次为1→3→2 顺序,以2→1→3 顺序连接最小。其余紧固顺序偏移量数值均保持在0.02 mm以内,其中以1→3→2 中间向外顺序连接产生的偏移变形最小。可见对称性连接比按顺序连接产生的偏移变形更小,单条翼肋螺栓顺序以中间向两端连接产生的变形更小。不同点位的对称连接中偏移变形以两侧向内的翼肋顺序连接更小,原因在于两侧翼肋连接好后壁板位置已提前确定,因此最终壁板偏移变形最小。
4.2 壁板法向变形分析
壁板x、y 两个方向出现空间偏移变形的同时,残余装配间隙的存在会导致贴合面产生“气泡效应”,紧固后产生法向装配变形,影响最终的装配质量。因此本文进行了加垫装配9 种紧固顺序壁板法向变形的分析,结果如图9 所示。

图9 壁板法向装配变形云图(mm)
Fig.9 Cloud map of normal assembly deformation for panels (mm)
结合图9 分析可知,壁板填隙补偿后相互贴合的壁板和翼肋间仍存在部分装配间隙,在螺栓载荷预紧力的作用下,壁板孔周区域材料挤压产生凹陷变形并向四周逐层递减,间隙量变化对应壁板内部区域法向变形变化,法向变形为负值。同时壁板四周区域材料由于内部凹陷变形使得径向处于拉伸状态,导致左右两侧出现翘曲变形,法向变形为正值。加垫后除壁板左右两侧和螺栓孔周围出现装配变形集中现象,其余测量区域内变形分布较为均匀,处于允许范围内。
对比加垫后法向变形的正负值及其分布位置可知,对于壁板内部凹陷变形区域大小不同、紧固顺序存在差异,其中以1→2→3 正向顺序凹陷变形区域最大,以2→1→3 中间向外顺序紧固凹陷变形区域最小,总体来说多螺栓按顺序连接的变形区域最大,其次为两侧向内进行对称连接,变形区域最小的是从中间向外对称连接。壁板内部9 种紧固顺序凹陷变形最大值均为0.208 mm,说明凹陷变形与间隙量变化直接相关,紧固顺序对间隙处凹陷变形最大值无明显影响。而壁板左右边缘翘曲变形差别较大,与凹陷变形区域大小分布一致,无论螺栓顺序还是翼肋顺序,按顺序依次连接边缘的翘曲变形区域最大,其次为两侧向内进行对称连接,以中间向外对称连接的翘曲变形最小。9 种紧固顺序中以1→2→3正向顺序紧固的边缘变形最大,为0.637 mm,以2→1→3 中间向外顺序紧固的边缘变形最小,为0.233 mm。通过改变螺栓紧固顺序,壁板法向变形值最大值减小约63.4%,可见改变紧固顺序能有效减小装配变形。总体来说,装配时以对称形式进行螺栓紧固比按顺序依次连接装配导致的变形小,以两侧向内顺序对称连接会导致装配间隙集中于一点,而从间隙值最大处向外对称连接使得间隙向两端传递减弱,呈气泡效应,因此对称连接中以中间向外连接较两侧向内顺序更有优势。
4.3 壁板装配应力分析
加垫后随着螺栓夹紧力紧固壁板表面依然会产生一定的法向变形,从而导致壁板表面出现残余应力集中情况,影响最终的装配质量。因此本文进行了9 种紧固顺序下壁板装配应力集中情况的分析,应力云图如图10 所示。

图10 壁板装配应力云图(MPa)
Fig.10 Cloud map of assembly stress for panels (MPa)
由图10 可知,加垫处理后不同紧固顺序对应的装配应力大小及分布情况存在差异,以2→1→3 中间向外顺序连接产生的最大应力值最小,为262.377 MPa。以1→3→2 两侧向内顺序连接产生的最大应力值最大,为266.895 MPa。规划的9 种紧固顺序应力分布云图相似度高,平均最大应力值接近,说明螺栓连接顺序对壁板整体应力分布的影响相对较小。局部壁板装配应力主要分布在螺栓孔周区域,其余区域应力集中情况较小。为能更清晰对比分析紧固顺序对孔周应力分布影响情况,选择1 号翼肋的1#、2#、3#螺栓孔进行分析,绘制图11 所示的9 种连接顺序下1#、2#、3#孔周应力分布云图。

图11 壁板孔周装配应力云图
Fig.11 Cloud map of hole perimeter assembly stress for panels
由图11 横向对比可知,按照1 →2 →3 和1 →3 →2 顺序装配翼肋(即先装配1 号翼肋),3 种螺栓紧固顺序所得孔周应力大体相同;而先装配2 号翼肋所得孔周应力则与上述两种情况存在明显不同。这说明翼肋的装配顺序对连接孔周应力有较大影响。竖向对比分析可知,3 种顺序孔周应力分布存在差异,其中以两侧向内顺序紧固2#孔周围较另外两种顺序应力值小,说明单条翼肋上螺栓紧固顺序对应力值有一定影响。综上,局部壁板在填隙状态下的螺栓紧固顺序对应力分布的影响相对较小,而对螺栓孔周应力分布和结构整体在空间上的变形影响较大。螺栓连接孔周的应力分布与壁板翼肋的间隙跨度和间隙量密切相关,连接孔周仅在与螺栓接触的部位产生较大应力,随着间隙量的提高,应力值和传递的范围逐渐增大。主要原因在于,特定结构与配合间隙下无论何种连接顺序都是将壁板与翼肋的间隙压平,因此产生的整体应力相近。面内偏移和面内变形等空间变形也会导致应力改变,然而这种改变更多的是作用在螺栓与连接孔的界面处,导致界面应力急剧增加。
5 结论
(1)加垫后以正向顺序紧固螺栓壁板偏移变形较大,其中以1→2→3翼肋顺序连接最大,其余紧固顺序偏移量数值均保持在0.02 mm 以内。翼肋两端壁板边缘较其他位置向内偏移严重,上下边缘偏移量曲线除翼肋两端位置外相互对称,说明壁板在xoy 面内偏移主要表现为以右上端点为圆心向左下方旋转变形,左下端点偏移量最大可达0.05547 mm。针对偏移变形,对称性连接比按顺序连接产生的变形更小,单条翼肋螺栓顺序以中间向外连接的变形更小。
(2)加垫后除壁板左右两侧和螺栓孔周围出现装配变形集中现象,其余测量区域内变形分布较为均匀。以1→2→3 正向顺序紧固边缘产生的变形最大,为0.637 mm;以2→1→3 中间向外顺序紧固边缘产生的变形最小,为0.233 mm。装配时以对称形式进行螺栓紧固比按顺序依次连接的法向变形小,改变螺栓紧固顺序,法向变形值最大值减小约63.4%,可见改变紧固顺序能有效减小装配变形,对称连接中以中间向外连接较两侧向内顺序更有优势。
(3)加垫填隙后螺栓紧固顺序对壁板整体应力集中情况影响相对较小,以2→1→3 中间向外顺序连接时的最大应力值最小,为262.377 MPa;以1→3→2 两侧向内顺序连接时的最大应力值最大,为266.895 MPa。紧固顺序对螺栓孔周应力分布和壁板结构在空间上的变形影响较大。连接孔周应力分布与间隙跨度和间隙量密切相关,连接孔周仅在与螺栓接触的部位产生较大应力,随着间隙量的提高,应力值和传递的范围逐渐增大。
本文仅针对已规划的9 种紧固顺序连接情况进行分析,后续若采用遗传算法进行连接路径次序优化,壁板整体装配质量还有较大提升空间,即便在实际装配中螺栓和连接孔存在一定间隙,通过紧固顺序的优化亦可对装配质量实现均衡控制。
[1] BARAN I, CINAR K, ERSOY N,et al.A review on the mechanical modeling of composite manufacturing processes[J].Archives of Computational Methods in Engineering: State of the Art Reviews, 2017, 24(2): 365–395.
[2] BATUWITAGE C, FAWZIA S,THAMBIRATNAM D, et al.Durability of CFRP strengthened steel plate double-strap joints in accelerated corrosion environments[J].Composite Structures, 2017, 160: 1287–1298.
[3] SÖDERBERG R, WÄRMEFJORD K, LINDKVIST L.Variation simulation of stress during assembly of composite parts[J].CIRP Annals, 2015, 64(1): 17–20.
[4] D H Ô T E J X, C O M E R A J,STANLEY W F, et al.Investigation into compressive properties of liquid shim for aerospace bolted joints[J].Composite Structures,2014, 109: 224–230.
[5] 曾祥钱.复合材料构件螺栓连接二次损伤建模与分析[D].大连: 大连理工大学,2018.
ZENG Xiangqian.Modeling and analysis on secondary-damage of composite bolted joints[D].Dalian: Dalian University of Technology, 2018.
[6] CHENG L, WANG Q, KE Y L.Experimental and numerical analyses of the shimming effect on bolted joints with nonuniform gaps[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science,2019, 233(11): 3964–3975.
[7] YUE X D, AN L L, CHEN Z T,et al.Effect of preload and shim types on the mechanical properties of composite-aluminium bolted joints[J].Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(2):1099–1118.
[8] CHANG J H, LIU X, YANG Y X,et al.The influence of the assembly gaps and tightening operations on the stress distribution during the assembly process[J].IOP Conference Series: Materials Science and Engineering,2018, 408: 012008.
[9] LIU C N, LI Y, CHENG Y, et al.Investigation on deformation of composite multi-bolted joints considering influences of hole-location errors and installation sequence[J].Engineering Failure Analysis, 2022, 140:106592.
[10] POGARSKAIA T, LUPULEAC S, SHINDER J, et al.Optimization of the installation sequence for the temporary fasteners in the aircraft industry[J].Journal of Computing and Information Science in Engineering, 2022,22(4): 040901.
[11] KAPIDŽIĆ Z, NILSSON L,ANSELL H.Finite element modeling of mechanically fastened composite-aluminum joints in aircraft structures[J].Composite Structures, 2014, 109: 198–210.
[12] 叶鑫, 安鲁陵, 岳烜德, 等.填隙补偿对碳纤维/环氧树脂复合材料–铝合金装配结构力学性能的影响[J].复合材料学报,2020, 37(9): 2183–2199.
YE Xin, AN Luling, YUE Xuande, et al.Effect of gap-filling compensation on mechanical properties of carbon fiber/epoxy composite–aluminum assembly structure[J].Acta Materiae Compositae Sinica, 2020, 37(9):2183–2199.
[13] 熊明洋, 向忠, 胡旭东, 等.基于ABAQUS 的CCF300 碳纤维层合板低速冲击破坏数值模拟[J].轻工机械, 2017, 35(4):27–32.
XIONG Mingyang, XIANG Zhong, HU Xudong, et al.Numerical simulation of low velocity impact failure of CCF300 carbon fiber laminate based on ABAQUS[J].Light Industry Machinery, 2017, 35(4): 27–32.
[14] XU W C, WANG D F.Static and dynamic impact performance optimization of CFRP/Al bolt joint coupling structure–lay-up–connection parameters[J].Archives of Civil and Mechanical Engineering, 2022, 22(3): 118.
[15] 部标准编制组.部标准《高锁螺栓、螺母》介绍[J].航空标准化, 1981(3): 1–4.
Department Standard Establishment Group.Introduction of ministry standard “high lock bolt and nut”[J].Aeronautic Standardization &Quality, 1981(3): 1–4.
[16] MCCARTHY M A, MCCARTHY C T, LAWLOR V P, et al.Three-dimensional finite element analysis of single-bolt, singlelap composite bolted joints: Part I—Model development and validation[J].Composite Structures, 2005, 71(2): 140–158.
[17] FAROOQ U, MYLER P.Finite element simulation of carbon fibre-reinforced composite laminates subjected to low velocity impact using damage induced static loaddeflection methodology[J].Thin-Walled Structures, 2015, 97: 63–73.
