精密主轴是航空制造机床的核心功能部件，被广泛用于压气机叶片抛光等重要航空零部件的加工制造过程中，其回转误差对航空零部件的加工精度具有巨大影响[1]。然而，由于主轴的结构特性，其回转误差在加工过程中难以通过数控系统进行补偿。因此，在设计阶段开展主轴回转精度分析，预测装配后的精度性能指标，对主轴的性能保障至关重要。
回转精度作为主轴的重要性能指标，长期以来得到了研究人员的广泛关注。一些学者尝试开发各类测量系统及误差分离算法以获得更加精确的主轴回转误差，例如Cui 等[2]开发了一种基于唐纳森反转法测量主轴径向回转误差的纳米系统。Ni等[3]提出了一种基于复合激光目标的主轴误差测量方法，该法能够测量主轴运动误差，包括轴向、径向和倾斜运动误差。张华等[4]使用Lion Precision 公司的主轴回转精度测试仪对砂轮动静压主轴系统的回转精度进行测试，并基于有限元方法分析了该型主轴的静刚度等性能指标。另一些学者则尝试探究主轴回转精度的影响因素，Hu 等[5]使用可变预紧试验台研究了预紧力和方法对主轴旋转精度的影响。Fang 等[6]探讨了中推力轴承结构精密静压主轴中转子同轴度误差对主轴精度的影响。然而这些基于试验的方法仅能探究单个因素对主轴回转精度的影响，无法建立主轴的回转精度模型。而主轴的回转误差归根结底来源于零部件的制造和装配，零件的制造误差在装配阶段的传递、累积使得主轴各零部件偏离名义位置，从而在运转时产生了回转误差，这与零部件的加工精度和主轴的公差设计紧密相关。因而从公差角度出发，建立主轴的回转精度模型对于预测、调控主轴的回转误差具有重要意义。
长期以来，学者们在公差建模及分析方面做了许多工作。在零件公差建模方面，小位移旋量理论（Small displacement torsor，SDT）[7]、雅克比旋量法[8–10]、矢量环法[11]、T–Map法[12]和多面体理论[13–14]是当前进行公差建模和分析的主要方法。其中，SDT理论基于自由度约束的思想，将特征面的制造误差等效为偏离名义位置的理想表面。使用旋量理论对公差进行建模并与雅克比矩阵相结合，能够便捷高效地进行误差传递的计算。一些学者基于上述理论方法尝试建立了主轴的精度模型，例如Huang等[15]提出了一种考虑轴承配合误差的车床主轴回转误差综合模型，但该方法极大地简化了主轴的结构因而难以用于实际产品分析。Guo 等[16]基于SDT 理论建立了更全面的主轴精度分析模型，该模型综合考虑了定位、定向和轴承回转误差但无法兼顾形状误差，这是由于上述公差建模方法在表征形状误差方面存在着“先天不足”所导致的。因为包含形状误差的零件表面往往是非理想表面，无法通过名义表面的等效位姿变换进行表示，也即无法简单地通过一组矢量或矩阵进行数学表达。尽管T–Map 和多面体理论基于集合交并集运算的方法可以考虑形状误差，其中的T–Map 法也完全满足ASME 标准，能对各类误差进行建模[17]；但这些方法无法考虑零件的误差分布情况，仅能进行极值分析，更无法分析零件之间装配的相对定位关系，使得此类方法在指导公差设计方面存在一定的局限性。
为了在精度建模中更好地考虑形状误差，肤面模型（Skin model，SM）的概念被引入了装配精度分析领域[18]。与名义模型不同，肤面模型是零件与其环境之间的物理界面模型[19]，使用无限数量的点对特征进行描述，可以考虑从宏观到纳米尺度的各种几何偏差，但是无限数量的点在实际分析和计算中难以实现。因此，Schleich 等[20]进一步提出了肤面模型形状（Skin model shape，SMS）的概念，使用有限数量的点对零件特征面进行描述，能够很好地表征零件因加工而产生的非理想表面。与以往研究中将理想面进行偏移来对形状误差进行等效不同，肤面模型形状使用点云对非理想表面进行表征，这使得在进行装配误差分析中精确考虑形状误差成为可能。基于肤面模型形状的装配仿真，可以使用Samper等[21]提出的差表面法进行分析，通过计算差值表面进行接触仿真分析。另一种分析方法则是点云处理领域广泛使用的配准（Registration）技术，例如迭代最近点算法（Iterative closest point，ICP）[22–23]。与从ICP 方法中衍生而来的约束配准方法相比，差表面法在计算柱面特别是涉及过盈配合时有着很大的局限性，因而并不适用于存在大量柱面和过盈配合的主轴分析中。许多学者基于肤面模型开展了装配精度分析的研究，例如应用肤面模型形状表征航空发动机中的形状误差，并使用碰撞检测算法进行模拟来分析装配偏差[24]。Wang 等[25]基于肤面模型形状建立了零件数字孪生模型，并在负载敏感多路阀的泄漏分析上取得了良好的应用效果。Yi等[26]则进一步将肤面模型形状的应用推广到包含有局部并行连接装配体的公差分析中。上述研究尝试使用肤面模型方法建立能考虑形状误差的精度分析模型，然而该方法在精密主轴精度分析领域的研究仍然较少，特别是对考虑主轴内部过约束结构所导致的复杂连接关系的研究仍然不足。
综上所述，过往的研究尚不能很好地在主轴回转精度分析中综合考虑零部件形位误差，也无法解决主轴系统中存在的完全并行连接关系。基于此，本文综合运用小位移旋量理论和肤面模型方法表征主轴零部件的形位误差，分析了主轴中存在的完全并行连接关系，并提出使用优化的方法求解完全并行连接关系下的主轴回转误差。最后以某型磨削主轴为案例，研究了公差与主轴回转精度之间的关系，并通过敏感度分析改进了该型主轴的设计公差，证明了该方法在主轴回转精度分析中的有效性。
1 主轴回转误差
作为一种典型的转子系统，主轴通常由轴承、转子、轴承座及隔套等零件组成。由于存在零部件制造误差，导致转子在旋转过程中并不是沿着理想轴线旋转，而是呈现非理想的空间轨迹，如图1 所示（蓝色实线代表主轴轴心的空间轨迹）。主轴的空间轨迹包括轴向窜动和径向跳动两部分，工程上常将径向轨迹投影的最小包络圆直径定义为主轴径向跳动[17]，使用主轴装夹标准棒并用千分表进行检测。而轴向窜动则为轨迹沿轴向方向投影的区间极值。例如，对于图1 中轴心轨迹而言，其径向跳动约为8 μm，轴向窜动约为7 μm。
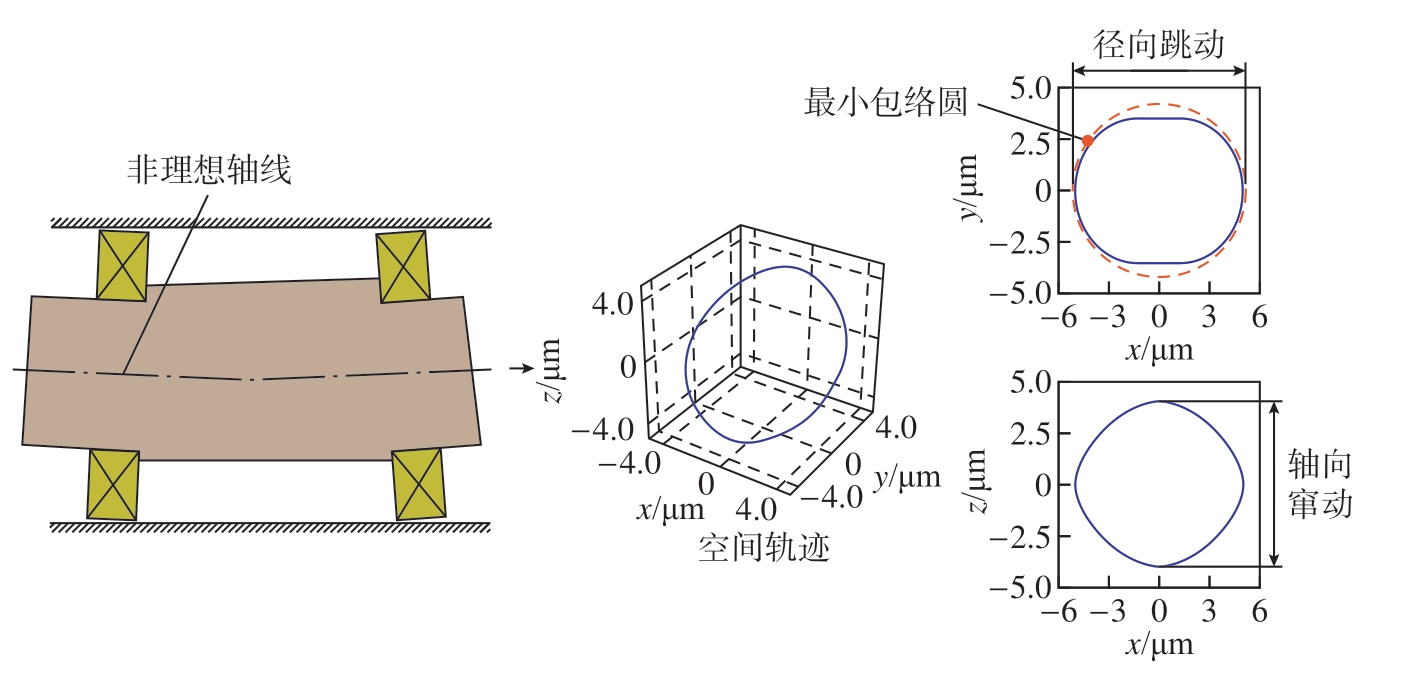
图1 回转误差示意图
Fig.1 Diagram of rotation error
2 零部件公差建模
由于零部件不可避免地存在制造误差，因此，零部件在设计阶段的理想表面会转变为非理想表面，从而偏离设计目标而影响产品的功能要求并导致装配偏差。公差分析是为了在设计阶段对产品最终的装配分析进行预测，从而保障产品的装配精度，因而公差分析的第1 步就是对零部件进行公差建模。
2.1 定向及定位公差建模
定向及定位公差是指特征表面相对于名义基准的偏离量，因而很适合使用小位移旋量理论进行建模。几何特征的偏离可以用2 组矢量表示，即平移矢量ρ =（u v w）T 和旋转矢量ε =（α β γ）T。根据齐次矩阵理论，可以很方便地将其表示为齐次坐标变换矩阵的形式
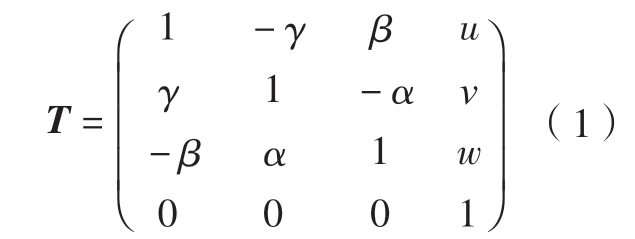
式中，α、β、γ 分别为绕x、y、z 轴的转角；u、v、w 分别为绕x、y、z 轴方向的位移。由于主轴的公差域是微小量，因此矩阵中的三角函数被线性化为角度值。在主轴中，常见的定向及定位公差有平行度、垂直度和同轴度，对上述公差进行建模[17]的结果如表1所示，其中T为公差值的大小。
表1 定向及定位公差建模
Table 1 Modeling for orientation and positioning tolerance
公差种类 示意图 齐次矩阵形式 约束条件A - T d ≤α≤T d垂直度d2 d1 T ＝10β0 0 1 -α 0-β α 1 0- T■■■■■■■■■■d ≤β≤T d 0 0 0 1 TA ［αsinφ+βcosφ］d ≤T A TA - T d ≤α≤T d平行度d T ＝■■■■■10β0 0 1 -α 0-β α 1 0- T■■■■■d ≤β≤T d 0 0 0 1［αsinφ+βcosφ］d ≤T- T L - T L ≤β≤T L d2 d1同轴度T T ＝■■■■■10βu 0 1 -α v-β α 1 0■■■■■■■■■■ ■■L ≤α≤T- T 2 ≤u≤T■2 - T 2 ≤v≤T 2 0 0 0 1 2 L u±β× L( )( )2+ v ±α× L 2 2≤T 2
2.2 形状公差建模
虽然基于小位移旋量理论可以有效地对定位和定向公差建模，但是并不能有效表征形状误差，这是由于形状误差对应的几何要素通常是非理想表面。然而形状误差对于主轴这样的精密机械而言又至关重要，因而本文通过引入肤面模型形状理论来解决这一问题。
使用肤面模型形状对形状公差进行建模相较于定向及定位公差建模而言更加复杂，这是因为该方法需要表征更多的特征面信息。图2 为柱面和平面形状公差的示意图，Tol1和Tol2 为形状公差域，使用肤面模型形状对形状公差进行建模的关键是确定公差域内肤面模型形状上每个点相较于名义位置的偏差量。本文使用基于模态函数的方法[27]仿真各类特征表面的形状误差，分别采用离散余弦变换（Discrete cosine transform，DCT）、Zernike 多项式和勒让德–傅里叶多项式对矩形平面、圆环平面和圆柱面的形状公差进行建模。
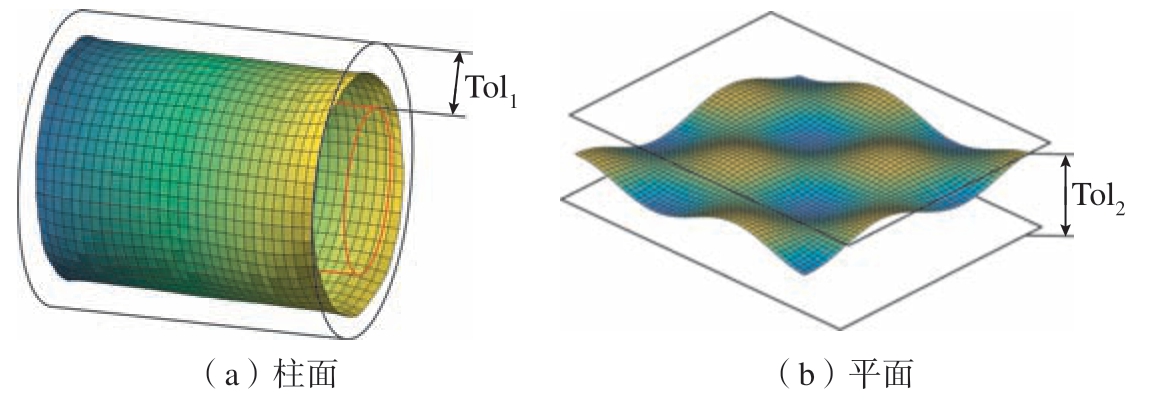
图2 形状公差示意图
Fig.2 Diagram of form tolerance
2.2.1 矩形平面
DCT 的基函数相互正交且线性无关，并且其形状与加工制造时产生的形状误差密切相关[28]，因而很适合用于矩形平面形状误差的建模。DCT 基函数的数学形式如式（2）所示：式中，E 和F 分别为沿x 和y 方向的采样点数量；e 和f 分别是沿x 和y方向采样点的序号，e = 0，1，…，E–1且f = 0，1，…，F–1；g 和h 分别是x和y 方向的频率，g = 0，1，…，E–1 且h= 0，1，…，F–1。前4 阶DCT 基函数的形状如图3 所示，其中g=h=0 时为无形状误差的理想平面。对于矩形平面，其形状误差可以由不同阶次的DCT 基函数通过线型叠加得到。
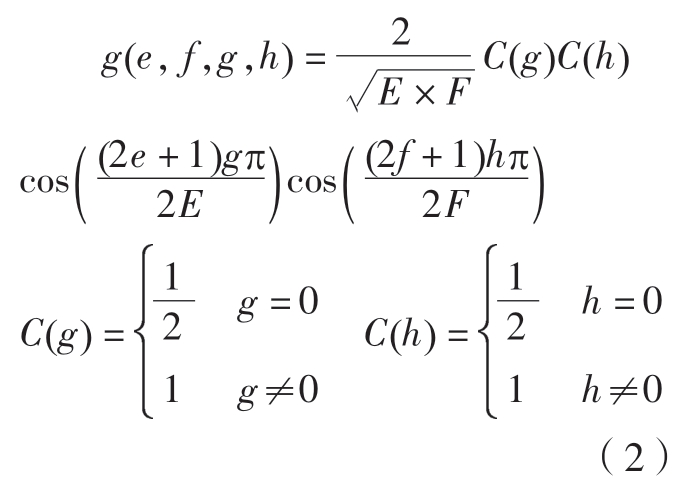
图3 DCT 基函数形状
Fig.3 Shapes of DCT basis functions
2.2.2 圆柱面
圆柱面的形状公差主要是同轴度，因而需要确定圆柱表面上各位置的点偏离名义位置的大小。从制造角度出发，圆柱表面通常是由车床加工成型。在这个过程中，除了刀具的回转运动外，还有沿轴向的进给运动，故而表面误差由径向误差和轴向误差两部分构成。径向误差也即圆度误差，可以使用二维傅里叶级数表示。而轴向误差是非周期性的，一般使用勒让德多项式进行表征。因此，本文使用勒让德–傅里叶多项式对圆柱表面的形状公差进行建模。勒让德–傅里叶多项式的表达式如下。
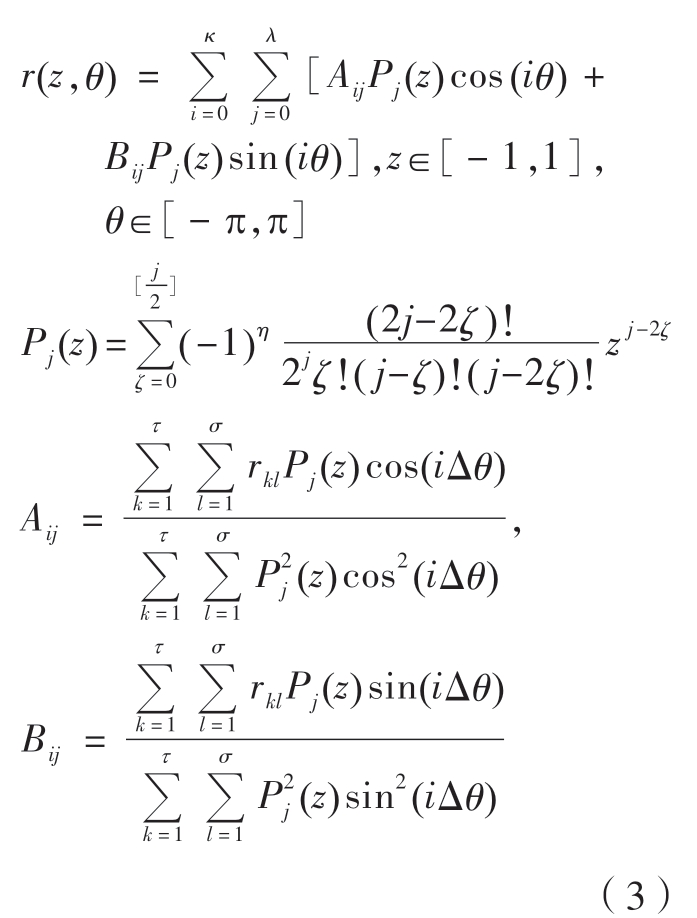
式中，r 代表圆柱面上的点与轴线之间的距离；θ 为圆柱坐标系中的极角；Pj（z）是j 阶勒让德多项式；ζ 是求和索引；Aij 和Bij 是系数；rkl 是第k行第l 列采样点的半径；τ 和σ 分别为轴向和径向的采样点数；Δθ 是径向相邻采样点之间的角度间隔。图4 展示了各阶勒让德–傅里叶多项式基函数形状。
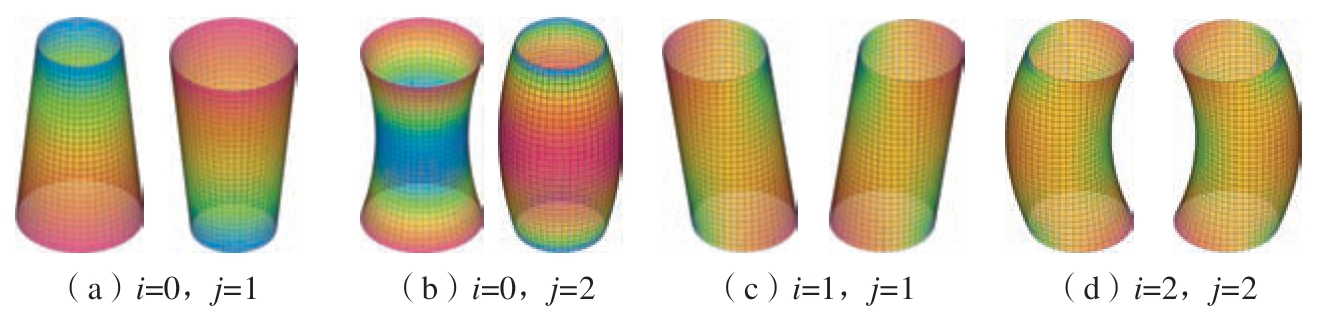
图4 勒让德–傅里叶多项式基函数形状
Fig.4 Shapes of Legendre–Fourier polynomial basis functions
2.2.3 圆环平面
圆环平面通常存在于主轴的轴向定位元件中，主轴中通常使用隔圈、端盖及锁紧螺母等零部件进行轴向定位，这些零部件的配合面一般为圆环平面。Zernike 多项式是一组可以被线性叠加的相互正交且完全独立的基函数，这些基函数可用于表示圆形平面和圆环形平面的形状误差。本文使用Zernike 多项式对圆环平面形状公差进行仿真建模，在极坐标系中，Zernike 多项式可表示为
其中，
式中，m′和n′（|m′|≤n′）分别是方位角频率和径向阶数；ρ ∈[0，1]和θ ∈[0，2π]分别为极半径和极角；s′为求和角标。Zernike 多项式基函数的形状如图5 所示。
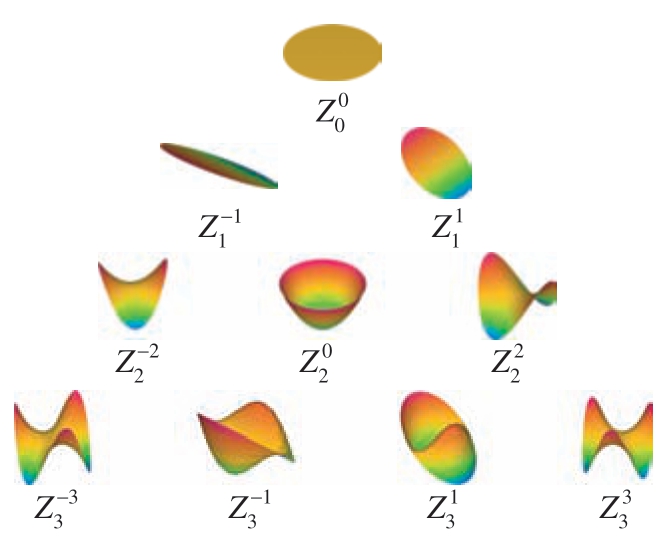
图5 Zernike 多项式基函数形状
Fig.5 Shape of Zernike polynomial basis functions
2.3 轴承回转轨迹建模
在主轴系统中，轴承一般作为成品部件直接外购而来。由于对精度有着极高的要求，主轴往往选用较高精度等级的轴承。以公称直径30 mm 的P4 精度等级的轴承为例，其内外圈配合柱面粗糙度要求Ra = 0.25 μm[29]，因而轴承本身的形状误差可以忽略不计。然而轴承的回转误差往往达数μm，这对于主轴的回转精度分析而言不可忽略，因此需要对轴承的回转轨迹进行建模。轴承中心轨迹复杂，一般可以分解为重复性回转误差和非重复性回转误差2部分，而其中非重复性回转误差相对较小[17]，因而本文只对轴承的重复性回转进行建模。以轴承外圈几何中心为原点建立轴承零件坐标系，取轴承内圈中心轨迹的径向投影为椭圆且轴向窜动为正弦规律变换进行分析，则轴承回转轨迹半径为
式中，r 和w 分别为轴承轨迹的径向半径和轴向位移；el 和er 分别为椭圆的半长轴和半短轴；ea 为轴向窜动轨迹的幅值；θr 为轴承的旋转角度。
3 考虑完全并行连接的主轴精度分析
通过装配累积的零部件制造误差导致了主轴的回转误差，因而从零部件的设计公差出发，对主轴进行装配误差传递计算是分析回转精度的重要手段。本文使用前述基于肤面模型的方法对主轴零部件的配合面进行建模，提出完全并行连接关系的辨识及处理方法，完成考虑形状误差的主轴误差传递计算。
3.1 考虑形状误差的装配仿真
装配误差是由多个零部件的制造误差在装配阶段的传递而来，单对配合表面的接触是装配误差传递计算的最小单元，所以进行误差传递计算的第1 步就是要解决单对配合表面的接触误差计算。在理想情况下，一对配合表面是在空间中重合于名义位置的理想表面。然而由于制造误差的存在，特征面往往呈现为公差域内的非理想表面。以图6 所示的2 个矩形平面的肤面模型形状为例，其特征面上的点由于形状误差而偏离了名义位置。SA 和SB 分别是包含制造误差的2 个平面的肤面模型形状。其中，SA 为固定基准；SB 为待装配表面与SA 接触。SA 和SB 均是由一系列点构成的，
和
分别是SA 和SB 点的集合，其中λ为点的个数，i 为点的索引角标。当SB 面装配到SA 面上，由于几何误差的存在，将会偏离名义位置到S′B 的位置。本文采用约束配准方法[30]求解装配后S′B 相对于SA 的位姿，具体为利用优化方法求解配合面之间所有点欧氏距离之和的最小值，其数学表达如下。
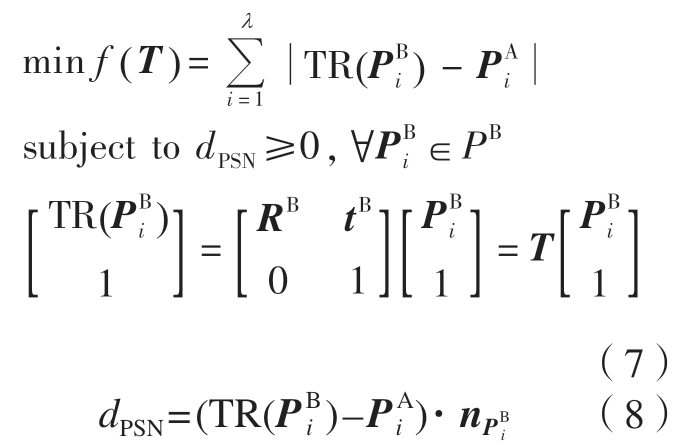
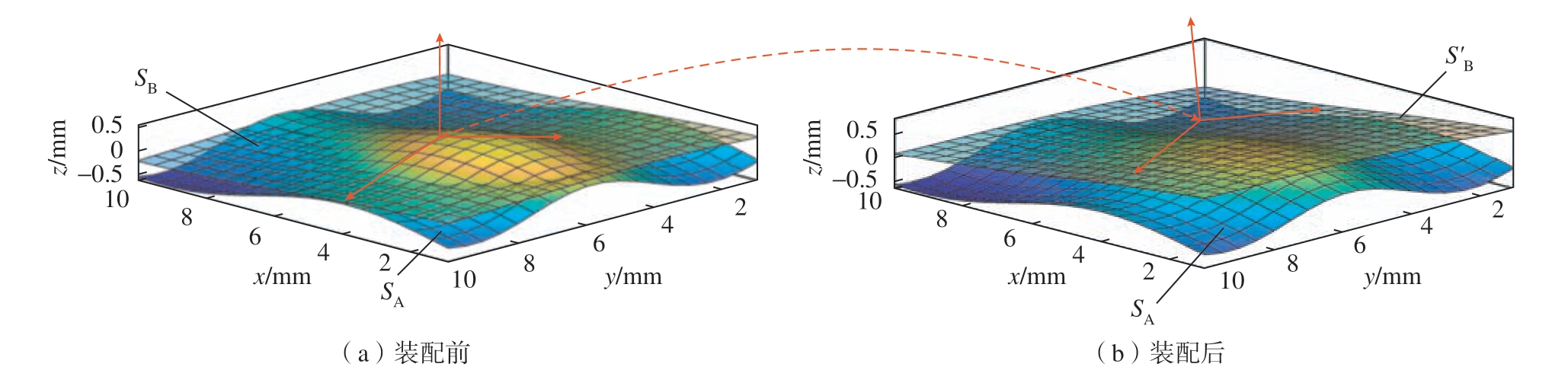
图6 基于约束配准方法的装配仿真
Fig.6 Assembly simulation based on constrained registration method
式中，RB 和tB 分别为SB 的旋转和平移矩阵；
为移动后
点的坐标。该方法的物理含义为寻找到一个装配位姿T，使得该装配位姿下2 个肤面间所有点的距离之和最小。dPSN 为有符号的法向投影距离（Projected signed normal distance），用以约束配合面之间可能存在的干涉。图6 展示了基于约束配准方法的装配仿真。
3.2 完全并行连接分析
特征面配合计算是误差传递的基本单元，下一步是对装配体进行误差传递计算，从而得到产品功能需求的误差变动范围。绝大多数装配连接关系可以被分为以下4 类：串行链、并行链、部分并行链和混合链[31]，不同的装配连接关系有着不同的误差传递计算方法。但是对于主轴而言，其装配连接关系更为复杂，以图7 所示的双轴承支撑主轴为例，该主轴由转轴、隔圈、轴承座和2 个轴承组成，图中1.1、1.2 等数字表示装配位置，具体可见图8。轴承一前一后分别安装在轴承座上，内圈依靠轴肩进行轴向定位，外圈使用隔圈进行轴向定位。其中隔圈与轴承座通常为间隙配合，因而轴承座并不会影响隔圈的位姿，该柱面配合不参与误差传递的计算。
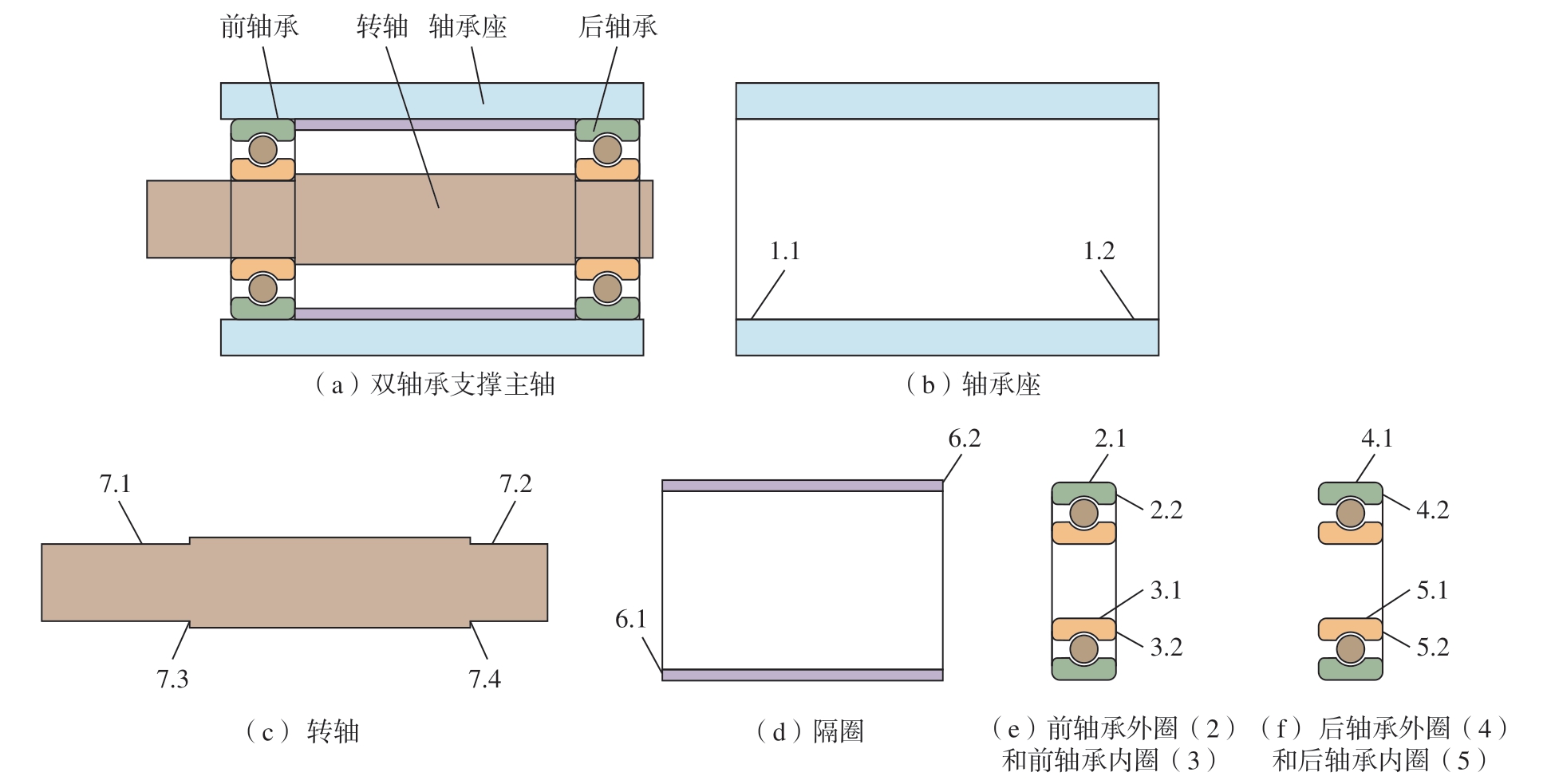
图7 双轴承支撑主轴结构示意图
Fig.7 Schematic diagram of double bearing supported spindle structure
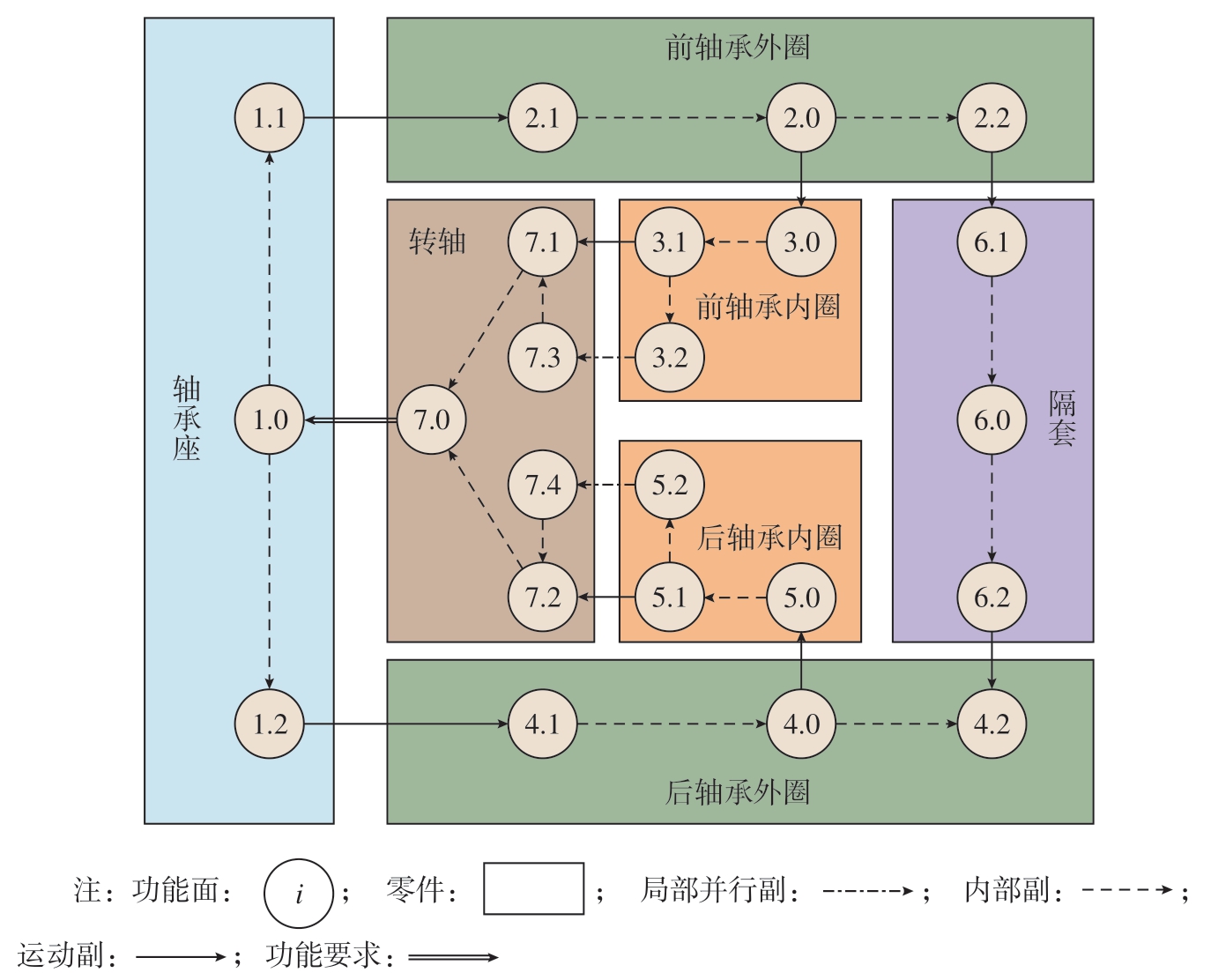
图8 装配连接关系图
Fig.8 Connection diagram of assembly
由 图8（其 中，1.0、2.0、3.0、4.0、5.0、6.0、7.0 分别为轴承座、前轴承外圈、前轴承内圈、后轴承外圈、后轴承内圈、隔圈和转轴的零件基准）所示的装配连接关系图可以看出，在忽略隔圈和轴承外圈接触的情况下可以得到2 条误差传递路径：路径1（1.0→1.1→2.1→2.0→3.0→3.1→7.1→7.0）和路径2（1.0→1.2→4.1→4.0→5.0→5.1→7.2→7.0）。每条路径都可以认为是一条包含局部并行连接（3.1→3.2→7.3→7.1/5.1→5.2→7.4→7.2）的局部并行链，并共同组成了混合链。然而由于存在隔圈的影响，2 条原本独立的误差传递路径产生了相互作用并耦合在一起，即完全并行连接。隔圈和前轴承接触产生的误差将不仅沿着路径1 传递，也会影响路径2。同理，路径2 也会影响路径1。在实际工程中，主轴的轴承常常成对配置并使用多组隔圈进行定位，这使得耦合关系更加紧密。因此，主轴内的各零部件相对位姿是一个相互协调的过程，对于包含完全并行连接关系的主轴，仅仅依靠传统的串行链中的单向累积误差传递计算则无法准确计算其装配精度。本文基于肤面模型的公差模型，提出使用优化的方法来计算完全并行连接装配体的装配精度。
对于一个含有完全并行连接的装配体，设其有n 个零件和m 组配合面，每组配合面大小形状完全一致（名义表面）但分属于2 个不同的零件，分别记为
和
和
是对应配合面肤面模型形状的点云集合，其中，λj 表示第j 个肤面的点的个数。每个零件装配后的位姿都可以使用相对于名义位置的齐次坐标变换矩阵Ts（s =1，2，…，n）表示，其中，s为零件索引角标。由于完全并行链内部的相互作用，因此使用整体优化的方法求解装配后各零件的相对位姿。将完全并行连接副上所有零件的位姿作为变量，求解使得装配后所有肤面模型形状配合面均处于距离最小的装配位姿，从而达到整体最优的装配情况。其中，目标函数为所有零件配合面肤面模型对应点距离之和，约束条件为避免配合面干涉，即有符号的法向投影距离≥0。该优化问题可以表达为如下数学形式。
式中，X=（T1，T2，…，Tn）为所有待求零件空间位姿的齐次坐标变换矩阵组成的优化变量。
对于精密主轴而言，其零部件按照运动与否可以分为定子和转子。以图7 主轴为例，其定子部分由轴承座、轴承外圈和隔圈组成，转子部分则包含转轴和轴承内圈。由于主轴的装配功能要求（Assembly functional requirement，AFR）为回转误差，而主轴的回转误差则是由定子的安装误差和转子的回转运动误差共同造成的。因此在计算过程中，对定子和转子分别进行计算，从而得到旋转一周的误差。首先对定子的装配进行分析，由于在主轴旋转过程中定子保持静止，因此可以以轴承座为基准，使用式（9）直接计算得到定子各个零件的空间位姿，进而得到轴承外圈的安装误差。而转子的误差计算则更加复杂，由于旋转运动的原因，需要将转子的计算离散为多个旋转相位角进行分别计算。转子首先受到外圈安装误差的影响，在初始相位下会偏离其名义位置。其次，由于转子还受到轴承回转误差的影响，在旋转过程中的每个相位角均会产生不同程度的运动误差。因此对于转子每个相位角的计算，都需要综合考虑轴承外圈安装误差和轴承回转误差的影响，因而转子误差计算的数学表达式为
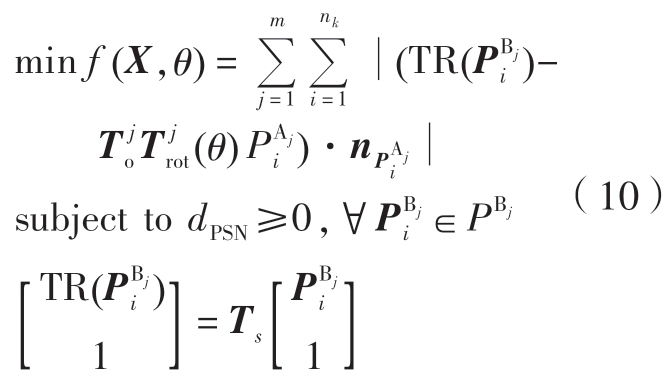
对于轴承内圈而言，
为定子计算中得到的对应轴承外圈安装误差，而对于转子其他零件的配合面而言，
为单位矩阵；同理对于轴承内圈特征面而言，
为轴承在转角θ处的回转误差矩阵，而对于非轴承内圈特征面则为单位矩阵。对转子在每个旋转角度（θ）分别求解式（10），便可以得到一系列不同旋转角度下主轴的回转轨迹点，进而可以得到回转误差的大小。以图7 所示的主轴为例，其回转精度分析流程如图9所示。首先根据式（9）计算得到定子部分（零件1、2、4 和6）各个零部件的装配位姿，从而得到前后轴承外圈的安装误差位姿矩阵T2 和T4。对于转子的计算，先将主轴旋转一圈离散为ε 个相位，则转角θ 满足：θ（k）=2π（k–1）/ε。而后根据式（10）分别计算出各个旋转角度下的转轴位姿，即可得到主轴的回转轨迹。
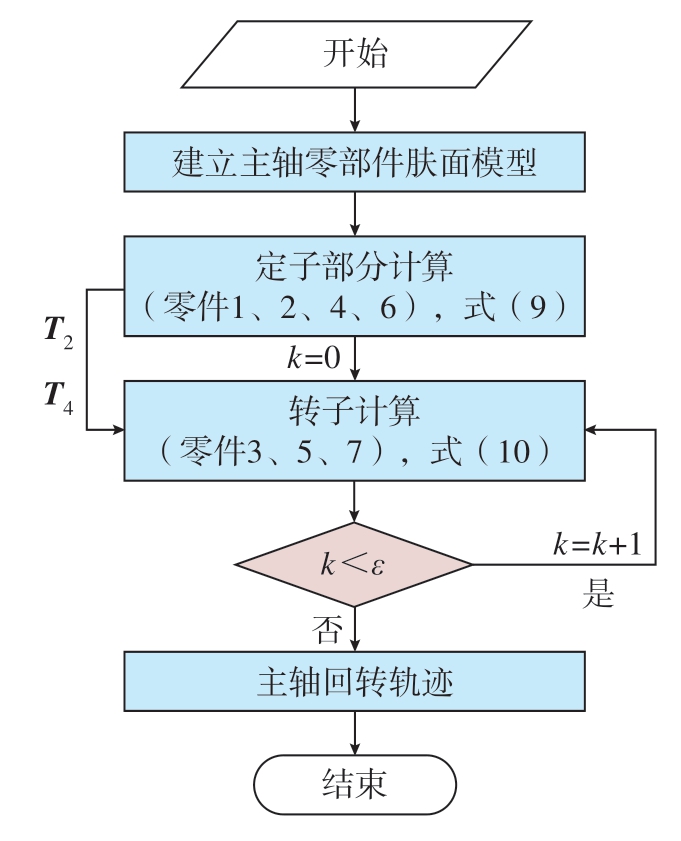
图9 主轴回转精度分析流程图
Fig.9 Flow chart of the spindle rotation accuracy analysis
4 案例研究
4.1 主轴回转精度仿真分析
磨削主轴是数控机床制造高/低压压气机叶片及其他航空零件的核心基础部件，其回转精度控制对于保障航空器性能至关重要，典型磨削电主轴在低速空载工况下的径向回转精度一般小于10 μm，轴向窜动一般小于2 μm[32]。选用秦川机床工具集团股份公司某型磨削电主轴进行公差分析，主轴基本结构如图10 所示（部分不影响精度分析的结构已略去）。该主轴的轴承配置为前4 后2，分别安装在前后轴承座上，轴承之间使用隔圈和锁紧螺母进行轴向定位。图11 给出了该型主轴零件的相关公差标注信息；其中，A～H 对应零件见表 2。
图10 主轴结构
Fig.10 Structure of the spindle
图11 零件公差标注（μm）
Fig.11 Tolerance dimensioning of the component (μm)
由于磨削主轴此类机械产品结构的复杂性，导致其公差大小往往完全依赖于设计人员的经验，这使得在主轴的研发过程中需要反复经历“设计–加工–调整”的过程，增加了企业产品开发和制造的成本。而公差分析可以在设计阶段就提前获知产品的最终精度性能，能够有效解决该问题。基于所提出的公差建模和误差传递计算方法，使用蒙特卡洛方法对主轴回转精度进行分析。主要流程：首先随机生成Q 组肤面模型形状，其次使用优化方法分别求解每组肤面模型形状定子和转子的装配误差，从而得到Q 组回转误差数据，最终得到主轴回转精度的公差值，蒙特卡洛公差分析的流程如图12 所示。
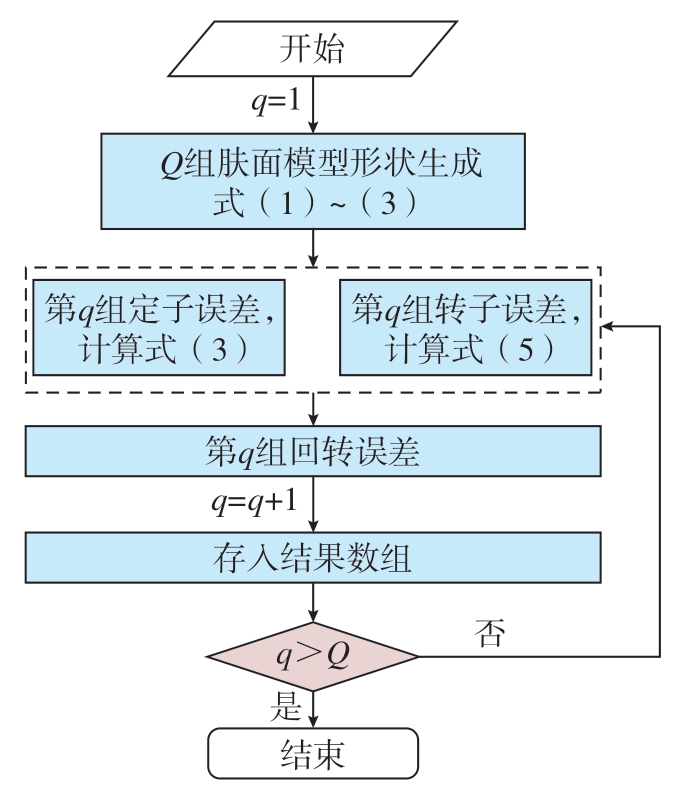
图12 蒙特卡洛公差分析流程图
Fig.12 Flow chart of the tolerance analysis based on Monte-Carlo method
使用蒙特卡洛方法在表2 给定的设计公差下对该型磨削主轴进行精度分析，仿真结果如图13 所示。径向跳动误差符合正态分布，均值μ=3.2，标准差σ =1.2。计算得到主轴的径向跳动公差为2.34 μm，同理可得轴向窜动公差为2.14 μm。
表2 零件公差值
Table 2 Tolerance value of components
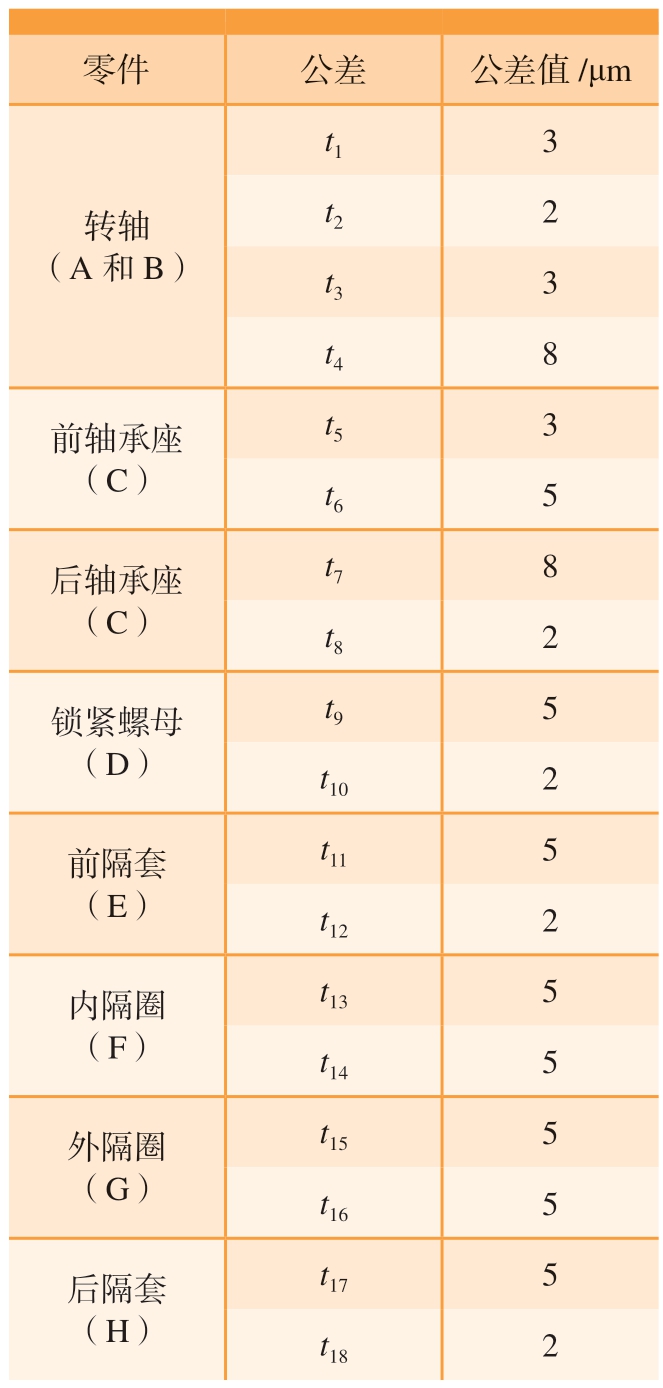
零件 公差 公差值/μm转轴（A 和B）t1 3 t2 2 t3 3 t4 8前轴承座（C）t5 3 t6 5后轴承座（C）t7 8 t8 2锁紧螺母（D）t9 5 t10 2前隔套（E）t11 5 t12 2内隔圈（F）t13 5 t14 5外隔圈（G）t15 5 t16 5后隔套（H）t17 5 t18 2
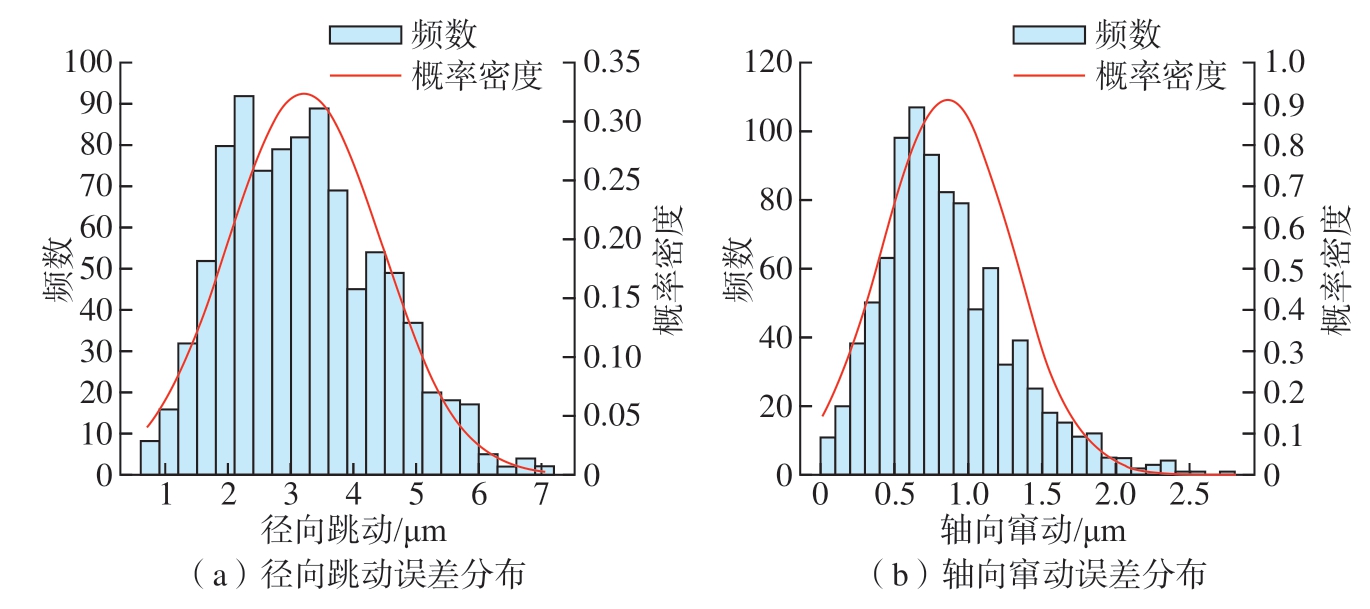
图13 蒙特卡洛仿真结果
Fig.13 Result of the Monte-Carlo simulation
4.2 试验验证
为了验证公差分析结果的合理性，选取同一批次的7 根主轴进行测量。以径向跳动的测量为例，具体方法：将标准棒装夹于主轴前端，千分表通过表架固定于轴承座上，使用千分表获取主轴的径向跳动。测量过程中缓慢旋转主轴，记录主轴转动一周过程中千分表的示数，示数变化范围即为径向跳动值。如此依次测量7 根主轴的径向跳动值，测量结果如表3 所示。该批次7 根主轴的径向跳动和轴向窜动值均位于公差分析区间内，且径向跳动和轴向窜动的均值分别为2.34 μm 和1.21 μm，均与公差分析结果接近，证明了所提出方法的有效性。
表3 径向跳动和轴向窜动测量结果
Table 3 Measurement results of radial runout and axial movement μm
类别 主轴1 主轴2 主轴3 主轴4 主轴5 主轴6 主轴7径向跳动 2.3 2.0 2.1 2.0 2.5 3.0 2.5轴向窜动 1.0 1.3 1.2 1.2 1.2 1.3 1.3
4.3 关键误差敏感度分析
该型主轴径向跳动的设计值是4 μm，而从图13 的分析结果可知，该型主轴的径向跳动精度合格率仅为74.3%，说明零件设计公差存在不合理之处，需要进一步改进。在设计阶段，通过误差敏感度分析可以评估产品设计中各个组件的尺寸和几何公差对最终产品性能或功能的影响程度。进行此类分析的一个常用方法是计算敏感度系数，该系数通常可通过偏导数或差分方法确定，以揭示装配误差与形位误差之间的关联。由于本文所采用的基于优化的计算方法难以获得敏感度系数的解析解，因而本节采用差分方法进行误差敏感度分析。
对于装配体中的一项形位误差t 而言，通过装配误差建模，最终的装配偏差可以被表示为t 的函数即f（t）。在本文中，f（t）的输出可以通过式（10）得到。选择一个小的变化量Δt，计算f（t +Δt），即改变输入误差后计算模型输出的装配误差。敏感度系数可以通过变化量除以Δt来近似得到
式中，sc 为计算得到的近似敏感度系数。使用上述分析方法，对该型主轴前后轴承座的同轴度（t7）和转轴前后轴承安装圆柱面的同轴度（t4）进行敏感度分析。选取Δt 在1～9 μm的区间内，计算径向跳动与对应误差项之间的关系，结果如图14 所示，曲线的斜率即为对应点处敏感度系数。由图14 可知，转轴同轴度对主轴径向跳动影响很大而前后轴承座同轴度影响则相对较小。因而将t4公差值更改为3 μm 并保持其他公差不变，重新进行蒙特卡洛仿真分析，得到的公差分析结果如图15 所示，可知，主轴径向跳动的精度合格率上升至88.2%，有效提高了产品合格率。
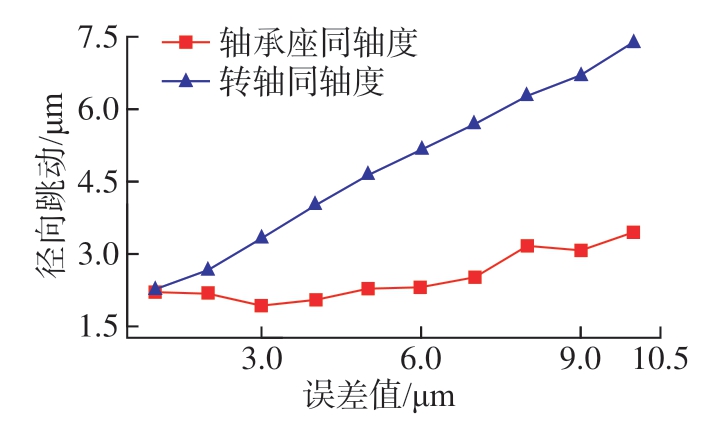
图14 同轴度对径向跳动的影响
Fig.14 Influence of coaxiality on radial runout
图15 优化主轴公差后的蒙特卡洛仿真分析结果
Fig.15 Monte-Carlo simulation analysis results after optimizing the spindle tolerance
5 结论
（1）基于肤面模型方法，结合小位移旋量理论建立了零件的全公差模型。所建立的模型能够全面地表征零件定位、定向和形状误差，并通过建立轴承的回转轨迹模型，为主轴的回转精度分析提供全面的误差源表征方法。
（2）针对精密主轴中广泛存在的完全并行连接，提出一种优化方法的误差传递计算方法。该方法基于肤面模型形状表征的误差源模型，使用优化方法求解完全并行连接下的主轴各零部件相对装配定位位姿，有效解决了复杂主轴系统误差耦合难以解算的问题。
（3）将所提出的方法应用于某型磨削主轴的精度分析中，发现该型主轴设计公差的缺陷，通过计算关键公差项的敏感度系数改进了设计参数，从而提高了径向跳动的精度合格率，有效提高了产品的合格率。
[1] HU L, LI Y P, ZHA J, et al.A “double accuracy theory” and experimental research on precision grinding[J].Applied Sciences, 2020,10(6): 2030.
[2] CUI H L, LEI D J, ZHANG X J, et al.Measurement and analysis of the radial motion error of aerostatic ultra-precision spindle[J].Measurement, 2019, 137: 624–635.
[3] NI H, ZHAO W Q, QIU L R.Measurement method of spindle motion error based on composite laser target[J].International Journal of Machine Tools and Manufacture,2022, 174: 103860.
[4] 张华, 郭力.高效精密磨床动静压主轴回转精度的测试研究[J].制造技术与机床, 2020(6): 131–133.
ZHANG Hua, GUO Li.Research on rotation accuracy test of grinding wheel hybrid spindle in high accuracy grinder[J].Manufacturing Technology & Machine Tool,2020(6): 131–133.
[5] HU G F, GAO W G, CHEN Y, et al.An experimental study on the rotational accuracy of variable preload spindle-bearing system[J].Advances in Mechanical Engineering,2018, 10(5): 168781401877617.
[6] FANG C G, HUO D H, HUANG X D.A comprehensive analysis of factors affecting the accuracy of the precision hydrostatic spindle with mid-thrust bearing layout[J].The International Journal of Advanced Manufacturing Technology, 2021, 114(3): 949–967.
[7] 刘壮壮, 韩东.基于小位移旋量的旋翼系统公差建模及分析[J].航空工程进展,2021, 12(3): 144–152.
LIU Zhuangzhuang, HAN Dong.Modeling and analysis of rotor system tolerance based on small displacement torsor[J].Advances in Aeronautical Science and Engineering, 2021,12(3): 144–152.
[8] 戴宏玮, 陈琨, 于慧, 等.雅克比旋量的装配体并联结构公差分析方法研究[J].西安交通大学学报, 2022, 56(5): 156–222.
DAI Hongwei, CHEN Kun, YU Hui, et al.Research on tolerance analysis method of assembly parallel structure based on Jacobian spinor[J].Journal of Xi’an Jiaotong University,2022, 56(5): 156–222.
[9] DING S Y, JIN S, LI Z M, et al.Multistage rotational optimization using unified Jacobian–Torsor model in aero-engine assembly[J].Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2019, 233(1): 251–266.
[10] 丁司懿, 周文波, 毛新华.基于改进雅克比–旋量模型的航空发动机转子–叶片结构装配精度分析[J].航空制造技术,2023, 66(8): 65–77.
DING Siyi, ZHOU Wenbo, MAO Xinhua.Assembly precision analysis for rotor–blade structure of aero-engine based on improved Jacobian–torsor model[J].Aeronautical Manufacturing Technology, 2023, 66(8): 65–77.
[11] LIU Z Y, ZHOU S E, QIU C, et al.Assembly variation analysis of complicated products based on rigid–flexible hybrid vector loop[J].Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2019, 233(10): 2099–2114.
[12] MUJEZINOVIĆ A, DAVIDSON J K, SHAH J J.A new mathematical model for geometric tolerances as applied to rectangular faces[C]//Volume 2A: 27th Design Automation Conference.Pennsylvania: American Society of Mechanical Engineers, 2001: 355–372.
[13] HOMRI L, TEISSANDIER D,BALLU A.Tolerance analysis by polytopes:Taking into account degrees of freedom with cap half-spaces[J].Computer-Aided Design, 2015,62: 112–130.
[14] 刘检华, 张志强, 夏焕雄, 等.考虑表面形貌与受力变形的装配精度分析方法[J].机械工程学报, 2021, 57(3): 207–219.
LIU Jianhua, ZHANG Zhiqiang, XIA Huanxiong, et al.Assembly accuracy analysis with consideration of form defects and surface deformations[J].Journal of Mechanical Engineering, 2021, 57(3): 207–219.
[15] HUANG Q, WEI K.Modeling and analysis on the rotation accuracy of lathe spindle[J].Advanced Materials Research, 2012,602–604: 1757–1760.
[16] GUO J K, HONG J, YANG Z H, et al.A tolerance analysis method for rotating machinery[J].Procedia CIRP, 2013, 10: 77–83.
[17] 孙岩辉, 洪军, 刘志刚, 等.考虑零部件制造误差的精密主轴几何回转精度计算方法[J].机械工程学报, 2017, 53(3):173–182.
SUN Yanhui, HONG Jun, LIU Zhigang,et al.A calculating method for the geometric rotation accuracy of precision spindles considering the manufacturing errors of component parts[J].Journal of Mechanical Engineering, 2017, 53(3): 173–182.
[18] ANWER N, BALLU A, MATHIEU L.The skin model, a comprehensive geometric model for engineering design[J].CIRP Annals,2013, 62(1): 143–146.
[19] AFJEHI-SADAT A, NOMAK A.Dimensional and geometrical measurements and interpretation of measuring results on the basis of the skin-model[J].Measurement Science Review, 2001, 1(1): 89–92.
[20] SCHLEICH B, ANWER N,MATHIEU L, et al.Skin Model Shapes: A new paradigm shift for geometric variations modelling in mechanical engineering[J].Computer-Aided Design, 2014, 50: 1–15.
[21] SAMPER S, ADRAGNA P A,FAVRELIERE H, et al.Modeling of 2D and 3D assemblies taking into account form errors of plane surfaces[J].Journal of Computing and Information Science in Engineering, 2009,9(4): 1.
[22] BESL P J, MCKAY N D.A method for registration of 3-D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992, 14(2): 239–256.
[23] FLÖRY S, HOFER M.Surface fitting and registration of point clouds using approximations of the unsigned distance function[J].Computer Aided Geometric Design,2010, 27(1): 60–77.
[24] ZHAO G, LI J Y, ZHANG B, et al.An aero-engine assembly deviation analysis method based on skin model shapes[M]//DING H F, ed.Aerospace Mechatronics and Control Technology.Singapore: Springer Nature Singapore, 2022: 78–89.
[25] WANG K, LIU D X, LIU Z Y, et al.An assembly precision analysis method based on a general part digital twin model[J].Robotics and Computer-Integrated Manufacturing, 2021,68: 102089.
[26] YI Y, LIU T Y, YAN Y H, et al.A novel assembly tolerance analysis method considering form errors and partial parallel connections[J].The International Journal of Advanced Manufacturing Technology, 2024,131(11): 5489–5510.
[27] YAN X Y, BALLU A.Review and comparison of form error simulation methods for computer-aided tolerancing[J].Journal of Computing and Information Science in Engineering, 2019, 19(1): 010802.
[28] ZHANG T Y, ZHANG Z J, JIN X,et al.An innovative method of modeling plane geometric form errors for precision assembly[J].Proceedings of the Institution of Mechanical Engineers, Part B.Journal of Engineering Manufacture, 2016, 230(6): 1087–1096.
[29] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会.滚动轴承 通用技术规则: GB/T 307.3—2017[S].北京: 中国标准出版社, 2017.
General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration.Rolling bearings—General technical regulations: GB/T 307.3—2017[S].Beijing: Standards Press of China, 2017.
[30] SCHLEICH B, WARTZACK S.Novel approaches for the assembly simulation of rigid skin model shapes in tolerance analysis[J].Computer-Aided Design, 2018, 101: 1–11.
[31] JIN S, DING S Y, LI Z M, et al.Pointbased solution using Jacobian-Torsor theory into partial parallel chains for revolving components assembly[J].Journal of Manufacturing Systems,2018, 46: 46–58.
[32] 丁浩, 王鹏武, 刘保国, 等.磨削电主轴动态回转精度分析及实验[J].机床与液压, 2022, 50(21): 114–119.
DING Hao, WANG Pengwu, LIU Baoguo,et al.Analysis and experimental study on dynamic rotation accuracy of grinding motorized spindle[J].Machine Tool & Hydraulics, 2022,50(21): 114–119.
