飞机大部件对接技术难度大、涉及学科领域多，很大程度上决定了飞机装配最终质量和制造周期[1]。飞机机身对接是大部件对接的典型环节，使用柔性工装进行位姿调整，通过测量系统对测量点坐标进行位姿计算，根据计算结果使用控制系统驱动机构运动。机身对接过程中的变形会使对接测量点产生偏移，难以快速准确入位，需要反复测量、多次调整位姿，直至完成对接，导致对接效率较低。
虚实相映、以虚控实是数字孪生的主要思想，虚实融合更强调物理系统与信息系统之间的实时交互，可以将现场实测数据引入虚拟模型中，通过实时数据驱动转化为操作指令，调控物理实体实现在线仿真[2–4]。数据驱动是数字空间虚拟模型控制物理实体的传输通道，很多新型的数据驱动方法近年来被提出，比如面向对象的动态数据驱动[5]和基于并联长短期记忆的网络处理[6]。具有多层次的三维可视化监控虚拟车间[7]和基于Unity3D 建立的数字化车间[8]实现了车间全流程、全要素的动态监控。黄华等[9]使用了智能优化算法更新模型做到参数同步。Stojanovic等[10]提出一种面向多维海量数据的大数据分析方法，对生产流程状态进行预测。目前在机身对接仿真的研究中，主要利用理论模型进行运动过程仿真，将机身视为刚体，难以体现实际对接过程中的机身变形，同时将虚实融合技术应用于机身对接仿真的研究较少。
有限元仿真技术广泛应用于变形计算，但会耗费大量计算时间与资源，利用代理模型技术[11]可快速计算得到变形数据。目前代理模型在不同场景中被应用，Jiang 等[12]使用有限元法和Kriging 模型进行不锈钢316L 的激光焊接工艺参数优化；Gaspar 等[13]提出了一种主动优化的自适应Kriging 代理模型，来解决随机变量的结构可靠性问题；Zhang等[14]基于折叠正态分布的主动学习函数，对自适应截断采样区域进行有效主动学习迭代；南凯刚等[15]利用多元线性回归多项式构建代理模型，并利用代理模型进行装配精度预测。综上所述，仿真计算可以预测机身对接中的变形情况，从而进行调整和补偿，代理模型可以提升仿真数据的计算速度，如果应用在机身对接中，可以减少对接过程中测量和调姿频次，提高对接效率。
本文以机身对接过程为研究对象，搭建机身对接仿真环境，实现仿真计算结果与仿真环境、仿真计算结果与实际调姿机构的实时数据传输，进行数据驱动的机身对接过程仿真；建立机身有限元模型从而得到机身变形值数据，将数据作为输入以构建Kriging 代理模型并验证有效性；最后开发了机身对接过程仿真系统，根据机身对接实例进行验证。
1 飞机机身对接仿真
1.1 运动学模型构建
机身对接过程采用六自由度平台作为机身调姿工装，如图1 所示。该平台结构主要包括上平台、下平台（基座）、电动缸、伺服电机等，在运行时通过改变6 个电动缸推杆的长度来控制上平台产生不同位置和姿态，以此带动机身完成对接过程。
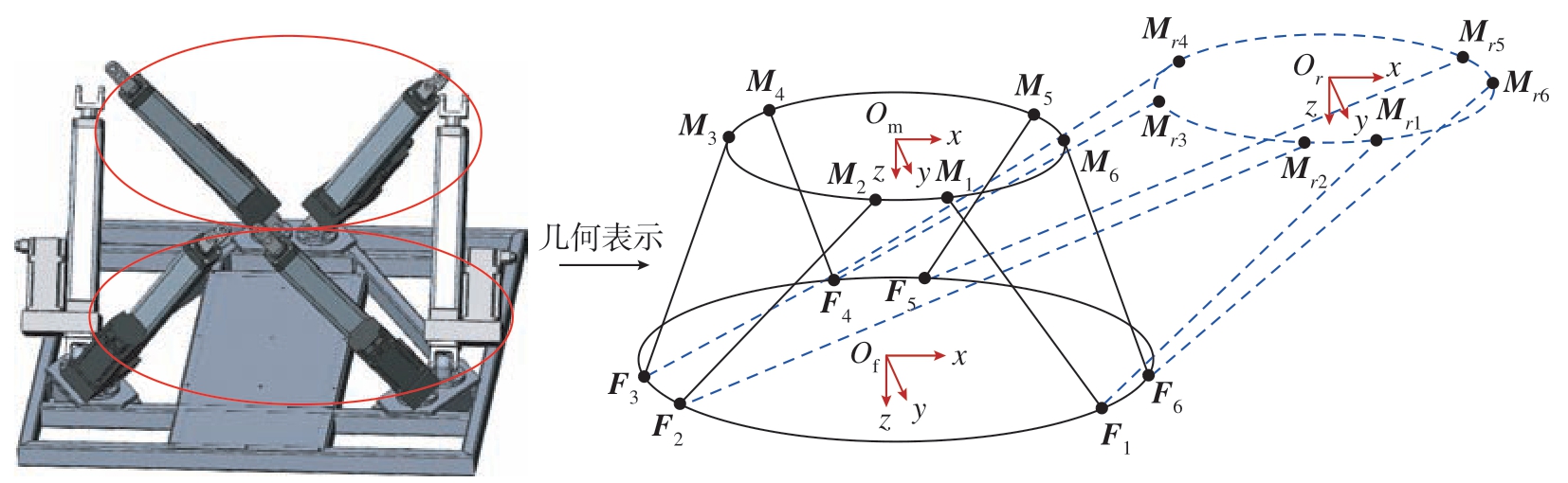
图1 六自由度平台坐标系变换示意图
Fig.1 Schematic diagram of coordinate system transformation for a six-degree of freedom platform
在已知调姿前和调姿后上平台位姿的条件下，由式（1）可以得到上平台初始坐标系{Om}相对于下平台坐标系{Of}的初始旋转矩阵Rm 与平移矩阵Tm；上平台移动后坐标系{Or}相对于下平台坐标系{Of}的移动后旋转矩阵Rr 与平移矩阵Tr。
在调姿过程中上平台各铰点相对于上平台坐标系和下平台各铰点相对于下平台坐标系的位置是不变的，其位置矢量表示为
式中，R 为上平台半径；r 为下平台半径；αi 为坐标系{Om}内上平台各铰点与x 轴的夹角；βi 为坐标系{Of}内下平台各铰点与x 轴的夹角。则初始状态与调姿后上平台铰点相对于下平台的位置矢量分别为
因此，六自由度平台初始与调姿后推杆长度L 分别为
则推杆调整量分别为
在六自由度平台驱动机身运动时，机身位姿与上平台位姿不重合，因此需要根据六自由度平台位姿变化量求解其推杆调整量，根据机身位姿相对于上平台位姿的关系，得到其转换关系。
设机身在全局坐标系下位姿为
，上平台在全局坐标系下位姿为
。将两个位姿按照平移量T=（x，y，z）T 与位姿角E=（α，β，γ）T 两个维度进行分析。对位姿平移量变化进行分析，若机身与六自由度平台的平移量变化相同且未发生角度改变，即TC=TM，EC=EM；然后对位姿角度变化情况进行分析，当机身产生旋转变化时，即位姿角EC 改变，此时机身平移量TC 不改变，而上平台位姿角EM 与平移量TM 均发生改变，上平台旋转角变化与机身旋转角变化相同，即EM=EC，可推得平移量变化如式（5）～（7）所示，其中，L1 为机身轴线到六自由度上平台中点的距离，L2 为机身端面到六自由度上平台中点的垂直距离。
由以上分析可知，在进行六自由度平台平移量计算时，需要将机身位姿转化为上平台位姿，转化公式为
。
1.2 数据交互与数据驱动技术
1.2.1 数据交互环境搭建
内部交互分为MATLAB 与MySQL 的 数 据 交 互、MATLAB 与Unity3D 的数据交互和Unity3D 与MySQL 的数据交互；外部交互为虚拟模型与物理实体间的数据交互，具体内容为虚拟模型与双相机测量系统的数据交互和虚拟模型与六自由度平台的数据交互。虚拟模型之间、虚拟模型与物理实体之间的交互关系及其通信协议如图2 所示。
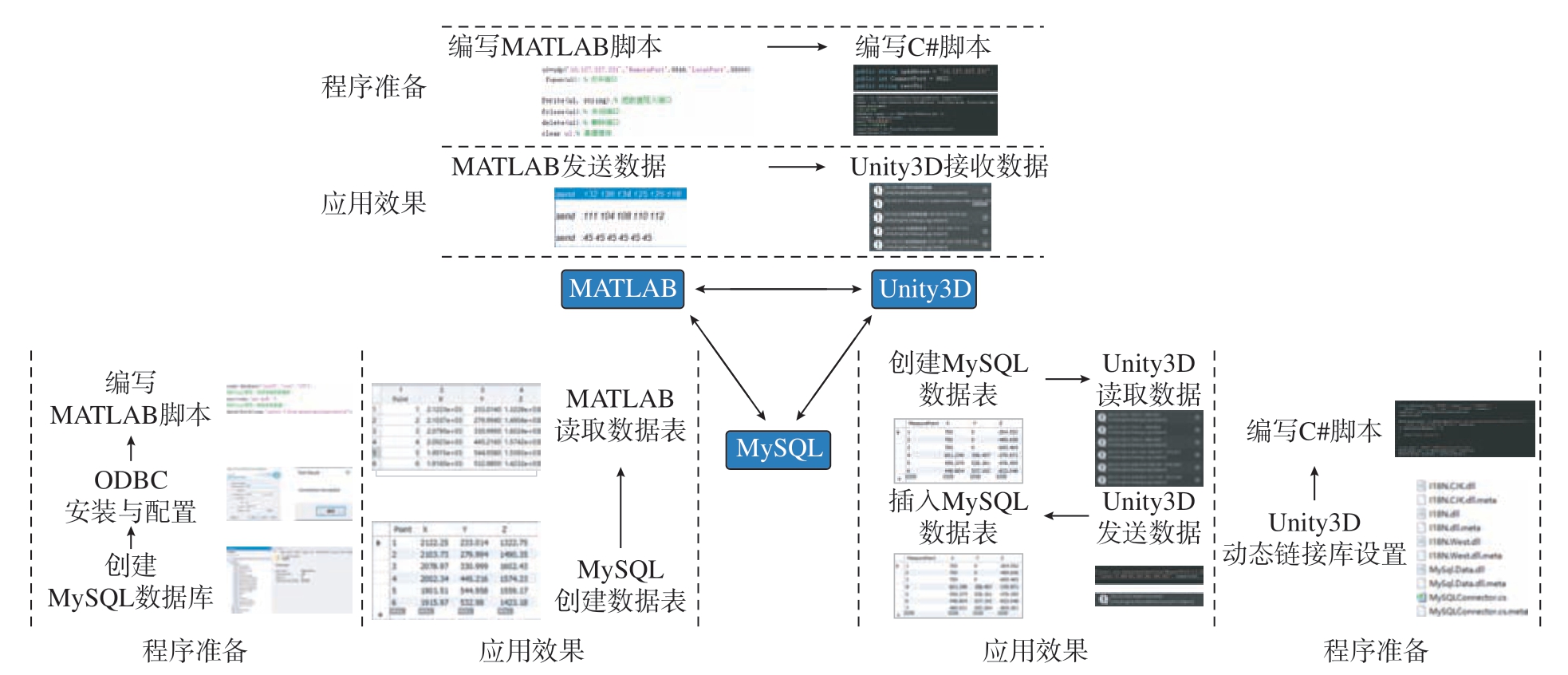
图2 内部交互示意图
Fig.2 Internal interaction diagram
MATLAB 与MySQL 的 数 据 交互采用MATLAB 代码实现数据读取，测试通过后对数据库进行操作；MATLAB 与Unity3D 的数据交互采用IP 地址和端口号实现数据接收和传输；Unity3D 与MySQL 的数据交互在Unity3D 中添加动态链接库建立链接，进行数据库操作。
虚拟模型与物理实体数据交互，使用双相机测量系统获取数据，将测量坐标值数据导入数据库中，然后读取表中数据使实测坐标数据参与仿真系统运算；利用UDP 通信协议将仿真结果传输到六自由度调姿平台，实现数据交互，具体过程如图3 所示。
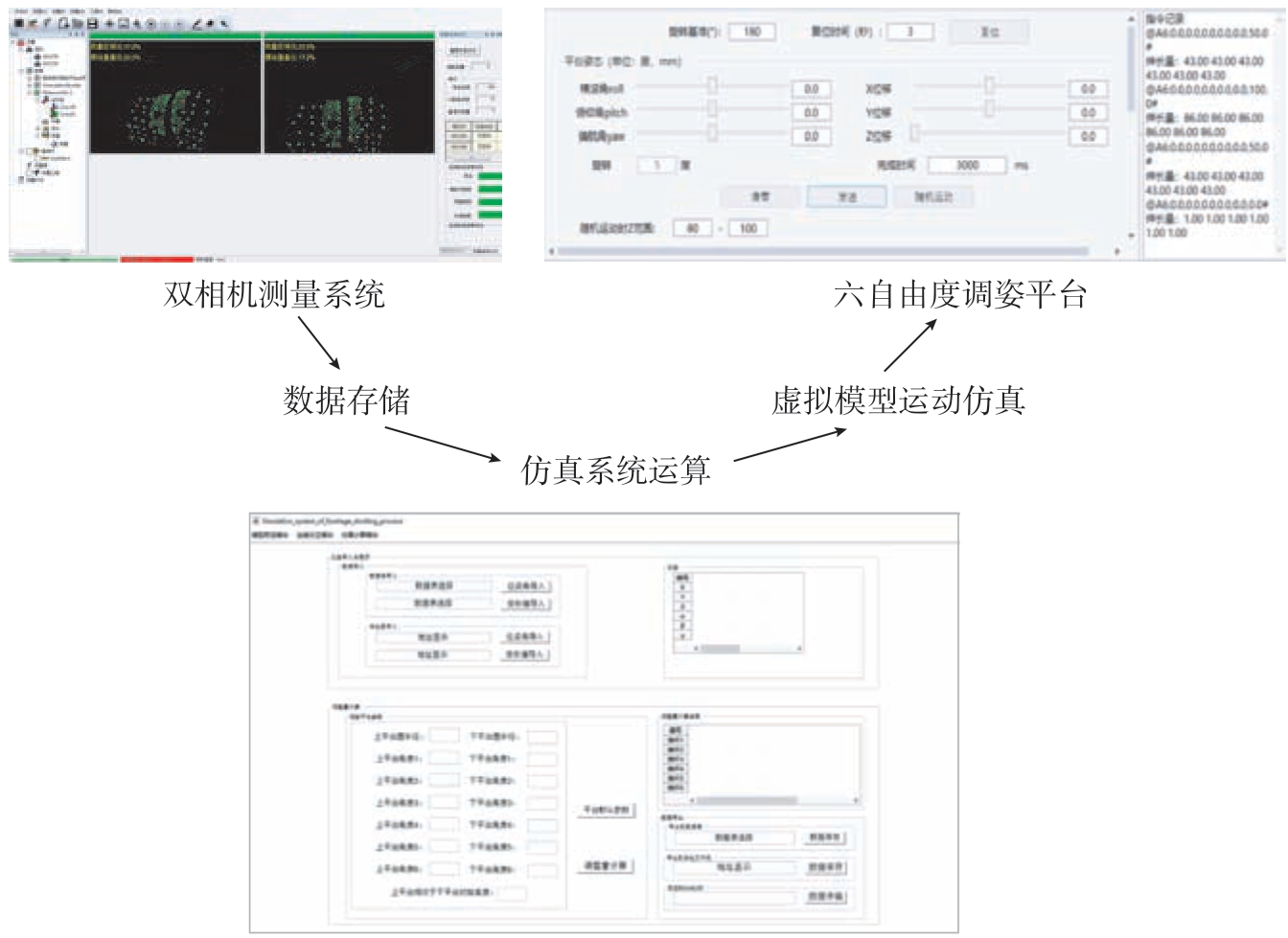
图3 虚拟模型与物理实体交互
Fig.3 Interaction between virtual model and physical entity
1.2.2 数据驱动方法
实现机身对接需要六自由度调姿平台驱动中机身运动完成调姿对接，控制对象为平台6 个推杆。模型导入Unity3D 时，需要进行运动副约束实现机构间的联动。约束完成后在Unity3D 中通过数据驱动虚拟模型进行运动，而要实现运动过程，需先定义Unity3D 中的坐标系及模型位置表达方式。通过控制Position、Rotation 和Scale 3 个属性可实现对象的移动、旋转和缩放。
1.3 机身运动过程仿真
在虚拟模型构建完成后，即可进行机身对接仿真，其过程为“获取机身测量点坐标—机身初始位姿解算—调姿路径规划—调姿平台调整参数计算—虚拟模型对接仿真”；之后虚拟模型将会与实体机身进行数据交互，从而推动实体机身运动。
（1）机身测量点坐标获取与机身初始位姿解算。
要得到机身位姿值需要获取机身测量点分别在全局坐标系和局部坐标系下的坐标值，该坐标值分别由双相机测量系统和虚拟模型获得。本文在中机身与前机身表面各取8个点作为机身测量点，得到中机身、前机身测量点分别在测量坐标系和局部坐标系下的坐标值，如表1 和2所示。
表1 机身测量点在全局坐标系下坐标值
Table 1 Coordinate values of measurement points on the fuselage in the global coordinate system
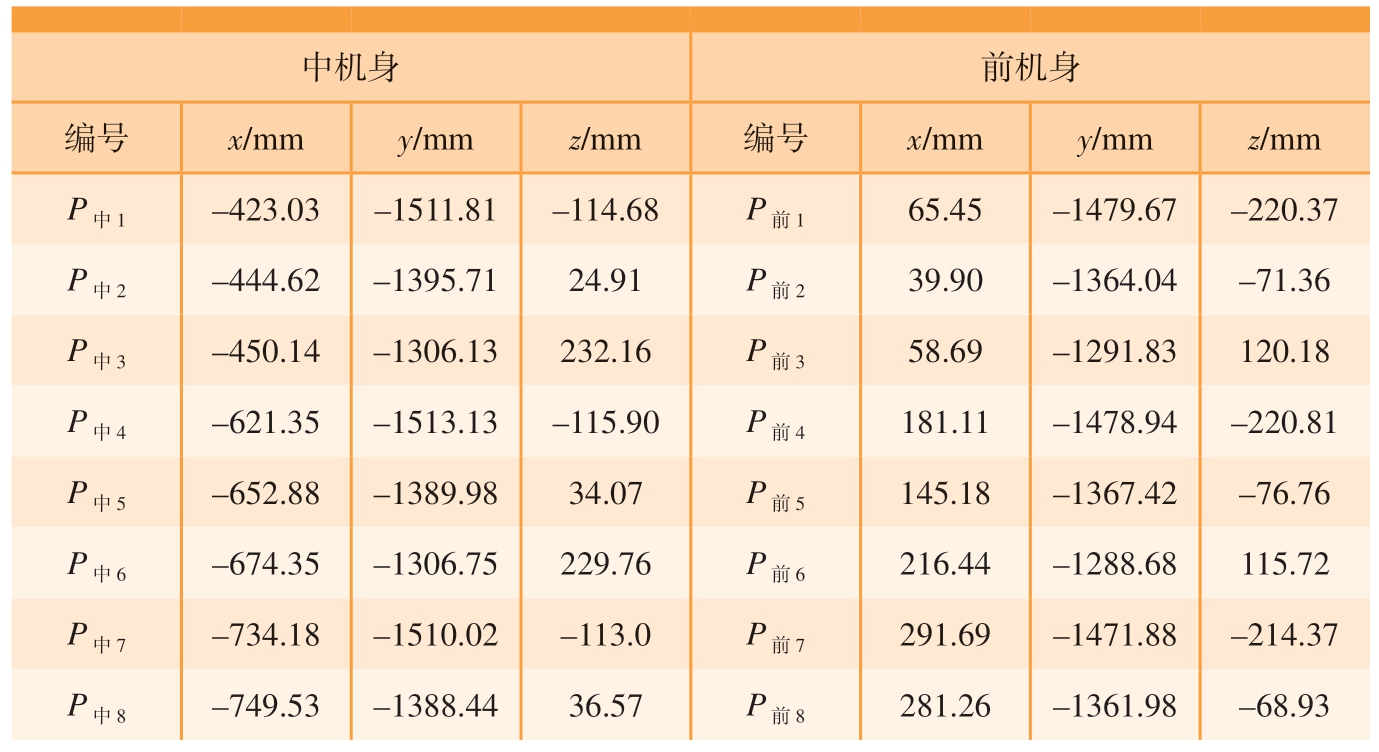
中机身 前机身编号 x/mm y/mm z/mm 编号 x/mm y/mm z/mm P中1 –423.03 –1511.81 –114.68 P前1 65.45 –1479.67 –220.37 P中2 –444.62 –1395.71 24.91 P前2 39.90 –1364.04 –71.36 P中3 –450.14 –1306.13 232.16 P前3 58.69 –1291.83 120.18 P中4 –621.35 –1513.13 –115.90 P前4 181.11 –1478.94 –220.81 P中5 –652.88 –1389.98 34.07 P前5 145.18 –1367.42 –76.76 P中6 –674.35 –1306.75 229.76 P前6 216.44 –1288.68 115.72 P中7 –734.18 –1510.02 –113.0 P前7 291.69 –1471.88 –214.37 P中8 –749.53 –1388.44 36.57 P前8 281.26 –1361.98 –68.93
表2 机身测量点在局部坐标系下坐标值
Table 2 Coordinate values of measurement points on the fuselage in the local coordinate system
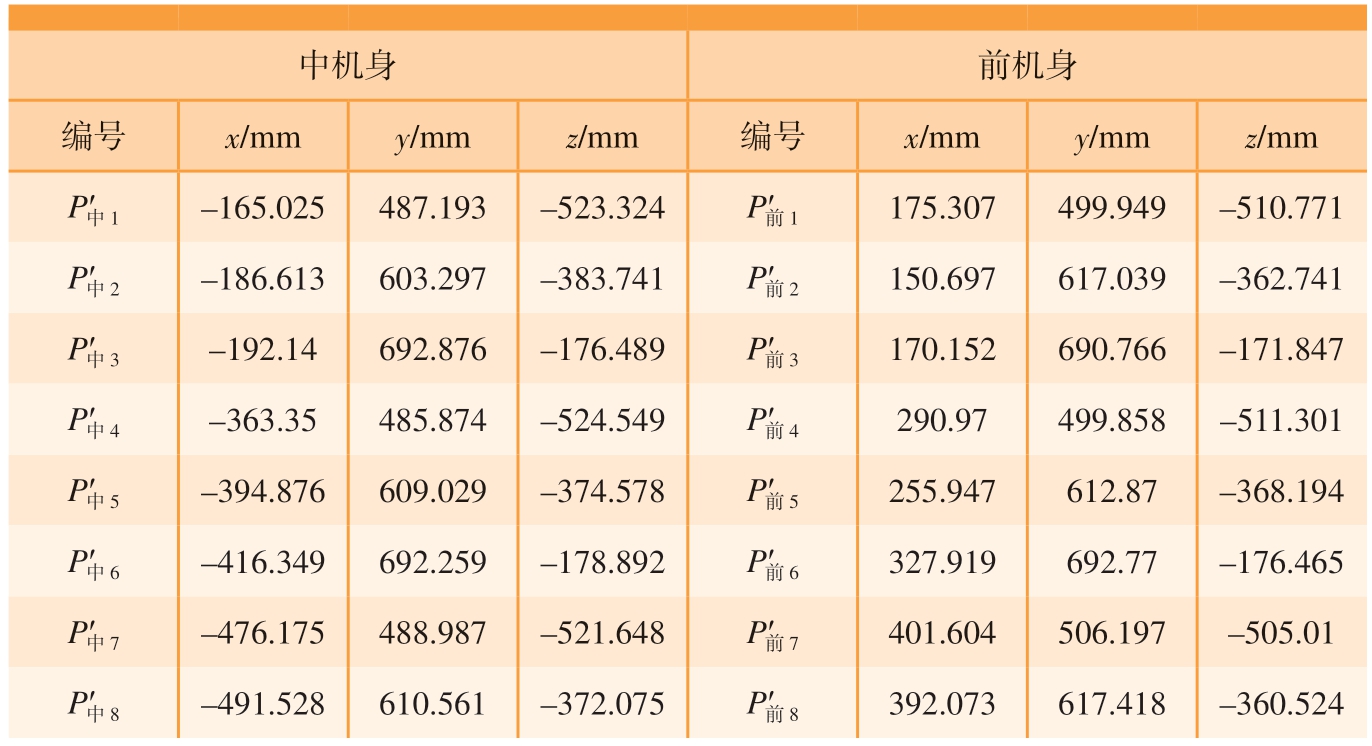
中机身 前机身编号 x/mm y/mm z/mm 编号 x/mm y/mm z/mm P′中1 –165.025 487.193 –523.324 P′前1 175.307 499.949 –510.771 P′中2 –186.613 603.297 –383.741 P′前2 150.697 617.039 –362.741 P′中3 –192.14 692.876 –176.489 P′前3 170.152 690.766 –171.847 P′中4 –363.35 485.874 –524.549 P′前4 290.97 499.858 –511.301 P′中5 –394.876 609.029 –374.578 P′前5 255.947 612.87 –368.194 P′中6 –416.349 692.259 –178.892 P′前6 327.919 692.77 –176.465 P′中7 –476.175 488.987 –521.648 P′前7 401.604 506.197 –505.01 P′中8 –491.528 610.561 –372.075 P′前8 392.073 617.418 –360.524
在得到两机身段的测量点在全局坐标系和局部坐标系下坐标值后，根据位姿解算公式得到相应位姿量。由表1 与2 计算出的中机身和前机身初始位姿如表3 所示。
表3 机身初始位姿
Table 3 Initial pose of the fuselage
位姿参数 中机身 前机身x/mm –258.001 –114.470 y/mm –1999.005 –1975.017 z/mm 408.648 296.584 α/（°） 0 –0.52 β/（°） 0 0.06 γ/（°） 0 –0.4
（2）调姿路径规划。
以中机身为移动端，前机身为固定端，六自由度平台为调姿机构，通过固定工装与机身连接，表2 中以前机身的初始位姿作为中机身的目标位姿，根据得到的初始位姿和目标位姿，结合本文六自由度平台尺寸参数进行调姿路径规划，确定机身中间位姿。每次调姿需要先将平台向上移动50 mm，在对接过程的最后时刻中机身与前机身为插入式对接，为防止调姿时参数输入有误从而产生碰撞或摩擦等损伤工件的情况，在最后插接过程中，本文选择每隔5 mm 左右前进1 次，最终拟定的调姿路径如表4 所示。
表4 机身调整过程位姿
Table 4 Pose during fuselage adjustment process
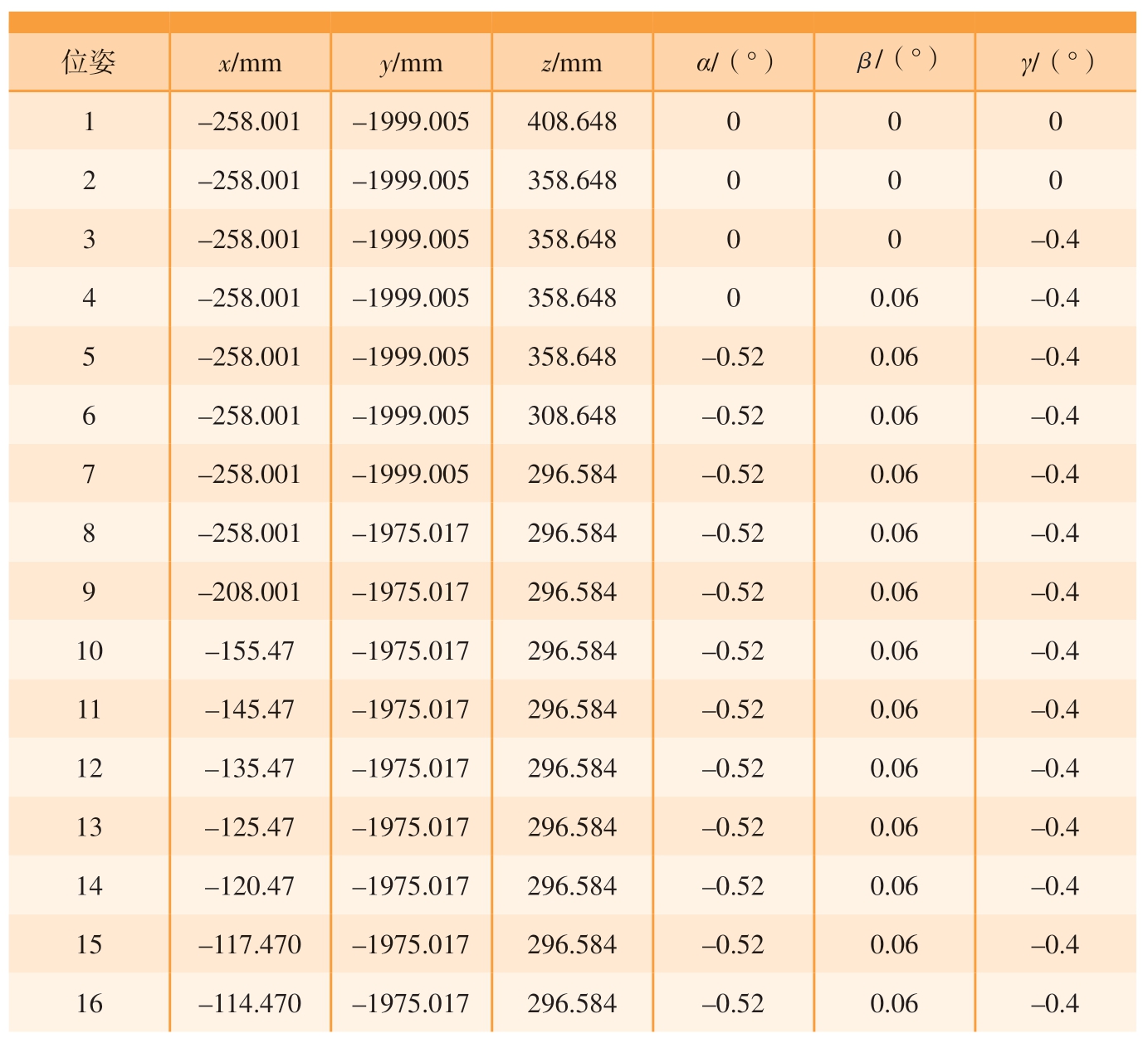
位姿 x/mm y/mm z/mm α/（°） β/（°） γ/（°）1 –258.001 –1999.005 408.648 0 0 0 2 –258.001 –1999.005 358.648 0 0 0 3 –258.001 –1999.005 358.648 0 0 –0.4 4 –258.001 –1999.005 358.648 0 0.06 –0.4 5 –258.001 –1999.005 358.648 –0.52 0.06 –0.4 6 –258.001 –1999.005 308.648 –0.52 0.06 –0.4 7 –258.001 –1999.005 296.584 –0.52 0.06 –0.4 8 –258.001 –1975.017 296.584 –0.52 0.06 –0.4 9 –208.001 –1975.017 296.584 –0.52 0.06 –0.4 10 –155.47 –1975.017 296.584 –0.52 0.06 –0.4 11 –145.47 –1975.017 296.584 –0.52 0.06 –0.4 12 –135.47 –1975.017 296.584 –0.52 0.06 –0.4 13 –125.47 –1975.017 296.584 –0.52 0.06 –0.4 14 –120.47 –1975.017 296.584 –0.52 0.06 –0.4 15 –117.470 –1975.017 296.584 –0.52 0.06 –0.4 16 –114.470 –1975.017 296.584 –0.52 0.06 –0.4
（3）六自由度平台调整参数计算。
六自由度平台通过6 个电动缸推杆的变化推动上平台运动，进而带动中机身运动，因此需要根据机身位姿变化计算出六自由度平台各推杆伸长量。在计算时首先需要将表4 中机身理论位姿按式（5）～（7）转化为六自由度平台的上平台位姿，转化结果如表5 所示，根据式（1）～（4）计算出在各个位姿状态下六自由度平台各个推杆的调整量如表6所示。
表5 六自由度平台理论位姿
Table 5 Theoretical poses of a six-degree of freedom platform
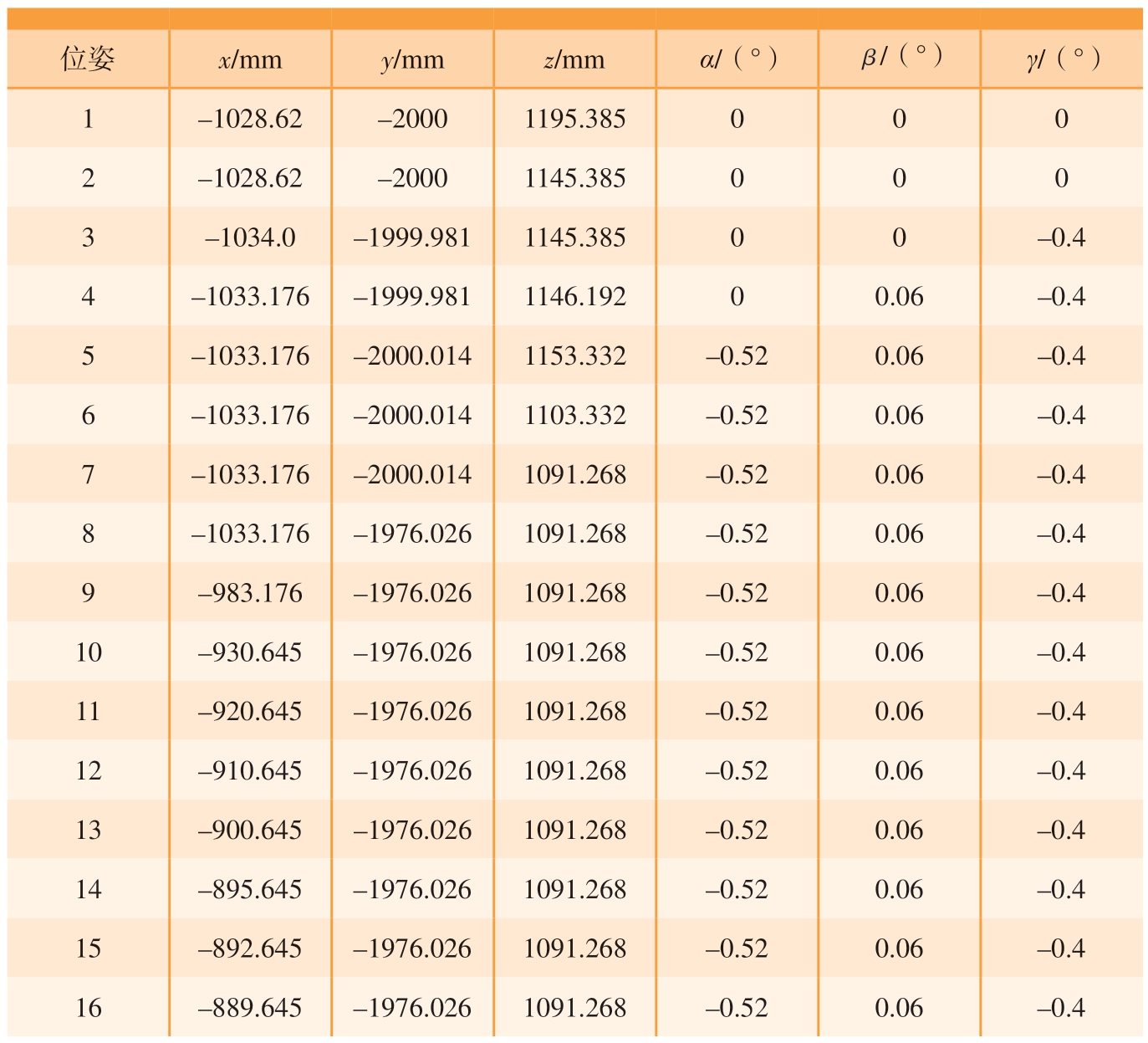
位姿 x/mm y/mm z/mm α/（°） β/（°） γ/（°）1 –1028.62 –2000 1195.385 0 0 0 2 –1028.62 –2000 1145.385 0 0 0 3 –1034.0 –1999.981 1145.385 0 0 –0.4 4 –1033.176 –1999.981 1146.192 0 0.06 –0.4 5 –1033.176 –2000.014 1153.332 –0.52 0.06 –0.4 6 –1033.176 –2000.014 1103.332 –0.52 0.06 –0.4 7 –1033.176 –2000.014 1091.268 –0.52 0.06 –0.4 8 –1033.176 –1976.026 1091.268 –0.52 0.06 –0.4 9 –983.176 –1976.026 1091.268 –0.52 0.06 –0.4 10 –930.645 –1976.026 1091.268 –0.52 0.06 –0.4 11 –920.645 –1976.026 1091.268 –0.52 0.06 –0.4 12 –910.645 –1976.026 1091.268 –0.52 0.06 –0.4 13 –900.645 –1976.026 1091.268 –0.52 0.06 –0.4 14 –895.645 –1976.026 1091.268 –0.52 0.06 –0.4 15 –892.645 –1976.026 1091.268 –0.52 0.06 –0.4 16 –889.645 –1976.026 1091.268 –0.52 0.06 –0.4
表6 6 个推杆的调整量
Table 6 Adjustment amount of six push-rods
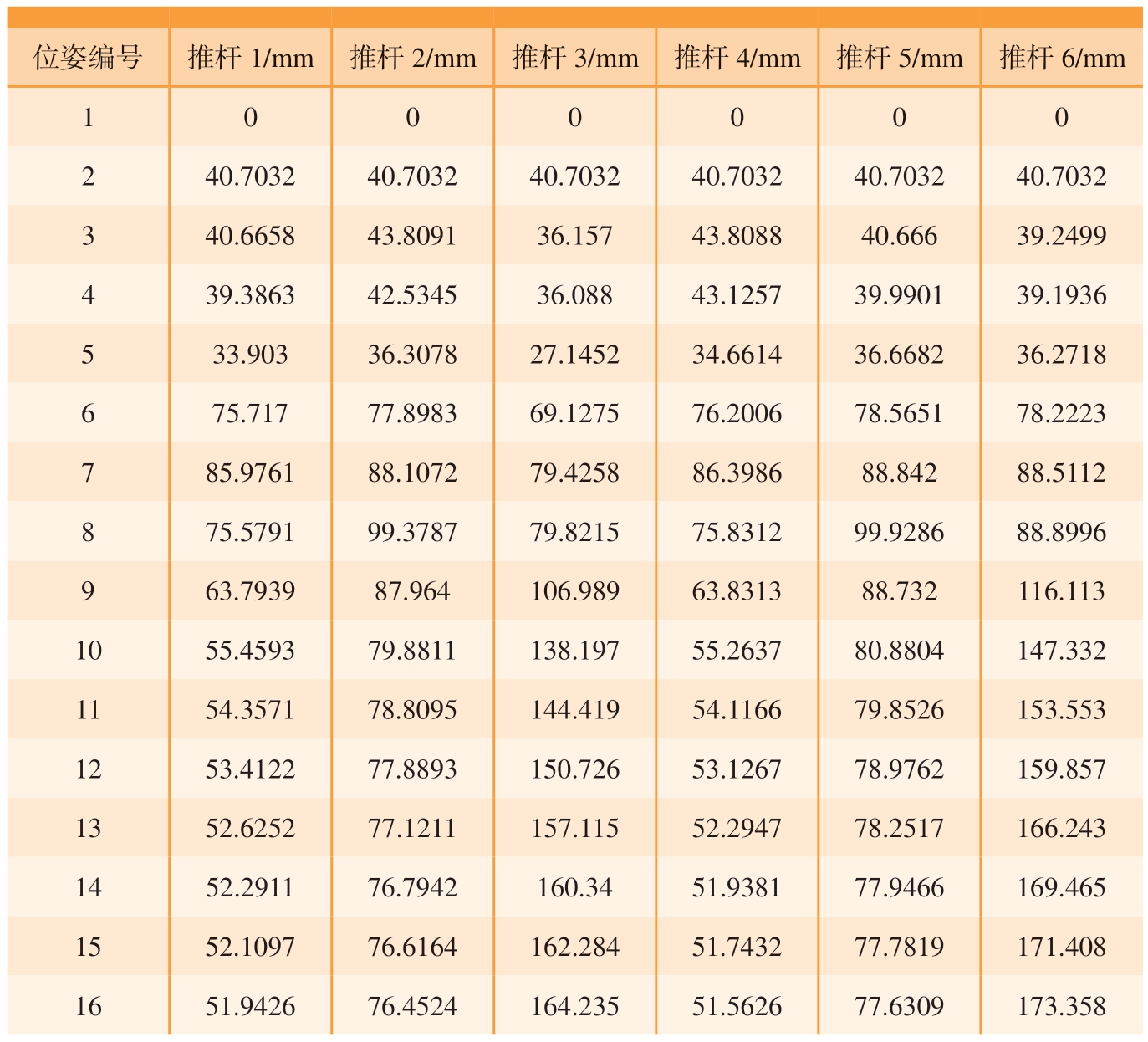
位姿编号 推杆1/mm 推杆2/mm 推杆3/mm 推杆4/mm 推杆5/mm 推杆6/mm 1 0 0 0 0 0 0 2 40.7032 40.7032 40.7032 40.7032 40.7032 40.7032 3 40.6658 43.8091 36.157 43.8088 40.666 39.2499 4 39.3863 42.5345 36.088 43.1257 39.9901 39.1936 5 33.903 36.3078 27.1452 34.6614 36.6682 36.2718 6 75.717 77.8983 69.1275 76.2006 78.5651 78.2223 7 85.9761 88.1072 79.4258 86.3986 88.842 88.5112 8 75.5791 99.3787 79.8215 75.8312 99.9286 88.8996 9 63.7939 87.964 106.989 63.8313 88.732 116.113 10 55.4593 79.8811 138.197 55.2637 80.8804 147.332 11 54.3571 78.8095 144.419 54.1166 79.8526 153.553 12 53.4122 77.8893 150.726 53.1267 78.9762 159.857 13 52.6252 77.1211 157.115 52.2947 78.2517 166.243 14 52.2911 76.7942 160.34 51.9381 77.9466 169.465 15 52.1097 76.6164 162.284 51.7432 77.7819 171.408 16 51.9426 76.4524 164.235 51.5626 77.6309 173.358
（4）虚拟模型对接仿真。
得到调姿平台各推杆伸长量后，将其输入到虚拟模型中驱动虚拟模型进行机身对接运动仿真，其中每1 组6 个推杆的伸长量都对应1 个机身状态，图4 为虚拟模型分别处于位姿1、6、11、16 的机身状态，可见构建的虚拟模型可以由数据驱动进行相应运动，且运动趋势符合需求。
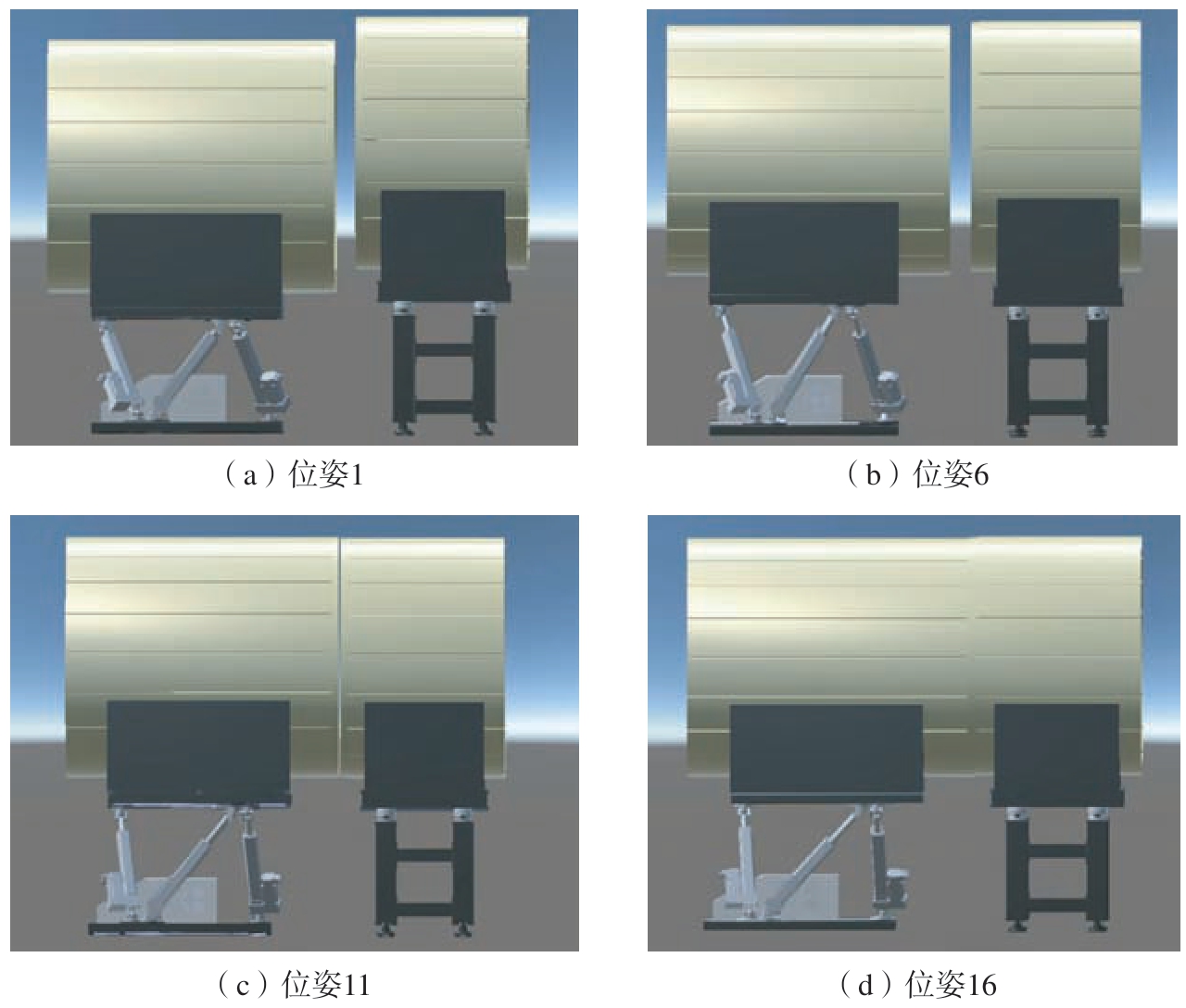
图4 虚拟模型状态变化
Fig.4 Virtual model state changes
2 基于Kriging 代理模型的机身对接快速计算
2.1 Kriging 模型
Kriging 模型主要由两部分组成：一部分是确定性且具有多项式变化趋势的简单回归模型（Regression model with polynomial trend）；而另一部分则是代表多项式变化趋势周围波动的系统偏离（Systematicdeparture），其一般表达式为
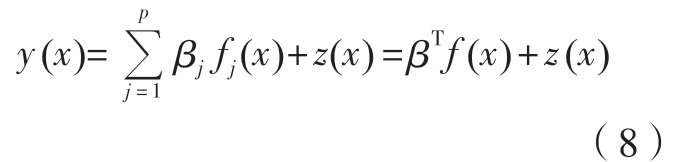
式中，fj（x）为基函数；βj 为基函数系数；z（x）为拟合偏差函数，其均值为0，方差为σ2；任意两点t 和u 的协方差函数定义为
给定相关函数ρ 及样本观察值后，需根据样本观察值确定基函数系数、随机过程方差、相关函数参数的估计值 
、
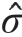2、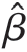
，常用最大似然估计法确定；建立样本观察值的联合概率分布函数p（y），通过该函数值最大化确定参数值大小。
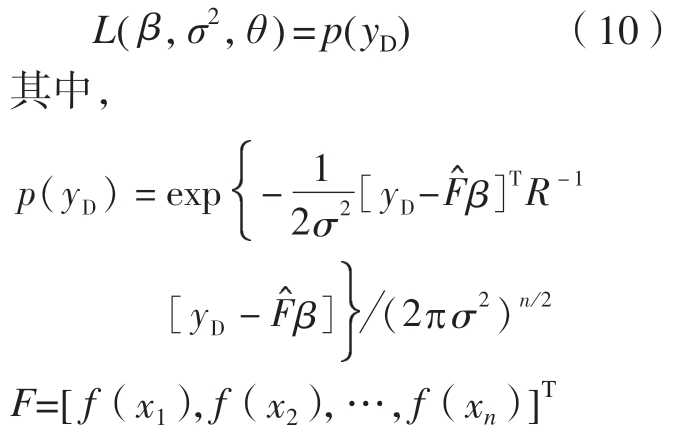
相关系数θ 采用数值求解方法，借助最大似然函数求极值确定其数值大小。记r（x）=[ ρ（x，x1），ρ（x，x2），…，ρ（x，xn）]，则Kriging 模型在任意设计参数样点x 处的响应预测表达式为
2.2 机身有限元模型构建
由于机身筒段具有尺寸大、形状复杂、易变形等特点，对接时通常会因重力、制造误差等原因产生变形，使得测量点实际位置与理论位置出现偏差，机身在横滚和俯仰阶段重力载荷分布影响较大，在偏航阶段无影响。针对机身运动端在ABAQUS 中进行有限元建模及计算分析，载荷选择重力载荷，边界条件根据机身托架与定位接头的位置进行相应设置，然后划分网格，检查无误后提交计算，其中重力载荷施加与网格划分情况如图5 所示。
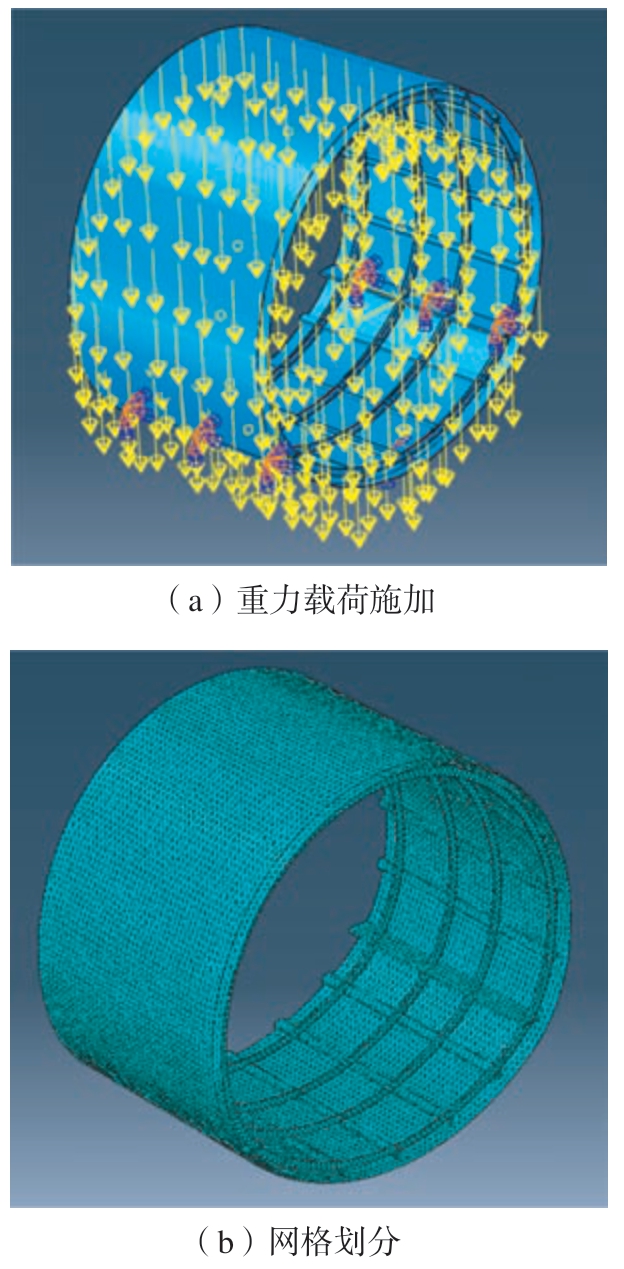
图5 机身有限元模型
Fig.5 Finite element model of fuselage
施加重力载荷时，可通过设置重力场在3 个方向的分量模拟姿态角变化情况，按照姿态角无变化；横滚角α 为10°，其他角为0°；俯仰角β 为10°，其他角为0°；偏航角为10°，其他角为0°这4 种情况分别设置重力载荷，结合本文ABAQUS 中的模型坐标系，转化成的重力场分量形式分别为（0，0，–g）T、（0.174g，0，–0.985g）T、（0，–0.174g，–0.985g）T、（0，0，–g）T，将上述4 个不同的状态分量分别输入到有限元模型中进行仿真计算，最终得到结果如图6 所示，证明了不同的横滚角、俯仰角会影响机身变形。因此，下文中以横滚角、俯仰角为输入，机身位置变化量为输出构造代理模型。
图6 不同姿态角下有限元仿真结果
Fig.6 Finite element simulation results under different attitude angles
2.3 机身姿态–位置Kriging 代理模型构建
首先确定变量空间，选择取样范围。本文采用六自由度平台作为机身调姿工装，其旋转角度参数如图7所示，该机构绕单一坐标轴的旋转角度为单边伸出23.1°、一边伸出一边收缩30°。为保证结构安全，以单边旋转角度23.1°的80%作为取样范围，即（–18°，18°），在该范围内进行拉丁超立方抽样设计。完成抽样后得到36 个二维变量样本点，样本点分布情况如图8 所示，其中每1 个抽样点代表机身的1 个姿态。
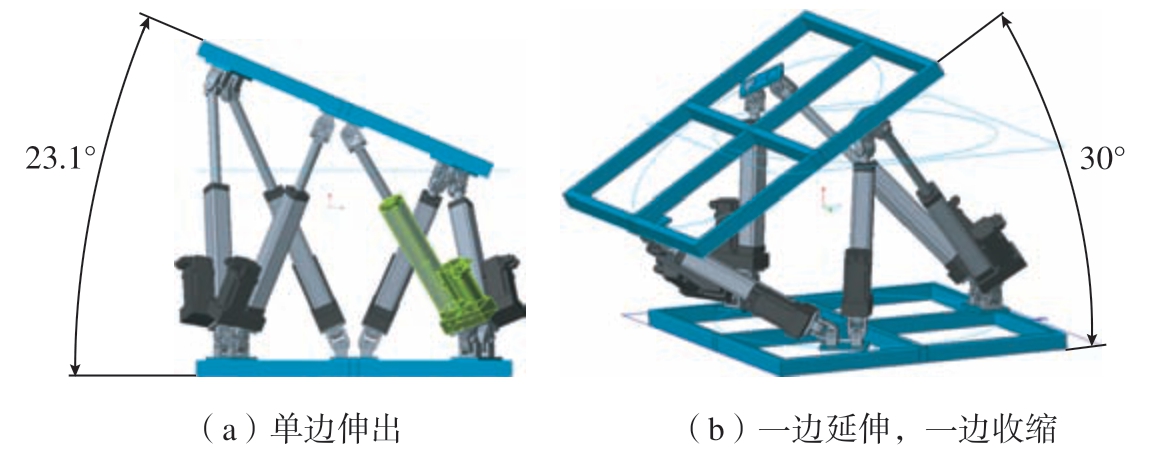
图7 六自由度平台旋转角度参数
Fig.7 Rotation angle parameters of six-degree of freedom platform
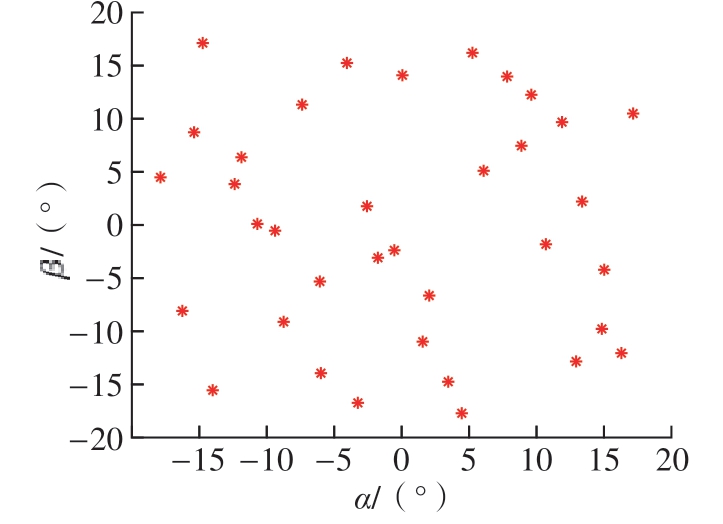
图8 拉丁超立方抽样样本点分布情况
Fig.8 Distribution of sample points generated by Latin hypercube sampling
经试验设计产生样本点后得到对应的响应值，然后以设计变量和对应响应值为输入、输出构造出代理模型。首先将图8 中36 个抽样点的机身横滚角α 与机身俯仰角β 转化为重力场分量形式；然后将它们分别输入到机身有限元模型中，经仿真计算后得到机身测量点在不同姿态下3 个方向的变形值，其中部分变形值数据如表7 所示。
表7 测量点在不同姿态下的部分变形值
Table 7 Partial deformation values of measurement points under different poses
位置靶标T1/mm T2/mm T3/mm T4/mm T5/mm T6/mm T7/mm T8/mm部分抽样点0.293 0.256 0.331 0.373 0.408 0.621 0.649 0.317 0.726 0.624 0.366 0.430 0.485 0.018 0.153 0.345 0.095 0.096 0.193 0.193 0.192 0.319 0.295 0.193 P1 P2–0.003 0.066 0.279 0.205 0.143 0.651 0.380 0.303–0.542 –0.363 –0.736 –0.854 –0.953 –1.190 –1.225 –0.697–0.164 –0.164 –0.339 –0.339 –0.339 –0.568 –0.524 –0.339 P3 0.448 0.384 0.349 0.420 0.478 0.528 0.643 0.325 1.629 1.456 1.423 1.533 1.627 1.216 1.380 1.387 0.161 0.162 0.327 0.326 0.326 0.541 0.500 0.327 P4 0.356 0.394 0.348 0.308 0.274 0.463 0.308 0.361 1.649 1.745 1.963 1.898 1.846 1.837 1.823 1.985–0.085 –0.084 –0.179 –0.180 –0.180 –0.304 –0.281 –0.179 P5 0.124 0.137 0.297 0.283 0.272 0.642 0.526 0.299–0.050 –0.019 –0.379 –0.401 –0.419 –0.798 –0.744 –0.375–0.029 –0.028 –0.061 –0.061 –0.061 –0.104 –0.095 –0.061 0.278 0.334 0.336 0.277 0.227 0.493 0.285 0.356 1.239 1.381 1.516 1.421 1.343 1.336 1.298 1.548–0.129 –0.128 –0.268 –0.269 –0.269 –0.452 –0.418 –0.268 P6
得到机身测量点变形值后按位姿解算公式将它们转化为位姿平移量改变值，转化结果如表8 所示。
表8 机身位置变化量
Table 8 Variation of fuselage position
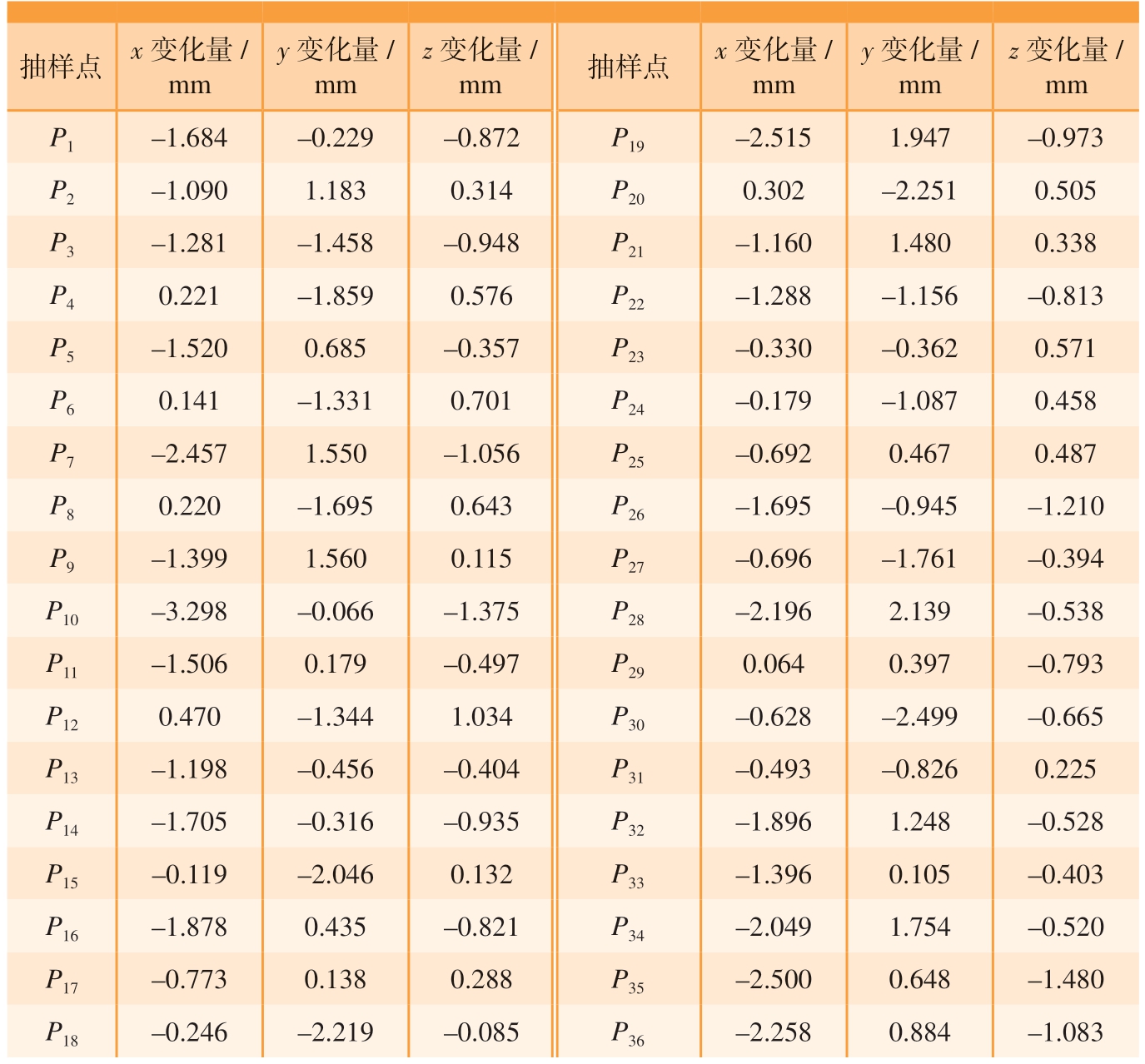
抽样点 x 变化量/mm z 变化量/mm P1 –1.684 –0.229 –0.872 P19 –2.515 1.947 –0.973 P2 –1.090 1.183 0.314 P20 0.302 –2.251 0.505 P3 –1.281 –1.458 –0.948 P21 –1.160 1.480 0.338 P4 0.221 –1.859 0.576 P22 –1.288 –1.156 –0.813 P5 –1.520 0.685 –0.357 P23 –0.330 –0.362 0.571 P6 0.141 –1.331 0.701 P24 –0.179 –1.087 0.458 P7 –2.457 1.550 –1.056 P25 –0.692 0.467 0.487 P8 0.220 –1.695 0.643 P26 –1.695 –0.945 –1.210 P9 –1.399 1.560 0.115 P27 –0.696 –1.761 –0.394 P10 –3.298 –0.066 –1.375 P28 –2.196 2.139 –0.538 P11 –1.506 0.179 –0.497 P29 0.064 0.397 –0.793 P12 0.470 –1.344 1.034 P30 –0.628 –2.499 –0.665 P13 –1.198 –0.456 –0.404 P31 –0.493 –0.826 0.225 P14 –1.705 –0.316 –0.935 P32 –1.896 1.248 –0.528 P15 –0.119 –2.046 0.132 P33 –1.396 0.105 –0.403 P16 –1.878 0.435 –0.821 P34 –2.049 1.754 –0.520 P17 –0.773 0.138 0.288 P35 –2.500 0.648 –1.480 P18 –0.246 –2.219 –0.085 P36 –2.258 0.884 –1.083 y 变化量/mm z 变化量/mm 抽样点 x 变化量/mm y 变化量/mm
得到机身位置变化量后，以高斯函数为相关函数构造代理模型，输入为姿态角α、β；输出为机身位置变化量3个分量x、y、z，其中第6组、12组、18 组、24 组、30 组和36 组数据用来比较预测结果和模拟结果之间的拟合程度，其余数据参与代理模型构造，最终得到的Kriging 代理模型如图9 所示。
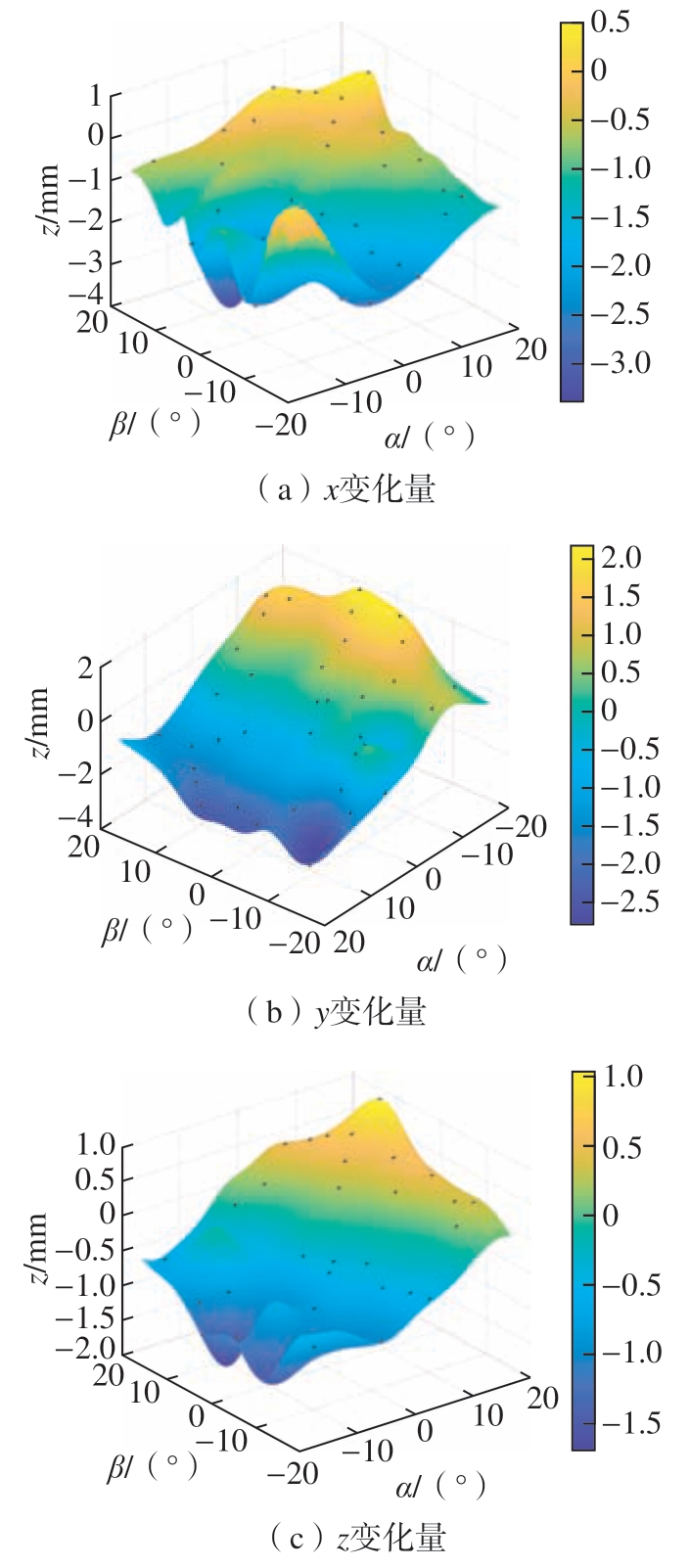
图9 姿态–位置Kriging 代理模型
Fig.9 Attitude–position Kriging surrogate model
构造代理模型后，需要检验代理模型精度，本文通过比较预测结果和模拟结果之间的拟合程度来表示。将上文中列举的第6组、12组、18组、24 组、30 组和36 组样本点利用代理模型得到相应预测值，模拟结果与预测结果如表9 所示。
表9 模拟结果与预测结果
Table 9 Results of simulation and prediction
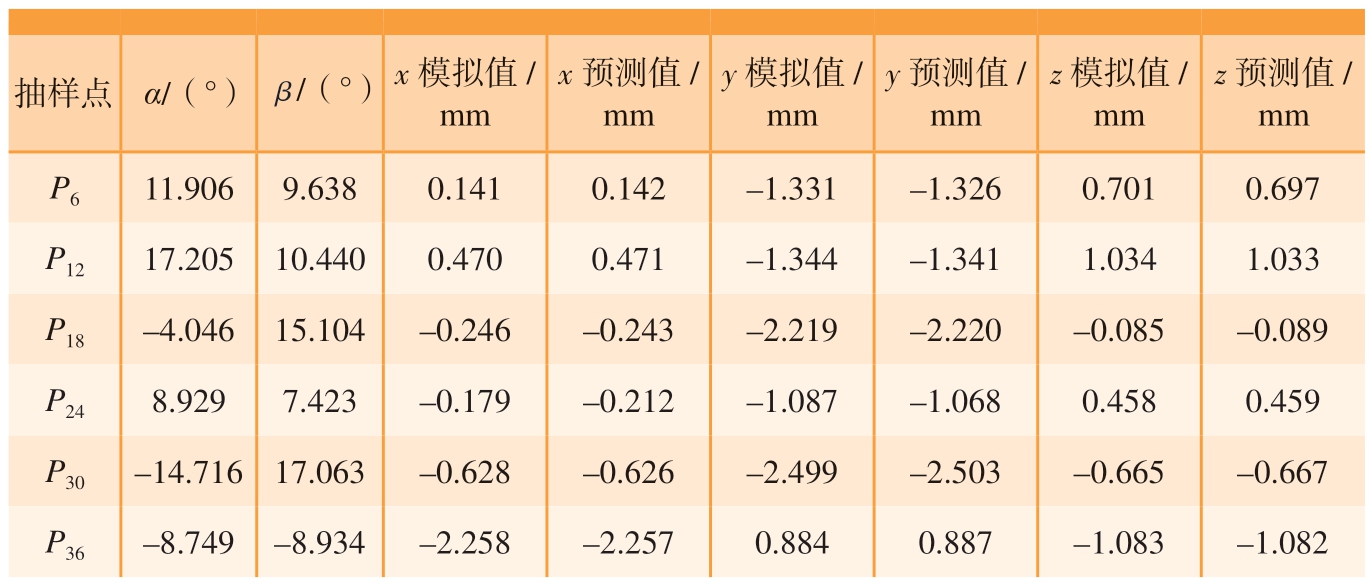
抽样点 α/（°） β/（°）x 模拟值/mm x 预测值/mm y 模拟值/mm y 预测值/mm z 模拟值/mm z 预测值/mm P6 11.906 9.638 0.141 0.142 –1.331 –1.326 0.701 0.697 P12 17.205 10.440 0.470 0.471 –1.344 –1.341 1.034 1.033 P18 –4.046 15.104 –0.246 –0.243 –2.219 –2.220 –0.085 –0.089 P24 8.929 7.423 –0.179 –0.212 –1.087 –1.068 0.458 0.459 P30 –14.716 17.063 –0.628 –0.626 –2.499 –2.503 –0.665 –0.667 P36 –8.749 –8.934 –2.258 –2.257 0.884 0.887 –1.083 –1.082
与模拟结果相比，预测结果在趋势和数值上符合度较高，其中x、y、z模拟结果与预测结果的平均相对误差分别为0.61%、0.27%、1.33%，可见所构造代理模型的有效性。
3 机身对接仿真系统开发与试验验证
3.1 系统需求分析
在进行机身对接仿真时，需要根据测量点坐标值解算出机身位姿，利用代理模型快速获得机身位置变化量并进行补偿，然后根据补偿后机身位姿得到调姿工装的6 个推杆调整量并将它们传输到可视化仿真平台中驱动虚拟模型运动。为了能便捷直观地实现这一过程，搭建了1套“机身对接过程仿真系统”，为用户提供1个实现机身对接数据计算的平台。
3.2 机身对接仿真系统功能实现
模型预览功能模块用来浏览参与仿真的三维模型，通过调用回调函数中编写好的网格化算法，将模型文件中的点数据互相连接组成大量网格，然后将网格着色获得重构模型，在预览框中也能实现对模型的放大、缩小、旋转操作。
连接交互模块主要建立计算程序与MySQL及Unity3D的连接关系，使数据计算时可更高效地进行读取与存储。登录所需数据库及要查看的数据表，即可对数据库进行操作，在数据发送窗口中进行数据传输。
仿真计算模块的功能为读取机身测量点坐标进行位姿解算，经过位姿补偿后计算得到六自由度平台推杆调整量，并输出至可视化环境中的虚拟模型中。该模块包含位姿解算、位姿补偿、调整量计算3 个子模块。
位姿解算窗口通过调用奇异值分解算法，由导入的测量点坐标值求解机身位姿，并显示结果；数据保存窗口可实现数据存储功能；位姿补偿子模块窗口界面在数据导入后，调用回调函数相关算法，构建出代理模型并显示图形。之后导入位姿数据，调用回调函数中的数据查询算法获取补偿值，将补偿结果显示在表中并保存。调整量计算子模块首先导入位姿，输入调姿平台参数，之后运行程序得到调整量计算结果并显示，最后可导出或传输到可视化界面中，机身对接过程仿真系统结构树如图10所示。
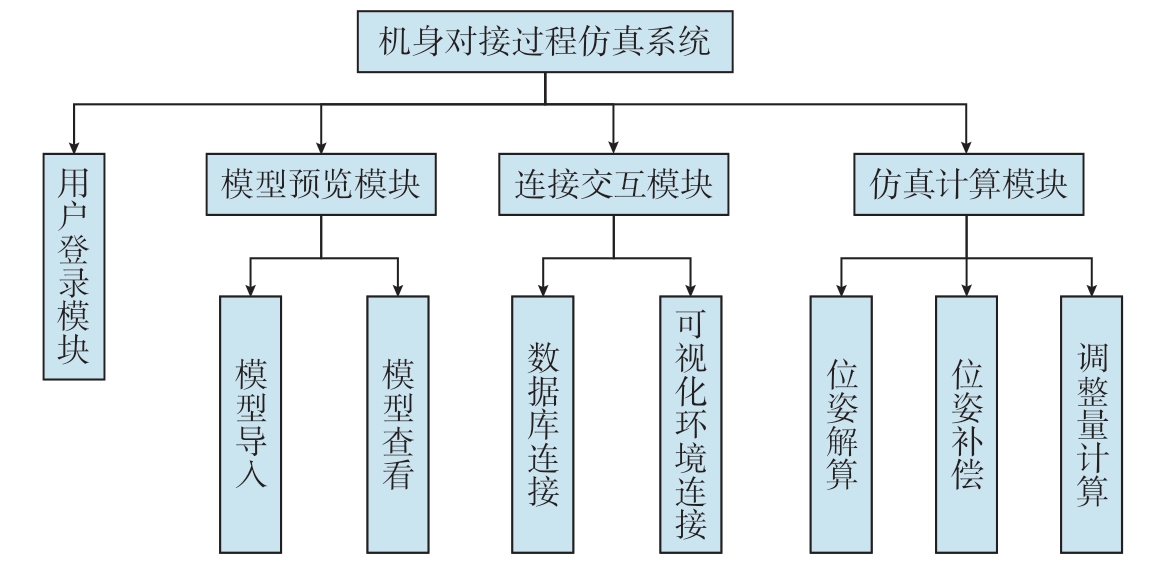
图10 机身对接过程仿真系统结构树
Fig.10 Structure tree of simulation system for fuselage docking process
3.3 机身对接试验验证
3.3.1 试验环境搭建
将六自由度平台和固定工装布置在试验场地内，然后连接支撑托架和固定工装，机身试验件通过定位接头和螺栓与支撑托架进行定位并连接，完成机身试验件与工装的布置，试验现场如图11 所示。
图11 机身对接试验现场
Fig.11 Experiment site of fuselage docking
测量前将两台M20 高精度实时摄影相机布置到位，调节相机角度使其视场覆盖机身表面，调节角度为沿基线垂直方向偏转15°，布置完后将相机与PC 端连接。
相机布置完成后进行编码标志点布设，在两机身端表面相距30 cm处均匀布设编码标志点，保证双相机系统能同时拍摄两机身段表面多个标志点。完成标志点布设工作后，启动双相机系统软件，使用定向尺定向，通过移动标定多个位置，软件自动标定两相机的位置关系。
3.3.2 系统应用验证
上述试验环境搭建完成后，使用开发的机身对接仿真系统进行机身调姿平台调整量计算，驱动机身试验平台进行对接操作。
（1）测量点坐标获取。
试验环境搭建完成后，机身及工装均处于初始状态，此时利用双相机测量系统获取机身表面测量点坐标值；由虚拟模型得到局部坐标系坐标值。
（2）位姿解算。
登录系统后在菜单栏中切换至仿真计算模块，首先选择位姿解算模块，将测量点坐标导入后进行位姿解算，并将解算结果显示在表格中，如图12 所示。
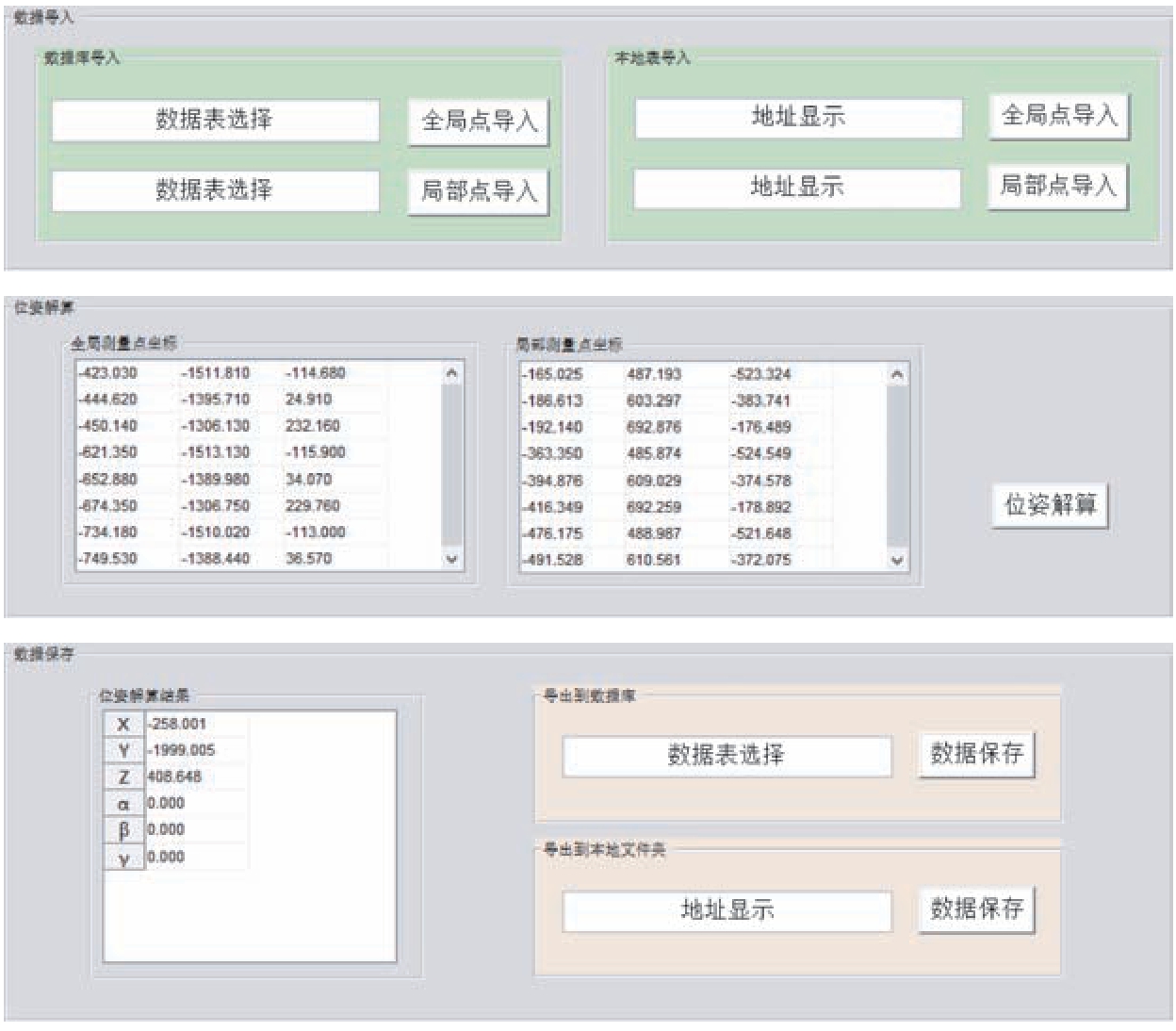
图12 位姿解算结果显示
Fig.12 Display of pose calculation results
（3）位姿补偿。
在菜单栏中切换至位姿补偿模块，导入姿态角及变形数据，选择构造元素后进行Kriging 代理模型搭建，在完成全部代理模型构建后进行位姿补偿，最后将补偿后位姿结果以表格化的形式显示，如图13 所示。
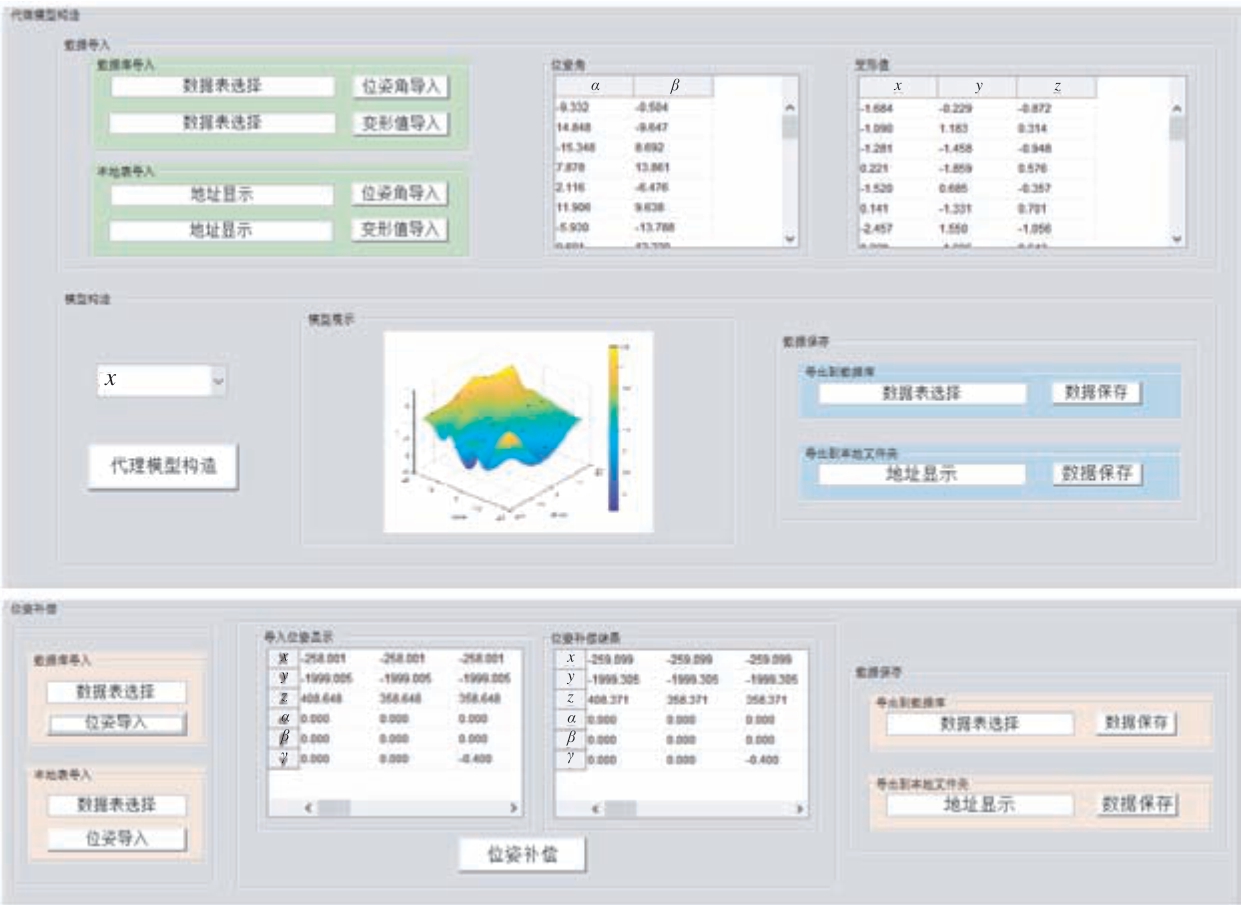
图13 代理模型构造及位姿补偿显示
Fig.13 Proxy model construction and pose compensation display
（4）调整量计算。
在菜单栏中切换至调整量计算模块，在数据导入窗口完成机身位姿导入，输入调姿平台参数后进行调整量计算，并将计算结果显示在表格中，如图14 所示。
图14 六自由度平台调整量数据显示
Fig.14 Display of adjustment data for a six-degree of freedom platform
（5）机身对接。
得到调姿平台各推杆调整量后，将它们传输到六自由度平台控制软件中，驱动六自由度平台运动带动机身完成对接，试验机身段对接过程如图15 所示。
图15 机身试验件对接过程
Fig.15 Docking process of the fuselage test piece
（6）应用效果分析。
在完成机身对接情况下，对提出的关键特征数据驱动的虚实融合机身对接快速仿真方法及机身对接仿真系统应用效果进行分析，结果如表10 所示，利用搭建的数据交互通道与代理模型位姿补偿方法，将计算过程集成到系统中，可更加高效地指导操作，提高对接效率和对接精度。
表10 方法与系统应用效果分析
Table 10 Effectiveness analysis of the method and system application
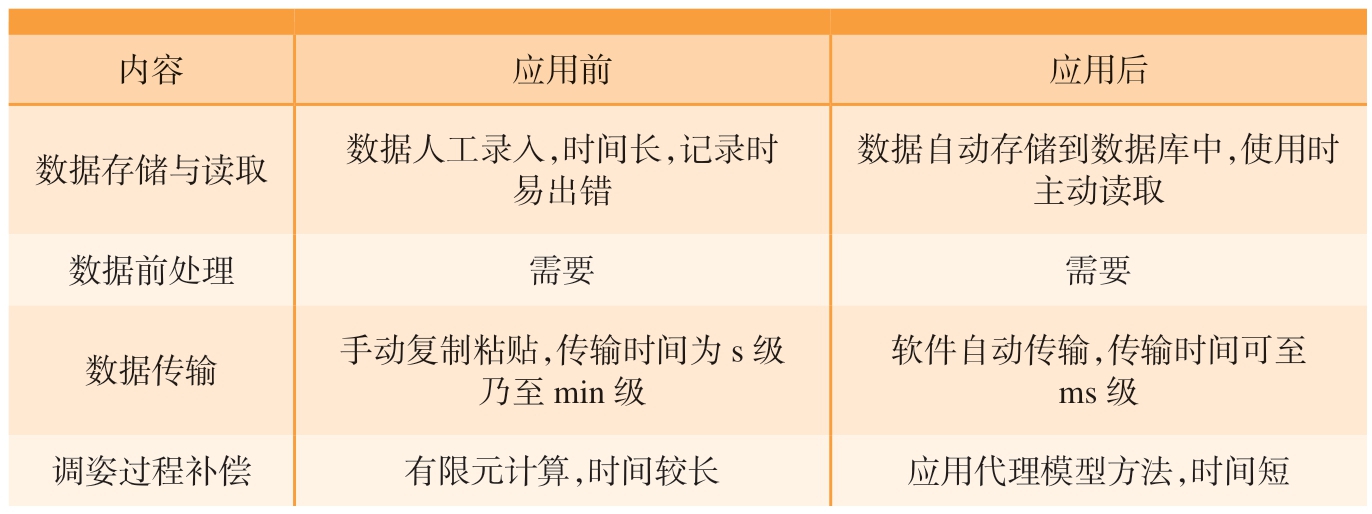
内容 应用前 应用后数据存储与读取 数据人工录入，时间长，记录时易出错数据自动存储到数据库中，使用时主动读取数据前处理 需要 需要数据传输 手动复制粘贴，传输时间为s 级乃至min 级软件自动传输，传输时间可至ms 级调姿过程补偿 有限元计算，时间较长 应用代理模型方法，时间短
4 结论
针对传统飞机虚拟装配仿真传统机身对接仿真中理论模型偏差较大、有限元模型消耗时间长的问题，本文开展了基于数据驱动技术的机身对接仿真方法研究，为机身对接过程快速仿真提供试验方法，并进行了试验验证，得出以下3 项主要研究内容和成果。
（1）针对飞机机身对接过程，构建机身与工装几何模型并搭建了仿真可视化环境；搭建数据交互环境以实现仿真数据的实时传输；利用测量数据与虚拟模型进行了对接仿真，确定了对接过程的位姿参数，为调姿参数补偿提供了数据基础。
（2）对仿真计算得到的变形情况，基于Kriging 代理模型，以机身姿态角和位置变化量分别作为输入、输出值构建代理模型，对机身位置变化量进行预测，结果对比显示代理模型方法有效。
（3）开发了机身对接过程仿真系统，设计了系统的基本架构、主要功能模块以及系统应用流程，最后以机身试验件的对接过程为例，验证了系统的可行性。
[1] 秦宇, 黄翔, 邓正平, 等.基于激光测距的大部件对接方法及误差分析[J].计算机集成制造系统, 2021, 27(3): 728–738.
Q I N Yu, H U A N G X i a n g, D E N G Zhengping, et al.Novel posture alignment method and error analysis for large component assembly based on laser range sensing[J].Computer Integrated Manufacturing Systems,2021, 27(3): 728–738.
[2] 郭飞燕, 刘检华, 邹方, 等.数字孪生驱动的装配工艺设计现状及关键实现技术研究[J].机械工程学报, 2019, 55(17):110–132.
GUO Feiyan, LIU Jianhua, ZOU Fang, et al.Research on the state-of-art, connotation and key implementation technology of assembly process planning with digital twin[J].Journal of Mechanical Engineering, 2019, 55(17):110–132.
[3] 王安洋, 王仲奇, 夏松, 等.基于数字孪生模型的可配置装配偏差分析方法[J].航空制造技术, 2021, 64(20): 65–75.
WANG Anyang, WANG Zhongqi, XIA Song, et al.Configurable assembly deviation analysis technology based on digital twin model[J].Aeronautical Manufacturing Technology, 2021, 64(20): 65–75.
[4] 王仲奇, 杨盼, 陈世洁, 等.飞机舱门数字孪生模型构建及偏差传递分析研究[J].航空制造技术, 2022, 65(12): 36–47.
WANG Zhongqi, YANG Pan, CHEN Shijie, et al.Research on construction of digital twin model and deviation transfer analysis of cabin door of airplane[J].Aeronautical Manufacturing Technology, 2022, 65(12):36–47.
[5] 王鹏, 杨妹, 祝建成, 等.面向数字孪生的动态数据驱动建模与仿真方法[J].系统工程与电子技术, 2020, 42(12): 2779–2786.
WANG Peng, YANG Mei, ZHU Jiancheng,et al.Dynamic data driven modeling and simulation method for digital twin[J].Systems Engineering and Electronics, 2020, 42(12):2779–2786.
[6] LIU Z Y, ZHANG D H, JIA W Q, et al.An adversarial bidirectional serial–parallel LSTM–based QTD framework for product quality prediction[J].Journal of Intelligent Manufacturing, 2020, 31(6): 1511–1529.
[7] 赵浩然, 刘检华, 熊辉, 等.面向数字孪生车间的三维可视化实时监控方法[J].计算机集成制造系统, 2019, 25(6): 1432–1443.
ZHAO Haoran, LIU Jianhua, XIONG Hui,et al.3D visualization real-time monitoring method for digital twin workshop[J].Computer Integrated Manufacturing Systems, 2019, 25(6):1432–1443.
[8] 胡凡成.基于Unity 3D 的实时数据驱动数字化车间研究[D].长沙: 湖南大学, 2018.
HU Fancheng.Research on real-time data driven digital workshop based on unity 3D[D].Changsha: Hunan University, 2018.
[9] 黄华, 李嘉然, 赵秋舸, 等.基于混合驱动的进给系统数字孪生模型自适应更新法[J].计算机集成制造系统, 2023, 29(6):1840–1851.
HUANG Hua, LI Jiaran, ZHAO Qiuge,et al.Adaptive update method of digital twin model for feed system based on hybrid drive[J].Computer Integrated Manufacturing Systems,2023, 29(6): 1840–1851.
[10] STOJANOVIC N, MILENOVIC D.Data-driven digital twin approach for process optimization: An industry use case[C]//2018 IEEE International Conference on Big Data (Big Data).Seattle: IEEE, 2018: 4202–4211.
[11] 韩忠华.Kriging 模型及代理优化算法研究进展[J].航空学报, 2016, 37(11):3197–3225.
HAN Zhonghua.Kriging surrogate model and its application to design optimization: A review of recent progress[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197–3225.
[12] JIANG P, WANG C C, ZHOU Q,et al.Optimization of laser welding process parameters of stainless steel 316L using FEM, Kriging and NSGA–Ⅱ[J].Advances in Engineering Software, 2016, 99: 147–160.
[13] GASPAR B, TEIXEIRA A P,GUEDES SOARES C.Adaptive surrogate model with active refinement combining Kriging and a trust region method[J].Reliability Engineering & System Safety, 2017, 165: 277–291.
[14] Z H A N G X F, WA N G L,SØRENSEN J D.REIF: A novel active-learning function toward adaptive Kriging surrogate models for structural reliability analysis[J].Reliability Engineering & System Safety, 2019,185: 440–454.
[15] 南凯刚, 闫如玉, 李光明, 等.大型桁架天线装配精度仿真与代理模型的构建[J].成组技术与生产现代化, 2021, 38(4):27–36.
NAN Kaigang, YAN Ruyu, LI Guangming,et al.Assembly error simulation and proxy model construction of large-scale truss antenna[J].Group Technology & Production Modernization, 2021, 38(4): 27–36.
