点阵结构由大量周期性桁架状的点阵单胞组成，其设计灵感来源于自然界中的轻质结构，如鸟骨、竹子等，这类轻质结构在细观层面上均展现出“疏松多孔”的特性[1]。这类“多孔”结构具有优良的力学性能 （如高比强度、高比刚度、抗冲击等），同时还具有更多的功能属性，如隔热、降噪等[2]。点阵结构在设计中可根据当地载荷，通过调整该处点阵“支杆”的几何参数实现结构力学性能优化，因而越来越被航空航天、汽车制造及医疗行业关注[3]。尽管点阵结构拥有诸多优异的性能，但传统点阵结构在“支杆”交点处几何过渡剧烈，造成该处过大的应力集中，导致整体结构力学性能下降，使其过早的屈服、蠕变或破坏[4–5]。近年来，已有很多针对提高点阵结构力学性能的研究，Park 等[6]提出一种新型均质化方法，可在计算点阵单胞等效力学性能时，同时考虑点阵节点的“强化”作用，研究结果表明，“弯曲”型点阵单胞力学性能对支杆节点“强化”更加敏感，而节点“强化”对“拉伸”型点阵单胞的力学性能影响不大。为了降低点阵结构节点处应力集中，设计人员应该尽量避免交点处剧烈的几何突变以保证应力梯度平滑过渡。Bai[5]构建了一种新型BCC点阵结构，可提高点阵结构刚度及塑性破坏强度38.2%及34.12%以上。Cao 等[7]将变截面支杆引入到菱形十二面体点阵中，并通过仿真及试验验证了新型菱形十二面体点阵结构具有更好的力学及吸能性能。姚定烨等[8]通过提高点阵节点处制备激光功率，使节点处的有效截面积比常规节点增大143%，相较于常规点阵，节点增强型点阵结构的相对密度提高了24.8%，弹性模量增加了112%，抗压强度增加了52%，30%应变时的吸能提升了88%。Dallago 等[9]通过引入节点圆角增强显著改善了点阵结构的疲劳性能。通过改变点阵交点几何形状以提高点阵单胞力学性能的其他研究工作可参考文献[10–12]。
本研究以体心立方 （BCC）点阵结构为研究对象，研究圆角化节点增强对BCC 点阵结构力学性能的影响。研究主要分为3 步： （1）给出圆角化节点增强点阵结构的设计方法及设计参数； （2）基于数值均匀化方法采用有限元仿真计算得到圆角化节点增强对点阵单胞等效力学性能的影响； （3）针对不同构型的BCC点阵结构进行单轴正压试验，通过对圆角化节点增强前后的点阵结构试验结果对比，得到圆角化节点增强对BCC 点阵结构力学性能的影响。
1 圆角化节点增强BCC 点阵结构设计
根据麦克斯韦 （Maxwell）判据，BCC 点阵结构属于“弯曲型”点阵，通过增加支杆交点处面–面倒圆角以获得更加光顺的几何过渡，减小交点处应力集中以提高点阵结构的承载能力。图1 展示了2×2×2 的传统BCC 点阵及圆角化后的BCC-F点阵结构。传统BCC 点阵结构支杆节点处“剧烈”几何过渡，而圆角化节点增强BCC-F 点阵结构通过圆角半径r 对点阵结构支杆交点处进行“光滑”几何过渡。
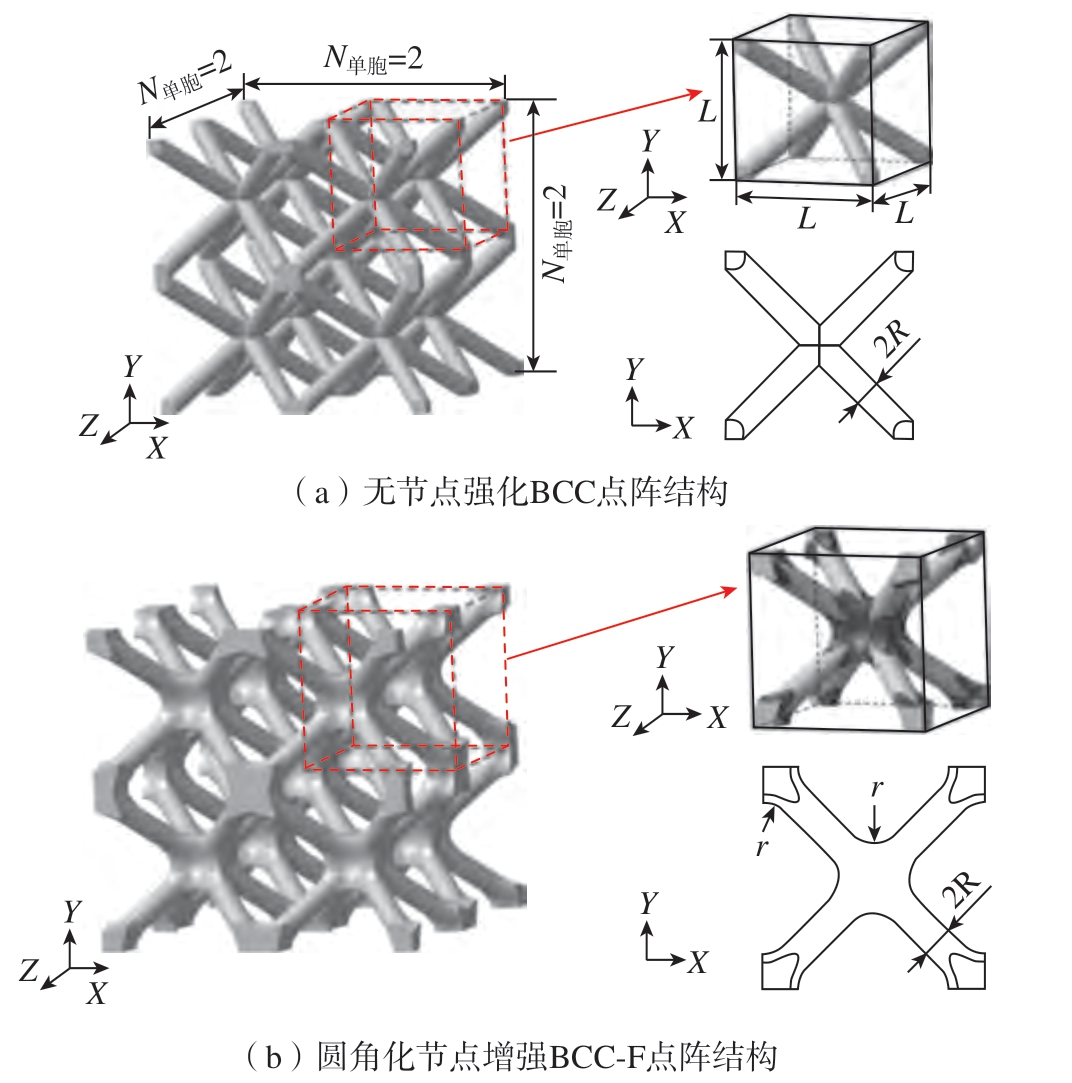
图1 传统BCC 点阵结构与圆角化节点增强BCC 点阵结构
Fig.1 Conventional and filleted BCC lattice structures
圆角化节点增强BCC-F 点阵单胞的主要几何设计参数为支杆半径R 及圆角半径r。常用的几何倒圆方法是“滚球法”，即假设一个半径为r的圆球从相交曲面靠近交线处滚过，通过计算圆球轨迹从而获得倒圆角曲面几何图形[13]。在商业CAD 软件中，通常只需定义圆角的位置及半径尺寸便可快速获得倒圆几何模型。本研究采用无量纲参数相对密度ρ、支杆相对半径R 及圆角相对半径r来表征BCC 点阵结构设计，其定义为
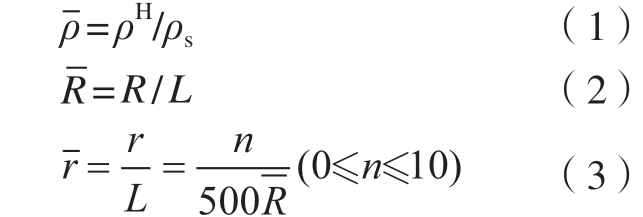
式中，ρH 及ρs 分别为点阵单胞及母材密度；R 和L 分别为单胞支杆半径及单胞的立方体尺寸；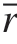
与r 分别为BCC 点阵结构圆角相对半径及圆角真实半径。点阵结构交点处倒圆角的最大尺寸受点阵单胞拓扑类型及支杆半径影响，对于BCC 点阵结构，倒圆角尺寸与杆件半径呈反比例关系，杆件半径越大，倒圆角尺寸越小，为便于工程设计引用，引入圆角系数n（n = 0、1、2、3…）来表征节点圆角设计，通过圆角系数及点阵相对半径计算得到圆角尺寸。当n = 0 时，
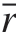= 0，点阵结构即为传统的无圆角化节点增强的点阵单胞。圆角尺寸随n 增加而增大，考虑到BCC 点阵结构的拓扑构型及支杆节点圆角处空间尺寸限制，本研究中n 的最大值取10[14]。图2 展示了不同支杆相对半径及圆角系数对应的BCC 点阵结构单胞构型，其中
（ 
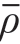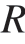= 0.072，n = 0） = 10%，
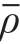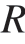（ = 0.188，n = 0）= 50%。
图2 不同几何设计参数的BCC 点阵单胞
Fig.2 BCC lattice cells with different geometric design parameters
2 圆角化节点增强对BCC 点阵结构力学性能的影响
2.1 点阵单胞等效力学性能计算
基于数值均匀化方法，对点阵结构代表体元 （RVE）进行分析，通过对RVE 施加周期性边界条件，采用应变能等效的原则即可求解点阵结构等效性能[15]。图3 展示了尺寸为L 的立方体RVE 在受到1 方向单轴拉伸尺寸变化图，L1、L2 及L3 分别为RVE 在单轴拉伸应变作用下单元尺寸变化。利用Omairey 等[15]的方法对ABAQUS 进行二次开发，可实现点阵RVE 快速施加周期性边界条件。通过对单胞进行单轴拉伸数值仿真试验，在点阵单胞线弹性变形范围内，其1 方向等效杨氏模量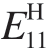
由式（4）计算。
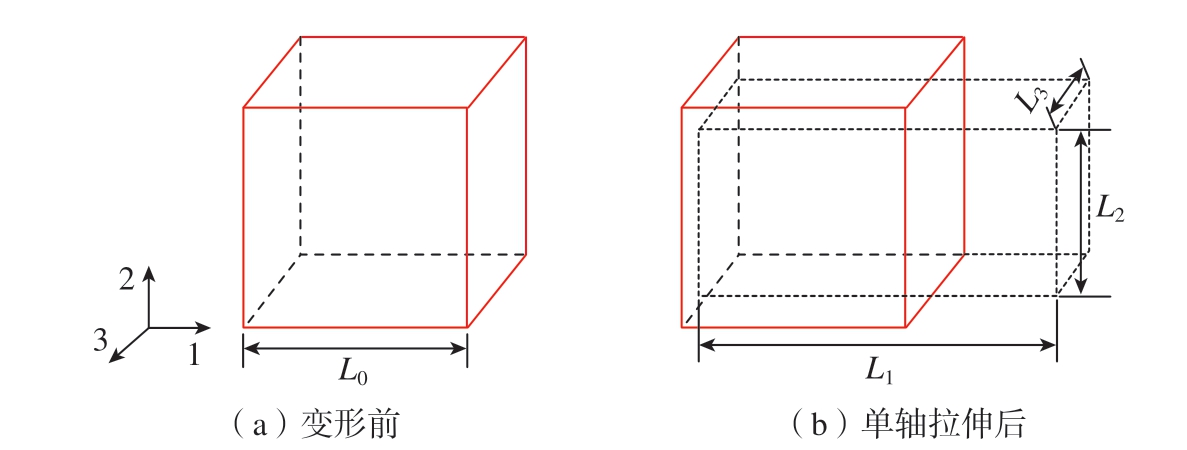
图3 周期性RVE 均匀化方法边界条件示意图
Fig.3 Schematic diagram of boundary conditions for the periodic RVE homogenization method
式中，
为施加在RVE 上1 方向的单位应变；
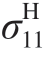为单元1 方向的等效平均应力，该应力可通过有限元中提取参考节点1 方向的支反力F1计算。
等效泊松比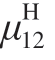
及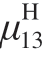
由式 （5）和 （6）得到。
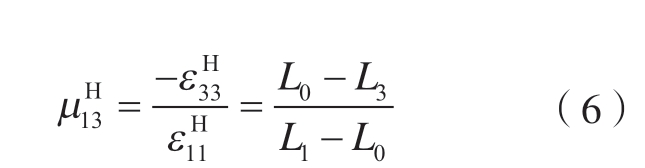
BCC 点阵RVE 元均具有3 个正交的对称平面，并考虑到同一个点阵单胞内支杆半径均相同，这种点阵结构可等效为准各向同性的点阵结构，因此其杨氏模量及泊松比满足式（7）和 （8）。
有限元仿真采用四面体C3D4 单元类型，通过网格敏感度分析可确定网格尺寸，以平衡精度和效率[16]。点阵结构母材为Ti – 6Al – 4V，对采用激光选区熔化（ Selective laser melting，SLM）制备的Ti – 6Al – 4V 标准拉伸试样进行准静态单轴拉伸试验，确定母材的力学性能。母材的应力–应变曲线如图4（a）所示，杨氏模量E0=110 GPa，泊松比μ0=0.34，屈服应力σ0.2=939.625 MPa。图4（b）为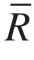
=0.072，n = 4 时，BCC 及BCC-F 点阵单胞在单轴拉伸载荷下的等效应力–应变曲线，将0.2%塑性应变时的等效应力作为单胞的等效屈服应力
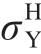，可以看出，BCC-F 的等效杨氏模量及屈服应力相较于BCC 点阵均有了大幅度提高，详细讨论见2.2 节。
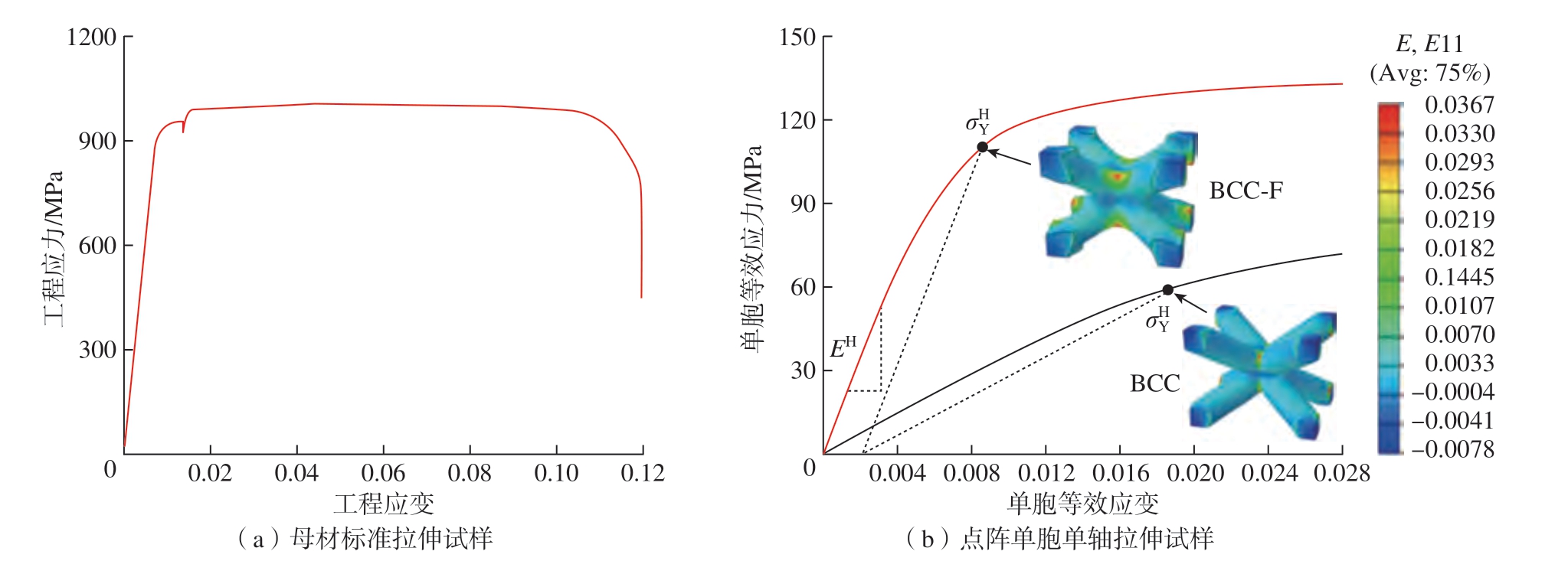
图4 母材、BCC 和BCC-F 试样的应力–应变曲线
Fig.4 Stress – strain curves of base material, BCC, and BCC-F samples
2.2 圆角化节点增强对点阵单胞力学性能的影响
图5 展示了归一化后的点阵单胞等效杨氏模量
及等效屈服应力柱状图，归一化方法如式（ 9）和（ 10）所示，相同相对支杆半径的点阵单胞的等效杨氏模量及等效屈服应力按无圆角化增强的点阵单胞的模量及屈服应力进行归一化处理。
图5 圆角系数对点阵单胞等效杨氏模量及屈服应力的影响
Fig.5 Effect of the fillet parameter on effective Yong’s Modulus and yield stress of lattice cells
从图5（a）可以看出，经过圆角化节点增强后的BCC 点阵单胞等效杨氏模量随圆角系数显著增长，但其增长趋势随点阵单胞相对密度增加而减缓。当R = 0.072和R= 0.188 时，圆角系数n 从0 增加到10，BCC 点阵单胞的等效杨氏模量分别增加了约334%和37%。由图5（b）可以看出，随着圆角系数n 等增大，点阵单胞的等效屈服应力提高，且支杆相对半径越小等效屈服应力提高越明显，当R= 0.072和R= 0.188 时，圆角系数n 从0 增加到10，点阵单胞的等效屈服应力分别提高了213%和24%。
3 BCC 点阵准静态单轴压缩试验
3.1 试样制备
点阵试样采用Gd5 等级的Ti –6Al – 4V 粉末制造，粉末粒径为15 ～53 μm，层厚0.04 mm。激光功率320 W、光斑直径100 μm、扫描间距0.14 mm、扫描速度1200 mm/s。采用电火花切割将试样从打印平台取下，并在800 ℃下保温4 h 进行热处理。图6（a）为点阵试样示意图，试样为40 mm×40 mm×40 mm 的立方体结构，由8 层8×8 的PC 点阵单胞组成。点阵单胞如图6（b）所示,单胞尺寸为5 mm。试样分组及相对密度设计值与实测值见表1。由于在激光选区熔化成形过程中，金属点阵结构表面粘有部分未熔化的合金粉末，导致实测值相较相对密度设计值偏大。
表1 点阵试样列表
Table 1 Lists of lattice samples
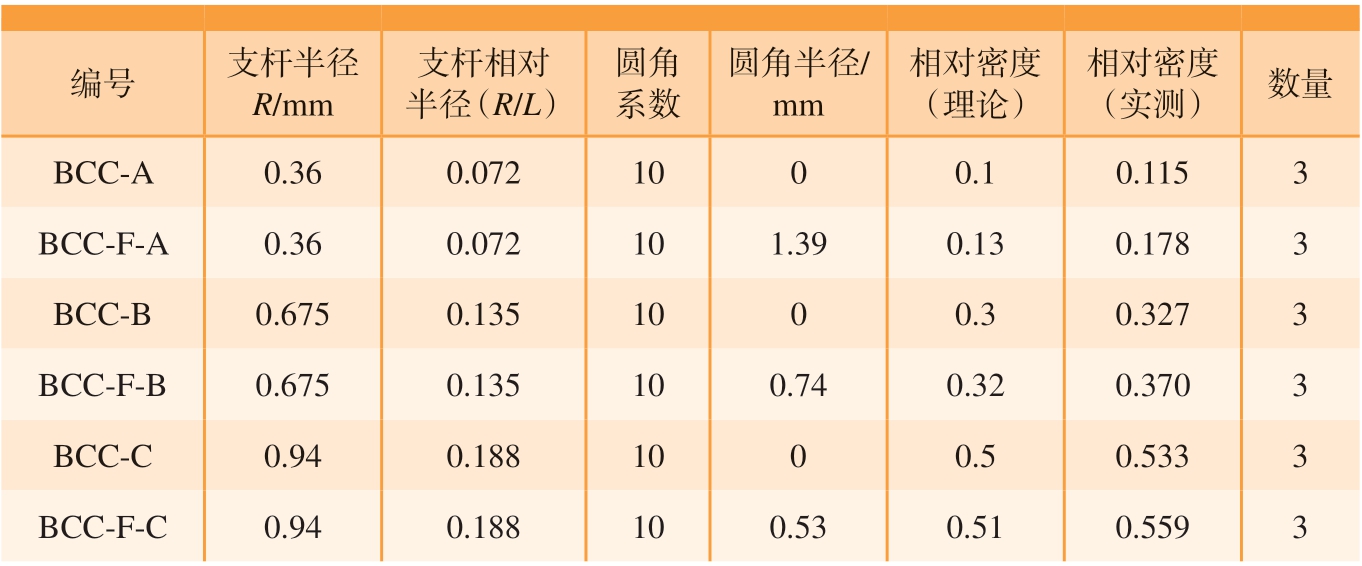
编号支杆半径R/mm支杆相对半径（R/L）圆角系数圆角半径/mm相对密度（理论）相对密度（实测）数量BCC-A0.360.0721000.10.1153 BCC-F-A0.360.072101.39 0.130.1783 BCC-B0.6750.1351000.30.3273 BCC-F-B0.6750.135100.74 0.320.370 3 BCC-C0.940.1881000.50.5333 BCC-F-C0.940.188100.53 0.510.5593
图6 BCC 和BCC-F 点阵试样尺寸及实物图
Fig.6 Dimensions and physical images of BCC and BCC-F lattice samples
3.2 试验过程
采用MTS E64 电子万能试验机对点阵结构进行单轴压缩试验，试验在室温下进行，位移加载速度为1.5 mm/min。压缩试验按照ISO 13314∶2011 标准执行，试验装置如图7 所示。试验中，将BCC 点阵试样放置在上、下压台之间，压台与试样之间的接触面使用二硫化钼润滑剂润滑，以减少压缩过程中试样垂直于加载方向膨胀时接触界面之间的摩擦力。试验中采用固定在两个压板上的位移引伸计测量试样沿加载方向的位移。为保证测量精度，同时对与压板接触的试样表面进行线切割精加工，保证两个接触面的平面度及平行度不大于0.3。
图7 点阵试件准静态单轴压缩试验的试验装置
Fig.7 Experimental setup of the quasi-static uniaxial compression test on the lattice specimens
3.3 试验结果讨论
点阵试样的工程应变–应力曲线试验结果如图8 所示，所有试样在变形初始阶段，应力均随应变线性增加，直到试件屈服，随后以非线性增加直至第1 个应力峰值。从线性变形阶段可以看出，圆角化节点增强后点阵试样的等效杨氏模量及等效屈服应力相较于增强前均出现较大幅度增长。对于相对密度较低的无圆角化增强点阵试样 （BCC-A 及BCC-B），在达到应力峰值后，直接沿对角线呈45°剪切破坏，整个破坏过程仅一个应力峰值。然而，BCC-F-A及BCC-F-B 试样在加载到第1 个应力峰值时仅产生局部层间的坍塌破坏，并未产生整体破坏，在经历过数个波峰（逐层坍塌）后最终沿对角线呈45°剪切整体破坏。对于相对密度较高的BCC-C 及BCC-F-C 组试样，在破坏过程中同样呈现出逐层坍塌的“多波峰”破坏模式。“多波峰”破坏模式是在增材制造过程中引入不可避免的制造缺陷或过高的残余应力，造成“薄弱层”，在加载过程中该层率先坍塌导致[17]。随着点阵结构相对密度的增大以及圆角化节点增强引起局部几何过于致密，在SLM成形过程中，致密的点阵结构造成过高的温度梯度，造成试样内部存在较高的残余应力或几何缺陷，最终造成了各组试样破坏过程的差异[16]。
图8 点阵试样试验应力–应变曲线
Fig.8 Stress–strain curve of the lattice samples
图9 为等效杨氏模量及等效屈服应力的试验结果与仿真结果对比图，可以看出，试验件的等效杨氏模量及等效屈服应力相较仿真结果普遍偏低，且随着点阵结构相对密度的增大，试验件等效杨氏模量及等效屈服应力与仿真结果的差异变大，该现象由增材制造中不可避免的制造缺陷引起。在低相对密度时，等效杨氏模量仿真结果能保证较高精度，例如相对密度为 0.115 的 BCC-A 及相对密度 0.178 的 BCC-F-A 点阵结构，等效杨氏模量仿真结果分别为0.2286 GPa 和1.6356 GPa，等效杨氏模量试验结果分别为0.2027 GPa和1.5039 GPa，误差分别为12.8%及8.8%。点阵结构的等效屈服应力的仿真结果与试验结果接近，屈服应力仅与结构局部应力集中有关，通过采用文献[14]的仿真方法可以得到较精确的仿真结果。
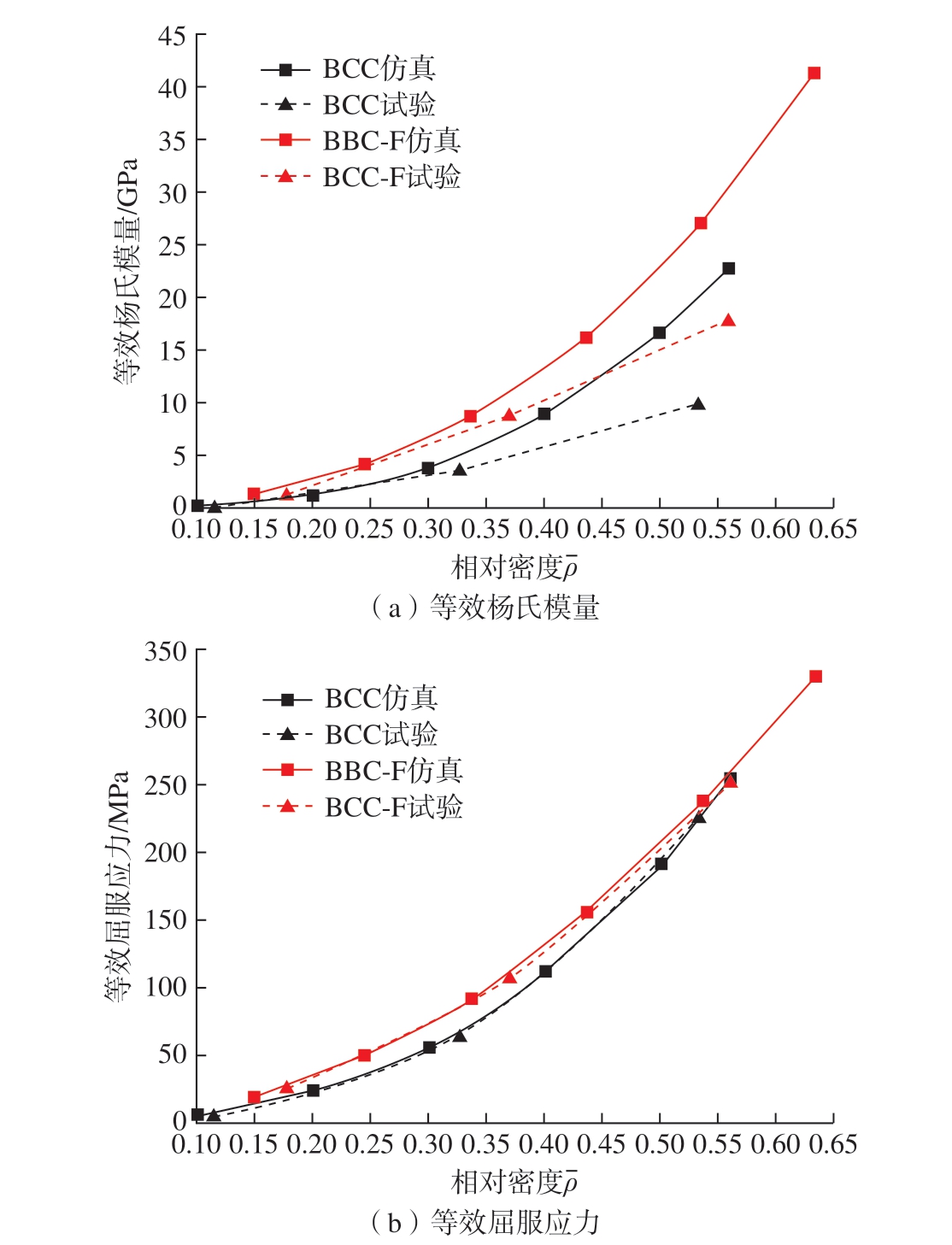
图9 仿真结果与试验结果对比
Fig.9 Comparison between simulation results and test results
4 结论
本文提出的圆角化节点增强方法可以通过控制点阵结构无量纲设计参数，即支杆相对半径及圆角系数来实现点阵支杆交点处几何光滑过渡，从而提高点阵结构的力学性能。对BCC 及BCC-F 点阵结构分别进行数值仿真及单轴压缩试验，试验结果表明，在BCC 及BCC-F 相对密度分别为0.327 及0.370 时，二者等效杨氏模量及等效屈服应力分别为3.71 GPa 和66.32 MPa， 8.98 GPa 和109.04 MPa。可以看出通过增加支杆节点倒圆角，等效杨氏模量及等效屈服应力分别增加了142%和64%，且BCC-F 的破坏模式呈现出“多波峰”的坍塌特点。本研究对提高点阵结构的安全性及点阵结构优化设计具有重要的意义。
[1]ABATE K M, NAZIR A, YEH Y P, et al.Design, optimization, and validation of mechanical properties of different cellular structures for biomedical application[J].The International Journal of Advanced Manufacturing Technology, 2020, 106(3): 1253–1265.
[2]HELOU M, KARA S.Design,analysis and manufacturing of lattice structures:An overview[J].International Journal of Computer Integrated Manufacturing, 2018, 31(3): 243–261.
[3]王向明.飞机新概念结构设计与工程应用[J].航空科学技术, 2020, 31(4): 1–7.WANG Xiangming.New concept structure design and engineering application of aircraft[J].Aeronautical Science & Technology, 2020,31(4): 1–7.
[4]M E Y E R G, WA N G H X,MITTELSTEDT C.Influence of geometrical notches and form optimization on the mechanical properties of additively manufactured lattice structures[J/OL].Materials & Design.[2022–08–22] DOI: 10.1016/j.matdes.2022.111082.
[5]BAI L, YI C, CHEN X, et al.Effective design of the graded strut of BCC lattice structure for improving mechanical properties[J].Materials(Basel), 2019, 12(13): E2192.
[6]PARK S I, ROSEN D W.Homogenization of mechanical properties for material extrusion periodic lattice structures considering joint stiffening effects[J].Journal of Mechanical Design,2018, 140(11): 111414.
[7]CAO X F, DUAN S Y, LIANG J,et al.Mechanical properties of an improved 3D-printed rhombic dodecahedron stainless steel lattice structure of variable cross section[J].International Journal of Mechanical Sciences,2018, 145: 53–63.
[8]姚定烨, 兰彦宇, 马宇立, 等.基于选区激光熔化的Ti–6Al–4V钛合金节点增强型点阵结构及其力学行为[J].热加工工艺, 2023,52(13): 121–126.YAO Dingye, LAN Yanyu, MA Yuli, et al.Ti–6Al–4V node-enhanced lattice structure prepared by selective laser melting and its mechanical behavior[J].Hot Working Technology,2023, 52(13): 121–126.
[9]DALLAGO M, RAGHAVENDRA S, LUCHIN V, et al.The role of node fillet, unitcell size and strut orientation on the fatigue strength of Ti–6Al–4V lattice materials additively manufactured via laser powder bed fusion[J].International Journal of Fatigue, 2021, 142:105946.
[10]DALLAGO M, RAGHAVENDRA S, FONTANARI V, et al.Stress concentration factors for planar square cell lattices with filleted junctions[J].Material Design & Processing Communications, 2020, 2(2).[2019–07–30]https://doi.org/10.1002/mdp2.98.
[11]雷鹏福, 戴宁, 汪志鹏.基于复杂点阵结构的节点强化技术研究[J].机械设计与制造工程, 2018, 47(12): 1–4.LEI Pengfu, DAI Ning, WANG Zhipeng.Research on node enhancement technology of the lattice structure[J].Machine Design and Manufacturing Engineering, 2018, 47(12): 1–4.
[12]朱健峰, 戴宁, 刘乐乐.功能性点阵结构设计优化技术研究[J].机械设计与制造工程, 2020, 49(7): 1–6.ZHU Jianfeng, DAI Ning, LIU Lele.Research on the design and optimization technology of functional lattice structure[J].Machine Design and Manufacturing Engineering,2020, 49(7): 1–6.
[13]SANGLIKAR M A, KOPARKAR P, JOSHI V N.Modelling rolling ball blends for computer aided geometric design[J].Computer Aided Geometric Design, 1990, 7(5): 399–414.
[14]WANG X Y, ZHU L, SUN L, et al.Optimization of graded filleted lattice structures subject to yield and buckling constraints[J].Materials & Design, 2021, 206: 109746.
[15]OMAIREY S L, DUNNING P D,SRIRAMULA S.Development of an ABAQUS plugin tool for periodic RVE homogenisation[J].Engineering with Computers, 2019, 35(2):567–577.
[16]张升, 桂睿智, 魏青松, 等.选择性激光熔化成形TC4钛合金开裂行为及其机理研究[J].机械工程学报, 2013, 49(23): 21–27.ZHANG Sheng, GUI Ruizhi, WEI Qingsong,et al.Cracking behavior and formation mechanism of TC4 alloy formed by selective laser melting[J].Journal of Mechanical Engineering, 2013, 49(23):21–27.
[17]ONAL E, FRITH J, JURG M, et al.Mechanical properties and in vitro behavior of additively manufactured and functionally graded Ti6Al4V porous scaffolds[J].Metals, 2018, 8(4):200.
