为提升飞机作战性能和战场生存能力，飞机主结构对轻量化设计和增加有效载荷的需求日益迫切，而复合材料以可设计性、轻质、高强、抗疲劳、耐腐蚀、易修补等优点成为飞机结构的首选材料，并进一步使飞机复杂结构大部件一体化成形制造成为必然，这也使得复合材料在飞机制造中的用量日趋增加[1]。
目前大型复杂复合材料构件成型精度差，在成型过程中通常在构件边缘留有余量，固化之后再进行铣削去除 （铣边），以满足与其他零部件的装配及连接要求。然而，复合材料由纤维和基体复合而成，其力学性能呈现出明显的各向异性，层间强度低，且碳纤维硬度高、强度大，为铣边带来了极大困难，铣削过程中极易出现撕裂、毛刺、分层、烧伤等加工缺陷[2]。其次，飞机大型复合材料构件产品具有尺寸大、结构复杂、壁厚不均匀、品种多、加工区域可达性差等特点，生产中几乎不能采用现有的通用数控机床完成大型复杂复合材料构件的铣边任务，且人工铣边效率低、精度差，造成产品报废率高[3]。
此外，在传统的生产模式中，大型复合材料构件产品的铣边均采用固定实体模具，每个产品在生产过程中均需要专用模具，而且这些固定实体模具尺寸规格大、制造周期长、存放占用场地大、利用率低，一旦飞机外形设计有微小改动，就要重新制作模具，导致大量工时的耗费，使整个零件的生产开发成本提高。采用柔性工装进行加工是解决此问题的最佳方法[4]。
国外对阵列式柔性工装的研究已较为深入且成熟，西班牙M-Torres公司开发的飞机柔性装配工具TORRESTOOL阵列式柔性工装，以及与之配套的TORRESMILL龙门铣床已被大量应用于实际飞机生产，达到提高飞机零部件的生产效率、降低成本的目的[5]。国内也对阵列式柔性工装技术进行了一定研究，清华大学的陆俊百等[6]设计制造了基于机器人驱动的阵列式柔性工装系统，并研究了柔性工装支承的运行优化方法，但并未涉及复合材料铣边加工的相关研究内容。北京航空航天大学的胡福文等[7]对蒙皮柔性夹持数控切边工艺进行了研究，提出了多点夹持下的工艺设计方法，然而并未对柔性工装布局优化方面的内容进行研究。南京航空航天大学的朱明华[8]提出了面向蒙皮切边定位的动态多点定位方法，不过同样缺少柔性工装的布局优化相关的研究。国内有关柔性工装的研究还较为初步，大多处于应用研究和试验上，且并未涉及复合材料薄壁件铣边加工的相关内容。
本文在以上研究的基础上，利用有限元法进一步研究复合材料铣边加工过程中POGO柱间距、POGO柱到零件边沿距离及复合材料纤维角度对铣边变形的影响规律，提出铣边变形预测方法，为解决柔性工装布局优化提供重要依据。
1 柔性工装系统组成
针对大型复合材料薄壁件铣边的特殊性，本文开发了面向复合材料铣边的阵列式柔性工装系统，其基本结构如图1所示。
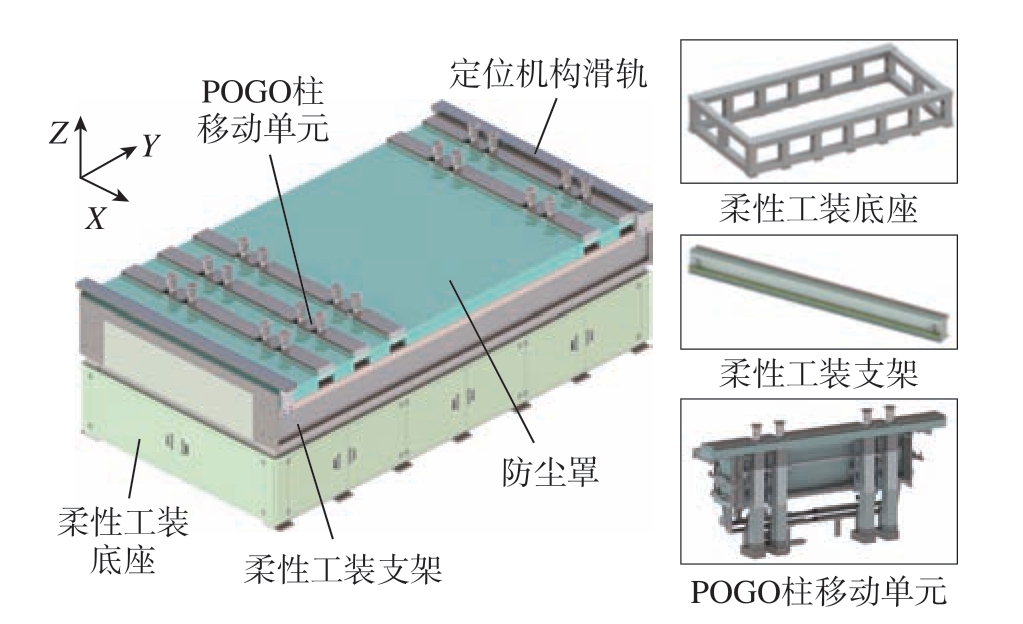
图1 柔性工装示意图
Fig.1 Schematic diagram of flexible tooling system
POGO柱移动单元可以在柔性工装底座上沿Y方向运动，POGO柱Y向最小间距400 mm；单根POGO柱可以在各移动单元上沿X方向运动，POGO柱X向最小间距200 mm，并可以伸缩改变顶端吸盘的Z向高度。在3个方向的运动组合下，POGO柱顶点可以形成拟合待装夹复合材料工件底部曲面的5×4个支承点，并与薄壁件底部紧密贴合。
2 铣边变形有限元模型创建
在柔性工装使用有限数量的POGO柱对工件进行吸附装夹的情况下，由于铣边加工时切削力等外力引起的薄壁件变形与柔性工装支承分布之间的关系，采用有限元仿真的方法研究复合材料薄壁件铣边变形规律，为优化柔性工装支承分布提供依据。
本文中，实际需要采用柔性工装进行铣边加工的复材薄壁件零件尺寸较多，其中最大的零件尺寸达到4 m×2 m，最小的零件尺寸仅为2 m×1 m。
为研究相同材料、不同尺寸的薄壁件零件铣边变形的共性，将柔性工装系统简化为图2所示的复合材料薄壁件及离散分布的支承柱。因为只研究复材薄壁件在铣边过程中的变形，且支承柱本身的变形相比复材薄壁件变形可以忽略不计，因此可认为支承为刚体，在有限元仿真中将支承简化为直径100 mm的解析刚性部件。
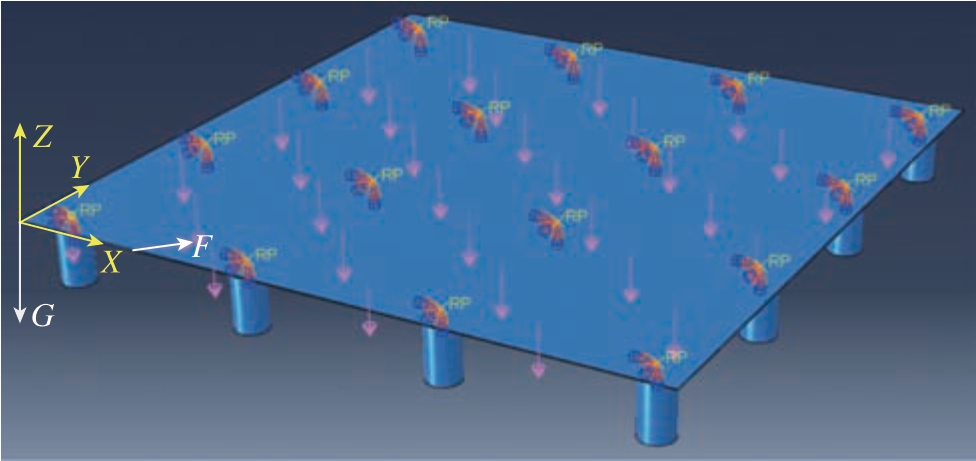
图2 柔性工装系统的简化模型
Fig.2 Simplified model of flexible tooling system
支承柱以4×4等间距排布，其上表面与复材薄壁件下表面之间设置为表面接触，接触属性的切向行为中摩擦采用“罚”公式，根据复材摩擦系数相关研究文献，取摩擦系数为0.3[9]。在复材薄壁件下表面施加垂直向下的表面载荷，以作为支承柱真空吸盘的吸力，大小为0.07 MPa。由于吸附力应当只施加在支承柱与薄壁件表面接触的圆形区域内，故调用ABAQUS提供的UTRACLOAD子程序接口，对表面载荷有效区域进行设置，具体方法：计算节点坐标距离各个支承柱顶部圆心坐标的距离，当距离小于50 mm时，设置该节点载荷α为0.07 MPa，载荷方向为Z的负方向，此外的节点的载荷大小设置为0。在本文所进行的仿真试验中，采取让真空吸盘同时起到定位以及支承作用的方式，仅通过真空吸附力达到限制工件水平方向自由度的目的。
复合材料铺层顺序按照某实际产品中使用的铺层方式，采用厚度0.341 mm的双向碳布材料1与厚度0.166 mm的单向碳布材料2混合铺层，共13层。实际产品固化后厚度测量值为2.898 mm，整体密度为319.7 kg/m3。其中第1、4、7、10、13层为材料1，其余为材料2；第1、7、13层夹角45°，其余层0°。具体铺层方式见图3。铺层中使用的两种材料及其力学性能见表1[10]。
表1 复合材料力学性能[10]
Table 1 Mechanical properties of composite materials[10]
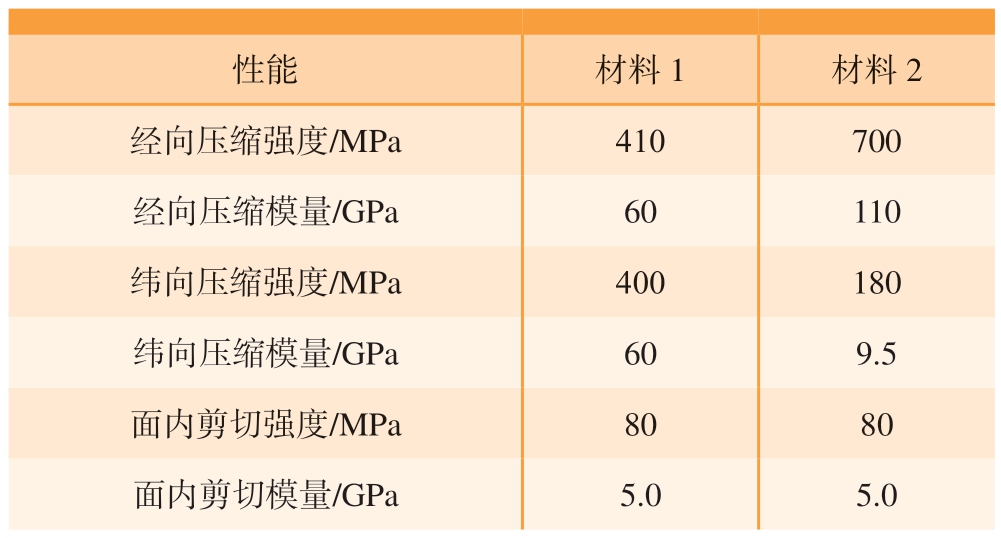
性能 材料1 材料2经向压缩强度/MPa 410 700经向压缩模量/GPa 60 110纬向压缩强度/MPa 400 180纬向压缩模量/GPa 60 9.5面内剪切强度/MPa 80 80面内剪切模量/GPa 5.0 5.0
图3 复材薄壁件铺层方式
Fig.3 Laying method of thin-walled composite parts
铣边加工的过程中，水平方向的分力Fx和Fy为主要铣削力，在ABAQUS中设置切削力F，加载于最左侧两个支承柱的中点宽度0.05 mm的区域内，类型为表面载荷，与边之间的夹角为ψ，本文采用瞬时切削力进行仿真，取ψ=45°，铣削力加载方式如图4所示。
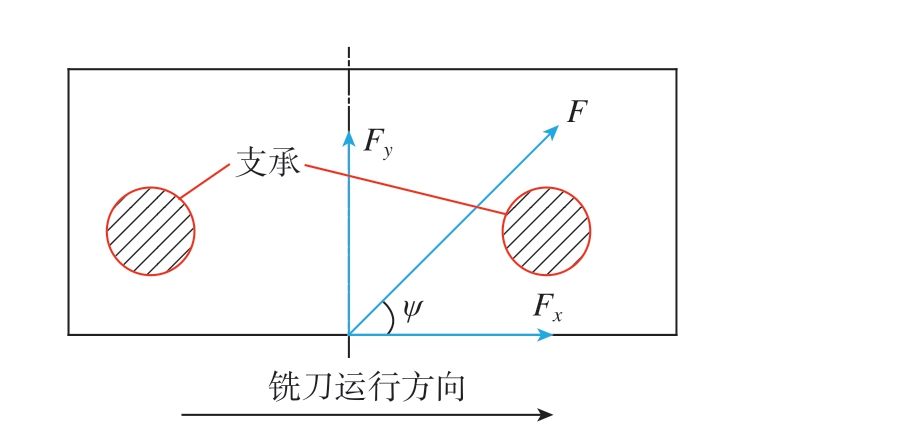
图4 铣削力加载方式
Fig.4 Milling force loading mode
薄壁件的截面属性设置为复合壳，网格尺寸设置为20 mm，为支承柱附加刚性约束，分析步为静力学-通用。采用ABAQUS/STANDARD模式进行仿真分析。
3 仿真结果
由于复合材料薄壁件在柔性工装上装夹时，支承之间的部分处于悬空状态，因此存在两个主要变形，即复合材料构件的自重变形及外力载荷引起的外力变形。
3.1 自重变形仿真
对支承间距400 ～ 800 mm时由于薄壁件自重而引起的变形进行仿真，以初步研究支承间距对于复材薄壁件变形的影响趋势。
对复材薄壁件施加整体自重载荷，此时薄壁件由于自重导致的变形情况如图5（a）所示，其中“×”的位置是支承，A、B两点为薄壁件两条边上支承之间悬空区域的中点，此时支承距离两条边的距离相同。复材薄壁件整体的最大自重变形，以及薄壁件边沿A、B两点处的自重变形与支承柱间距的关系如图5（b）所示。可以看出，自重引起的最大变形出现在4个支承之间悬空区域的中心位置，且与支承间距呈现出近似满足二次多项式关系。此外，复材壁板件边沿A、B两点处的变形并不相等，其中B点处的变形较大，主要原因是该类型复材薄壁件铺层时，双向碳布材料1经纬方向力学性能相同，而单向碳纤维材料2经纬方向力学性能不同，且材料2全部朝向相同方向，导致复材薄壁件整体力学性能呈现各向异性。复材薄壁件的纤维角度示意图如图6所示。
图5 自重变形仿真结果
Fig.5 Simulation results of self-weight deformation
图6 纤维角度示意图
Fig.6 Fiber angle diagram
由图6可知，A、B分别为相互垂直的边1、2上的点；θ为边与纤维方向之间的夹角，可以看出，B所在边纤维角度为A所在边的纤维角度加90°。当θ = 0时，薄壁件铺层状态与图5中自重变形仿真时薄壁件状态相同。因该类型复合材料存在各向异性特点，对主要纤维方向θ和自重变形的关系进行研究。通过在ABAQUS软件中为复材铺层方向附加旋转角度，即可改变主要纤维方向的朝向，进行纤维方向对自重变形影响的仿真研究，其结果如图7所示。
图7 纤维角度–自重变形关系
Fig.7 Relationship between fiber angle and self-weight deformation
由图7可以看出，纤维角度对复材薄壁件内部区域的最大变形影响较小，变形变化量在0.005 mm以内。边沿上A、B两点处的自重变形与纤维角度关系以纤维角度45°为对称线轴对称，从图6可知，B点处纤维角度为θA + 90°，故可认为边沿处的自重变形与纤维方向与边沿的夹角以180°为周期的规律变化。对于A点来说，由于变形与角度相关，且在0°时自重变形最小，90°时最大，故可以用近似公式表示，即
式中，Ae为与复合材料性能有关的系数；δπ/4为纤维角度45°时的边沿自重变形。
3.2 铣边变形仿真
薄壁件铣边中的另一主要变形为外力载荷引起的变形。通过在两排支承正中央A点处施加45°方向载荷，模拟铣边过程中的切削力，在不施加重力载荷的情况下，对支承间距400 ～ 800 mm、支承到边沿70 ～ 140 mm时边沿水平方向最大变形进行仿真，以研究支承间距、边距 （指最外侧支承到复材薄壁件边沿的垂直距离）对加工点变形的影响。
首先，研究了载荷大小对铣边变形的影响，选取支承间距400 mm、500 mm、600 mm 3种支承分布，分别施加大小不同的载荷，其仿真结果如图8所示。可以看出，在各个间距下载荷与水平变形之间都呈现明显的线性关系，因此在之后的仿真研究中，只选取外力载荷100 N作为标准，其他外力载荷下的变形量可以由100 N的变形计算得到。
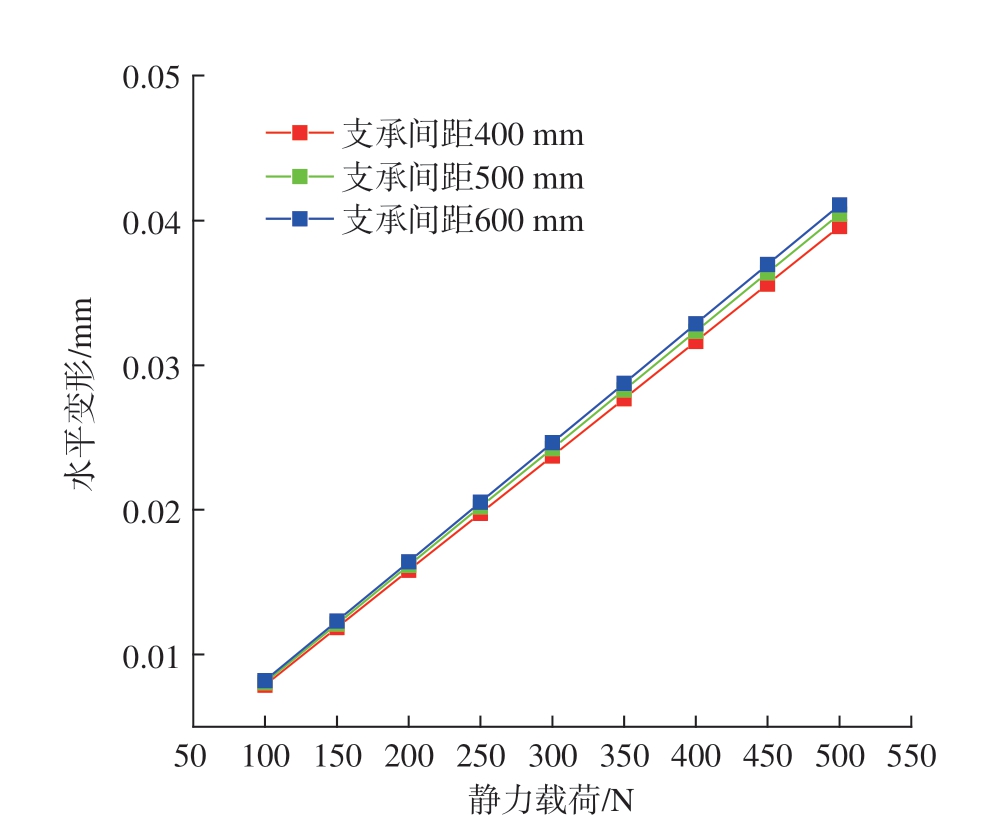
图8 载荷–水平变形关系
Fig.8 Relationship between load and horizontal deformation
其次，对间距、边距对水平变形的影响进行仿真。对间距400～800 mm，以及边距70～140 mm的各个分布组合夹持下的薄壁件施加外力载荷100 N。仿真结果如图9所示。可以看出，水平变形与间距、边距呈正相关关系，得到的图像近似存在起伏的倾斜平面，最大变形出现在间距800 mm、边距140 mm的组合下，为0.008645 mm，最小变形出现在间距400 mm、边距70 mm的组合下，为0.007445 mm，二者相差0.0012 mm。为更具体研究间距、边距对水平变形的影响，在间距600 mm处与边距100 mm 处分别做截面，得到仅间距、边距对水平变形的影响，其结果如图10所示。可以看出，二者都呈现近似线性的正相关关系，但存在一定的起伏，有可能是有限元软件会将受力转换到各节点上进行计算，而网格尺寸一致的情况下，由于间距、边距不同导致其变形出现一定偏差，其具体原因有待进一步研究。铣边变形与边沿处自重变形相同，会受纤维方向影响。通过在ABAQUS软件中部件属性内修改铺层方向的附加旋转角，针对0 ～ 180°各纤维角度对铣边变形的影响进行了仿真研究，结果如图11所示。
图9 间距–边距仿真结果
Fig.9 Simulation results of support spacing–edge distance
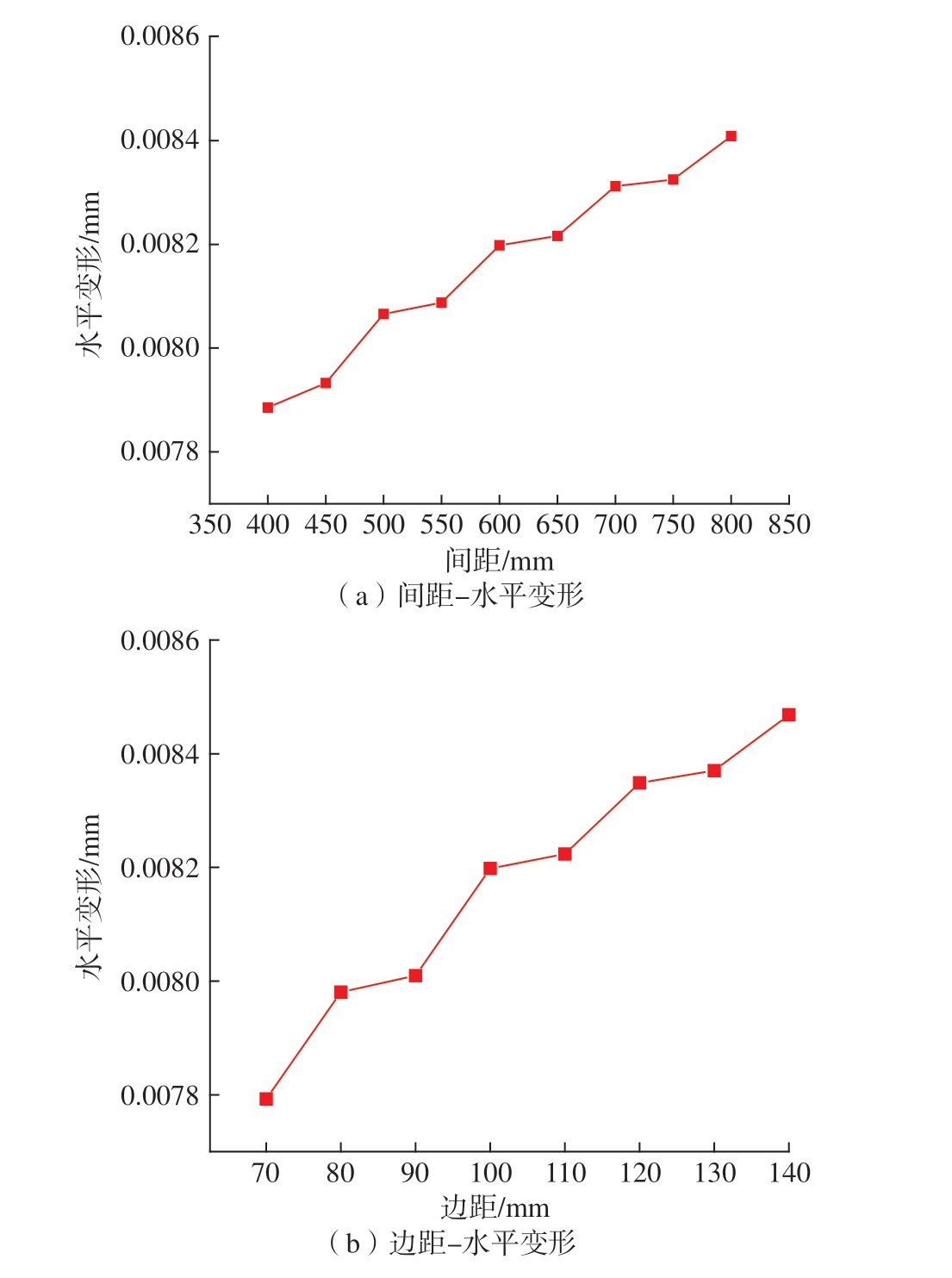
图10 间距–边距对水平变形的影响
Fig.10 Effect of spacing-edge distance on horizontal deformation
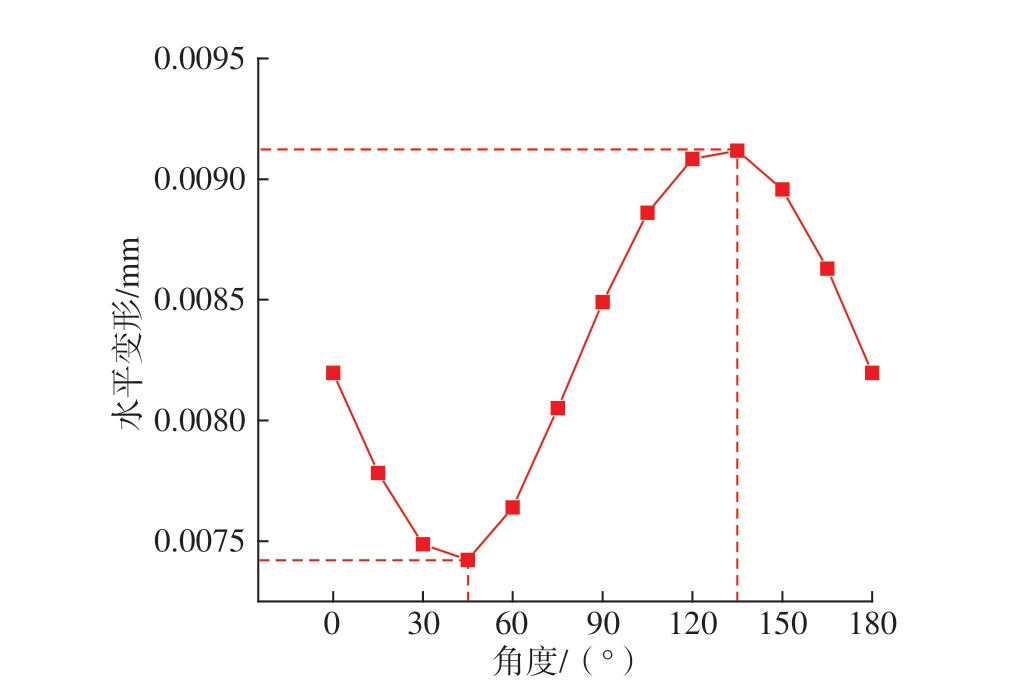
图11 纤维角度–水平变形图
Fig.11 Relationship between fiber angle and horizontal deformation
主要纤维角度对水平方向变形的影响曲线近似正弦曲线，在45°时，即外力方向与主要纤维方向相同时，铣边变形最小；在135°时，即外力方向垂直于主要纤维方向时，铣边变形最大。因复材薄壁件主要纤维方向与受力方向的夹角不同，产生不同的变形量 （Δθ），因此采用正弦函数近似描述该关系，即
式中，k2为与复合材料性能有关的系数；δπ/2为纤维角度90°时外力载荷引起的变形。
4 复合材料薄壁件变形预测拟合方程
基于3.1节与3.2节中的仿真数据，综合间距、边距、纤维方向等参数，对复合材料薄壁件变形的整体影响关系进行研究，建立薄壁件铣边变形拟合方程，以实现对任何支承分布下该铺层方式薄壁件的变形预测。
4.1 自重引起的变形
基于仿真数据规律，构建以下预测方程：
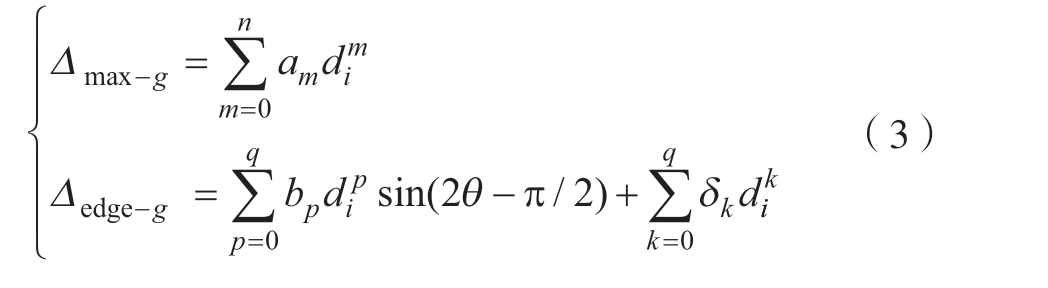
预测方程的具体构造方法如下：Δmax-g为复材薄壁件因重力引起的最大变形，由图5可以看出，间距与最大变形近似多项式关系，故采用多项式
对其进行拟合，am（m = 0，…，n）为间距
项的系数，采用相关软件可以快速计算拟合结果；Δedge-g为边沿自重变形，其同时受到间距以及纤维角度的影响，且由图7可知，边沿自重变形图像可以写作如式 （1）所示的周期为180°的三角函数Ae sin（2θ - π/2） + δπ/4，同时，由图5可以看出，间距与边沿处自重变形也近似多项式关系，令式 （1）中系数Ae等于多项式
等于多项式
，必须首先确定两个多项式在各个间距下的值。而纤维角度0时，点B处的变形等于纤维角度90°时点A的变形，将此时的变形代入式 （3），则有
式中，ΔA，0与ΔB，0分别为纤维方向0°时A、B点处自重变形。
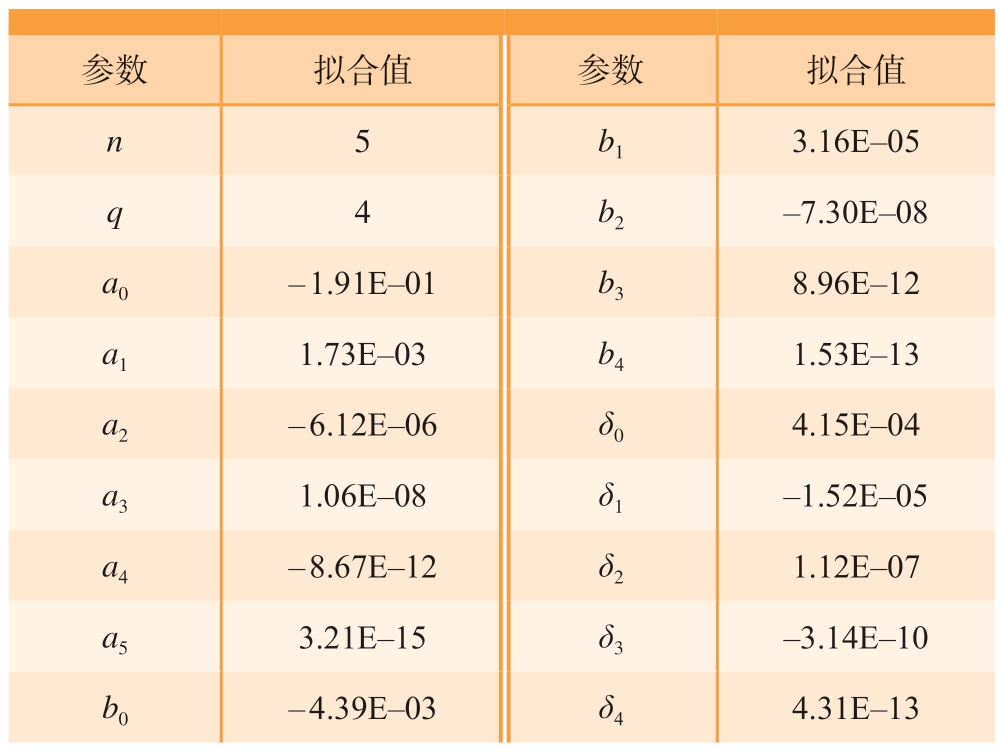
通过已有数据，对式 （4）和 （5）中各参数进行拟合，最后得到的参数值如表2所示。
表2 自重变形预测方程拟合参数
Table 2 Fitting parameters of self-weight deformation prediction equation
参数 拟合值 参数 拟合值n 5 b1 3.16E-05 q 4 b2 -7.30E-08 a0 - 1.91E-01 b3 8.96E-12 a1 1.73E-03 b4 1.53E-13 a2 - 6.12E-06 δ0 4.15E-04 a3 1.06E-08 δ1 -1.52E-05 a4 - 8.67E-12 δ2 1.12E-07 a5 3.21E-15 δ3 -3.14E-10 b0 - 4.39E-03 δ4 4.31E-13
为验证预测方程的准确性，设置如表3所示的3组参数，在前文已进行过仿真计算的间距与角度组合的基础上，分别为只改变间距、只改变角度、两个参数都改变，通过式 （3）的预测方程及有限元仿真的方法进行计算。
表3 自重变形预测值与仿真值对比
Table 3 Comparison between predicted and simulated self-weight deformation values
参数 第1组 第2组 第3组间距/mm 900 600 900角度/（°） 0 45 45最大变形-预测值/mm 0.3196 0.0505 0.3196最大变形-仿真值/mm 0.3106 0.0479 0.2995最大变形预测误差/% 2.9 5.43 6.71边沿变形-预测值/mm 0.0600 0.0215 0.1317边沿变形-仿真值/mm 0.0579 0.0223 0.1340边沿变形预测误差/% 3.6 3.59 1.72
通过表3 可以看出，建立的薄壁件自重变形预测方程能一定程度上符合仿真结果，边沿变形预测值与仿真值的误差最大为3.6%。而最大变形预测值误差达到了6.71%，主要原因是最大变形预测方程忽略了角度的影响，故最大误差较大。自重变形预测方程对边沿变形的预测则有较好的效果。
4.2 外力载荷引起的边沿变形
基于仿真数据规律，构建预测方程为
预测方程的具体构造方法：水平方向最大变形Δ受到纤维角度影响，由图11可知，水平变形曲线可以写作式 （2）所示的周期为180°的三角函数k2sin（2θ - π）+δπ/2，同时由于图9中曲面近似为平面，采用平面方程进行拟合，使式 （2）中系数k2等于 （adi + bde + c），δπ/2等于（mdi + nde + q），这两个参数受支承间距与边距影响。
与自重预测方程相同，同理可得
式中，Δ0与Δ45分别为受力点0、45°时的水平方向变形。
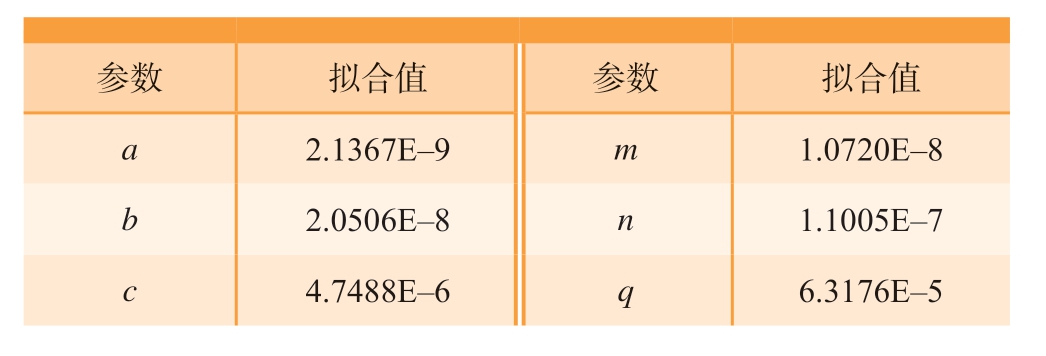
使用已有数据对式 （6）和 （7）中各参数进行拟合，最后得到的参数值如表4 所示。
表4 铣边变形预测方程拟合参数
Table 4 Fitting parameters of milling edge deformation prediction equation
参数 拟合值 参数 拟合值2.1367E-9 m 1.0720E-8 b 2.0506E-8 n 1.1005E-7 c 4.7488E-6 q 6.3176E-5 a
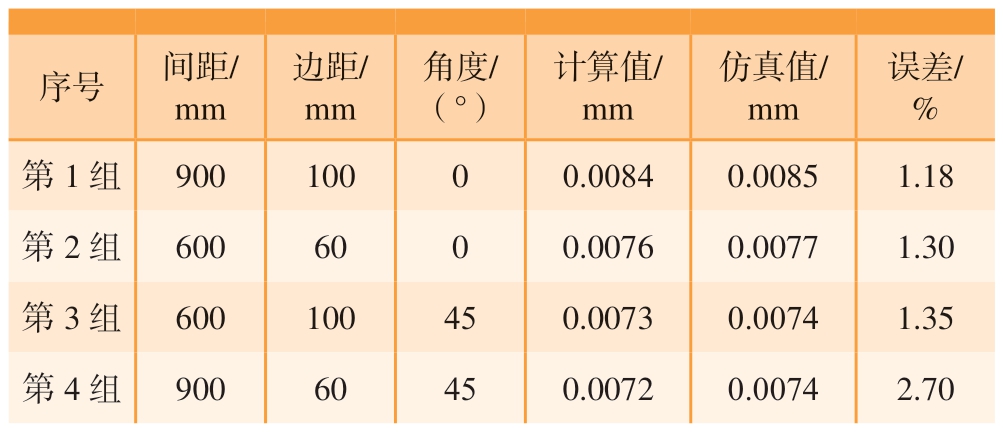
为验证预测方程的准确性，设置如表5所示的4组参数，在前文已进行过仿真计算的间距、边距与角度组合的基础上，分别为只改变间距、只改变边界、只改变角度及3个参数都改变，通过式 （5）的预测方程及有限元仿真的方法分别进行计算。
表5 铣边变形预测值与仿真值对比
Table 5 Comparison of predicted value and simulation value of milling edge deformation
序号 间距/mm边距/mm角度/（°）计算值/mm仿真值/mm误差/%第1组 900 100 0 0.0084 0.0085 1.18第2组 600 60 0 0.0076 0.0077 1.30第3组 600 100 45 0.0073 0.0074 1.35第4组 900 60 45 0.0072 0.0074 2.70
从表5可以看出，铣边变形预测方程可以较好地预测任意间距、边距以及纤维角度组合下的边沿变形，与仿真结果的误差在3%以内，可以认为铣边变形预测方程具有较高的准确性。
5 结论
基于有限元方法对多点式柔性工装夹持复合材料薄壁件进行铣边加工的过程中，柔性工装支承分布对边沿变形产生的影响进行了仿真研究，并提出了薄壁件铣边变形的预测方法。
（1）薄壁件最大自重变形出现在相近4个支承之间的悬空区域的中心，且变形值随支承间距增大而增大；薄壁件边沿自重变形会随纤维方向与边沿之间的夹角以180°为周期变化，并在纤维角度为90°时变形量最大。
（2）铣边变形同时受纤维角度与支承间距、边距影响，并在纤维角度与受力方向垂直时变形最大，在本文的仿真试验中该角度为135°；支承间距、边距对铣边变形的影响可以采取近似线性关系进行处理。
（3）本文提出的铣边变形预测方法可以较为准确地预测柔性工装各支承分布下薄壁件相应的最大自重变形、边沿自重变形及铣边变形大小，预测值与仿真值间最大误差分别为6.71%、3.6%、2.70%。
[1] 游军权, 周富民, 乔鹏. 浅析复合材料在武装直升机上的应用[J]. 中国科技信息, 2013(18): 138.YOU Junquan, ZHOU Fumin, QIAO Peng. Application of composite materials in armed helicopter[J]. China Science and Technology Information,2013(18): 138.
[2] 康永峰, 陈树巍, 袁士平, 等. 大型碳纤维复合材料壁板轮廓数控铣削工艺技术[J]. 航空制造技术, 2013, 56(15): 70-73.KANG Yongfeng, CHEN Shuwei, YUAN Shiping, et al. NC milling technology for large carbon fiber composites panel contour[J]. Aeronautical Manufacturing Technology, 2013, 56(15): 70-73.
[3] 高航, 王奔, 黄均亮, 等. 大型复合材料构件数字化加工工装与装置的开发与应用[J]. 航空制造技术, 2012, 55(18): 38-43.GAO Hang, WANG Ben, HUANG Junliang, et al. Development and application of digital machining device and equipment for large composites component[J]. Aeronautical Manufacturing Technology, 2012, 55(18): 38-43.
[4] 周凯. 飞行器大型薄壁件制造的柔性工装技术[J]. 航空制造技术, 2012, 55(3): 34-39.ZHOU Kai. Flexible tooling and fixture technology of large thinwall part manufacturing for aircraft[J]. Aeronautical Manufacturing Technology, 2012, 55(3): 34-39.
[5] 丁韬. TORRESMILL(R)和TORRESTOOL(R)系统蒙皮切边钻铣床及柔性夹具装置[J]. 航空制造技术, 2007, 50(2): 108-109.DING Tao. TORRESMILL(R) and TORRESTOOL(R) system skin trimming drilling and milling machine and flexible fixture device[J].Aeronautical Manufacturing Technology, 2007, 50(2): 108-109.
[6] 陆俊百, 周凯, 张伯鹏. 飞行器薄壁件柔性工装定位/支承阵列优化自生成研究[J]. 中国机械工程, 2010, 21(19): 2369-2374, 2378.LU Junbai, ZHOU Kai, ZHANG Bopeng. Research on optimization of location/support array of flexible tooling system for aircraft large-scale thin-wall workpiece[J]. China Mechanical Engineering, 2010, 21(19):2369-2374, 2378.
[7] 胡福文, 李东升, 李小强, 等. 蒙皮柔性夹持数控切边的工艺设计方法[J]. 北京航空航天大学学报, 2012, 38(5): 675-680.HU Fuwen, LI Dongsheng, LI Xiaoqiang, et al. Process planning of aircraft skins NC trimming based on reconfigurable fixture[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 675-680.
[8] 朱明华. 面向精准装配的飞机钣金零件成形关键技术研究[D]. 南京: 南京航空航天大学, 2016.ZHU Minghua. Research on key technology of aircraft sheet metal part forming technique for precise assembly[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016.
[9] 彭赫, 张锦光, 叶梦勇. 碳纤维复合材料摩擦性能试验研究[J]. 数字制造科学, 2021, 19(1): 22-25.PENG He, ZHANG Jinguang, YE Mengyong. Experimental investigation on the tribological properties of the carbon fiber composites[J].Digital Manufacture Science, 2021, 19(1): 22-25.
[10] 马子广, 王卫卫. 某国产复合材料层压板压缩稳定性研究[J]. 力学研究, 2017, 6(2): 9.MA Ziguang, WANG Weiwei. Study on compression stability of a domestic composites laminate[J]. International Journal of Mechanics Research, 2017, 6(2): 9.