近年来,高空长航时太阳能无人机发展迅猛,随着太阳能推进系统、电池技术、材料科学的进步,高空长航时太阳能无人机的载荷能力、航行时间不断提升,逐渐具备一定的商用价值[1]。为提高升限、延长留空时间[2]、减小能量消耗,太阳能无人机结构的重量控制面临新的挑战。来自不同国家及机构的太阳能无人机结构特征各有区别,共同点如下。
(1)大量采用复合材料来满足太阳能无人机苛刻的重量要求,复合材料使用率基本接近100%[3]。
(2)采用大展弦比设计降低诱导阻力,从而提供更高的整机升阻比及更低的翼载荷[4]。
(3)为满足太阳能板铺设及结构轻量化需求[5],一般采用轻质柔性蒙皮,且蒙皮不承载,载荷主要通过主梁承担。
对于大展弦比无人机而言,翼梁作为机翼的主承力结构,几乎承受机翼的全部载荷,对飞机的飞行性能至关重要,因此复合材料翼梁的设计是太阳能无人机结构设计的核心,当前应用较为成功的翼梁结构形式有圆管梁及夹芯板方管梁两种,其各自代表的型号见图1。

图1 两种太阳能无人机结构
Fig.1 Two kinds of solar-powered UAV structures
典型太阳能无人机型号中,复合材料圆管梁使用最多,主要代表包括空客的“Zephyr”,其结构如图1(a)所示。此外,美国NASA “Helios”系列飞机[6]及中国“彩虹”太阳能无人机等也均采用了圆管翼梁。空客“Zephyr”系列的最新型号“Zephyr S”翼展达到25 m、起飞重量62~65 kg、有效载荷5 kg,保持着平流层连续飞行64 d的最长纪录。
“Solar Impulse”太阳能载人飞机翼梁则采用蜂窝夹芯板方管梁结构,如图1(b)所示,方形管梁的对接接头采用了承弯承剪耳片对接。历经两代发展[7],“Solar Impulse 2”于2016年达成了仅用太阳能完成环球飞行的设计目标,其翼展达到了72 m,起飞重量约2400 kg[7]。“X-HALE”[8]无人机也采用方管梁的类似结构,上下缘贴合翼型外型面,从而实现最大的抗弯刚度,机翼中间采用铝合金接合段对接。
在太阳能无人机翼梁的优化设计方面,国内外学者做了较多研究工作,但研究对象及方法各有不同。昌敏等[9]研究了太阳能无人机复合材料梁典型截面承载能力的理论计算方法,并计算了不同参数组合的截面应力,提出仅考虑正应力约束,工字梁承载效率高于方形梁及圆管梁,但工字梁承扭能力较差,一般不使用,同时提出一种基于数值计算、展向分区、优化铺层的翼梁设计流程,但设计中未考虑结构稳定性。曹岩等[10]对比了不同梁的特征,结论和文献[9]相符,并通过有限元法对蜂窝夹芯方梁结构的设计参数组合进行了计算,但是并未涉及屈曲及铺层的设计。英国索尔福德大学的Alsahlani等[11]也利用与文献[9]中类似的解析方法计算分析了梁截面,研究了失效的区域,并给出了计算方法。北京航空航天大学的Zhang等[12]针对泡沫夹芯方管梁,先优化截面铺层层数再优化夹芯参数,完成了两阶优化并开展了试验,结果表明,夹芯结构相比于层压板结构可以减少刚度溢出和增加临界屈曲载荷,并改善了太阳能无人机的飞行效率,但在铺层优化时,未考虑翼梁整体尺寸变量及部分铺层约束要求。
本文提出了一种太阳能无人机复合材料翼梁的设计方法,避免了设计前期建立全机有限元模型的反复迭代计算,在满足铺层对称性和限制应变约束、稳定性约束的前提下实现了太阳能无人机翼梁结构选型及参数的快速优化设计。本文针对大尺寸复合材料圆管梁进行研究并提出了一种新型的专用工艺方法,制造出合格样件并进行了试验。
1 机翼结构及设计
本文研究的超大展弦比柔性机翼采用碳纤维复合材料翼梁、复合材料桁架肋、芳纶柔性蒙皮的典型复合材料轻质结构,薄膜蒙皮承受气动载荷,翼肋将气动载荷引起的弯矩、剪力和扭矩传递到主梁,由其全部承受。主梁位于距离机翼前缘约30%平均气动弦长位置处,基本在机翼的气动压心线上,从而尽可能减少附加扭矩。对于大展弦比太阳能无人机机翼结构而言,由于翼载荷低,以及动力电机、机身等部件对机翼的卸载作用,使得机翼剪力较小,但由于机翼翼展大,所以机翼根部弯矩大,因此本文以抗弯作为设计中主要考虑的载荷,另一方面,由于铺层对称性可能影响零件变形并导致内应力,本文同时考虑了铺层的对称性。
复合材料结构设计中首先需要满足强度要求,对于强度约束,工程计算中一般采用应变限制;考虑到屈曲问题,还需限制屈曲载荷值下限;为研究结构全部的承载特性,还需考虑破坏载荷。全部约束由式 (1)描述。

式中,Ldmg、Lblk分别为梁发生破坏、屈曲时的载荷,必须高于外部载荷的最大值Lmax;[ε]为翼梁任意一点的应变值的集合,在工程中,一般要大于限制的最小的压缩应变εmin,小于限制的最大拉伸应变εmax。
一般来说,应变值范围的确定与材料性能及工程要求有关系,本文取应变的上下限为±3500 με,对于截面对称的梁结构,由于在纯弯矩作用下,最大拉应变和最大应变值十分接近,一般考虑受压部分即可。在满足上述约束条件时,使得设计结构达到最轻为设计目标。
2 翼梁承载能力分析
2.1 计算方法
对于匀质材料而言,通过计算截面形状的惯性矩即可得到截面的抗弯刚度,并可以根据外部载荷计算截面不同点的应力、应变值。
圆形、方形典型截面的设计变量如图2所示。
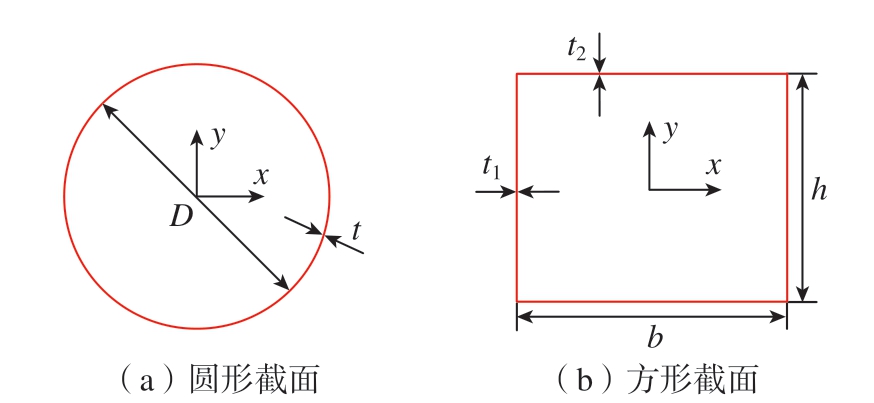
图2 截面及其设计参数
Fig.2 Section and design parameters
惯性矩IA的基本计算公式为
式中,y为截面任意点的纵向坐标;A为截面几何区域。
通过材料的杨氏模量可计算出对应弯矩下截面的应力、应变。而对于复合材料层压板结构,根据复合材料层压板理论,通过层压板的单层力学性能和铺层方案计算出层压板的等效模量Ex,其方向垂直于梁的截面,计算方法为[12]
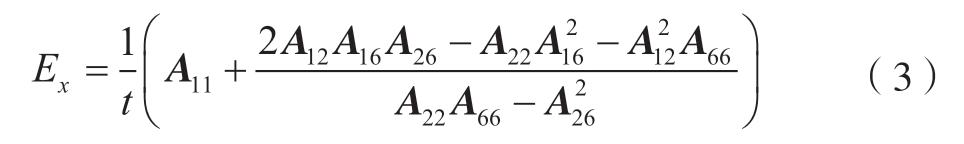
式中,t为层压板总厚度;Aij为总铺层结构的面内刚度矩阵值[13],计算方式为
式中,i、j取1、2、6。折算刚度矩阵Qij由单层铺层材料的基础力学参数决定;tk则为第k层铺层的厚度[13]。对于可以分为多个层压板计算的截面形式,可以通过截面各部分的Ex和对应部分的惯性矩IA计算总截面抗弯能力表征值![]() ,即[11]
,即[11]
式中,Ei代表截面的第i部分层压板的Ex;Ii为截面第i部分层压板对应的惯性矩IA。对于连续形状的截面,可以写为积分形式,即
此时的Ex为对应位置的层压板等效模量。当确定了截面的限制应变ε,则可以根据式 (7)计算出截面对应的弯矩载荷值Mx。
式中,Mx是截面上承载的弯矩;Y为截面应变最大或最小点距离形心的纵向高度。
2.2 梁截面方案承载特性解析计算分析
在复合材料薄壁结构中,屈曲的发生常在材料强度极限之前,对于太阳能无人机的大展弦比机翼,梁的屈曲问题需要重点考虑。圆管梁由于拉压面都为曲面,有效提高了其抗屈曲能力;对于方形梁而言,面板则可以采用夹芯结构提升抗屈曲能力,相比无夹芯结构,能够有效提高其屈曲特征值。因此后续的研究选择层压板圆管梁和夹芯板方管梁作为研究对象。
本文针对这两种典型构型的梁截面,利用2.1节中的方法计算其应变对应载荷。考虑外形几何限制、工艺要求等因素,设计圆管梁截面直径D = 240 mm,夹芯方管梁边长为L= 240 mm,四边圆角内径r = 24 mm,外径R = 32 mm,芯材厚度为8 mm,腹板和上下板铺层相同,截面形状见图3。为了尽量降低机翼的变形,提高刚度和强度,材料的选用遵循轻质、高强、高模量的原则。本文选择具有较高纤维方向模量的M40J单向带预浸料;考虑到结构局部加强、切削加工及铺层成型的要求,还需有织物参与铺层,综合成本及材料性能,选用W3021织物预浸料;夹芯结构材料选择芳纶纸蜂窝,在相同密度时,芳纶纸蜂窝比常用的PMI泡沫夹芯材料具有更高的支撑方向模量。材料参数见表1和2,截取样段长度1000 mm。
表1 单层复合材料弹性力学参数
Table 1 Elastic parameters of single layer composite
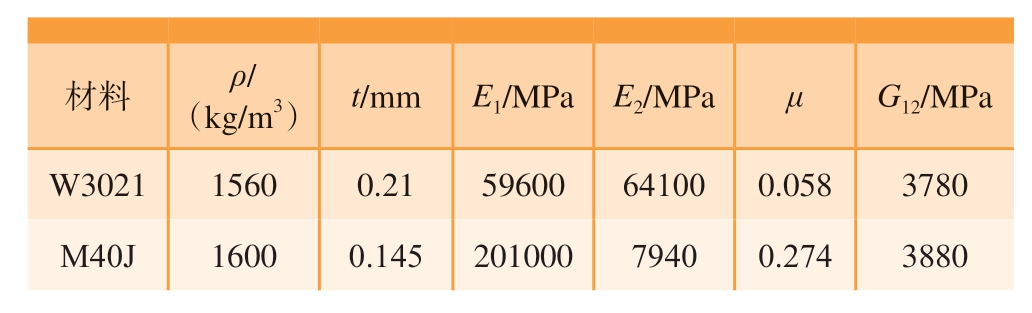
注:ρ为密度;t为厚度;μ为泊松比;E1、E2为1、2方向的弹性模量;G12为12面内的剪切模量。
材料 ρ/(kg/m3) t/mm E1/MPa E2/MPa μ G12/MPa W3021 1560 0.21 59600 64100 0.058 3780 M40J 1600 0.145 201000 7940 0.274 3880
表2 芳纶纸蜂窝芯材料等效弹性力学工程常数
Table 2 Equivalent elastic engineering constant of aramid paper honeycomb core material

注:E3为3方向的弹性模量;μ12、μ13、μ23分别为12、13、23面内的泊松比。
E1/MPa E2/MPa E3/MPa μ12 μ13 μ23 G12/MPa 1 1 148 0.37 0.01 0.01 3.6
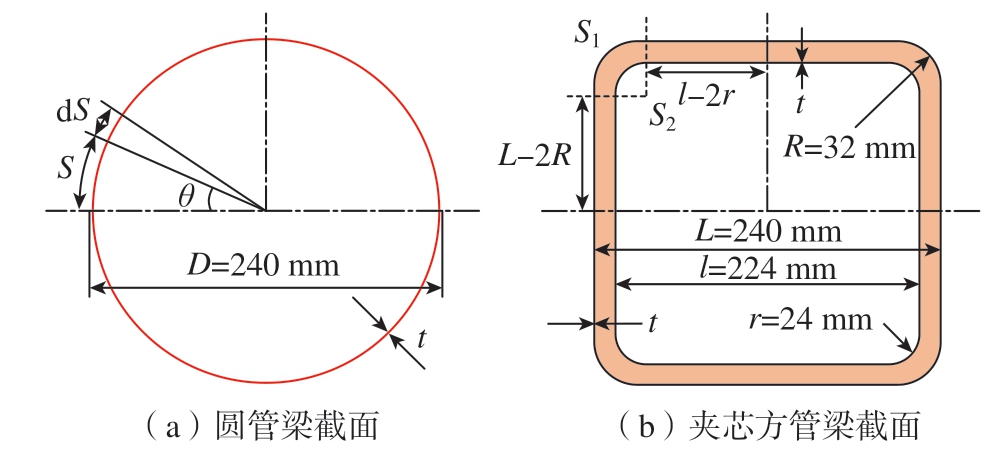
图3 样段截面示意图
Fig.3 Cross-section diagram
通过计算不同铺层对应的载荷来研究不同截面梁的承载特性,并为后续展向铺层设计做基础工作。其中不同厚度对应的铺层利用文献[14]中的方法生成,其基本思路:先生成多种铺层比例交叉融合的铺层库,再对铺层顺序根据约束条件进行筛选,根据设计指标确定最优核心层组,最后基于此层组进行加层和丢层,形成完整铺层库。本文基于此方法对生成的铺层库进行设计,从而保证铺层对称性并提高了结构稳定性,生成的铺层库结果见表3,两种不同截面梁的铺层均从中选取。
表3 铺层库
Table 3 Lay up library
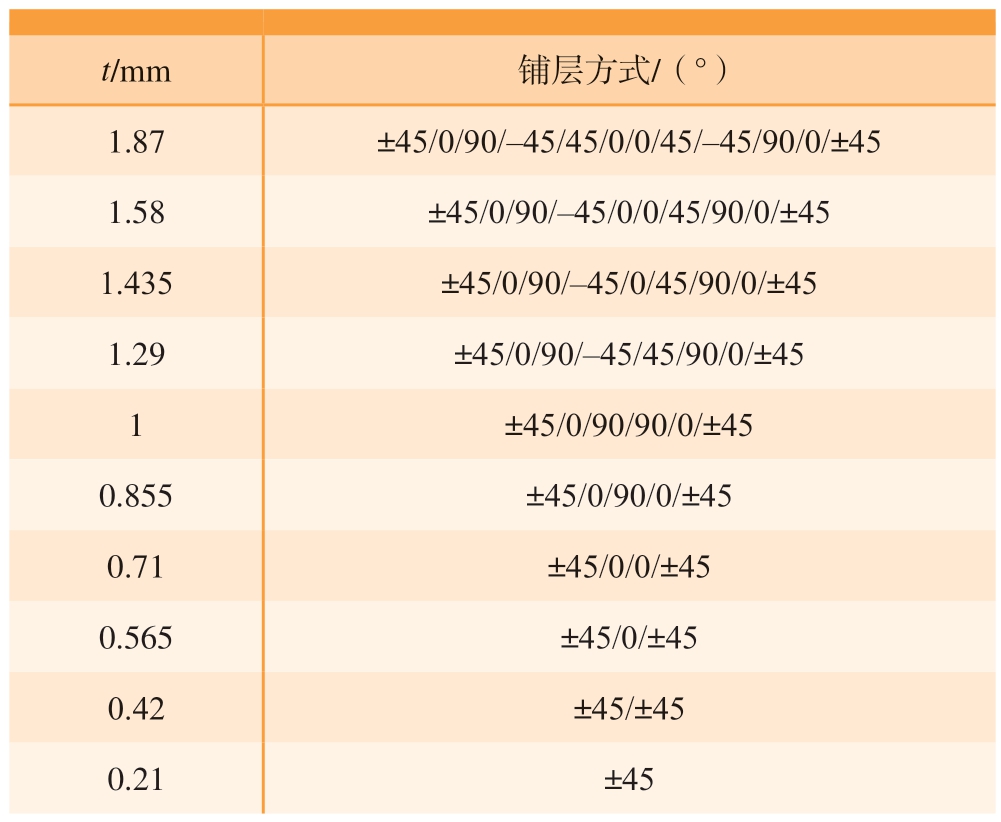
t/mm 铺层方式/(°)1.87 ±45/0/90/-45/45/0/0/45/-45/90/0/±45 1.58 ±45/0/90/-45/0/0/45/90/0/±45 1.435 ±45/0/90/-45/0/45/90/0/±45 1.29 ±45/0/90/-45/45/90/0/±45 1±45/0/90/90/0/±45 0.855 ±45/0/90/0/±45 0.71 ±45/0/0/±45 0.565 ±45/0/±45 0.42 ±45/±45 0.21 ±45
针对两种不同截面,通过式 (5) ~(7)计算其不同铺层在设计应变下的载荷值,其中![]() 、Mx1对应圆管梁,
、Mx1对应圆管梁,![]() 、Mx2对应夹芯板方管梁。如图3(a)所示,圆管梁的
、Mx2对应夹芯板方管梁。如图3(a)所示,圆管梁的![]() 为
为
对于图3(b)所示带圆角的蜂窝夹芯板方管梁,由于夹芯材料相比面板材料在面内方向杨氏模量极小,所以对整体抗弯刚度几乎没有贡献,分析时可以忽略芯材,只考虑两层面板,即在计算![]() 时仅求和内外面板对应的项,从而简化计算,与非夹芯结构的计算方法相同。将截面分为内外 (S2、S1)两部分,对每部分的1/4进行分段线积分并求和
时仅求和内外面板对应的项,从而简化计算,与非夹芯结构的计算方法相同。将截面分为内外 (S2、S1)两部分,对每部分的1/4进行分段线积分并求和![]() 计算化简结果为
计算化简结果为
计算结果统计见表4。
表4 计算结果统计
Table 4 Calculation result statistics
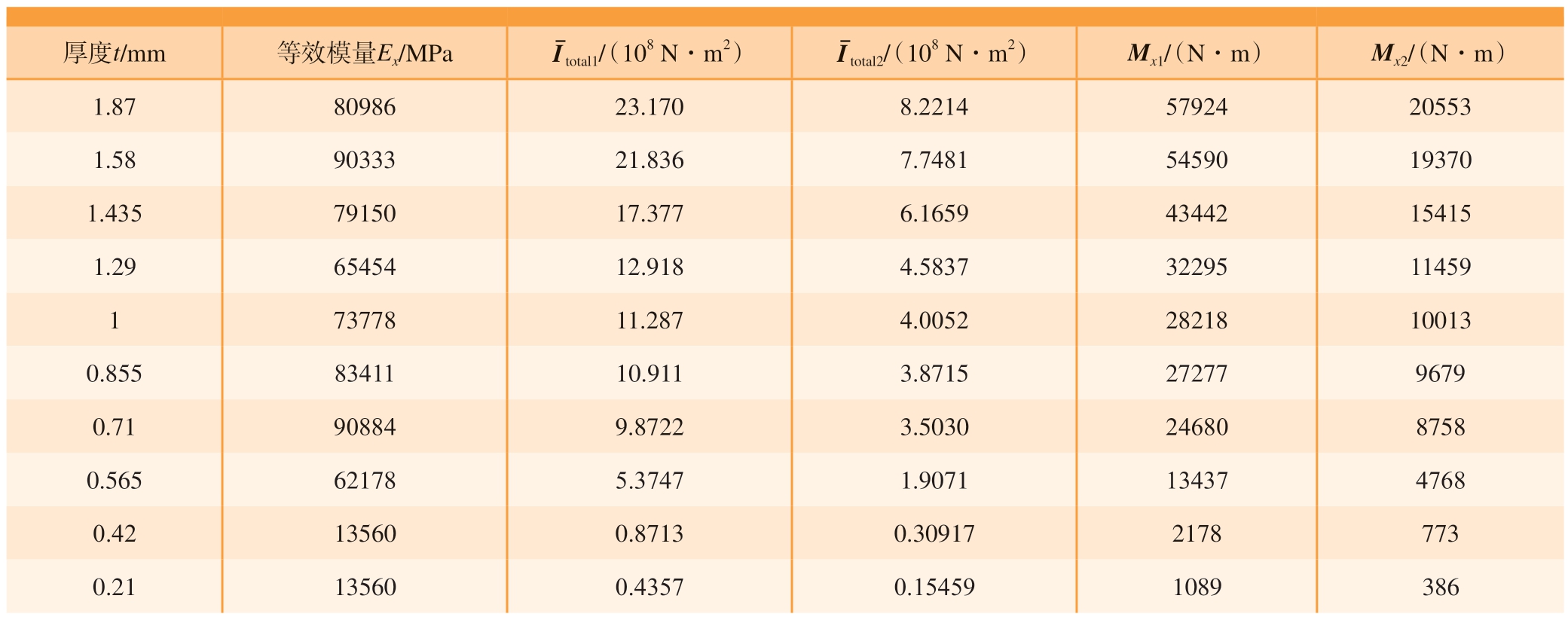
厚度t/mm 等效模量Ex/MPa I total1/(108 N·m2) I total2/(108 N·m2) Mx1/(N·m) Mx2/(N·m)1.87 80986 23.170 8.2214 57924 20553 1.58 90333 21.836 7.7481 54590 19370 1.435 79150 17.377 6.1659 43442 15415 1.29 65454 12.918 4.5837 32295 11459 1 73778 11.287 4.0052 28218 10013 0.855 83411 10.911 3.8715 27277 9679 0.71 90884 9.8722 3.5030 24680 8758 0.565 62178 5.3747 1.9071 13437 4768 0.42 13560 0.8713 0.30917 2178 773 0.21 13560 0.4357 0.15459 1089 386
2.3 梁截面方案承载特性仿真分析
为进一步验证解析法的计算精度,并研究梁的屈曲和破坏载荷,本文通过ABAQUS有限元分析软件对梁样段模型进行计算分析。样段的约束方式为一端固支,在悬臂梁的另一端施加纯弯矩载荷,模拟翼梁实际受载状态。层压板圆管梁采用S4R壳单元模拟;夹芯方管梁则采用SC8R单元模拟层压板面板,将蜂窝夹芯视为各向异性匀质材料,用C3D8R体单元进行模拟,单元共节点约束,厚度方向单元数4个。在分析中,做如下假设:(1)夹芯和面板的胶接面足够牢固,不会先于面板发生失效; (2)蜂窝单元大小相比整体尺寸足够小,可以忽略其尺寸影响。
针对两种结构选取不同铺层参数进行Dynamic-Explicit非线性分析,研究其承载特性。得到其在限制应变、屈曲及破坏时的载荷,其中破坏行为由Hashin准则[15]定义,材料破坏相关参数见表5,加载时载荷由0加载至最大弯矩,载荷采样单元位置处于样段中点上缘以排除边界条件影响。分析结果云图见图4。
表5 材料破坏相关参数
Table 5 Related parameters of material failure MPa
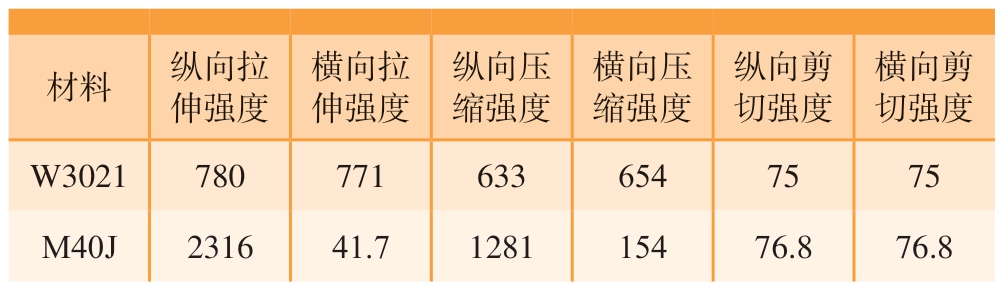
材料 纵向拉伸强度横向拉伸强度纵向压缩强度横向压缩强度纵向剪切强度横向剪切强度W3021 780 771 633 654 75 75 M40J 2316 41.7 1281 154 76.8 76.8

图4 不同承载状态的有限元分析云图
Fig.4 Contour plot of finite element analysis in different bearing states
不同铺层厚度对应的截面积见表6,解析法、有限元法得到的限制应变载荷见图5。圆管梁取样点的平均误差为3.86%,而夹芯方管梁为3.45%。可见,解析法精度与有限元结果误差极小,考虑到计算方便,限制应变载荷采用解析法结果。
表6 铺层厚度与截面积对应表
Table 6 Lamination thickness and cross-sectional area correspondence table

构型铺层厚度t 1.87 mm 1.58 mm 1.435 mm 1.29 mm 1 mm 0.855 mm 0.71 mm 0.565 mm 0.42 mm 0.21 mm夹芯方管梁截面积/mm2 3292 2781 2526 2271 1760 1505 1250 994 739 370圆管梁截面积/mm2 1410 1191 1063 973 754 641 535 422 317 159
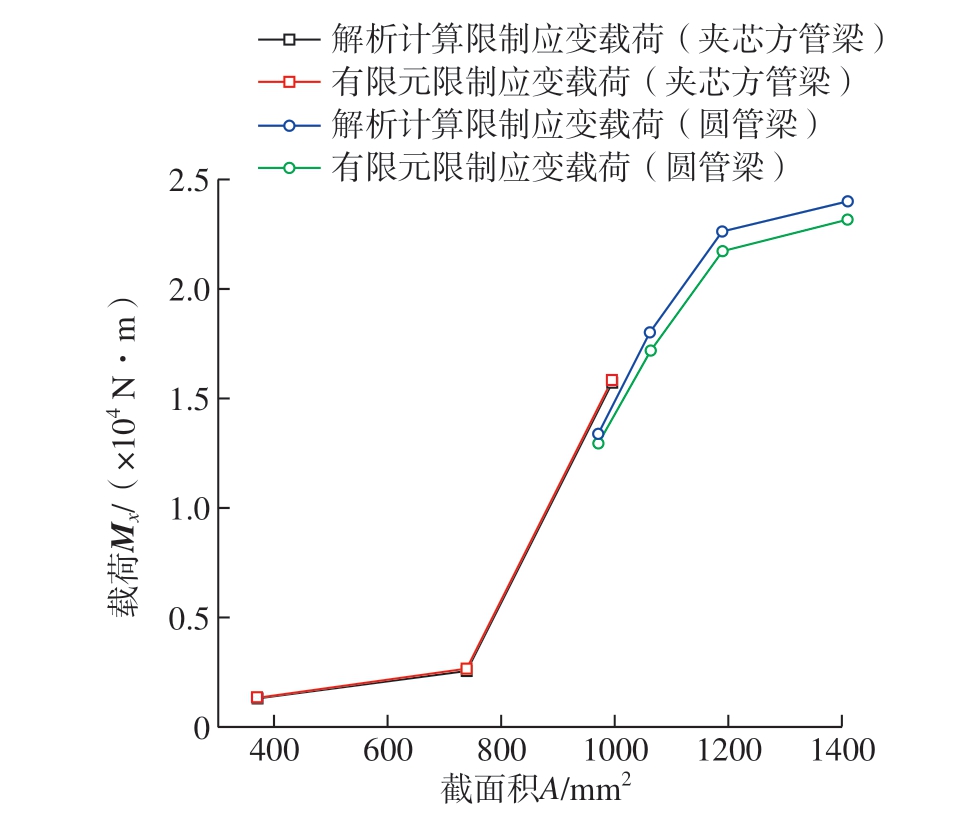
图5 解析法及有限元法3500 με限制应变下载荷值对比
Fig.5 Comparison of analytical method and finite element method for load values at 3500 με
不同截面积、不同截面构型在不同限制条件下的载荷见图6。可以看出,在采用同一铺层库时,夹芯板方管梁的屈曲出现在较高面板厚度及以上,而圆管梁则出现在1 mm厚度以下。分析认为,对于圆管梁而言,随着铺层厚度降低,厚度与尺寸之比更小,屈曲更容易发生在材料破坏之前;而夹芯方管梁则相反,由于夹芯材料的支撑作用,厚面板更容易先发生屈曲,薄面板材料则更容易先发生破坏。计算发现,夹芯方管梁在屈曲之后还能继续承载直至结构破坏,圆管梁在屈曲之后几乎立刻失去承载能力,继而完全失效,说明夹芯方管梁后屈曲承载能力更强。
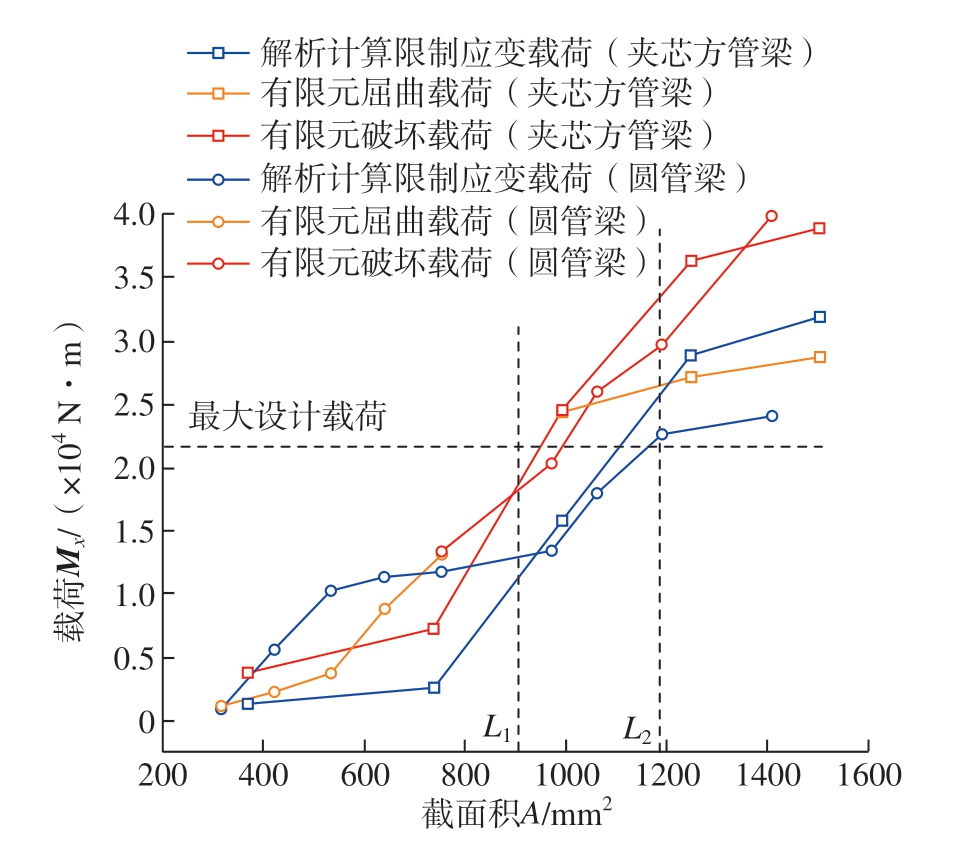
图6 承载能力统计
Fig.6 Statistical chart of bearing capacity
结合表6分析图6,分别比较夹芯板方管梁和圆管梁任一截面积对应的3条载荷曲线中的最低值,此值为当前截面积对应的铺层的承载能力。从理论计算来说,虽然方形截面有利于提高抗弯刚度,但如图6所示,用L1、L2将图按截面积分为低、中、高3个区域,分析结果中仅在右边较高面板厚度时承载能力有优势,在中间厚度时和圆管梁承载能力区别不大,在厚度较低时反而不如圆管梁。
究其原因,夹芯板方管梁由于双侧面板的存在,在相同载荷的前提下,单侧面板厚度低,铺层数量少,导致面内刚度矩阵的优化空间小,造成面板整体模量较低,限制应变载荷小;另一方面,蜂窝夹芯的存在虽然提高了结构抗屈曲能力,但低面板厚度时屈曲载荷溢出,最终承载能力还是由应变限制决定,且蜂窝芯与其粘接胶膜共同造成了重量的大幅增加,因此不是优选方案。
3 总体铺层参数设计及制造工艺方案实施
3.1 总体铺层参数设计
在结构参数设计时,基于第2节中的计算方法得到图6曲线,即得到不同铺层参数的限制应变载荷、屈曲载荷及破坏载荷,可以得知不同铺层和截面对应的失效形式,从而得到其承载能力。
与机翼的展向弯矩图进行对比,可以确定展向铺层设计方案,如图7所示,其中结构安全系数取1.3(图中各数值表示机翼展向范围对应的铺层厚度)。对于图7中翼梁根部的最大设计载荷,比对图6可知,在应变限制条件下,圆管梁根部铺层厚度为1.58 mm,可选铺层有8组,且1.2 mm铺层厚度以下具有明显承载优势。在此载荷以下,夹芯板方管梁可选铺层参数仅有4组,且根部载荷裕度大,中间过渡也不平滑。因此圆管梁在设计空间、承载能力、重量方面都具有明显的优势,此参数即为后续工艺制造的结构参数。
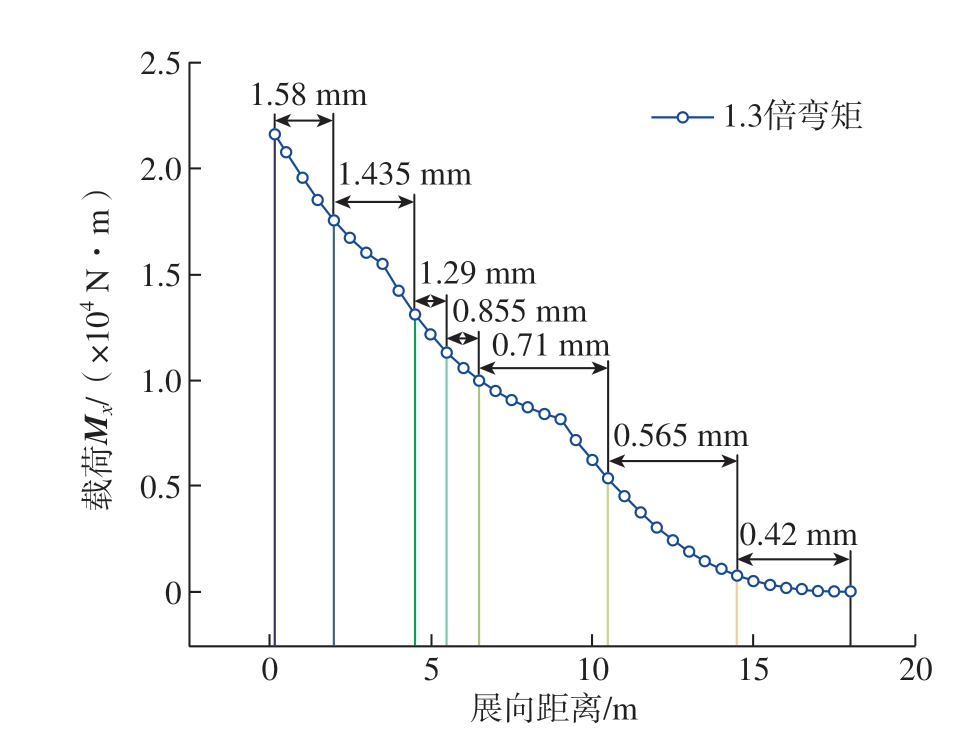
图7 展向弯矩及铺层示意图
Fig.7 Spanwise bending moment and lamination diagram
3.2 制造工艺方案及实施
根据图7的设计结果,圆管梁越靠近尖部,铺层厚度越薄,越容易发生变形和损坏,对制造工艺提出了较高的要求。
复合材料零件成型方法较多,其中碳纤维管的常见成型工艺有缠绕、卷制、模压、拉挤成型等。传统碳纤维管的卷制、缠绕工艺成型方法一般需要将预浸料铺于阳模表面后固化成型,对于大型复合材料圆管梁部件的成型,可能存在脱模困难、外表面精度不满足要求的问题,纤维方向也无法完全满足设计要求。而模压成型工艺模具及机械成本较高,拉挤成型也难以适用。
本文针对大型复合材料圆管梁结构提出专用成型工艺方法,如图8和9所示。采用柱状EPS泡沫作为管梁内部芯模,芯模外部包裹离型风管真空袋,真空袋外侧包裹铺层后,合紧上下外侧阴模,端口密封。之后利用端口加压孔对风管真空袋进行内部加压,模具整体抽真空,将预浸料铺层压在外侧模具内壁,使预浸料铺层与外侧模具之间的气体排出,以减少成品缺陷。将模具与预浸料铺层整体置于大型烘箱中加温固化。中间的EPS泡沫芯模在120 ℃时融化,无须抽芯,从而降低了零件损坏率。通过保证模具加工精度、控制密封质量、调节工艺参数,提高成品质量,达到设计要求。
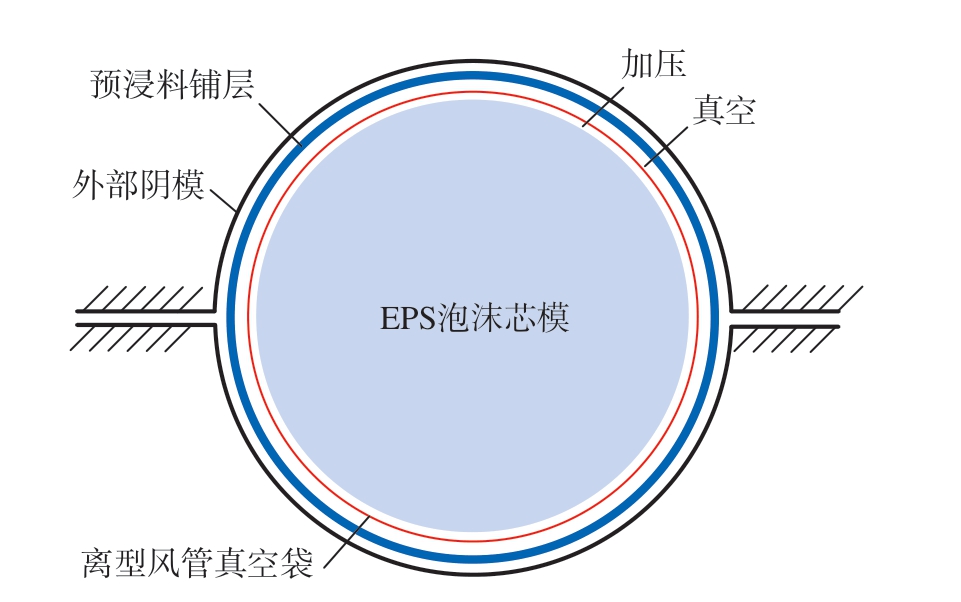
图8 成型工艺方案示意图
Fig.8 Schematic diagram of molding process
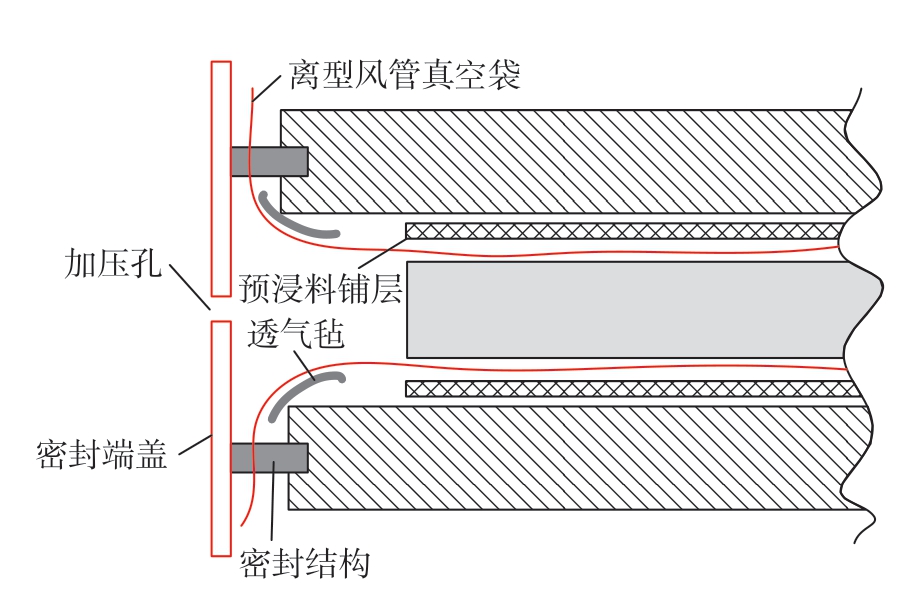
图9 工艺装备安装图
Fig.9 Process equipment installation diagram
试制成品如图10所示,经测量圆柱度、直线度、表面粗糙度可知,成品件能够满足大尺寸管梁加工质量要求。采用本文的阴模成型方法,能够良好地满足纤维取向的要求,由于内部加压,外部贴合模具,保证了装配面精度,同时降低了孔隙率,零件成型质量高。经无损检测,成型样件能够满足HB 7224—1995复合材料构件通用技术条件规定的A级缺陷标准。

图10 成品样件
Fig.10 Finished beam samples
4 试验验证
4.1 样件加载试验
利用3.2节中的方法制造试验件并进行试验验证。图11中绿色部分为厚度1.58 mm的完整层铺层。蓝色、紫色部分分别为实际结构中挂载段及对接段增强区。如图12所示,在试验件样段不同截面圆周的上下左右4个位置各布置一组3个不同方向的应变片,与梁轴线夹角分别为45°、90°、0°。
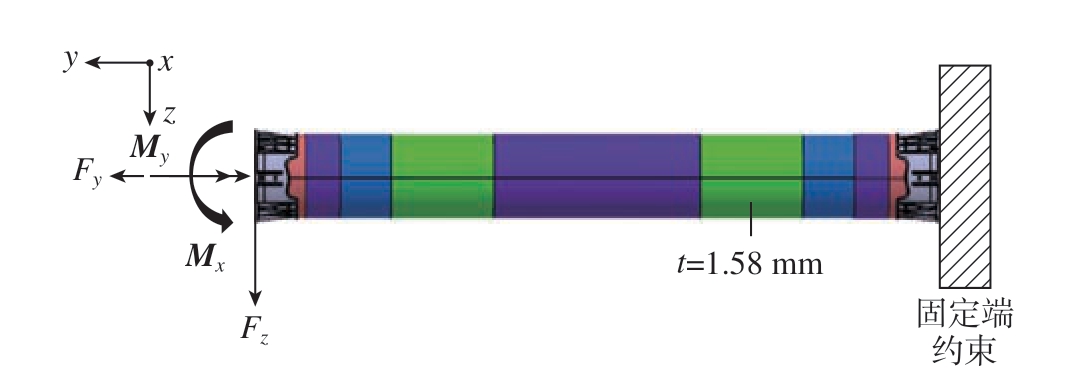
图11 试验件设计及加载示意图
Fig.11 Schematic diagram of specimen design and loading

图12 梁样段试验件
Fig.12 Beam segment specimen
如图13所示,试验时,试验件右端通过支持夹具固定在承力墙上,试验加载端通过专用夹具固定,使用MTS FlexTest 32通道协调加载系统、RT-ETS-1152通用数据采集系统进行加载试验及数据采集。加载误差小于1%,数据采集系统误差小于0.1%。

图13 试验现场
Fig.13 Test site
为方便试验中加载操作及数据处理,参考实际载荷量级,选择10000 N·m弯矩及-230 N剪力作为参考载荷值,以此值为100%进行加载。实际加载到100%时的载荷值:Fz = 230.71 N,Mx = 10011.89 N·m。
加载过程分为两步。
(1)分别按照10%、7%的梯度加载至60%和67%并记录数据,最后按照10%的梯度卸载并记录数据,卸载完成后等待120 s再测量位移和应变数据。
(2)加载完成后继续按照3%的梯度加载至70%并记录数据,之后按照连续加载的方式加载至试验件破坏,并记录数据。
4.2 试验结果
加载过程中样件未出现异响,全程未见屈曲。加载直至断裂,断裂位置出现在右侧基本铺层区域,断面如图14所示,纤维发生断裂和脱出,断裂截面垂直于轴线。

图14 试验件断面形貌及断裂位置
Fig.14 Cross-section morphology and fracture location of specimen
完整层段应变-载荷曲线见图15,可见,随着载荷的增大,材料应变呈现出近似线性增加,试验应变结果和解析法计算结果误差不超过10%。
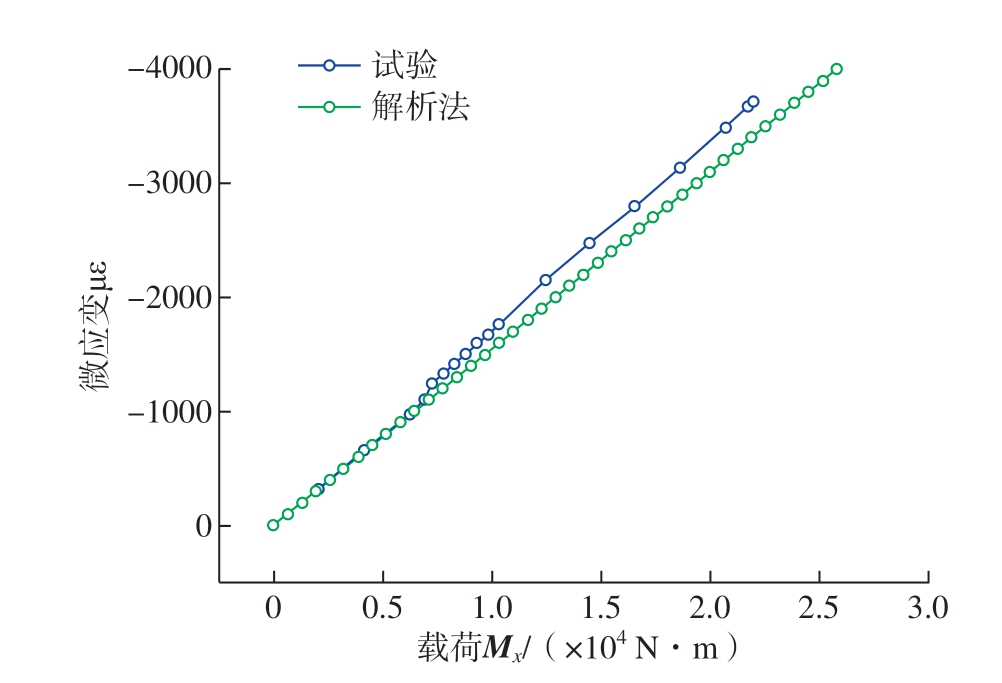
图15 试验应变载荷及计算载荷对比
Fig.15 Test strain corresponding to load and theoretical analysis
试验结果证明,上述方法设计的根部样段达到了设计要求。分析认为,试验和理论计算的误差主要来源于实际加载状态和理论分析状态的区别。同时,试验中圆管梁根部样段未发生屈曲,验证了2.3节中仿真分析的正确性。
5 结论及展望
5.1 结论
(1)提出了一种复合材料翼梁的结构快速设计方法,基于研究不同梁截面的承载能力,避免了设计前期建立复杂优化模型或有限元模型反复迭代。针对本文算例,在考虑铺层对称性、应变约束条件、屈曲约束条件的前提下完成了截面构型选型及圆管梁参数的优化设计,为太阳能无人机的梁结构设计提供了参考。研究表明,在本研究的载荷量级下,圆管梁相比夹芯方管梁具有铺层设计空间大、重量轻的构型优势,但后屈曲承载能力不如夹芯方管梁。
(2)针对大尺寸复合材料圆管梁结构进行研究并设计了一种新型的专用制造工艺方案,通过结合泡沫芯模与外部阴模,加压固化成型,制造了符合设计质量要求的样件,为类似的复合材料大型结构提供了参考。制造试验件对翼梁根部设计参数进行了试验验证,试验结果在线性范围内与理论计算结果的误差不超过10%,试验中未出现屈曲,验证了设计方法的可行性和准确性。分析认为,试验误差主要来源于实际加载状态和理论分析状态的区别。
5.2 展望
(1)设计技术方面。大展弦比太阳能无人机复合材料翼梁结构精细化程度高、重量要求苛刻,常规设计方法往往难以满足要求。需要研究专用设计流程与规范,基于复合材料结构的多层级耦合优化,可引入复合材料翼盒弯扭耦合效应,针对性放宽铺层设计约束条件,从而进一步开发材料潜力,提高结构的承载效率。
(2)材料技术方面。对于重量敏感、载荷量级低的太阳能无人机复合材料结构,亟须通过降低预浸料厚度,提高铺层总层数来改善铺层设计空间,从而需要进一步发展小丝束碳纤维技术。然而小丝束碳纤维目前应用面小、价格高昂,丝束的减小也为预浸过程调配等方面带来工艺难点,尚待整个产业链的进一步发展支撑。
(3)制造工艺方面。对于超薄、多层预浸料的复合材料零件来说,精度控制难度增大,放开铺层设计时,还需要深入研究成型过程的变形抑制技术。同时层数增多导致生产效率降低,针对性发展自动铺丝、自动铺带设备等的研制,能够推进基于超薄预浸料的复合材料制造工艺的成熟,进一步支持太阳能无人机的未来发展与应用。
[1] 马东立, 张良, 杨穆清, 等. 超长航时太阳能无人机关键技术综述[J]. 航空学报, 2020, 41(3): 29-58.MA Dongli, ZHANG Liang, YANG Muqing, et al. Review of key technologies of ultra-long-endurance solar powered unmanned aerial vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(3): 29-58.
[2] MONTAGNIER O, BOVET L. Optimisation of a solar-powered high altitude long endurance UAV[C]//27th Congress of the International Council of the Aeronautical Sciences 2010. Nice: 2010, 1: 177-186.
[3] 董鑫. 太阳能无人飞机复合材料机翼结构设计优化[D]. 西安: 西安工业大学, 2016.DONG Xin. Optimization design of composite material wing structure of solar-powered unmanned aerial vehicle[D]. Xi’an: Xi’an Technological University, 2016.
[4] ZHU X F, GUO Z, HOU Z X. Solar-powered airplanes: A historical perspective and future challenges[J]. Progress in Aerospace Sciences, 2014, 71: 36-53.
[5] ZHANG W W, ZHANG L G, YAN Z W, et al. Structural design and difficulties of solar UAV[C]//IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2019, 608(1): 012016.
[6] 赵迪. 某型太阳能无人机复合材料夹芯翼梁优化设计[D].西安: 西安工业大学, 2019.ZHAO Di. Optimal design of composite sandwich wing beam of a solar unmanned aerial vehicle[D]. Xi’an: Xi’an Technological University, 2019.
[7] 强磁力. 某型太阳能无人机气动与结构优化[D]. 南京: 南京航空航天大学, 2021.QIANG Cili. Aerodynamics and structural optimization of a certain type of solar-powered unmanned aerial vehicle[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2021.
[8] CESNIK C E S, SENATORE P J, SU W H, et al. X-HALE: A very flexible unmanned aerial vehicle for nonlinear aeroelastic tests[J].AIAA Journal, 2012, 50(12): 2820-2833.
[9] 昌敏, 汪辉, 金朋, 等. 高空太阳能无人机设计与动力学[M].北京: 机械工业出版社, 2023.CHANG Min, WANG Hui, JIN Peng, et al. Design and dynamics of high-altitude solar-powered unmanned aerial vehicles[M]. Beijing: China Machine Press, 2023.
[10] 曹岩, 沈冰, 刘红军. 某太阳能无人机复合材料机身结构梁选型与优化[J]. 机械设计与制造, 2016(7): 205-208, 212.CAO Yan, SHEN Bing, LIU Hongjun. Selection and optimization of new solar UAV composite fuselage structural beams[J]. Machinery Design & Manufacture, 2016(7): 205-208, 212.
[11] ALSAHLANI A, RAHULAN T, ABDULHASSAN N.Composite structural analysis of a high altitude, solar powered unmanned aerial vehicle[J]. International Journal of Mechanical Engineering and Robotics Research, 2017: 71-76.
[12] ZHANG L, MA D L, YANG M Q, et al. Optimization and analysis of composite sandwich box beam for solar drones[J]. Chinese Journal of Aeronautics, 2021, 34(10): 148-165.
[13] (荷)克里斯托斯 · 卡萨波格罗. 飞机复合材料结构设计与分析[M]. 颜万亿, 译. 上海: 上海交通大学出版社, 2011.KASSAPOGLOU Christos. Design and analysis of composite structures with applications to aerospace structures[M]. YAN Wanyi,trans. Shanghai: Shanghai Jiao Tong University Press, 2011.
[14] 徐荣章, 朱胜利, 余明, 等. 基于屈曲稳定性的复合材料铺层库优化设计[J]. 航空科学技术, 2023, 34(6): 26-34.XU Rongzhang, ZHU Shengli, YU Ming, et al. Optimization design of the composite layup library base on buckling[J]. Aeronautical Science& Technology, 2023, 34(6): 26-34.
[15] 林中照, 盛冬发, 方雨汀, 等. 含孔纤维增强镁合金层合板制备和拉伸时渐进损伤模式研究[J/OL]. 航空制造技术, 2023: 1-9.[2024-02-03]. https://kns.cnki.net/kcms2/article/abstract. LIN Zhongzhao, SHENG Dongfa, FANG Yuting, et al. Preparation of hole-containing fiber-reinforced magnesium alloy laminates and progressive damage mode study during tension[J/OL]. Aeronautical Manufacturing Technology, 2023: 1-9[2024-02-03]. https://kns.cnki.net/kcms2/article/abstract.