自20世纪70年代开始,随着复合材料网格结构的应用范围逐渐增加,其优异的性能被国内外航空航天领域学者、专家广泛关注。同时,作为新兴的结构形式,其力学性能及结构形式也相继被国内外学者深入研究[1]。
Jaunky等[2–3]以网格最小质量为设计目标,以筋条高度、宽度、间距、蒙皮铺层和网格构型为设计变量,在整体屈曲约束下,利用遗传算法的离散优化器优化得到设计变量最佳值。Vasiliev[4]、Totaro[5]、何景轩[6]等同样以网格质量最小为优化目标,以缠绕角度、筋条高度、筋条间距比等为优化变量,利用模拟分析法对网格结构尺寸进行优化,推导出在特定外载荷下的变量最佳组合。Afonso[7]和张卫红[8]等提出了板壳加筋结构的系统优化方法,对壳结构与筋条布局进行拓扑优化并在此基础上对加筋壳进行了尺寸和形状优化。意大利的Sano等[9]对机身结构进行了网格加强优化,机身形状为非对称双曲率网格加强结构,与本文所用不规则结构相似。荷兰ATG公司的Maes等[10]通过分析网格结构节点位置的特点,提出了一种较为有效的网格结构优化方法,相比于传统的试错法,该方法可实现大于20%的结构减重设计,并且该方法成功地在阿里安6号运载火箭的级间段得以应用。
梁东平[11]和黄蔚[12]等利用遗传算法对网格加筋板进行布局优化研究,将环筋与纵筋的高度、宽度、厚度及排布作为设计变量,通过参数化的等效平铺刚度进行计算,之后通过有限元分析进行验证。荣晓敏等[13]利用进化神经网络找到优化变量与优化目标值之间的非线性关系,代替了优化过程中的大量有限元计算,并以遗传算法为优化求解器,最终得到了一种可解决大型复合材料结构优化的高效方法。林再文等[14]通过对锥壳的光壳、纵筋与螺旋筋的研究,发现螺旋筋可大幅提升整个构件的承载能力。何景轩等[6]对轴压载荷下的复合材料圆柱网格结构进行优化,通过引入网格整体、局部屈曲及压缩强度安全系数,优化得到网格结构参数,此方法针对网格结构优化非常有效。北京航空航天大学任康熙等[15]针对等格栅圆柱壳结构,在结构质量不变的情况下,优化筋条的结构参数,并建立了CATIA、ABAQUS从建模到分析的整套优化流程,为网格加筋结构的设计及优化提供了参考和依据。
综上,目前国外针对复合材料网格筋结构的研究已经成熟,并取得了较为理想的效果。而国内由于复合材料的研究起步较晚,目前针对复合材料网格结构大多停留在研究阶段,并未过多地投入实际使用。综合国内外的研究发现,针对复合材料网格结构的应用大多是在圆柱、圆锥等规则回转体或曲面板上,在复杂、不规则回转体上的应用并未过多涉及。
网格结构作为一种新兴的复合材料结构形式,由于其结构的复杂性和成型工艺的难度较高,试验所花费的时间较长、成本较高,故在设计时以数值模拟为主。本文通过建模、有限元前/后处理建立完整的非线性屈曲分析流程,基于结构参数进行单因素分析,找到各因素影响规律,确定变量取值。针对复杂回转体的网格筋结构参数进行优化,以最大载荷质量比为优化目标,以筋条尺寸及数量为设计变量,将连续变量变为离散变量,利用正交试验找出最优参数组合。
1 复杂回转体网格筋结构分析及方法
1.1 复杂回转体网格筋结构分析
1.1.1 材料
本文选择的材料为江苏恒神股份有限公司生产的T800/BH108碳纤维树脂基预浸料,材料密度为1.56 g/mm3,材料的弹性性能参数如表1所示。
表1 T800/BH108碳纤维树脂基的弹性性能参数
Table 1 Elastic property parameters of T800/BH108 carbon fiber resin base

注:E1、E2为复合材料1、2方向的弹性模量;μ为复合材料的泊松比;G12、G13、G23为复合材料12、13、23面的剪切模量。
E1/GPaE2/GPaμG12/GPaG13/GPaG23/GPa 120 9 0.3 7 7 7
1.1.2 复杂回转体结构分析
本文研究的模型为给定的复合材料复杂回转体网格结构,下端为直径1120 mm的圆,上端为对称分布的不规则曲线,整体高度为1010 mm,壁厚约3.5 mm。由于构件高度及直径都远大于壁厚,因此在建模及分析时,将构件作为薄壳单元处理,模型具体形状如图1所示。主要设计工况为承受轴向压缩载荷,加载至上线端框的连接孔处。
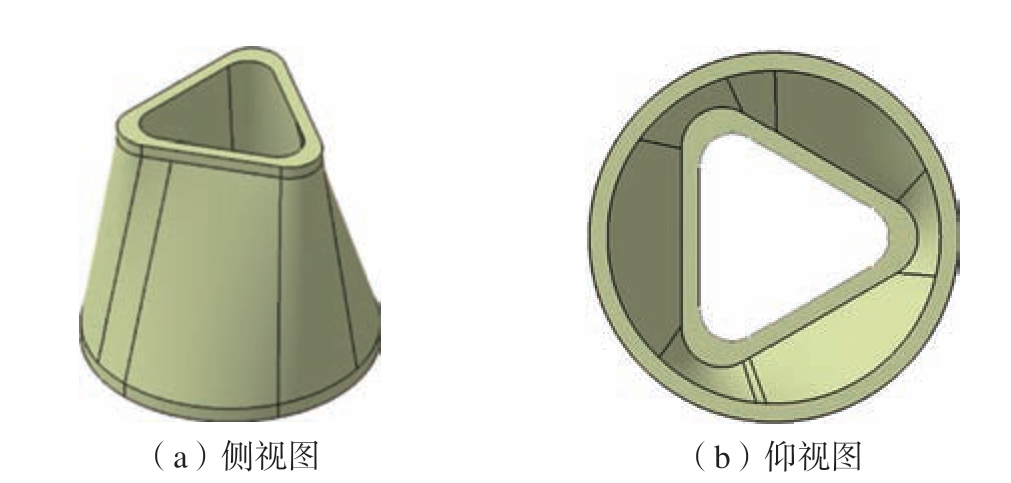
图1 模型外形示意图
Fig.1 Schematic diagram of model shape
筋条分为环筋和纵筋,且筋条分布位置只在蒙皮区域内,不涉及端框位置。在蒙皮区域内,环筋由上至下根据筋条数量不同均匀分布,纵筋以蒙皮与下端框连接处为基准,呈圆周状均匀分布,具体形式如图2所示。

图2 筋条结构示意图
Fig.2 Schematic diagram of rib structure
1.1.3 网格筋结构形式及参数选择
(1)网格筋结构形式选择。
复合材料网格筋结构主要有菱形、三角形、矩形、三角形与六边形相间,网格的工艺难度、力学性能及结构对比如表2所示。本文所用复杂回转体构件的构型基于实际生产设计,因此在选择网格结构时优先考虑工艺性及生产效率。菱形和三角形网格筋结构简单,但菱形结构承载效率较低,在轴压载荷作用下稳定性差;三角形结构由于在每个节点处都是3根筋条相交,使整体力学性能及稳定性降低。而三角形与六边形相间的结构虽稳定性好,但结构及制造工艺较为复杂,不适用于本文模型。矩形结构可通过连续纤维缠绕成型,也可通过铺放成型、手糊成型,成型方式多变、自动化程度高、生产效率高,并且整体承载效率较高,环纵筋交错结构可满足多种工况的承载要求。但由于本文构件结构的复杂性,在某些区域并不能确保构型是规整的矩形结构,因此,本文的网格结构选择以矩形结构为主的类矩形结构进行设计优化。
表2 典型网格结构对比
Table 2 Comparison of typical grid structures

网格形式 工艺难度 力学性能 结构示意图菱形 可通过纤维缠绕成型,自动化程度高 缺少环向筋,承载能力差images/BZ_30_1367_510_1500_688.png三角形 可通过纤维缠绕成型,节点处堆积较高,影响性能结构稳定,但节点处3筋条相交,稳定性差images/BZ_30_1367_712_1500_887.png矩形可通过连续纤维缠绕、铺放成型,工艺实现容易,自动化程度高整体承载能力足够,但无斜向肋,部分工况不适用images/BZ_30_1362_911_1496_1087.png三角形与六边形相间可通过连续纤维缠绕获得,自动化程度高,但工艺复杂 结构稳定,承载力好images/BZ_30_1362_1110_1496_1287.png
(2)网格筋参数选择。
本文采用矩形网格筋结构形式,筋条包括环筋、纵筋两种。在蒙皮区域内,环筋由上至下根据筋条数量不同均匀分布,纵筋以蒙皮与下端框连接处为基准,呈圆周状均匀分布,因此对于筋条的分布参数值使用筋条数量来表示。考虑工艺实现成本,将环筋与纵筋设置相同高度。具体筋条参数为纵筋数量NL、纵筋宽度aL、筋条高度b、环筋数量NC、环筋宽度aC。由于蒙皮外形需要满足装配要求,且作为承压构件,网格筋的结构效率远高于蒙皮,因此本文仅针对网格筋参数进行优化,蒙皮的设计参数不作为变量。
1.2 网格筋结构分析方法
1.2.1 经典复合材料层合板基本理论
(1)层合板的基本假设。
复合材料由纤维和基体组合制造而成,其结构如图 3所示,1轴表示单向纤维长度方向; 2轴表示垂直于纤维方向; 3轴表示材料厚度方向。复合材料由高强度、高模量的纤维作为增强体通过树脂结合成为整体。由于纤维材料具有各向异性,且纤维材料作为增强体与基体之间性能差距较大,使复合材料呈明显各向异性的特点。本文所研究的内容均在复合材料宏观力学的基础上开展。

图3 复合材料结构示意图
Fig.3 Schematic diagram of composite structure
在研究复合材料相关力学性能时应遵循以下3种基本假设。
直线假设法:层合板垂直于中面(复合材料层合板厚度方向上的中间平面)的法线,在载荷作用下变形后,该法线仍垂直于变形后的中面,即层合板截面上剪切应力为0。
等线假设法:层合板受载发生形变时,垂直于中面的法线长度不变,即沿3方向的应变为0。
平面应力假设:与单层板中面垂直的应力远小于面内应力分量。
(2)经典复合材料层合板合力及合力矩。
层合板中第k层应力表示为

式中,σi为对应方向的应力;εi为对应方向上的应变;τij为对应方向的剪切应力;γij为对应方向的剪切应变;κxy为扭曲率,表示中面在x方向的斜率随y方向的变化率,也就是中面在y方向的斜率随x方向的变化率;Qij为化简后刚度系数,可由材料本身工程常数获得,如式 (5)所示。
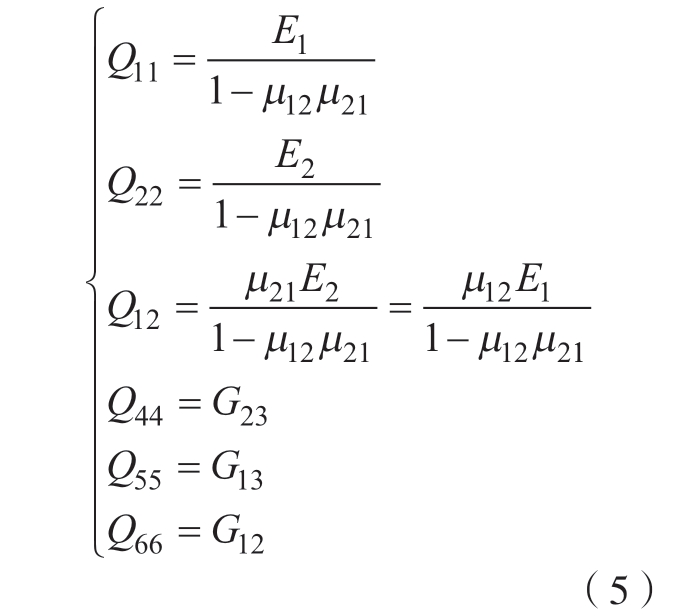
复合材料层合板是由多层不同方向的单层板铺叠而成,单层板的材料方向往往与层合板坐标系不同。针对不同于坐标系的单层板应力–应变关系可通过坐标转换矩阵进行转换。假设如图 4所示,材料方向与层合板坐标系夹角为θ。
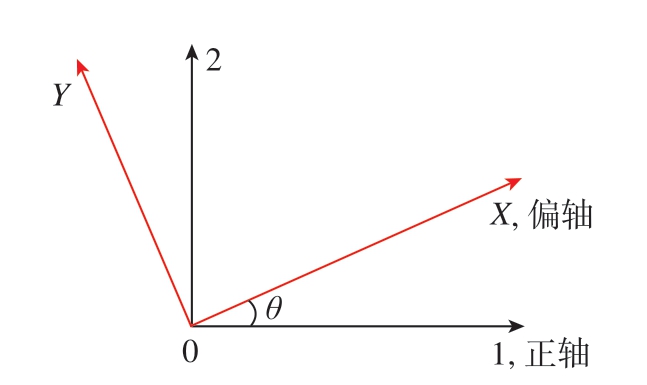
图4 偏轴坐标系
Fig.4 Off-axis coordinate system
偏轴状态下,应力与一般正交状态下的应力转换关系如下。
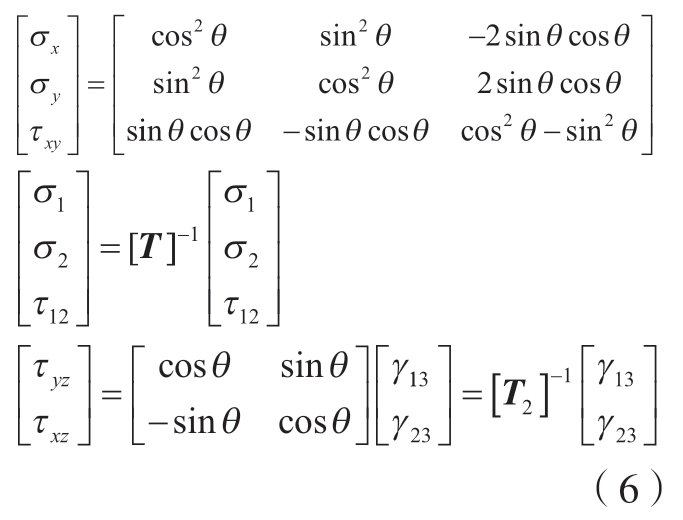
式中,T为转换坐标矩阵,T1、T2分别定义为

综合式(7),偏轴状态下应力–应变关系为

层合板的合力与合力矩就是层合板中各单层板在某一方向上的合力与合力矩,如图 5所示。
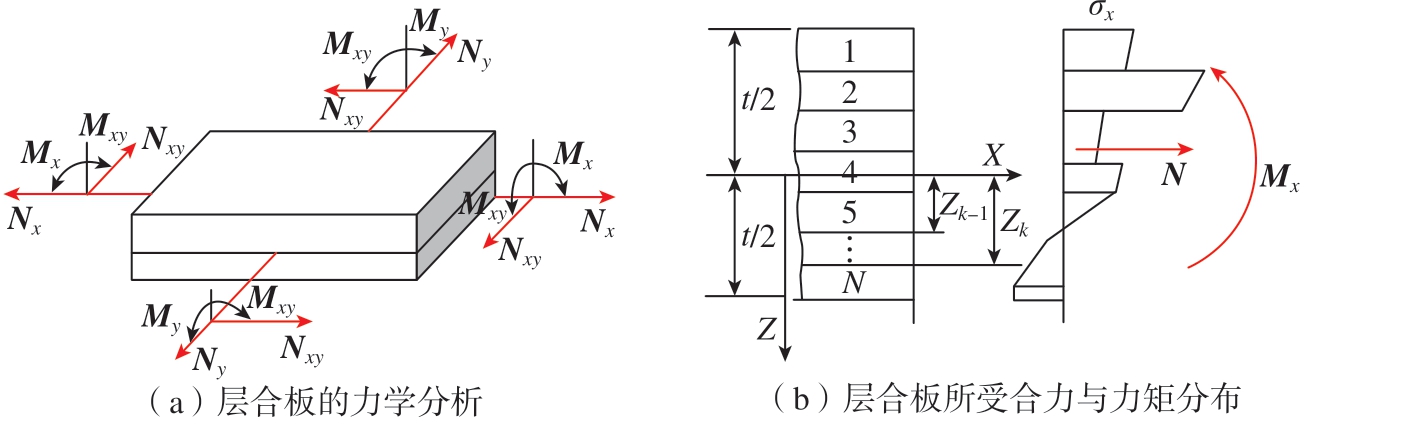
图5 层合板的合力与合力矩
Fig.5 Resultant force and resultant moment of laminates
层合板面内合力为
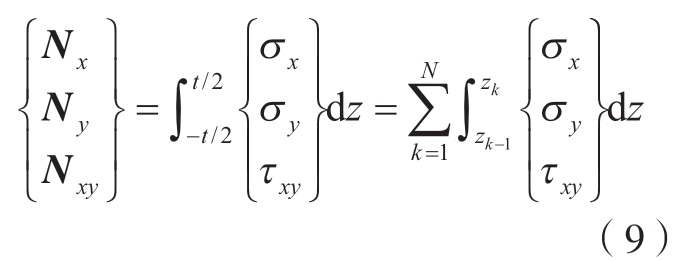
层合板的合力矩为
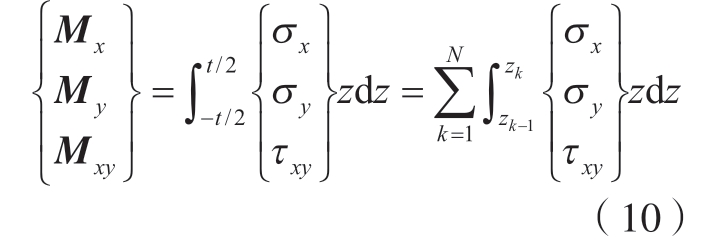
式中,Ni为层合板面内合力;Mi为层合板面内合力矩;t为层合板的厚度;Zk为层合板中面到第k层板底部的距离。将式 (8)代入到式 (9)和式 (10)中并化简得到

其中,
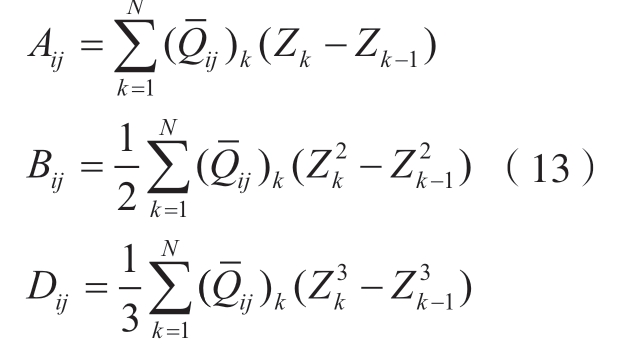
用矩阵的形式表示为
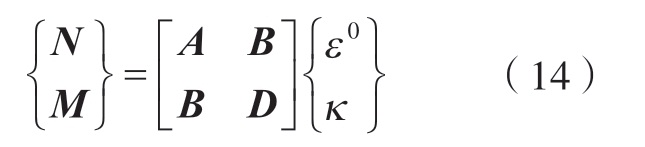
式中,A为面内刚度矩阵;B为耦合刚度矩阵;D为弯曲刚度矩阵。
1.2.2 强度失效准则
复合材料的破坏形式较为复杂,在结构设计中强度破坏准则有10多种,常见的有Hoffman准则、Puck准则、Hashin准则、Tsai-Hill准则、Tsai-Wu准则、最大应变准则等,不同构件、不同工况下适用不同的失效准则。本文主要应用Hashin准则,可以将复合材料纤维与基体之间的失效有效区分,包括以下4种失效模式。
纤维拉伸失效 (σ11≥0):
纤维压溃 (σ11< 0):
基体开裂 (σ22≥ 0):
基体压溃 (σ22< 0):
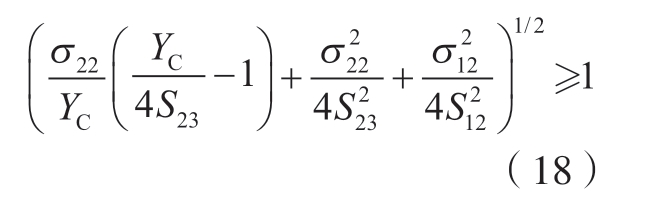
式中,XT、XC为轴向拉伸强度、轴向压缩强度,MPa;YT、YC为横向拉伸强度、横向压缩强度,MPa;S12、S23为横向剪切强度、轴向剪切强度,MPa;σ11、σ22别为1、2方向应力分量,N;τ12为1、2方向切应力分量,N。
1.2.3 非线性屈曲分析
为探究模型结构的实际屈曲极限,本文采用非线性屈曲分析,需从分析开始就引入微小干扰,使分析过程更加接近于实际情况。非线性屈曲方程为
式中,KT为模型在某增量步上的切线刚度矩阵;Δp为构件当前外在增量;Δq为结构当前的位移增量。
在实际工况下,该模型作为连接段构件,主要承受拉伸、压缩、扭转载荷,且在实际应用中拉伸及压缩所受载荷最大。对于薄壳结构,拉伸往往不是使其发生失效的主要原因,在压缩载荷下更容易发生屈曲失效,因此本文主要对模型进行压缩屈曲分析。
2 复杂回转体网格筋结构有限元仿真及结构参数分析
2.1 有限元屈曲分析
基于二维Hashin失效准则,在ABAQUS中利用用户USDFLD子程序与Static General分析步实现复合材料的非线性屈曲分析,材料在不同失效模式下的退化模型如表3所示。
表3 材料Camanho退化模型
Table 3 Camanho degradation model of materials
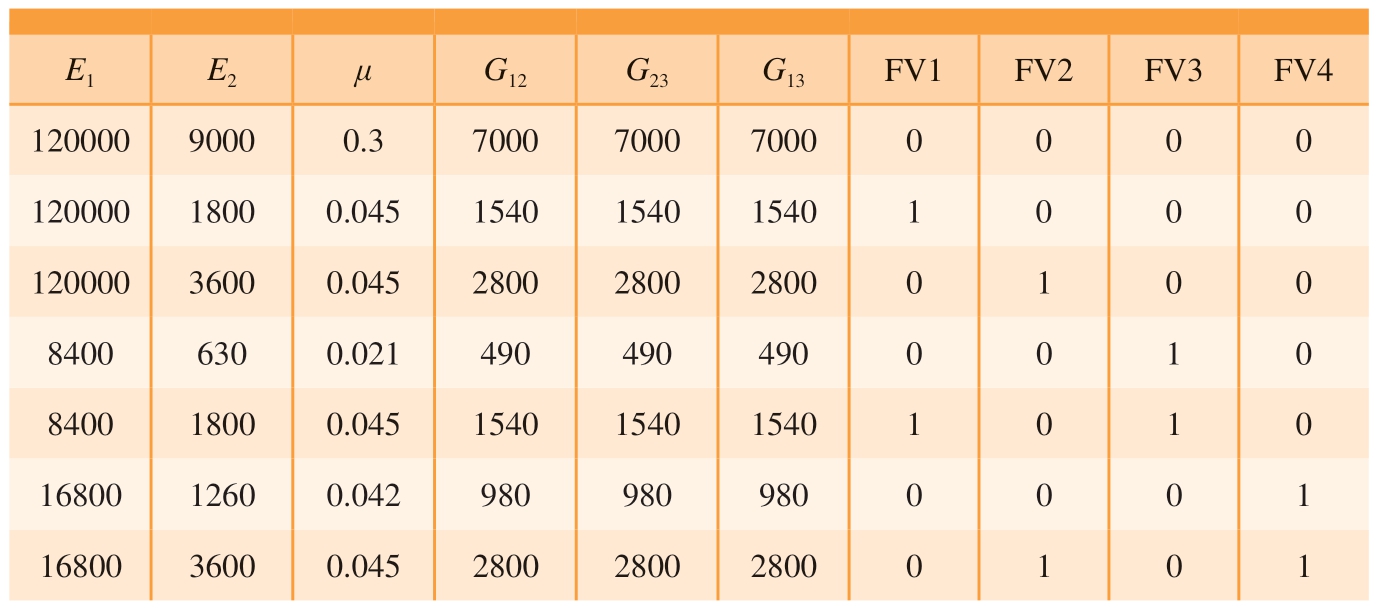
注:FV表示预定义场变量,即引入的初始损伤。FV1为基体拉伸损伤;FV2为基体压缩损伤;FV3为纤维拉伸损伤;FV4为纤维压缩损伤。
E1E2μG12G23G13FV1FV2FV3FV4 120000 9000 0.3 7000 7000 7000 0 0 0 0 120000 1800 0.045 1540 1540 1540 1 0 0 0 120000 3600 0.045 2800 2800 2800 0 1 0 0 8400 630 0.021 490 490 490 0 0 1 0 8400 1800 0.045 1540 1540 1540 1 0 1 0 16800 1260 0.042 980 980 980 0 0 0 1 16800 3600 0.045 2800 2800 2800 0 1 0 1
表4 试验因素水平表
Table 4 Experimental factor level table
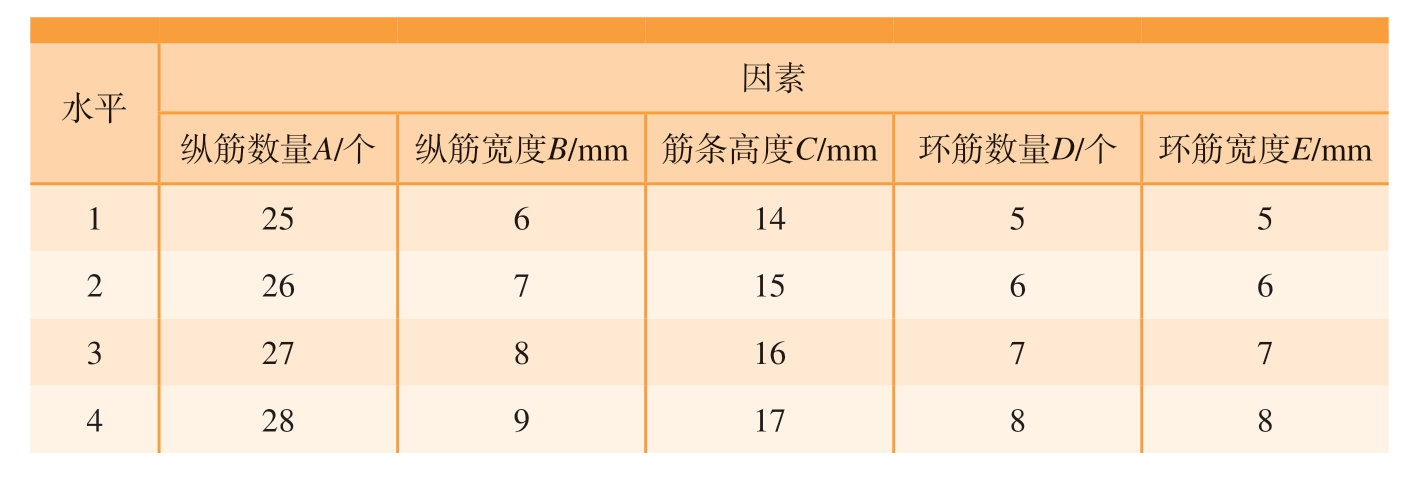
水平 因素纵筋数量A/个 纵筋宽度B/mm 筋条高度C/mm 环筋数量D/个 环筋宽度E/mm 1 25 6 14 5 5 2 26 7 15 6 6 3 27 8 16 7 7 4 28 9 17 8 8
根据实际压缩工况,本文设置模型边界条件:上端固定,下端位移边界条件为位移量30 mm,如图6所示。
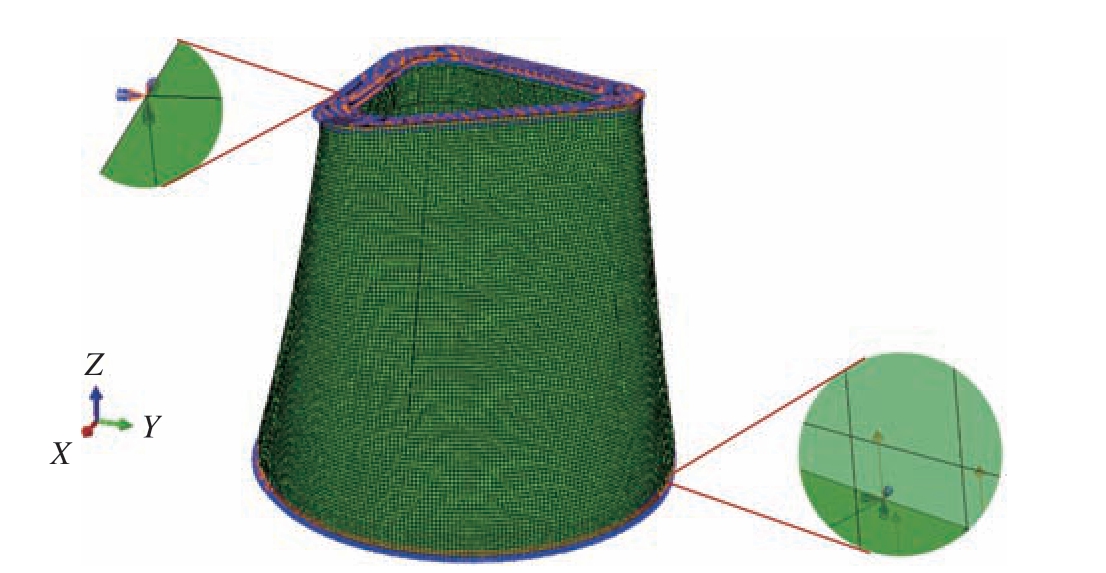
图6 模型有限元分析边界条件
Fig.6 Model finite element analysis boundary conditions
有限元分析结果如图7所示,由于载荷直接传递至端框,同时端框与蒙皮件具有几何不连续性,此处存在应力集中,因此有限元结果显示端框区域出现基体损伤。之后随着载荷位移的增加,模型所受载荷也增加,直至达到材料强度极限,所承受压缩载荷开始下降,最终得到模型承受的轴向压缩载荷随位移变化情况,最大载荷Fmax = 1511.02 kN,载荷–位移曲线如图8所示。
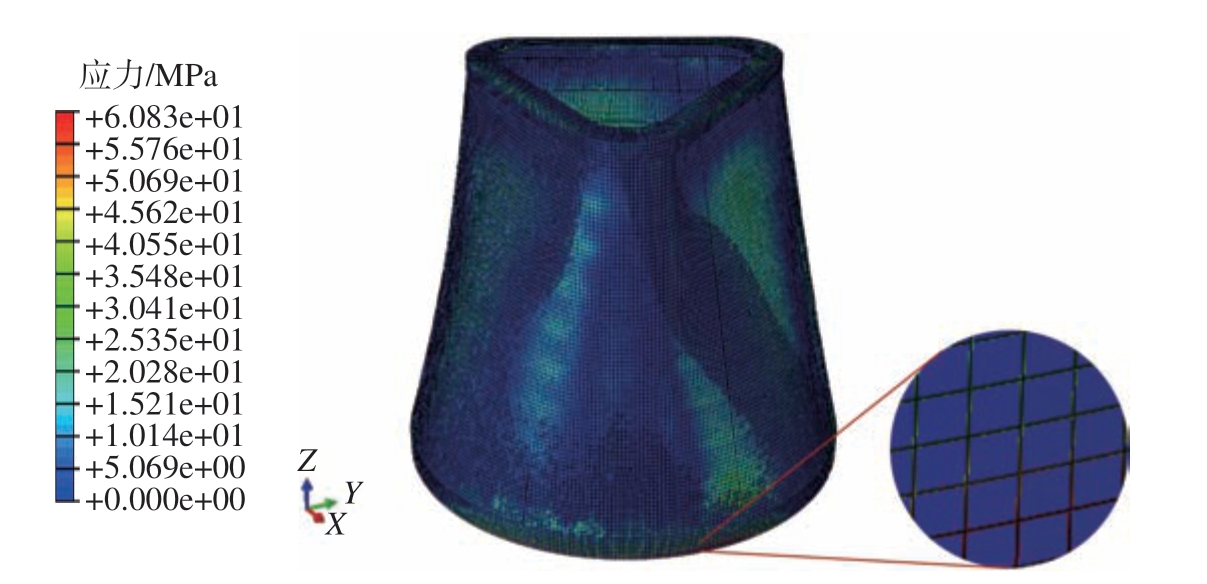
图7 非线性屈曲分析
Fig.7 Nonlinear buckling analysis
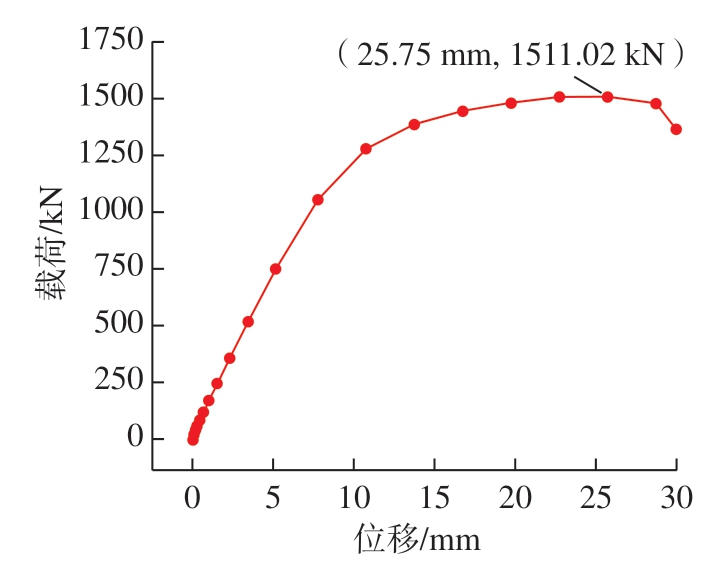
图8 载荷–位移曲线
Fig.8 Load–displacement curve
2.2 单因素对复杂回转体网格筋承载能力的影响研究
复合材料网格结构具有轻质、高强的特点,理论上增加纵筋与环筋的数量,以及横截面的长度、宽度会使模型压缩载荷增加,但模型重量也会增加,增加材料成本[16–17]。在航天领域,降低飞行器质量会增加运载能力、减少推进剂消耗,以及加大飞行距离或射程,因此使构件具有更高的承载效率是优化的更好方向。
本文将采用最大屈曲载荷表征模型的轴向承载能力,同时采用载荷质量比,即最大屈曲载荷除以模型总质量来表示整个构件的轴向承载效率。变量初始值:NL=29个、aL=7 mm、b=15 mm、NC=7个、aC=5 mm。进行单因素分析时,只对需要分析的变量取不同值,其他变量值保持不变。
2.2.1 纵筋数量的影响研究
纵筋数量NL对模型轴向承载能力具有最直接的影响。根据工程经验,初步确定纵筋数量的范围为25~32个,有限元分析结果见图9。

图9 纵筋数量对载荷与载荷质量比的影响
Fig.9 Effect of the number of longitudinal ribs on load and the ratio of load to mass
分析有限元模拟数据,模型所受最大屈曲载荷在NL达到29个之前增加较为明显,后续增加较为缓慢,甚至有下降趋势。这是因为纵筋数量NL的增加必然带来纵筋位置的改变,对于复杂回转体而言,筋条位置不同也会给所受载荷分布带来改变,在曲率较大处排布筋条,会使承载能力增加的幅度较大,而在曲率较小处排布筋条所增加的承载能力较少。纵筋数量NL越大,曲率较小处排布的筋条就越多,回转体承受最大载荷增量变小,质量增加越多,使载荷质量比增量减少甚至下降。在NL=26时,承载效率达到拐点,最大值为43.58 kN/kg,之后NL的增加会使载荷质量比下降。纵筋优化时,可取NL=26为基点,取其前后几组数据进行分析。
2.2.2 纵筋宽度的影响研究
根据工程经验及自动化缠绕的机械限制,纵筋宽度aL设定范围为5~10 mm,分析结果如图10所示。根据有限元模拟结果分析,纵筋宽度的增加会使模型轴向承载效率下降,但同时会使整体承载能力上升,对于纵筋数量及环筋数量,其对承载能力的提升更加显著,因此在做正交试验时将其作为考虑因素之一。另根据实际生产情况,选取aL正交试验取值范围6~9 mm。
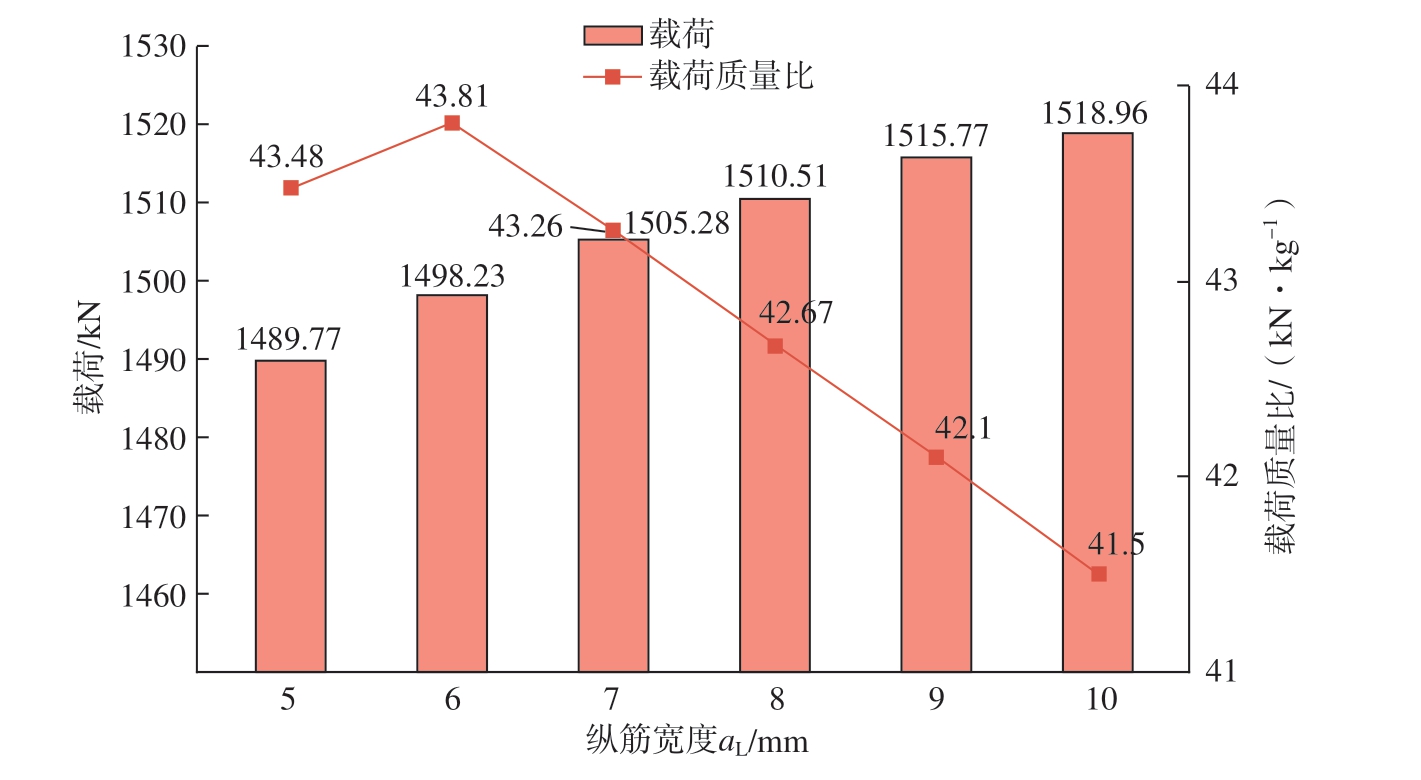
图10 纵筋宽度对载荷与载荷质量比的影响
Fig.10 Effect of longitudinal reinforcement width on load to load mass ratio
2.2.3 筋条高度的影响研究
在设计优化过程中,考虑到生产工艺的可行性,故设置相同的环筋高度和纵筋高度。根据工程经验,设定筋条高度b范围为12~17 mm,分析结果如图11所示。根据有限元模拟结果分析,模型的承载能力随着筋条高度b的增加而增加,载荷质量比随着筋条高度b的增加而先增后降,在b = 14 mm时承载效率到达最高值。筋条高度b对模型承载效率有着显著影响,但筋条过高会使承载效率降低。因此在正交试验选择因素水平时,以b = 14 mm为基准,取相应组数进行试验分析。

图11 筋条高度对载荷与载荷质量比的影响
Fig.11 Effect of rib height on load to load mass ratio
2.2.4 环筋数量的影响研究
根据工程经验,环筋数量NC对模型轴向承载能力影响力较低,确定环筋数量NC的范围为3~10个,分析数据及结果如图12所示。可以看出,随着环筋数量NC增加,模型的载荷质量比下降,因为从施加载荷开始至载荷最高处,环筋所承受的应力较小,因此对于本模型,环筋数量NC的增加并不能使结构的轴向承载效率增加。在正交试验分析时,环筋数量需作为因素之一,以获得最佳参数组合。在试验数据中载荷质量比的平均值为43.49 kN/kg,基于工程经验与平均值取值,可选NC正交试验因素水平组为5~8个。

图12 环筋数量对载荷与载荷质量比的影响
Fig.12 Effect of the number of ring ribs on ratio of load to mass
2.2.5 环筋宽度的影响研究
环筋宽度aC根据工程经验及自动化缠绕技术限制,设定范围为4~9 mm,分析结果如图13所示。根据试验结果分析,环筋宽度aC的增加会使模型轴向承载效率下降,且aC的增加并未使承载能力有显著的提升,与纵筋宽度aL相比,aL每增加1 mm,其承载效率平均降低1.32%,而aC每增加1 mm,其承载效率平均降低1.28%。因此在做正交试验时,需将环筋宽度aC作为因素之一,以便获得最佳参数组合。根据实际生产情况可选取正交试验因素水平组为5~8 mm。
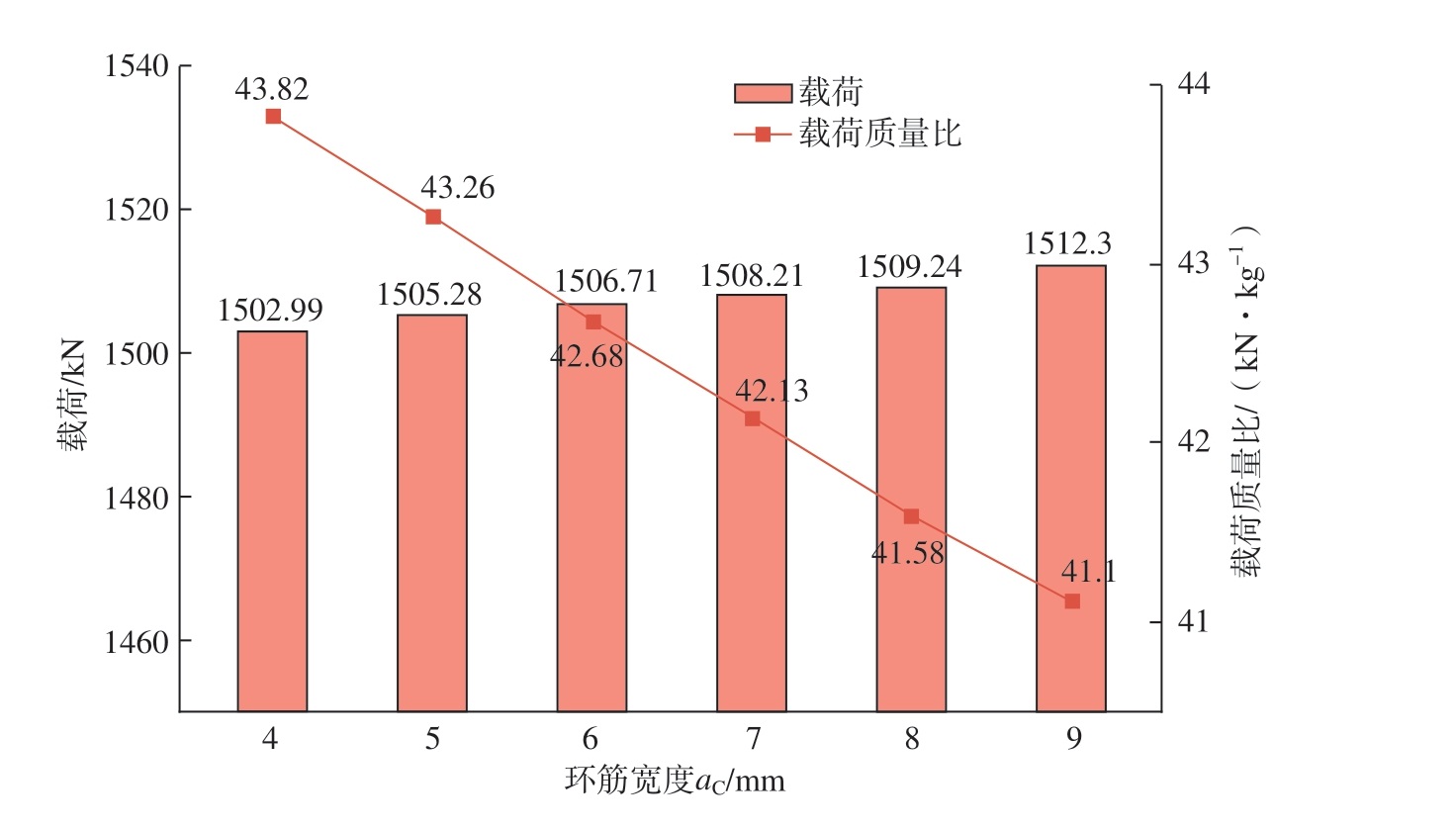
图13 环筋宽度对载荷与载荷质量比的影响
Fig.13 Effect of ring reinforcement width on load to load to mass ratio
3 基于正交试验的网格筋结构参数优化
正交试验是在概率论与数理统计的基础上,运用标准化的正交表格,在所有可能的试验中,选择一定数量且具代表性的因素组合来进行试验,进而分析各因素的影响规律,并将试验结果进行数学处理的一种科学方法[18]。本文分析了网格筋各结构参数对模型承载效率的影响程度,结合分析结果与实际生产经验,找出了参数的合理范围。但在设计时,各个参数并不是独立存在,而是存在相互作用关系的。为更好地提高结构的承载效率,需要对各种参数组合进行研究,全因素分析工作量大且耗时较长,因此采用正交试验法,可在保证试验结果准确性的同时,减少试验分析次数,从而对各参数组合进行优化。
3.1 试验因子及水平
本文所优化的网格筋模型采用矩形网格筋,筋条包括环筋与纵筋。由单因素试验分析得知,网格筋结构参数包括纵筋数量、纵筋宽度、筋条高度、环筋数量、环筋宽度。本文选取以上5种工艺参数为此正交试验的试验因子,并且每个因子都选出4个水平,具体如表 4所示。
3.2 正交试验及结果分析
3.2.1 正交试验方案
由表 3选定的因素与水平数可知,本次试验为5因素4水平正交试验,所以选用L16(45)正交表。仿真试验结果见表5。
表5 正交试验仿真结果
Table 5 Orthogonal test simulation results
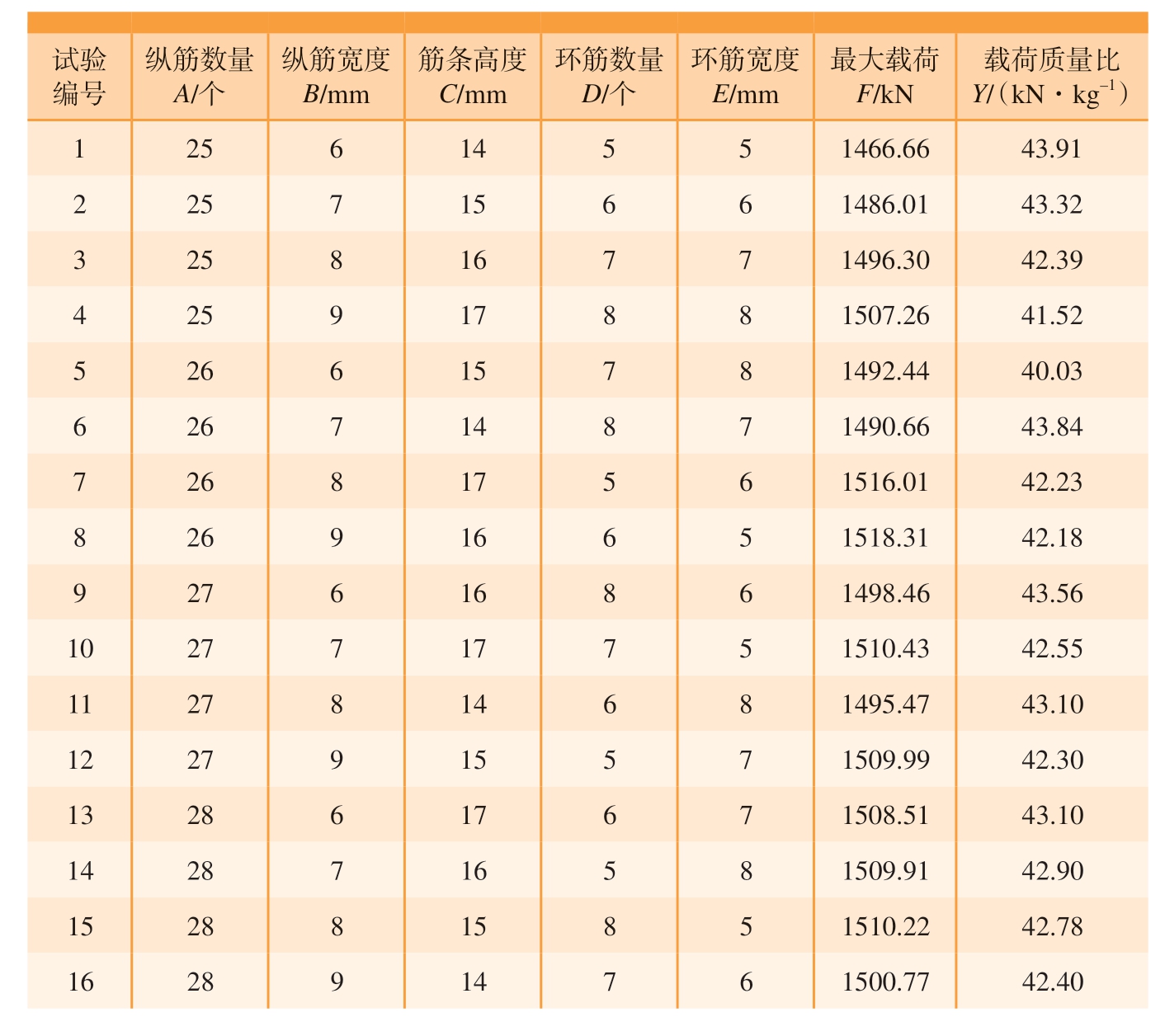
试验编号纵筋数量A/个纵筋宽度B/mm筋条高度C/mm环筋数量D/个环筋宽度E/mm最大载荷F/kN载荷质量比Y/(kN·kg–1)1 25 6 14 5 5 1466.66 43.91 2 25 7 15 6 6 1486.01 43.32 3 25 8 16 7 7 1496.30 42.39 4 25 9 17 8 8 1507.26 41.52 5 26 6 15 7 8 1492.44 40.03 6 26 7 14 8 7 1490.66 43.84 7 26 8 17 5 6 1516.01 42.23 8 26 9 16 6 5 1518.31 42.18 9 27 6 16 8 6 1498.46 43.56 10 27 7 17 7 5 1510.43 42.55 11 27 8 14 6 8 1495.47 43.10 12 27 9 15 5 7 1509.99 42.30 13 28 6 17 6 7 1508.51 43.10 14 28 7 16 5 8 1509.91 42.90 15 28 8 15 8 5 1510.22 42.78 16 28 9 14 7 6 1500.77 42.40
3.2.2 试验优化结果分析
常用的正交试验分析法有极差分析法和方差分析法两种,两种方法均可单独使用,亦可联合运用。本文使用极差分析法。
通常在同一正交试验中,各因素对目标函数的作用程度不同,其极差值也不同,且极差值的大小与对目标函数的作用程度成正比,表6为正交试验结果的极差分析表。根据表6数据绘制模型承载效率的极差关系,如图14所示。可以看出,各结构参数对模型承载效率的极差影响大小排序为纵筋宽度B >筋条高度C >纵筋数量A >环筋数量D >环筋宽度E。对于连接段模型来说,模型承载效率越高越好,故得出的最佳工艺参数组合为A2B1C1D4E3,即纵筋数量26个、纵筋宽度6 mm、筋条高度14 mm、环筋数量8个、环筋宽度7 mm。
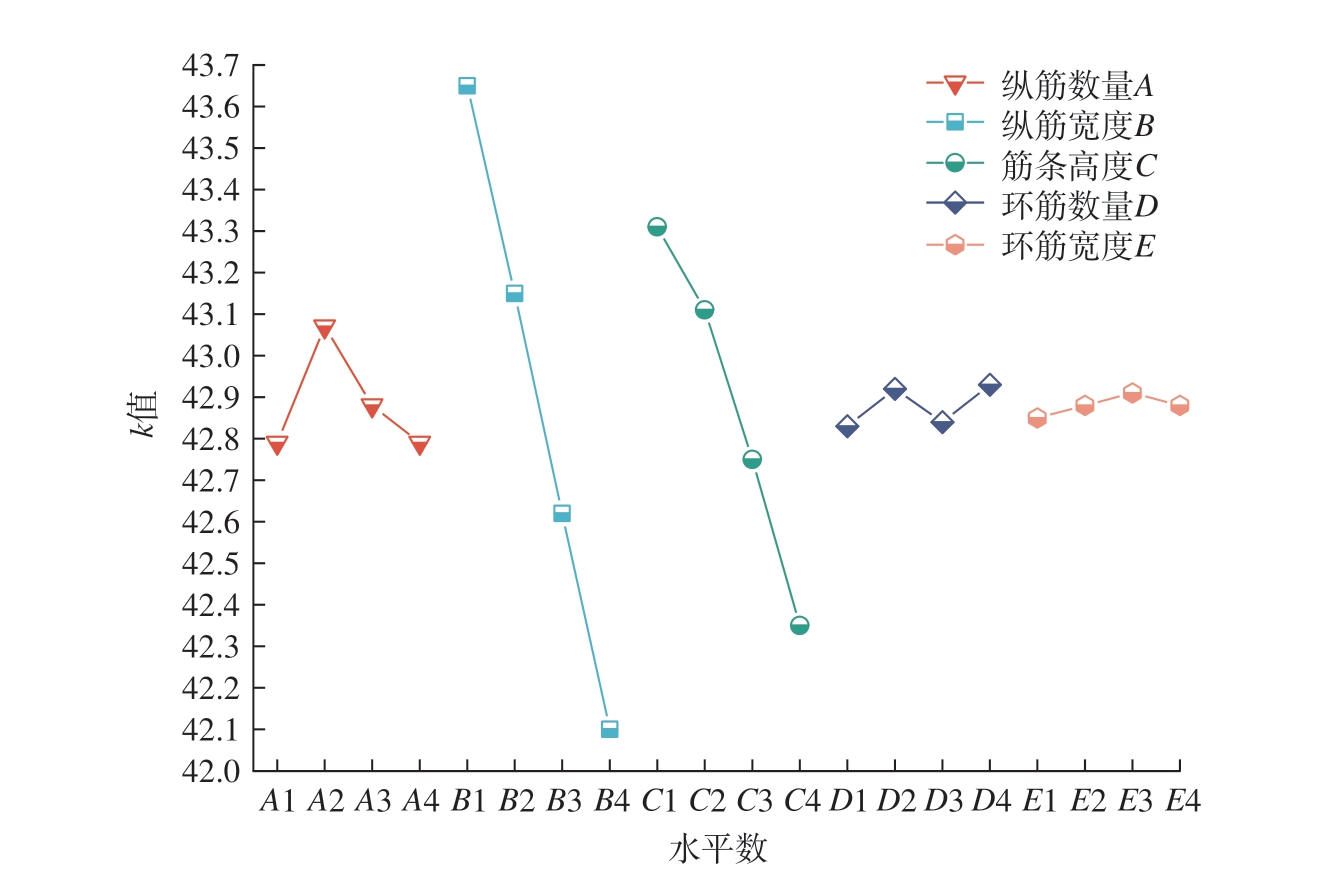
图14 极差关系
Fig.14 Range relationship
表6 极差分析表
Table 6 Range analysis table
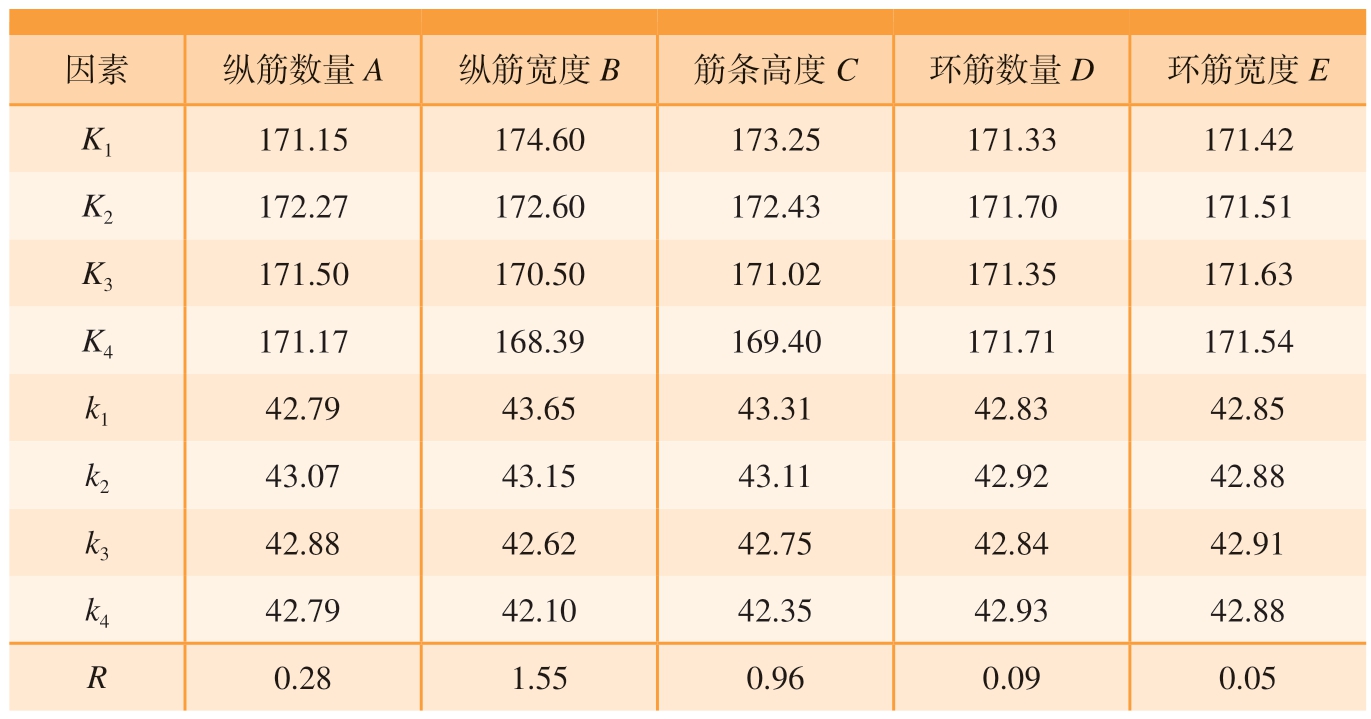
因素 纵筋数量A 纵筋宽度B 筋条高度C 环筋数量D 环筋宽度E K1 171.15 174.60 173.25 171.33 171.42 K2 172.27 172.60 172.43 171.70 171.51 K3 171.50 170.50 171.02 171.35 171.63 K4 171.17 168.39 169.40 171.71 171.54 k1 42.79 43.65 43.31 42.83 42.85 k2 43.07 43.15 43.11 42.92 42.88 k3 42.88 42.62 42.75 42.84 42.91 k4 42.79 42.10 42.35 42.93 42.88 R 0.28 1.55 0.96 0.09 0.05
为验证优化参数的可靠性,依照网格筋最佳结构参数,重新建模并进行有限元分析,得到载荷–位移曲线,如图15所示。经过分析,得到优化后模型的最大载荷为1539.71 kN,对应模型质量为34.9 kg,载荷质量的比值为44.12 kN/kg,如图 16所示,优化后的模型载荷相较于正交试验组的平均载荷增加了38.62 kN,且载荷质量比比正交试验组增加1.24 kN/kg,同时质量相较于正交试验组的平均质量减轻了0.3 kg。综合比较,优化后的模型拥有更好的结构参数组合,力学性能更优秀,更符合需求。
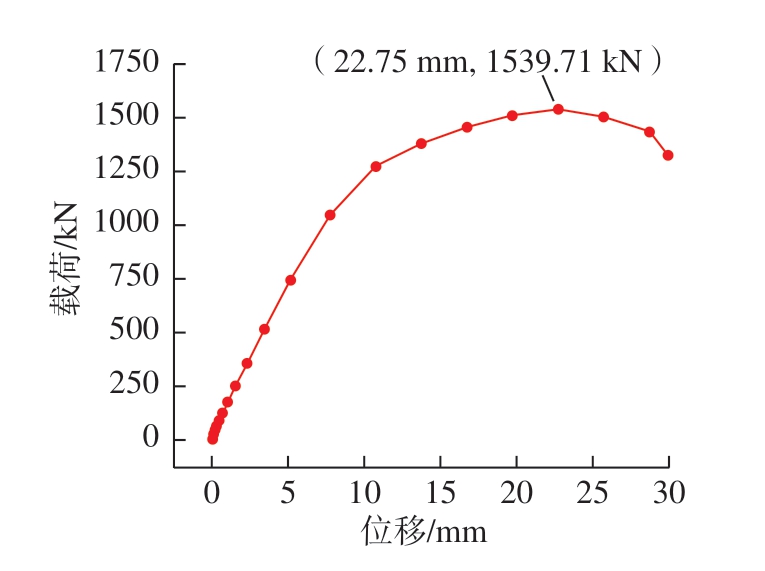
图15 载荷–位移曲线优化结果
Fig.15 Optimization result of load–displacement curve
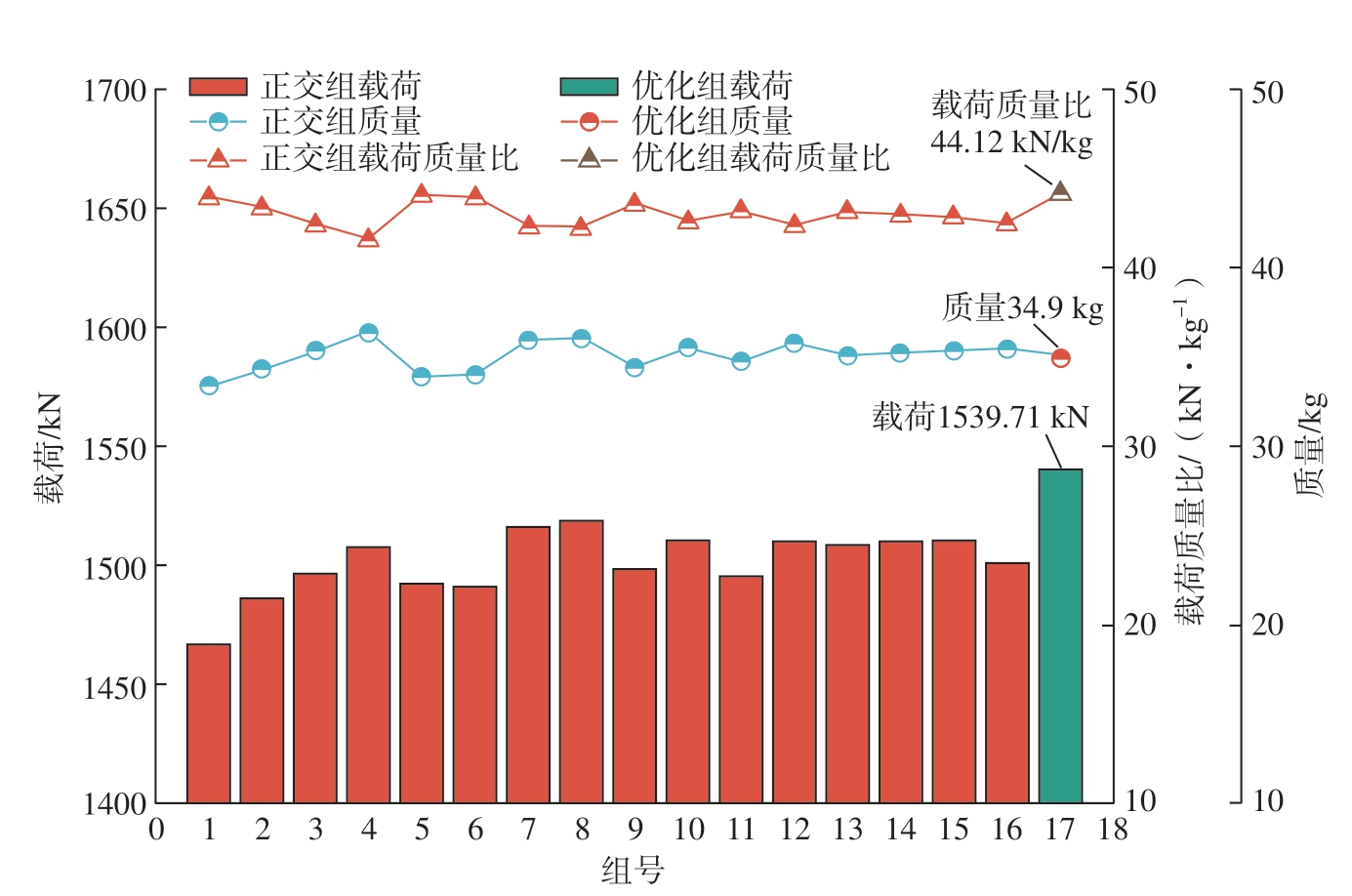
图16 初始组与优化组数据对比
Fig.16 Comparison of original and optimized group data
4 复杂回转体网格筋构件制备及性能测试
4.1 复杂回转体网格筋构件制备工艺
4.1.1 成型方法选择
常见复合材料网格结构成型方法有人工铺放、纤维缠绕、纤维铺放。本文选用纤维铺放技术进行复杂回转体网格筋结构成型。将预浸料以一定方式铺放在模具相应位置,压辊与模具接触,可通过提供一定的压力及温度实现产品的制备,最终使制件拥有更好的成型性能。纤维铺放技术不仅能使产品拥有更好的成型性能,且能完成复杂曲面结构产品的生产,其切断与重送功能也大大提高了生产效率。
4.1.2 模具准备
在网格筋结构铺放成型过程中,影响构件质量的重要因素之一是成型模具。一般根据成型的过程所选模具不同,可以将网格筋结构成型方法分为自由成型法、轻质泡沫模具成型法、硅橡胶模具成型法、金属模具成型法、石膏模具成型法等。考虑到模具成本和制备的难易程度,本文采用硅橡胶–金属组合模具成型方法,如图17所示。金属芯模的作用是提供整个模具的承载刚度,同时用来安装外围的硅胶模具,最后可在模具两端安装法兰,为后期模具固定于主轴配合自动化成型做准备。硅橡胶模具能够铺覆在硬质金属模具表面,同时具有良好的耐高温性能。在固化过程中,硅胶模具会受热膨胀变形,对肋条产生较大的侧向挤压力,使纤维更加密实,减少肋条中的孔隙率。此外为了便于脱模与模具安装,模具采用分段式安装。

图17 硅橡胶–金属组合模具
Fig.17 Silicone rubber–metal combination mold
4.2 制备及性能测试
本文设计的复杂回转体网格筋结构使用多丝束网格筋铺丝设备及16丝束卧式铺丝设备成型,根据网格结构的形状尺寸,编写了筋条铺放相应程序并生成数控系统的NC代码。再利用CATIA二次开发自动生成蒙皮自动铺放轨迹点,经过后置处理生成卧式机床NC代码。铺放成型前,要将模具表面清理干净,涂刷脱模剂,方便固化成型后脱模。铺放过程中筋条及端框铺放局部图如图18所示,筋条节点处采用的是堆叠铺放形式。

图18 筋条及端框铺放局部图
Fig.18 Partial diagram of rib and end frame laying
构件铺放完成之后采用热压罐工艺固化,如图19所示。固化工艺:从室温加热至 (90±5) ℃,保温3 h;升至 (120±5) ℃,保温3 h;升至(150±5) ℃,保温4 h;升至(180±5)℃,保温4 h;升至 (195±5) ℃,保温5 h;之后随炉冷却降温。固化后产品如图20所示。

图19 固化过程示意图
Fig.19 Schematic diagram of curing process

图20 固化后产品
Fig.20 Cured product
固化结束后,会对产品再次进行一系列的加工,包括边切削、打孔、去除毛刺等。之后进行多项性能测试,本文只关注在轴压作用下的最大载荷。通过测试得到最大载荷为1418.27 kN,而本产品实际制造后的质量为35.9 kg,实际载荷质量比为39.51 kN/kg。其中实际载荷达到理论载荷的92.1%。通过分析,实际载荷低于理论计算载荷可能存在的原因:首先,理论计算时选取的是Hashin失效准则,涉及基体及纤维的失效,失效强度均为单层板的强度,但是复合材料结构有分层现象出现,尤其是在筋条与蒙皮之间存在一定的分层现象;其次,在实际制造过程中,由于设备、材料、环境等因素,不可避免地造成一定的夹杂、重叠、褶皱等缺陷,使得实际载荷低于理论计算载荷;此外,对产品进行边切削、打孔等机械加工也会使实际载荷低于理论计算载荷。
5 结论
本文利用有限元屈曲分析方法对复杂回转体的网格筋结构进行单因素分析,设计了适用于复杂网格筋结构的正交试验方案,通过数值模拟,以及对试验结果进行极差分析,发现各因素对目标值影响程度的排序为:纵筋宽度>筋条高度>纵筋数量>环筋数量>环筋宽度,得出最优参数组合:纵筋数量26个、纵筋宽度6 mm,筋条高度14 mm、环筋数量8个、环筋宽度7 mm。优化后的模型载荷相较于正交试验组的平均载荷增加38.62 kN,且载荷质量比相较于正交试验组的平均值增加1.24 kN/kg,同时质量相较于正交试验组的平均质量减轻了0.3 kg。最后对优化模型进行了试验验证,实际载荷达到理论载荷的92.1%,发现使用最优参数组合的回转体承受最大载荷理论值与实际值间的差异并分析差异出现的原因:理论计算时未考虑复合材料结构不可避免的分层现象的出现;实际制造过程中由于设备、材料、环境等因素,不可避免地造成一定的夹杂、重叠、褶皱等缺陷。
[1] GIUSTO G, TOTARO G, SPENA P, et al. Composite grid structure technology for space applications[J]. Materials Today: Proceedings,2021, 34: 332–340.
[2] AMBUR D R, JAUNKY N. Optimal design of grid-stiffened panels and shells with variable curvature[J]. Composite Structures, 2001,52(2): 173–180.
[3] JAUNKY N, KNIGHT Jr N F,AMBUR D R. Optimal design of general stiffened composite circular cylinders for global buckling with strength constraints[J]. Composite structures,1998, 41(3–4): 243–252.
[4] VASILIEV V V, MOROZOV E V. Optimal composite structures[J]. Advanced Mechanics of Composite Materials, 2007, 74:437–480.
[5] TOTARO G, GÜRDAL Z. Optimal design of composite lattice shell structures for aerospace applications[J]. Aerospace Science and Technology, 2009, 13(4-5): 157-164.
[6] 何景轩, 何国强, 侯晓. 复合材料格栅圆柱结构优化设计[J]. 固体火箭技术, 2009,32(1): 87–89, 99.HE Jingxuan, HE Guoqiang, HOU Xiao.Optimization design of composite cylindrical lattice structure[J]. Journal of Solid Rocket Technology, 2009, 32(1): 87-89, 99.
[7] AFONSO S, BELBLIDIA F, SIENZ J. Design of plates and shells using several optimization strategies[C]//Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2004:AIAA2004–4416.
[8] 张卫红, 章胜冬, 高彤. 薄壁结构的加筋布局优化设计[J]. 航空学报, 2009, 30(11):2126–2131.ZHANG Weihong, ZHANG Shengdong,GAO Tong. Stiffener layout optimization of thin walled structures[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2126–2131.
[9] SANO T, CATALANO J, CASEM D,et al. Microstructural and mechanical behavior characterization of ultrasonically consolidated titanium-aluminum laminates[C]//TMS Annual Meeting, TMS2008-137th Annual Meeting and Exhibition Supplemental Proceedings: Materials Processing and Properties. Boise, 2009.
[10] MAES V K, PAVLOV L, SIMONIAN S M S. An efficient semi-automated optimisation approach for (grid-stiffened) composite structures:Application to Ariane 6 interstage[J]. Composite Structures, 2019, 209: 1042–1049.
[11] 梁东平, 徐元铭, 彭兴林. 复合材料格栅加筋板布局优化设计[J]. 固体火箭技术,2008, 31(5): 527–530, 542.LIANG Dongping, XU Yuanming, PENG Xinglin. Configuration optimum design of gridstiffened composite panels[J]. Journal of Solid Rocket Technology, 2008, 31(5): 527-530, 542.
[12] 黄蔚, 杨勇, 王立朋, 等. 层合复合材料网格加筋结构有限元分析方法研究[C]// 中国力学大会. 2017暨庆祝中国力学学会成立60周年大会. 北京, 2017.HUANG Wei, YANG Yong, WANG Lipeng,et al. Study on finite element analysis method of grid-reinforced structures of laminated composite materials [C]//Chinese Mechanics Congress.2017 and Celebrating the 60th Anniversary of the Establishment of Chinese Mechanics Society.Beijing, 2017.
[13] 荣晓敏, 徐元铭, 吴德财. 进化神经网络在复合材料格栅结构设计中的应用[J].固体火箭技术, 2006, 29(4): 305–309.RONG Xiaomin, XU Yuanming, WU Decai.Application of evolutionary neural networks to grid-stiffened composite structure design[J].Journal of Solid Rocket Technology, 2006, 29(4):305–309.
[14] 林再文, 杜善义, 侯涤洋. 纤维增强聚合物基复合材料网格加筋锥壳[C]//2011中国材料研讨会论文摘要集. 北京: 冶金工业出版社, 2011.LIN Zaiwen, DU Shanyi, HOU Diyang.Fiber reinforced polymer matrix composite mesh reinforced conical shell[C]//2011 China Materials Conference abstracts. Beijing: Metallurgical Industry Press, 2011.
[15] 任康熙, 李星, 何为. 先进复合材料格栅加筋(AGS)圆柱壳结构优化设计[C]//第十五届中国科协年会. 贵阳, 2013.REN Kangxi, LI Xing, HE Wei. Optimal design of advanced composite grid reinforced(AGS) cylindrical shell structure [C]//The 15th Annual Meeting of China Association for Science and Technology. Guiyang, 2013.
[16] AHMADI H, RAHIMI G. Analytical and experimental investigation of transverse loading on grid stiffened composite panels[J].Composites Part B: Engineering, 2019, 159: 184-198.
[17] MOBASHERI ZAFARABADI M M,AGHDAM M M. Semi-analytical solutions for buckling and free vibration of composite anisogrid lattice cylindrical panels[J]. Composite Structures,2021, 275: 114422.
[18] 张毅. 基于CAE技术的车灯面罩翘曲变形分析与优化[D]. 长春: 吉林大学, 2020.ZHANG Yi. Analysis and optimization of warping deformation of car lamp mask based on CAE technology[D]. Changchun: Jilin University,2020.
