随着航空航天、核电、风电、船舶动力等领域对复杂型腔类零件的设计需求不断增加，特别是在高温、高压、高速等特殊工况下的需求，推动了复杂型腔类零件的广泛应用[1–2]。火箭氢氧发动机中的整体带叶冠涡轮盘是提高涡轮盘强度、刚度、极限转速和工作可靠性的一个设计实例[3]。叶片和轮盘由同一块材料整体加工而成，使得暴露在空气中的表面积更小，运行速度更快，减少了组装过程中的接缝和连接处的磨损，提高了叶盘的可靠性和性能，通常用于对强度、刚度和效率要求较高的高性能应用场合[4]。整体带叶冠涡轮盘因其内部叶冠的存在，导致叶片之间的通道狭窄而封闭，限制了材料选择和刀具可及性。若采用传统切削加工方法，易发生干涉，增加了加工的难度[5]。电火花加工可以用软的工具加工硬得多的工件，加工时不会产生切削力[6]，可以实现“以柔克刚”，多用于制作难加工材料[7]，是加工整体带叶冠涡轮盘等复杂型腔类零件的最佳方案之一[8]。
复杂型腔类零件电火花加工的关键是复杂型腔流道的加工，加工轨迹一般为空间复杂轨迹，编程难度大，电极与工件易发生干涉，能否规划出最佳电极进给路径对工件制造精度和效率具有重要影响。在电极进给轨迹规划中，轨迹搜索算法是前提，不少国内外学者对该技术进行了相应的研究。哈尔滨工业大学的Li 等[9]提出主运动轴法规划电极的运动轨迹，选取XYZ 3 个直线轴中的1 个作为主运动方向，优先保证电极沿该方向进行移动，结合辅助方向运动及加工参数调节实现对工件的加工，并基于该算法开发了BliskCad/Cam 软件。詹涵菁[10]基于顺序二次规划法对带冠整体涡轮叶盘的电极加工路径进行了研究，提出了一种通用算法，在约束范围内优化变量Xi=[yi Zi Bi Ci Hi],能够在复杂的约束条件下获得无干涉的电极运动轨迹，可实现复杂零件的轨迹搜索。庞鹏等[11]基于随机方向法求解每个节点处电极上端面中心点的无干涉运动轨迹坐标并使用NURBS 曲线拟合优化，得到电极无干涉的运动轨迹，可以满足闭式整体叶盘的技术指标要求。南京航空航天大学赵建社等[12]针对带冠整体叶盘提出沿主方向运动、辅助方向旋转的路径规划方法，在UG 平台上自主开发了数控电火花加工仿真模块，并进行了试验验证，验证结果可以满足加工需求。上海交通大学赵万生等 [13–17]在对某型号高性能液体火箭发动机中涡轮叶盘研究的基础上，提出了切向追随方法来完成电极的进给路径规划，并在UG 软件上开发了专用模块，成功完成了叶盘试件的加工。田喜明等[5]针对造型复杂的叶盘通道，提出一种电极纵向拆分的方法，将电极与工件干涉问题设为约束条件，构建轨迹搜索的最优化模型，求解得到电极无干涉的撤出轨迹，并进行带冠整体叶轮的加工试验验证，加工结果满足设计要求。Jia 等[18]提出了一种以流道内的最大旋转实体为基本几何形状的电极设计方法，满足高压冲洗、刀具磨损补偿和易于制造等要求，并提出了行星运动的四轴联动加工刀具路径，以整体导向叶环为例进行加工验证，试验证明该方法能够显著减少加工流道的时间。Ayesta 等[19]提出将低成本与获得电极最大尺寸相结合，给出了基于信赖域法的混合遗传算法，将其应用于电极运动轨迹搜索，可计算出电极平滑的运动轨迹。
目前主要的轨迹搜索算法采用直线轴作为主运动方向，轨迹搜索耗时长、效率低，生成的轨迹光滑度不高，具有工件局限性。本文以型腔流道狭小弯曲的闭式叶盘为例，基于非均匀有理B 样条（Non-uniform rational B-splines，NURBS）参数化曲线曲面建模方法提出计算流道中心线的通用算法。将流道中心线作为主运动方向进行电极进给轨迹优化搜索，有效避免电极干涉，从而提高轨迹搜索效率，并使用NURBS 曲线拟合无干涉的电极运动坐标。基于该算法开发了复杂型腔类零件电火花加工专用CAM 系统，并进行整体带叶冠涡轮盘的加工试验验证。
1 闭式叶盘电极设计方案
图1 为整体带叶冠涡轮盘的三维模型，由叶片、轮盘和叶冠构成，众多叶片分布于叶冠与轮盘之间，形成半封闭式的复杂弯曲通道。由于叶片弧度大且通道狭窄，使用单一电极加工易造成干涉，故需拆分电极，对同一通道依次进行加工。叶片间变截面型腔流道具有狭窄特征，流道上宽下窄。若将电极进行上下拆分，位于下侧的电极将无法进入流道内部进行加工。因此，设计电极拆分方案为左右拆分，拆分后的4 块电极分别从左右两侧进入叶盘通道进行加工，电极拆分如图2 所示。
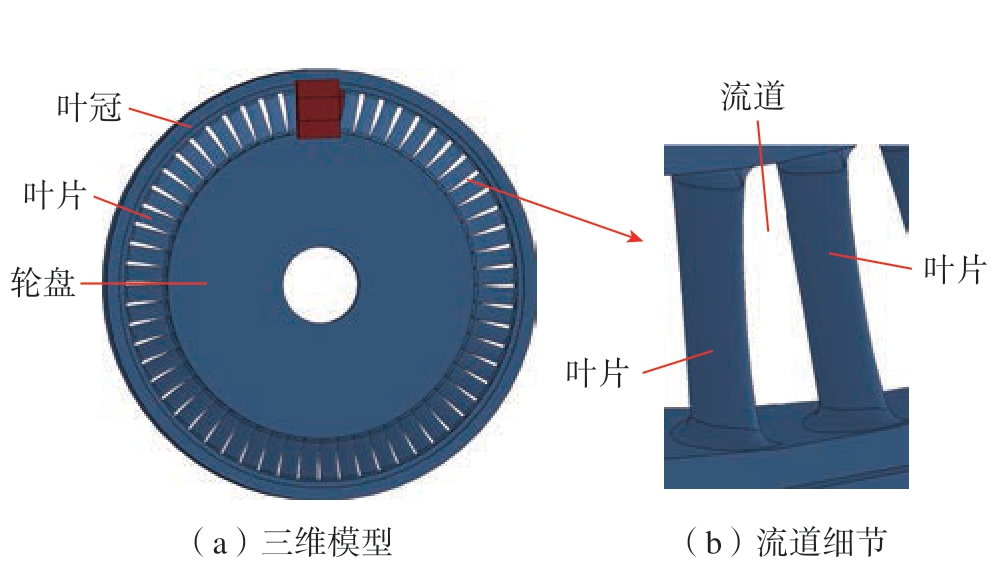
图1 整体带叶冠涡轮盘三维模型及流道细节
Fig.1 3D model and channel details of integral turbine disk with blade crown
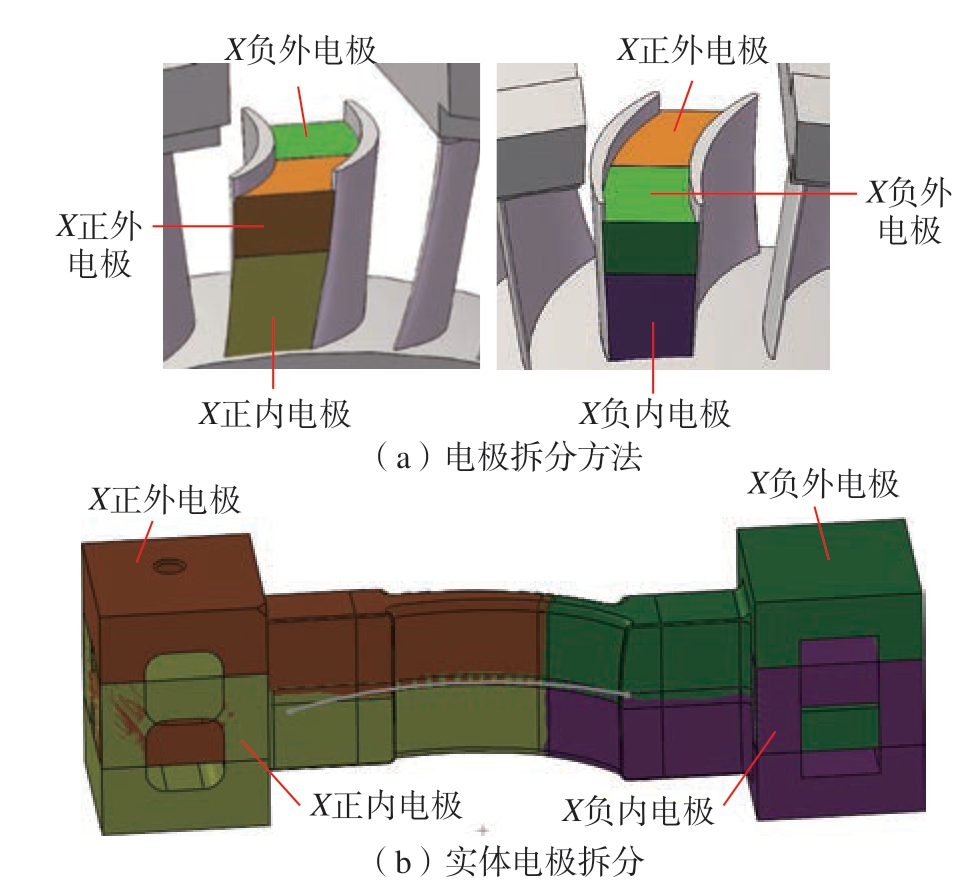
图2 电极拆分示意图
Fig.2 Schematic diagram of electrode splitting
为确保加工的准确性、效率和质量，拆分电极时应遵循以下原则。
（1）平衡电极厚度。
尽量保证拆分后的电极厚度相似，确保每块电极都能充分移动，避免部分电极受到限制而影响加工的均匀性和稳定性。
（2）电极部分重叠。
拆分后的各电极之间应保留重叠部分，以确保被加工表面的完整性。
（3）精简电极数量。
在保证成功加工的前提下，尽量减少电极的数量，以提高加工的精度和效率。
2 基于NURBS 的叶片型线重构
在整体带叶冠涡轮盘的设计与制造过程中，叶片的设计对于整个系统的性能和效率至关重要。一般情况下涡轮盘的实物模型与理论模型之间存在差异，通过比较根据原位测量数据重建的模型与理论模型之间的偏差，确定叶片的型面质量是否符合预定要求。根据叶片型面测量数据重建叶片模型是获得加工余量、评估叶片型面加工精度是否合格的关键步骤，也是获取流道中心线和刀具路径规划的前提[20]。叶片轮廓可通过一组型值点来描述，叶片轮廓拟合方法的选择取决于所需的拟合精度和复杂程度[21]。NURBS 方法使用控制点、节点和权重拟合曲线的形状，在处理复杂几何形状拟合时具有灵活性和数学表达优越性。本文采用NURBS 参数化曲线曲面建模方法重建整体带叶冠涡轮盘中的叶片模型，以有理的方式表示控制点，通过调整权重影响曲线，更好地适应叶盘的复杂曲面并通过局部控制参数曲线方法求取叶盘流道中心线，有助于优化叶盘的流动性能和设计效果。
2.1 NURBS 参数化曲线定义
一条p 次NURBS 曲线定义为[22]
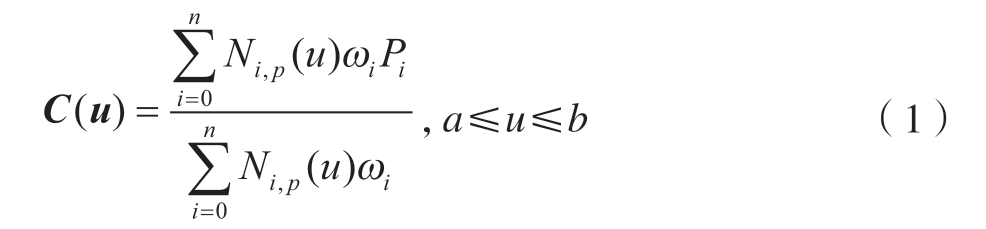
式中，{Pi} 为控制顶点，权重{ωi} 与{Pi} 相对应；{Ni，p（u）}[22]是定义在非周期（且非均匀）节点矢量U上的p 次B 样条基函数，其定义为
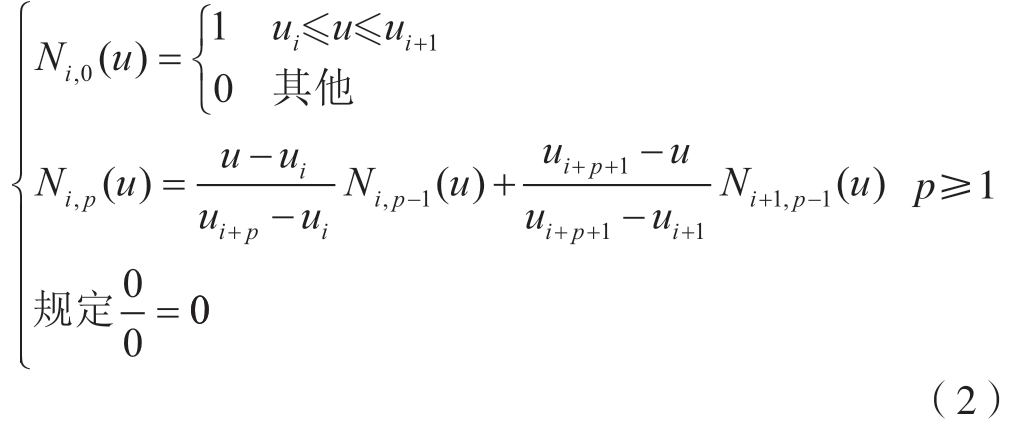
满足U={a，…，a，up+1，…，un，b，…，b}，在实际应用中节点矢量的首尾取p 重节点，分别为0 与1。
2.2 参数化构造叶片型线
针对闭式叶盘叶片叶型的参数组成部分，标注如图3 所示。
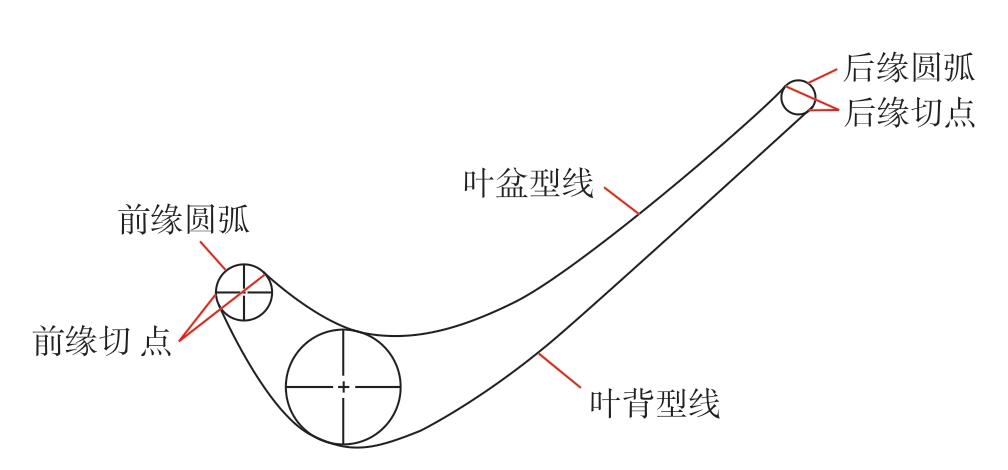
图3 参数化叶片叶型
Fig.3 Parameterized blade profile
叶片截面主要组成包括叶盆型线、叶背型线、前缘小圆、后缘小圆，在进行参数化叶型构造时选用五次多项式近似样条曲线。前缘小圆和后缘小圆直接由给定的圆心位置和半径确定，叶盆和叶背采用五阶多项式表示，多项式系数通过分析特殊点的位置及其导数确定，从而得到叶盆和叶背型线的参数化表示。
设叶盆型线和叶背型线分别为ys=f（x）、yt=g（x）的五次多项式，两者具有以下形式，即
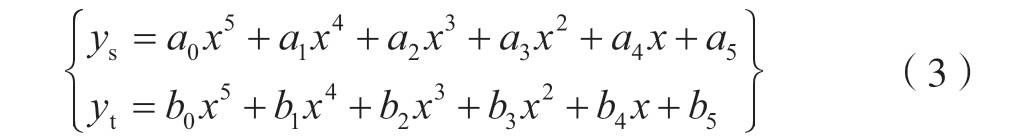
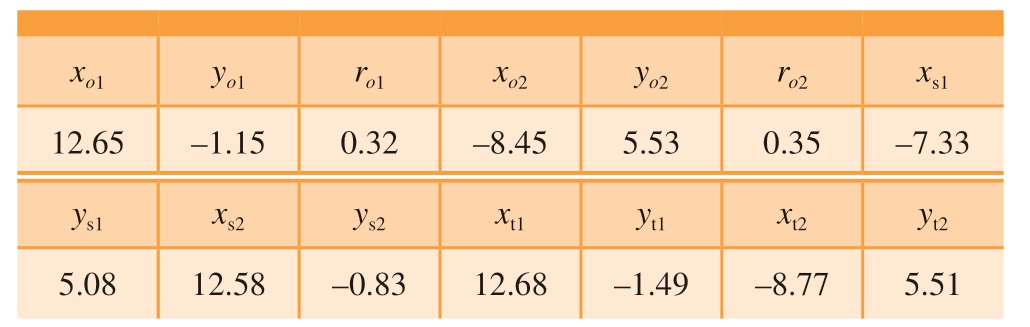
选取前缘切点和后缘切点为4 个特殊点，同时也是叶盆叶背型线的起始点和终止点。求取型线的相关参数，如表1 所示，将参数表示的前后缘切点代入叶盆叶背型线及其一阶、二阶导数中，即可计算出多项式的各项系数，并得到表2 所示参数。
表1 求解型线相关参数设置
Table 1 Parameter settings related to solving the profile line
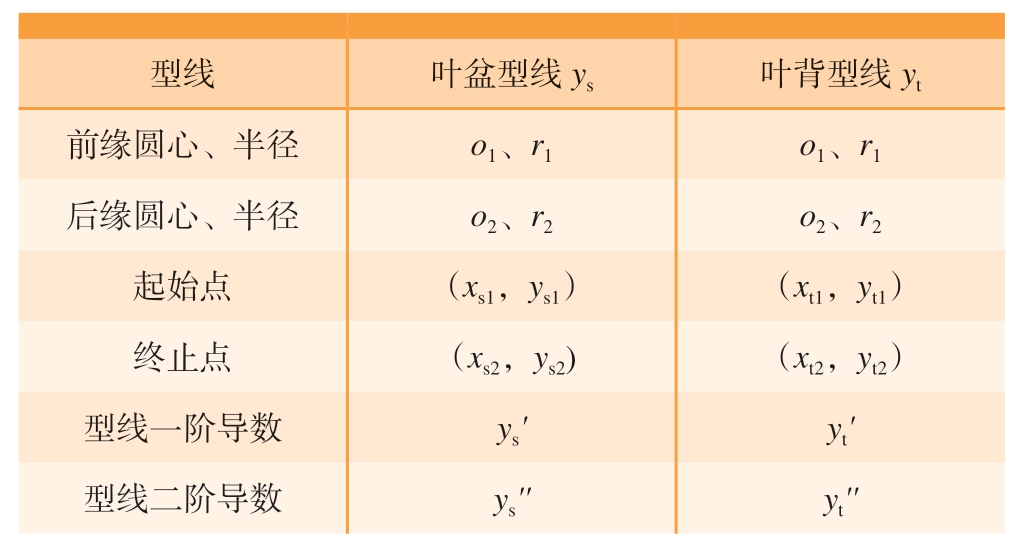
表2 代入起始点和终止点后型线相关参数设置
Table 2 Parameter settings for the profile after bring in the start point and end point
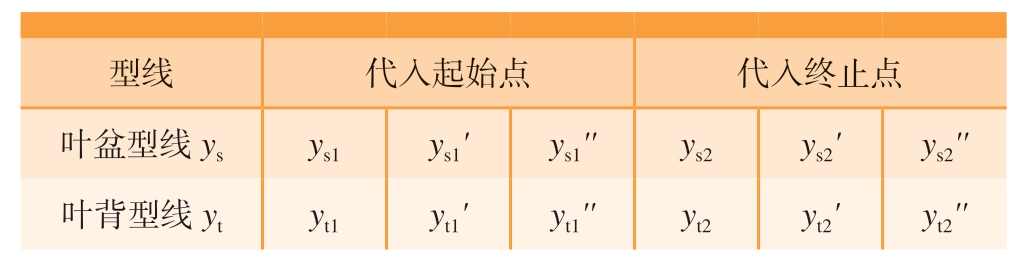
分别将叶盆、叶背型线的起始点和终止点代入型线、一阶导数、二阶导数中，则有
由式（4）和（5）可得叶盆叶背型线参数系数为[a0 a1 a2 a3 a4 a5]T 和[b0 b1 b2 b3 b4 b5]T，代入到叶盆和叶背型线函数中可以得到确切的叶盆和叶背型线。
在完成求解型线的准备工作后，确定叶型中各参数的初始值，并使用MATLAB 编写程序。计算所需初始参数，如表3 所示。
表3 计算所需初始参数
Table 3 Initial parameters required for calculation
根据得到的参数值，代入求解叶盆叶背多项式系数，得到叶盆叶背的参数化表示为
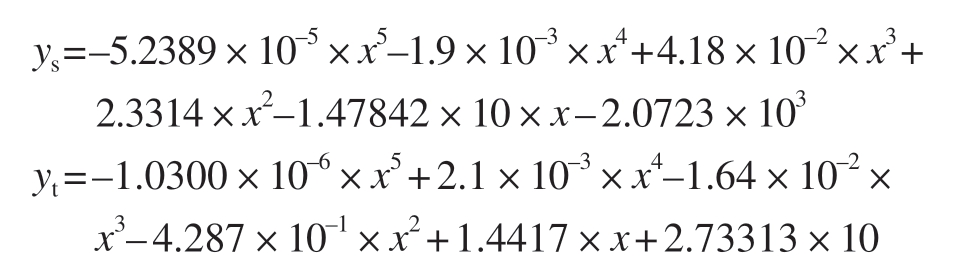
3 叶片自由曲面重构
叶片复杂曲面模型重构通过叶片型面测量数据重构叶片曲面模型，是判断叶片加工是否合格的重要方法，也是获取流道几何中心线、规划加工轨迹等工作的前提。通过曲线曲面重构算法，利用叶片截面线上的数据点来描述叶片的几何形状。
3.1 NURBS 曲面的矩阵表示
在进行NURBS 曲线曲面重构时，通常会利用C2连续的3 次B 样条曲线作为插值曲线，以重建给定型值点的曲面。由于数据量大，使用有理分式进行NURBS曲面的求值和求导容易出错，因此采用矩阵表达式形式来简化NURBS 曲面的计算过程[23]。
给定空间（n+1）×（m+1）个控制顶点di，j（i=0，1，…，n；j=0，1，…，m），采用3×3 次NURBS 曲面的矩阵表达形式为
式中，U = [1 u u2 u3]，V =[1 v v2 v3]（0≤u，v≤1）为U、V 方向上的节点矢量。
Wi，j 为控制顶点对应的权因子矩阵，即
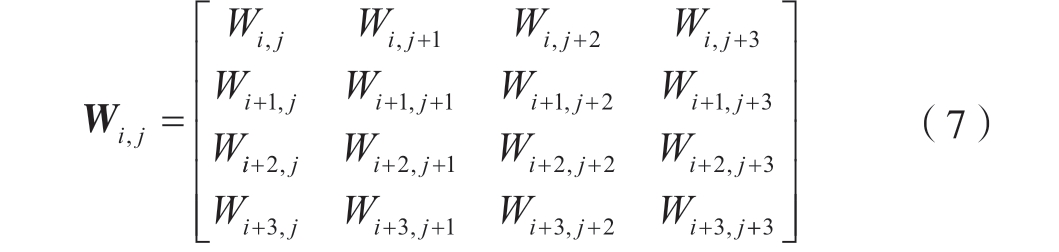
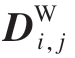为带权控制网格顶点，对应每一个控制顶点，即
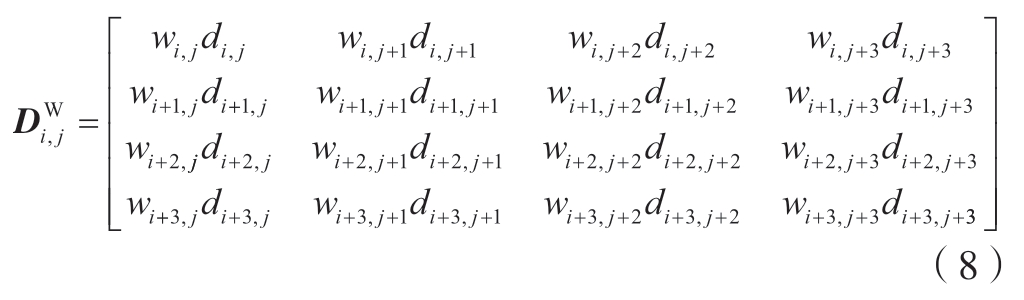
为了方便计算，引入节点系数矩阵Ni 和算子Δ，并规定
类似定义V 向算子Δ，同理可得
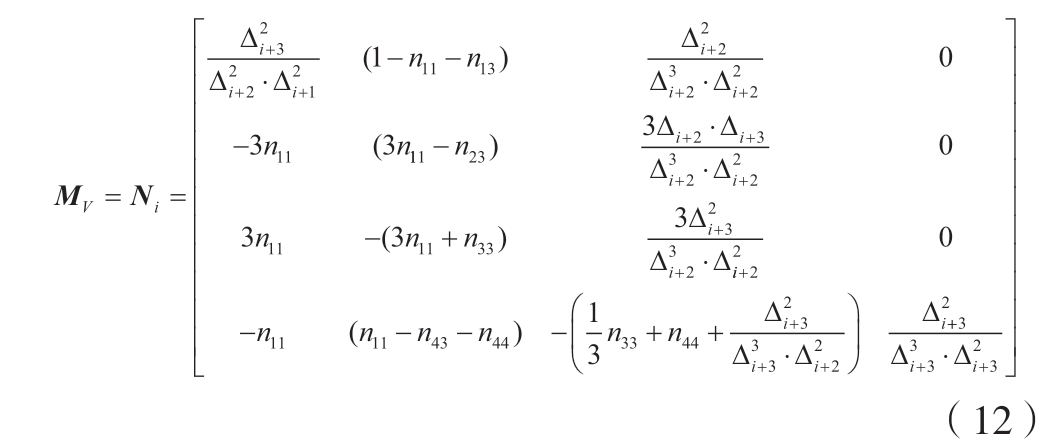
通过参数化型值点得到节点矢量，反求出控制顶点和权因子，即可确定叶片的曲面方程。
3.2 数据点参数化与节点矢量求解
参数化方法的选择会影响插值曲线的形状。因此，数据点的参数化应尽可能地反映出插值曲线的性质。本文采用累积弦长参数化法参数化U、V 方向节点矢量，能够较好地反映测量数据点按弦长分布的情况。
令d 为曲线总弦长，可得
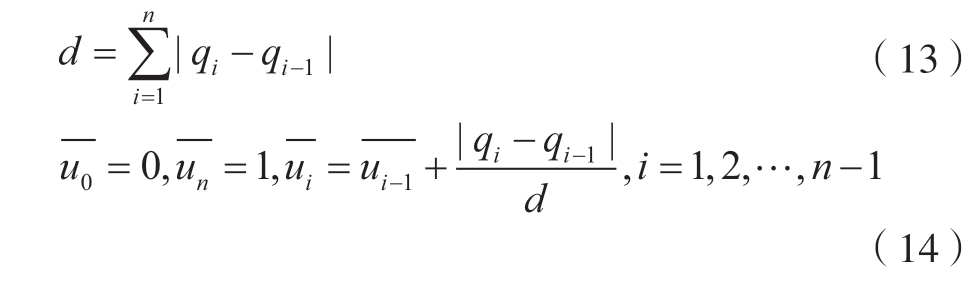
通过累积弦长法对型值点参数化得到
采用平均节点矢量的方式建立节点矢量与数据点参数值的关系，如式（15）所示。
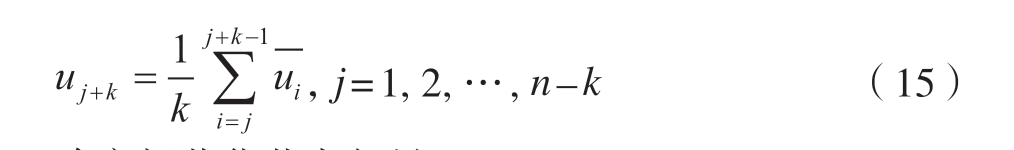
确定规范化节点矢量
3.3 反求控制顶点
对一组离散的型值数据点qi（i=0，1，…，n）拟合，选用（n+2）个控制顶点di（i = 0，1，…，n+2）与节点矢量U=[u0，u1，…，un+6]求解曲线，控制顶点di 与型值点qi 需满足式（16），即
选择切矢条件作为边界条件，可知首末控制顶点与首末数据点重合，即d0=q0，dn+2=qn，且首末端点处的切矢条件如式（17）所示。
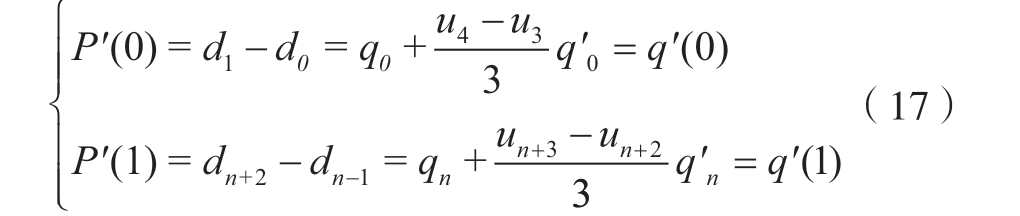
式中，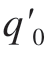
和
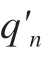为型值数据点首末端点的一阶导数，可得线性方程组，即
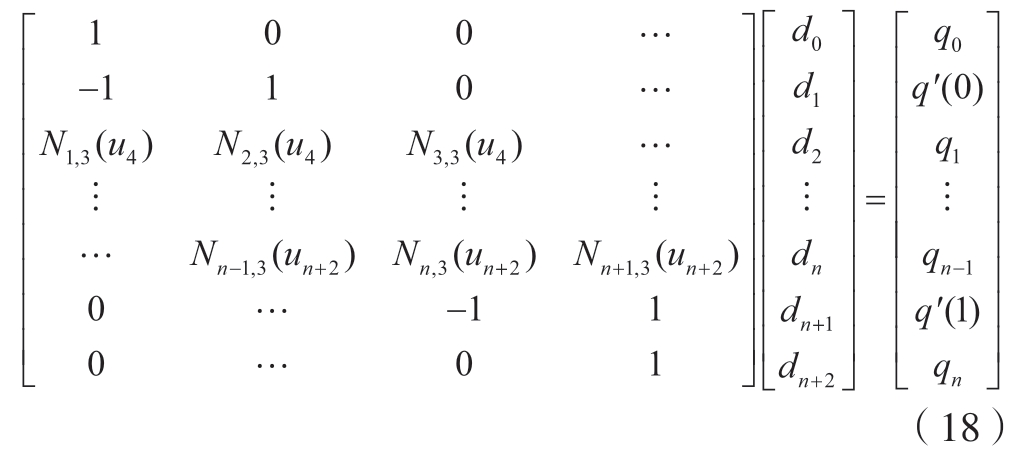
将根据型值数据点参数化得到的节点矢量和基函数值，代入式（18）即可反算出全部控制顶点。分别将控制顶点、权因子和系数矩阵代入式（6）中，即可得到叶片的参数表达式。在MATLAB 中进行拟合，得到叶片型面，如图4 所示。
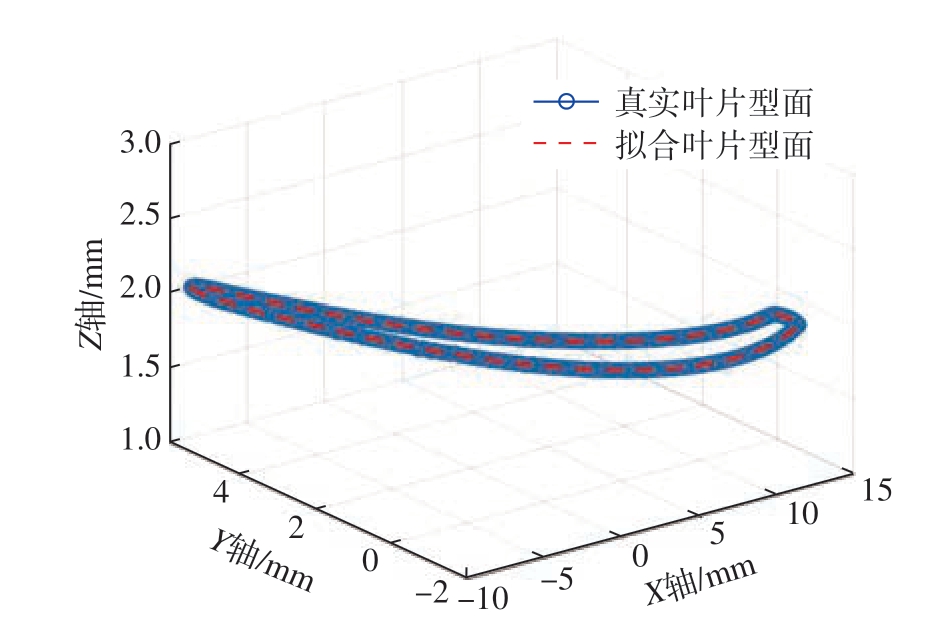
图4 叶片型面Fig.4 Blade profile
4 轨迹搜索算法研究
4.1 总体流程设计
电极运动轨迹是影响加工件最终形状、尺寸和精度的关键因素。对于复杂型腔类零件的电火花加工，找到一条无干涉的、优化的加工轨迹至关重要，一般加工的起点是任意的，而加工的终点是唯一确定的。根据电火花加工的特点来看，只要能确保电极从被加工型腔中无干涉地抽出，其反向运动轨迹就可以用于电极的加工路径。本研究采用逆向搜索方法，以叶盘通道形状作为电极的初始形状，并将左右拆分后的成形电极放置于加工完成时的位置（即流道的内部）。在搜索无干涉运动轨迹的同时，逐步撤出电极，确保电极与工件不会发生碰撞。最后通过反向电极撤出轨迹，获得实际加工中电极的进给轨迹。
在实施电极运动轨迹搜索之前，需考虑放电间隙补偿问题。由于放电过程中电极放电面与工件被加工型面之间存在一定的放电间隙δ，一般在0.01～ 0.50 mm 之间。需对电极运动轨迹搜索中使用的电极模型进行“缩小偏置”处理，偏置距离为放电间隙δ，从而避免被加工零件模型和电极模型因放电间隙造成电极运动轨迹干涉。
基于NURBS 参数化曲线曲面建模方法的复杂型腔类零件电极运动轨迹搜索算法总体流程如图5 所示。首先基于NURBS 曲面重构方法得到流道中心线数学表达式，使电极沿流道中心线方向以一定的步长移动，并在每个特定位置处做干涉检查。对无干涉的运动点坐标使用NURBS 曲线拟合得到电极运动轨迹。记录无干涉点的坐标，使用NURBS 拟合。
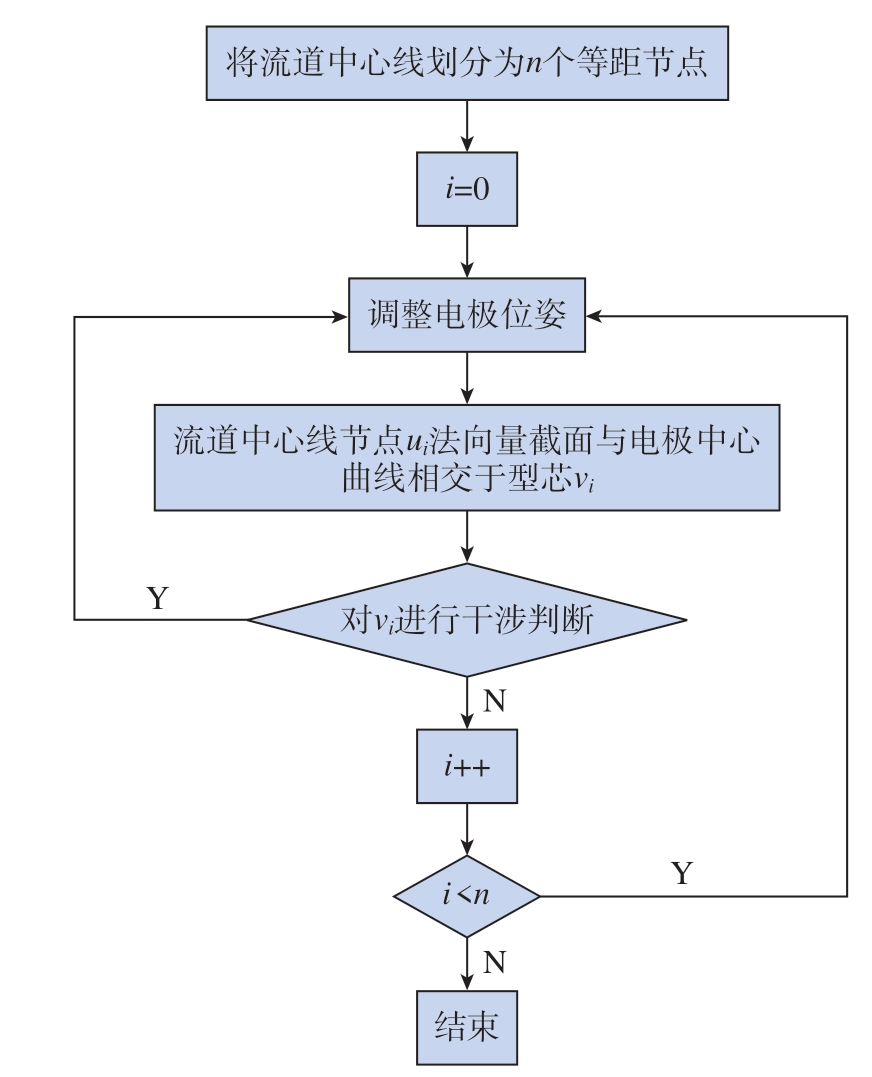
图5 轨迹搜索算法流程图
Fig.5 Flowchart of trajectory search algorithm
4.2 理论算法研究
成形电极在运动过程中存在4 个自由度，分别是沿X、Y、Z 轴的直线自由度Mx、My、Mz 和绕C 轴的旋转自由度θC。为了使电极运动轨迹适用于尽可能厚的电极，定义电极撤出的主方向r为沿叶盘流道中心线方向。本文基于NURBUS 曲面重构方法给出复杂型腔类零件求取流道中心线的通用算法步骤如下。
对于给定的叶片型面（x，y，z）=S（u，v），考虑在其上寻找一组内切圆Ci（i=1，2，…，n），满足以下条件。
（1）内切圆Ci（i=1，2，…，n）与叶片型面S 相切于两点s1=（x1，y1，z1）和s2=（x2，y2，z2），且s1∈ys（ys为叶盆型线），s2∈yt（yt 为叶背型线）。
（2）在相切点s1、s2 处满足圆心c =（x0，y0，z0）到相切点的连线向量与叶片型面S 在相切点处的梯度向量方向相同，即
式中，
f（x1，y1，z1）为叶片型面S 在相切点（x1，y1，z1）处的梯度向量。
（3）内切圆Ci（i=2，3，…，n – 1）两两相切于一点。
由于叶盘型腔的叶片是由一个叶片通过圆周方式散布于叶盘中，所有叶片除位置信息外，其余均相同。对于相邻叶片的型面，对每个叶片分别进行内切圆构造。如图6 所示，设第j（j =1，2，…，m）个内切圆分别为Ci，j（i =1，2，…，n），分别连接相邻叶片内切圆圆心ci，j（i =1，2，…，n）和ci，j+1（i =1，2，…，n），得到直线Li（i =1，2，…，n）。依次连接各Li（i =1，2，…，n）的中点Mi，使用NURBS 曲线拟合即可获得复杂型腔类零件的流道中心线。
图6 流道中心线
Fig.6 Runner centerline
将流道中心线F（x，y，z，）以电极运动步长Δs 划分为n 个等距节点{u0，u1，…，un–1}。电极运动到第i步时，调整电极姿态，使得流道中心线节点ui 处法向量截面与电极型面相交于线段li（i=0，1，…，n–1），取线段li 的中心点定义为“型芯”vi。电极进给运动轨迹搜索的目标是计算出一组vi，控制电极无干涉地从加工终了位置抽出运动至加工起始位置。电极从初始点出发，沿运动方向r 以步长Δs 进行迭代计算，依次对每个型芯点vi（i=0，1，…，n–1）采用最短距离算法进行干涉判断。
定义流体通道的叶盆、叶背、轮毂外圆、叶冠内圆型面与相应的电极型面之间的最小距离分别为δ1、δ2、δ3、δ4，设定一个安全距离阈值，判断在任意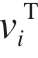
（x，y，z，c）下最短距离δi1、δi2、δi3、δi4 是否小于。若任意最短距离小于设定的安全距离阈值，即电极与实体过于接近，可能发生干涉。
如果发现干涉问题，可通过及时调整电极姿态、增加安全间隙或缩短步长等方法消除干涉，直到找到一组无干涉的型芯点位姿，即
最后使用NURBS 曲线对运动轨迹坐标差补运算，拟合得到无干涉的电极撤出轨迹。
4.3 CAM 系统仿真
为了验证基于NURBS 参数化曲线曲面建模方法的电极运动轨迹搜索算法的正确性，使用VB.NET 语言对该算法编程，得到复杂型腔类零件多轴联动电火花加工专用CAM 系统。开发电极运动轨迹优化搜索模块和加工过程仿真模块，输入轨迹搜索参数如表4所示，针对4 轴、5 轴、6 轴复杂型腔类零件分别进行图7 所示的电极运动轨迹优化搜索。导入机床文件，通过仿真加工过程有无碰撞验证轨迹搜索的正确性。如图8 所示，不同轴系工件加工过程仿真中电极进出均无碰撞，证明该轨迹搜索算法可有效避免干涉，工况适应性强，可用于复杂型腔类零件无干涉的电极运动轨迹优化搜索。
表4 CAM 系统轨迹搜索参数
Table 4 CAM system trajectory search parameters
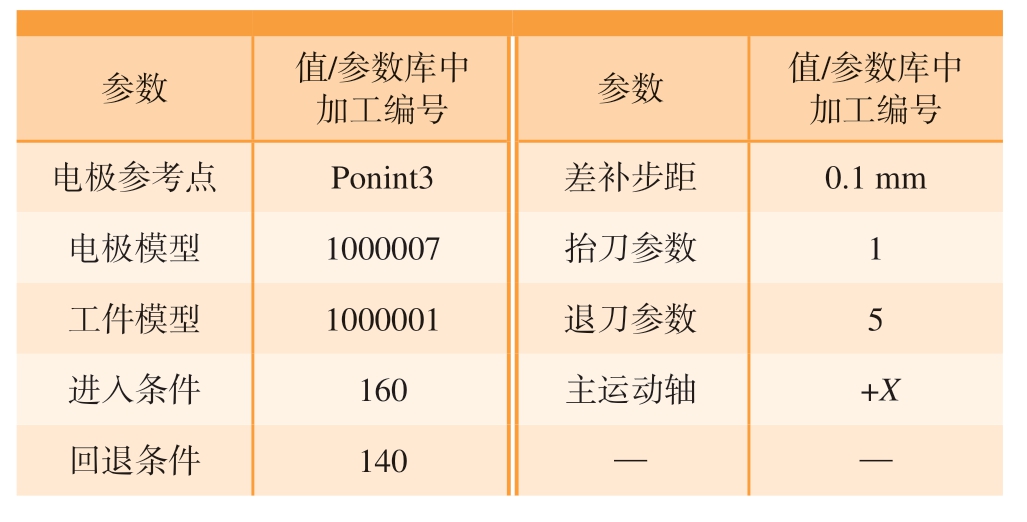
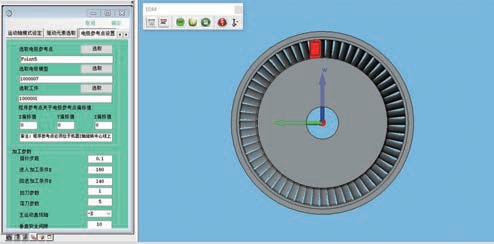
图7 CAM 系统轨迹搜索界面
Fig.7 CAM system trajectory search interface
图8 CAM 系统不同轴系工件加工过程仿真
Fig.8 Simulation of machining process of workpieces with different axes in CAM system
5 试验验证
为验证本文提出的轨迹搜索算法的正确性和优越性，以图1 所示闭式叶盘为例，首先在CAM 系统中导入叶盘与电极模型，计算涡轮盘流道中心线表达式，沿流道中心线方向以步长0.1 mm 搜索电极运动轨迹，拟合得到电极无干涉的运动曲线。在CAM 系统中使用5轴机床仿真加工过程确认叶盘模型与电极模型无干涉后，使用表5 中的加工参数进行多轴联动电火花闭式叶盘加工试验验证，全部放电参数都采用正极性加工。叶盘材料为钛合金，加工电极采用第1 节中提到的分体电极，电极材料为紫铜，加工机床采用自主研发的5 轴联动精密数控电火花成形机床，试验设备和试验过程如图9 所示。
表5 电极加工参数
Table 5 Electrode processing parameters
图9 试验设备与试验过程
Fig.9 Experimental equipment and experimental process
基于上述试验条件，叶盘成形加工流程如下：
（1）根据本文提出的轨迹搜索算法和分体电极搜索电极无干涉运动路径，得到多轴联动加工轨迹；
（2）将叶盘基体材料和分体电极分别装卡在转台和夹具上，进行拉直、找正等操作；
（3）使用左内、外电极和右内、外电极进行叶盘的五轴联动电火花加工。
叶盘共计60 个通道，各通道加工具体时间如图10（a）所示，其中单通道最长耗时4.25 h，最短耗时4.07 h，总耗时249.3 h，平均每个通道耗时4.16 h。
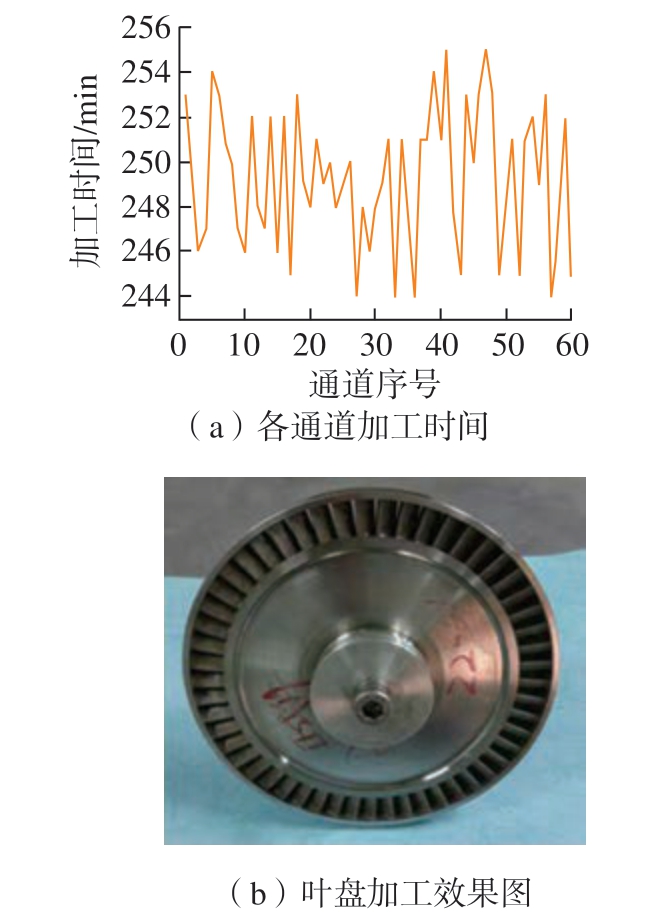
图10 加工结果分析
Fig.10 Analysis of machining results
叶盘最终加工效果如图10（b）所示，加工过程中叶盘放电稳定，测量叶形加工精度≤0.03 mm，满足闭式整体叶盘类零件指标要求。试验结果证明，该算法可快速搜索电极无干涉运动轨迹，可用于该类复杂型腔零件的电火花成形加工。
6 结论
（1）以某火箭发动机中的闭式叶盘为例，建立电极拆分原则，采用NURBS 参数化曲线曲面建模方法，通过参数化数据点、求解节点矢量和控制顶点等重构叶片型面，建立了叶片的精确数学模型。
（2）基于叶片精确数学模型，构建计算流道中心线的方法，提出以流道中心线为主运动方向的电极运动轨迹搜索算法，使用该算法编程开发了复杂型腔类零件多轴联动电火花加工专用CAM 系统，能够搜索不同轴系工件无干涉的电极运动轨迹，并进行加工过程的仿真。
（3）进行闭式叶盘多轴联动电火花加工试验验证，平均每个通道加工耗时4.16 h，测量叶形加工精度≤0.03 mm，满足闭式整体叶盘类零件指标要求。试验证明该算法可以快速搜索电极无干涉运动轨迹，有效避免干涉，从而提高轨迹搜索效率，轨迹拟合精度高，工况适应能力强，可用于4～ 6 轴各种工况下叶轮、叶盘等复杂型腔类零件的电极运动轨迹搜索。
[1] 吴彦农,赵建社,唐兰剑,等.闭式复杂流道类零件数控电火花加工电极设计[J].中国机械工程,2012,23(20): 2430–2433.WU Yannong,ZHAO Jianshe,TANG Lanjian,et al.Design method of NC-EDM electrode for components with closed complex flow channel[J].China Mechanical Engineering,2012,23(20): 2430–2433.
[2] 刘辰,徐家文,赵建社,等.三元流闭式叶轮组合电加工技术研究Ⅰ——总体方案设计及关键技术[J].航空学报,2010,31(3):650–654.LIU Chen,XU Jiawen,ZHAO Jianshe,et al.Research on combined electrical machining of 3D-flow closed impeller Ⅰ—Overall scheme design and key technology[J].Acta Aeronautica et Astronautica Sinica,2010,31(3): 650–654.
[3] 赵万生,康小明,顾琳,等.放电加工技术在航空航天制造中的应用[J].航空学报,2022,43(4): 32–46.ZHAO Wansheng,KANG Xiaoming,GU Lin,et al.Application of electrical discharge machining technology in aerospace manufacturing[J].Acta Aeronautica et Astronautica Sinica,2022,43(4): 32–46.
[4] 贾雨超,迟关心,张昆,等.闭式整体叶盘成组电极高效电弧成形加工技术[J].航空学报,2022,43(4): 285–295.JIA Yuchao,CHI Guanxin,ZHANG Kun,et al.High-efficiency electrical arc machining of integral shrouded blisk using grouped electrode[J].Acta Aeronautica et Astronautica Sinica,2022,43(4): 285–295.
[5] 田喜明,张云鹏,陈阳.带冠整体叶轮电火花加工电极结构与运动轨迹设计方法[J].电加工与模具,2019(1): 12–15.TIAN Ximing,ZHANG Yunpeng,CHEN Yang.Electrode structure and motion path design method for EDM with cowled integral impeller[J].Electromachining &Mould,2019(1): 12–15.
[6] UHLMANN E,DOMINGOS D C.Development and optimization of the die-sinking EDM-technology for machining the nickel-based alloy MAR-M247 for turbine components[J].Procedia CIRP,2013,6: 180–185.
[7] 候少杰,白基成,刘晓萌,等.电火花加工放电状态特性试验研究[J].航空制造技术,2021,64(10): 80–85.HOU Shaojie,BAI Jicheng,LIU Xiaomeng,et al.Experimental investigation on discharge states characteristics of EDM[J].Aeronautical Manufacturing Technology,2021,64(10): 80–85.
[8] KLINK A,HLAVAC M,HERRIG T,et al.Technological and economical assessment of alternative process chains for turbocharger impeller manufacture[J].Procedia CIRP,2018,77: 586–589.
[9] LI G,ZHAO W S,WANG Z L,et al.A special CAD/CAM software for electro-discharge machining of shrouded turbine blisks[J].Journal of Shanghai University (English Edition),2007,11(1): 74–78.
[10] 詹涵菁.带冠扭叶片涡轮叶盘CAD/CAM 与加工仿真[D].哈尔滨: 哈尔滨工业大学,2001.ZHAN Hanjing.CAD/CAM and machining simulation of turbine blades with crown twisted blades[D].Harbin: Harbin Institute of Technology,2001.
[11] 庞鹏,张云鹏,王豆豆.闭式整体叶盘电火花加工电极运动轨迹搜索优化方法[J].机械科学与技术,2020,39(9): 1379–1384.PANG Peng,ZHANG Yunpeng,WANG Doudou.Electrode motion path search and optimization method for EDM with closed blisk[J].Mechanical Science and Technology for Aerospace Engineering,2020,39(9): 1379–1384.
[12] 赵建社,周学德,周旭娇,等.带冠整体叶轮电火花加工电极及其运动轨迹同步设计方法[J].兵工学报,2017,38(4): 744–749.ZHAO Jianshe,ZHOU Xuede,ZHOU Xujiao,et al.Synchronous design of electrode and its feeding path in EDM for cowled integral impeller[J].Acta Armamentarii,2017,38(4): 744–749.
[13] LIU X,KANG X M,ZHAO W S,et al.Electrode feeding path searching for 5-axis EDM of integral shrouded blisks[J].Procedia CIRP,2013,6: 107–111.
[14] LIU X,KANG X M,XI X C,et al.Electrode feed path planning for multi-axis EDM of integral shrouded impeller[J].The International Journal of Advanced Manufacturing Technology,2013,68(5): 1697–1706.
[15] 刘晓,康小明,赵万生.闭式整体涡轮叶盘多轴联动电火花加工电极运动路径规划[J].电加工与模具,2012(1): 11–14,50.LIU Xiao,KANG Xiaoming,ZHAO Wansheng.Electrode path searching for multi-axis NC EDM of shrouded blisk[J].Electromachining&Mould,2012(1): 11–14,50.
[16] KANG X M,LIANG W,ZHAO W S,et al.Feeding with perturbations in the EDM process of an integral shrouded blisk[J].The International Journal of Advanced Manufacturing Technology,2018,96(9): 3951–3957.
[17] KANG X M,LIANG W,YANG Y X,et al.Maximum free distance method for electrode feeding path planning in EDM machining of integral shrouded blisks[J].Precision Engineering,2018,51: 514–520.
[18] JIA Y C,CHI G X,SHEN Y,et al.Electrode design using revolving entity extraction for high-efficiency electric discharge machining of integral shrouded blisk[J].Chinese Journal of Aeronautics,2021,34(6): 178–187.
[19] AYESTA I,IZQUIERDO B,SANCHEZ J A,et al.Optimum electrode path generation for EDM manufacturing of aerospace components[J].Robotics and Computer-Integrated Manufacturing,2016,37(C): 273–281.
[20] 何申伟.叶片自由曲面重构技术研究[D].长春: 吉林大学,2018.HE Shenwei.Research on the reconstruction technology for freeform surface of blade[D].Changchun: Jilin University,2018.
[21] BRUJIC D,AINSWORTH I,RISTIC M.Fast and accurate NURBS fitting for reverse engineering[J].The International Journal of Advanced Manufacturing Technology,2011,54(5): 691–700.
[22] 王玉莲.面向叶片复杂曲面的加工测量及NURBS曲面重构研究[D].沈阳: 东北大学,2020.WANG Yulian.Research on machining measurement of blade complex surfaces and NURBS surface reconstruction[D].Shenyang:Northeastern University,2020.
[23] 乐英,王璋奇,韩庆瑶.基于非均匀有理B样条曲面重构汽轮机扭曲叶片[J].动力工程学报,2010,30(12): 926–931.YUE Ying,WANG Zhangqi,HAN Qingyao.Reconstruction of turbine blade twisted based on NURBS surface[J].Journal of Chinese Society of Power Engineering,2010,30(12): 926–931.