SiCp/Al 复合材料因其良好的耐磨性、耐热性和导电性,较低的热膨胀系数和材料密度[1–2],被广泛应用于航空航天、光学仪器、汽车和电子封装等领域[3–6]。然而,SiC 颗粒在增强材料物理力学性能的同时增加了它的切削加工难度,且材料的硬度和脆性随着SiC 颗粒体积分数的增加而增加,是一种典型的难加工材料。因此,有必要采取合适的加工工艺及方法,提高SiCp/Al 复合材料的加工质量。
切削力和切削热是监测SiCp/Al复合材料加工状态和质量的重要指标,表面粗糙度是控制加工质量的重要因素,因此,有必要对其进行准确的研究和预测。Yin 等[7]在分析SiCp/Al 复合材料车削过程中不同区域的力学机制以及剪切源和摩擦源产热机制的基础上,建立了SiCp/Al复合材料的动态切削力模型,该模型讨论了SiCp/Al 复合材料车削时切削参数对平均切削力的影响。Tosun等[8]在不同的主轴转速、进给速度条件下进行了SiCp/Al 复合材料钻削试验,通过方差分析确定钻削参数的重要程度,通过信噪比分析,确定了最优的钻削参数组合。Wang 等[9]对体积分数为20%的SiCp/Al 进行了正交试验,研究了铣削速度、进给速度和铣削深度对铣削力的影响,建立了铣削力经验模型。Cui 等[10]研究了铣削深度和铣削速度等参数对切削力、切削温度的影响,并根据切削力、切削温度的变化规律对工艺参数进行优化,得到最佳的工艺参数组合。
人工神经网络因具有自学习、信息存储、联想记忆及高速寻求最优解等能力而广泛应用于材料性能预测、工艺条件最优参数确定等科学技术研究方面,改变了采用“试错法”的传统研究方法[11]。Zhu 等[12]设计了高体积分数SiCp/Al 复合材料的钻孔试验,获得了不同转速和进给速率下的钻削力,采用改进神经网络算法对钻削力进行预测,结果表明预测精度较高。Paturiu 等[13]采用回归分析和人工神经网络分别建立了车削AlSl 52100 钢的表面粗糙度预测模型,结果表明两种预测方法都具有较好的预测效果,但人工神经网络所建立的预测模型具有更高的准确度。李鑫等[14]通过端铣铝合金试验,以切削参数为自变量,采用人工神经网络建立了切削力的预测模型,与经验公式相比,人工神经网络具有更高的预测精度。
随着高体积分数SiCp/Al 复合材料的应用愈加广泛,传统加工工艺难以满足现代工业的加工要求。纵扭超声振动辅助铣削(Longitudinaltorsion ultrasonic vibration assisted milling,LTUVAM)结合了铣削与超声振动的优势,且与常规单向超声辅助铣削相比,LTUVAM 具有更高的加工效率,更高的加工精度及更高的加工质量[15]。马亚健等[16]建模仿真了LTUVAM 的刀刃运动轨迹,并采用单因素法分析了SiCp/Al 复合材料在不同主轴转速、进给速度和铣削深度条件下的表面粗糙度和表面形貌,得到了影响加工表面质量机制及规律;试验结果表明,过低或过高的主轴转速都会导致加工表面质量的恶化。Xiang 等[17]通过有限元分析了常规铣削(Conventional milling,CM)和LTUVAM 中SiCp/Al 复合材料边缘缺陷的形成机理,并通过试验研究了加工参数对边缘缺陷和表面质量的影响规律;随着切削深度和每齿进给量的增加,边缘缺陷值增加,随着切削速度的增加,边缘缺陷值先减小后增加;此外,只有在施加适当的超声振幅条件下,边缘缺陷和表面质量才会得到显著改善。Peng等[18] 研究了SiCp/Al 复合材料在LTUVAM 和CM 过程中边缘缺陷的形成机理和缺陷特征,结果表明,在一定超声振幅范围内,LTUVAM 可有效降低表面颗粒破碎率和铣削力,减缓裂纹扩展,抑制毛刺产生,增加材料的塑性流动,获得更好的表面形貌与边缘质量。
综上所述,与CM 相比,LTUVAM可有效提高加工质量,且参数的选择对LTUVAM 的切削性能有着重要影响,但目前针对材料切削力、热及表面粗糙度的预测及参数优化主要集中于传统工艺,且未对切削力、热及表面粗糙度进行综合分析及多目标优化。因此,本文通过开展LTUVAM 60% SiCp/Al 正交试验,采用响应曲面法(Response surface method,RSM)建立了切削力、切削温度和表面粗糙度的预测模型,分析了4 个参数变量中两个指标的交互影响作用,并与人工神经网络(Artificial neural network,ANN)所建立的预测模型进行了准确性对比验证。通过熵权法建立了切削力、热及表面粗糙度的多目标优化函数,通过遗传算法(Genetic algorithm,GA)进行多目标参数优化,优选了超声振幅、切削速度、每齿进给量和切削深度的最佳参数组合。
1 试验条件及结果
1.1 试验平台
试验材料为60% SiCp/Al 复合材料,SiC 颗粒平均尺寸为5~10 μm,工件尺寸为30 mm×25 mm×20 mm。刀具采用四齿立铣刀,基体材料为硬质合金,涂层材料为NaNoTiAlXN,刀具直径为6 mm,刃长16 mm,总长50 mm。
试验系统如图1 所示。超声电源产生高频交流电并通过非接触式能量传输系统将电流传递给换能器,换能器中的压电陶瓷片由于逆压电效应产生高频轴向振动,在斜槽式变幅杆中,轴向振动所产生的部分纵波将被转化为横波,纵波与横波相互叠加从而使得刀具产生纵扭超声振动。整个试验在VMC850E 三轴立式加工中心进行。试验开始前对超声振幅进行了测量,振动频率为33 kHz,扭纵比为超声振动系统固有属性,当扭转振幅在1~5 μm 变化时,扭纵比恒定为1∶0.6,因此下文中的振幅均为扭振振幅。试验过程中,采用Kistler9257B 记录进给方向切削力,采用Optirs PI 红外热像仪测量铣削温度。试验完成后,采用表面粗糙度测量仪JITAI820 测量加工表面粗糙度。
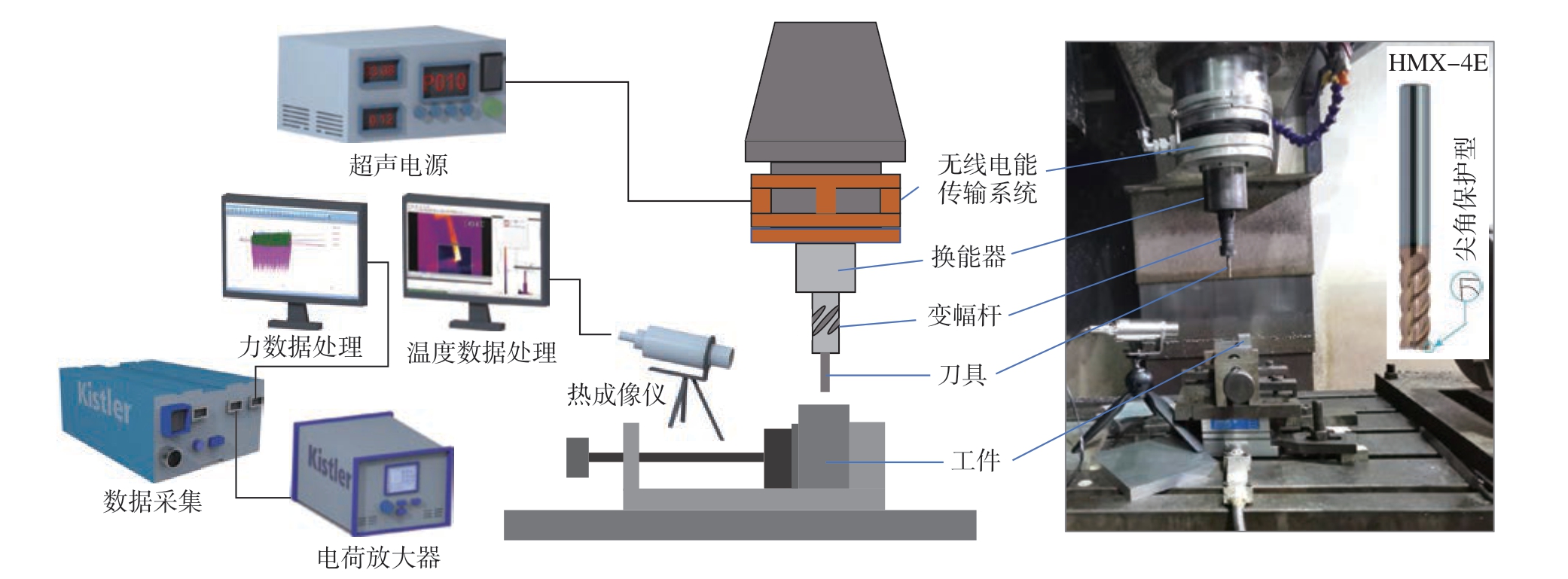
图1 试验系统
Fig.1 Test system
1.2 试验方案及结果
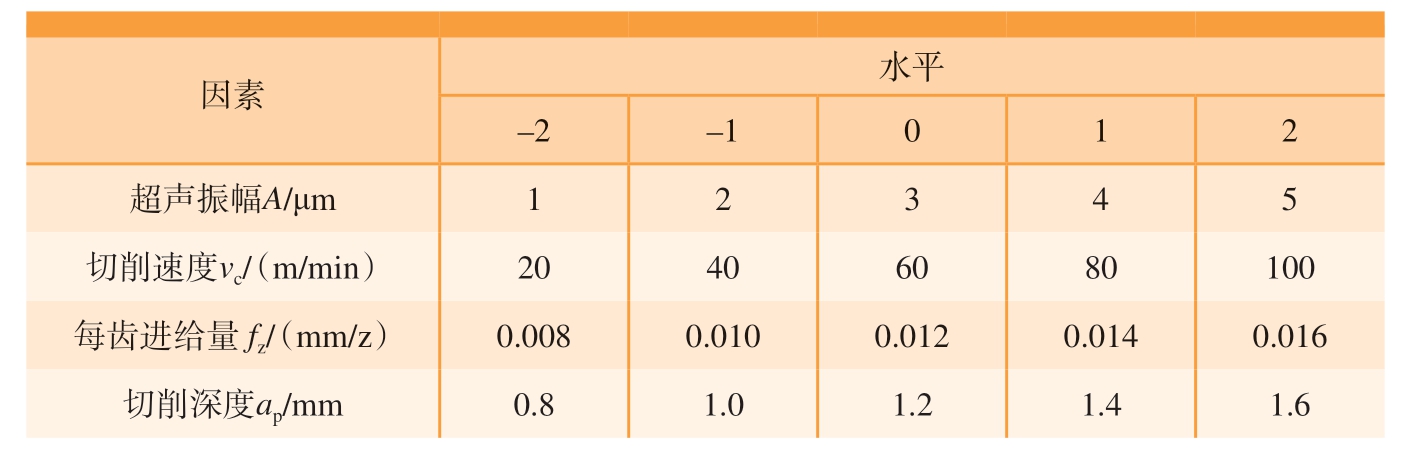
试验以超声振幅、切削速度、每齿进给量和切削深度为变量,切削宽度为定值0.3 mm,设置了四因素五水平正交试验,参数选取范围由铣削经验与刀具性能确定,具体参数如表1 所示。
表1 正交试验因素水平
Table 1 Factors and levels of orthogonal experimental
以整个切削过程的平均切削力和平均切削温度作为最终试验结果。在测量表面粗糙度Ra 时,随机选取5个不同位置进行测量,取其平均值作为结果。各组试验参数选取情况及试验结果如表2 所示。
表2 各组试验参数选取及试验结果
Table 2 Parameter selection and experimental results for each group experiment

2 响应曲面数学模型
RSM 是优化随机过程的统计学试验方法,充分考虑了因素之间交互作用对响应结果的影响,并可通过所建立的数学回归模型选取最佳响应结果[19]。
本文通过RSM 研究了响应结果(Ft、T、Ra)与自变量(A、vc、fz、ap)之间的数学关系,考虑到自变量之间的线性作用、交互作用及二次作用,其通用数学模型可表示为
式中,y 为响应结果;xi、xj 为自变量;k 为自变量水平数;β0、βi、βij、βii 分别为常数项、线性项、交互作用项和二次项;ε 为误差项。
2.1 数学模型的建立与可靠性分析
将25 组试验数据导入Design-Expert 软件中进行数据分析,分别建立了切削力Ft、切削温度T 和表面粗糙度Ra 的数学回归方程。为了使预测更加准确,又对每个响应结果建立了3种类型的数学方程,分别为线性方程、线性与交互作用方程和二次方程。
切削力Ft 的回归方程如式(2)~(4)所示。
线性方程:
线性与交互作用方程:

二次方程:

切削温度T 的回归方程如式(5)~(7)所示。
线性方程:
线性与交互作用方程:

二次方程:
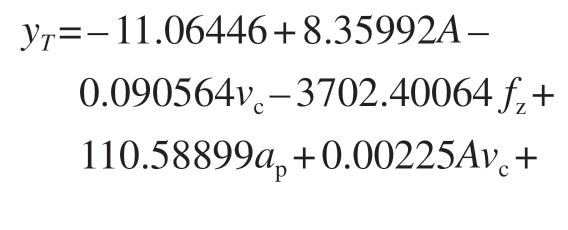
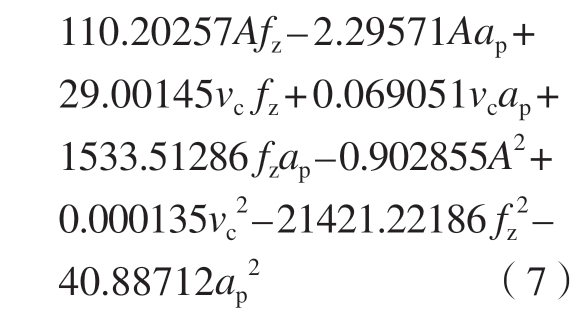
表面粗糙度Ra 的回归方程如式(8)~(10)所示。
线性方程:
线性与交互作用方程:

二次方程:

为了评价各模型拟合的可靠性和准确性,对所建立的回归方程进行方差分析和显著性检验,结果如表3 所示。其中,F 值为回归方程均平方和与残差均平方和的比值,P 值为F 值对应的概率。F 值越大,P 值越小,方程与因素的显著性就越强。当P<0.05 时,表示该项显著;当P<0.01时,表示该项非常显著。通过调整系数(Adj R2)和预测系数(Pr R2)来验证模型的拟合程度,各项系数值越高表示拟合程度越高,且当Adj R2 与Pr R2 的差值小于0.2 时,表示各组数据准确可靠。而Adj R2 考虑了自变量数量的影响,用来作为最优回归方程的决定性系数。
表3 回归方程各项系数
Table 3 Coefficients of regression equation
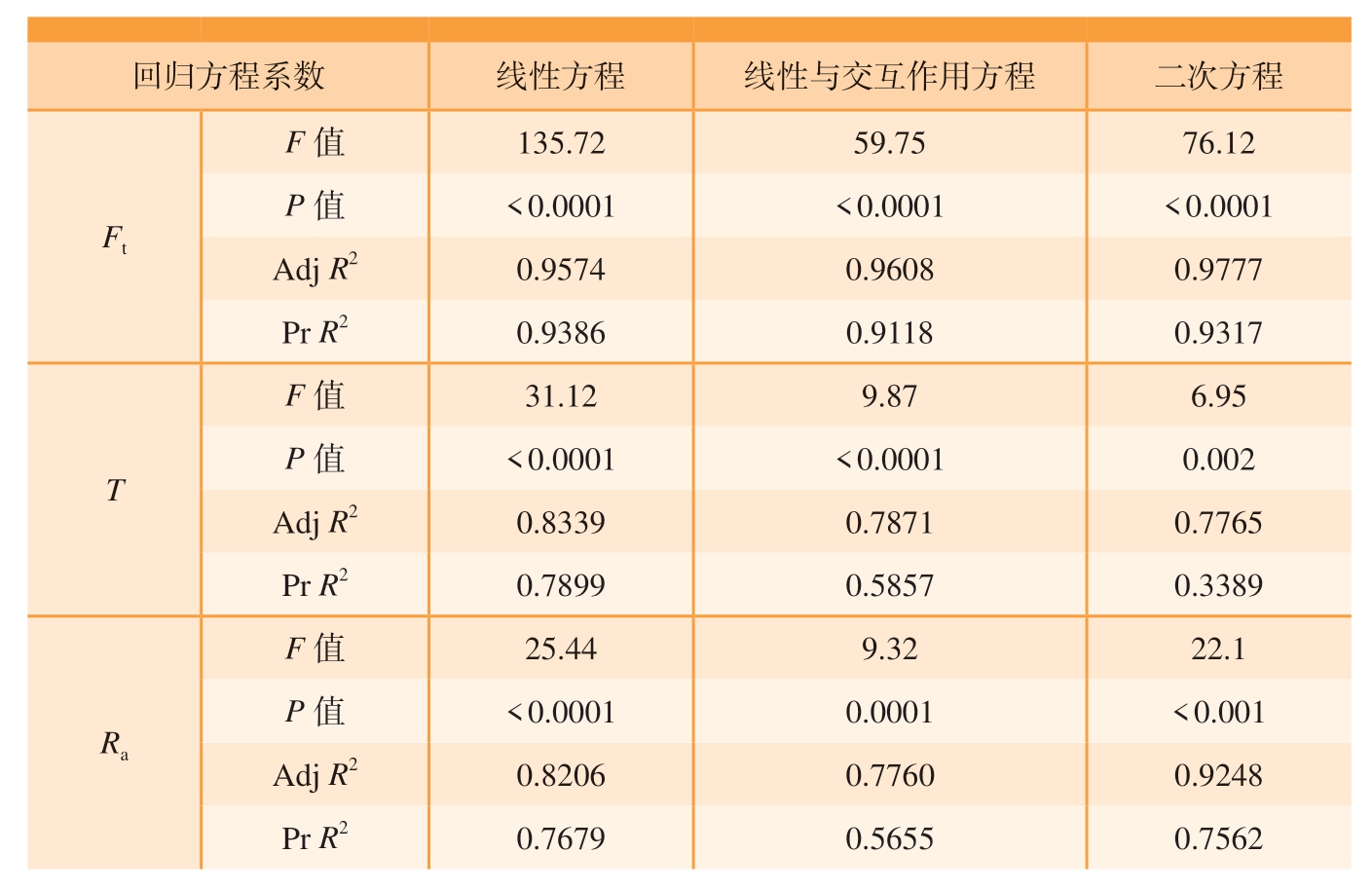
由表3 可知,在Ft 与Ra 的3 种数学模型中,二次方程具有更高的Adj R2值,且其P 值均小于0.001,Adj R2 与Pr R2 的差值均小于0.2,说明模型显著性强,拟合程度高。而在T 的3 种回归方程中,选择线性方程更优。因此,Ft、T、Ra 的最优数学模型分别为式(4)、(5)、(10)。
2.2 回归系数的显著性分析
为了研究各加工参数对Ft、T 和Ra 的影响程度,根据所选取的最优回归方程进行了回归系数显著性分析,结果如表4 所示。
表4 回归系数的显著性分析
Table 4 Significance analysis of regression coefficients
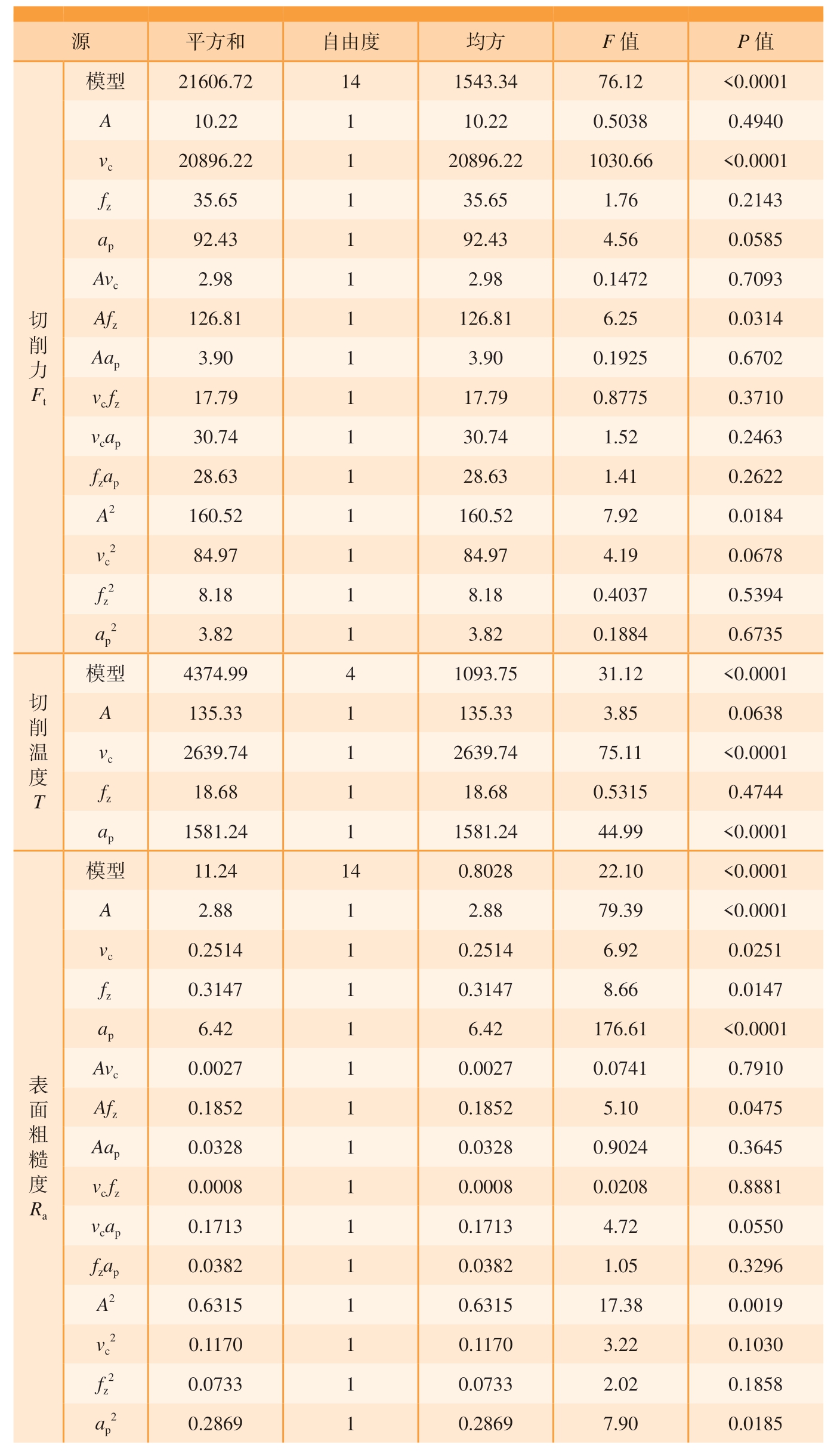
根据表4 的分析结果可知,在切削力Ft 的回归模型中,各项影响程度如下。
(1)线性作用影响:vc >ap >fz >A;
(2)交互作用影响:Afz >vcap >fz ap >vc fz >Aap >Avc;
(3)二次作用影响:![]() 。
。
值得注意的是,在切削力的回归模型中,超声振幅的个体影响最小。这是因为超声振幅的增大会使得占空比增大,平均切削力减小,而且振动对材料的冲击效应也会增强,使得切削力增大[20],因此,不同超声振幅对切削力的影响差异不大。
在切削温度T 的回归模型中,各项影响程度分别为vc >ap >A >fz。
在表面粗糙度Ra 的回归模型中,各项影响程度如下。
(1)线性作用影响:ap >A >fz >vc;
(2)交互作用影响:Afz >vcap >fzap >Aap >Avc >vc fz;
(3)二次作用影响:![]()
2.3 响应曲面及等高线图
为了研究各因素之间交互作用对切削力和表面粗糙度的影响,根据最优回归方程和交互作用影响程度绘制排列出了切削力和表面粗糙度的响应曲面及等高线图(图2 和3),每个响应曲面中的其他两个加工参数采用表1 中的0 级别水平。
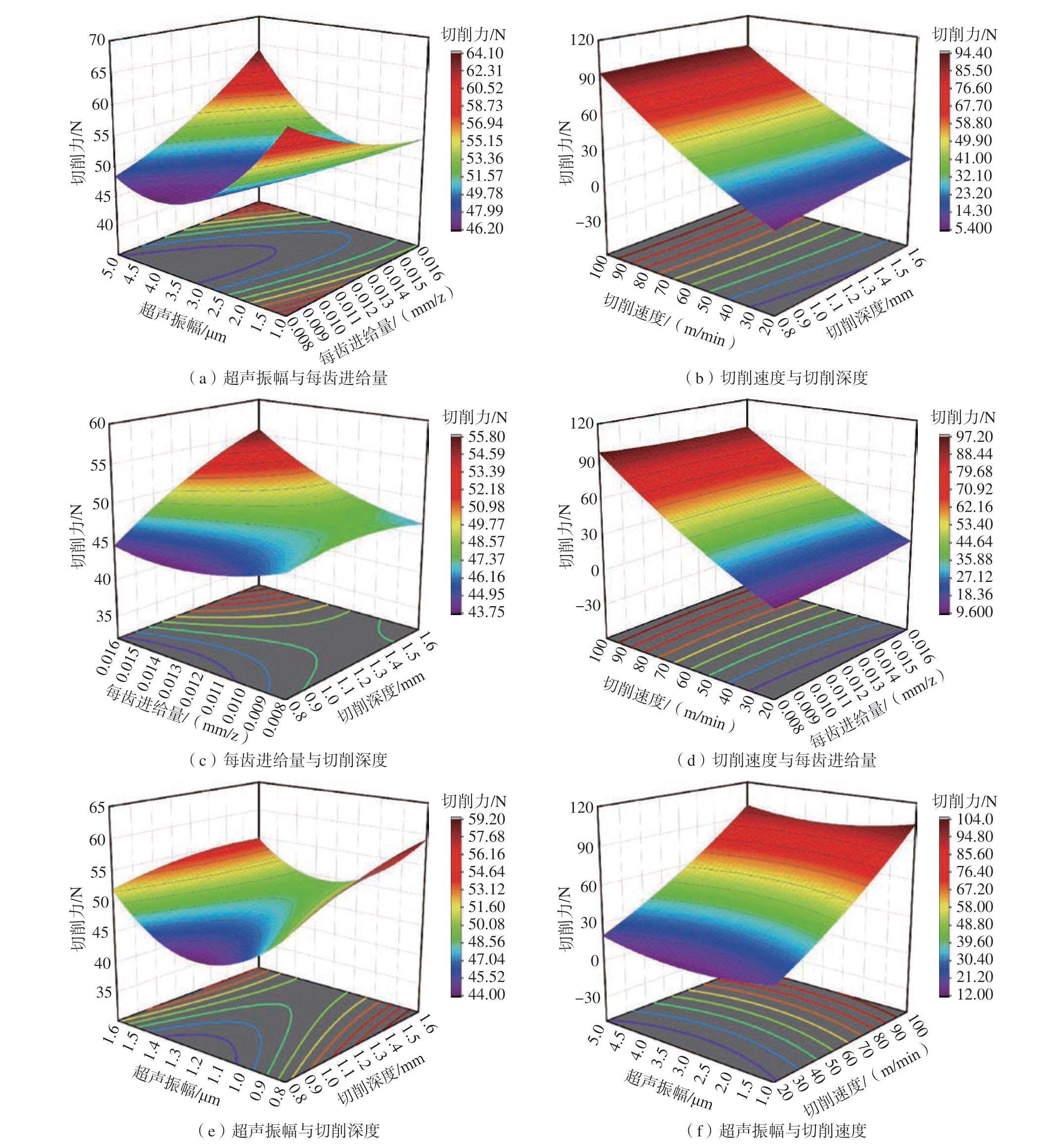
图2 切削力Ft 的响应曲面及等高线图
Fig.2 Response surface and contour diagram of cutting force Ft
如图2(a)所示,随着超声振幅的增大,切削力先减小后增大,图2(e)和(f)也能得出同样结论。这是因为随着超声振幅的增大,振动效果增强,周期性振动能够使得碎状SiC颗粒脱离刀面,减少刀具磨粒磨损,保持刀具锋利性[21]。同时,超声振幅的增大使得刀具空切及回转作用增强,平均切削力减小。但随着超声振幅进一步增大,刀具由剪切作用逐渐向挤压作用转变[22],材料由剪切去除转变为挤压脱落,加剧了刀具与工件的摩擦,使得平均切削力增大。因此,当超声振幅较小时,刀具以剪切作用为主,增大每齿进给量,使得刀具与SiC 颗粒剪切接触时间缩短,减小了平均切削力;当超声振幅较大时,刀具以挤压冲击作用为主,增大每齿进给量,使得刀具与材料挤压冲击作用增强,且单位时间内材料去除体积增大,平均切削力增大。
由图2(b)可知,增大切削速度,切削力增大,图2(d)和(f)中也能得出同样结论。这是因为随着切削速度的增大,材料应变率增大,刀具与工件摩擦加剧,且刀具占空比减小,回转现象逐渐弱化[23],使得切削力增大。从图2(b)和(e)中可以发现,随着切削深度的增大,切削力整体上呈现出增大的趋势。这是因为增大切削深度,单位时间内材料去除体积增大,使得切削力增大。但值得注意的是,在图2(b)中,采用较大切削速度时,切削力随着切削深度增大而增加的趋势有所减缓。由切削温度T 的回归模型(式(5))可知,切削速度对切削温度的影响程度最大,切削深度其次,且随着切削速度与切削深度的增大,切削温度升高。因此,当切削速度较高时,切削温度较高,加之切削深度的增加,使得切削温度进一步升高,Al 基体软化,材料更易去除,减缓了切削力增长趋势。
在图2(c)中,每齿进给量和切削深度对切削力的影响并不均匀。当采用较小的每齿进给量或切削深度时,增大另一因素,切削力变化比较平缓。当每齿进给量或切削深度较大时,刀具单位时间内与材料接触体积较大,与SiC 颗粒接触概率增大,系统刚度下降,切削条件较差,因此,此时随着另一因素的增大,切削力急剧上升。
图3 为各因素之间交互作用对表面粗糙度的影响规律。如图3(a)、(d)和(e)所示,随着超声振幅的增大,表面粗糙度先减小后增大。这是由于增大超声振幅有利于保持刀具锋利性、减小切削力,使得表面加工质量较好。但随着超声振幅的进一步增大,刀具冲击作用过强,材料由剪切去除转变为挤压脱落,基体与颗粒界面被破坏,造成大面积撕裂与大孔洞现象[24],反而恶化了表面质量。因此,在图3(a)中,采取较小的超声振幅时,刀具以剪切作用为主,每齿进给量对于表面粗糙度的影响程度不大,但当采取较大超声振幅时,随着每齿进给量的增加,表面粗糙度急剧增大。

图3 表面粗糙度Ra 的响应曲面及等高线图
Fig.3 Response surface and contour diagram of surface roughness Ra
增大切削速度,表面粗糙度先增大后减小,如图3(e)和(f)所示。这是由于增大切削速度,材料去除率增大,且LTUVAM 占空比减小,切削条件恶化,使得表面粗糙度增大。但进一步增大切削速度,在刀具高速切削以及超声振动作用下,材料去除更加完全,SiC 颗粒破碎细化程度高,加之切削温度的增大,使得铝基体更易黏结在工件表面,表面粗糙度减小。因此,在图3(b)中,切削深度作为影响切削温度的第二因素,在低切削深度下,切削温度不足以使得铝基体黏结在工件表面,随着切削速度的增大表面粗糙度并未出现减小现象,只是刀具剪切作用的增强使得表面粗糙度增大趋势得以缓和。
增大切削深度,摩擦力和切削力增大,加剧了刀具不规则振动,导致表面粗糙度值增大,如图3(c)和(d)所示。而在图3(b)中,当切削速度较大时,由于切削温度的影响,增大切削深度,表面粗糙度呈现先增大后减小的趋势。
3 人工神经网络预测模型
人工神经网络因具有自组织、自学习、联想记忆能力,能够处理非线性自适应信息问题,是目前科学研究中应用最广泛、最成熟的机器学习算法[25]。本文采用BP 神经网络建立了切削力、切削温度及表面粗糙度的预测模型,并与响应曲面所建立的模型进行了准确性对比。
BP 人工神经网络是一种单向传播的神经网络,具有多层结构和信号前向传递、误差反向传递的特点,广泛应用于非线性系统的研究[26],主要由输入层、隐含层和输出层组成。本文中将超声振幅、切削速度、每齿进给量和切削深度作为输入层参数,隐含层内含10 个神经元,对输入层参数进行接收、处理并连接输出层,从而将切削力、切削温度和表面粗糙度作为计算结果输出,其结构如图4 所示。
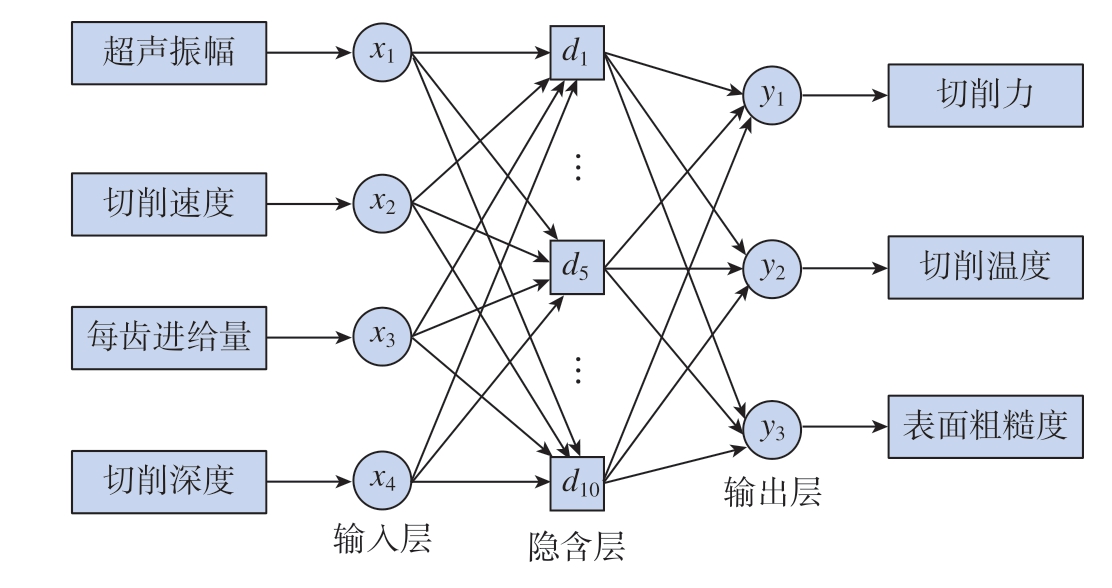
图4 BP 人工神经网络结构示意图
Fig.4 Schematic diagram of BP artificial neural network structure
为了确保预测模型的准确性,从表2 所示的25 组试验数据中,选择17 组数据作为训练集,4 组作为验证集,4 组作为测试集。经过BP 人工神经网络多次的训练–反馈–训练,获得了较为准确的预测模型,其训练结果如图5 所示,其中All 代表全部25 组数据,R 为拟合程度,Y=T 即直线Output=Target,用于对比观察数据拟合程度。可以看出,各集拟合程度高,模型整体训练结果良好。
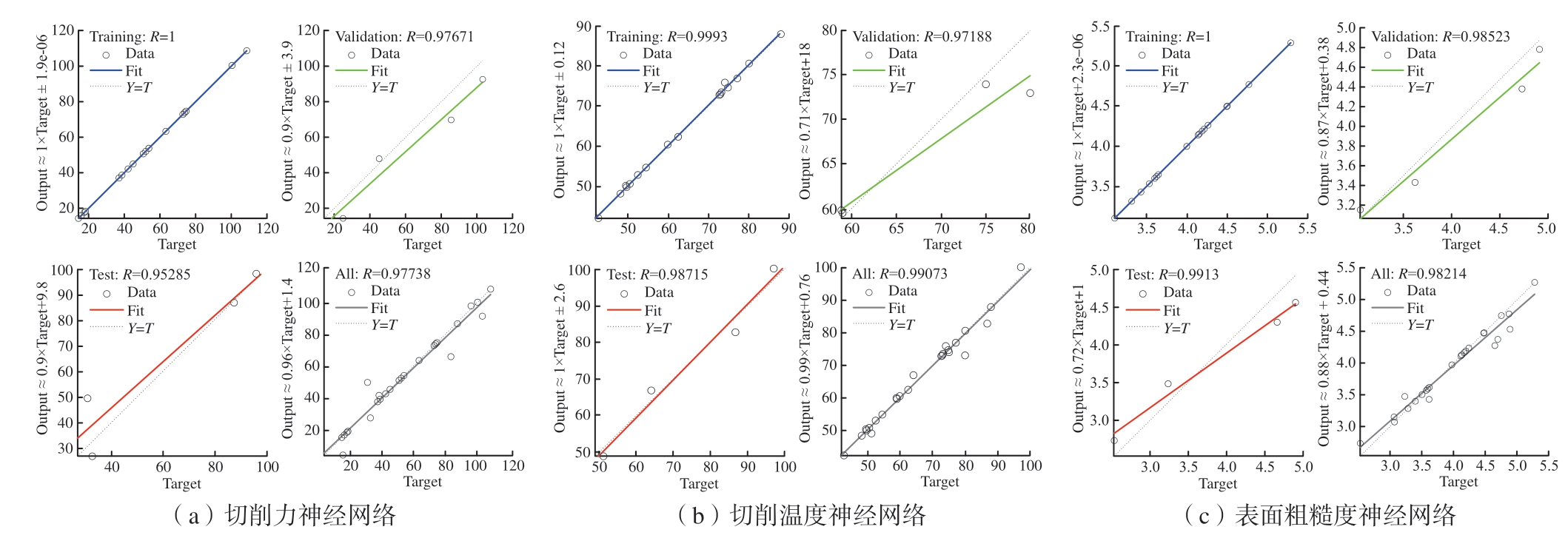
图5 BP 人工神经网络训练结果
Fig.5 BP artificial neural network training results
对所建立的响应曲面数学模型与BP 人工神经网络预测模型进行了准确性分析与对比,如表5~ 7 及图6 所示。由于试验组数较多,在表5~ 7 中只列举了前10 组数据,其中,PExp 代表试验值,为了更直观地表示预测值与试验值的差距以及预测模型的准确性,采用K 值代表模型准确度。PRSM 与KRSM 分别代表响应曲面预测值与准确度,PANN 与KANN 分别代表人工神经网络预测值与准确度。K 值可根据式(11)得出。
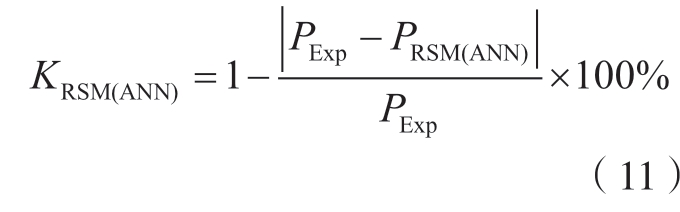
表5 响应曲面与神经网络模型的切削力预测结果及准确度
Table 5 Cutting force prediction results and accuracy of response surface and neural network model
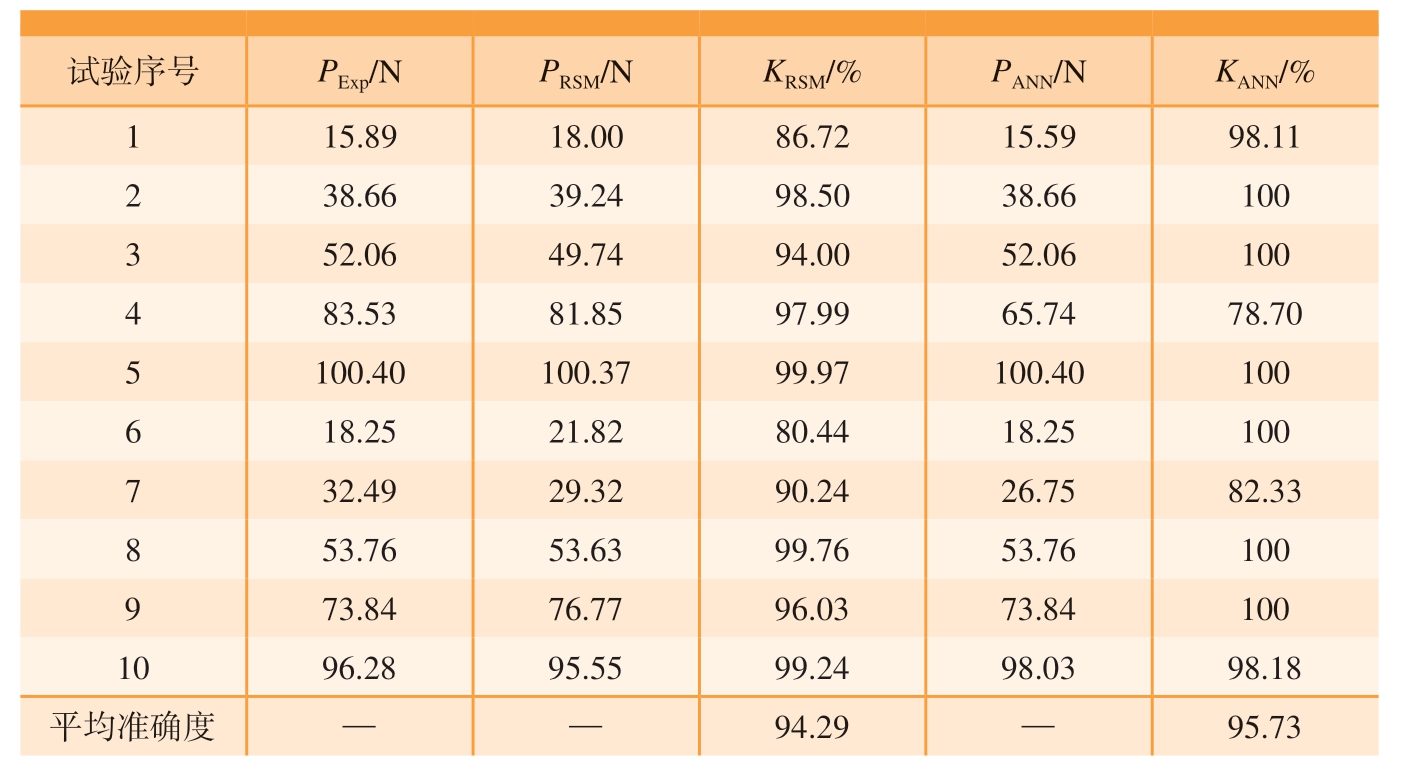
表6 响应曲面与神经网络模型的切削温度预测结果及准确度
Table 6 Results and accuracy of cutting temperature prediction by response surface and neural network model
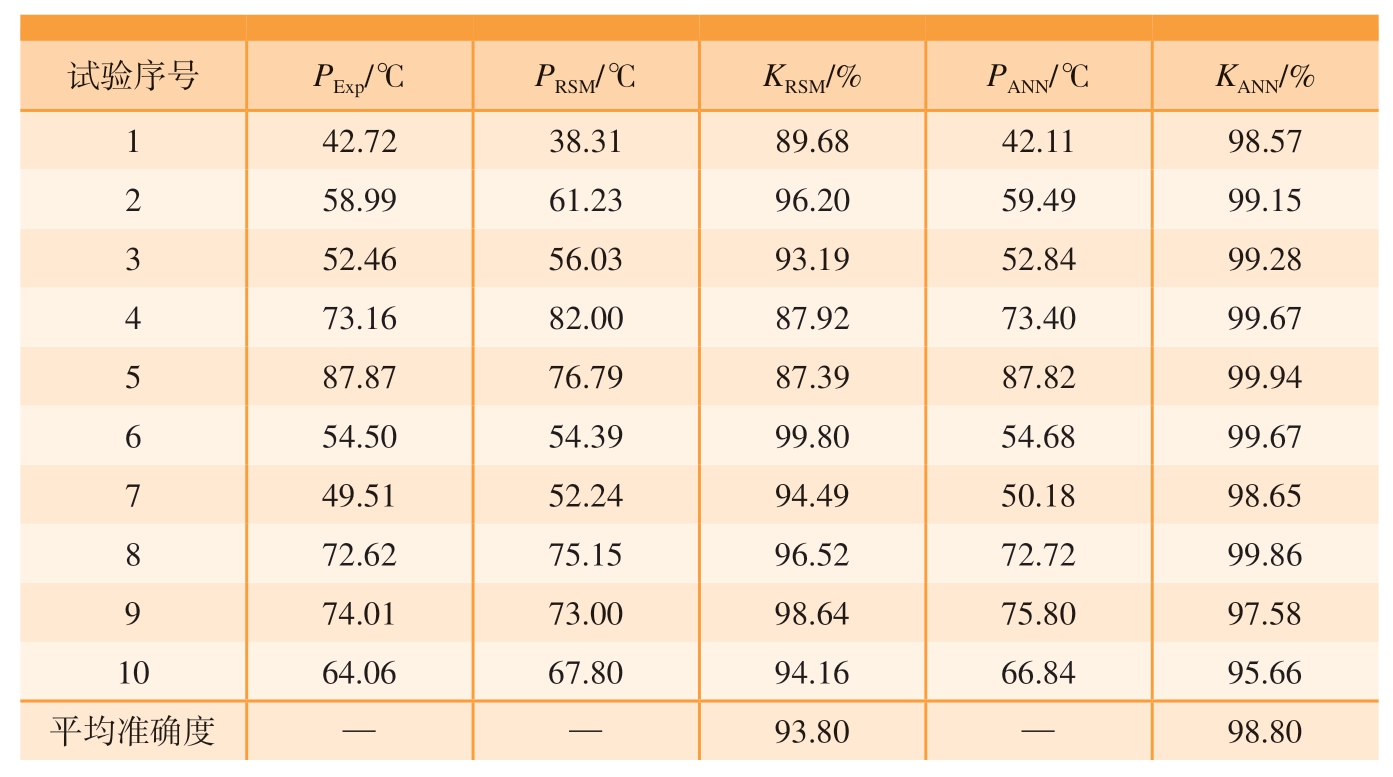
表7 响应曲面与神经网络模型的表面粗糙度预测结果及准确度
Table 7 Results and accuracy of surface roughness prediction of response surface and neural network model
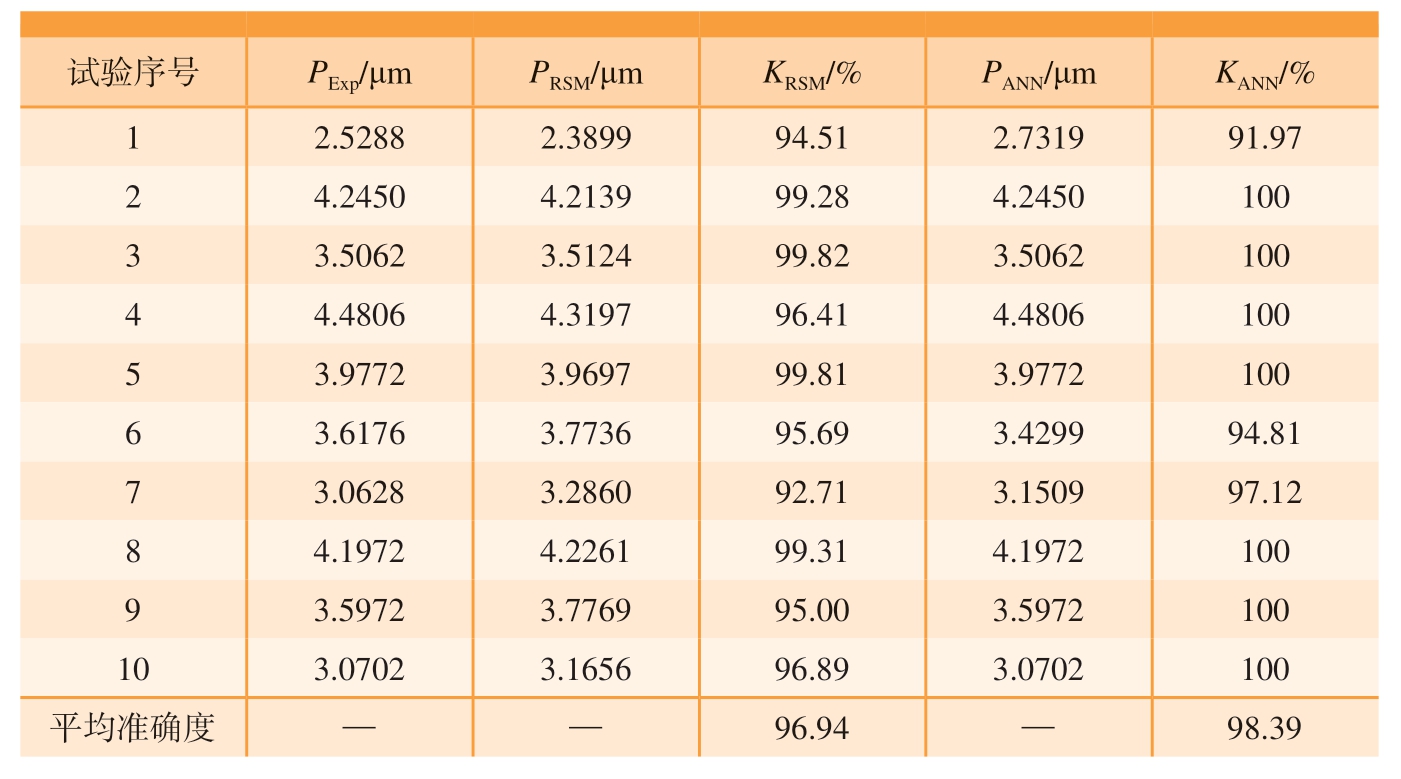
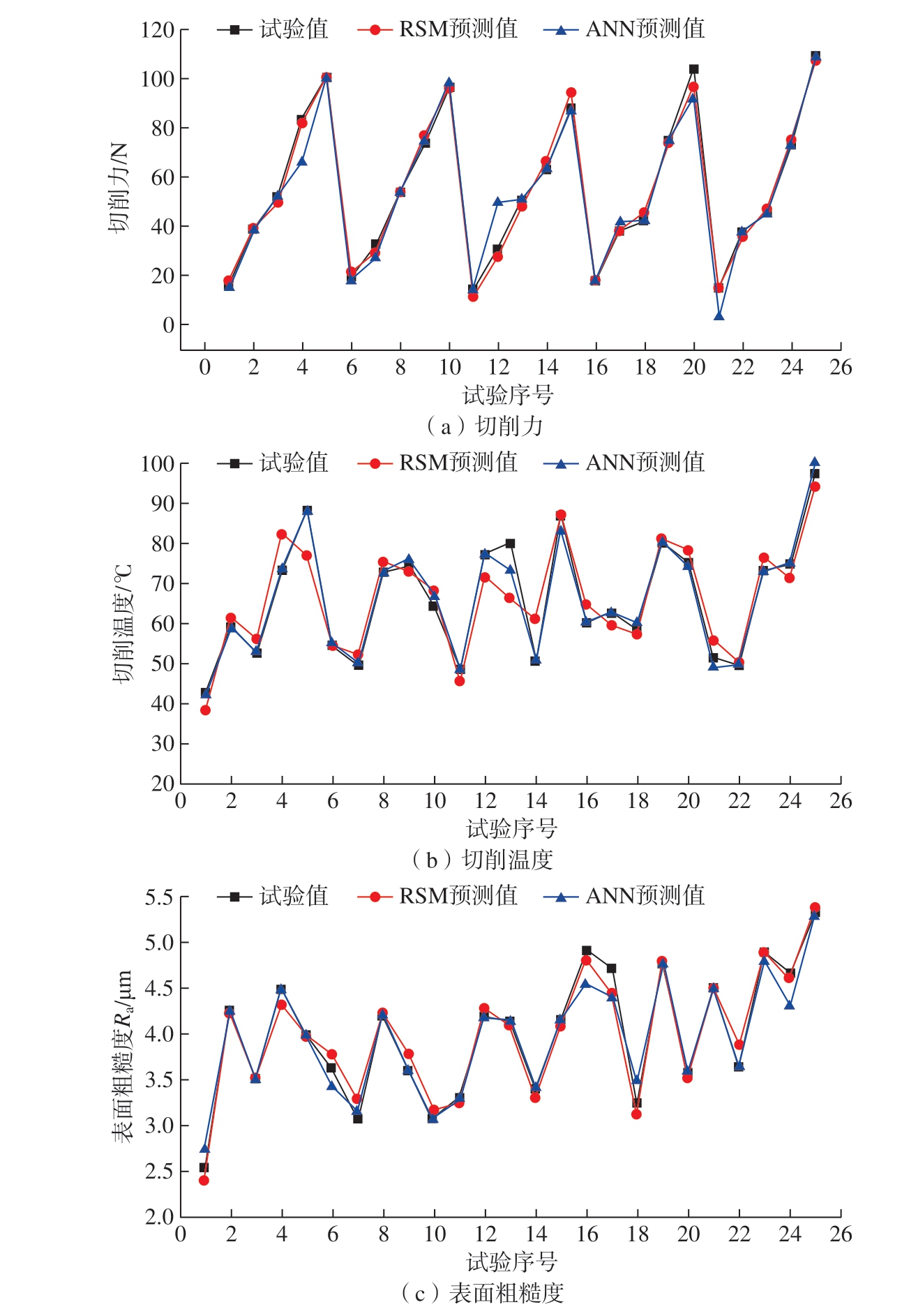
图6 试验值与RSM、ANN 预测值对比
Fig.6 Comparison of test values with predicted values of RSM and ANN
由表5~ 7 可知,所建立的RSM数学模型与ANN 预测模型对于切削力、切削温度和表面粗糙度都有着较好的预测能力,误差在可接受范围之内。由图5 可知,在神经网络的训练过程中,有个别集与拟合结果差距较大,但ANN 具有更高的平均准确度,且多组数据预测准确度达到了100%。同时,从图6 中也可以发现,25 组试验整体上ANN 预测值与试验值吻合程度更高,预测精度更好。
4 基于遗传算法的多目标参数优化
遗传算法的核心原理是引入自然生物界优胜劣汰的进化法则,将待优化的参数进行编码串联形成群体,按复制、交叉与变异等生物遗传进化机制对数据进行优化筛选,同时通过预设次数的遗传交叉与迭代,使各参数值逐渐接近目标解[27]。遗传算法在进行多目标参数优化求解上具有独特优势,能够以简便高效的计算过程获得准确结果,其基本流程如图7 所示。
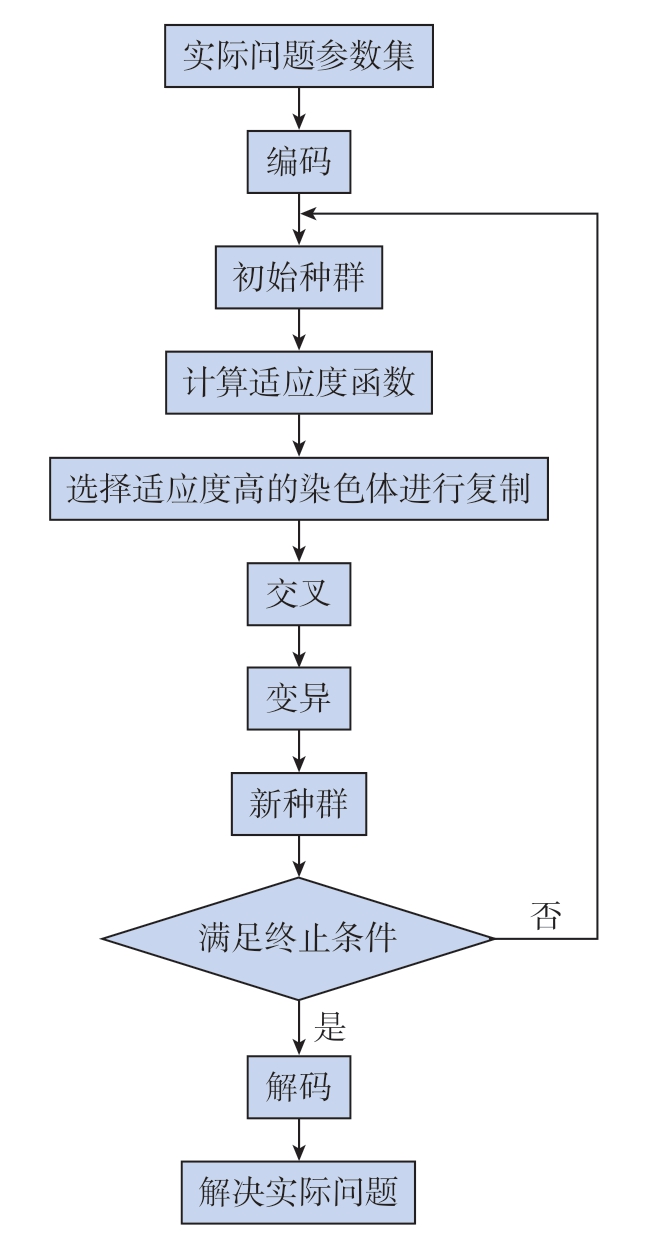
图7 遗传算法流程
Fig.7 Process of genetic algorithm
(1)编码:在进行搜索优化之前先将解空间的参数转化成遗传空间的基因型串结构数据,从而形成染色体或个体。
(2)初始种群:由一定数量个体组成的群体特征,遗传算法在此基础上开始进化计算。
(3)适应度评估:表明个体对于环境的适应度。
(4)选择:从当前种群中选择优良的个体作为父代,并使其具有更大概率来贡献出多个子代,体现出了达尔文的适者生存概念。
(5)交叉:通过交叉操作获得具有父辈特征的新一代个体。
(6)变异:对种群中的个体随机改变串结构数据中某个串的值,同生物界一样,变异发生的概率很低,在进行操作过程中取值较小。
上述流程便是一次迭代计算的全部内容,通过解集是否满足终止条件来判断迭代是否继续。如果满足,则此时的解集便是所寻最优解;如果不满足,则将继续重复迭代过程。
通过遗传算法优选最佳参数组合的过程中,为了综合考虑加工参数对切削力、切削温度和表面粗糙度的影响,采用熵权法将2.1 节中所建立的3 个单目标最优数学模型转化为多目标优化函数。一般来说,某个指标的信息熵Hj 越小,表明指标值的变异程度越大,提供的信息量越多,在综合评价中所起的作用越大,因此其权重Wj 也越大[28]。
在所评价的3 个指标中,切削力、切削温度和表面粗糙度值越小越好,属于逆向指标,因此需按照式(12)对各组数据进行标准归一化处理,使各试验值位于[0,1]区间之内。
式中,x 为原始数据列;y 为标准归一化值。切削力、切削温度和表面粗糙度的标准归一化值如表8 所示。
表8 切削力、切削温度和表面粗糙度的标准归一化值
Table 8 Standard normalized values of cutting force,cutting temperature and surface roughness
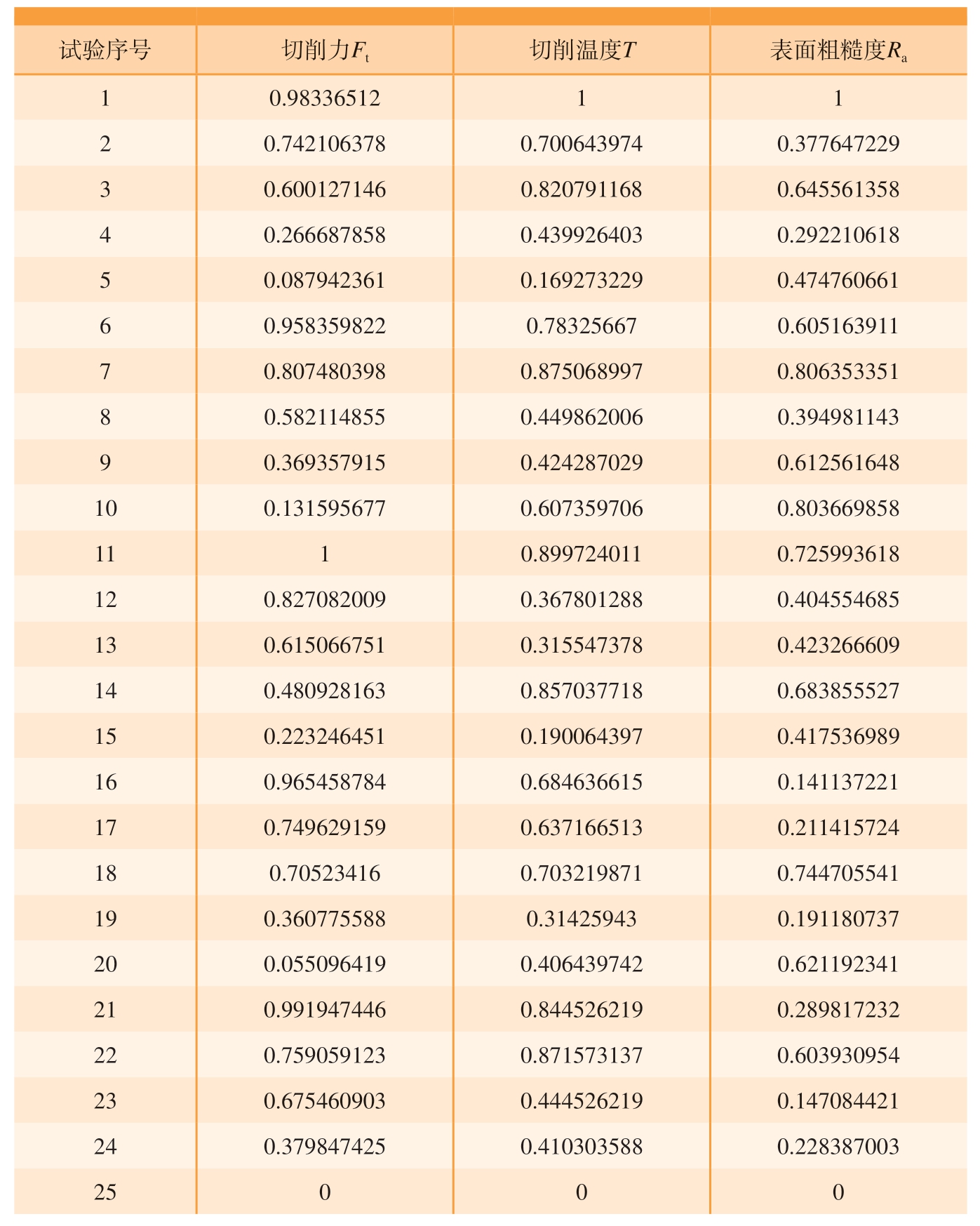
根据表8 的归一化结果,可以得到一个具有25 个评价对象、3 个评价指标的标准化矩阵R=[rij]25×3,则切削力、切削温度和表面粗糙度3 个评价指标的信息熵Hj可以根据式(13)和(14)获得,其中j 取值1 为切削力;2 为切削温度;3 为表面粗糙度。
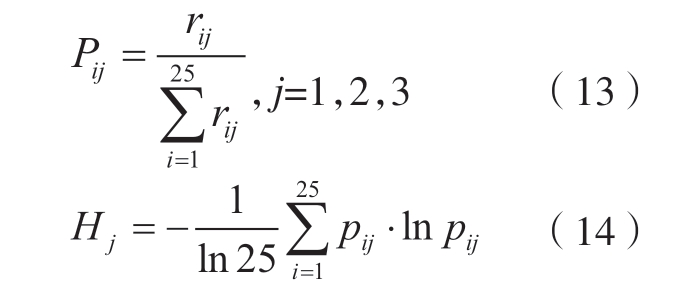
将3 个指标的信息熵Hj 代入式(15)中,得到切削力、切削温度和表面粗糙度的权重分别为0.3842、0.2842、0.3316。
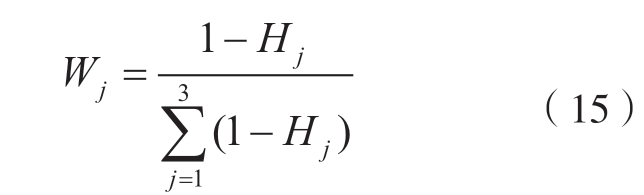
因此,多目标优化函数为
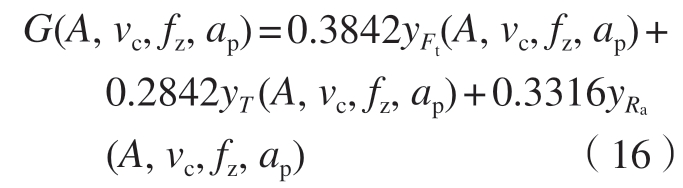
将式(16)导入MATLAB 自带工具Optimization 中,采用GA 函数求解最佳参数组合,使得切削力、切削温度和表面粗糙度综合值最小。在MATLAB 中设置约束条件与本文中参数选取范围相同。种群数量、交叉率、变异率为遗传算法中重要参数。种群数量太少,可能发生近交,遗传质量下降,种群数量太大,导致难以收敛,稳定性下降;随着迭代次数的增加,变异概率太大会使种群原始性被破坏的可能性增大,过小则会导致种群多样性降低。同理,过小的交叉概率会使得种群有效更新效率降低。因此,经过参考赵海越等[29]的研究及多次测试,设置初始种群数量为50,交叉概率为0.7,变异概率为0.01,进行5 次遗传算法操作后选取综合值最小的一组参数作为最终结果,其经历了110 次迭代,Parteo前沿如图8 所示,最佳参数组合及预测结果如表9 所示。
表9 最佳参数组合及试验值预测结果
Table 9 Optimal parameter combination and experimental value prediction results

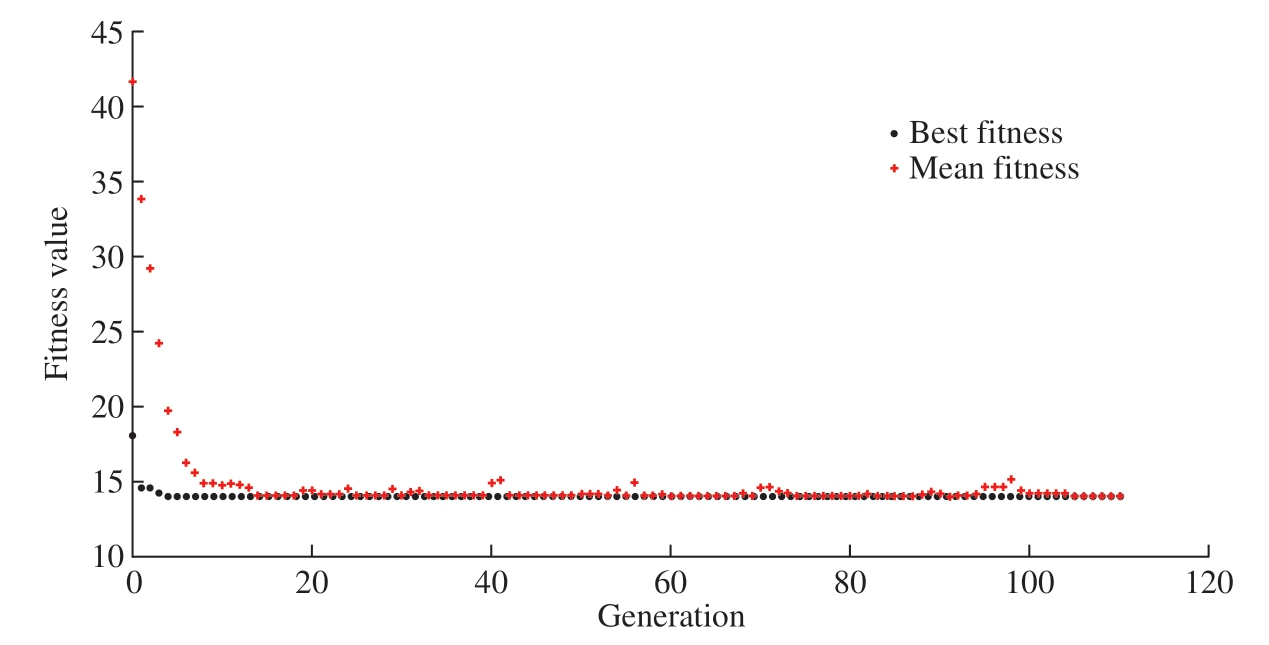
图8 多目标优化Parteo 前沿曲线
Fig.8 Parteo frontier curve for multi-objective optimization
采用最佳参数组合进行了切削参数性能验证试验,试验结果表明,切削力Ft=7.23 N,切削温度T=40.18℃,表面粗糙度Ra=2.4673 μm,预测误差分别为6.91%、6.53%、2.53%。各目标值误差均在可接受范围之内,进一步验证了预测模型的准确性与优化参数的有效性。
5 结论
本文在60% SiCp/Al 的切削加工中引入了LTUVAM,通过正交试验,综合考虑了超声振幅、切削速度、每齿进给量和切削深度对切削力、切削温度及表面粗糙度的影响,建立了切削力、切削温度和表面粗糙度预测模型与多目标优化函数,优选出了最佳参数组合,显著提升了加工质量。得出结论如下。
(1)响应曲面法所建立的预测模型中,二次方程式为切削力与表面粗糙度的最佳预测模型,而切削温度的线性方程预测模型具有更高的可靠性和准确性。所选取的最佳预测模型中,切削速度为切削力和切削温度的主要影响因素,切削深度对表面粗糙度的影响最为显著。
(2)在切削力与表面粗糙度的二次方程式预测模型中,Afz 为影响最显著的交互作用项。随着超声振幅的增大,切削力与表面粗糙度先减小后增大。当超声振幅较小时,增大每齿进给量,切削力减小,当超声振幅较大时,增大每齿进给量,切削力增大。而采取较小的超声振幅时,每齿进给量对于表面粗糙度的影响程度不大,但当超声振幅较大时,随着每齿进给量的增加,表面粗糙度急剧增大。
(3)人工神经网络与响应曲面法所建立的各目标预测模型均具有较好的预测能力,但人工神经网络预测模型准确度更高,其在所取的试验样本中,切削力、切削温度和表面粗糙度的预测准确度分别为95.73%、98.80%、98.39%。
(4)采用熵权法建立了切削力、切削温度和表面粗糙度的多目标优化函数,并通过遗传算法优化出的最佳组合为A=1.84 μm,vc=20 m/min,fz=0.015 mm/z,ap=0.8 mm,验证试验结果表明,切削力Ft=7.23 N,切削温度T=40.18 ℃,表面粗糙度Ra=2.4673 μm,预测误差分别为6.91%、6.53%、2.53%。有效降低了切削力、切削温度和表面粗糙度,为60% SiCp/Al 纵扭超声振动辅助铣削加工提供了借鉴。
[1] 董小磊,高国富,马星辉.颗粒增强金属基复合材料加工表面质量的研究[J].工具技术,2008,42(12): 22–25.DONG Xiaolei,GAO Guofu,MA Xinghui.Study for machining surface quality of particle reinforced metal matrix composites[J].Tool Engineering,2008,42(12): 22–25.
[2] WANG Y F,LIAO W H,YANG K,et al.Simulation and experimental investigation on the cutting mechanism and surface generation in machining SiCp/Al MMCs[J].The International Journal of Advanced Manufacturing Technology,2019,100(5): 1393–1404.
[3] 周岩,张冬云,王卫东,等.选区激光熔化成形碳化硅颗粒增强铝基复合材料研究现状及航空航天应用[J].航空制造技术,2018,61(10): 68–73.ZHOU Yan,ZHANG Dongyun,WANG Weidong,et al.Current situation and aerospace applications analysis based on SiC particle reinforced aluminum matrix composites manufactured by selective laser melting[J].Aeronautical Manufacturing Technology,2018,61(10): 68–73.
[4] 杨睿.铝基复合材料制备方法与增强体颗粒的形成机制[J].内燃机与配件,2021(17): 31–32.YANG Rui.Preparation method of aluminum-based composite material and formation mechanism of reinforcement particles[J].Internal Combustion Engine &Parts,2021(17): 31–32.
[5] LIAO Z R,LA MONACA A,MURRAY J,et al.Surface integrity in metal machining—Part I: Fundamentals of surface characteristics and formation mechanisms[J].International Journal of Machine Tools and Manufacture,2021,162: 103687.
[6] LA MONACA A,MURRAY J W,LIAO Z R,et al.Surface integrity in metal machining—Part II: Functional performance[J].International Journal of Machine Tools and Manufacture,2021,164: 103718.
[7] YIN W D,DUAN C Z,LI Y J,et al.Dynamic cutting force model for cutting SiCp/Al composites considering particle characteristics stochastic models[J].Ceramics International,2021,47(24): 35234–35247.
[8] TOSUN G.Statistical analysis of process parameters in drilling of AL/SICP metal matrix composite[J].The International Journal of Advanced Manufacturing Technology,2011,55(5): 477–485.
[9] WANG R,ZHAO M,MAO J,et al.Force prediction and material removal mechanism analysis of milling SiCp/2009Al[J].Micromachines,2022,13(10): 1687.
[10] CUI Y,GAO S,WANG F,et al.Study on the high-speed milling performance of highvolume fraction SiCp/Al composites[J].Materials(Basel),2021,14(15): 4143.
[11] 杨西荣,权强强,田倩炆,等.人工神经网络在材料加工中的应用及展望[J].中国材料进展,2023,42(11): 896–901.YANG Xirong,QUAN Qiangqiang,TIAN Qianwen,et al.Application and prospect of artificial neural network in material processing[J].Materials China,2023,42(11): 896–901.
[12] ZHU C M,WU Y Y,GU P,et al.Prediction of drilling force for high volume fraction SiCp/Al composite based on neural network[J].Procedia CIRP,2021,99: 414–419.
[13] MAHESHWERA REDDY PATURI U,DEVARASETTI H,KUMAR REDDY NARALA S.Application of regression and artificial neural network analysis in modelling of surface roughness in hard turning of AISI 52100 steel[J].Materials Today: Proceedings,2018,5(2): 4766–4777.
[14] 李鑫,史振宇,蒋森河,等.人工神经网络预测刀具磨损和切削力[J].控制理论与应用,2018,35(12): 1731–1737.LI Xin,SHI Zhenyu,JIANG Senhe,et al.Artificial neural network predicts tool wear and cutting force[J].Control Theory &Applications,2018,35(12): 1731–1737.
[15] 冯平法,王健健,张建富,等.硬脆材料旋转超声加工技术的研究现状及展望[J].机械工程学报,2017,53(19): 3–21.FENG Pingfa,WANG Jianjian,ZHANG Jianfu,et al.Research status and future prospects of rotary ultrasonic machining of hard and brittle materials[J].Journal of Mechanical Engineering,2017,53(19): 3–21.
[16] 马亚健,聂文忠,陆建民,等.纵扭复合超声振动铣削SiCp/Al 表面质量研究[J].机床与液压,2020,48(8): 45–48.MA Yajian,NIE Wenzhong,LU Jianmin,et al.Study on surface quality of SiCp/Al by longitudinal and torsional composite ultrasonic vibration milling[J].Machine Tool &Hydraulics,2020,48(8): 45–48.
[17] XIANG D H,LI B,PENG P C,et al.Study on formation mechanism of edge defects of high-volume fraction SiCp/Al composites by longitudinal-torsional ultrasonic vibrationassisted milling[J].Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2022,236(11):6219–6231.
[18] PENG P C,XIANG D H,LEI X F,et al.Study on the edge defects of high volume fraction 70% SiCp/Al composites in ultrasonicassisted milling[J].The International Journal of Advanced Manufacturing Technology,2022,122(1): 485–498.
[19] LI Z P,ZHANG F H,LUO X C,et al.Material removal mechanism of laserassisted grinding of RB-SiC ceramics and process optimization[J].Journal of the European Ceramic Society,2019,39(4): 705–717.
[20] YE Z,WEN X,WAN W,et al.Precision grinding technology of silicon carbide(SiC) ceramics by longitudinal torsional ultrasonic vibrations[J].Materials (Basel),2023,16(16): 5572.
[21] 童志强,皮钧.纵扭共振旋转超声端铣碳纤维复合材料的试验研究[J].机械科学与技术,2016,35(3): 425–430.TONG Zhiqiang,PI Jun.Experimental study on longitudinal-torsional resonance rotary ultrasonic face milling of CFRP[J].Mechanical Science and Technology for Aerospace Engineering,2016,35(3): 425–430.
[22] GAO G F,XIA Z W,SU T T,et al.Cutting force model of longitudinal-torsional ultrasonic-assisted milling Ti–6Al–4V based on tool flank wear[J].Journal of Materials Processing Technology,2021,291: 117042.
[23] 张存鹰,赵波,王晓博.纵扭复合超声端面铣削表面微结构建模与试验研究[J].表面技术,2019,48(10): 52–63,79.ZHANG Cunying,ZHAO Bo,WANG Xiaobo.Modeling and experiment of surface microstructure by longitudinal-torsional compound ultrasonic end milling[J].Surface Technology,2019,48(10): 52–63,79.
[24] LI Y Q,XIANG D H,FENG H R,et al.Surface characteristics investigation of ultrasonic longitudinal-torsional milling of high–volume fraction SiCp/Al[J].The International Journal of Advanced Manufacturing Technology,2020,110(7): 2119–2130.
[25] 赵崇文.人工神经网络综述[J].山西电子技术,2020(3): 94–96.ZHAO Chongwen.A survey on artificial neural networks[J].Shanxi Electronic Technology,2020(3): 94–96.
[26] 任子为,刘彦杰,张仕进.基于BP神经网络的碳钢激光切割工艺参数预测模型及验证[J].工业控制计算机,2023,36(9): 53–54,57.REN Ziwei,LIU Yanjie,ZHANG Shijin.Prediction model and verification of carbon steel laser cutting process parameters based on BP neural network[J].Industrial Control Computer,2023,36(9): 53–54,57.
[27] 陈虹松,董定乾,黄兵,等.基于遗传算法的航空叶片铣削加工工艺参数优化[J].工具技术,2021,55(9): 68–73.CHEN Hongsong,DONG Dingqian,HUANG Bing,et al.Optimization of process parameters for Ti–Al alloy milling simulation processing based on genetic algorithm[J].Tool Engineering,2021,55(9): 68–73.
[28] 姚忠.采用熵权TOPSIS 模型的电火花线切割电参数优化[J].机械设计与制造,2018(10): 184–186.YAO Zhong.Electrical parameters optimization of WEDM using entropy weight TOPSIS model[J].Machinery Design &Manufacture,2018(10): 184–186.
[29] 赵海越,曹岩,黄亮,等.基于遗传算法的ZL205A 铝合金切削参数多目标优化[J].兵器材料科学与工程,2023,46(5): 58–65.ZHAO Haiyue,CAO Yan,HUANG Liang,et al.Multi-objective optimisation of cutting parameters of ZL205A aluminium alloy based on genetic algorithm[J].Ordnance Material Science and Engineering,2023,46(5): 58–65.
