在铣削加工过程中,由时滞再生效应引起的铣削颤振是一种自激振动现象,是导致铣削加工颤振的主要原因[1]。铣削颤振会导致被加工对象表面质量差,加快铣刀磨损甚至加工效率低下等问题[2]。考虑再生时滞效应的铣削动力学模型可用时滞微分方程表示,对时滞微分方程求解可以获得铣削深度与主轴转速之间临界关系的稳定性叶瓣图[3],为铣削加工提供合适的工艺参数,保持铣削稳定,达到高精度、高效率的铣削加工目的。
Insperger[4]和Li[5]等对时滞微分方程中时滞项用半离散法(Semi-discretization method,SDM)离散;Ding等[6]对时滞微分方程中时滞项和状态项用全离散法(Full-discretization method,FDM)进行线性插值。SDM和FDM大幅度提高了预测方法的计算效率及计算精度,被用于评判其他计算方法的优劣[7]。Li等[5]基于四阶龙格库塔法,把铣削时滞项进行完全离散,且用数值迭代方法得到时滞转移矩阵,可高效预测铣削稳定性。Dai等[8]利用显式精细积分方法可降低对时滞项的离散化误差,提高稳定性预测精度。智红英等[9]用Hamming线性多步法离散时滞项,同等离散数时,计算截断误差小,求解时滞微分方程时具有更快的收敛速度。黄超等[10]利用精细积分全离散算法,不用对时滞矩阵进行求逆运算,可快速精确预测铣削加工稳定性。于福航等[11]对每个离散时间间隔采用多步回溯的方法来逼近时滞项和状态项,能高效准确预测铣削稳定性边界参数。
本文基于数值积分方法求解时滞微分方程,探究数值积分方法对铣削稳定性预测的适用性,旨在保证其预测精度、提高预测效率。
1 铣削动力学模型
考虑时滞再生效应的铣削动力学模型为
式中,M为铣刀模态质量矩阵;C为铣刀模态阻尼;K为铣刀模态刚度矩阵;q(t)为铣刀模态坐标;Kc(t)为周期系数矩阵;ap为轴向铣削深度;T为时滞量。令
通过矩阵变换,式(1)变为
其中,
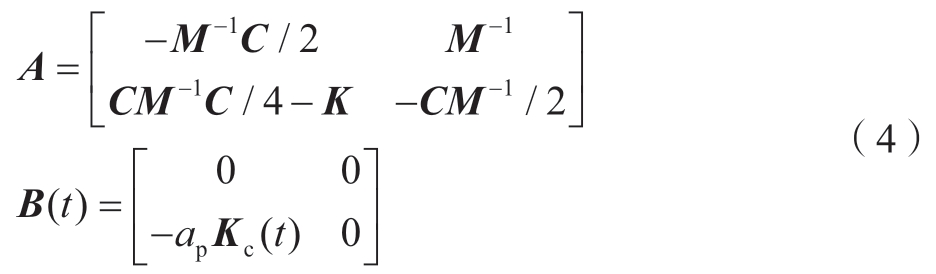
式中,A为常数矩阵;B(t)为随时间变化的周期系数矩阵,且A(t)=A(t+T),B(t)=B(t+T),是螺旋切削刃的铣削周期。在单自由度和双自由度铣削加工中,主要区别是状态向量x(t)、常数矩阵A和周期系数矩阵B(t)的不同。
1.1 单自由度铣削加工模型
单自由度铣削加工模型为
其中,
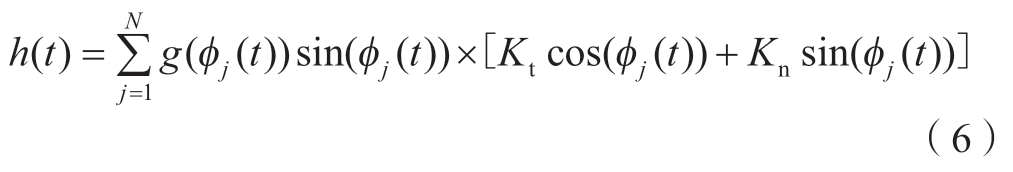
式中,ζ为铣刀的结构阻尼比;mt是为铣刀模态质量;ωn为铣刀的固有频率;Kt为切向切削力系数;Kn为径向切削力系数;φj(t)为铣刀第j个刀齿的位置角,有
式中,n为转速;N为螺旋切削刃数。由于在铣削加工中,当螺旋切削刃与被加工对象接触时才会有铣削产生,所以引入阶跃函数判断是否产生铣削,阶跃函数为
式中,φst、φex为铣削加工过程中立铣刀铣削被加工对象的切入角和切出角。φst、φex为
令x(t)=[x(t)mx˙(t)+mζωn x(t )]T,则单自由度铣削模型的状态空间为
则式(10)中的常数矩阵A和周期系数矩阵B(t)分别为
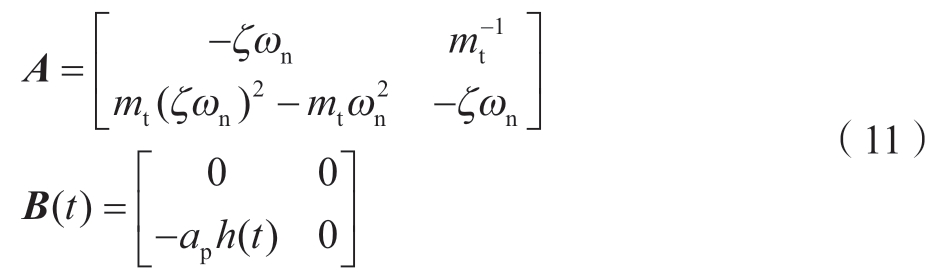
1.2 双自由度铣削加工模型
双自由度模型为

其中,
其中,

令
则双自由度铣削模型的状态空间为
式中,常数矩阵A和周期系数矩阵B(t)分别为
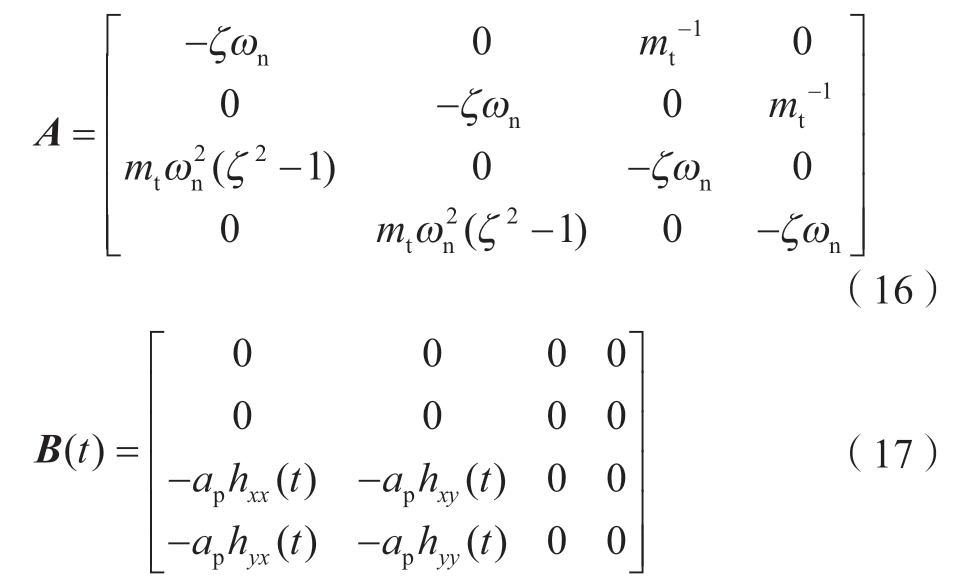
2 多步数值积分方法
将螺旋切削刃的铣削周期T划分为m个相等的时间间隔,则每个时间间隔的离散点为
式中,η表示时间间隔,η=T/m。令
则式(10)和(15)为
由数值积分思想[12]可知,在每段时间间隔(ti,ti+1)内,可得
当m=1时,由式(22)可得
由梯形公式知
联立式(20)和(24)得

式中,I为单位矩阵,当m=2时,由式(22)可得
由1/2辛普森公式知
联立式(20)和(27)得
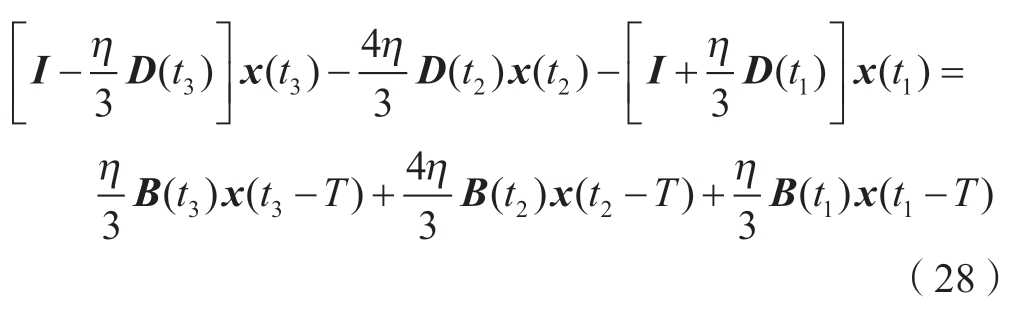
当m=3时,由式(22)可得
由辛普森3/8公式知
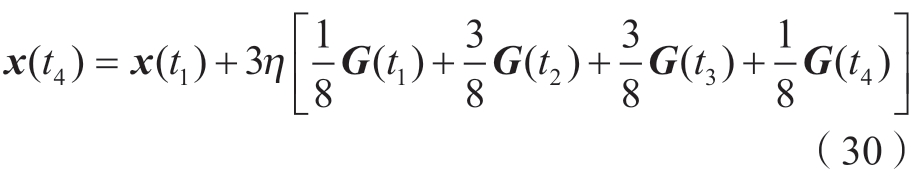
联立式(20)和(30)得

当m=4时,由式(22)可得
由Newton-Cotes公式知
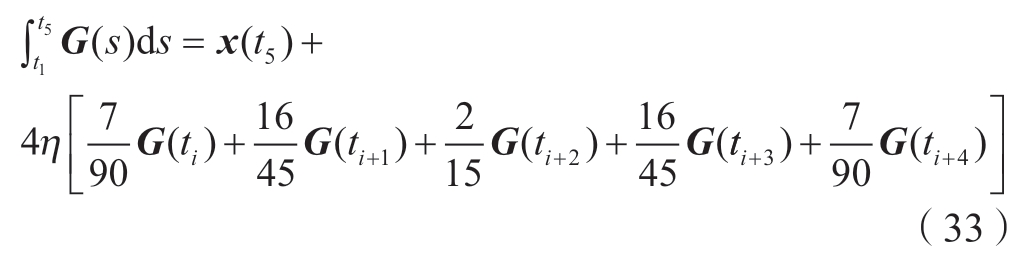
联立式(20)和(33)得
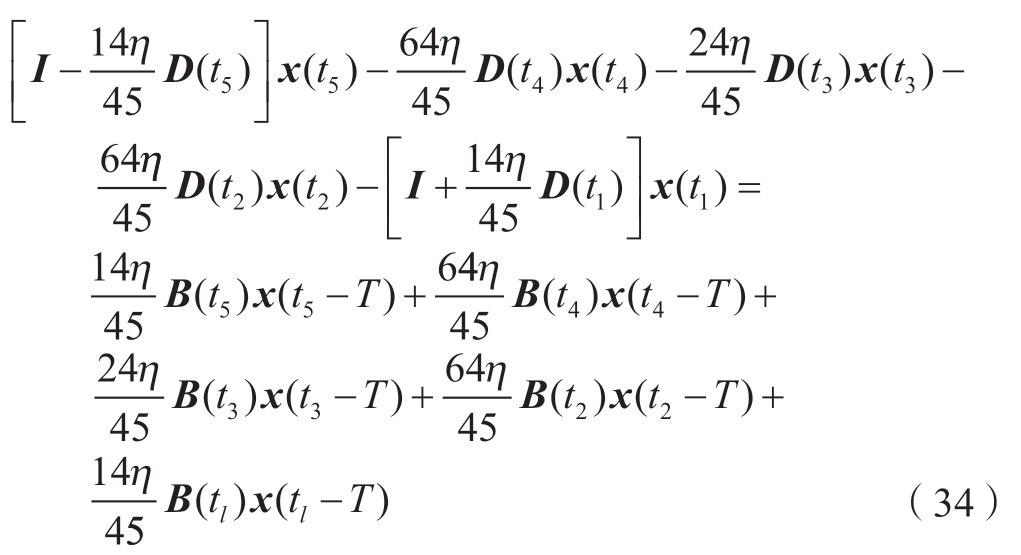
当m≥5时,由积分系数可知

将式(25)、(28)、(31)、(34)联立可得
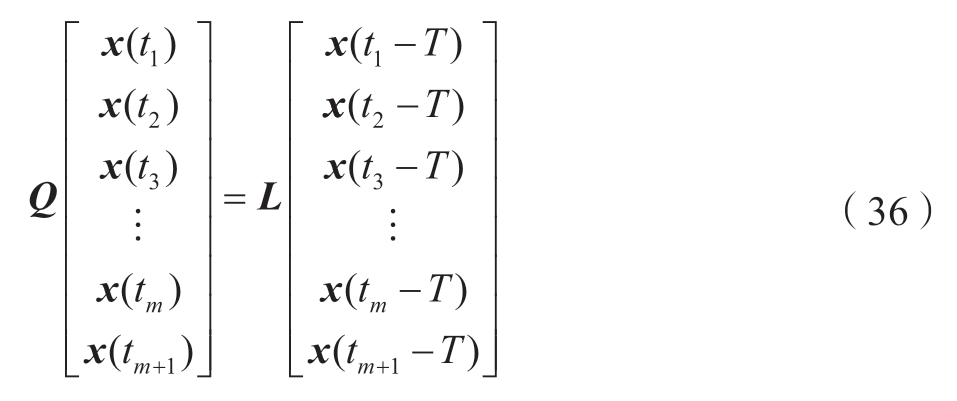
其中,

可得状态转移矩阵为
根据 Floquet 理论,当|Λ|<1时,铣削加工处于稳定状态;|Λ|=1时,铣削系统处于边界状态;|Λ|>1时,铣削系统处于不稳定状态。
3 Matlab数值仿真结果分析
本铣削加工系统中所需的仿真参数采用参考文献[12]中仿真参数:ζ=0.011,mt=0.3993 kg,ωn=922 Hz,Kt=6×108 N/m2,Kn=2×108 N/m2。
3.1 收敛率分析
不同方法的局部离散误差,可以反映计算方法的收敛效率。局部离散误差由|| μ |–| μ0 ||表示,其中| μ0 |是一阶半离散方法(1st-SDM)在m取300时特征值的模。使用Matlab 软件分别对1st-SDM、一阶全离散方法(1st-FDM)和数值积分3种方法进行编程。为比较3种不同数值分析方法的收敛性,铣削宽度和铣刀直径之比ae/R设置为1,机床主轴转速n分别设为5000 r/min和10000 r/min,铣刀轴向铣削深度ap分别为0.7 mm、1.0 mm、1.5 mm。在不同机床主轴转速和不同轴向铣削深度下,1st-SDM、1nd-FDM、数值积分3种方法所对应的局部离散误差如图1所示。
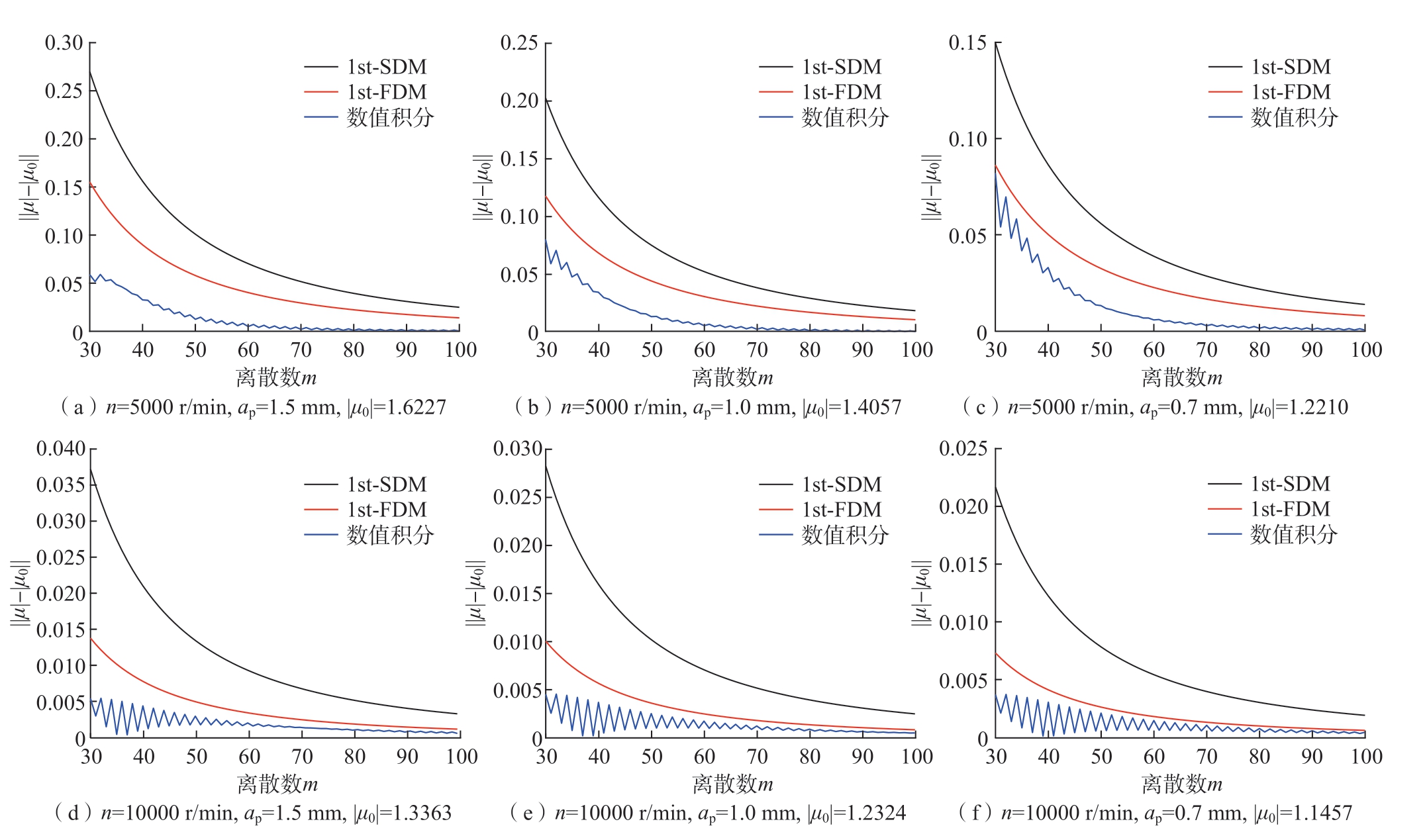
图1 1st-SDM、1st-FDM、数值积分的收敛速度比较
Fig.1 Convergence rate comparisons of 1st-SDM, 1st -FDM and numerical integration
可以看出,随着离散数的不断增加,预测方法的特征值模| μ |快速接近于特征值模| μ0 |,验证了数值积分方法的有效性和精确性。例如,n=5000 r/min,ap=0.7 mm,| μ0 |=1.221,m=50时,1st-SDM方法的局部离散误差为0.05581,1st-FDM 方法的局部离散误差为0.03246,数值积分方法的局部离散误差为0.01316,比1st-SDM 方法的局部离散误差减少76.42%,比 1st-FDM 方法的局部离散误差减少59.46%,因此数值积分方法计算精度高于1st-SDM方法和1st-FDM方法。
3.2 单自由度铣削加工模型叶瓣图
在单自由度铣削加工模型中,为了3种计算方法的效率和准确性,将机床主轴转速n设置为5000~10000 r/min,轴向铣削深度ap设置为0~4 mm。将铣削宽度和立铣刀直径比值ae/R设置成1,离散数m设置为40和60。离散数m越大,局部误差越小,将m=200时1st-SDM方法计算得出的曲线作为理想参考曲线。在不同离散数值下,3种计算方法仿真结果对比如图2所示。
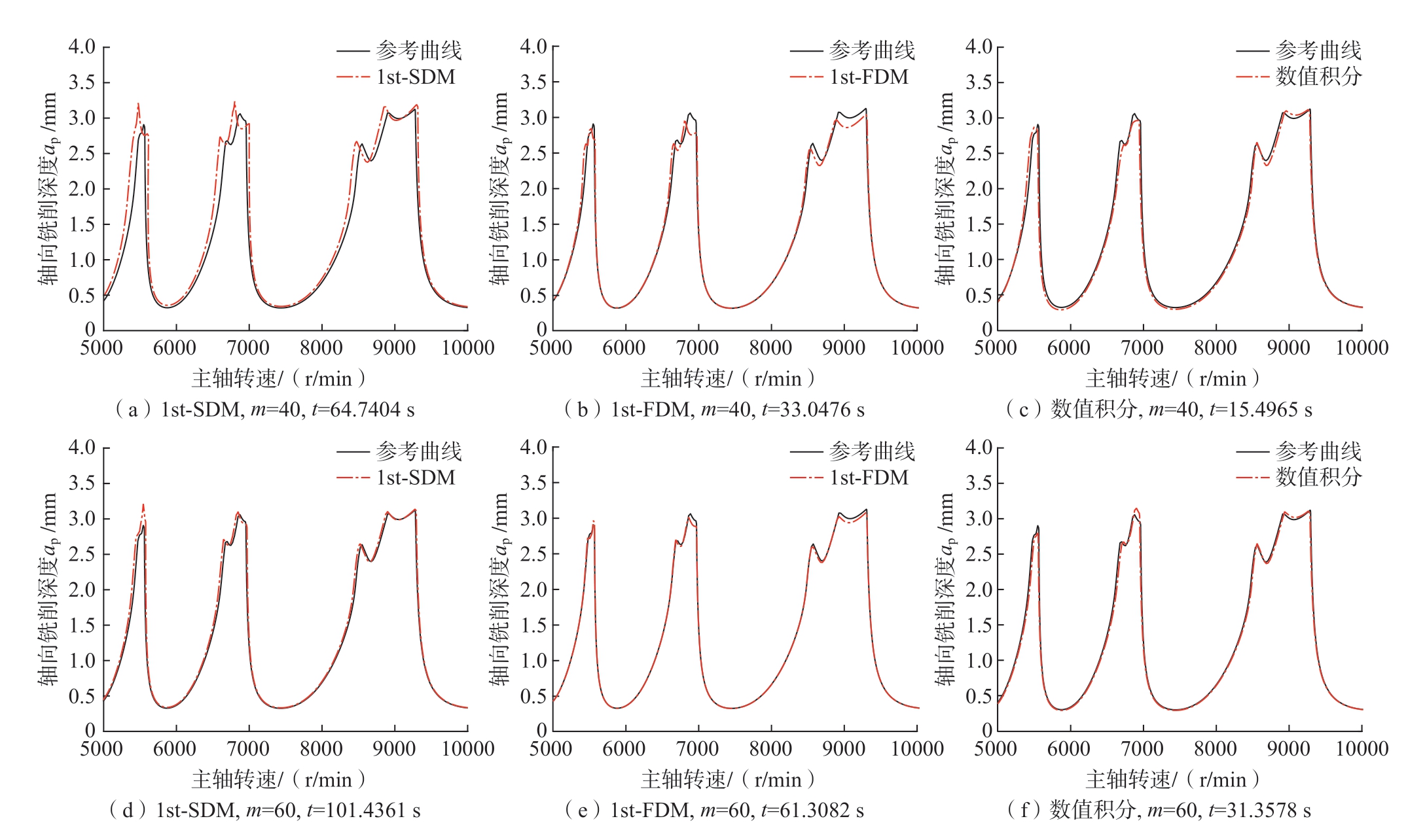
图2 单自由度稳定性叶瓣图
Fig.2 Stability lobe diagrams of single degree-of-freedom milling model
可以看出,在单自由度铣削加工的模型下,同一种计算方法中,随着铣削周期的离散数m的增加,3种方法的计算精度都越来越接近理想参考曲线,且当m=40时,数值积分方法计算时间要比1st-SDM、1st-FDM方法缩短76.06%、53.11%。当 m=60时,数值积分方法计算时间要比1st-SDM、1st-FDM方法缩短69.09%、48.85%。因此,在离散数m相同时,数值积分方法的计算效率要比1st-SDM 方法和 1st-FDM 方法的计算效率要高。
3.3 双自由度铣削加工模型叶瓣图
双自由度铣削加工过程的铣削系统参数与单自由度的铣削参数相同。将铣削宽度和立铣刀直径的比值ae/R设置成0.5,离散数m设置为40和60。主机床主轴转速n设置为5000~10000 r/min,轴向铣削深度ap设置为0~4 mm。在不同离散数值m下,3种计算方法仿真所得结果对比如图3所示。
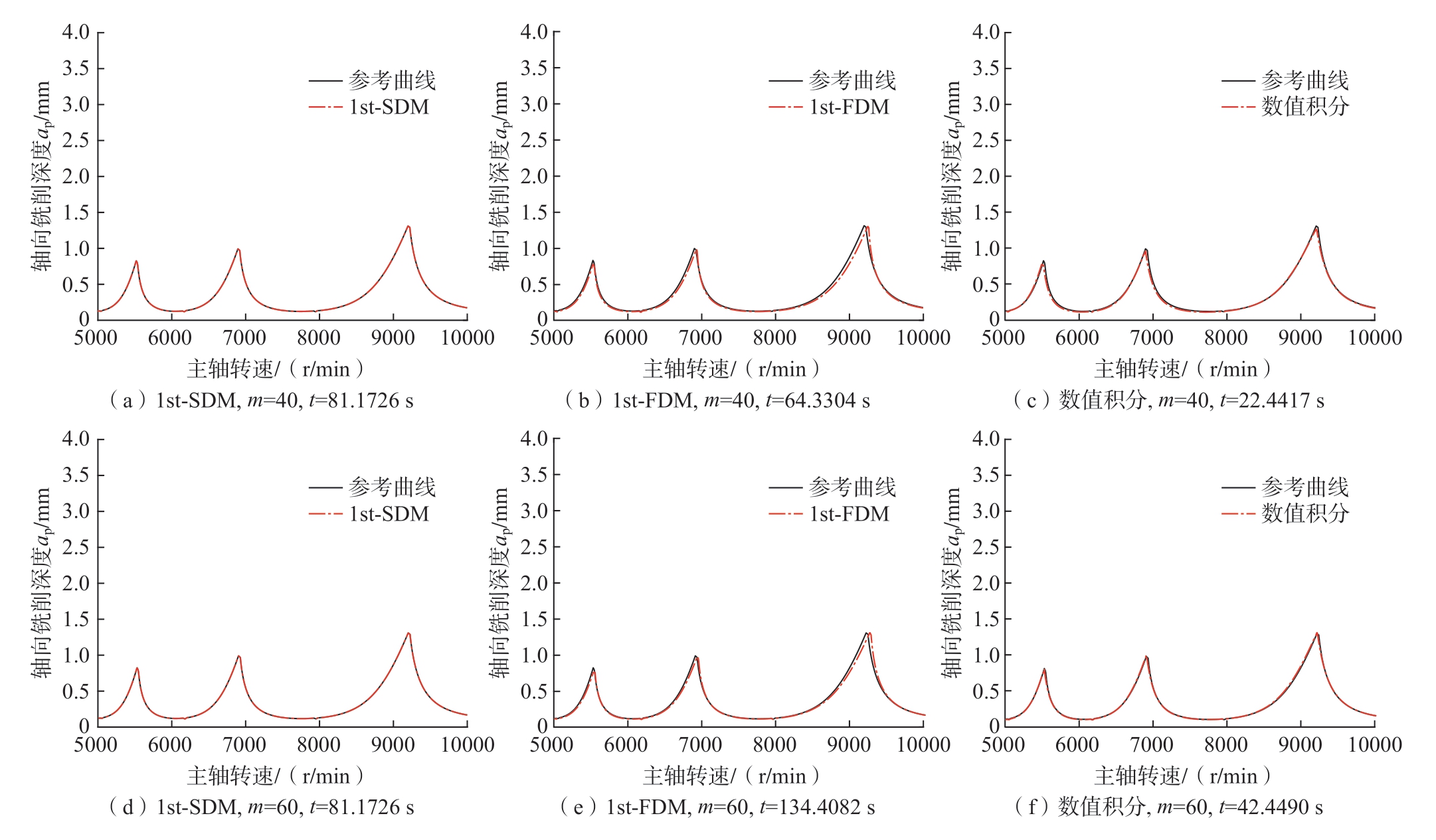
图3 双自由度稳定性叶瓣图
Fig.3 Stability lobe diagrams of double degree-of-freedom milling model
可以看出,在双自由度铣削加工的模型下,在同一种计算方法中,随着铣削周期的离散数m的增加,3种方法的计算精度都越来越接近理想参考曲线,且当m=40时,数值积分方法计算时间要比1st-SDM、1st-FDM方法缩短72.35%、65.11%。当m=60时,数值积分方法的计算时间比1st-SDM,1st-FDM方法缩短47.71%、68.42%。因此,在离散数m相同时,数值积分方法的计算效率要比1st-SDM 方法和1st-FDM 方法的计算效率要高。
4 参数识别
4.1 铣削力参数获取试验
通过机械模型法求解,保持机床主轴转速和轴向铣削深度不变,测量每个刀齿周期下在不同进给量的平均切削力,用线性回归分析来求解铣削力系数,即

Kte、Kre为径向和切向犁耕力系数,试验在数控铣床VM–600上进行,试验现象如图4所示。采用3齿硬质合金立铣刀,R=10 mm,螺旋角=45°,工件材料铝合金(7075T),测量仪器为Kistler9257B动态测力仪、Kistler5070A电荷放大器、Kistler5697A1数据采集仪,分析软件为Kistler2825A(图4(a))。采用全齿铣削,即ae=10 mm,保持机床主轴转速和轴向铣削深度不变,测得平稳铣削时,每齿进给量为0.02 mm/z、0.04 mm/z、0.06 mm/z、0.08 mm/z、0.10 mm/z时,X、Y和Z方向平均铣削力如表1所示。
表1 X和Y方向平均铣削力
Table 1 Average milling force in X and Y directions

序号fz /(mm/z)Fx /NFy /NFz /N 0.0214.3229.459.46 2 0.0418.5338.5210.32 3 0.0622.4748.2712.11 4 0.0828.2960.7913.26 5 0.131.7672.8114.73 1

图4 试验现场
Fig.4 Testing site
4.2 模态参数获取试验
通过锤击试验获取刀尖频响函数曲线,采用LC–02A冲击力锤和1A803E加速度传感器(东华),数据采集及分析软件为DH5930便携式模态测试分析系统(东华),锤击试验现场如图4(b)所示。力锤对刀尖产生激励,传感器收集激励和响应信号,经过电荷放大器放大后输入数据采集仪,电脑软件分析处理得到实测刀尖频响函数曲线,如图5所示。

图5 刀尖频响函数实测曲线
Fig.5 Measured curve of tool tip frequency response function
将表1中X和Y方向平均铣削力代入式(40),经过线性回归分析计算得Kt=795.64 N/mm2,Kn=325.63 N/mm2。
有多种方法可以从刀尖频响函数曲线中获取模态参数,本次试验采用峰值辨识法获得对应的模态刚度和阻尼比等参数,如表2所示。
表2 刀具模态参数
Table 2 Tool modal parameters
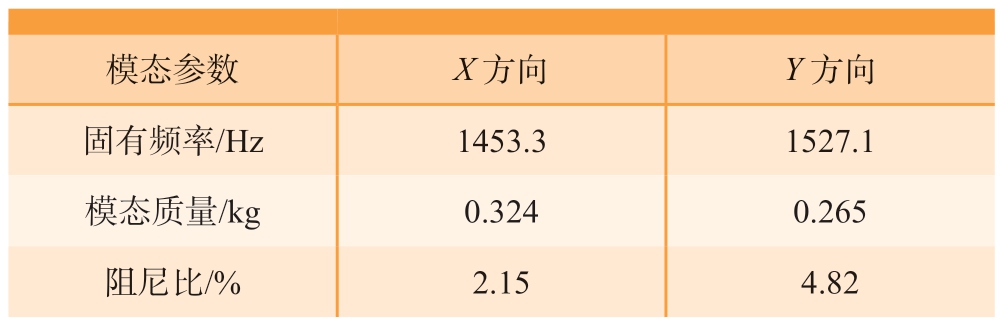
模态参数X方向Y方向固有频率/Hz1453.31527.1模态质量/kg0.3240.265阻尼比/%2.154.82
5 铣削试验验证
采用3齿硬质合金立铣刀,R=10 mm,螺旋角45°,工件材料铝合金(7075T),将铣削宽度和立铣刀直径比值ae/R设置成1,机床主轴转速设置为5000~10000 r/min,轴向铣削深度ap设置为0~4.5 mm,离散数m设置为50,并将铣削力系数获取试验和模态参数获取试验得到的试验参数进行数值仿真,结果如图6所示。

图6 稳定性叶瓣图验证试验图
Fig.6 Stability leaflet diagram verification experiment diagram
通过对铣削力时域信号进行傅里叶变换得到铣削力的频域信号,由此可以判断铣削加工系统是否稳定。根据图6中稳定性叶瓣图,固定点A(n=6000 r/min、ap=2 mm)和固定点B(n=7500 r/min,ap=1 mm)。将在A点和B点所测得的Y方向铣削力时域信号通过快速傅里叶变换转换到频域进行分析,试验结果分析如图7所示。
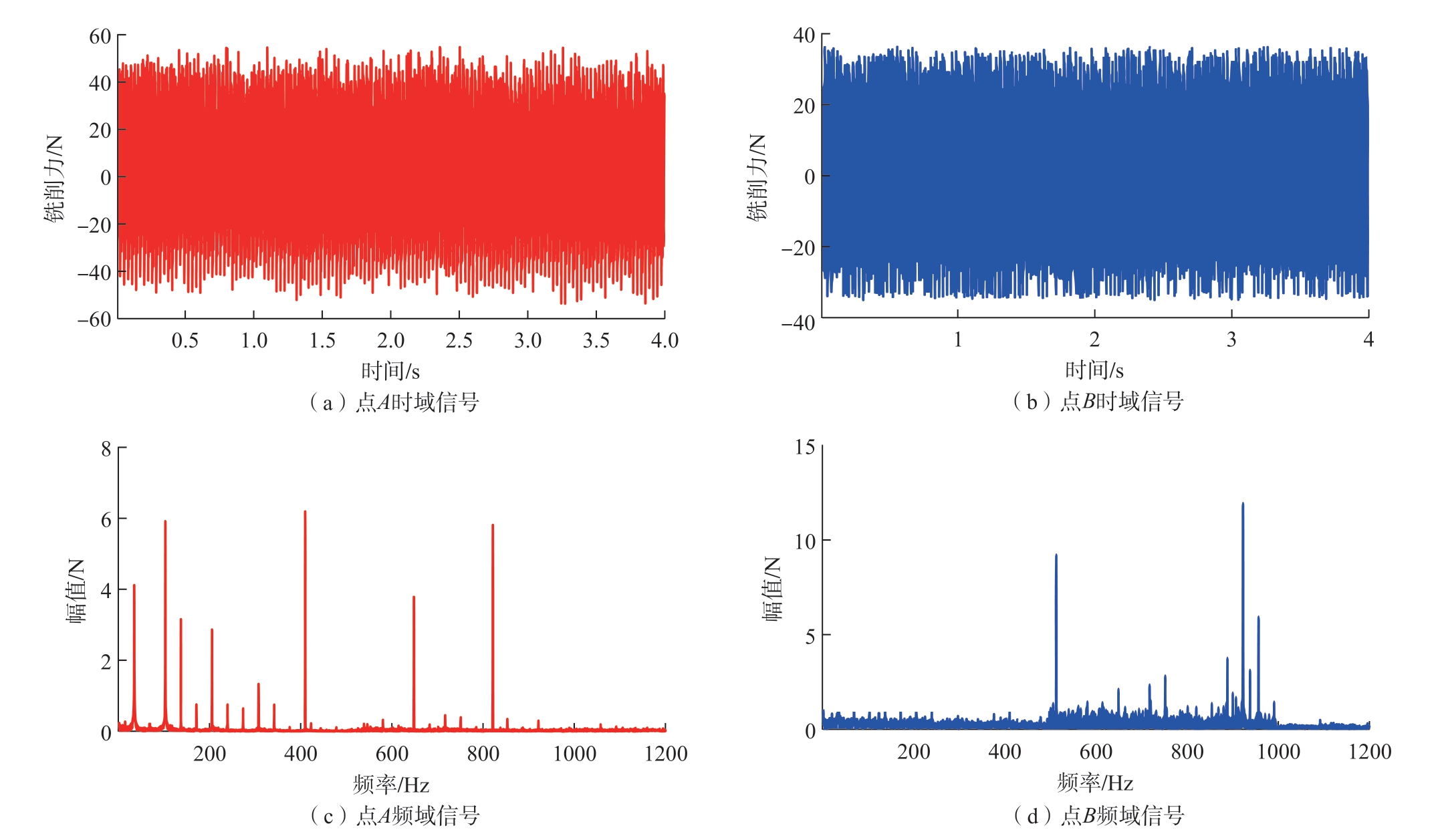
图7 固定点A和固定点B信号图
Fig.7 Fixed point A and fixed point B signal diagram
从图7(a)和(b)铣削力的时域图中可以看出,固定点B的时域铣削力波形相对于固定点A的时域铣削力波形更为平稳;把固定点A和固定点B时域信号转化到频域信号进行分析,由图7(c)和(d)可以看出,采用点B的加工参数对被加工对象进行切削时,频率集中在主轴转频和倍频处。采用点A的加工参数对被加工对象进行铣削时,频率从主轴转频和倍频处发生转移,可以得出点B处于稳定铣削状态,点A处于不稳定铣削状态。
试验表明,数值积分方法的仿真结果和铣削试验结果是吻合的,数值积分方法可以作为预测铣削加工稳定性的一种方法。
6 结论
本文针对铣削加工过程中颤振现象,基于数值积分法预测立式加工中心刀具铣削加工过程稳定性。
(1)通过与全离散法和半离散法局部离散误差仿真结果比较可知,数值积分方法具有更快的收敛速度。数值积分方法在离散数较小的情况能达到1st-SDM和1st-FDM在离散数较高时的局部离散误差。
(2)同一离散数时,数值积分方法的求解效率要高于 1st-SDM 方法和 1st-FDM 方法。
(3)铣削试验和仿真结果一致,数值积分方法可以用来预测铣削加工的稳定性。
[1] 杨昀, 张卫红, 党建卫, 等.航空薄壁件铣削加工动力学仿真技术[J].航空制造技术, 2018, 61(7): 42–47, 69.YANG Yun, ZHANG Weihong, DANG Jianwei, et al.Dynamic modelling technology on milling process of aerospace thin-walled workpiece[J].Aeronautical Manufacturing Technology, 2018, 61(7):42–47, 69.
[2] 李文霞, 杨德云, 邓斌, 等.大型结构件镗孔加工颤振检测与改善试验研究[J].现代制造工程, 2020(12): 105–110.LI Wenxia, YANG Deyun, DENG Bin, et al.Experimental study on testing and improvement of machining chatter for large structure components boring process[J].Modern Manufacturing Engineering,2020(12): 105–110.
[3] 智红英, 闫献国, 杜娟, 等.预测铣削稳定性的隐式Adams方法[J].机械工程学报, 2018, 54(23): 223–232.ZHI Hongying, YAN Xianguo, DU Juan, et al.Prediction of the milling stability based on the implicit Adams method[J].Journal of Mechanical Engineering, 2018, 54(23): 223–232.
[4] INSPERGER T, STÉPÁN G.Semi-discretization method for delayed systems[J].International Journal for Numerical Methods in Engineering, 2002, 55(5): 503–518.
[5] LI M Z, ZHANG G J, HUANG Y.Complete discretization scheme for milling stability prediction[J].Nonlinear Dynamics, 2013,71(1): 187–199.
[6] DING Y, ZHU L M, ZHANG X J, et al.A full-discretization method for prediction of milling stability[J].International Journal of Machine Tools and Manufacture, 2010, 50(5): 502–509.
[7] 李忠群, 彭岳荣, 夏磊, 等.基于三阶龙格库塔法的铣削稳定性半解析法预测[J].航空制造技术, 2016, 59(23/24): 30–33.LI Zhongqun, PENG Yuerong, XIA Lei, et al.Prediction of chatter stability for milling process using semi-analytical approach based on three-order Runge–Kutta method[J].Aeronautical Manufacturing Technology, 2016, 59(23/24): 30–33.
[8] DAI Y B, LI H K, XING X Y, et al.Prediction of chatter stability for milling process using precise integration method[J].Precision Engineering, 2018, 52: 152–157.
[9] 智红英, 闫献国, 杜娟, 等.预测铣削稳定性的Hamming线性多步法[J].振动与冲击, 2018, 37(22): 67–74, 110.ZHI Hongying, YAN Xianguo, DU Juan, et al.Prediction of the milling stability based on the Hamming linear multistep method[J].Journal of Vibration and Shock, 2018, 37(22): 67–74, 110.
[10] 黄超, 杨文安, 蔡旭林, 等.基于精细积分全离散法的变齿距铣削稳定性研究[J].航空制造技术, 2022, 65(7): 110–115.HUANG Chao, YANG Wenan, CAI Xulin, et al.Stability prediction of milling with variable pitch cutter using precise integration-based fulldiscretization method[J].Aeronautical Manufacturing Technology, 2022,65(7): 110–115.
[11] 于福航, 李茂月, 严复钢, 等.一种基于多步回溯算法的铣削稳定性预测方法[J].振动与冲击, 2021, 40(1): 102–109.YU Fuhang, LI Maoyue, YAN Fugang, et al.A prediction method of milling stability based on multi-step backtracking algorithm[J].Journal of Vibration and Shock, 2021, 40(1): 102–109.
[12] 张奇.铣削加工颤振稳定性分析和颤振辨识研究[D].上海:上海交通大学, 2022.ZHANG Qi.Study on stability analysis and identification and detection of chatter in milling process[D].Shanghai: Shanghai Jiao Tong University, 2022.