大底脚螺纹抽钉是一种单面连接紧固件,可解决飞机机体不开敞结构的连接问题。大底脚螺纹抽钉通常由4个及以上分件装配组成,各分件在铆接时共同作用,相互协调,通过将芯杆的旋转运动转换为大底脚对夹层的夹紧力来实现铆接效果。与传统拉拔型抽芯铆钉不同,具有螺纹副的大底脚螺纹抽钉可提高夹紧力,带来更好的连接强度和抗振动性能,安装工具结构也更简单。因为具有铆接成形后底脚面积大,对复合材料损伤小的独特优势,被广泛应用于飞机复合材料结构的连接。复合材料虽已成为飞机结构最主要的材料之一[1–2],如舱门[3]、发动机风扇叶片[4]、飞机机翼蒙皮等[5],但复合材料为层状结构,存在抗剪强度低、塑性差、抗冲击力差、连接接头强度低等缺点,使用大底脚螺纹抽钉可减少复合材料的连接损伤,对于结构设计、质量、可靠性和飞机轻量化具有积极作用[6]。
由于大底脚螺纹抽钉安装过程较为复杂,目前国内尚未实现自主研发,但国内研究人员开展过一些研究。2009年,孙钢[7]介绍了5种国内外航空复合夹层用抽芯铆钉,指出国内复材用抽芯铆钉与国外的差距很大,体现在品种过少、工艺标准不足、制造水平不高、缺乏抽芯铆钉技术和结构力学模型等方面的理论依据。2014年,西北工业大学的魏景超[8]研究了单面抽钉紧固件的不同干涉量配合对复合材料连接结构疲劳寿命的影响。2016年,李荣霞[9]从螺纹抽钉铆接工艺的角度分析故障率高的原因,制定相应改进措施,达到降低故障率的目的。2021年,首都航天机械有限公司的檀甜甜等[10]通过试验对比了不同连接方式下碳纤维复合材料结构件的结构强度,结果表明螺纹抽芯铆钉的抗剪切强度高、不损伤材料表面,且指出单面连接的场合应尽量采用大底脚螺纹抽钉连接。2022年,天津大学的Li等[11]使用试验和数值模拟结合的方法,研究了抽钉和铆孔间不同干涉量的配合对CFRP/Al材料损伤的演变过程。
目前我国紧固件体系中有2004年实施的关于普通型抽芯铆钉标准GB/T 3098.18—2004《紧固件机械性能盲铆钉试验方法》和GB/T 3098.19—2004《紧固件机械性能抽芯铆钉》;航标体系中有2002年实施的由俄罗斯国产化形成的HB8001~HB8005,但以上标准中的铆钉无法满足航空领域对复合材料连接性能的需求。
综上所述,我国目前缺乏对复材用螺纹抽钉的设计制造及使用标准,复材用抽钉和安装工具普遍采用英制系列设计,而使用国外标准则存在英制和米制换算精度不准确,以及国内外材料力学性能不同导致的精确性和稳定性的问题。此外,对紧固件的研究重点集中在铆接后材料的力学性能,对抽钉的研究手段以试验分析为主,导致对抽钉安装过程受力特点、各因素影响规律等关键理论研究不透彻,实现大底脚螺纹抽钉的自主研发较为困难。
本文从材料力学理论分析和有限元仿真计算的角度,通过对此种结构的大底脚螺纹抽钉进行受力分析、芯杆关键位置处最大应力数学建模、有限元建模计算和参数影响规律分析,实现了大底脚螺纹抽钉芯杆强度计算方法的研究,以期为提升大底脚螺纹抽钉安装质量、连接可靠性和合格率提供技术支撑,进而促进飞机的轻量化发展,提升飞机的安全性能和经济效益。
1 抽钉安装过程及受力分析
1.1 抽钉结构
本文的研究对象为大底脚螺纹抽钉,由芯杆、成型套、插入件、钉套和驱动螺母5部分组成,5个分件在进行铆接时共同作用,相互协调,形成一个完整的系统,抽钉整体和分件结构如图1所示。芯杆上下两段螺纹(完整段螺纹和非完整段螺纹)都为UNJF螺纹,区别是大径不同。完整段螺纹牙型完整,只能与钉套内螺纹啮合;而非完整段螺纹牙型不完整,大径小于完整段螺纹大径,可同时与钉套内螺纹和驱动螺母内螺纹啮合。两段不同螺纹使得安装时驱动螺母无法攻入完整段螺纹,卡在断颈槽与完整段螺纹过渡端面,达到随扭矩增加,芯杆沿断颈槽断裂的目的。
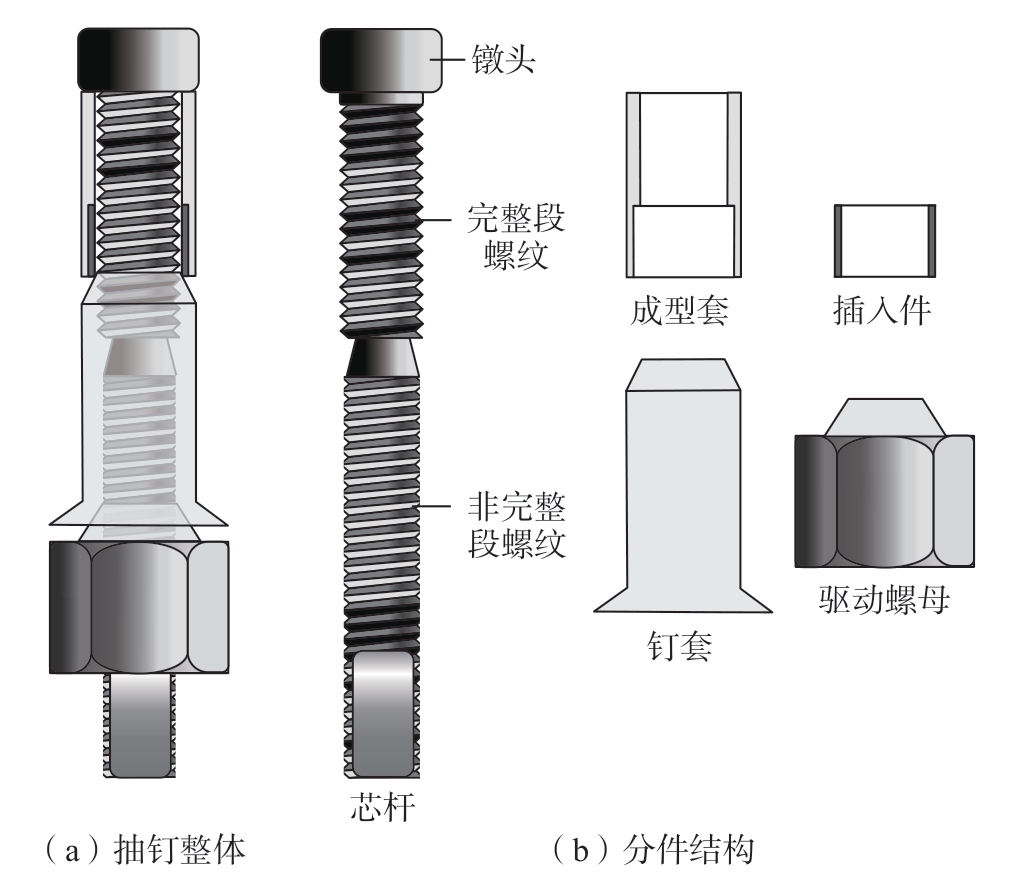
图1 大底脚螺纹抽钉整体和分件结构
Fig.1 Structure and components of blind bolted rivets
1.2 抽钉安装过程
图2为铆接安装过程。
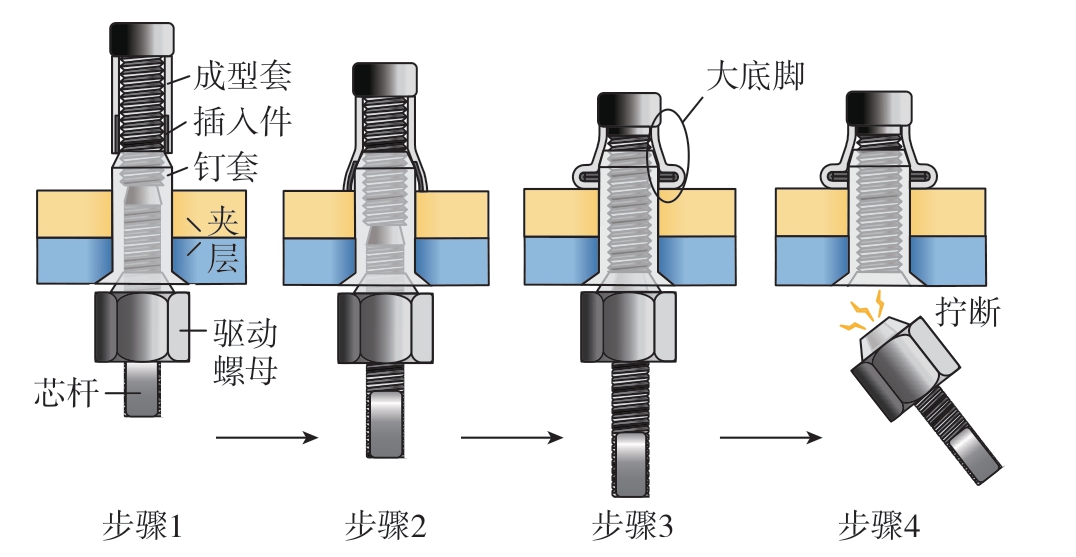
图2 大底脚螺纹抽钉安装过程
Fig.2 Setting process of blind bolted rivets
步骤1:抽钉整体插入铆孔,铆枪套筒固定驱动螺母,驱动螺母顶在钉套上,螺母和钉套都被固定不发生转动,铆枪夹头夹持芯杆尾部平面,驱动芯杆旋转;
步骤2:芯杆的转动通过螺纹副转换为对成型套和插入件向下的压力,成型套和插入件在压力作用下被压入钉套,沿径向发生膨胀;
步骤3:成型套和插入件在与被夹紧件接触后形成一个大底脚,从而产生夹紧力;
步骤4:驱动螺母的内螺纹无法与完整段螺纹啮合,螺母上端面抵在芯杆完整螺纹段的端面,当铆枪扭转力矩产生的铆接力达到断颈力的值,断颈槽发生断裂,非完整段芯杆和驱动螺母脱离,铆接完成。
1.3 受力分析
图3为铆接安装过程步骤3~4中各分件的受力图。步骤3~4中各分件间力的相互作用和力矩数量最多,且包括步骤1~3过程中所有外力和力矩,因此进行受力分析时选择步骤3~4,各分件在外力作用下满足力的平衡。成型套三力平衡为
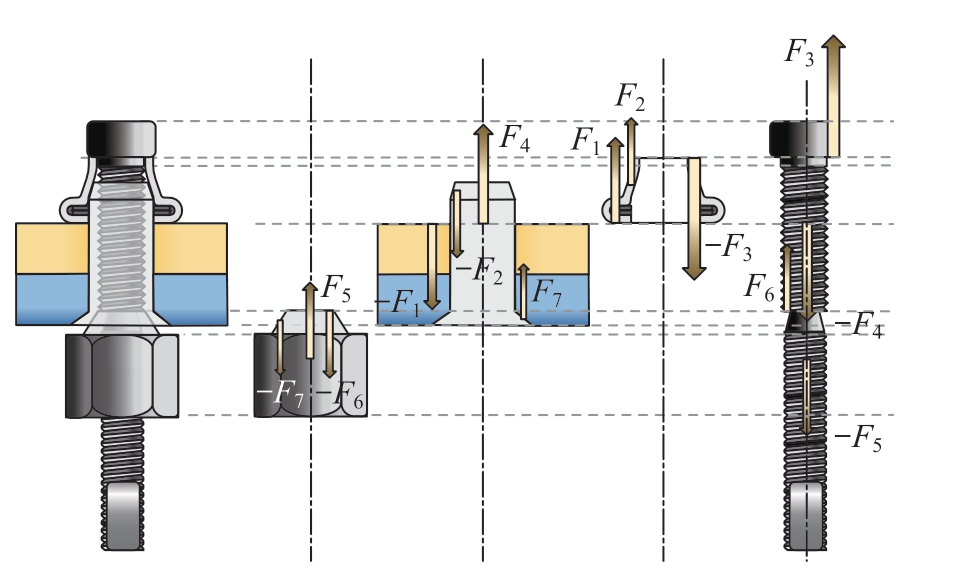
图3 步骤3~4的过程中各分件受力图
Fig.3 Step 3–4 in the process of each part of the force diagram
式中,F1为被夹紧件对底脚的反作用合力,即产生的夹紧力(预紧力);F2为成型套与钉套接触面上摩擦力沿芯杆轴向分力的合力;F3为芯杆镦头对成型套端面压力的合力。
芯杆四力平衡为
式中,F4为钉套与螺纹完整段芯杆拧紧,沿轴线上产生拉力的合力;F5为驱动螺母与螺纹非完整段芯杆拧紧,沿轴线上产生拉力的合力;F6为驱动螺母顶在芯杆断颈槽处端面产生拉力的合力。
驱动螺母和钉套分别满足
式中,F7为驱动螺母顶在钉套斜面产生拉力的合力。
图4为步骤3~4安装过程中各分件受扭矩的示意图。M1~M7分别为F1~F7对应的扭矩;M为铆枪施加力矩减去损耗后作用于芯杆尾部平面的输入扭矩。
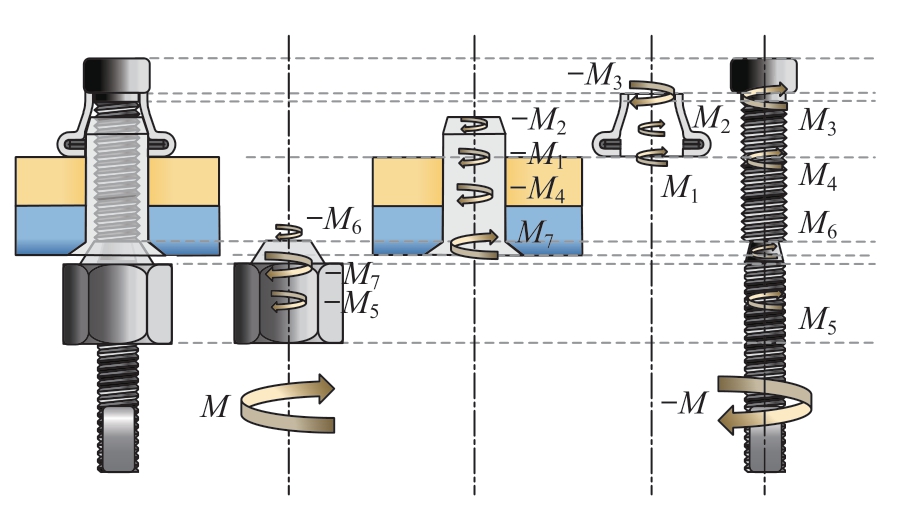
图4 步骤3~4的过程中各分件受扭矩图
Fig.4 Step 3–4 in the process of each part of the torque diagram
2 芯杆关键部位应力分析
大底脚螺纹抽钉作为由5个单独分件装配而成的复杂单边连接系统,安装过程中禁止出现掉头、翻边、撕裂、脱落和翘曲现象,且安装完成后,须保证底脚成形后的最小直径尺寸ΦJ值、最大高度K值和断面高度I值(图5),以满足底脚面积大、对复材损伤小、夹紧力大、连接强度高、抗振动性能和密封性能好、断面齐平度好的要求。
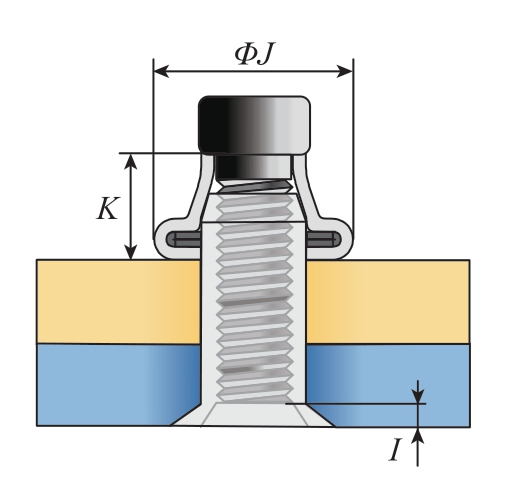
图5 大底脚外观尺寸
Fig.5 External dimensions of blind head
在上述禁止出现的现象中,掉头(图6)指芯杆尚未沿断颈槽扭断之前,镦头断裂、脱离芯杆的现象,通常发生在安装步骤3~4,扭矩即将达到断颈槽扭断力矩(驱动螺母上端面已抵在芯杆完整螺纹段端面)之时,且断裂位置位于与镦头连接的第一牙螺纹处。根据强度理论,原因是芯杆第一牙螺纹处的应力值早于断颈槽的应力值达到材料的抗拉强度。因此为防止镦头断裂,建立断裂时刻芯杆螺纹和断颈槽在外力作用下产生的应力的理论模型,以及分析关键因素对最大应力值的影响规律尤为重要。
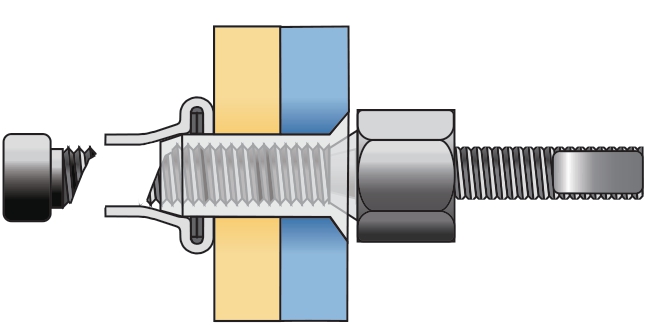
图6 芯杆镦头断裂失效
Fig.6 Torsion failure of screw head
根据上节内容,芯杆共承受了5个扭矩:M3、M4、M5、M6和M,计算公式分别为
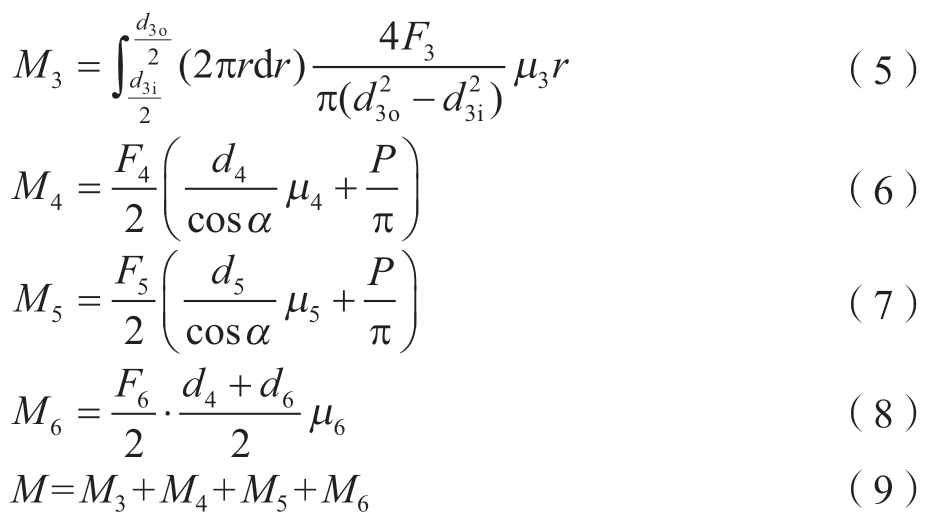
式中,r为半径;μ3、μ4、μ5和μ6分别为镦头与成型套接触面、钉套与芯杆完整段螺纹副、驱动螺母与芯杆非完整段螺纹副和驱动螺母与芯杆端面的摩擦因数;α为牙型半角;P为螺距;d4、d5、d6、d3i和d3o分别为完整段螺纹中径、非完整段螺纹中径、断颈槽直径、成型套内径和外径。
2.1 芯杆关键部位应力分析
在步骤3~4过程中,芯杆在成型套、螺母和钉套对芯杆外力作用下,各横截面的内力图和扭矩图如图7所示。从0点往上(图7(a)):a为芯杆非完整段受拉,力由0非线性增加至F5;b为断颈槽处无螺纹副及其他接触,力保持F5不变;c为完整段端面受到向上的力F6,力瞬间减小至F5–F6;d为芯杆完整段受拉,力由F5–F6非线性增加至F3,增加的量为F4;e为镦头与螺纹过渡处无螺纹副,力保持F3不变。从0点往上(图7(b)),扭矩由输入扭矩M,依次减小了M5、M6、M4、M3。
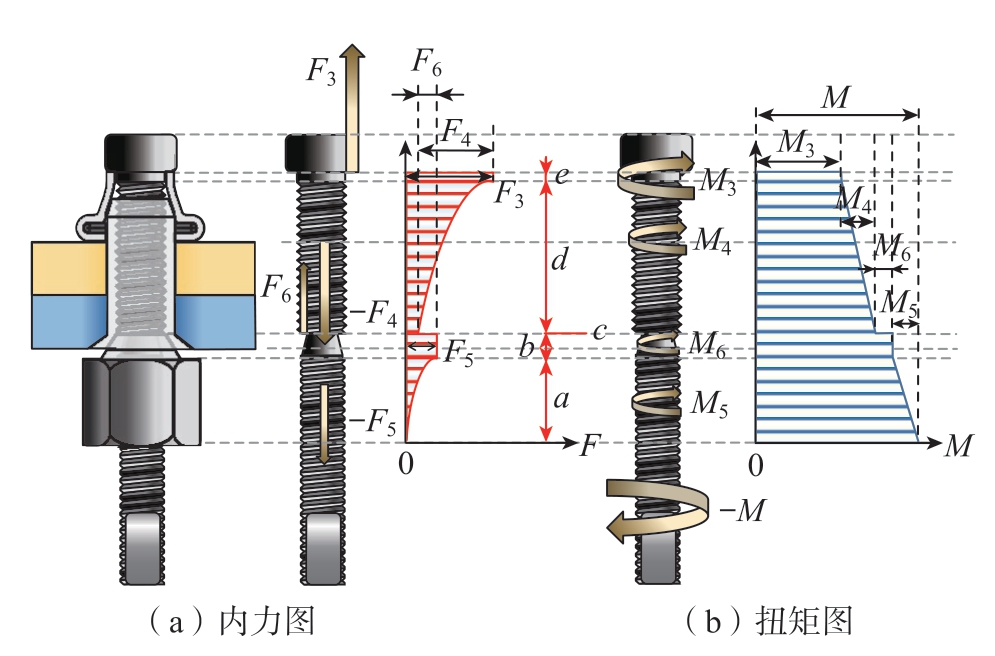
图7 芯杆内力图和扭矩图
Fig.7 Internal force and torque diagram of screw
由此可知,断颈槽处应力取决于拉力F5和扭矩M3+M4+M6值的大小,第一牙螺纹处应力由拉力F3和扭矩M3共同决定。
基于材料力学第四强度理论,结合M3~M6表达式,给出的断颈槽最大应力σr4和第一牙螺纹最大应力σ'r4分别如下。
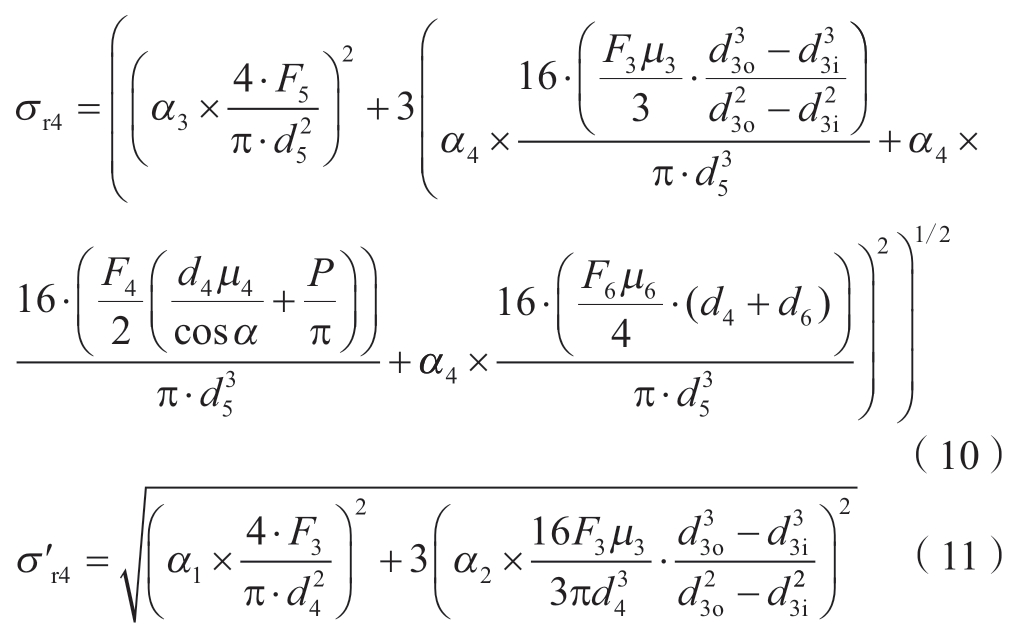
式中,α1、α2、α3和α4分别为螺纹处受拉力、螺纹处受扭矩、断颈槽受拉力、断颈槽受扭矩时的应力集中系数,应力集中系数只与结构本身有关。
《应力集中》(增补版)[12]中给出了固定直径、不同牙型角和螺距的惠氏螺纹在受拉时的应力集中系数,缺少芯杆对应直径的螺纹在受扭时的应力集中系数。因此,下文建立了精细化的螺纹结构有限元模型,将仿真得到的应力集中系数α1、α2、α3和α4代入到上述公式中,从而计算和分析关键部位的应力及各因素的影响规律。
2.2 有限元建模及应力集中系数计算
由于螺纹紧固件几何形状的特殊性,建立螺纹三维网格模型较为困难。本课题组已形成一套成熟的考虑螺牙几何型线和螺旋形状,可生成六面体网格的建模方法[13–15]。方法的思路为:
(1)根据几何尺寸建立不考虑螺纹的圆柱基体;
(2)绘制螺纹横截面网格;
(3)将此横截面网格沿螺杆轴线映射得到形状规则的网格模型;
(4)根据螺牙几何型线方程计算考虑螺纹的螺杆网格节点坐标,将不考虑螺纹的圆柱基体网格节点移动到对应的考虑螺纹的螺杆网格节点。
该方法可得到精细的螺纹三维网格模型,通过轴向网格数量和螺距间网格数量控制网格规模,通过合理协调网格规模和计算精度,大大提高了求解精度和求解效率。本文对大底脚螺纹抽钉分件芯杆完整和非完整段螺纹的建模过程都基于此思路。
UNJF不同于普通英制螺纹,它的根部圆角比普通英制螺纹更大,完整段螺纹牙型几何尺寸关系如图8(a)所示。
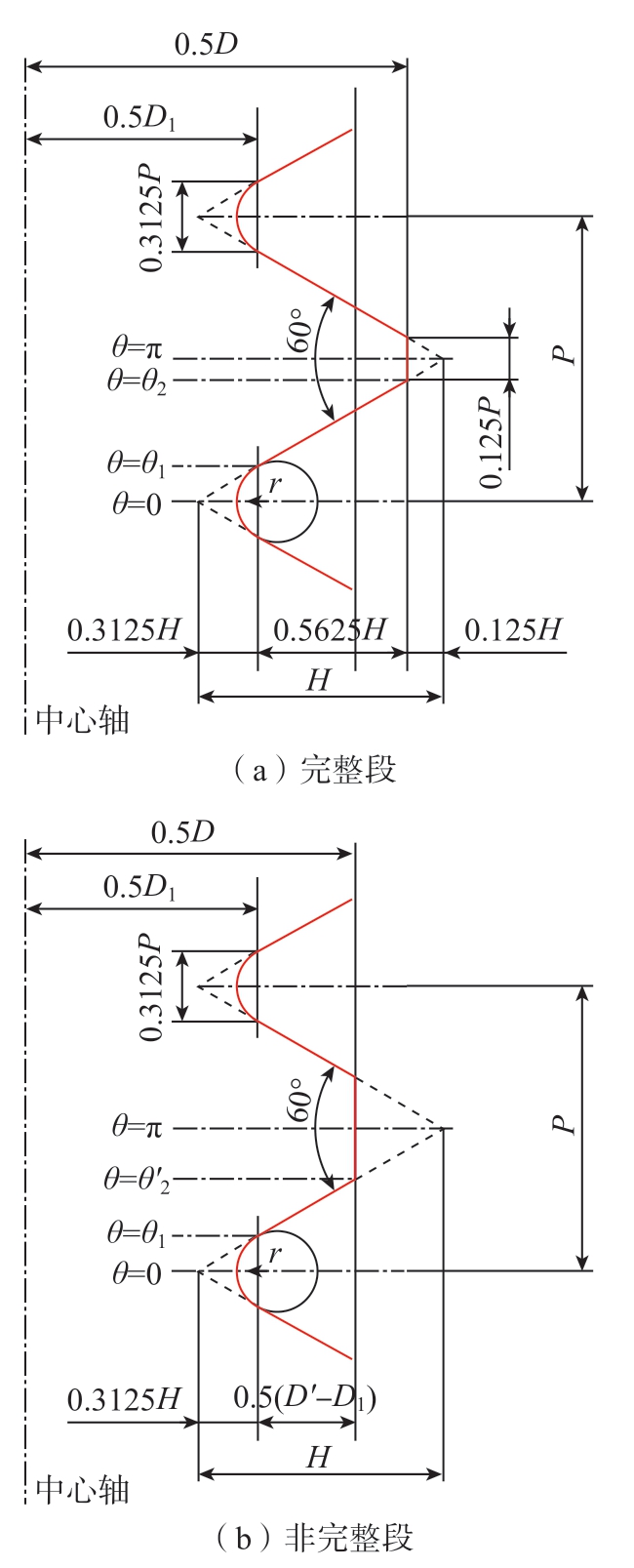
图8 UNJF螺纹完整段及非完整段牙型
Fig.8 Profile of basic and modified UNJF thread
注:D1为小径。
完整段螺牙的几何型线方程l(θ)为
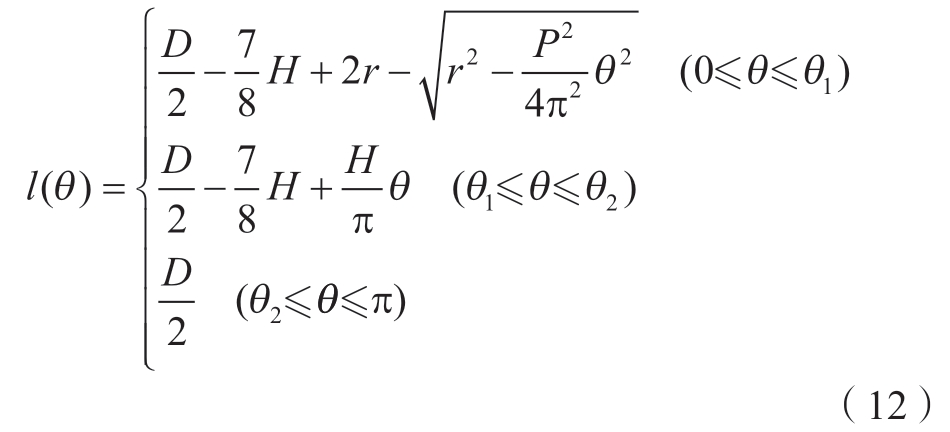
式中,H为牙高;D为大径。其中,![]()
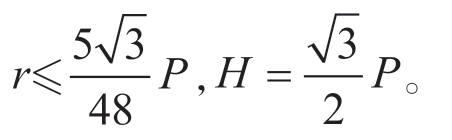
非完整段螺纹牙型几何尺寸关系如图8(b)所示,与完整段相比,几何型线方程大径、由大径不同导致的θ1和部分参数不同。
该网格建模方法将芯杆划分为形状规则的六面体网格,如图9所示。

图9 芯杆几何和网格模型
Fig.9 Geometric and mesh model of screw
有限元仿真过程中,添加4个参考点,分别为参考点和4个承力面(f、g、h、i)建立耦合,如图10所示。通过在参考点上施加成对拉力或扭矩(F3与F4、M3与M4、F5与F6、M5与M6)分别获得芯杆螺纹处受拉力、螺纹处受扭矩、断颈槽受拉力、断颈槽受扭矩时对应方向的应力值,除以对应螺纹中径的基准应力,得到应力集中系数α1、α2、α3和α4。

图10 芯杆边界条件
Fig.10 Boundary conditions
3 影响因素分析
由上述断颈槽处应力σr4和第一牙螺纹处应力σ'r4表达式可知(式(10)和(11)),σr4和σ'r4受较多因素影响,且σr4大于σ'r4是避免镦头断裂的必要条件,因此必须明确式中各因素(拉力、直径和摩擦因数)对σr4和σ'r4大小关系的影响规律。
3.1 拉力
拉力大小由抽钉几何尺寸、摩擦因数等其他因素共同决定,不属于可改变σr4和σ'r4的独立变量,因此,对拉力采取定性而非定量分析。
3.1.1 F4、F5
σr4与F4和F5呈正相关,σ'r4与F4和F5无关,因此,增加F4和F5均有利于σr4>σ'r4成立。根据芯杆受力平衡已知,F4和F5之和始终等于F3+F6,但F4和F5的值未知,因此,拉力分析时无法单独看F4或F5,选择以F4/F5为横坐标(F4+F5的值固定),以σr4和σ'r4为纵坐标绘制关系曲线来图形化F4和F5对σr4和σ'r4的影响规律,如图11所示。F4/F5=1处,σr4有小于σ'r4的极小值,因此,F4和F5数值越接近,安装过程中出现掉头的概率越大。
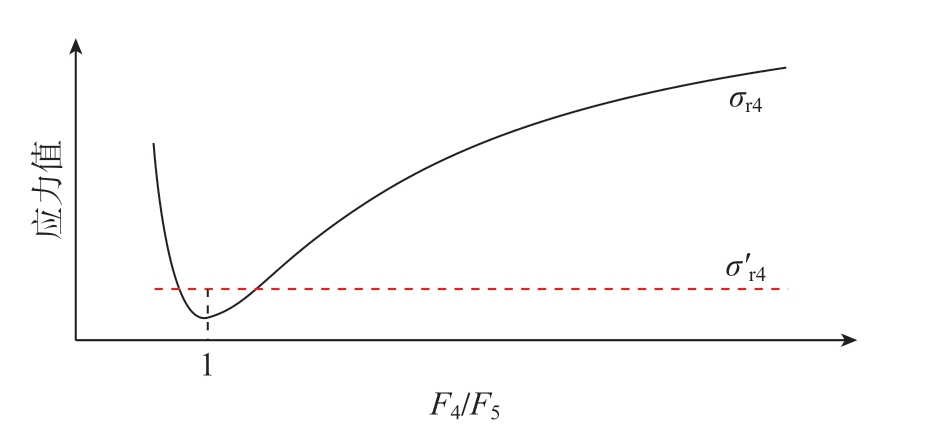
图11 不同F4/F5比值下,σr4和σ'r4的变化趋势
Fig.11 Trends of σr4 and σ'r4 under different F4/F5
3.1.2 F3
F3增加,σr4和σ'r4同时增加,且F3变化对于σr4和σ'r4值的变化幅度影响基本相同,即在图12中,F3增加,σr4和σ'r4曲线同时沿应力变大的方向移动,两者不会发生较大相对运动,σr4 < σ'r4的区间保持不变。

图12 不同F3下,σr4和σ'r4的变化趋势
Fig.12 Trends of σr4 and σ'r4 under different F3
3.1.3 F6
因为F6只影响σr4,不影响σ'r4,所以F6会改变σr4和σ'r4间的应力关系。如图13所示,F6增大,σr4曲线沿应力变大的方向移动,σ'r4曲线不变,两者发生明显相对运动。F6越小,出现σr4<σ'r4的可能性越大,且F6满足F6=F4+F5–F3,因此,F4+F5的值越接近F3,安装过程中出现掉头的概率越大。
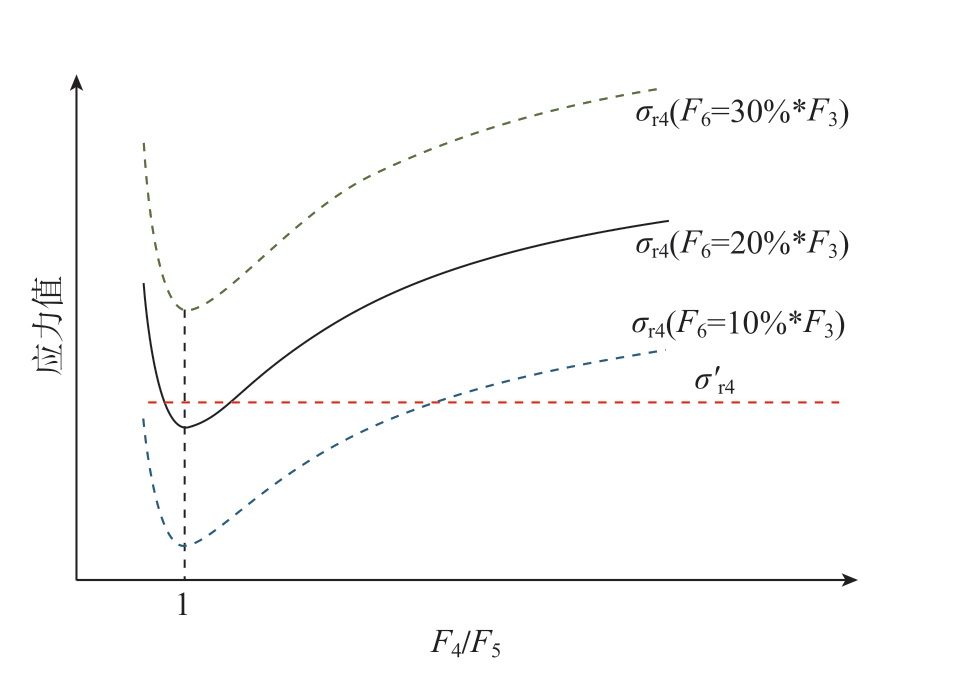
图13 不同F6下,σr4和σ'r4的变化趋势
Fig.13 Trends of σr4 and σ'r4 under different F6
3.2 直径
(1)直径d4、d5和d6。σr4与d4、d6呈正相关,与d5呈负相关,σ'r4与d4呈负相关,与d5和d6无关。
(2)成型套内外径d3i和d3o。如图14所示,分为3种情况:d3i不变,d3o变大;d3o不变,d3i变大;d3i、d3o同时变大但d3o–d3i的值不变。3种情况都会引起σr4和σ'r4同时增加,且σr4增加幅度> σ'r4,更有利于σr4>σ'r4,原因是d3i和d3o增加使得成型套和镦头接触面等效有效直径增大。

图14 不同d3i和d3o下,σr4和σ'r4的值
Fig.14 Values of σr4 and σ'r4 under different d3i and d3o
3.3 摩擦因数
在分析摩擦因数对最大应力σr4和σ'r4影响规律之前,首先给出一个假设:芯杆沿断颈槽扭断时的力矩M断不随摩擦因数改变而改变,然后用此假设来判断摩擦因数的影响规律,影响规律反过来又可以验证假设的可靠性。图15为不同摩擦因数下,拉力、扭矩、应力的变化趋势。
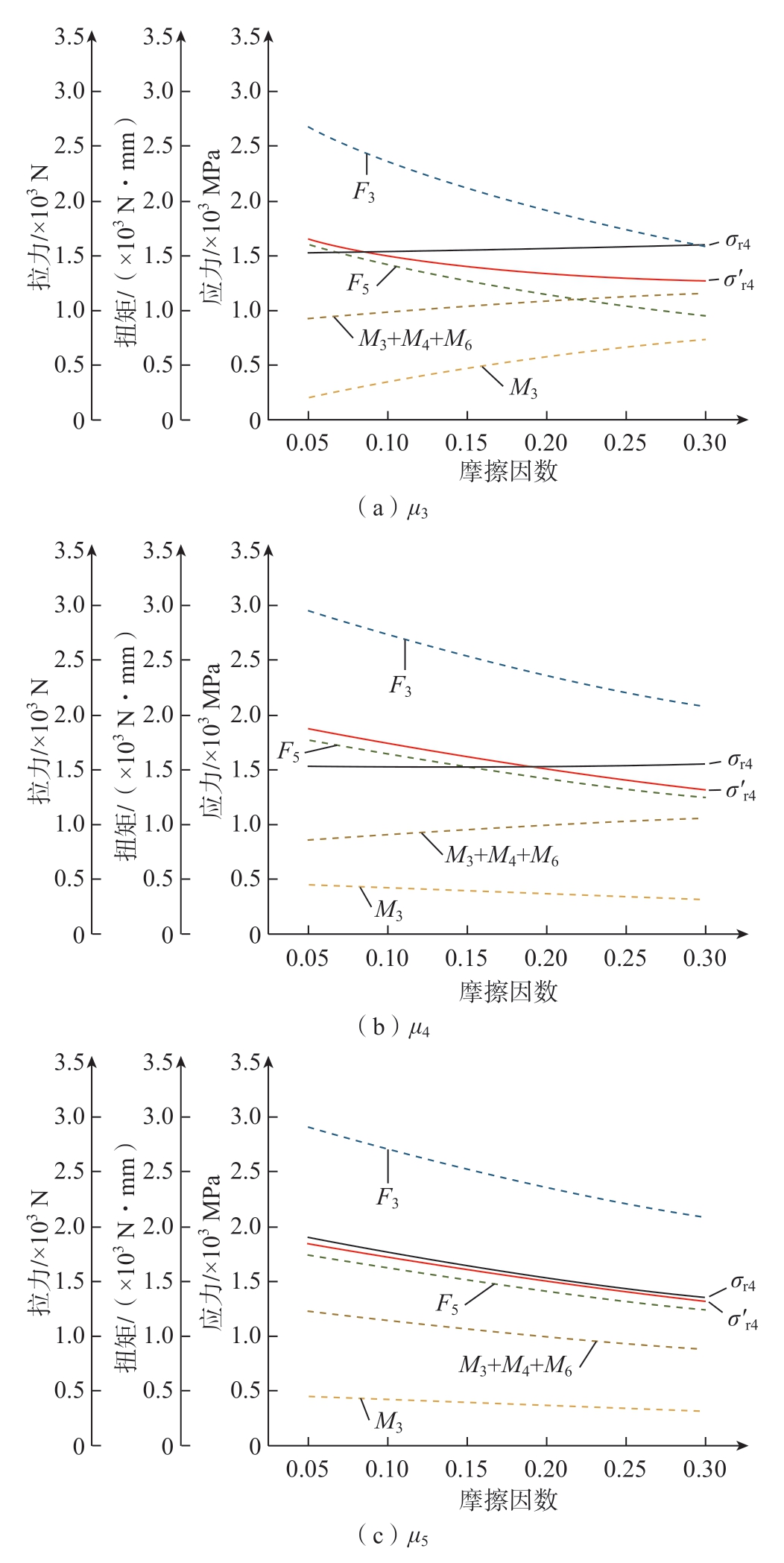
图15 不同摩擦因数下,拉力、扭矩和应力的变化趋势
Fig.15 Trends of tension, torque and stress under different coefficients of friction
(1)μ3。对此芯杆进行多次扭断试验,得到M断,为固定值。当输入扭矩M等于M断时,随μ3增加,F3和F5减小,M3和M3+M4+M6增加,如图15(a)所示。在F3减小和M3增大共同变化下,σ'r4减小了377 MPa,σr4在F5减小和M3+M4+M6增大共同变化下略有上升但变化不明显(数值变化过程见表1)。μ3增加,有利于σr4>σ'r4,但会明显降低对夹层的夹紧效果,夹紧力下降了40%,因此,在满足夹紧力要求的前提下,应适当增加μ3。
表1 应力值σr4、σ'r4和夹紧力随μ3、μ4和μ5变化对比
Table 1 Comparison of stress values σr4 and σ'r4 with the change of μ3, μ4 and μ5
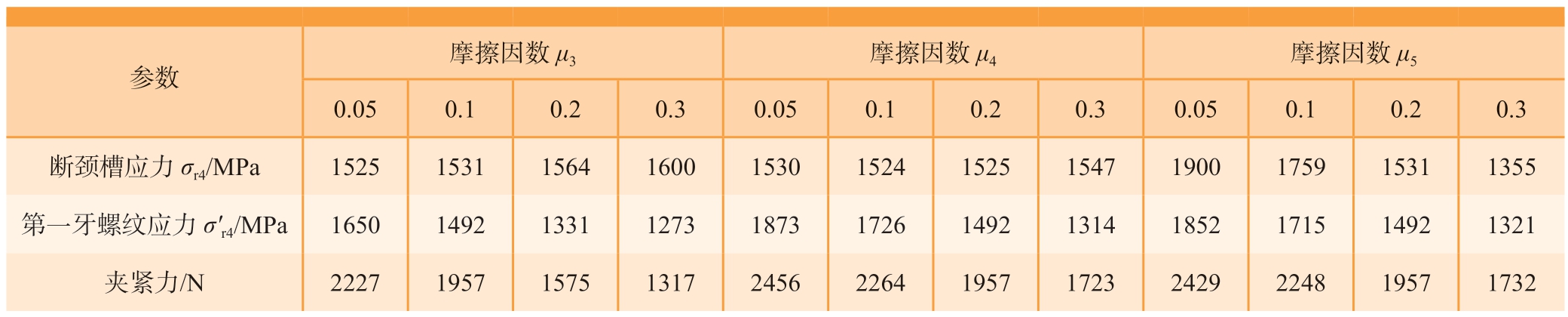
参数摩擦因数μ3摩擦因数μ4摩擦因数μ5 0.050.10.20.30.050.10.20.30.050.10.20.3断颈槽应力σr4/MPa152515311564160015301524152515471900175915311355第一牙螺纹应力σ'r4/MPa165014921331127318731726149213141852171514921321夹紧力/N222719571575131724562264195717232429224819571732
(2)μ4和μ6。μ4增加,F3、F5和M3减小,M3+M4+M6增加,σ'r4在F3和M3都减小的情况下减小;σr4在F5减小和M3+M4+M6增加共同变化下基本保持不变(图15(b))。μ6和μ4同理。μ4和μ6增加,同样带来一利一弊,利于避免镦头脱落的同时降低了夹紧力(30%)。
(3)μ5。μ5增加,F3、F5、M3和M3+M4+M6都减小,σ'r4和σr4的差值几乎不变,不会改善掉头。
断颈槽应力σr4对于μ3、μ4和μ6变化的敏感程度较低,因此本文认为假设合理,上述基于假设对μ3、μ4和μ6的影响规律的分析可靠。断颈槽应力σr4对于μ5变化的敏感程度高,μ5增加必定会增加扭断力矩M断的值,输入扭矩M到达M断值附近时,芯杆不会沿着断颈槽扭断,所以用假设分析μ5影响规律(图15(c))与实际情况不符,但即使M断随μ5改变,σ'r4和σr4的差值几乎不发生变化,因此μ5对σ'r4和σr4的影响规律的分析同样可靠。
4 结论
本文针对某结构类型大底脚螺纹抽钉芯杆强度计算方法进行研究,通过受力分析并基于材料力学第四强度理论,给出了芯杆断颈槽和第一牙螺纹处的最大应力表达式,式中的应力集中系数通过对芯杆的有限元分析获得。分析了拉力、直径和摩擦因数对最大应力的影响规律,得到以下结论。
(1)F4和F5的值越接近,F6越小,安装过程中出现掉头的概率越大,F3几乎不改变σr4和σ'r4的关系。
(2)摩擦因数μ5越大,芯杆沿断颈槽扭断时所需的力矩M断就越大,单独改变μ5不会改善掉头现象;μ3、μ4和μ6增加,所需的扭断力矩M断不发生明显变化,有利于避免掉头发生,但以降低夹紧力为代价,因此,在满足夹紧力要求的前提下,应适当增加μ3、μ4和μ6。
(3)增加成型套内外径d3i和d3o会降低夹紧力,但有利于避免掉头现象。
本文所建立的芯杆强度计算方法可避免抽钉安装过程中发生掉头失效,对于提升大底脚螺纹抽钉安装质量、连接可靠性和合格率,以及提升飞机的安全性能和经济效益具有重要意义。
[1] 曹增强, 张铭豪, 谭学才, 等.航空复合材料结构铆接技术综述[J].航空制造技术, 2023, 66(1/2): 26–37.CAO Zengqiang, ZHANG Minghao, TAN Xuecai, et al.Overview of riveting technology for aviation composite structure[J].Aeronautical Manufacturing Technology, 2023, 66(1/2): 26–37.
[2] 胡俊山, 张开富.力热耦合的复合材料干涉连接结构松弛演化与失效机理[J].机械工程学报, 2022, 58(1): 60–68.HU Junshan, ZHANG Kaifu.Relaxation evolution and failure mechanism of composite interferometric connection structures with mechanothermal coupling[J].Journal of Mechanical Engineering, 2022,58(1): 60–68.
[3] 孙阔.碳纤维复合材料滑动舱门刚度试验与仿真分析[J].材料导报, 2020, 34(S1): 161–163.SUN Kuo.Test and simulation analysis on stiffness of carbon fiber composite sliding door[J].Materials Reports, 2020, 34(S1): 161–163.
[4] 周何, 李小兵, 张婷, 等.航空发动机复合材料风扇叶片制造工艺应用进展[J].航空制造技术, 2022, 65(13): 84–91.ZHOU He, LI Xiaobing, ZHANG Ting, et al.Application progress on manufacturing technology of composite fan blades for aero-engine[J].Aeronautical Manufacturing Technology, 2022, 65(13): 84–91.
[5] 李海洲.复合材料连接件的参数化仿真和试验分析[D].哈尔滨: 哈尔滨工业大学, 2021.LI Haizhou.Parametric simulation and experimental analysis of composite connectors[D].Harbin: Harbin Institute of Technology, 2021.
[6] 刘风雷, 刘丹, 刘健光.复合材料结构用紧固件及机械连接技术[J].航空制造技术, 2012, 55(1/2): 102–104, 111.LIU Fenglei, LIU Dan, LIU Jianguang.Fasteners and mechanical connection technology for composite structures[J].Aeronautical Manufacturing Technology, 2012, 55(1/2): 102–104, 111.
[7] 孙钢.抽芯铆钉用于复合材料夹层的研究与探讨[J].航空标准化与质量, 2009(4): 16–18.SUN Gang.Research and discussion on the application of corepulling rivets in composite sandwich[J].Aeronautic Standardization &Quality, 2009(4): 16–18.
[8] 魏景超.复合材料结构新型紧固件连接强度与失效机理[D].西安: 西北工业大学, 2014.WEI Jingchao.Strength and failure mechanisms of bolted composite joints with new fastener[D].Xi’an: Northwestern Polytechnical University, 2014.
[9] 李荣霞.大底脚螺纹抽钉铆接工艺研究[J].科技创新与应用, 2016(16): 113.LI Rongxia.Study on rivet drawing process of large foot thread[J].Technology Innovation and Application, 2016(16): 113.
[10] 檀甜甜, 杨鹏, 曹娜, 等.碳纤维复合材料结构件在不同铆接方式下的连接强度对比分析[J].航空精密制造技术, 2021, 57(3):14–18.TAN Tiantian, YANG Peng, CAO Na, et al.Comparative analysis of connection strength of carbon fiber composite structural parts under different riveting methods[J].Aviation Precision Manufacturing Technology, 2021, 57(3): 14–18.
[11] LI S P, ZHANG S G, LI H, et al.Numerical and experimental investigation of fitting tolerance effects on bearing strength of CFRP/Al single-lap blind riveted joints[J].Composite Structures, 2022, 281: 115022.
[12] 西田正孝.应力集中[M].李安定, 译.北京: 机械工业出版社,1986.NISHIDA Masataka.Stress concentration[M].LI Anding, trans.Beijing: China Machine Press, 1986.
[13] 侯世远.螺纹联接松动机理研究[D].北京: 北京理工大学,2015.HOU Shiyuan.Study on mechanism of loosening of threaded connection[D].Beijing: Beijing Institute of Technology, 2015.
[14] 邬杰.螺纹连接结构横向松动寿命预测模型研究[D].北京:北京理工大学, 2019.WU Jie.Research on prediction model of transverse looseness life of threaded joint structure[D].Beijing: Beijing Institute of Technology,2019.
[15] 王桢.螺栓连接结构抗松动性能评价指标研究[D].北京:北京理工大学, 2021.WANG Zhen.Research on evaluation index of anti-looseness performance of bolted joints[D].Beijing: Beijing Institute of Technology,2021.