随着航空航天等尖端技术的不断推动,复合材料的制备及其成型技术日渐成熟[1],而编织技术因其简单稳定、自动化程度高和近净成形的特点,广泛用于制备复合材料的各种三维纺织预成型体[2]。复合材料编织预成型体无须任何连接或切割,就能得到质量更轻的复杂零件,该零件不仅能够承受不同载荷,也具有更高的损伤容限,因而更加稳定可靠[3–6]。在复合材料的编织过程中,预成型体由顺时针运动和逆时针运动的纱线相互交叉缠绕形成,其中,编织角是纱线与芯模轴线形成的角度,复合材料能否拥有期望的机械性能与编织角的误差值有很大关系。目前,在机器人牵引异形结构芯模的编织过程中,如何合理地对机器人牵引速度进行控制来保证编织角稳定成为亟须解决的关键问题之一。
编织角作为复合材料预成型体的一个重要参数,研究者进行了一系列有关编织角的研究。Nishimoto等[7]提出了圆柱形编织织物编织角的阶跃响应模型,试验表明,编织角会影响织物的弯曲弹性模量和最大弯曲应力等机械性能,可以通过改变编织角来设计不同的机械性能。Tate等[8]通过试验表明,材料的拉伸强度、模量、泊松比等都与编织角有关。
但是,在对芯模进行编织时,经常会出现编织角难以达到期望值的情况,研究人员通过对编织过程中牵引速度的调整来修正编织角。舒展翔[9]给出了速度曲线反解算法,运用二分法来寻找目标卷曲速度,通过控制卷曲速度来增大编织部位的编织角,达到增大构件强度的目的。陈燕婷等[10]研究了二维编织机的运动规律,提出调整等截面芯轴的移动速度来减少收敛长度的波动幅度,但是这种速度控制方法局限于等截面芯模。吴修可等[11]通过对编织工艺进行分析,建立了牵引速度与编织角、覆盖率等参数的数学模型。王晓明等[12]通过数学建模的方法得出,改变二维编织时的卷绕速度,实际编织角会逐渐向期望的编织角变化。Du等[13]发现,编织直径变化时会产生极其不规则的编织角,提出改变轴向速度来确保编织角稳定,但并没有给出相应的数学模型。Chi等[14]得出了异形芯模编织不稳定阶段纱线在芯模上形成的编织长度与时间的关系,并通过两个速度分别保证收敛长度和织物的编织长度,但是在保证织物长度时需要再次调整速度,这会导致编织角波动。
在异形结构芯模编织的过程中,编织点平面到编织环平面之间的距离为收敛长度,由于芯模的半径连续变化,如果对收敛长度不进行调整,则得到的编织角与期望值间会存在较大的误差。使用机器人调整收敛长度的过程比较复杂,同时在对异形结构芯模编织时,通过多次启停编织设备来调整收敛长度会严重影响生产效率与产品质量,并且在编织过程中存在不稳定阶段,因此很难设计出异形结构芯模的编织模式。
本文提出一种适用于编织异形结构芯模的机器人牵引速度及推进距离的控制策略,建立了编织不稳定阶段机器人牵引速度的数学模型,通过控制牵引速度使收敛长度达到期望收敛长度,同时使编织进入稳定状态,然后在编织稳定状态下通过期望编织速度对机器人推进芯模的距离进行控制,在保证编织角稳定的同时通过机器人推进距离对编织长度进行补偿,使芯模上编织长度达到预期长度,同时整体的编织角误差更小,对于变截面任意曲率芯模的编织具有重大意义。
1 牵引速度模型
图1所示为云路复材144锭三维径向编织机及KUKA六自由度机器人牵引装置,机器人夹持芯模以设定的轨迹和计算出的牵引速度推进,纱线从携纱器出发穿过导向环,形成一段收敛距离后覆盖在芯模表面,形成复合材料预成型体。编织过程如图2所示,编织机的携纱器按照设定的转速ω携带纱线沿着编织机内的轨道做近似圆周运动,机器人则以设定的轨迹保证芯模时刻垂直于编织点平面,同时以牵引速度V进给。
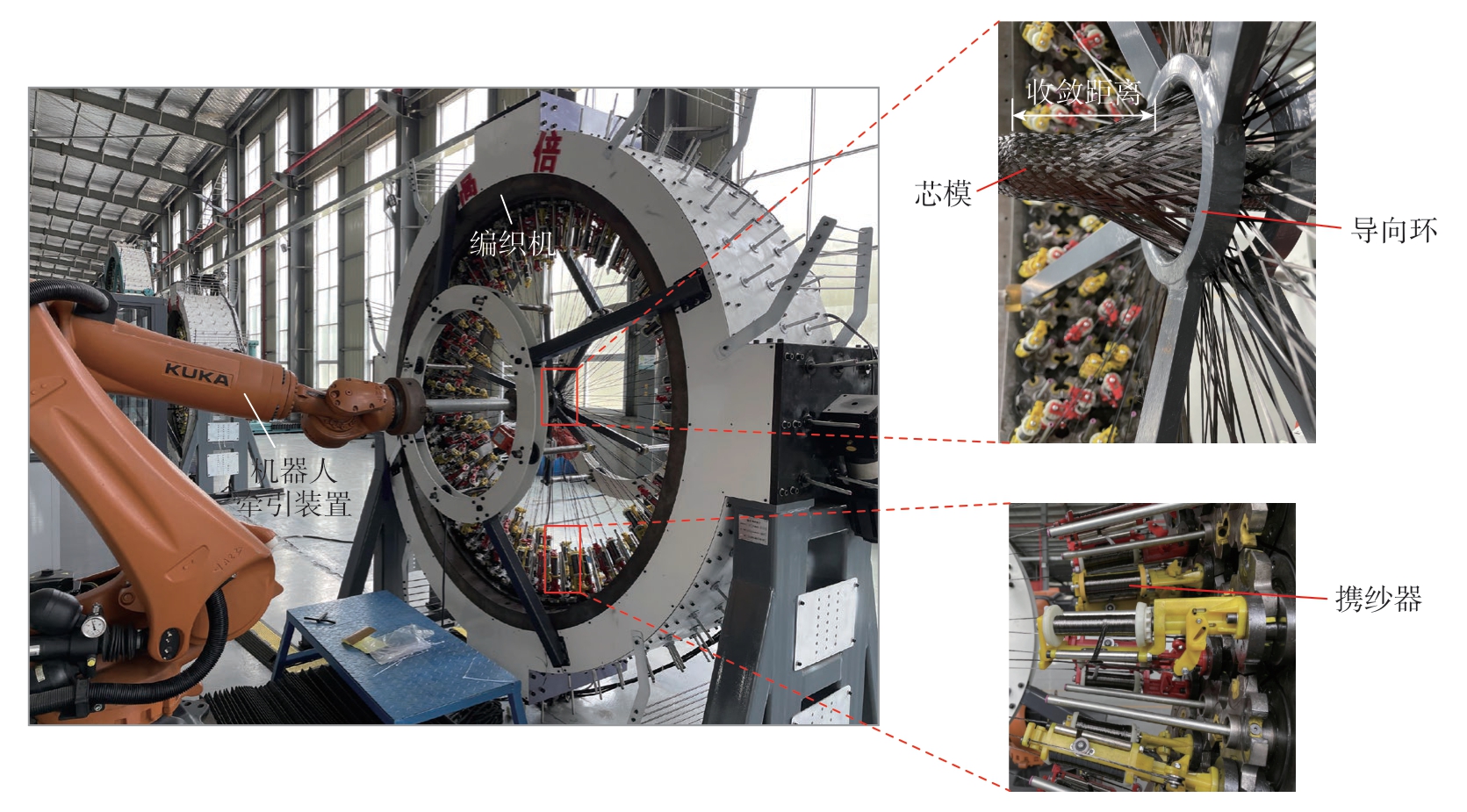
图1 KUKA六自由度机器人与云路复材144锭三维径向编织机
Fig.1 KUKA six-degree-of-freedom robot and Yunlu composite 144-spindle 3D radial braiding machine

图2 编织过程及芯模离散化
Fig.2 Braiding process and mandrel discretization
1.1 模型假设
对于异形芯模的编织,本文提出的模型基于以下假设:
(1)忽略纱线间及纱线与编织环间的摩擦力和相互作用力;
(2)纱线厚度忽略不计;
(3)纱线与芯模表面完全贴合,且编织在芯模上的纱线不发生滑动;
(4)忽略携纱器编织过程的蜿蜒运动;
(5)不考虑机器人轨迹的规划过程,默认机器人夹持芯模时刻垂直通过编织点所在平面。
1.2 等效芯模
将横截面积变化的芯模等效为长度相等的N个离散圆柱体。如图2所示,对芯模进行离散化处理,分为多段进行计算,同时将O(i–1)与O(i)之间的芯模形状近似为圆柱体,圆柱体的长度固定为d,则圆柱体半径的计算公式为
式中,rO(i–1)和rO(i)分别表示在O(i–1)与O(i)处芯模截面的半径。
1.3 数学模型推导
编织角与导向环半径、芯模半径及收敛长度有关,满足以下数学关系,即
式中,θ为编织角,表示预成型体上纱线与牵引速度方向上芯模轴线所形成的角度;R为导向环半径;r为该编织时刻芯模的半径;h为收敛长度。编织时由于芯模的横截面积不断变化,由式(2)可以看出,在芯模半径变化时,需要对收敛长度进行调整才能保证编织角稳定。但编织过程中编织机处于连续工作状态,通过启停编织机对收敛长度反复调整难以实现。而编织角与牵引速度满足式(4)所示关系,故最好通过调整牵引速度来保证编织角稳定。
异形芯模的编织过程分为编织不稳定阶段和编织稳定阶段,刚开始编织时处于编织不稳定阶段,等收敛长度到达期望收敛长度时,对应的速度会到达期望编织速度,进入编织稳定状态;在编织不稳定阶段,牵引速度V由编织速度Vb与编织点移动速度Vp组成,且满足
在编织稳定阶段,编织点不再移动,机器人夹持芯模推进的牵引速度V=Vb,Vp=0;同时编织角与携纱器圆周速度和编织速度满足以下数学关系,即
当编织角等于期望编织角θe时,编织稳定阶段的期望编织速度Ve为
当第i段编织时,由于半径突然变化,收敛长度仍然为h0,通过式(2)和(4)可以得出突变编织速度Vb0为
每段开始编织时,h=h0。同时,在编织不稳定阶段,收敛长度在很短一段时间Δt内的变化长度与编织点移动速度的关系满足:
将微分方程转换为一阶线性微分方程得:
求得微分方程的通解为
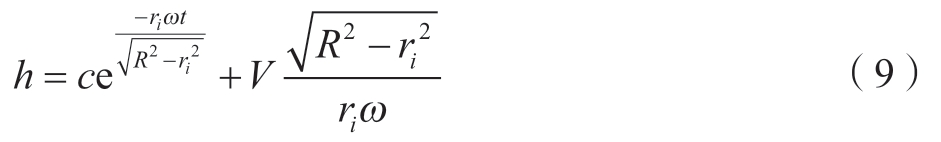
式中,c为常数。
代入初始条件t=0,h=h0,解得
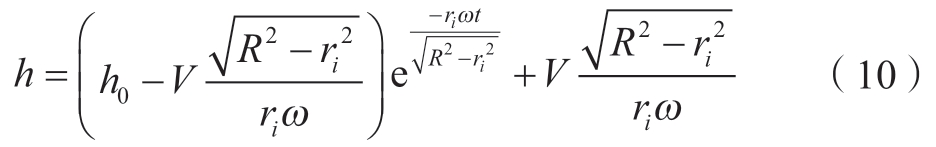
对时间t求导得编织点移动速度Vp为
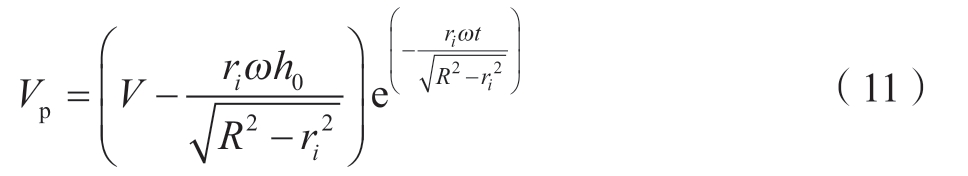
由式(3)和(11)可得织物的编织速度Vb与时间t的关系为
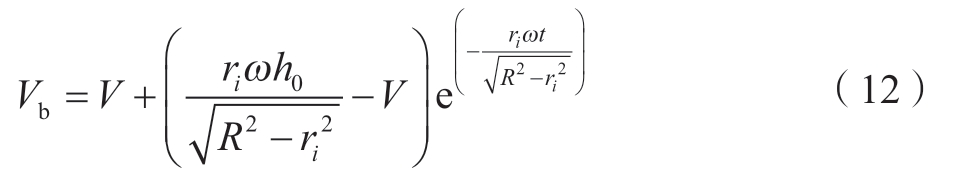
由上述方程式可知,机器人牵引芯模进行编织过程中,在某一时间点,机器人的牵引速度V对织物的编织速度Vb有很大的影响,同时通过式(5)可以看出,牵引速度对编织角也有很大影响。
2 牵引速度控制优化
现有研究中在编织异形结构芯模时,确定初始收敛长度后,通过调整牵引速度使编织速度趋于期望编织速度,对应的收敛长度趋于期望的收敛长度,使编织进入稳定状态。但是为保证每段芯模上织物的编织长度趋于稳定,之后需要再次调整速度使每段芯模的期望收敛长度向初始收敛长度调整,这会导致编织速度不等于期望编织速度,使得编织再次进入不稳定状态,编织角出现波动。
本文基于动态收敛长度的思想,确定初始收敛长度后,通过调整牵引速度使编织速度达到期望编织速度,收敛长度达到期望收敛长度,进入编织稳定状态后以期望编织速度继续运行,并且不对收敛长度进行回调,使编织一直处于编织稳定状态,保证编织角的稳定,然后通过机器人推进距离的补偿保证织物的编织长度,并且当前段的期望收敛长度作为下一段的初始收敛长度。
根据图2的方式将芯模分为多段长度为d的圆柱体后,在编织处于不稳定状态时,机器人推进的相同时间内,推进距离d1和芯模上形成的编织长度l1不相等,而进入编织稳定状态后,相同时间内机器人推进距离d2与芯模上的编织长度l2相等。欲使每段长度为d的芯模上也形成长度d的织物长度并且保证编织角的稳定,只能在进入编织稳定状态后通过调整机器人的推进距离d2来弥补不稳定阶段造成的偏差。
牵引速度控制流程如图3所示。首先使机器人推进d1=d/2,通过调整机器人牵引速度V使突变编织速度Vb0快速趋近期望编织速度Ve,同时使收敛长度h=he,在此期间芯模上织物的编织长度为l1;后半段机器人以期望牵引速度Ve运行,再根据l1与d1的大小对机器人后半段推进的距离进行对应的调整得到d2,最终使芯模上形成的编织长度稳定为d。

图3 牵引速度控制流程图
Fig.3 Control flow diagram of take-up speed
每段编织开始时的起始编织速度为Vb0,收敛长度为h0,编织稳定后编织速度Vb1=Ve,收敛长度为h1。并且第i段编织完成后稳定的Vi(b1)和hi(1)分别等于第i+1段编织起始的Vi+1(b0)和hi+1(0),也就更加保证了编织的连续性,并且使得在编织任意曲率变化的芯模时也能对其编织角进行严格把控。
设每段芯模所需的牵引速度为V1,结合式(12),根据机器人的运行时间d1/V1和期望编织速度Ve可求出该段需要的牵引速度V1;对式(12)求积分,得到机器人牵引速度为V1时,芯模上形成的编织物长度l1为
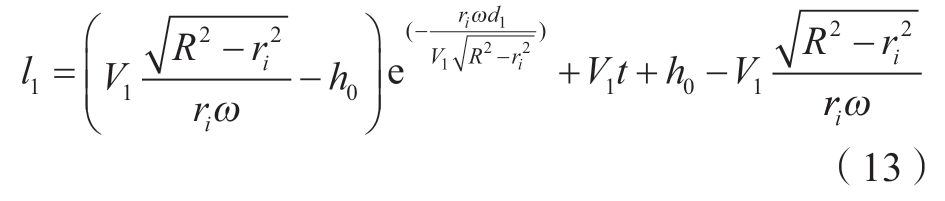
由式(10)可得稳定后的收敛长度h1为
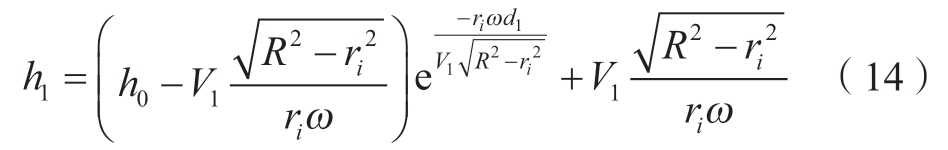
式中,d1=d/2。此时,已知l1与d1的大小满足下列关系,即
要保证在调整牵引速度时,不能使l1大于d,因此还要满足以下约束条件:
对应的速度约束为
因此可得后半段机器人推进距离d2为
3 试验验证
以异形结构的芯模(图2)为例,验证提出的牵引速度控制策略的适用性。芯模起始端的截面半径为26 mm,截止端的截面半径为59 mm,将此芯模离散成10段圆柱体后分段控制,图4为离散后芯模的几何形状(芯模离散后各段长度d=50 mm),以及将芯模离散后得到的各段芯模的半径长度。试验中用到的设备有球面编织机、六自由度工业机器人。其中球面编织机含有144个锭子,每个锭子上有一个携纱器,编织机的运动系统包括4个伺服电机、2个振动电机及其各自的控制器。在编织过程中,主机转速为320 r/min,锭子转动的角速度为0.07 rad/s,振动电机频率为46 Hz。

图4 芯模几何形状
Fig.4 Mandrel geometry
编织角为60°时,通过本文的控制方法得出的动态收敛长度变化如图5所示,每段的期望收敛长度作为下一段的初始收敛长度。计算得出机器人各段牵引速度和期望速度,如图6所示。

图5 异形结构芯模各段对应的收敛长度
Fig.5 Convergence length corresponding to each segment of special-shaped mandrel
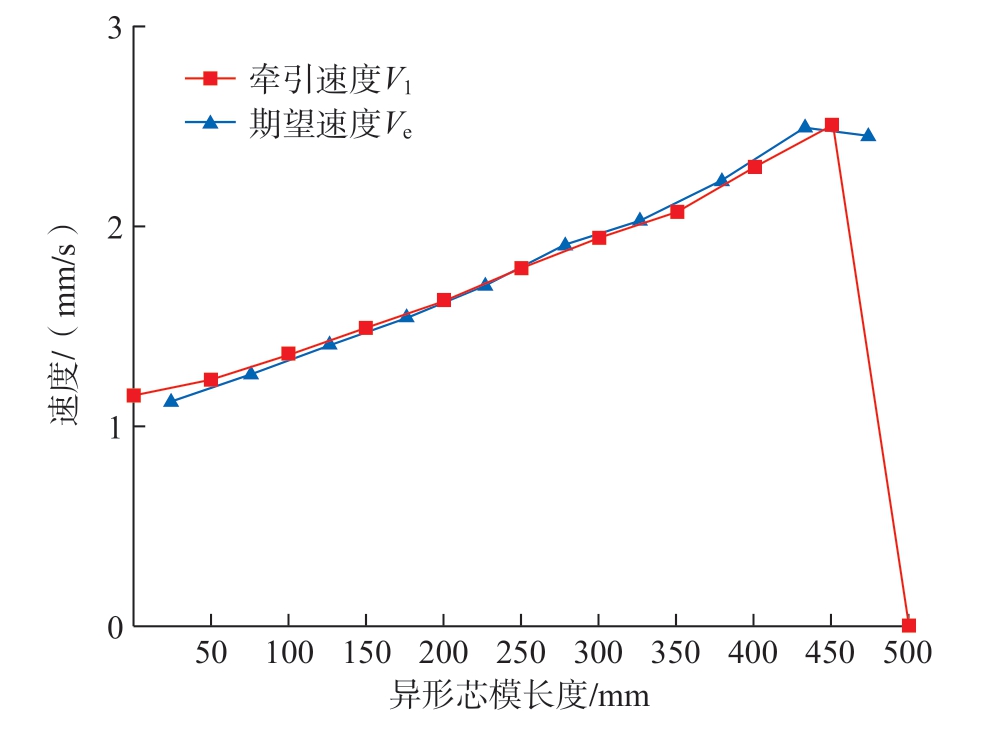
图6 异形结构芯模各段对应的机器人牵引速度与期望速度
Fig.6 Take-up speed and expected speed corresponding to each segment of the special-shaped mandrel
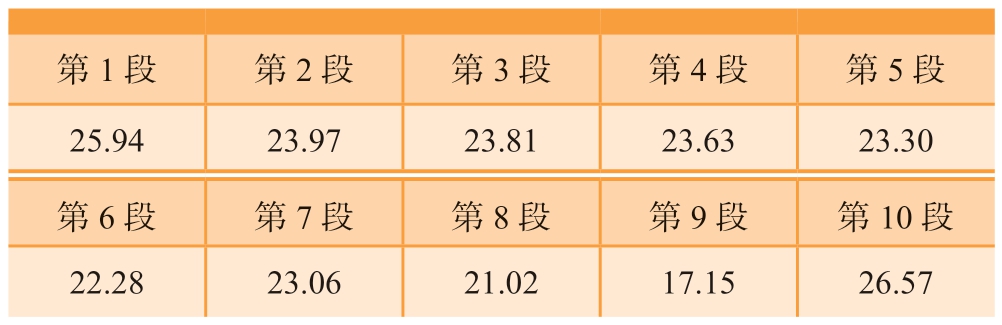
编织各段芯模时,设置机器人第1段推进距离统一为d1=25 mm,通过图6的牵引速度计算出第2段推进距离d2,如表1所示。通过所得数据设置机器人的牵引速度V1和推进距离d1,使各段芯模快速调整到期望速度Ve,同时设置机器人牵引速度为V1,用推进距离d2来保持织物的编织长度。整个编织过程是连续的,机器人各段的牵引速度V1和期望牵引速度Ve,以及推进距离d1和d2在芯模确定后就已经确定。
表1 异形结构芯模各段机器人推进距离
Table 1 Robot advancing distance of each segment of the special-shaped mandrel mm
第1段第2段第3段第4段第5段25.9423.9723.8123.6323.30第6段第7段第8段第9段第10段22.2823.0621.0217.1526.57
图7(a)为使用传统控制方法对图4所示异形结构芯模进行编织后的实物图片及编织角测量。可以看出,传统控制方法由于编织过程中没有考虑异形结构芯模截面半径的变化,导致编织出的预成型体上编织角非常不稳定,而且编织角误差很大;图7(b)为使用本文提出的控制方法对异形芯模进行编织后的实物图片及编织角测量。可以明显看出,采用本文控制方法编织出的预成型体结构紧密,编织角稳定,误差很小。

图7 不同控制方法下的预成型体及其编织角
Fig.7 Preforms and their braiding angles under different control methods
通过编织角测量工具分别对图7编织后的预成型体上随机一相同的点进行编织角的测量并进行对比,如图8所示。
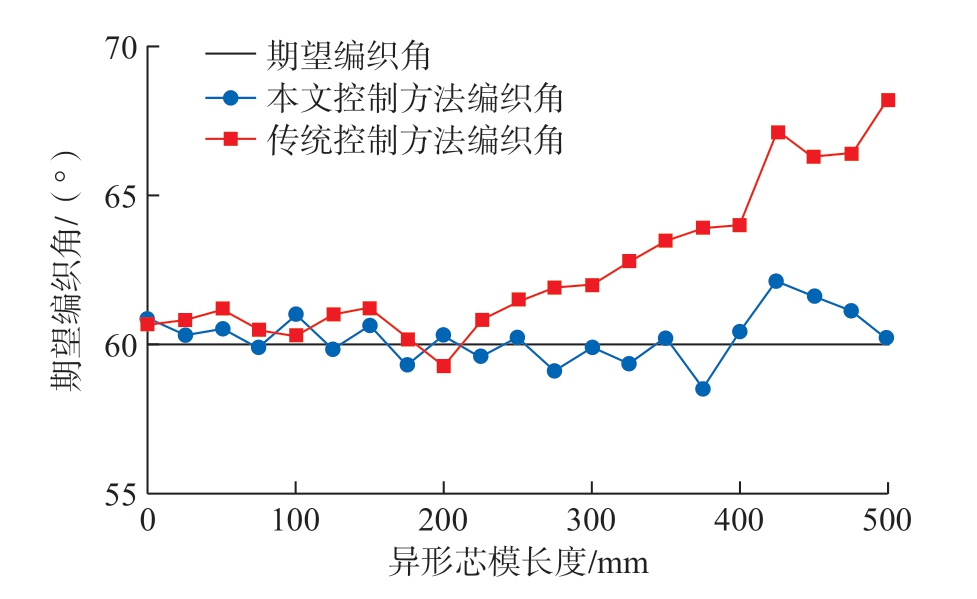
图8 不同控制方法的编织角的对比
Fig.8 Comparison of braiding angles of different control methods
可以看出,传统控制方法没有考虑异形结构芯模截面半径的变化,编织角与期望编织角最大相差8°以上,编织角不稳定也就导致预成型体的质量不高;而本文提出的控制方法考虑了芯模半径方向的变化,并通过调整牵引速度使编织角稳定,可以看出,编织角与期望编织角最大相差在±3°以内,由此可知预成型体的编织质量很高,对异形芯模以及任意曲率芯模的编织有重要意义,异形结构芯模的编织更高效、编织角更准确、复合材料性能更优良。
4 结论
本文提出了一种编织异形结构芯模的机器人牵引速度以及推进距离的控制策略。针对异形结构芯模编织过程中编织角不稳定的情况,提出的控制策略如下:
(1)将异形结构芯模离散化后,求解出所需的收敛长度、机器人牵引速度以及推进距离;
(2)在动态收敛长度的基础上,通过机器人牵引速度和推进距离的联合控制来保证编织角的稳定,降低编织角的误差在±3°以内。
通过试验证明,本文提出的控制方法能够有效减小异形结构芯模编织过程中的编织角误差,同时编织出的预成型体质量优良,能够达到现实生产中的要求。
[1] 王巧玲, 魏栋, 李光俊, 等.FRP复合材料管材航空应用及成型技术研究现状[J].航空制造技术, 2020, 63(22): 92–101.WANG Qiaoling, WEI Dong, LI Guangjun, et al.Application of FRP composite tubes in aerospace field and developments of manufacturing technology: A review[J].Aeronautical Manufacturing Technology, 2020,63(22): 92–101.
[2] NA W J, AHN H C, JEON S Y, et al.Prediction of the braid pattern on arbitrary-shaped mandrels using the minimum path condition[J].Composites Science and Technology, 2014, 91: 30–37.
[3] ABOUNAIM M.Process development for the manufacturing of flat knitted innovative 3D spacer fabrics for high performance composite applications[M].Elsevier Science, 2010.
[4] HUFENBACH W, BÖHM R, KROLL L, et al.Theoretical and experimental investigation of anisotropic damage in textile-reinforced composite structures[J].Mechanics of Composite Materials, 2004, 40(6):519–532.
[5] POTLURI P, RAWAL A, RIVALDI M, et al.Geometrical modelling and control of a triaxial braiding machine for producing 3D preforms[J].Composites Part A: Applied Science and Manufacturing, 2003,34(6): 481–492.
[6] SONG S J, WAAS A M, SHAHWAN K W, et al.Braided textile composites under compressive loads: Modeling the response, strength and degradation[J].Composites Science and Technology, 2007, 67(15–16): 3059–3070.
[7] NISHIMOTO H, OHTANI A, NAKAI A, et al.Prediction method for temporal change in fiber orientation on cylindrical braided preforms[J].Textile Research Journal, 2010, 80(9): 814–821.
[8] TATE J S, KELKAR A D, WHITCOMB J D.Effect of braid angle on fatigue performance of biaxial braided composites[J].International Journal of Fatigue, 2006, 28(10): 1239–1247.
[9] 舒展翔.轴向梯度结构环形编织物设计方法研究[D].杭州:浙江理工大学, 2019.SHU Zhanxiang.Study on design method of annular braided fabric with axial gradient structure[D].Hangzhou: Zhejiang Sci-Tech University,2019.
[10] 陈燕婷, 李雪清, 孙志宏, 等.分叉结构管状编织物编织机的运动分析[J].东华大学学报(自然科学版), 2019, 45(1): 109–114.CHEN Yanting, LI Xueqing, SUN Zhihong, et al.Motion analysis of tubular braided fabric knitting machine with bifurcated structure[J].Journal of Donghua University (Natural Science), 2019, 45(1): 109–114.
[11] 吴修可, 孟婥, 姚灵灵, 等.基于齐次坐标变换的编织工艺及芯模牵引轨迹分析[J].东华大学学报(自然科学版), 2019, 45(3): 425–430.WU Xiuke, MENG Chuo, YAO Lingling, et al.Analysis of braiding process and mandrel’s traction trajectory based on homogeneous coordinate transformation[J].Journal of Donghua University (Natural Science Edition),2019, 45(3): 425–430.
[12] 王晓明, 邹婷, 李超婧, 等.基于编织点起始位置及牵拉速度变化的编织角预测模型[J].纺织学报, 2015, 36(9): 28–33.WANG Xiaoming, ZOU Ting, LI Chaojing, et al.Predicting model for braiding angle based on initial braiding height and take-up speed[J].Journal of Textile Research, 2015, 36(9): 28–33.
[13] DU G W, POPPER P.Analysis of a circular braiding process for complex shapes[J].The Journal of the Textile Institute, 1994, 85(3): 316–337.
[14] CHI X F, LI Q Y, YAN H X, et al.Robot trajectory optimization control of braiding for three-dimensional complex preforms[J].Journal of Engineered Fibers and Fabrics, 2021, 16: 155892502110432.