工业机器人作为工业领域常用的自动化设备，可用于执行各种生产任务。工业机器人能够完成高精度、高效率和高可靠性的生产任务，提高生产效率，在智能制造、“工业4.0”等领域发挥着重要的作用[1]。同时，随着虚拟仿真技术和数字孪生技术的迅速发展[2]，工业机器人常常与数字孪生技术结合。数字孪生技术是将物理实体与其数字化虚拟模型相结合的创新方法，在工业机器人领域，数字孪生技术能够模拟、优化和监控机器人的运行，提高其效率和可靠性[3]。通过实时数据和模拟的反馈，数字孪生技术能够使工业机器人的设计、维护和工作过程更加精确，同时保证其可靠性。
但是，随着工业机器人的使用损耗、零部件的磨损以及实际场景的不断更新等，使得原先建立的数字孪生模型难以长期保持高度仿真精度，因此工业机器人的数字孪生模型更新研究尤为迫切[4]。
目前，针对数字孪生模型的更新问题，国内外研究的主要处理方式是利用改进的最小二乘法或专用模型对其进行函数拟合。黄华等[5]提出了一种带有遗忘因子的递推最小二乘法（Recursive least squares，RLS），对数控机床进给系统的数字孪生模型参数进行自适应更新，提高了数字孪生模型仿真结果和物理实体运行结果的一致性。Wu等[6]提出了一种基于核心的在线极限学习机，用于构建电力变压器的数字孪生模型，并使其通过学习新数据的输入输出关系进行模型自我更新，以保持数字孪生模型的精度。刘新宇等[7]提出了一种改进的自适应加权权重的渐消记忆RLS，其主要目标是实现高速列车悬挂系统的数字孪生模型的实时自适应修正，能够有效解决运行过程中随机波动和动态参数突变对模型参数同步的影响。Liu等[8]提出了一种基于记忆遗忘模型的数字孪生知识更新方法，用于解决复杂产品定制过程面临的高数据管理成本和数据浪费问题。
已报道的数字孪生模型更新方法研究大都基于固定的运行场景，通过函数拟合方法对关键参数进行更新。当模型样本特征过大或拟合函数非线性时，传统方法会受到限制，导致优化效果不理想。
工业机器人的功能和动作主要通过多个关节的角度变化实现，因此具有较高的自由度。相比于其他工业设备，工业机器人更加强调灵活性，需要多个关节协调动作。此外，由于其工作场景多变的特点，对工业机器人数字孪生模型进行更新研究有着迫切需求。然而，工业机器人的数字孪生模型更新将会面临模型样本特征过大、多重共线性等严重影响更新效果的难题。
然而，当前关于数字孪生模型更新方法的研究仍然匮乏，特别是缺乏针对工业机器人这类特殊装备的数字孪生模型更新方法。已有方法大多是为特定系统或结构而设计的专用模型，通用性较差。在处理不同目标类型数字孪生模型的更新问题时，一般难以直接应用或通过简单的调整再应用，通常均需要为特定模型定制解决方案，难以有效应用于工业机器人的数字孪生模型更新。
作为一种机器学习方法，深度强化学习能够处理高维度和非结构化数据，可直接采用原始数据进行学习，通过让智能体与工作场景不断交互，学习最优决策策略，最大化预期的累积奖励。智能体通过观察环境状态、执行动作和接收奖励来学习，这些经验被用于不断优化策略，使智能体在特定任务上的表现逐步提高[9–10]。近年来不断有学者将深度强化学习算法与数字孪生技术结合进行策略优化[11–12]或轨迹优化[13]等。目前尚无文献报道将深度强化学习应用于数字孪生模型更新，提高模型仿真精度。
为此，本文利用深度确定性策略梯度（Depth deterministic strategy gradient，DDPG）算法处理大规模连续动作空间问题的卓越性能，提出了基于深度强化学习的工业机器人数字孪生模型更新方法。以工业机器人为研究对象，利用DDPG算法在深度学习和强化学习上的优点，有效处理具有复杂和大规模参数的目标对象的数字孪生模型优化问题。构建了工业机器人数字孪生模型框架，并结合DDPG设计了工业机器人数字孪生模型更新算法，对深度强化学习算法进行了关于工业机器人的适应性改进，为数字孪生模型更新提供了更为通用的方法。所构建更新模型配合传感器实时采集数据，进行数字孪生模型的参数更新。以某型工业机器人为对象开展了仿真试验，验证了所提模型更新方法的有效性。
1 工业机器人数字孪生模型框架
本文设计的工业机器人数字孪生模型框架如图1所示，主要由物理空间、数据层、数字孪生空间和服务层组成。其中，物理空间由工业机器人实体及由多种传感器构成的感知模块、网络模块、控制模块组成；数据层主要负责处理和传输数据，对从物理空间和数字孪生空间采集到的数据进行清洗、融合等处理，以确保数据的准确性和可靠性；数字孪生空间包括机器人虚拟模型和算法更新模块；服务层具备人机交互功能，用户能够直接进行状态监控和参数设置等操作。
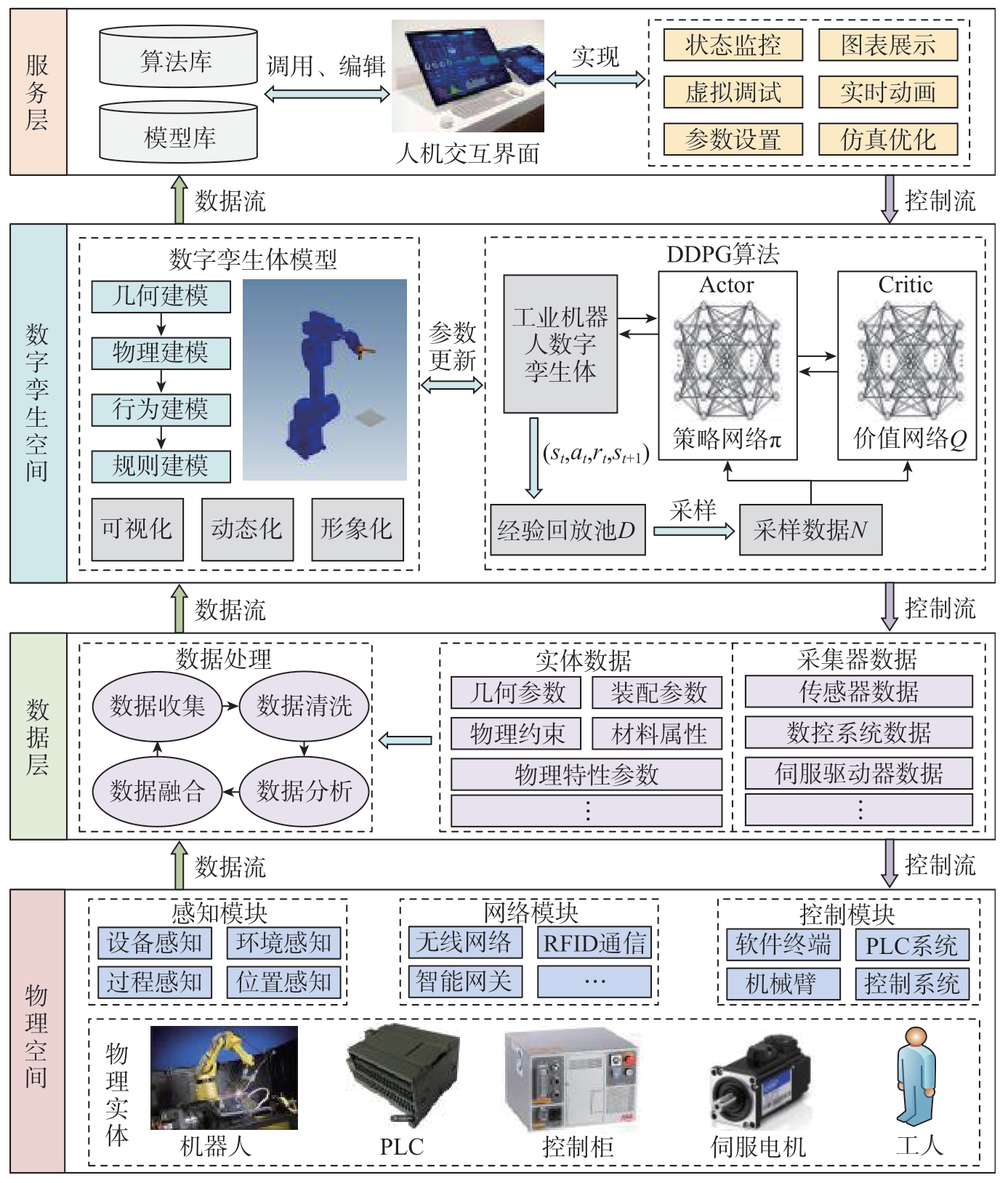
图1 工业机器人数字孪生模型框架
Fig.1 Industrial robot digital twin model framework
通过实时采集传感器、控制器等设备的物理数据，并经过适当处理，将处理后的数据输入到数字孪生空间。在数字孪生空间中，数字孪生模型能够实时监测和预测物理实体的运行状态。同时，用户可以通过用户层与数字孪生模型进行直接交互。利用数字孪生模型在虚拟空间中进行调试，并根据所获取的孪生虚拟数据为工业机器人提供决策反馈，从而形成整个过程的闭环机制。这种机制可以通过数字孪生的五维表达式[14]表示。
式中，RFDT表示工业机器人数字孪生框架；RPS表示工业机器人物理空间；RVS表示工业机器人数字孪生空间；RFDTD表示数字孪生模型仿真孪生数据；VRIS表示虚实交互空间，即服务层；CN表示连接。
2 基于深度强化学习的工业机器人数字孪生模型更新
2.1 模型更新方法
本文建立的工业机器人数字孪生模型，旨在通过实测数据完成对物理实体与虚拟模型之间的交互，以实现数字孪生模型的更新。首先将工业机器人数字孪生模型更新问题描述为马尔可夫决策过程（Markov decision process，MDP），使其能够被深度强化学习算法识别，再使用DDPG算法对其进行优化更新。在此基础上，提出了基于DDPG的工业机器人数字孪生模型参数更新框架，如图2所示。
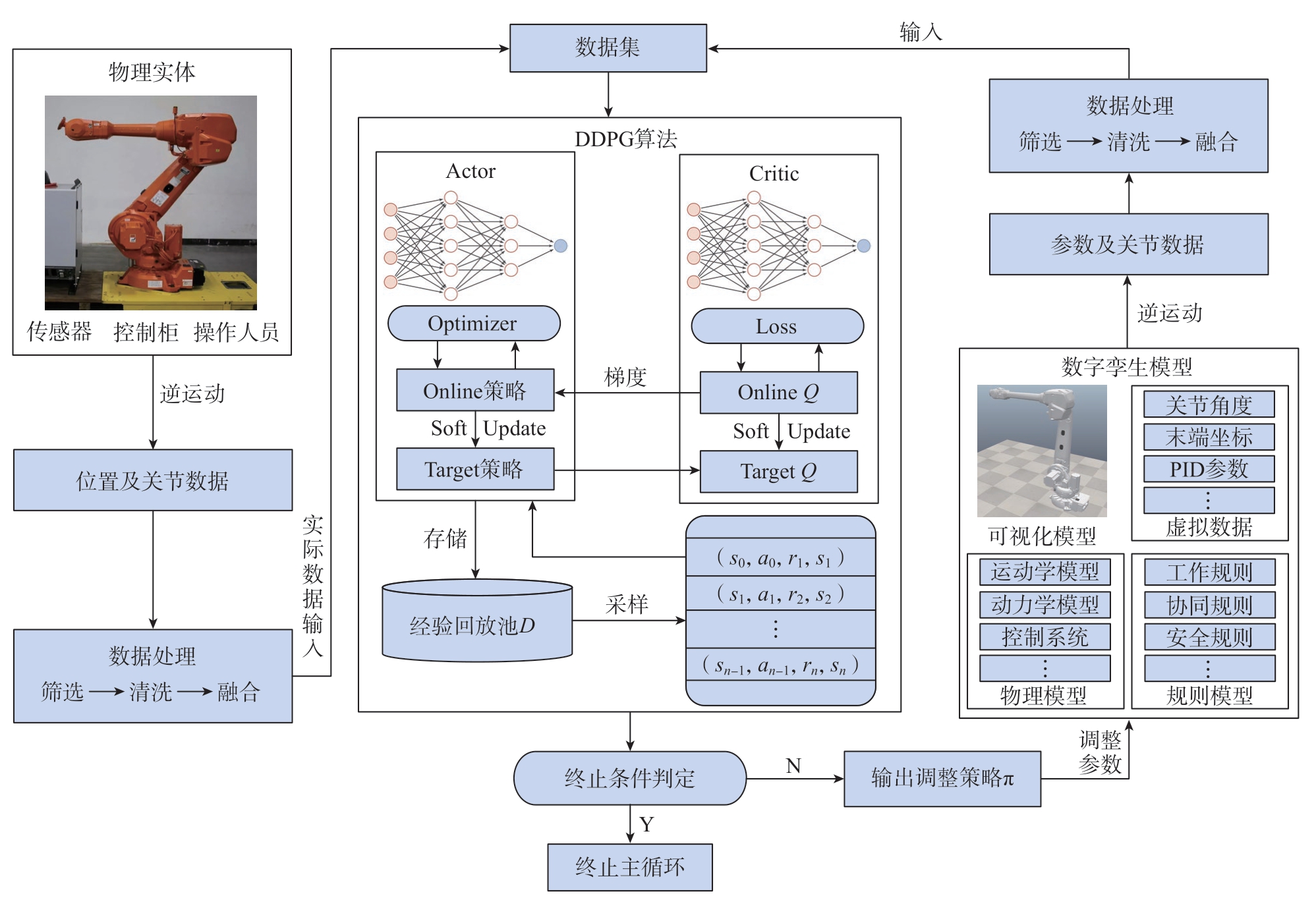
图2 数字孪生模型参数更新框架
Fig.2 Digital twin model parameter update process framework
此外，为了确保模型精度、稳定性及可调性，本文依据以下标准来确定需要更新的参数。
（1）对模型精度的影响：在选择更新参数时，首先要考虑的是那些对模型输出结果有显著影响的参数。
（2）参数的敏感性：容易因外界环境发生变化或产生误差的参数，对于模型的稳定性和准确性有较大影响。选择这些参数进行更新，可以确保模型在不同工况下的鲁棒性。
（3）参数的可调性：便于修改的参数能够使研究人员在模型更新过程中更加高效。选择这些参数有助于降低更新难度，提高操作便利性。
基于以上标准，本文选择以下4个参数作为工业机器人数字孪生模型的更新参数。
（1）比例系数：直接影响模型的放大或缩小效应，对模型输出精度有重要影响。
（2）积分时间常数：决定了模型对输入信号的积分速度，对于稳定性和响应速度至关重要。
（3）微分时间常数：影响模型对输入信号的微分动作，对于消除误差和调整动态特性十分关键。
（4）关节阻尼系数：关节阻尼系数对运动精度和防止振荡具有重要意义。
此框架主要由物理实体、数字孪生模型、DDPG算法、数据集和数据处理等组成。首先从物理实体采集目标工业机器人的实际运动数据，包括其逆运动的末端执行器位置和关节数据等，经过清洗和融合等数据处理步骤后，这些数据被输入到数据集中以备后续使用。数字孪生模型执行与物理实体相同的逆运动，并记录关节数据和相关参数。在数据处理阶段，筛选掉逆运动过程中的奇异点等异常数据，确保数据的质量和有效性，经过处理后的数据同样被输入到数据集中。将物理实体和数字孪生模型的同次动作作为初始数据，当收集到足够多的初始数据后，开始主循环。将数据集中的初始数据分批输入到DDPG算法中，在判定为未达成终止条件时，输出参数调整策略π，根据策略π对数字孪生模型的参数进行调整。参数更新后的数字孪生模型再次进行逆运动，并收集相关参数和关节数据。经过数据处理后，这些数据被输入到数据集中，并作为一条经验输入到DDPG算法中。整个参数更新过程形成一个闭环，并在主循环中不断执行，直到满足终止条件。终止条件设置为数字孪生模型相对于物理实体的误差缩小到指定值，或者达到指定的循环次数。
2.2 更新过程MDP建模
智能体通过MDP尝试不同的动作来最大化累积奖励，以训练智能体在与环境的交互中习得最优行为策略[15]。强化学习是一种机器学习方法，而MDP是强化学习中的一个基本概念，是一种用于描述序列决策问题的数学模型，它包含5个核心要素：状态集合、动作集合、状态转移函数、奖励函数和策略。这些要素共同决定了智能体在特定状态下应采取的动作，以及在执行动作后可能获得的奖励。
要将机器人数字孪生模型的更新改写为一个深度强化学习问题，首先要描述它的MDP，设置奖励函数为误差最小化，输入实际动作数据、虚拟动作数据和参数，输出参数调整策略。并通过调整数字孪生模型参数，达到更新模型的目的。为了简化操作过程并提高数据获取的效率，选择采用机器人逆运动的方式来执行动作，以获取关节角度和参数等关键数据。通过逆运动，本文可以快速地从环境中提取所需的数据，无须进行复杂的轨迹规划或任务执行，并且可以提高数据采集的准确性，从而更好地支持算法的学习和决策过程。
将工业机器人的数字孪生模型更新过程用MDP描述：在t时刻，状态集合由关节角度、末端坐标、PID参数及阻尼系数等其他参数组成。即
式中，St表示状态空间；J表示关节角度；n表示关节编号；CE表示工业机器人末端执行器坐标；KP、KI、KD分别为比例系数、积分时间常数和微分时间常数；ρ表示关节阻尼系数。将动作集合描述为调整各关节PID参数及关节阻尼系数，即
式中，At表示动作空间；
、
，
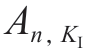，An，ρ 分别表示调整编号为n的关节比例系数的动作、关节积分时间常数、微分时间常数和关节阻尼系数的动作。
状态转移函数描述如式（4）所示，在不考虑调整参数失败或机器人故障等异常情况的前提下，状态转移概率始终为1，意味着智能体在执行动作后能够稳定地从当前状态转移到下一个状态。这种假设简化了问题的复杂性，使得智能体在面对环境变化时能够做出可靠的决策。
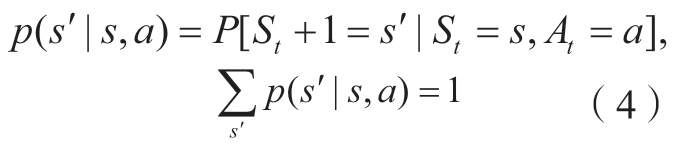
式中，p表示状态转移函数；P表示状态转移概率，即在状态s下，执行动作a转移到s'的概率。
为了提高奖励函数的精度，将奖励函数Rt设置为由调整参数后延迟增大和精度下降的惩罚和调整参数后延迟减小和精度上升的奖励组成，结合工业机器人动作之后的关节角度误差et、响应延迟dt和对应的变化率对动作进行奖励：
式中，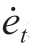
表示关节角度误差变化率；
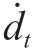表示延迟变化率；α1，α2，β1，β2 是控制各项因素对奖励的影响程度参数；f（et）和f（dt）是针对误差和延迟的惩罚函数，随着误差和延迟的增大，惩罚逐渐增加；γ1、γ2是控制误差和延迟增大时惩罚增长速度的参数。在奖励函数中，负号表示增大角度误差和延迟及其变化速率将导致奖励的减少，本文期望最小化这些因素，从而获得更高的奖励。惩罚函数采用平方函数，惩罚随着误差和延迟的增大呈二次增长，即误差或延迟每增大一点，惩罚会成倍增加。惩罚函数为
奖励函数中，误差et由均方根误差（Root mean squared error，RMSE）进行计算。
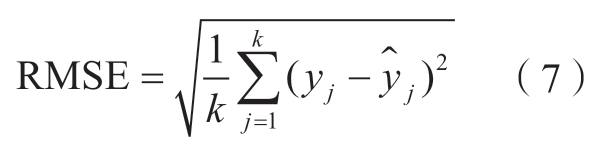
式中，k为样本数量；yj为物理实体的实测值；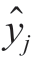
为虚拟模型的输出值。
2.3 模型更新算法设计
DDPG算法是DPG的改进版，采用Actor–Critic框架，是一种离线、无模型的深度强化学习算法[16]。这个算法结合了策略梯度和值函数方法，擅长处理连续状态空间问题，适用于机器人数字孪生模型更新问题。因此，本文选择DDPG算法作为参数优化的首选基础算法。
为了减少仅使用单一网络进行学习可能会出现的不稳定现象，DDPG引入了目标网络，DDPG算法由策略网络μ（s，a，θ）、价值网络Q（s，a，ω）、目标策略网络μ'（s，a，θ'）和目标价值网络Q'（s，a，ω'）4个网络构成。其中，价值网络用于评估Q值，对应A–C框架中的Critic评论家；策略网络用于选择策略，对应A–C框架中的Actor行动者；ω和θ分别表示价值网络和策略网络的权重。作为确定性的策略函数，当前策略网络会给出一个动作at。目标策略网络将根据经验回放池中的st+1选择的动作at+1与st+1一起输入目标价值网络，计算目标Q值的一部分，即Qπ（st+1，π（st+1））。随后，当前价值网络计算当前Q值，并基于目标价值网络计算目标Q值。
DDPG通过将经验回放、确定性策略、价值评估与神经网络结合，解决连续动作空间下的强化学习问题。算法使用策略网络指导动作选择，并通过经验回放训练价值网络。在经验采样和目标值计算后，通过最小化损失函数更新价值网络参数，并使用最大化目标函数更新策略网络参数。目标网络定期软更新以提高稳定性。
将DDPG与工业机器人数字孪生更新过程相结合，提出基于DDPG的工业机器人数字孪生模型更新算法。根据工业机器人数字孪生模型的具体参数、环境、关节值确定当前状态，通过策略网络生成参数调整动作并进入下一个参数状态，Actor利用当前和下一个状态计算Q值，然后更新各神经网络参数。不断重复此过程直至收敛或满足终止条件。具体伪代码如下。
初始化：
初始化策略网络μ（s，a，θ）、价值网络Q（s，a，ω）、目标策略网络μ'（s，a，θ'）、目标价值网络Q'（s，a，ω'）
网络参数分别为θ、ω、θ'←θ和ω'←ω
超参数：
软更新系数τ，折扣系数γ
经验回放池D容量为L，总迭代次数为M，随机采样样本数量n，实际动作数据库W
for episode=1，M do
初始化随机过程N，可用于初始的动作探索
设置初始状态S0
for t=1，T do（每一个episode中的每个时间步t）
根据目前的策略网络μ（s，a，θ）结合噪声选择参数调整动作At=μ（St，θ）+Lt
执行动作At调整模型参数，调整后模型执行数据库W中动作，获取虚拟数据
根据奖励函数获得奖励Rt+1，并进入下一个状态St+1
将从执行参数调整动作到进入下一状态作为一条经验（St，At，Rt+1，St+1），并存储在D中
从D中抽取n条经验样本（Si，Ai，Ri+1，Si+1），计算目标值：
yi=Ri+1+γQ'(Si+1,μ'(Si+1,θ'),ω')
根据最小化损失函数更新价值网络参数ω：
根据最大化目标函数更新策略网络参数θ
软更新目标网络：
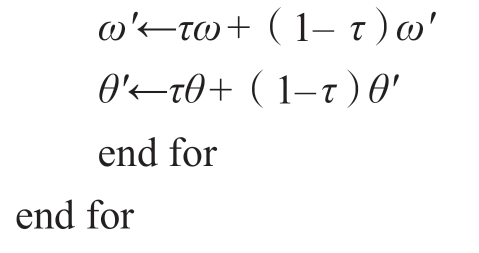
3 仿真验证结果与讨论
为验证所提方法的可行性，本文使用ABB–IRB2400工业机器人进行仿真验证。初始的物理数据来自ABB–IRB2400的实际逆运动学数据集，而仿真数据则由仿真工具Coppeliasim建立的ABB–IRB2400虚拟模型提供。
3.1 仿真环境及算法训练
试验环境如表1所示，DDPG算法参数Critic学习率设置为0.001，Actor学习率设置为0.0005，使用Adam参数优化器优化神经网络参数。为避免神经网络过拟合，采用 L2正则化，正则化参数设置为0.0001，通过在损失函数中添加正则化项，可以惩罚大的权重，使模型更加简单，从而避免过拟合。折扣系数γ设置为0.95，软更新系数τ设置为0.005，经验池大小为10000，用于参数更新的采样池大小为64，探索噪声采用Ornstein-Uhlenbeck噪声。Ornstein-Uhlenbeck噪声是一种随机过程，可以引导智能体在探索新动作和利用已知的高回报动作之间取得平衡，有助于智能体在连续动作空间中更有效地学习策略。激活函数采用修正线性单元（Rectified linear unit，ReLU），用于缓解梯度消失问题，有助于更快地收敛。
表1 仿真试验环境
Table 1 Simulation experiment environment
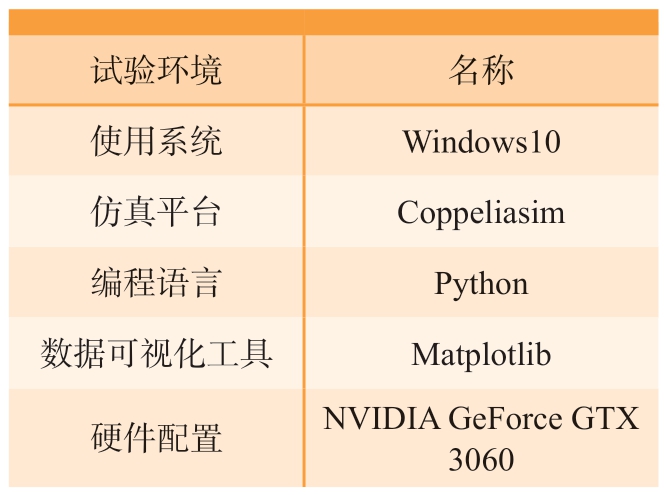
试验环境名称使用系统Windows10仿真平台Coppeliasim编程语言Python数据可视化工具Matplotlib硬件配置NVIDIA GeForce GTX 3060
将DDPG算法在工业机器人数字孪生虚拟模型中训练了500回合后，获得训练过程、收敛效果和累计奖励值如图3所示。在训练初期，即前100回合左右，累计奖励值出现了剧烈的波动，且并未呈现出明显的上升趋势。这是由于智能体在探索动作空间和环境中的初始阶段，尚未形成稳定的学习策略。这个阶段，智能体仍在尝试不同的动作，以逐步了解环境反馈和探索可能的动作空间。随着训练次数的增加，算法获得的累计奖励值逐渐增加，这表明智能体正在逐步学习到更有效的行为策略，并开始在环境中获得更高的回报。在第220回合左右，累计奖励值开始收敛，并稳定在57附近。这说明算法已经逐步找到了最优的行为策略，并在连续动作空间中实现了有效的学习。
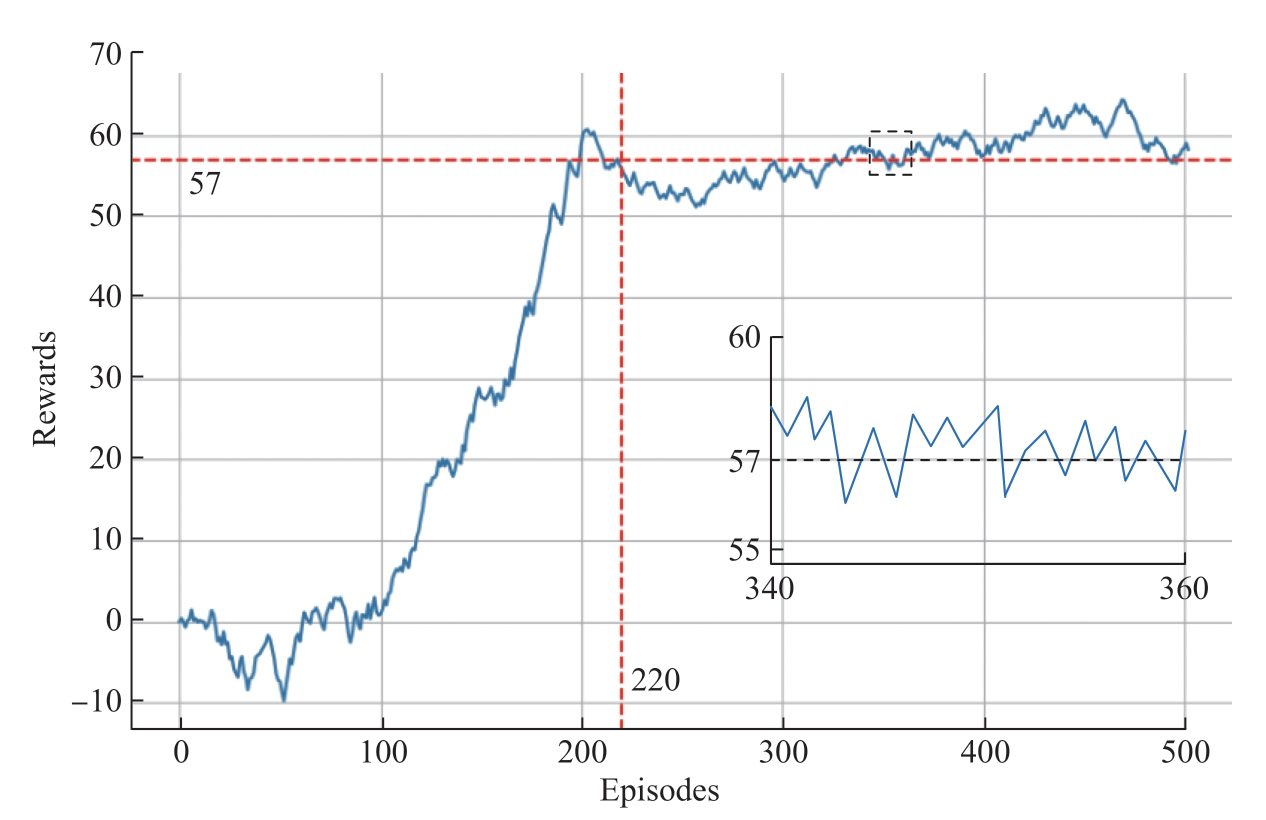
图3 DDPG训练过程
Fig.3 DDPG training process
3.2 仿真结果
为了检验参数更新后的工业机器人数字孪生模型的一致性，将工业机器人路径运动产生的角度数据和末端坐标数据与模型同路径运动数据进行误差对比。生成多段随机轨迹，对更新后的数字孪生模型输入路径运动信号，并取其中一段轨迹分析。以弧度为单位记录关节角度值，以编号a和b的两个关节角度为例，将其与更新前的模型角度数据和实际角度数据进行对比，如图4所示。其中，实线表示更新后数字孪生模型的角度数据；点画线表示更新前数字孪生模型的角度数据；虚线表示实际角度数据。
图4 仿真结果和实际数据对比
Fig.4 Comparison of simulation results with actual data
在整个位移过程中，关节a实际角度变化和更新后的数字孪生模型的角度变化都经过3 s平缓到达1.39 rad左右，并且在工业机器人动作过程中二者的曲线变化趋势基本一致。根据相对误差公式，在1.53 s时，机器人的实际角度和更新后的数字孪生模型的仿真角度值达到最大相对误差2.164%，整个过程的平均相对误差为1.803%，而更新前的数字孪生模型和实际数据间的平均相对误差为2.519%。关节b与关节a类似，经过3 s的时间，关节b的实际角度与数字孪生模型的仿真角度均逐渐趋近于–1.41 rad。在1.33 s时，实际角度值和数字孪生模型的仿真角度值的相对误差达到最大，为2.219%。在整个过程中，更新后的数字孪生模型与实际数据间的平均相对误差为1.816%，而更新前的模型与实际数据间的平均相对误差为2.463%。
图5为更新前后的模型仿真结果与实际数据的误差值。可以看出，基于混合驱动的进给系统数字孪生模型的仿真结果误差明显减小，基于DDPG的工业机器人数字孪生模型更新后的仿真结果误差明显减小。
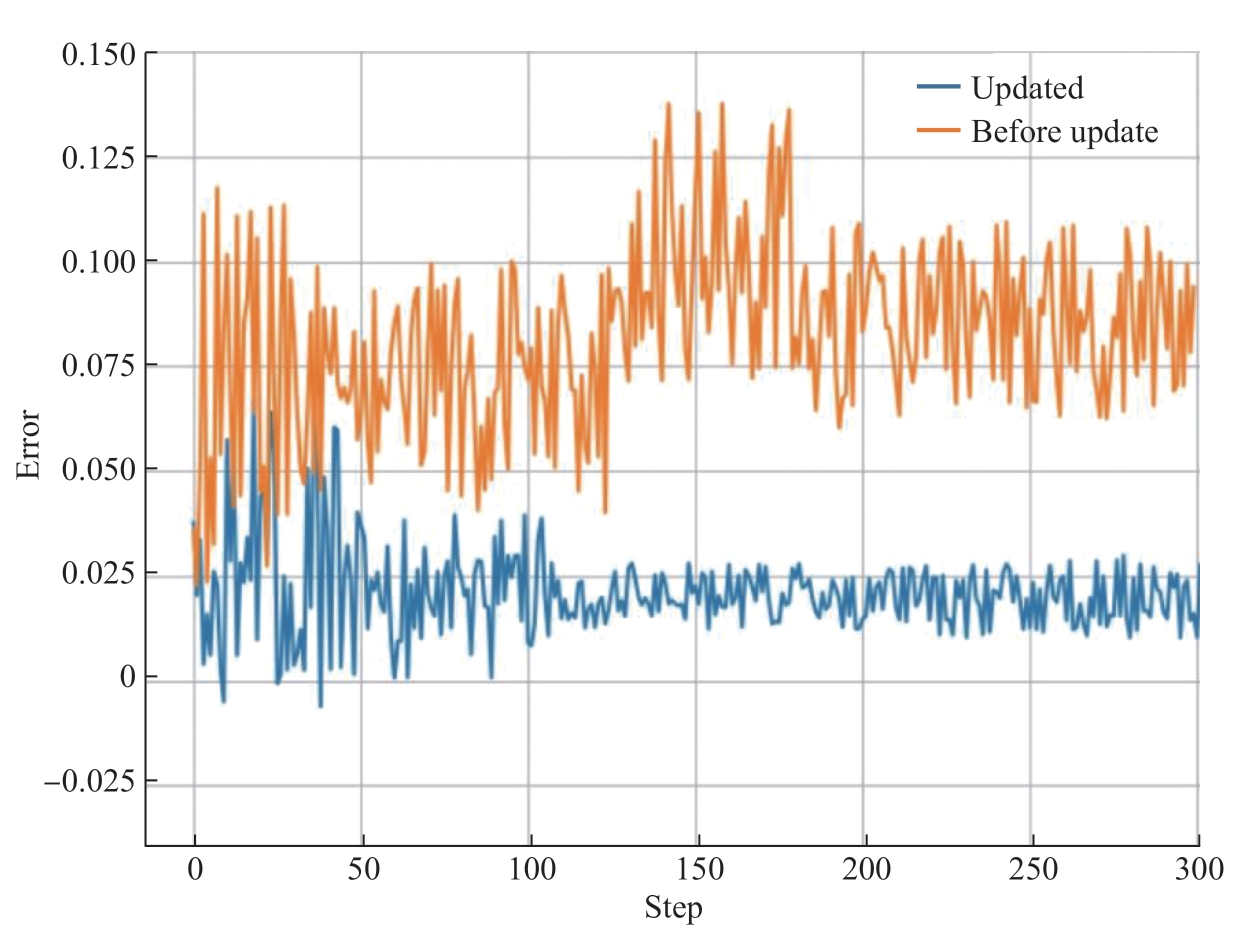
图5 更新前后仿真和实际数据的误差大小
Fig.5 Error magnitude of simulation and actual data before and after update
在相同环境下，针对ABB–IRB2400工业机器人数字孪生模型，分别采用基于DDPG的工业机器人数字孪生模型更新方法、基于深度Q网络（Deep Q–network，DQN）的工业机器人数字孪生模型更新方法进行更新后，将采样仿真数据和实际数据计算相对误差进行对比，如表2所示。
表2 不同算法更新效果对比
Table 2 Comparison of update effect of different algorithm
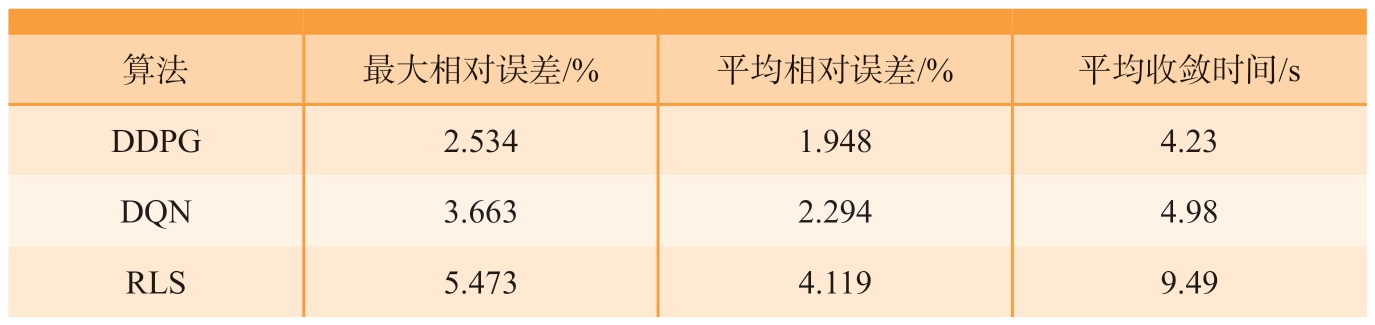
算法最大相对误差/%平均相对误差/%平均收敛时间/s DDPG2.5341.9484.23 DQN3.6632.2944.98 RLS5.4734.1199.49
使用本文提出的DDPG算法更新后的模型平均相对误差在2%左右，而RLS的平均相对误差为4.119%，且本文所提DDPG更新方法的平均收敛时间远低于RLS，表现出更好的模型精度和收敛速度。同时，对比使用相同方法但分别采取DDPG和DQN算法的结果，DDPG相对误差和收敛时间略优于DQN，说明DDPG算法更适合解决此类连续动作的工业机器人数字孪生模型更新问题。
4 结论
本文提出了一种基于深度强化学习的工业机器人数字孪生模型更新方法，用于解决因实际场景的更新和设备磨损等造成的工业机器人数字孪生模型与实际物理模型不一致，导致仿真精度下降的问题。通过对ABB–IRB2400工业机器人的仿真试验验证了所提方法的有效性，为工业机器人数字孪生模型参数的更新方法提供了一种新的思路。根据本文的研究结果，可以得到以下结论。
（1）研究了一种基于深度强化学习的工业机器人数字孪生模型更新方法。将物理实体传感器采集到的数据处理后输入到深度强化学习算法中，对数字孪生模型进行参数修正，达到更新数字孪生模型的目的。更新后的数字孪生模型相比于传统更新方法有较高的同步精度，以及较快的收敛速度。
（2）将工业机器人虚拟模型参数更新过程改写为马尔可夫决策过程，并将其在ABB–IRB2400工业机器人仿真验证更新中应用。试验结果表明，更新后的数字孪生模型能够更好地保持与物理实体运行结果的一致性，显著降低误差，使模型更贴近实际物理实体，有效提高了模型的输出精度，验证了所提方法的有效性。
[1] 王田苗, 陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报,2014, 50(9): 1–13.WANG Tianmiao, TAO Yong.Research status and industrialization development strategy of Chinese industrial robot[J].Journal of Mechanical Engineering, 2014, 50(9): 1–13.
[2] 陶飞, 刘蔚然, 刘检华, 等.数字孪生及其应用探索[J].计算机集成制造系统, 2018,24(1): 1–18.TAO Fei, LIU Weiran, LIU Jianhua, et al.Digital twin and its potential application exploration[J].Computer Integrated Manufacturing Systems, 2018, 24(1): 1–18.
[3] LIU Y K, XU H, LIU D, et al.A digital twin-based sim-to-real transfer for deep reinforcement learning-enabled industrial robot grasping[J].Robotics and Computer-Integrated Manufacturing, 2022, 102365.
[4] 刘伟, 刘顺, 邓朝晖, 等.工业机器人定位误差补偿技术研究进展[J].机械工程学报, 2023, 59(17): 1–16.LIU Wei, LIU Shun, DENG Zhaohui,et al.Research progress on positioning error compensation technology of industrial robot[J].Journal of Mechanical Engineering, 2023,59(17): 1–16.
[5] 黄华, 李嘉然, 赵秋舸, 等.基于混合驱动的进给系统数字孪生模型自适应更新法[J].计算机集成制造系统, 2023, 29(6): 1840–1851.HUANG Hua, LI Jiaran, ZHAO Qiuge,et al.Adaptive update method of digital twin model for feed system based on hybrid drive[J].Computer Integrated Manufacturing Systems,2023, 29(6): 1840–1851.
[6] WU T, YANG F, FAROOQ U, et al.An online learning method for constructing selfupdate digital twin model of power transformer temperature prediction[J].Applied Thermal Engineering, 2024, 237: 121728.
[7] 刘新宇, 韩旭, 王泓晖, 等.高速列车悬挂系统的数字孪生模型自适应实时修正方法[J/OL].计算机集成制造系统, 2023: 1–17.(2023–11–01).https://kns.cnki.net/kcms/detail/11.5946.TP.20231101.1151.004.html.LIU Xinyu, HAN Xu, WANG Honghui,et al.Adaptive real-time correction method for digital twin model of high-speed train suspension system[J/OL].Computer Integrated Manufacturing Systems, 2023: 1–17.(2023–11–01).https://kns.cnki.net/kcms/detail/11.5946.TP.20231101.1151.004.html.
[8] LIU S M, ZHENG P, XIA L Q, et al.A dynamic updating method of digital twin knowledge model based on fused memorizingforgetting model[J].Advanced Engineering Informatics, 2023, 57: 231–235.
[9] 刘建伟, 高峰, 罗雄麟.基于值函数和策略梯度的深度强化学习综述[J].计算机学报, 2019, 42(6): 1406–1438.LIU Jianwei, GAO Feng, LUO Xionglin.Survey of deep reinforcement learning based on value function and policy gradient[J].Chinese Journal of Computers, 2019, 42(6): 1406–1438.
[10] IBRAHIM A M, YAU K L A,CHONG Y W, et al.Applications of multiagent deep reinforcement learning: Models and algorithms[J].Applied Sciences, 2021, 11(22):10870.
[11] DUBBIOSO S, DE TOMMASI G,MELE A, et al.A deep reinforcement learning approach for vertical stabilization of Tokamak plasmas[J].Fusion Engineering and Design,2023, 194: 113725.
[12] LEE D M, LEE S, MASOUD N, et al.Digital twin-driven deep reinforcement learning for adaptive task allocation in robotic construction[J].Advanced Engineering Informatics, 2022, 53:101710.
[13] 王凤英, 陈莹, 袁帅, 等.自注意力机制结合DDPG的机器人路径规划研究[J/OL].计算机工程与应用, 1–12.[2024–01–03]http://kns.cnki.net/kcms/detail/11.2127.tp.20230920.0937.010.html.WANG Fengying, CHEN Ying, YUAN Shuai, et al.Since the attention mechanism combining DDPG robot path planning research[J/OL].Computer Engineering and Application,1–12.[2024–01–03] http://kns.cnki.net/kcms/detail/11.2127.tp.20230920.0937.010.html.
[14] 陶飞, 刘蔚然, 张萌, 等.数字孪生五维模型及十大领域应用[J].计算机集成制造系统, 2019, 25(1): 1–18.TAO Fei, LIU Weiran, ZHANG Meng,et al.Five-dimension digital twin model and its ten applications[J].Computer Integrated Manufacturing Systems, 2019, 25(1): 1–18.
[15] 刘全, 翟建伟, 章宗长, 等.深度强化学习综述[J].计算机学报, 2018, 41(1): 1–27.LIU Quan, ZHAI Jianwei, ZHANG Zongchang, et al.A survey on deep reinforcement learning[J].Chinese Journal of Computers, 2018,41(1): 1–27.
[16] WANG H N, LIU N, ZHANG Y Y,et al.Deep reinforcement learning: A survey[J].Frontiers of Information Technology and Electronic Engineering, 2020, 12: 1726–1744.
