近年来,复合材料在航空航天领域得到广泛应用。复合材料具有高比强度和比刚度、可设计性强、疲劳性能好、耐腐蚀和可整体成型等优点,但其较高的价格已经成为扩大复合材料应用规模的最大障碍。其中节约材料可对降低产品的制造成本产生明显影响。在复合材料构件的制造过程中,一般通过CAD/CAM软件生成各个铺层的二维展开图,再通过计算机对展开料片进行排样优化的方法来提高材料利用率。
优化排样问题属于具有最高计算复杂性的一类问题——非确定型的多项式算法 (Nondeterministic polynomial,NP)完全问题[1],很难在多项式时间内解决。排样零件形状复杂度越高,数量越多,计算复杂度会呈指数倍增长,这些问题制约了各类材料的自动化排样技术的发展。因此研究不规则料片的排样具有重要的实际应用价值。
由于零件本身的复杂性,零件间靠接关系描述、调整和对比等操作困难,使得不规则零件排样问题受到一定限制。其中临界多边形 (No-fit polygon,NFP)思想[2]已经成为优化问题的主流解决方法之一。国内外学者针对如何获得NFP提出了许多种方法,大体可分为移动碰撞法、轨迹线法、明科夫斯基矢量法、凹多边形凸化分割法等。
最早应用的移动碰撞法算法简单,但存在移动盲区,计算复杂度高,需要改进;轨迹线法适用于凹边形、凸边形,且能计算内外靠接多边形,可以有效生成NFP,但面对特殊情况时,由于需要求得多边形每个顶点的轨迹线,造成步骤过于复杂,耗时较高;明科夫斯基矢量法针对凸多边形简单有效,但当存在凹多边形时,算法将变得异常复杂;凹多边形凸化分割法将凹多边形分割为凸多边形,再将多个凸多边形的NFP合并得到最终NFP,但Agarwal等[3]证实了单多边形的分割重组会导致时间复杂度不减反增。本文将在充分研究各种求解NFP算法的基础上,提出一种基于轨迹线改进的临界多边形算法,用以降低几何计算复杂性,为实际排样做算法准备。
1 现有的求解算法
给定多边形A和多边形B,将A固定,在B中选择某个顶点作为参考点,在B绕着A做不旋转的环形运动的过程中,参考点形成的轨迹构成了B相对于A的临界多边形,记为NFPAB(图1)。
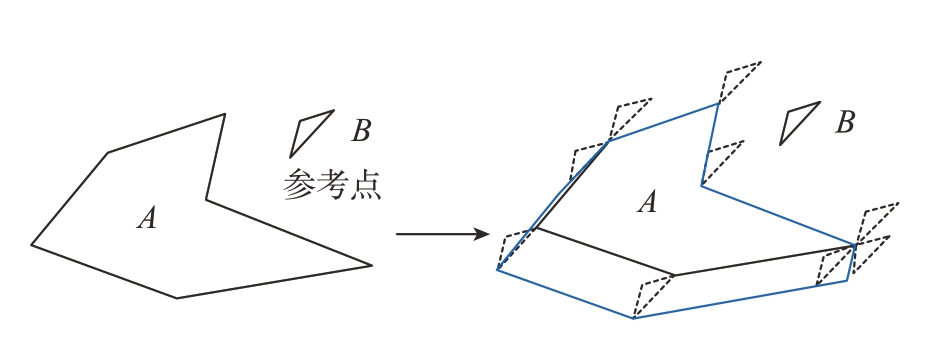
图1 临界多边形NFPAB的定义
Fig.1 Definition of no-fit polygon NFPAB
两个多边形的位置主要有重叠、接触、相离这3种关系[4]。临界多边形具有判别两个多边形位置关系的作用。若多边形B的参考点P0∈NFPAB,则B与A正好接触;若多边形B的参考点P0在NFPAB内侧,则B与A重叠;若多边形B的参考点P0在NFPAB外侧,则B与A相离。由于这个重要的几何性质,NFP已成为多种几何算法的基础。通过NFP可获得多边形之间所有可能的靠接位置,排样等问题可以转化为基于临界多边形的最佳定位点选择的问题。
移动碰撞法[5–6]的思路与NFP定义最为接近,主要分为两部分求解,包括移动方向和最小碰撞距离。对于外靠接NFP求解问题理论比较成熟,但遇到入口小的空腔等复杂图形时,因多边形B绕A移动无法进入A的空腔,会导致NFP结果不够准确。
轨迹法是刘胡瑶等[7]提出,通过分析两个多边形互相移动的轨迹线与临界多边形之间的关系得到了在轨迹集合中筛选NFP边界线的方法。通过对传统的NFP算法进行改进,使得NFP的求解过程大大简化。
明科夫斯基矢量法[8]是通过建立Minkowski矢量与临界多边形的联系,使用Minkowski sum来解决临界多边形的问题,但对于凹多边形,边的矢量顺序会被打乱,并不能正确合成一个临界多边形。后来在此基础上Ghosh[9]和佟德刚[10]针对凹多边形的问题提出一种斜率图 (Slope diagram)的算法,但当存在两个凹多边形时,点与点的干扰情况将无法确定,会导致算法复杂度提高[11]。
凹多边形凸化分割法[12]的基本原理是将凹多边形分割为多个凸多边形,分别求得对应的NFP后,合并成为最终的NFP。凸化分割的方法有多种,如三角分割、凹点分割等。Agarwal等[3]曾经对多种分割算法进行研究,设多边形A、B的边数为m、n,得出对于复杂凸多边形,凸化分割算法的时间复杂度会超过移动碰撞算法的复杂度O((m+n)mn)。
2 改进后的算法
虽然现有的算法在特定的情况下对排样的效率有明显的提升,但在复杂的排样数据下仍然有很多不足,存在或多或少的改进空间。求解NFP算法最基础的目标可分为两部分,包括移动方向和移动距离。移动碰撞法的主要计算量在于确定碰撞距离,而计算移动方向算法复杂度仅为O(m+n)。凹多边形凸化分割主要思想在于将难以计算碰撞距离的凹多边形分割为仅需计算移动方向的凸多边形,便于解决凹多边形问题。而轨迹线法可以有效地处理凹边问题以及孔洞和空腔等问题。
本文在现有算法的基础上提出并实现了一种基于轨迹线改进的临界多边形算法。针对NFP计算过程中所面临的效率低下问题,该算法整合并优化了轨迹线法和移动碰撞法的核心原理,简化了复杂的判断逻辑,减少了计算步骤,提升了NFP计算的整体效率。具体算法可分为如下5个部分。
2.1 多边形顶点的凹凸性判断
由于凸多边形能方便快捷得到NFP的几何特性,因而在计算过程中,多边形的凹凸性是一个非常重要的判定条件。过去很多学者通过判断整体多边形的凹凸性来设计算法,由于多边形外形复杂无法寻求一个整体的解决方案,需要通过判断顶点的凹凸性来使用对应的方法。
顶点的凹凸性判断方法:首先将多边形A的边按逆时针方向变成向量。以多边形A中的最低点pmin为起止点的两个向量的叉积Emin–1×Emin的Z轴分量为正方向。A中顶点pi为起始向量Ei和终止向量Ei+1的交点。由于极点必为凸点,若起始向量与终止向量的叉积Ei×Ei+1的Z轴分量与正方向相同时,顶点pi为凸点;若起始向量与终止向量的叉积Ei×Ei+1的Z轴分量与正方向相反时,顶点pi为凹点;若起始向量与终止向量的叉积Ei×Ei+1=0时,说明顶点pi与顶点pi+1和顶点pi–1共线,在此算法中将其归为凸点。
如图2所示,最低点p1为凸点,将以p1为起止点的两个向量的叉积E4×E1作为正方向,即E4到E1逆时针旋转为正。在凸多边形中,以各个顶点为起止点的两个向量的旋转方向应一致,与凸点旋转方向不一致的点即为凹点。因此可以得出,向量E1×E2和向量E3×E4的Z轴分量与正方向方向一致,为逆时针旋转,因此p2和p4为凸点。而向量E2×E3的Z轴分量与正方向方向相反,为顺时针旋转,因此p3为凹点。
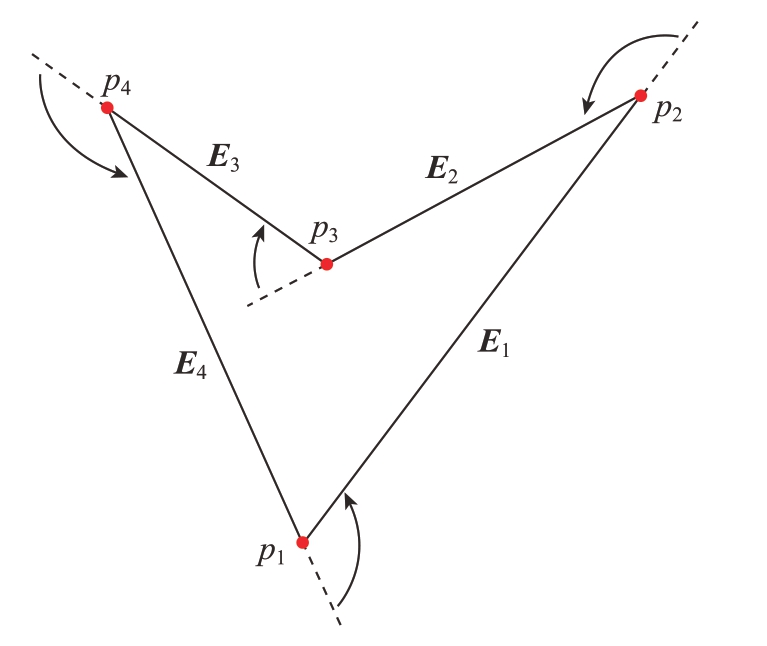
图2 多边形顶点凹凸性判断示意图
Fig.2 Schematic diagram of polygon vertex concavity and convexity judgment
2.2 凸化算法
由于凹多边形的局部NFP不易得到,并且直接去除凹点有时无法实现凹多边形凸化,因此利用此算法将部分顶点移除以达到形成凸多边形的目的。
定义1:设点集P=(p0,p1,p2,…,pn–1)逆时针方向组成简单多边形O,其中一个连续的点集Pt中存在凹点,在点集P中移除Pt后,将多边形开口进行连接,形成新的多边形,该处凹点消失,局部实现了凸化,存在多个满足该条件的Pt点集,将点数最小的点集Pt作为凹化点集。
凸化算法具体如下:
(1)顶点集P中存在一个或连续的多个凹点,其两侧凸点为点pa和点pb;
(2)设判断点ini_ p =pa,last_ p=pb;
(3)判断pa+1、pa–1和pb–1是否在ini_ p和last_ p两点的相同一侧;
(4)如pa+1、pa–1和pb–1 3点没有在两个判断点相同的一侧,则a=a–1,重复步骤 (2)和 (3),直到满足同侧条件;
(5)设判断点ini_ p=pa,last_ p=pb;
(6)判断pa–1、pb+1和pb–1是否在ini_ p和last_ p两点的相同一侧;
(7)如pa–1、pb+1和pb–1 3点没有在两个判断点相同一侧,则b=b+1,重复步骤 (5)和 (6),直到满足同侧条件;
(8)判断点之间的点集即为凹化点集。
如图3所示,在多边形A中p4和p5为凹点。若在A中直接移除p4和p5,连接p3和p6,在修改后的多边形A中,p3仍为凹点,不符合多边形凸化要求。通过凸化算法可获得凹化点集 (p3,p4,p5),移除凹化点集后,连接p2和p6,在修改后的多边形A中凹化点集附近的顶点p0、p1、p2、p6和p7均为凸点,满足多边形凸化要求并将p2 p6称为此组凹化点集的替换边。
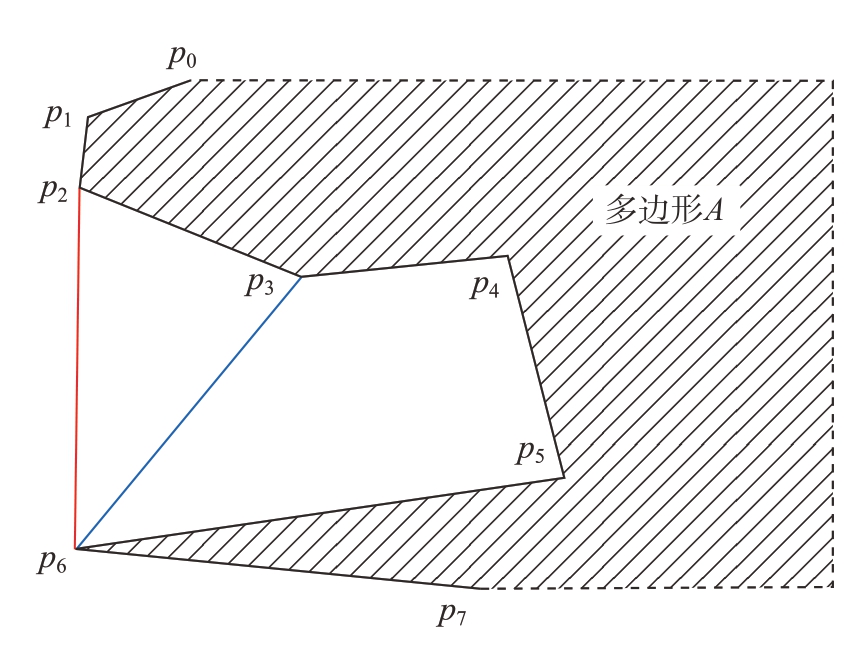
图3 凸化算法示意图
Fig.3 Schematic diagram of convex hull algorithm
2.3 移动碰撞算法
将多边形A、B的边按逆时针方向变成向量,其中多边形A和B均为凸多边形。当多边形B不旋转地移动在多边形A上,接触点为凸点时,求得其NFP。接触的情况分为点点接触和点线接触两种,如图4所示。
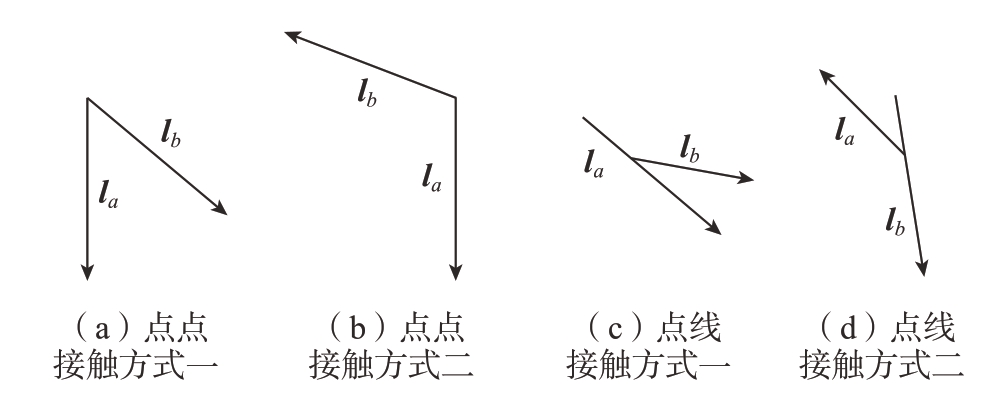
图4 接触方式示意图
Fig.4 Schematic diagram of contact mode
(1)点点接触。假设A、B的接触点分别为pa、pb,以pa、pb为顶点的向量分别为la、lb。如果向量lb与向量la的叉积Z分量小于0,即lb×la<0,则多边形B的下一步移动方向为–lb,如图4(a)所示;否则多边形B的下一步移动方向为la,如图4(b)所示。
(2)点线接触。如果是多边形B的顶点pb与A的边向量la接触,则多边形B的下一步移动方向为la,如图4(c)所示;如果是多边形A的顶点pa与多边形B的边向量lb接触,则多边形B的下一步移动方向为–lb,如图4(d)所示。
当凸多边形A、B一直处于凸点–凸点接触时,B沿着A的边移动,两个多边形不会相互重叠。并且移动距离无须二次计算,移动距离即为移动方向的向量模长。因此可通过上述方法得到多边形B每次的移动方向,直到终点与起点重合,在多边形B上的参考点移动轨迹便是对应的NFP。具体算法如下:
(1)将凸多边形A和B的边按照逆时针方向变为向量;
(2)将凸多边形A和B的接触 (将A中最低点pa–ymin和B中最高点pb–ymax接触);
(3)判断接触方式 (点点接触或点线接触),得到多边形B的移动方向;
(4)将多边形B按照移动方向移动至下一位置;
(5)重复步骤 (3)和 (4),直到运行至起始点。
2.4 基于局部轮廓的轨迹线NFP算法
在多边形A和多边形B的接触情况中,除上述的凸点–凸点接触的情况以外,还存在凹点–凹点和凸点–凹点等接触的情况。在多边形含有凹点的情况下,不仅会打乱移动碰撞法的移动方向,而且会产生空腔、空洞等移动碰撞法无法解决的情况。基于轨迹法的NFP算法可有效解决因凹点引起的上述问题。本文的基于局部轮廓的轨迹线NFP算法参考了文献[7]中的判断点线可能接触算法以及轨迹线生成算法,对基于轨迹线的临界多边形算法进行改进。
此算法用于生成多边形A相对于多边形B局部轮廓C的NFP。算法需要局部轮廓C满足以下条件:(1)局部轮廓C两端直线顶点皆为凸点; (2)需已知多边形B的两侧端点所对应的NFP线段,即已知局部轮廓C的NFP起始边向量lstart和终止边向量lend。
首先使用判断点线可能接触算法以及轨迹线生成算法获得相应的轨迹线集合后,求解NFP的问题就转化为了在轨迹线集合中求向量lstart与向量lend之间的临界多边形。求解基本原理:从起始边开始,得到与该边相交的线段,取离起点最近并与该边右侧夹角最小的交线作为下一边,循环执行该过程,直到执行到终止边,即可得到多边形A对应的临界多边形。算法如下:
(1)获得起始边向量lstart和终止边向量lend,以及轨迹线集合;
(2)得到与向量lstart相交的所有线段,取距离起点最近的交点为断点,并建立以当前边起点和断点为端点的线段,加入到线段集合中;
(3)得到与当前边在断点相交的所有线段,在交于断点的轨迹线段中,取与当前线段右侧夹角最小的线段,作为下一条边的向量lstart;
(4)不断执行步骤 (2)和 (3),直到下一条边为终止边向量lend;
(5)线段集合即为多边形A相对于局部轮廓C的NFP。
2.5 移动碰撞法与轮廓轨迹线算法的结合算法
根据研究可知,简单多边形中的凹化点集所在局部轮廓形成的NFP与凹化点集两侧顶点连接的直线 (即凹化点集的替换边)对应的NFP始末位置相同。在凸多边形A、B中,利用移动碰撞法得到的NFP由A、B各边平移至首尾相连组成。因此可利用标定替换边的方式来确定凹化点集所在局部轮廓形成的NFP的始末位置。
因此本文将轮廓较为复杂的多边形A转化为凸多边形和多边形A的多个局部轮廓。凸多边形使用具有时间复杂度低、算法效率较高的移动碰撞算法,局部轮廓使用有效解决凹点问题的基于局部轮廓的轨迹线NFP算法生成多边形局部轮廓的NFP。接下来详细说明一下整体算法。
设多边形A中最低点为初始点pa0,多边形B中最高点为初始点pb0。以pa0为起点的边为多边形A的初始边a0,以pb0为起点的边为多边形B的初始边b0。如图5所示,首先判断多边形A和多边形B顶点的凹凸性,凸点标识为0,凹点标识为1;其次利用凸化算法获得A和B的凹化点集,并标识在凹化点集的起始方向顶点上(即多边形起点存在标识的边为凹化点集的替换边);同时将多边形A和B转化为凸多边形At和Bt(图5中凸化算法内的方框表示凹化点集,箭头指向标识位置);最终使用移动碰撞法获得多边形Bt相对于多边形At的临界多边形NFPt。在获得NFPt的同时,可得到At和Bt中替换边的分布结果。另外由于NFP算法的特性,At、Bt一直保持接触,因此At的边向量la移动时接触的边是距离向量la顺时针最近的Bt边向量lb,Bt的边向量lb移动时接触的At边是距离向量lb顺时针最近的At边向量la。在图5中,ai和bi表示多边形A、B分别以a0和b0为起点的第i条边,移动碰撞法的结果为At、Bt各边在NFPt中的逆时针位置顺序。
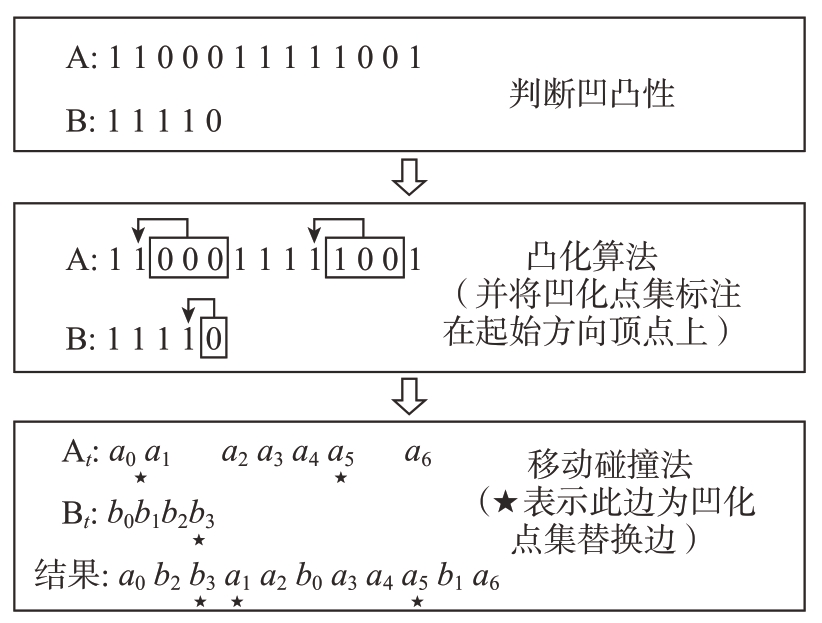
图5 凹化点集的生成及其替换边示意图
Fig.5 Schematic diagram of the generation of concave point set and its replacement edge
将移动碰撞法结果中每个替换边转化为多边形A中对应的局部轮廓。多边形A的边转化为对应的凹化点集,而多边形B的边按照顺时针最近的原则将接触的另一多边形A的边作为其对应的局部轮廓,如图6所示。确定了所有的局部轮廓后,将相邻的局部轮廓进行整合。整合后,将各个局部轮廓在多边形A中两侧相邻的直线加入局部轮廓中,用以生成顶点位置附近的轨迹线。
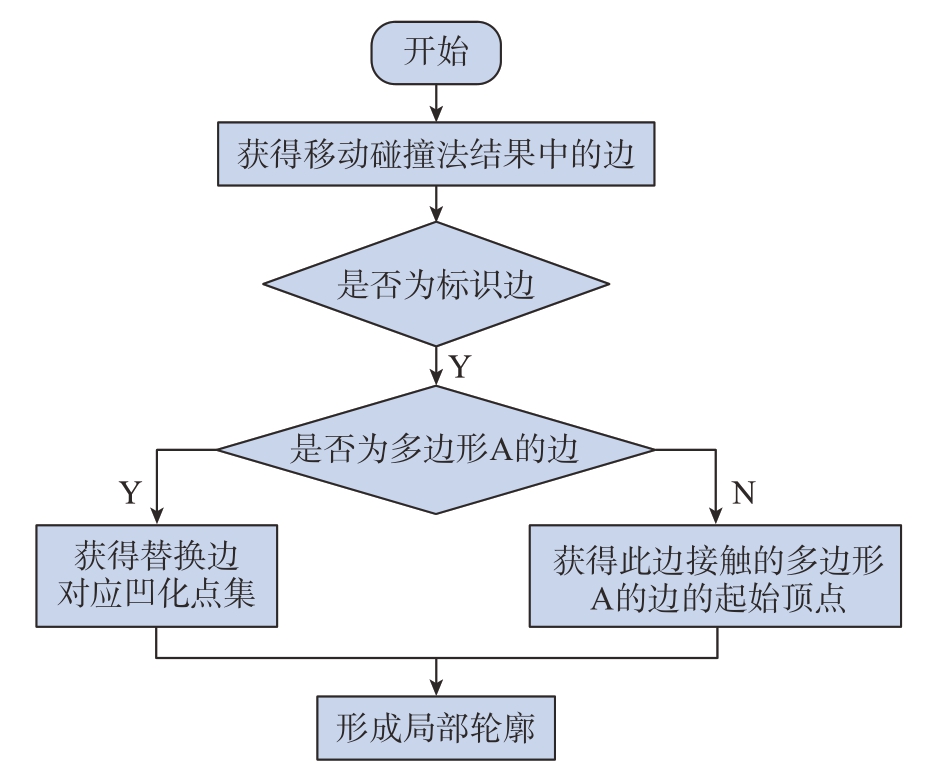
图6 替换边转换局部轮廓示意图
Fig.6 Schematic diagram of transforming replacement edge into local contour
再将整合后的各部分局部轮廓按照基于局部轮廓的轨迹线NFP算法生成对应NFP。利用替换边与凹化点集所对应的局部轮廓首末位置相同的特性,将NFPt中的替换边更换为对应的NFP,生成的结果即为最终的NFP。整体算法流程如图7所示。
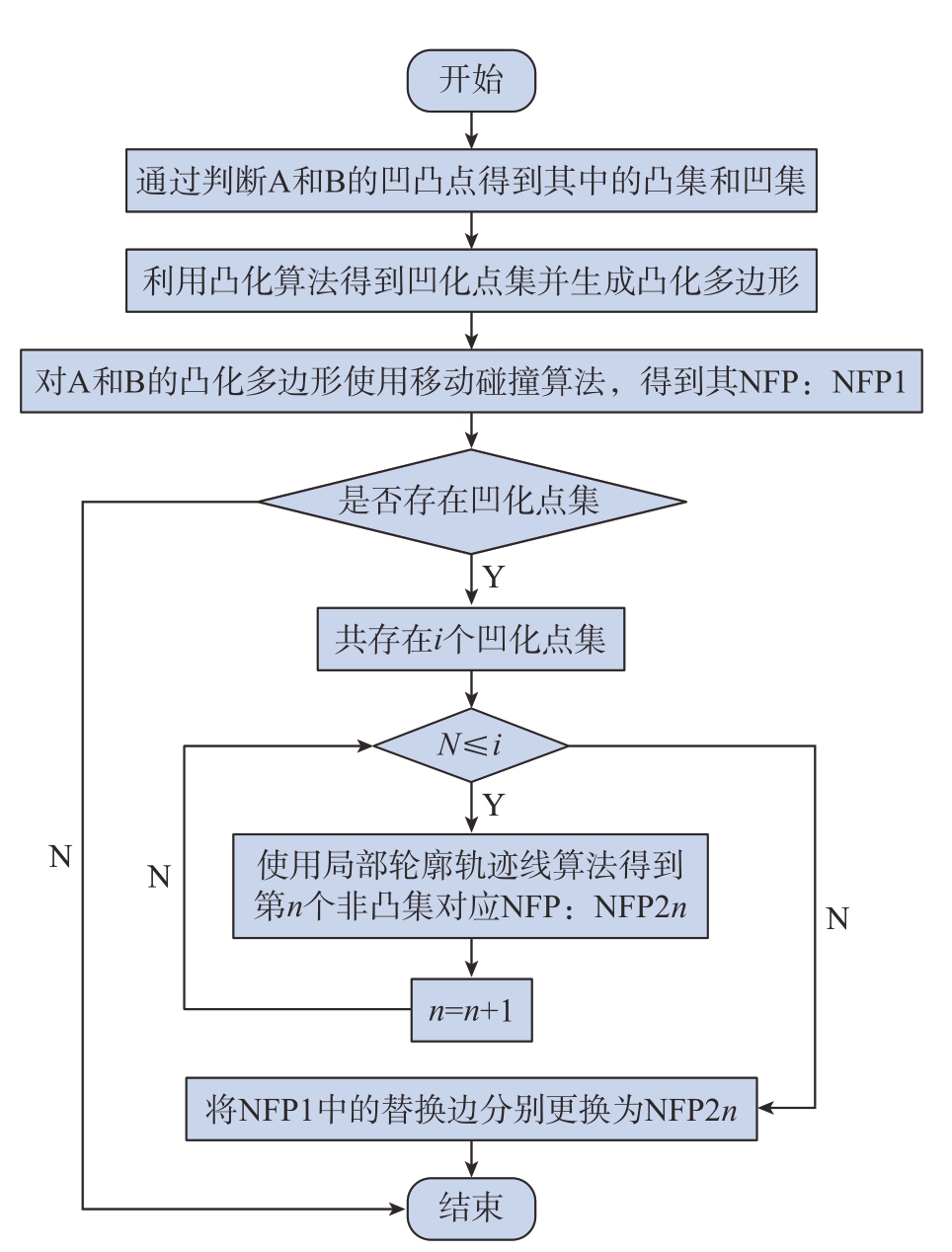
图7 改进算法流程图
Fig.7 Improved algorithm flowchart
3 实例与分析
对本文改进算法进行时间复杂度分析可知,本文采用的移动碰撞算法无须考虑移动距离,因此这部分算法的时间复杂度仅为O(m+n)。而改进的非封闭轨迹线NFP算法时间复杂度虽仍为O(mn),但因已经尽可能地将凹点排除,使得多边形的边数大量减少并有效地减少了轨迹线的生成数量,间接地减少了时间复杂度。最终计算可得本文改进算法总时间复杂度为O(m1+n+m2n)。由于多边形中内角和为 (n–2)×180°,且凹角角度大于180°,因此在多边形中凸点一定大于2个。在简单多边形顶点中凸点数量越多,越能缩短NFP生成时间。
为检验本文算法的性能,与刘胡瑶等[7]的算法进行对比。为保证对比结果准确有效,本文改进算法中的基于局部轮廓的轨迹线NFP算法及对比所用轨迹线算法均未采取其余优化手段。测试采用来自于ESICUP欧洲切割与包装事务委员会(https://www.euro-online.org/websites/esicup/)的2D不规则数据集Alban、Mao、Shirt。仿真运行平台为PC机,处理器为i5–8300H,2.30 GHz,8 GB内存。对于每组数据集中所有多边形,两两计算其临界多边形,生成的NFP总数S=N×N(N为数据集中多边形的个数)。算法运行20次,结果取其平均运行时间,如表1所示。
表1 改进算法与轨迹线算法运行时间对比
Table 1 Comparison of running time between the improved algorithm and the trajectory algorithm
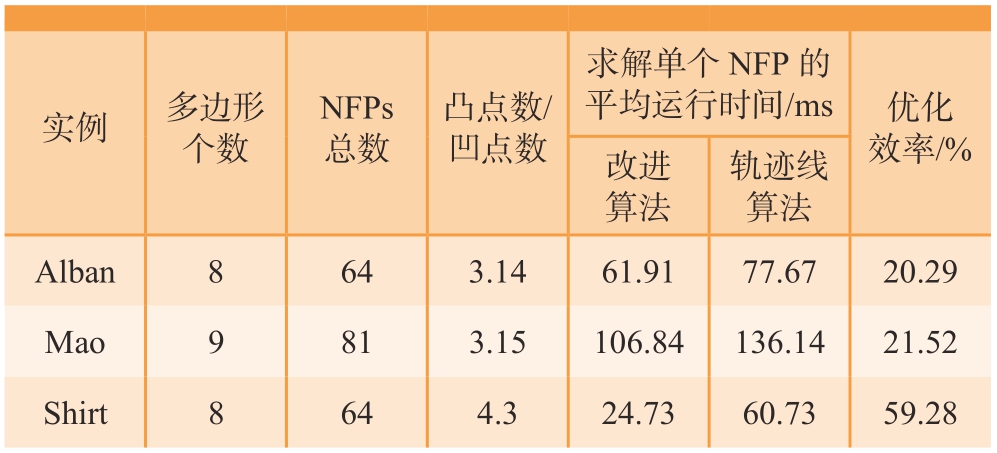
实例多边形个数NFPs总数凸点数/凹点数求解单个NFP的平均运行时间/ms优化效率/%改进算法轨迹线算法Alban8643.1461.9177.6720.29 Mao9813.15106.84136.1421.52 Shirt8644.324.7360.7359.28
由表1可知,本文改进算法略优于轨迹线算法,并且凸点数与凹点数比值越大,优化效果越明显。改进的算法在顶点为凸点的区域有较大简化,通过对顶点凹凸性的分析,再分别利用移动碰撞法和轨迹线算法的优点,有效地减少了算法的时间复杂度。
4 结论
求解临界多边形是各类排样问题中最关键的问题,在分析现有各类算法优缺点的基础上,提出一种基于轨迹线改进的临界多边形生成算法。对算法实现进行了描述,并对改进算法进行了仿真。理论与仿真结果均证明,改进算法可以有效降低算法的时间复杂度,其优化效率与多边形顶点凹凸性密切相关。改进算法将为二维排样中的定位问题提供更有效的技术支撑。
[1] BENNELL J A, OLIVEIRA J F.The geometry of nesting problems: A tutorial[J].European Journal of Operational Research, 2008,184(2): 397–415.
[2] ADAMOWICZ M, ALBANO A.Nesting two-dimensional shapes in rectangular modules[J].Computer-Aided Design, 1976, 8(1):27–33.
[3] AGARWAL P K, FLATO E, HALPERIN D.Polygon decomposition for efficient construction of Minkowski sums[J].Computational Geometry, 2002, 21(1–2): 39–61.
[4] 王静静.不规则件智能排样与数控切割系统的研究与实现[D].武汉: 华中师范大学, 2020.WANG Jingjing.Research and implementation of irregular intelligent layout and CNC cuting system[D].Wuhan: Central China Normal University,2020.
[5] 刘嘉敏, 张胜男, 黄有群.二维不规则形状自动排料算法的研究与实现[J].计算机辅助设计与图形学学报, 2000, 12(7): 488–491.LIU Jiamin, ZHANG Shengnan, HUANG Youqun.Research and implementation of two dimensional irregular auto nesting algorithm[J].Journal of Computer.Aided Design & Computer Graphics, 2000, 12(7):488–491.
[6] 杨卫波, 王万良, 张景玲, 等.基于遗传模拟退火算法的矩形件优化排样[J].计算机工程与应用, 2016, 52(7): 259–263.YANG Weibo, WANG Wanliang, ZHANG Jingling, et al.Packing optimization of rectangles based on improved genetic annealing algorithm[J].Computer Engineering and Applications, 2016, 52(7): 259–263.
[7] 刘胡瑶, 何援军.基于轨迹计算的临界多边形求解算法[J].计算机辅助设计与图形学学报, 2006, 18(8): 1123–1129.LIU Huyao, HE Yuanjun.New algorithm for No fit polygon calculation[J].Journal of Computer-Aided Design & Computer Graphics,2006, 18(8): 1123–1129.
[8] 高荣宇.二维不规则件排样优化系统研究与实现[D].长沙:湖南大学, 2019.GAO Rongyu.Research and implementation of two-dimensional irregular part nesting optimization system[D].Changsha: Hunan University,2019.
[9] GHOSH P K.An algebra of polygons through the notion of negative shapes[J].CVGIP: Image Understanding, 1991, 54(1): 119–144.
[10] 佟德刚.二维不规则形状排料算法研究与实现[D].沈阳:沈阳工业大学, 2005.TONG Degang.Research and implementation of two-dimensional irregular nesting algorithm[D].Shenyang: Shenyang University of Technology, 2005.
[11] BENNELL J A, DOWSLAND K A, DOWSLAND W B.The irregular cutting-stock problem—a new procedure for deriving the no-fit polygon[J].Computers & Operations Research, 2001, 28(3): 271–287.
[12] BURKE E K, HELLIER R S R, KENDALL G, et al.Complete and robust no-fit polygon generation for the irregular stock cutting problem[J].European Journal of Operational Research, 2007, 179(1): 27–49.