铆接由于其工艺过程简便、连接强度可靠、成本低廉等优点在航空工业等领域得到广泛应用[1]。一架普通民用飞机上的铆钉可达到100多万件,波音747客机机身更是有近200多万件铆钉,铆接装配工作量占整机制造工作量的20%以上[2]。普通铆接一般需要从板材两面进行铆接,对于开敞性差的场合不便使用,抽芯铆钉发明后,可以从一侧铆接板材,而无须在另一侧进行任何操作。抽芯铆接具有完成铆接安装简便、省时省力、铆接工具便携、铆接噪音小,产生的夹紧力更加均匀等优点,通常应用在机翼、尾翼前缘蒙皮、进气道蒙皮等处。作为飞机结构件的主要连接方式之一,铆接质量是影响飞机服役安全性、可靠性的重要因素。据统计,机体损伤的故障数量约占飞机全部安全故障总数的12%~ 30%,70%的飞机机体疲劳失效事故起源于结构的连接部位,其中又有80%的疲劳裂纹发生于连接孔处[3–4]。
为了提高连接结构整体力学性能,国内外学者对影响连接结构性能的生产变量、设计参数等进行了广泛研究。Qasim等[5]研究了抽芯铆接孔径、接头厚度、铆钉体长度以及在二次封头中使用垫圈等参数对结构强度结果的影响,发现铆钉长度会影响连接件的承载性能。Ma等[6]研究了工艺参数对铝合金搅拌摩擦盲铆接接头形成及力学性能的影响。Lubas等[7]研究了孔倒角对抽芯铆接连接件的强度影响,对单搭接铆接接头进行了试验分析,由于铆钉内部的应力状态更为复杂 (变形后期的剪切和弯曲结合),接头的破坏力增大。Li等[8]采用试验与数值模拟相结合的方法研究了CFRP/ Al单搭接抽芯铆接中铆孔公差的影响,选择合适的过盈配合率插入抽芯铆钉可以改善铆接接头的性能。黄志超等[9]进行抽芯铆接件的拉伸试验,分析了不同铆钉体长度和板料孔径对接头剪切强度的影响。Papuga等[10]研究了两个公司生产的同种铆钉的双剪静强度及疲劳强度,发现铆钉的力学性能与生产厂商以及毛刺对连接结构的力学性能均有影响。Yang等[11]研究了CFRP连接中铆钉的损伤,并对铆钉钉长进行了参数化研究。Lu等[12]研究了CFRP/Al异质盲铆接在静拉伸与循环载荷下的力学响应,并分析比较了接头的破坏形式、受力响应及力学性能,并通过数值模拟进行了仿真分析。Wang等[13]就铝合金铆接单剪疲劳破坏,基于MATLAB对结构循环相对位移幅值、刚度和耗散能量进行了分析,并进行了有限元仿真模拟。Wang等[14]对CFRP/Al单剪搭接接头通过动态响应的信号处理,研究分析了位移、刚度、耗散等不同破坏行为之间的关系。Mucha等 [15]对铆接接头的承载能力进行了分析。Lee等[16]建立了盲铆钉连接的宏观模型,并分析了板材的抗拉强度和厚度对单位接头强度的影响。
抽芯铆钉铆接最后的工艺过程是芯杆拉断,出于对飞机表面质量的考究,芯杆断面相对钉套头表面凸出量有定量规定标准,但关于芯杆齐平度这一标准对于结构力学性能的影响目前并未明确,且缺乏相关的研究去探究这一标准对结构强度是否存在影响。因此,本文以试验和数值模拟相结合,分别对抽芯铆钉装配合格与不合格试样进行了单钉双剪静强度以及疲劳强度试验,并对结构的静强度进行了有限元仿真,开展芯杆凸出量对于连接件的力学性能的影响研究。
1 抽芯铆钉单钉双剪静强度试验
1.1 抽芯铆钉装配
工艺试验所需的工艺试验件由3块135 mm×36 mm×1.6 mm的2024–T3铝板及一块尺寸为75 mm×36 mm×1.6 mm的2024–T3铝板与Cheery生产的NAS 1396M6–3抽芯铆钉装配而成,在试板上制4.88~4.97 mm的孔,安装抽芯铆钉后的装配示意图如图1所示。完成装配后分别在装配件标记,标记后的装配件如图2所示。
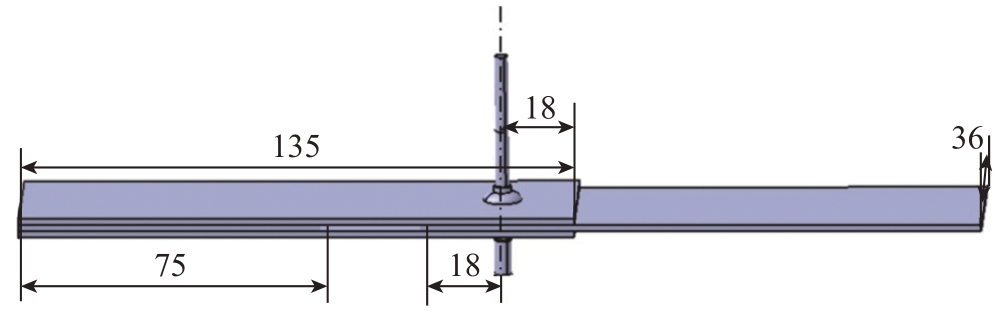
图1 装配件装配示意图(mm)
Fig.1 Assembly diagram of assembly parts (mm)

图2 试验件标记
Fig.2 Mark of test parts
抽芯铆钉安装完成后,采用游标卡尺对抽芯铆钉的芯杆齐平度进行检测。芯杆齐平度为±0.50 mm的试验件符合工程要求,将合格件与不合格件分为两组,测量情况和分组情况见表1,分别进行单钉双剪静强度试验以及疲劳试验。
表1 抽芯铆钉安装记录
Table 1 Installation record of core-pulling rivets
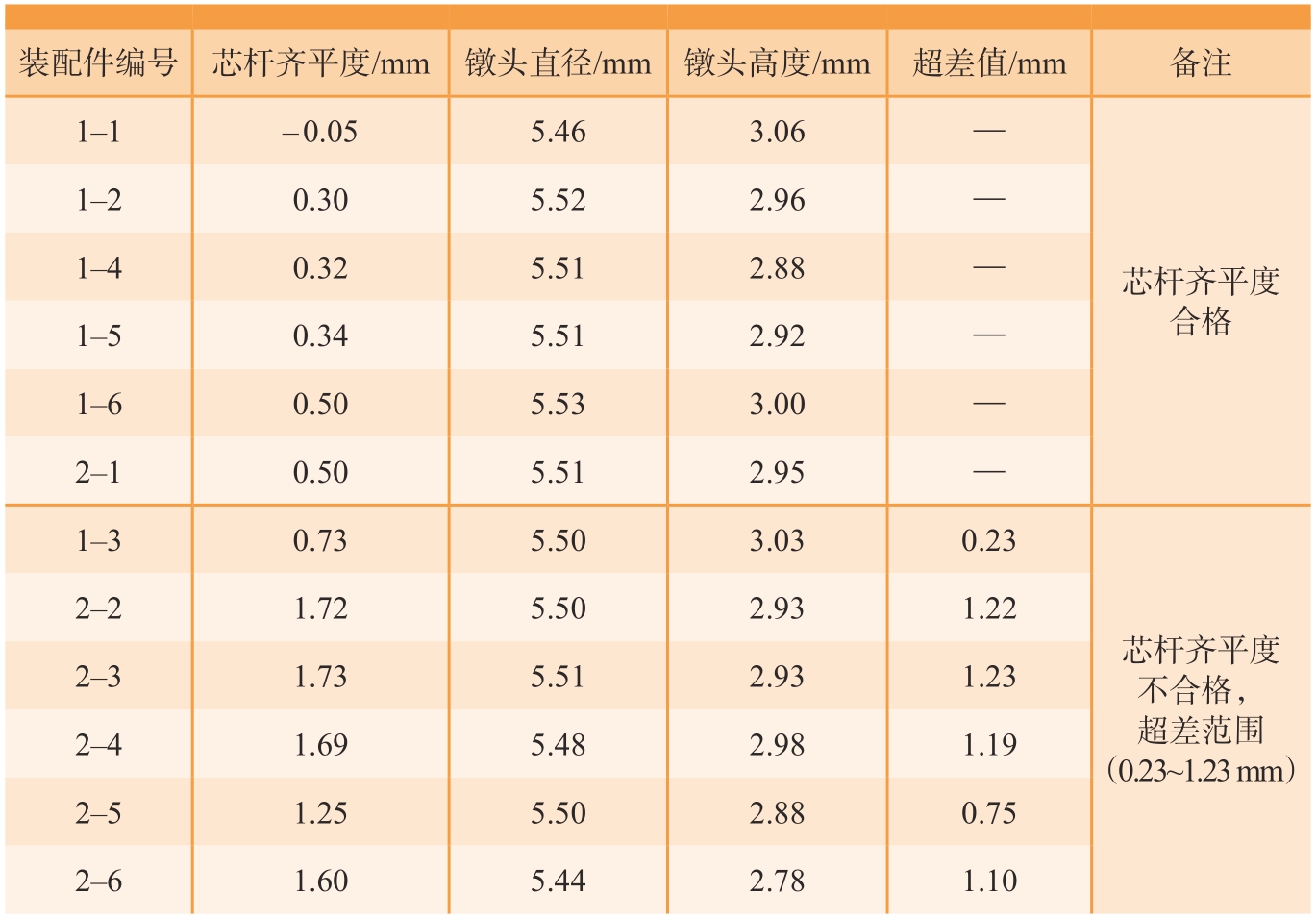
装配件编号芯杆齐平度/mm镦头直径/mm镦头高度/mm超差值/mm备注1–1–0.055.463.06—1–20.305.522.96—1–40.325.512.88—1–50.345.512.92—1–60.505.533.00—2–10.505.512.95—1–30.735.503.030.23芯杆齐平度合格2–21.725.502.931.22 2–31.735.512.931.23 2–41.695.482.981.19 2–51.255.502.880.75 2–61.605.442.781.10芯杆齐平度不合格,超差范围(0.23~1.23 mm)
1.2 试验过程及结果
单钉双剪连接静强度试验采用LD26.305拉力机,试验机外形及试件装夹方式如图3所示。

图3 试验机外形及试件装夹方式
Fig.3 Shape of testing machine and specimen clamping method
试验的基本步骤如下。
(1)装夹试件。先用上夹头夹紧试件上端,上下调节试件位置,将力值清零,然后闭合下夹头将试件固定,完成装夹。为防止试件打滑,夹持长度应控制在夹头总长度的2/3左右。
(2)设置试验参数。设置拉伸速度等试验参数。试验过程中,试验机的下夹头固定,上夹头以2 mm/min的速度向上拉伸试件。
(3)终止试验,记录数据。待试件完全破坏后终止试验,导出力–位移曲线,记录试件的最大静拉伸力作为疲劳载荷选取的参考。每组偏差水平重复3次试验。
单钉双剪连接静强度试验数据记录结果,以及芯杆齐平度合格与超差试样的最大剪切力平均值如表2所示。
表2 单钉双剪连接静强度试验数据记录
Table 2 Records of static strength test of single nail and double shear connection
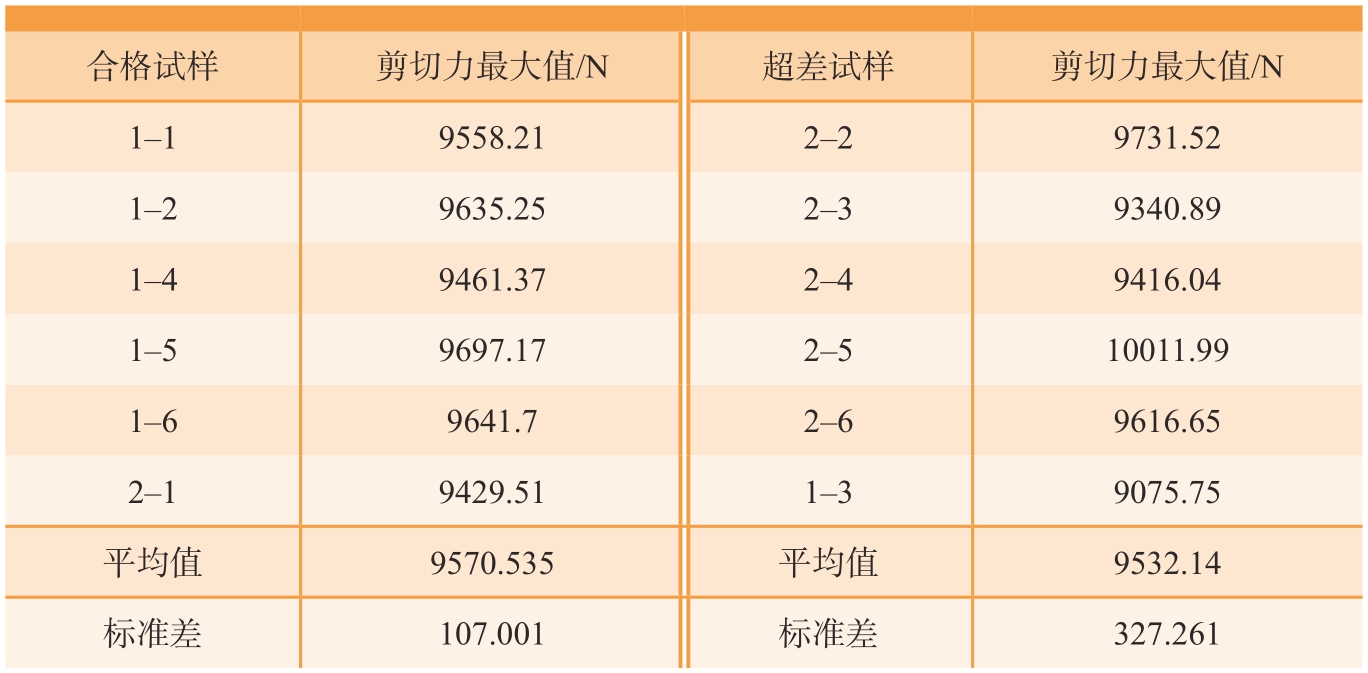
合格试样剪切力最大值/N超差试样剪切力最大值/N 1–19558.212–29731.52 1–29635.252–39340.89 1–49461.372–49416.04 1–59697.172–510011.99 1–69641.72–69616.65 2–19429.511–39075.75平均值9570.535平均值9532.14标准差107.001标准差327.261
图4为试验件发生失效后,试验件各部分的形变情况,发现失效试样钉头墩头以及试板部分均发生了一定的形变,可以认为,双剪试验的结果能够体现出抽芯铆钉的静剪切强度情况。将试验数据整合,力–位移曲线如图5所示。

图4 单钉双剪试验后铆钉及试板变形情况
Fig.4 Deformation of rivet and test plate after single nail and double shear test
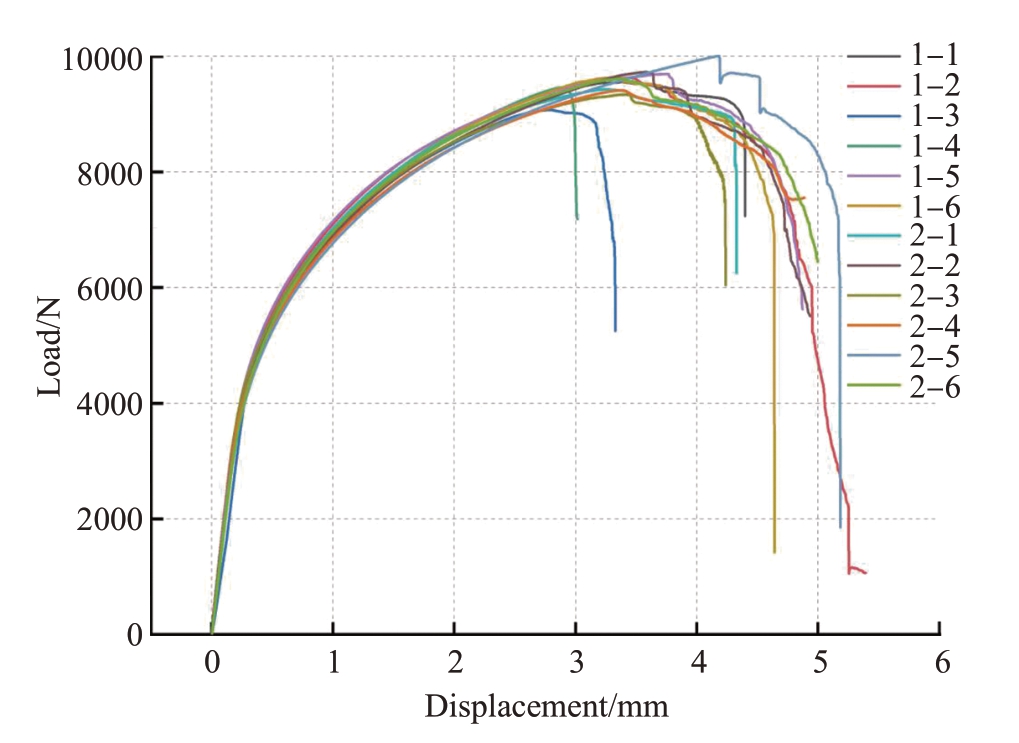
图5 单钉双剪连接静强度试验位移曲线
Fig.5 Displacement curves of static strength test of single nail and double shear connection
通过比较合格组与超差组的剪切力最大值,发现两者单钉双剪静强度差距不大,但两者的标准差存在显著差异。这证明虽然芯杆平齐度合格的结构的单钉双剪强度与芯杆齐平度超差的结构相差无几,但是相对于超差结构而言,合格组的结构静强度相对更为稳定。通过对曲线的分析发现两种情况下的力–位移曲线几乎没有区别,说明总体上芯杆凸出量对结构的双剪性能影响较小。
2 抽芯铆钉疲劳试验
2.1 疲劳试验条件与方案
为了研究芯杆凸出量对抽芯铆接连接件的疲劳性能的影响,对连接件进行疲劳试验。疲劳试验采用中机试验装备股份有限公司生产的SDS0100伺服液压动静疲劳试验机,最大动态试验力为±100 kN,最大静态试验力为±100 kN,示值精度误差不大于±1%,作动器最大振幅±75 mm。
选取合适的疲劳载荷水平开展拉–拉疲劳试验,采用力控模式,正弦波加载,加载频率为10 Hz,应力比为0.1,应力比的定义为
式中,R为应力比;σmin为最小载荷;σmax为最大载荷。
试验控制方式选用荷载控制,选取加载力波形为正弦波,以单钉双剪试验获得的最大载荷的0.6作为疲劳试验最大载荷水平即5753.76 N;载荷比为循环载荷中的最小值与最大值之比,本文试验载荷比采用q=0.1;疲劳试验加载频率一般小于20 Hz,本文采用频率f =10 Hz,试验环境为室温空气。疲劳试验件的铆钉和板材的材料、尺寸与静强度试验保持一致,其芯杆凸出量如表3所示,由于在工程中大部分的不合格试样超差值在0~0.5 mm范围内,故疲劳试验件的超差值定为0~0.5 mm。试验过程中,试验件上夹头固定,下夹头以固定频率做往复运动施加循环载荷,如图6所示。图7为疲劳试验的加载波形。试验初期,力以0.16 kN/s的速度线性增加,直至达到平均载荷,之后开始稳定循环加载。为保证结果可靠性,每组试样重复3次,试验终止条件为试样断裂。
表3 疲劳试验件
Table 3 Fatigue test parts
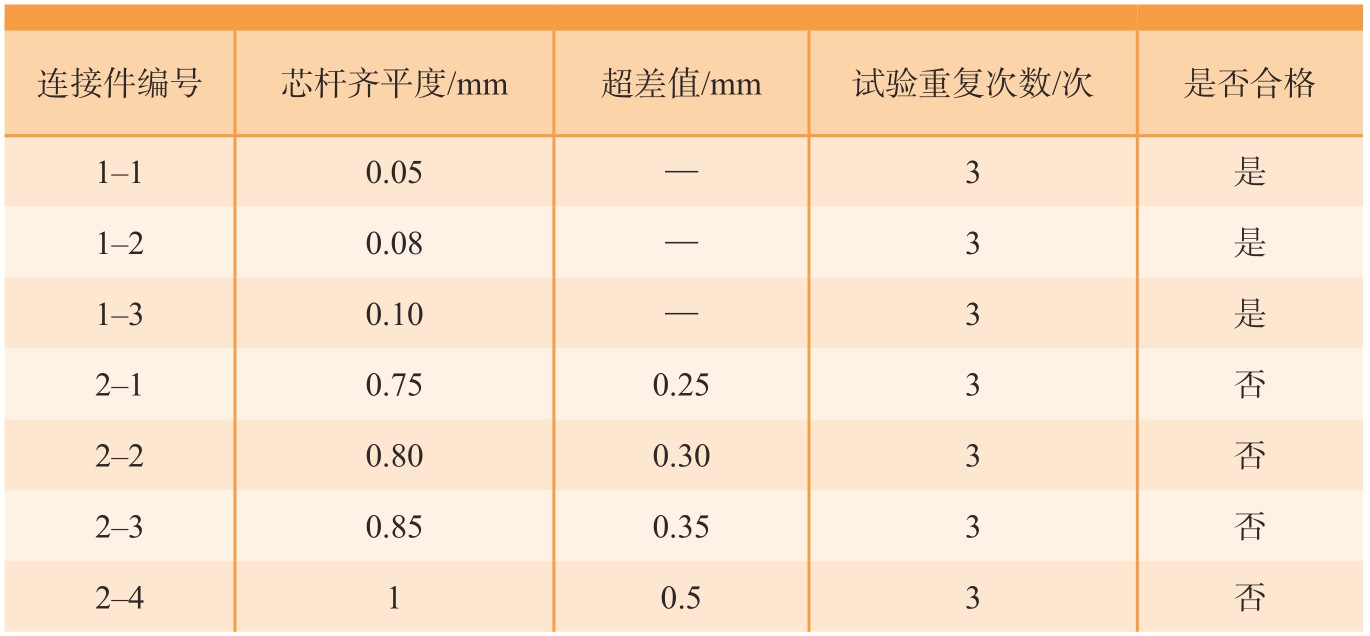
连接件编号芯杆齐平度/mm超差值/mm试验重复次数/次是否合格1–10.05—3是1–20.08—3是1–30.10—3是2–10.750.253否2–20.800.303否2–30.850.353否2–410.53否

图6 疲劳试验
Fig.6 Fatigue test
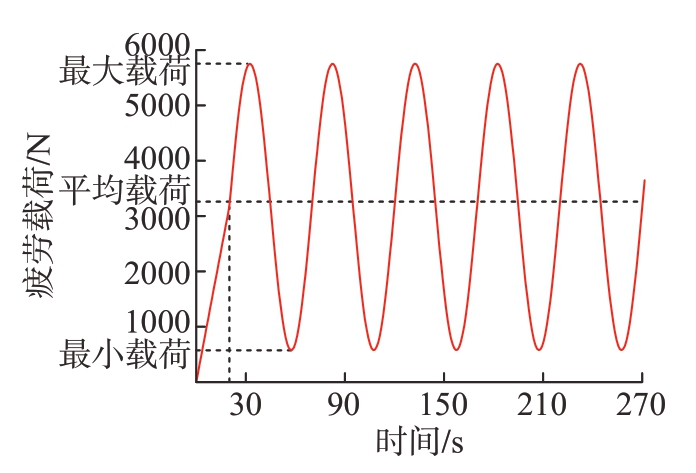
图7 疲劳试验加载波形图
Fig.7 Waveform diagram of fatigue test loading
2.2 疲劳试验结果
试验件在经历若干次循环加载后发生疲劳失效,图8为部分试验件连接结构疲劳试验后失效宏观图。可以看出,芯杆凸出量对连接结构的失效形式没有影响,所有试件破坏形式均为内夹板发生断裂,在层板接触面处可见微动磨损痕迹。

图8 连接结构疲劳失效
Fig.8 Fatigue failure of connected structures
表4为不同芯杆凸出量的抽芯铆接连接件疲劳试验结果,可见除个别数据因偶然因素差别较大,试验重复度良好。其中在试验条件下最大的疲劳循环次数为598169,最小循环次数为110944,取平均值后发现各组的疲劳循环次数在387123~502109浮动,波动幅度在100000次左右。对各组试验结果取标准差,最大的标准差为1–1组的251786.3次,最小值为2–4组的22798.8次。
表4 不同芯杆凸出量试验件疲劳循环次数
Table 4 Number of fatigue cycles of test parts with different core rod protrusion 次
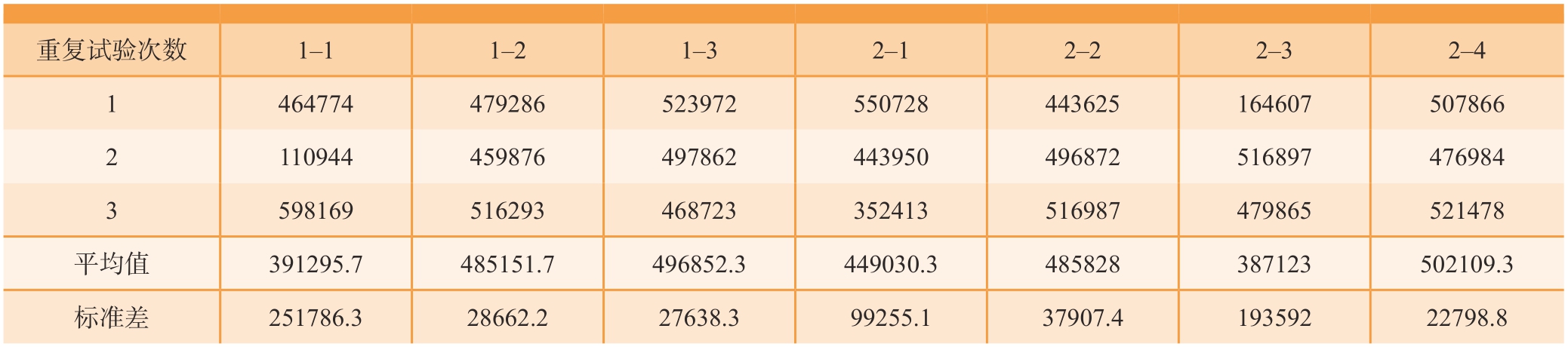
重复试验次数1–11–21–32–12–22–32–4 1 464774479286523972550728443625164607507866 2 110944459876497862443950496872516897476984 3 598169516293468723352413516987479865521478平均值391295.7485151.7496852.3449030.3485828387123502109.3标准差251786.328662.227638.399255.137907.419359222798.8
对比不同芯杆凸出量连接件疲劳寿命可知,在本文设置的疲劳试验条件下,连接件的疲劳寿命基本相近,基本上所有的试验件的疲劳寿命在500000次左右,所研究的凸出量超差没有较大的差距,因此,抽芯铆钉芯杆凸出量超差量在0 ~ 0.5 mm范围内对于连接件的疲劳性能影响不大。同时通过对疲劳试验结果的标准差进行研究发现,两组也没有很大的区别,综上所述,能够发现芯杆齐平度对连接件疲劳性能影响较小。
3 单钉双剪连接静强度仿真分析
3.1 抽芯铆钉模型建立
抽芯铆钉结构通过量取多个抽芯铆钉尺寸,并取均值的方式确定模型的抽芯铆钉尺寸,在CATIA力学建模软件中建模,建立的抽芯铆钉模型如图9所示。为满足两种不同工作状况需求分别设置不同的锁环与芯杆配合深度,以实现抽芯后存在芯杆齐平度超差以及合格两种抽芯结果,代表试验中芯杆齐平度超差与合格两种情况。由于在工程情况下大部分超差结构的超差量在0~0.5 mm,即芯杆凸出量在0.5~1 mm,故确定超差仿真的芯杆齐平度为1 mm。结构安装剖面图如图10所示。

图9 抽芯铆钉模型
Fig.9 Core-pulling rivet model
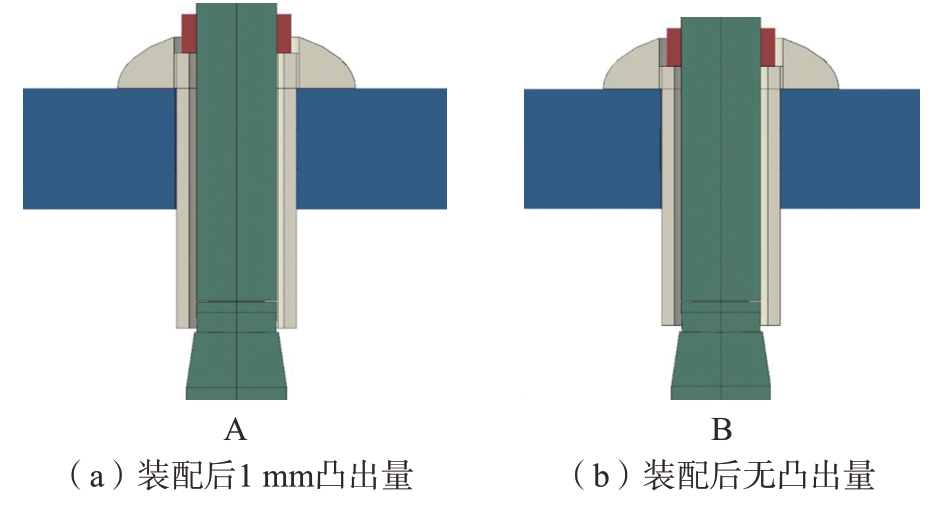
图10 两种锁环尺寸情况下的铆钉安装剖面图
Fig.10 Profile diagram of rivet installation under two lock-ring sizes
将三维模型导入到ABAQUS有限元仿真软件中,按实际工况进行装配,装配模型如图11所示。材料参数及工艺参数参考表5,将铆钉、钉套以及被连接件设置为变形体,锁环设置为刚体,单元类型为C3D8R,计算方法采用缩减积分,设置接触面摩擦系数为0.3。
表5 材料属性
Table 5 Material properties

参数蒙乃尔合金Al2020–T3弹性模量/MPa16900072400密度/(kg/m3)89102780泊松比0.2950.33屈服强度/MPa172345抗拉强度/MPa455—

图11 结构装配示意图
Fig.11 Schematic diagram of structural assembly
3.2 抽芯铆钉装配及双剪仿真
抽铆仿真分析步时长为0.1 s,载荷位移为15 mm,图12为A、B两种状况的安装结果。A状况下,抽芯铆钉完成装配后存在1 mm的凸出量;B状况下抽芯铆钉完成装配后无凸出量,能够满足实际工况要求。
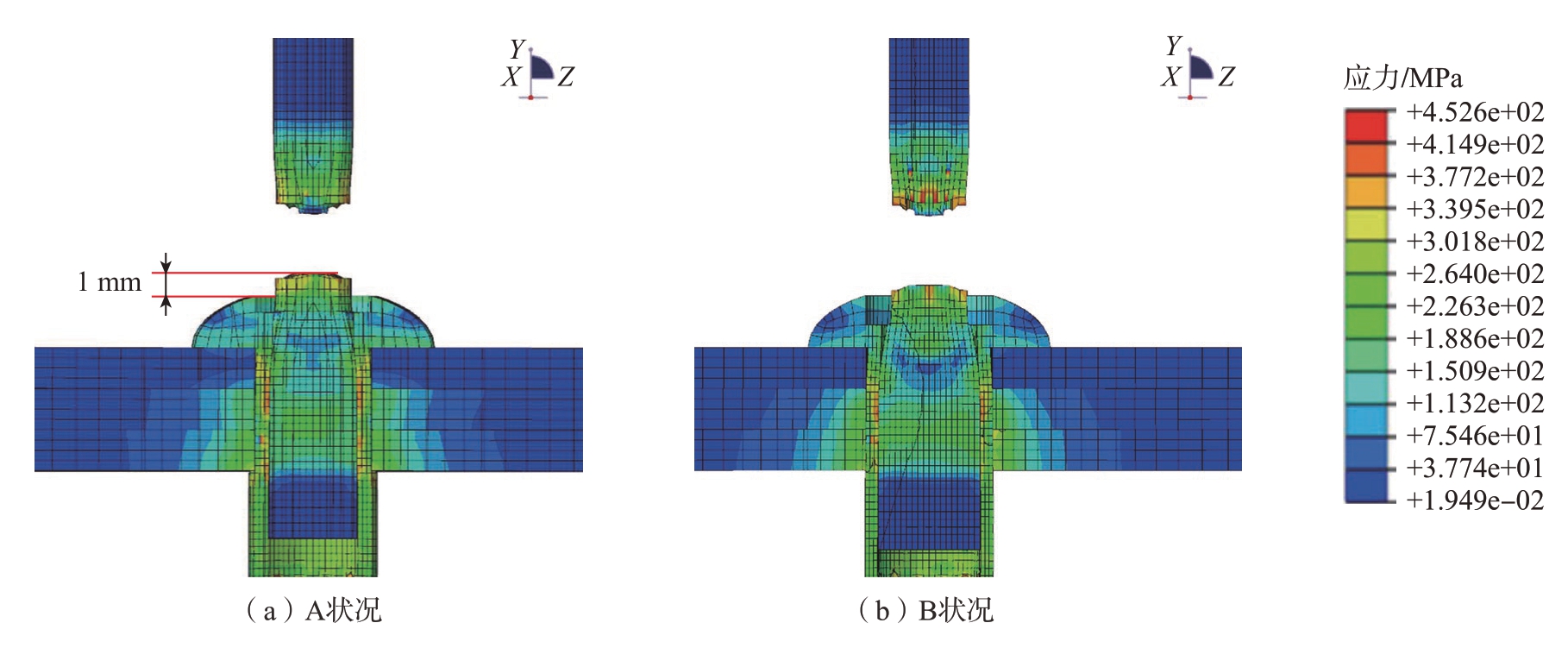
图12 抽芯铆钉安装仿真结果
Fig.12 Simulation results of core-pulling rivet installation
干涉配合铆接的干涉量是铆接后由于铆钉杆镦粗而使铆钉孔胀大的量。绝对干涉量是指铆接前后铝板孔径的差值,用绝对干涉量描述A、B两种状况下铝板孔直径的变化。绝对干涉量的计算公式为
式中,I为绝对干涉量;di为铆接后的铝板孔径;d为铆接前的铝板孔径。
抽铆后A、B两种状况的绝对干涉量与孔深的关系曲线如图13所示,可以看出,A状况下最大绝对干涉量在孔最底端,为0.09254 mm;最小绝对干涉量在孔最上端,为0.05632 mm。B状况下最大绝对干涉量也在孔最底端,为0.09001 mm;最小绝对干涉量也在孔最上端,为0.05737 mm。在孔深2.8~4 mm范围内,A状况下的绝对干涉量略大于B。A、B两种状况下绝对干涉量的趋势一致。
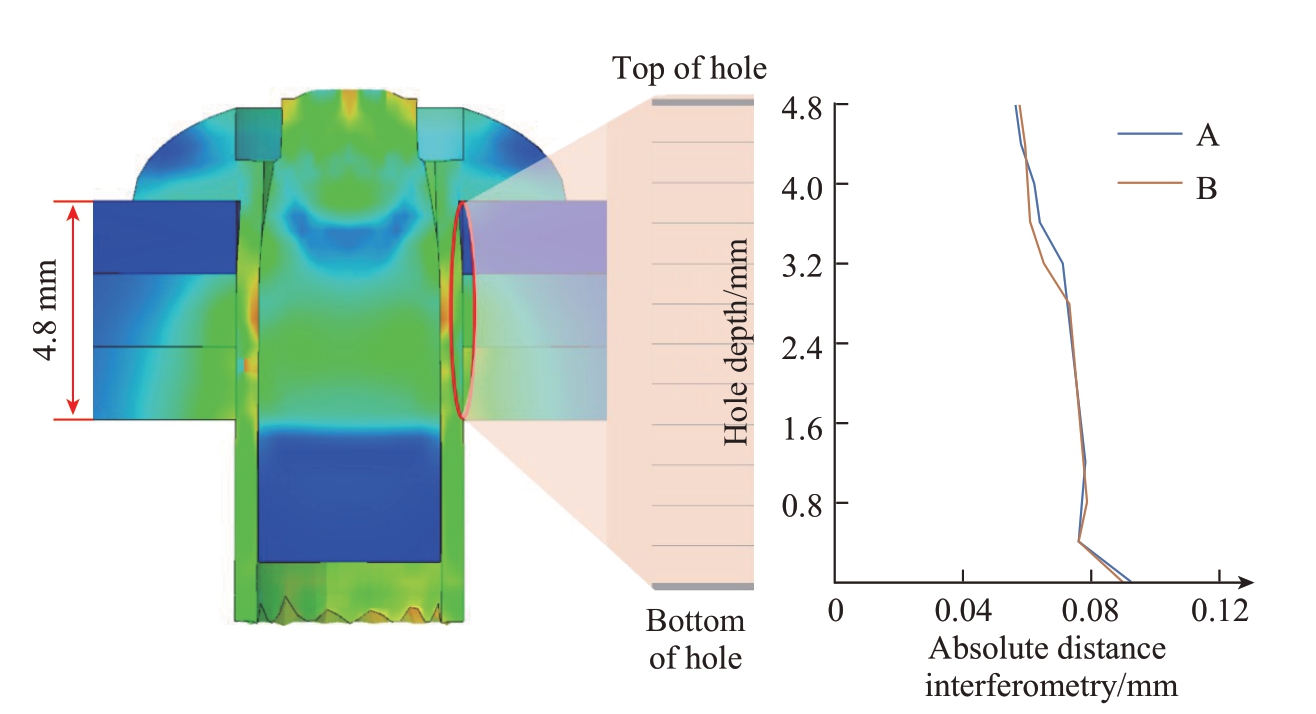
图13 抽铆后绝对干涉量与孔深关系曲线
Fig.13 Relationship curve between absolute interference and hole depth after riveting
图14为A、B两种状况在双剪位移1.25 mm、2.5 mm、3.75 mm、5.0 mm状态下的仿真对比图。通过比较发现在双剪静强度条件下,芯杆凸出量为1 mm时锁环较无凸出量时更容易脱落,故当芯杆凸出量较大时在位移量较大时会发生更为严重的变形。

图14 双剪静强度仿真过程对比
Fig.14 Comparison of the static strength simulation process of double shear
绘制A、B两种状况下的双剪强度仿真剪切力曲线,如图15所示,滤波前两条曲线上下起伏,规律性不明显,因此使用Origin软件对其滤波。滤波后A、B两种状况下的趋势一致,载荷位移在3.75 mm之前,A状况下的剪切力大于B状况;载荷位移在3.75 mm之后,B状况下的剪切力大于A,且载荷位移为5 mm时A、B两种状况下的最大剪切力分别为7884.83 N、7891.3 N。
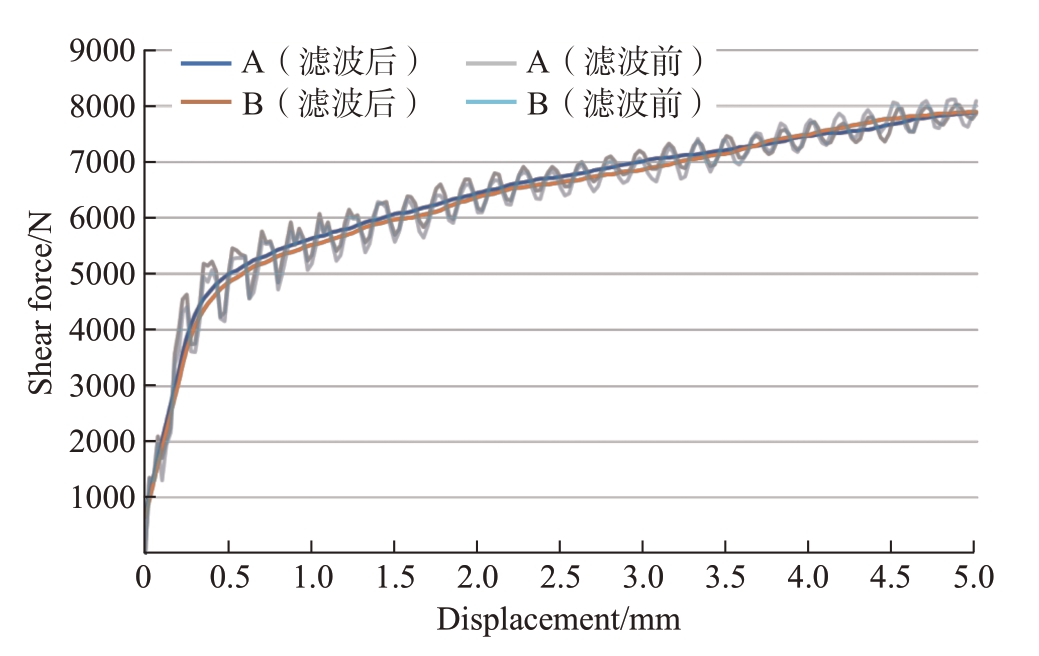
图15 双剪拉伸仿真剪切力曲线
Fig.15 Shear force curves of double shear tensile simulation
通过对抽芯铆钉单钉双剪仿真分析,首先发现两种情况下绝对干涉量区别不大,这是导致芯杆齐平度几乎对结构静强度以及疲劳强度没有影响的主要原因。当位移距离较大时,芯杆齐平度超差的模型锁环部位发生了较大的变形,且通过对滤波后的结构力–位移曲线进行分析,发现芯杆齐平度合格试样与超差试样的力–位移曲线几乎趋于一致,两种状况下的最大剪切力也几乎没有区别,齐平度合格的试样最大剪力稍大于超差试样。
4 结论
本文就抽芯铆钉装配后的芯杆齐平度对装配结构强度的影响分别进行了静拉伸与疲劳试验,并对装配结构就其静拉伸表现进行了仿真分析,通过试验以及仿真分析得到的结论如下。
(1)单钉双剪连接静强度试验中,芯杆齐平度合格样件剪切力破坏强度平均值为9570.535 N,芯杆齐平度不合格样件剪切力破坏强度平均值为9532.14 N。从力学方面分析两种情况下的单钉双剪静强度几乎没有区别,但是通过对试验的数据进行统计分析,相较于芯杆齐平度超差的试样,芯杆齐平度合格试样结构的稳定性更好,更容易控制整体结构的受力分布。
(2)疲劳试验中芯杆齐平度合格样件疲劳循环次数平均值为456770次,芯杆齐平度不合格样件疲劳循环次数平均值为456022.7次。单次疲劳试验循环次数最大值出现在芯杆齐平度合格试样的试验中,为598169次;单次疲劳试验循环次数最小值出现在芯杆齐平度合格试样的试验中,次数为110944。通过试验比较发现,抽芯铆钉芯杆凸出高度差值对结构疲劳强度影响较小。
(3)最后本文通过仿真试验,分别对芯杆凸出量为1 mm与无凸出量的抽芯铆钉进行了抽芯安装以及静拉伸试验仿真。通过对抽芯铆钉安装后铆钉的绝对干涉量的测算发现两种装配情况下绝对干涉量几乎没有区别,这点为芯杆齐平度对整体结构力学性能几乎没有影响的主要原因。仿真试验曲线验证了试验中芯杆齐平度对装配结构的力学性能影响不大这一结论。
[1] 曹增强, 张铭豪, 谭学才, 等.航空复合材料结构铆接技术综述[J].航空制造技术,2023, 66(1/2): 26–37.CAO Zengqiang, ZHANG Minghao,TAN Xuecai, et al.Overview of riveting technology for aviation composite structures[J].Aeronautical Manufacturing Technology, 2023,66(1/2): 26–37.
[2] 薛红前.飞机装配工艺学[M].西安:西北工业大学出版社, 2015.XUE Hongqian.Aircraft assembly technology[M].Xi’an: Northwestern Polytechnical University Press, 2015.
[3] 曹增强.应对我国大飞机研制的装配连接技术[J].航空制造技术, 2009, 52(2):88–91.CAO Zengqiang.Assembly connecting technology for the research of China large aircraft[J].Aeronautical Manufacturing Technology, 2009, 52(2): 88–91.
[4] 韦红余, 陈文亮, 蒋红宇, 等.面向现代飞机装配的长寿命机械连接技术[J].航空制造技术, 2009, 52(17): 34–37.WEI Hongyu, CHEN Wenliang, JIANG Hongyu, et al.Long-life mechanical connecting technology for modern aircaft assembly[J].Aeronautical Manufacturing Technology, 2009,52(17): 34–37.
[5] QASIM B M, KHIDIR T C,INCESU A.Study strength of blind riveted lap joint structure under tensile shear force[J].International Journal of Mechanical Engineering and Robotics Research, 2021, 10(7): 363–367.
[6] MA Y W, LI Y B, CARLSON B E, et al.Effect of process parameters on joint formation and mechanical performance in friction stir blind riveting of aluminum alloys[J].Journal of Manufacturing Science and Engineering, 2018, 140(6): 061007.
[7] LUBAS M, WITEK L.Influence of hole chamfer size on strength of blind riveted joints[J].Advances in Science and Technology Research Journal, 2021, 15(2): 49–56.
[8] LI S P, ZHANG S G, LI H, et al.Numerical and experimental investigation of fitting tolerance effects on bearing strength of CFRP/Al single-lap blind riveted joints[J].Composite Structures, 2022, 281: 115022.
[9] 黄志超, 谢春辉, 吕世亮.拉铆工艺过程数值模拟及实验[J].塑性工程学报, 2014,21(4): 28–32.HUANG Zhichao, XIE Chunhui, LÜ Shiliang.Numerical simulation and experiments on blind riveting process[J].Journal of Plasticity Engineering, 2014, 21(4): 28–32.
[10] PAPUGA J, STEJSKAL J.Reasons for different fatigue lives of riveted double-shear lap joints manufactured by two producers[J].Engineering Failure Analysis, 2023, 150:107308.
[11] YANG Z, JIANG R S, ZUO Y J.Riveting damage behavior and mechanical performance assessments of CFRP/CFRP singlelap gasket-riveted joints[J].Engineering Failure Analysis, 2023, 149: 107253.
[12] LU Y, LIU Q, ZHANG Z B, et al.Experimental and numerical investigation into tensile and cross tensile responses of CFRP/Al blind riveted-bonded hybrid joints[J].Composite Structures, 2023, 318: 117077.
[13] WANG H, LI H C, ZHAO Y, et al.Fatigue behaviour analysis of aluminium alloy riveted single-shear lap joints[J].International Journal of Fatigue, 2023, 172: 107610.
[14] WANG H, LI H C, FAN J F, et al, Numerical analysis of dynamic response:Fatigue behaviour analysis of Al alloy-CFRP riveted single-shear lap joints[J].International Journal of Fatigue, 2023, 170(5): 107515.
[15] MUCHA J, WITKOWSKI W.The structure of the strength of riveted joints determined in the lap joint tensile shear test[J].Acta Mechanica et Automatica, 2015, 9(1):44–49.
[16] LEE B, NAMGUNG H, SON S, et al.Joint strength prediction of multiple blind rivet connections with macroscopic model[J].Journal of Mechanical Science and Technology,2022, 36(2): 817–824.
